bitwise-operations/gray-code

Gray Code

描述

The gray code is a binary numeral system where two successive values differ in only one bit.

Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.

For example, given n = 2, return [0,1,3,2]. Its gray code sequence is:

00 - 0
01 - 1
11 - 3
10 - 2

Note:

• For a given n, a gray code sequence is not uniquely defined.
• For example, [0,2,3,1] is also a valid gray code sequence according to the above definition.
• For now, the judge is able to judge based on one instance of gray code sequence. Sorry about that.

分析

格雷码(Gray Code)的定义请参考 http://en.wikipedia.org/wiki/Gray_code

自然二进制码转换为格雷码：$$g0=b_0, g_i=b_i \oplus b{i-1}$$

保留自然二进制码的最高位作为格雷码的最高位，格雷码次高位为二进制码的高位与次高位异或，其余各位与次高位的求法类似。例如，将自然二进制码 1001，转换为格雷码的过程是：保留最高位；然后将第 1 位的 1 和第 2 位的 0 异或，得到 1，作为格雷码的第 2 位；将第 2 位的 0 和第 3 位的 0 异或，得到 0，作为格雷码的第 3 位；将第 3 位的 0 和第 4 位的 1 异或，得到 1，作为格雷码的第 4 位，最终，格雷码为 1101。

格雷码转换为自然二进制码：$$b0=g_0, b_i=g_i \oplus b{i-1}$$

保留格雷码的最高位作为自然二进制码的最高位，次高位为自然二进制高位与格雷码次高位异或，其余各位与次高位的求法类似。例如，将格雷码 1000 转换为自然二进制码的过程是：保留最高位 1，作为自然二进制码的最高位；然后将自然二进制码的第 1 位 1 和格雷码的第 2 位 0 异或，得到 1，作为自然二进制码的第 2 位；将自然二进制码的第 2 位 1 和格雷码的第 3 位 0 异或，得到 1，作为自然二进制码的第 3 位；将自然二进制码的第 3 位 1 和格雷码的第 4 位 0 异或，得到 1，作为自然二进制码的第 4 位，最终，自然二进制码为 1111。

格雷码有数学公式，整数n的格雷码是$$n \oplus (n/2)$$。

这题要求生成n比特的所有格雷码。

方法 1，最简单的方法，利用数学公式，对从 $$0\sim2^n-1$$的所有整数，转化为格雷码。

方法 2，n比特的格雷码，可以递归地从n-1比特的格雷码生成。如下图所示。

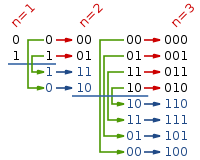
数学公式

// Gray Code
// 数学公式，时间复杂度O(2^n)，空间复杂度O(1)
public class Solution {
    public ArrayList<Integer> grayCode(int n) {
        final int size = 1 << n;  // 2^n
        ArrayList<Integer> result = new ArrayList<>(size);

        for (int i = 0; i < size; ++i)
            result.add(binary_to_gray(i));
        return result;
    }
    private static int binary_to_gray(int n) {
        return n ^ (n >> 1);
    }
}

// Gray Code
// 数学公式，时间复杂度O(2^n)，空间复杂度O(1)
class Solution {
public:
    vector<int> grayCode(int n) {
        const int size = 1 << n;  // 2^n
        vector<int> result;
        result.reserve(size);

        for (int i = 0; i < size; ++i)
            result.push_back(binary_to_gray(i));
        return result;
    }
private:
    static int binary_to_gray(int n) {
        return n ^ (n >> 1);
    }
};

Reflect-and-prefix method

// Gray Code
// reflect-and-prefix method
// 时间复杂度O(2^n)，空间复杂度O(1)
public class Solution {
    public ArrayList<Integer> grayCode(int n) {
        final int size = 1 << n;
        ArrayList<Integer> result = new ArrayList<>(size);

        result.add(0);
        for (int i = 0; i < n; i++) {
            final int highest_bit = 1 << i;
            for (int j = result.size() - 1; j >= 0; j--) // 要反着遍历，才能对称
                result.add(highest_bit | result.get(j));
        }
        return result;
    }
}

// Gray Code
// reflect-and-prefix method
// 时间复杂度O(2^n)，空间复杂度O(1)
class Solution {
public:
    vector<int> grayCode(int n) {
        const int size = 1 << n;
        vector<int> result;
        result.reserve(size);

        result.push_back(0);
        for (int i = 0; i < n; i++) {
            const int highest_bit = 1 << i;
            for (int j = result.size() - 1; j >= 0; j--) // 要反着遍历，才能对称
                result.push_back(highest_bit | result[j]);
        }
        return result;
    }
};