linear-list/array/next-permutation
优质
小牛编辑
139浏览
2023-12-01
Next Permutation
描述
Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).
The replacement must be in-place, do not allocate extra memory.
Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1
分析
算法过程如下图所示(来自http://fisherlei.blogspot.com/2012/12/leetcode-next-permutation.html)。
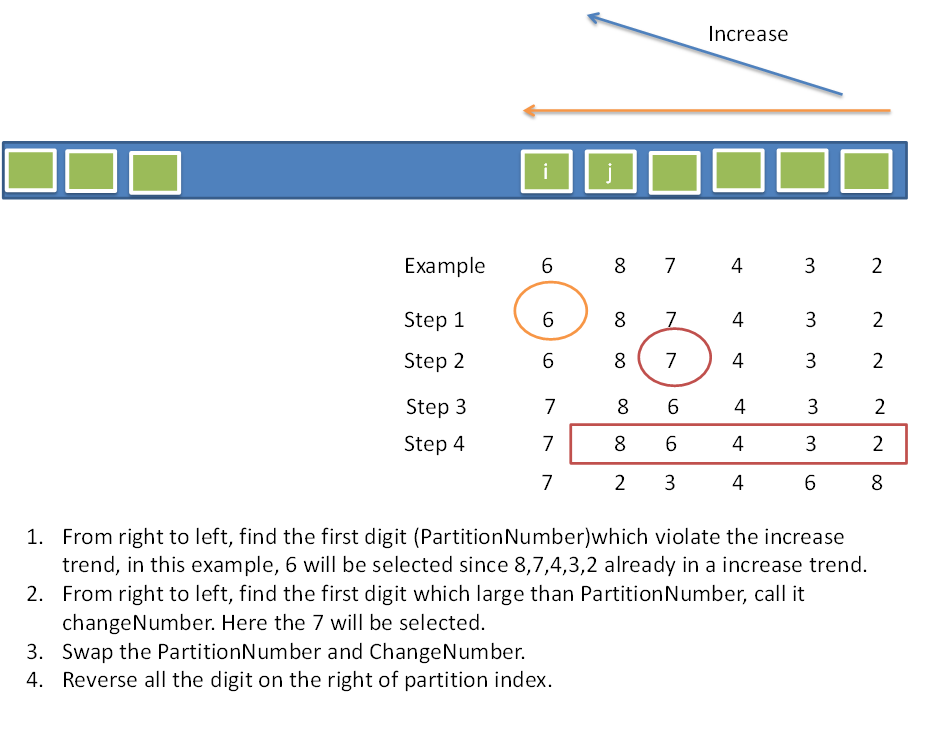
代码
// Next Permutation
// Time Complexity: O(n), Space Complexity: O(1)
public class Solution {
public void nextPermutation(int[] nums) {
nextPermutation(nums, 0, nums.length);
}
private static boolean nextPermutation(int[] nums, int begin, int end) {
// From right to left, find the first digit(partitionNumber)
// which violates the increase trend
int p = end - 2;
while (p > -1 && nums[p] >= nums[p + 1]) --p;
// If not found, which means current sequence is already the largest
// permutation, then rearrange to the first permutation and return false
if(p == -1) {
reverse(nums, begin, end);
return false;
}
// From right to left, find the first digit which is greater
// than the partition number, call it changeNumber
int c = end - 1;
while (c > 0 && nums[c] <= nums[p]) --c;
// Swap the partitionNumber and changeNumber
swap(nums, p, c);
// Reverse all the digits on the right of partitionNumber
reverse(nums, p+1, end);
return true;
}
private static void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
private static void reverse(int[] nums, int begin, int end) {
end--;
while (begin < end) {
swap(nums, begin++, end--);
}
}
};
// Next Permutation
// Time Complexity: O(n), Space Complexity: O(1)
class Solution {
public:
void nextPermutation(vector<int> &nums) {
next_permutation(nums, 0, nums.size());
}
private:
bool next_permutation(vector<int> &nums, int begin, int end) {
// From right to left, find the first digit(partitionNumber)
// which violates the increase trend
int p = end - 2;
while (p > -1 && nums[p] >= nums[p + 1]) --p;
// If not found, which means current sequence is already the largest
// permutation, then rearrange to the first permutation and return false
if(p == -1) {
reverse(&nums[begin], &nums[end]);
return false;
}
// From right to left, find the first digit which is greater
// than the partition number, call it changeNumber
int c = end - 1;
while (c > 0 && nums[c] <= nums[p]) --c;
// Swap the partitionNumber and changeNumber
swap(nums[p], nums[c]);
// Reverse all the digits on the right of partitionNumber
reverse(&nums[p+1], &nums[end]);
return true;
}
};

