graph/network-delay-time

Network Delay Time

描述

There are N network nodes, labelled 1 to N.

Given times, a list of travel times as directed edges times[i] = (u, v, w), where u is the source node, v is the target node, and w is the time it takes for a signal to travel from source to target.

Now, we send a signal from a certain node K. How long will it take for all nodes to receive the signal? If it is impossible, return -1.

Example 1:

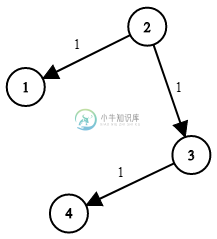
Input: times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
Output: 2

Note:

• N will be in the range [1, 100].
• K will be in the range [1, N].
• The length of times will be in the range [1, 6000].
• All edges times[i] = (u, v, w) will have 1 <= u, v <= N and 0 <= w <= 100.

分析

本题可以抽象为：给定图 G 和源顶点 v，找到从 v 至图中所有顶点的最短路径。这是经典的单源最短路径问题，用 Dijkstra 算法。时间复杂度 $O(E\log V)$，空间复杂度 $O(V+E)$，V 为顶点个数，E 为边条数。

代码

// Network Delay Time
// Dijkstra
// Time Complexity: O(ElogN), Space Complexity: O(N + E)
class Solution {
    public int networkDelayTime(int[][] times, int N, int K) {
        // adjacency list, map<vertex_id, map<vertex_id, weight>>
        Map<Integer, Map<Integer,Integer>> graph = new HashMap<>();
        for(int[] time : times){
            graph.putIfAbsent(time[0], new HashMap<>());
            graph.get(time[0]).put(time[1], time[2]);
        }

        Map<Integer, Integer> dist = dijkstra(graph, K);

        return dist.size() == N ? Collections.max(dist.values()) : -1;
    }

    /** Standard Dijkstra algorithm.
     *
     @param graph Adjacency list, map<vertex_id, map<vertex_id, weight>>.
     @param start The starting vertex ID.
     @return dist, map<vertex_id, distance>.
     */
    private static Map<Integer, Integer> dijkstra(Map<Integer, Map<Integer,Integer>> graph, int start) {
        // map<vertex_id, distance>
        Map<Integer, Integer> dist = new HashMap<>();
        // vertex_id -> father_vertex_id
        Map<Integer, Integer> father = new HashMap<>();

        // pair<distance, vertex_id>, min heap, sorted by distance from start to vertex_id
        Queue<Pair<Integer, Integer>> pq = new PriorityQueue<>((a, b) -> a.getKey() - b.getKey());

        // from start to start itself
        pq.offer(new Pair(0, start));
        dist.put(start, 0);

        while(!pq.isEmpty()){
            final int u = pq.poll().getValue();
            if (!graph.containsKey(u)) continue; // leaf node

            for(int v : graph.get(u).keySet()){
                final int w = graph.get(u).get(v);
                if (!dist.containsKey(v) || dist.get(u)+ w < dist.get(v)) {
                    final int shorter = dist.get(u)+ w;
                    dist.put(v, shorter);
                    father.put(v, u);
                    pq.offer(new Pair(shorter, v));
                }
            }
        }

        return dist;
    }
}

// TODO

相关题目

• Path with Maximum Probability