虽然这一形状的名字叫立方体（CubeGeometry），但它其实是长方体，也就是长宽高可以设置为不同的值。其构造函数是：

THREE.CubeGeometry(width, height, depth, widthSegments, heightSegments, depthSegments)

这里，width是x方向上的长度；height是y方向上的长度；depth是z方向上的长度；后三个参数分别是在三个方向上的分段数，如widthSegments为3的话，代表x方向上水平分为三份。一般情况下不需要分段的话，可以不设置后三个参数，后三个参数的缺省值为1。其他几何形状中的分段也是类似的，下面不做说明。

长宽高

创建立方体直观简单，如：new THREE.CubeGeometry(1, 2, 3);可以创建一个x方向长度为1，y方向长度为2，z方向长度为3的立方体。

为了更好地表现参数效果，我们在场景中用长度为1的红、绿、蓝线段分别表示x、y、z三个轴。在设置材质，并添加到场景之后（具体方法参见第4章及第5章）的效果是：

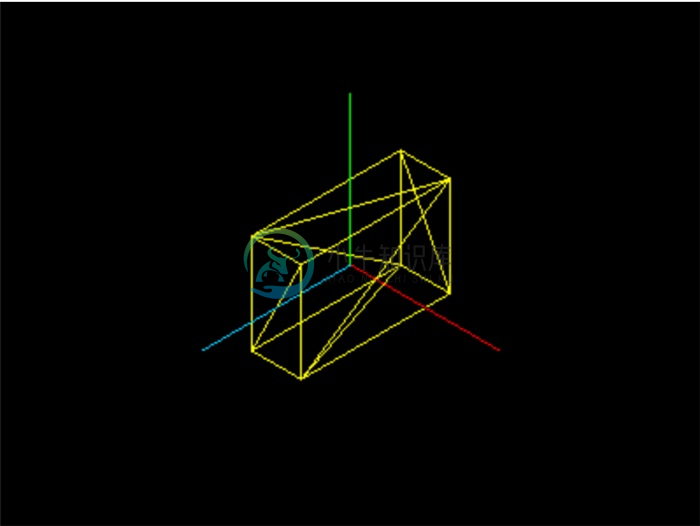
物体的默认位置是原点，对于立方体而言，是其几何中心在原点的位置。

分段

而在设置了分段new THREE.CubeGeometry(1, 2, 3, 2, 2, 3)后，效果如下：

注意这个分段是对六个面进行分段，而不是对立方体的体素分段，因此在立方体的中间是不分段的，只有六个侧面被分段。

平面

这里的平面（PlaneGeometry）其实是一个长方形，而不是数学意义上无限大小的平面。其构造函数为：

THREE.PlaneGeometry(width, height, widthSegments, heightSegments)

其中，width是x方向上的长度；height是y方向上的长度；后两个参数同样表示分段。

new THREE.PlaneGeometry(2, 4);创建的平面在x轴和y轴所在平面内，效果如下：

如果需要创建的平面在x轴和z轴所在的平面内，可以通过物体的旋转来实现，具体的做法将在5.2节作介绍。

球体

球体（SphereGeometry）的构造函数是：

THREE.SphereGeometry(radius, segmentsWidth, segmentsHeight, phiStart, phiLength, thetaStart, thetaLength)

其中，radius是半径；segmentsWidth表示经度上的切片数；segmentsHeight表示纬度上的切片数；phiStart表示经度开始的弧度；phiLength表示经度跨过的弧度；thetaStart表示纬度开始的弧度；thetaLength表示纬度跨过的弧度。

分段

首先，我们来理解下segmentsWidth和segmentsHeight。使用var sphere = new THREE.SphereGeometry(3, 8, 6)可以创建一个半径为3，经度划分成8份，纬度划分成6份的球体，如下图所示。

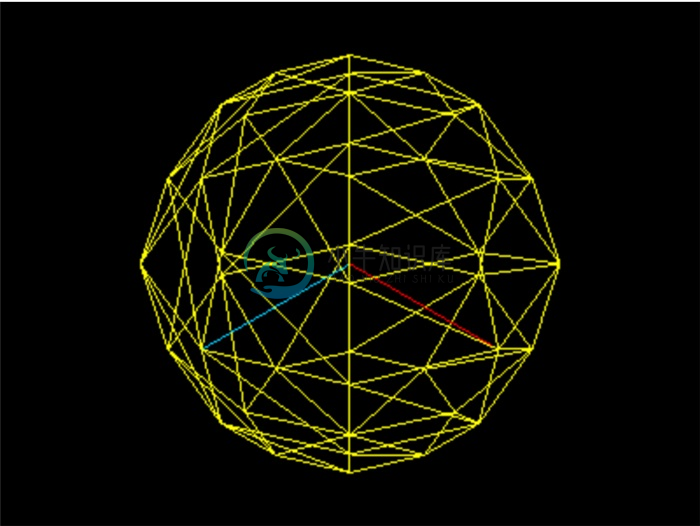
segmentsWidth相当于经度被切成了几瓣，而segmentsHeight相当于纬度被切成了几层。因为在图形底层的实现中，并没有曲线的概念，曲线都是由多个折线近似构成的。对于球体而言，当这两个值较大的时候，形成的多面体就可以近似看做是球体了。

new THREE.SphereGeometry(3, 8, 6)的效果：

new THREE.SphereGeometry(3, 18, 12)的效果：

经度弧度

new THREE.SphereGeometry(3, 8, 6, Math.PI / 6, Math.PI / 3)表示起始经度为Math.PI / 6，经度跨度为Math.PI / 3。效果如下：

需要注意的是，这里segmentsWidth为8意味着对于经度从Math.PI / 6跨过Math.PI / 3的区域内划分为8块，而不是整个球体的经度划分成8块后再判断在此经度范围内的部分。

纬度弧度

理解了经度之后，纬度可以同理理解。new THREE.SphereGeometry(3, 8, 6, 0, Math.PI * 2, Math.PI / 6, Math.PI / 3)意味着纬度从Math.PI / 6跨过Math.PI / 3。效果如下：

我们再来看一个经度纬度都改变了起始位置和跨度的例子：new THREE.SphereGeometry(3, 8, 6, Math.PI / 2, Math.PI, Math.PI / 6, Math.PI / 2)的效果为：

圆形

圆形（CircleGeometry）可以创建圆形或者扇形，其构造函数是：

THREE.CircleGeometry(radius, segments, thetaStart, thetaLength)

这四个参数都是球体中介绍过的，这里不再赘述，直接来看个例子。new THREE.CircleGeometry(3, 18, Math.PI / 3, Math.PI / 3 * 4)可以创建一个在x轴和y轴所在平面的三分之二圆的扇形：

圆柱体

圆柱体（CylinderGeometry）的构造函数是：

THREE.CylinderGeometry(radiusTop, radiusBottom, height, radiusSegments, heightSegments, openEnded)

其中，radiusTop与radiusBottom分别是顶面和底面的半径，由此可知，当这两个参数设置为不同的值时，实际上创建的是一个圆台；height是圆柱体的高度；radiusSegments与heightSegments可类比球体中的分段；openEnded是一个布尔值，表示是否没有顶面和底面，缺省值为false，表示有顶面和底面。

标准圆柱体

new THREE.CylinderGeometry(2, 2, 4, 18, 3)创建一个顶面与底面半径都为2，高度为4的圆柱体，效果如下：

圆台

将底面半径设为3创建一个圆台：new THREE.CylinderGeometry(2, 3, 4, 18, 3)，效果如下：

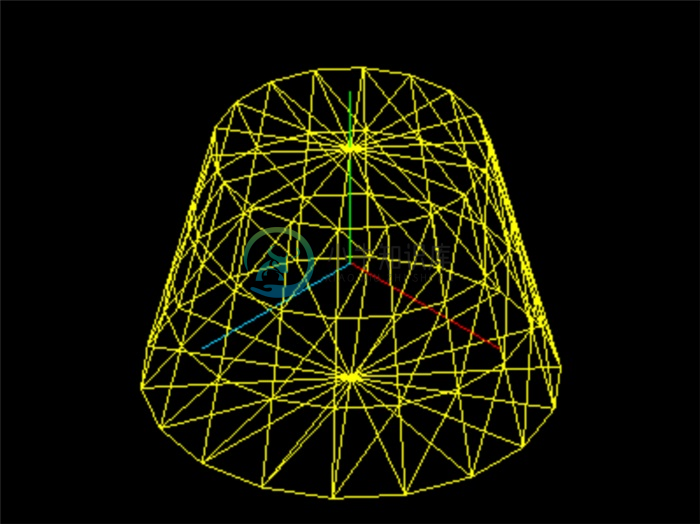
无顶面底面

new THREE.CylinderGeometry(2, 3, 4, 18, 3, true)将创建一个没有顶面与底面的圆台，效果如下：

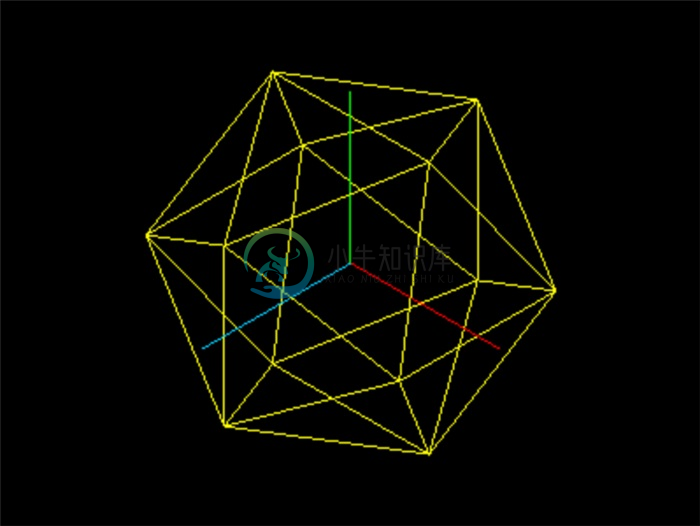
正四面体、正八面体、正二十面体

正四面体（TetrahedronGeometry）、正八面体（OctahedronGeometry）、正二十面体（IcosahedronGeometry）的构造函数较为类似，分别为：

THREE.TetrahedronGeometry(radius, detail)
THREE.OctahedronGeometry(radius, detail)
THREE.IcosahedronGeometry(radius, detail)

其中，radius是半径；detail是细节层次（Level of Detail）的层数，对于大面片数模型，可以控制在视角靠近物体时，显示面片数多的精细模型，而在离物体较远时，显示面片数较少的粗略模型。这里我们不对detail多作展开，一般可以对这个值缺省。

new THREE.TetrahedronGeometry(3)创建一个半径为3的正四面体：

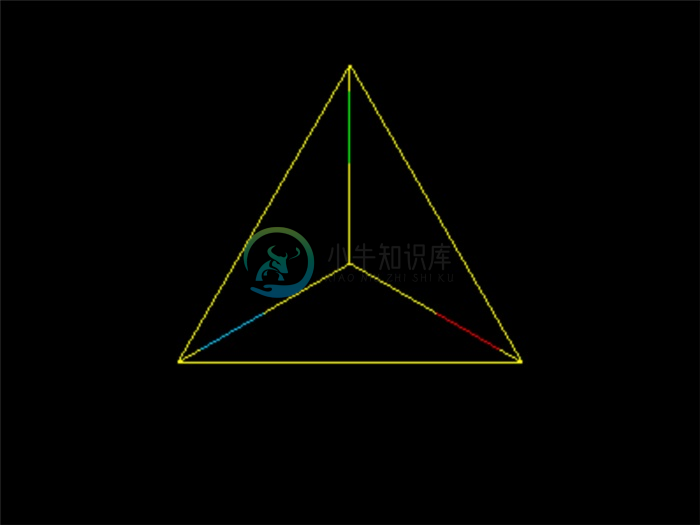
new THREE.OctahedronGeometry(3)创建一个半径为3的正八面体：

new THREE.IcosahedronGeometry(3)创建一个半径为3的正二十面体：

圆环面

圆环面（TorusGeometry）就是甜甜圈的形状，其构造函数是：

THREE.TorusGeometry(radius, tube, radialSegments, tubularSegments, arc)

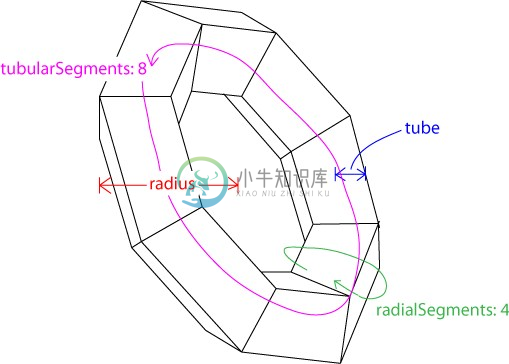
其中，radius是圆环半径；tube是管道半径；radialSegments与tubularSegments分别是两个分段数，详见上图；arc是圆环面的弧度，缺省值为Math.PI * 2。

new THREE.TorusGeometry(3, 1, 4, 8)创建一个粗糙的圆环面：

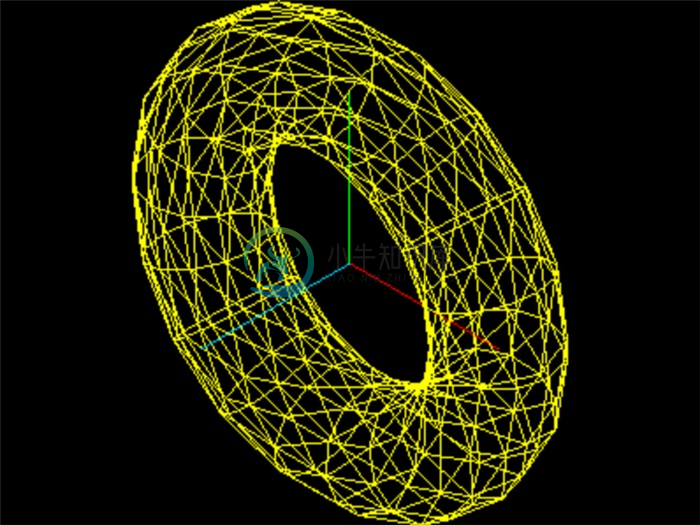
new THREE.TorusGeometry(3, 1, 12, 18)创建一个较为精细的圆环面：

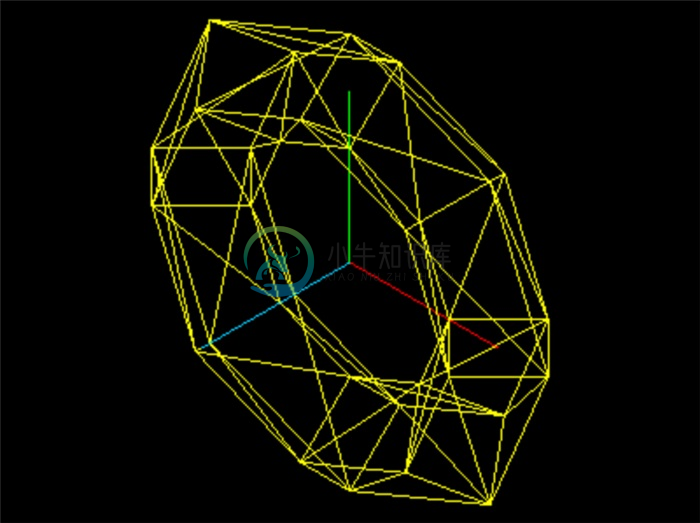
new THREE.TorusGeometry(3, 1, 4, 8, Math.PI / 3 * 2)创建部分圆环面：

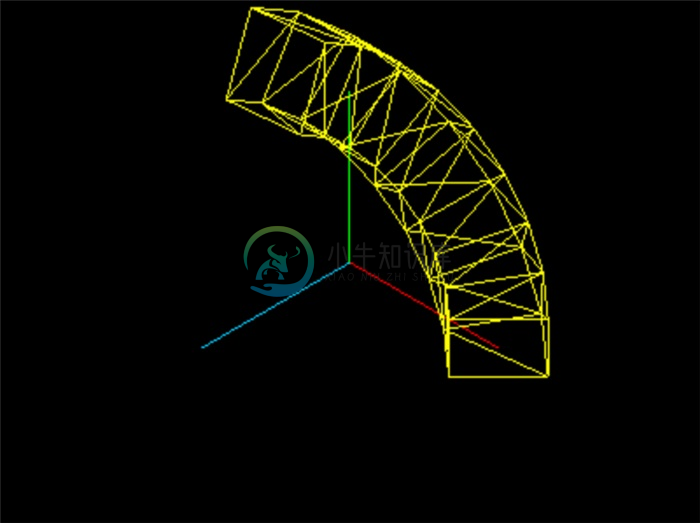
圆环结

如果说圆环面是甜甜圈，那么圆环结（TorusKnotGeometry）就是打了结的甜甜圈，其构造参数为：

THREE.TorusKnotGeometry(radius, tube, radialSegments, tubularSegments, p, q, heightScale)

前四个参数在圆环面中已经有所介绍，p和q是控制其样式的参数，一般可以缺省，如果需要详细了解，请学习圆环结的相关知识；heightScale是在z轴方向上的缩放。

new THREE.TorusKnotGeometry(2, 0.5, 32, 8)的效果：

本小节完整代码请参见例3.1.1