类神经网路 Neural_Networks - Ex 3: Compare Stochastic learning strategies for MLPClassifier

优质

小牛编辑

136浏览

2023-12-01

http://scikit-learn.org/stable/auto_examples/neural_networks/plot_mlp_training_curves.html

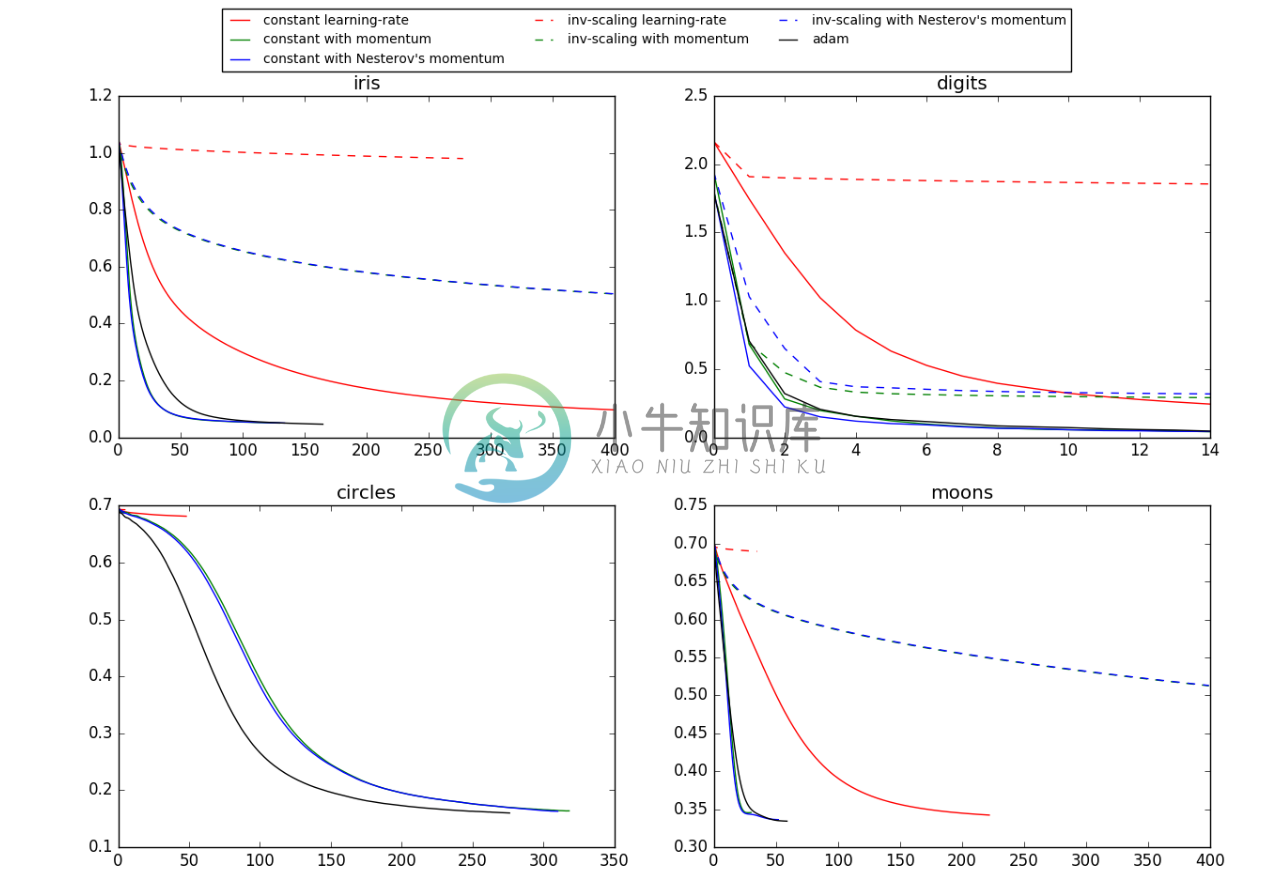
此范例将画出图表，展现不同的训练策略(optimizer)下loss curves的变化，训练策略包括SGD与Adam。

1.Stochastic Gradient Descent(SGD):

.Stochastic Gradient Descent(SGD)为Gradient Descent(GD)的改良，在GD里是输入全部的training dataset，根据累积的loss才更新一次权重，因此收歛速度很慢，SGD随机抽一笔 training sample，依照其 loss 更新权重。

2.Momentum:

Momentum是为了以防GD类的方法陷入局部最小值而衍生的方法，可以利用momentum降低陷入local minimum的机率，此方法是参考物理学动量的观念。

看图1蓝色点的位置，当GD类的方法陷入局部最小值时，因为gd=0将会使电脑认为此处为最小值，于是为了减少此现象，每次更新时会将上次更新权重的一部分拿来加入此次更新。如红色箭头所示，将有机会翻过local minimum。

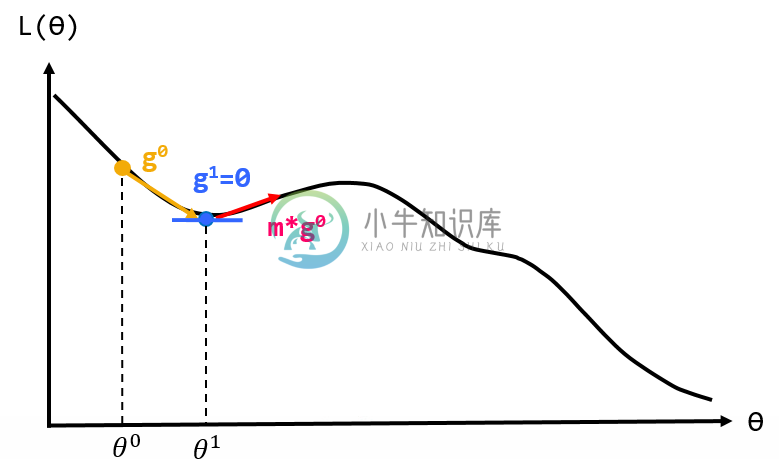
Ex 3: Compare Stochastic learning strategies for MLPClassifier - 图1

图1:momentum观念示意图

3.Nesterov Momentum:

Nesterov Momentum为另外一种Momentum的变形体，目的也是降低陷入local minimum机率的方法，而两种方法的差异在于下图:

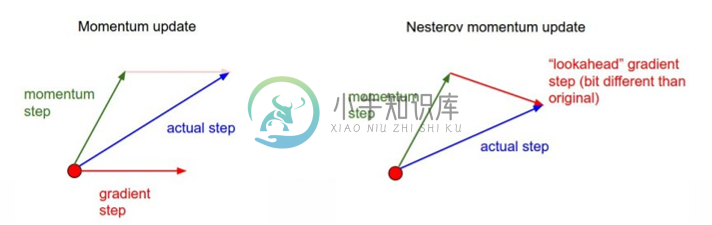
Ex 3: Compare Stochastic learning strategies for MLPClassifier - 图2

图2:左图为momentum，1.先计算 gradient、2.加上 momentum、3.更新权重

右图为Nesterov Momentum，1.先加上momentum、2.计算gradient、3.更新权重。

图2图片来源:http://cs231n.github.io/neural-networks-3/

4.Adaptive Moment Estimation (Adam):

Adam为一种自己更新学习速率的方法，会根据GD计算出来的值调整每个参数的学习率(因材施教)。

以上所有的最佳化方法都将需要设定learning_rate_init值，此范例结果将呈现四种不同资料的比较:iris资料集、digits资料集、与使用sklearn.datasets产生资料集circles、 moon。

(一)引入函式库

print(__doc__)
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import MinMaxScaler
from sklearn import datasets

(二)设定模型参数

# different learning rate schedules and momentum parameters
params = [{'solver': 'sgd', 'learning_rate': 'constant', 'momentum': 0,
           'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'constant', 'momentum': .9,
           'nesterovs_momentum': False, 'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'constant', 'momentum': .9,
           'nesterovs_momentum': True, 'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': 0,
           'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': .9,
           'nesterovs_momentum': True, 'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': .9,
           'nesterovs_momentum': False, 'learning_rate_init': 0.2},
          {'solver': 'adam', 'learning_rate_init': 0.01}]
labels = ["constant learning-rate", "constant with momentum",
          "constant with Nesterov's momentum",
          "inv-scaling learning-rate", "inv-scaling with momentum",
          "inv-scaling with Nesterov's momentum", "adam"]
plot_args = [{'c': 'red', 'linestyle': '-'},
             {'c': 'green', 'linestyle': '-'},
             {'c': 'blue', 'linestyle': '-'},
             {'c': 'red', 'linestyle': '--'},
             {'c': 'green', 'linestyle': '--'},
             {'c': 'blue', 'linestyle': '--'},
             {'c': 'black', 'linestyle': '-'}]

(三)画出loss curves

def plot_on_dataset(X, y, ax, name):
    # for each dataset, plot learning for each learning strategy
    print("\nlearning on dataset %s" % name)
    ax.set_title(name)
    X = MinMaxScaler().fit_transform(X)
    mlps = []
    if name == "digits":
        # digits is larger but converges fairly quickly
        max_iter = 15
    else:
        max_iter = 400
    for label, param in zip(labels, params):
        print("training: %s" % label)
        mlp = MLPClassifier(verbose=0, random_state=0,
                            max_iter=max_iter, **param)
        mlp.fit(X, y)
        mlps.append(mlp)
        print("Training set score: %f" % mlp.score(X, y))
        print("Training set loss: %f" % mlp.loss_)
    for mlp, label, args in zip(mlps, labels, plot_args):
            ax.plot(mlp.loss_curve_, label=label, **args)
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# load / generate some toy datasets
iris = datasets.load_iris()
digits = datasets.load_digits()
data_sets = [(iris.data, iris.target),
             (digits.data, digits.target),
             datasets.make_circles(noise=0.2, factor=0.5, random_state=1),
             datasets.make_moons(noise=0.3, random_state=0)]
for ax, data, name in zip(axes.ravel(), data_sets, ['iris', 'digits',
                                                    'circles', 'moons']):
    plot_on_dataset(*data, ax=ax, name=name)
fig.legend(ax.get_lines(), labels=labels, ncol=3, loc="upper center")
plt.show()

Ex 3: Compare Stochastic learning strategies for MLPClassifier - 图3

图3:四种资料对于不同学习方法的loss curves下降比较图

(四)完整程式码

print(__doc__)
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import MinMaxScaler
from sklearn import datasets
# different learning rate schedules and momentum parameters
params = [{'solver': 'sgd', 'learning_rate': 'constant', 'momentum': 0,
           'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'constant', 'momentum': .9,
           'nesterovs_momentum': False, 'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'constant', 'momentum': .9,
           'nesterovs_momentum': True, 'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': 0,
           'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': .9,
           'nesterovs_momentum': True, 'learning_rate_init': 0.2},
          {'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': .9,
           'nesterovs_momentum': False, 'learning_rate_init': 0.2},
          {'solver': 'adam', 'learning_rate_init': 0.01}]
labels = ["constant learning-rate", "constant with momentum",
          "constant with Nesterov's momentum",
          "inv-scaling learning-rate", "inv-scaling with momentum",
          "inv-scaling with Nesterov's momentum", "adam"]
plot_args = [{'c': 'red', 'linestyle': '-'},
             {'c': 'green', 'linestyle': '-'},
             {'c': 'blue', 'linestyle': '-'},
             {'c': 'red', 'linestyle': '--'},
             {'c': 'green', 'linestyle': '--'},
             {'c': 'blue', 'linestyle': '--'},
             {'c': 'black', 'linestyle': '-'}]
def plot_on_dataset(X, y, ax, name):
    # for each dataset, plot learning for each learning strategy
    print("\nlearning on dataset %s" % name)
    ax.set_title(name)
    X = MinMaxScaler().fit_transform(X)
    mlps = []
    if name == "digits":
        # digits is larger but converges fairly quickly
        max_iter = 15
    else:
        max_iter = 400
    for label, param in zip(labels, params):
        print("training: %s" % label)
        mlp = MLPClassifier(verbose=0, random_state=0,
                            max_iter=max_iter, **param)
        mlp.fit(X, y)
        mlps.append(mlp)
        print("Training set score: %f" % mlp.score(X, y))
        print("Training set loss: %f" % mlp.loss_)
    for mlp, label, args in zip(mlps, labels, plot_args):
            ax.plot(mlp.loss_curve_, label=label, **args)
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# load / generate some toy datasets
iris = datasets.load_iris()
digits = datasets.load_digits()
data_sets = [(iris.data, iris.target),
             (digits.data, digits.target),
             datasets.make_circles(noise=0.2, factor=0.5, random_state=1),
             datasets.make_moons(noise=0.3, random_state=0)]
for ax, data, name in zip(axes.ravel(), data_sets, ['iris', 'digits',
                                                    'circles', 'moons']):
    plot_on_dataset(*data, ax=ax, name=name)
fig.legend(ax.get_lines(), labels=labels, ncol=3, loc="upper center")
plt.show()