分类法 Classification - EX 3: Plot classification probability
优质
小牛编辑
140浏览
2023-12-01
分类法/范例三: Plot classification probability
这个范例的主要目的
- 使用iris 鸢尾花资料集
- 测试不同分类器对于涵盖特定范围之资料集,分类为那一种鸢尾花的机率
- 例如:sepal length 为 4cm 而 sepal width 为 3cm时被分类为 versicolor的机率
(一)资料汇入及描述
- 首先先汇入iris 鸢尾花资料集,使用
iris = datasets.load_iris()将资料存入 - 准备X (特征资料) 以及 y (目标资料),仅使用两个特征方便视觉呈现
import matplotlib.pyplot as pltimport numpy as npfrom sklearn.linear_model import LogisticRegressionfrom sklearn.svm import SVCfrom sklearn import datasetsiris = datasets.load_iris()X = iris.data[:, 0:2] # 仅使用前两个特征,方便视觉化呈现y = iris.targetn_features = X.shape[1]
iris为一个dict型别资料,我们可以用以下指令来看一下资料的内容。
for key,value in iris.items() :try:print (key,value.shape)except:print (key)
| 显示 | 说明 |
|---|---|
| (‘target_names’, (3L,)) | 共有三种鸢尾花 setosa, versicolor, virginica |
| (‘data’, (150L, 4L)) | 有150笔资料,共四种特征 |
| (‘target’, (150L,)) | 这150笔资料各是那一种鸢尾花 |
| DESCR | 资料之描述 |
| feature_names | 四个特征代表的意义 |
(二) 分类器的选择
这个范例选择了四种分类器,存入一个dict资料中,分别为:
- L1 logistic
- L2 logistic (OvR)
- Linear SVC
- L2 logistic (Multinomial)
其中LogisticRegression 并不适合拿来做多目标的分类器,我们可以用结果图的分类机率来观察。
C = 1.0# Create different classifiers. The logistic regression cannot do# multiclass out of the box.classifiers = {'L1 logistic': LogisticRegression(C=C, penalty='l1'),'L2 logistic (OvR)': LogisticRegression(C=C, penalty='l2'),'Linear SVC': SVC(kernel='linear', C=C, probability=True,random_state=0),'L2 logistic (Multinomial)': LogisticRegression(C=C, solver='lbfgs', multi_class='multinomial')}n_classifiers = len(classifiers)
而接下来为了产生一个包含绝大部份可能的测试矩阵,我们会用到以下指令。
np.linspace(起始, 终止, 数量)目的为产生等间隔之数据,例如print(np.linspace(1,3,3))的结果为[ 1. 2. 3.],而print(np.linspace(1,3,5))的结果为[ 1. 1.5 2. 2.5 3. ]np.meshgrid(xx,yy)则用来产生网格状座标。numpy.c_为numpy特殊物件,能协助将numpy 阵列连接起来,将程式简化后,我们用以下范例展示相关函式用法。
xx, yy = np.meshgrid(np.linspace(1,3,3), np.linspace(4,6,3).T)Xfull = np.c_[xx.ravel(), yy.ravel()]print('xx= \n%s\n' % xx)print('yy= \n%s\n' % yy)print('xx.ravel()= %s\n' % xx.ravel())print('Xfull= \n%s' % Xfull)
结果显示如下,我们可以看出Xfull模拟出了一个类似特征矩阵X, 具备有9笔资料,这九笔资料重现了xx (3种数值变化)及yy(3种数值变化)的所有排列组合。
xx=[[ 1. 2. 3.][ 1. 2. 3.][ 1. 2. 3.]]yy=[[ 4. 4. 4.][ 5. 5. 5.][ 6. 6. 6.]]xx.ravel()= [ 1. 2. 3. 1. 2. 3. 1. 2. 3.]Xfull=[[ 1. 4.][ 2. 4.][ 3. 4.][ 1. 5.][ 2. 5.][ 3. 5.][ 1. 6.][ 2. 6.][ 3. 6.]]
而下面这段程式码的主要用意,在产生一个网格矩阵,其中xx,yy分别代表着iris资料集的第一及第二个特征。xx 是3~9之间的100个连续数字,而yy是1~5之间的100个连续数字。用np.meshgrid(xx,yy)及np.c_产生出Xfull特征矩阵,10,000笔资料包含了两个特征的所有排列组合。
plt.figure(figsize=(3 * 2, n_classifiers * 2))plt.subplots_adjust(bottom=.2, top=.95)xx = np.linspace(3, 9, 100)yy = np.linspace(1, 5, 100).Txx, yy = np.meshgrid(xx, yy)Xfull = np.c_[xx.ravel(), yy.ravel()]
(三) 测试分类器以及画出机率分布图的选择
接下来的动作
- 用迴圈轮过所有的分类器,并计算显示分类成功率
- 将
Xfull(10000x2矩阵)传入classifier.predict_proba()得到probas(10000x3矩阵)。这裏的probas矩阵是10000种不同的特征排列组合所形成的数据,被分类到三种iris 鸢尾花的可能性。 - 利用
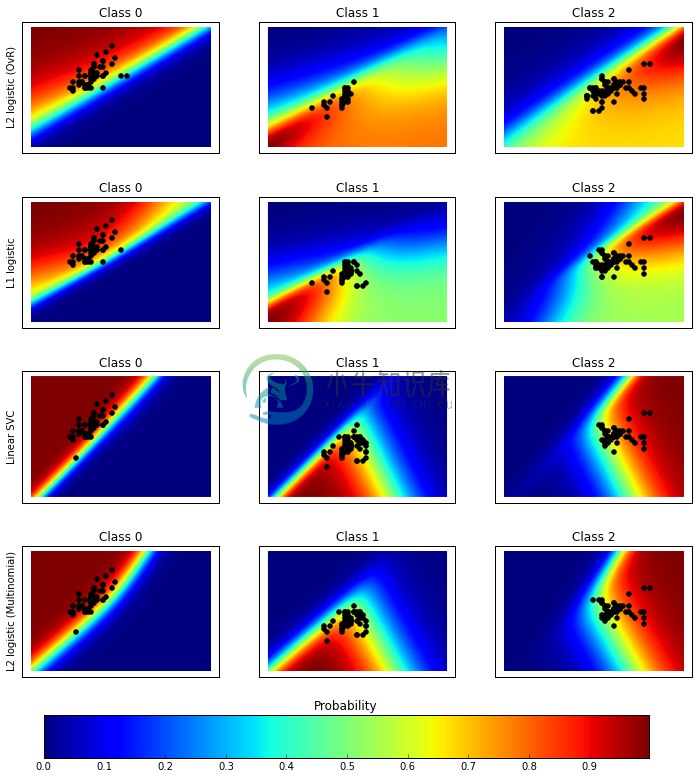
reshape((100,100))将10000笔资料排列成二维矩阵,并将机率用影像的方式呈现出来
#若在ipython notebook (Jupyter) 裏执行,则可以将下列这行的井号移除%matplotlib inline#原范例没有下列这行,这是为了让图形显示更漂亮而新增的fig = plt.figure(figsize=(12,12), dpi=300)for index, (name, classifier) in enumerate(classifiers.items()):#训练并计算分类成功率#然而此范例训练跟测试用相同资料集,并不符合实际状况。#建议採用cross_validation的方式才能较正确评估classifier.fit(X, y)y_pred = classifier.predict(X)classif_rate = np.mean(y_pred.ravel() == y.ravel()) * 100print("classif_rate for %s : %f " % (name, classif_rate))# View probabilities=probas = classifier.predict_proba(Xfull)n_classes = np.unique(y_pred).sizefor k in range(n_classes):plt.subplot(n_classifiers, n_classes, index * n_classes + k + 1)plt.title("Class %d" % k)if k == 0:plt.ylabel(name)imshow_handle = plt.imshow(probas[:, k].reshape((100, 100)),extent=(3, 9, 1, 5), origin='lower')plt.xticks(())plt.yticks(())idx = (y_pred == k)if idx.any():plt.scatter(X[idx, 0], X[idx, 1], marker='o', c='k')ax = plt.axes([0.15, 0.04, 0.7, 0.05])plt.title("Probability")plt.colorbar(imshow_handle, cax=ax, orientation='horizontal')plt.show()
classif_rate for L2 logistic (OvR) : 76.666667classif_rate for L1 logistic : 79.333333classif_rate for Linear SVC : 82.000000classif_rate for L2 logistic (Multinomial) : 82.000000
(四)完整程式码
Python source code: plot_classification_probability.py
http://scikit-learn.org/stable/_downloads/plot_classification_probability.py
print(__doc__)# Author: Alexandre Gramfort <alexandre.gramfort@inria.fr># License: BSD 3 clauseimport matplotlib.pyplot as pltimport numpy as npfrom sklearn.linear_model import LogisticRegressionfrom sklearn.svm import SVCfrom sklearn import datasetsiris = datasets.load_iris()X = iris.data[:, 0:2] # we only take the first two features for visualizationy = iris.targetn_features = X.shape[1]C = 1.0# Create different classifiers. The logistic regression cannot do# multiclass out of the box.classifiers = {'L1 logistic': LogisticRegression(C=C, penalty='l1'),'L2 logistic (OvR)': LogisticRegression(C=C, penalty='l2'),'Linear SVC': SVC(kernel='linear', C=C, probability=True,random_state=0),'L2 logistic (Multinomial)': LogisticRegression(C=C, solver='lbfgs', multi_class='multinomial')}n_classifiers = len(classifiers)plt.figure(figsize=(3 * 2, n_classifiers * 2))plt.subplots_adjust(bottom=.2, top=.95)xx = np.linspace(3, 9, 100)yy = np.linspace(1, 5, 100).Txx, yy = np.meshgrid(xx, yy)Xfull = np.c_[xx.ravel(), yy.ravel()]for index, (name, classifier) in enumerate(classifiers.items()):classifier.fit(X, y)y_pred = classifier.predict(X)classif_rate = np.mean(y_pred.ravel() == y.ravel()) * 100print("classif_rate for %s : %f " % (name, classif_rate))# View probabilities=probas = classifier.predict_proba(Xfull)n_classes = np.unique(y_pred).sizefor k in range(n_classes):plt.subplot(n_classifiers, n_classes, index * n_classes + k + 1)plt.title("Class %d" % k)if k == 0:plt.ylabel(name)imshow_handle = plt.imshow(probas[:, k].reshape((100, 100)),extent=(3, 9, 1, 5), origin='lower')plt.xticks(())plt.yticks(())idx = (y_pred == k)if idx.any():plt.scatter(X[idx, 0], X[idx, 1], marker='o', c='k')ax = plt.axes([0.15, 0.04, 0.7, 0.05])plt.title("Probability")plt.colorbar(imshow_handle, cax=ax, orientation='horizontal')plt.show()

