登录
目录
当前位置： 首页 > 文档资料 > 机器学习：使用 Python >

分类法 Classification - EX 5: Linear and Quadratic Discriminant Analysis with confidence ellipsoid

优质
小牛编辑
129浏览
2023-12-01

分类法/范例五：Linear and Quadratic Discriminant Analysis with confidence ellipsoid

线性判别以及二次判别的比较

http://scikit-learn.org/stable/auto_examples/classification/plot_lda_qda.html

(一)资料产生function

这个范例引入的套件，主要特点在：

  1. scipy.linalg:线性代数相关函式，这裏主要使用到linalg.eigh 特征值相关问题
  2. matplotlib.colors: 用来处理绘图时的色彩分布
  3. LinearDiscriminantAnalysis:线性判别演算法
  4. QuadraticDiscriminantAnalysis:二次判别演算法
  1. %matplotlib inline
  2. from scipy import linalg
  3. import numpy as np
  4. import matplotlib.pyplot as plt
  5. import matplotlib as mpl
  6. from matplotlib import colors
  7. from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
  8. from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis

接下来是设定一个线性变化的colormap，LinearSegmentedColormap(name, segmentdata) 预设会传回一个256个值的数值颜色对应关係。用一个具备有三个项目的dict变数segmentdata来设定。以'red': [(0, 1, 1), (1, 0.7, 0.7)]来解释，就是我们希望数值由0到1的过程，红色通道将由1线性变化至0.7。

  1. cmap = colors.LinearSegmentedColormap(
  2.     'red_blue_classes',
  3.     {'red': [(0, 1, 1), (1, 0.7, 0.7)],
  4.      'green': [(0, 0.7, 0.7), (1, 0.7, 0.7)],
  5.      'blue': [(0, 0.7, 0.7), (1, 1, 1)]})
  6. plt.cm.register_cmap(cmap=cmap)

我们可以用以下程式码来观察。当输入数值为np.arange(0,1.1,0.1)也就是0,0.1…,1.0 时RGB数值的变化情形。

  1. values = np.arange(0,1.1,0.1)
  2. cmap_values = mpl.cm.get_cmap('red_blue_classes')(values)
  3. import pandas as pd
  4. pd.set_option('precision',2)
  5. df=pd.DataFrame(np.hstack((values.reshape(11,1),cmap_values)))
  6. df.columns = ['Value', 'R', 'G', 'B', 'Alpha']
  7. print(df)
  1.     Value    R    G    B  Alpha
  2. 0     0.0  1.0  0.7  0.7      1
  3. 1     0.1  1.0  0.7  0.7      1
  4. 2     0.2  0.9  0.7  0.8      1
  5. 3     0.3  0.9  0.7  0.8      1
  6. 4     0.4  0.9  0.7  0.8      1
  7. 5     0.5  0.8  0.7  0.9      1
  8. 6     0.6  0.8  0.7  0.9      1
  9. 7     0.7  0.8  0.7  0.9      1
  10. 8     0.8  0.8  0.7  0.9      1
  11. 9     0.9  0.7  0.7  1.0      1
  12. 10    1.0  0.7  0.7  1.0      1

接着我们产生两组资料, 每组资料有 600笔资料，2个特征 X: 600x2以及2个类别 y:600 (前300个元素为0，余下为1)：

  1. dataset_fixed_cov():2个类别的特征具备有相同共变数(covariance)
  2. dataset_fixed_cov():2个类别的特征具备有不同之共变数
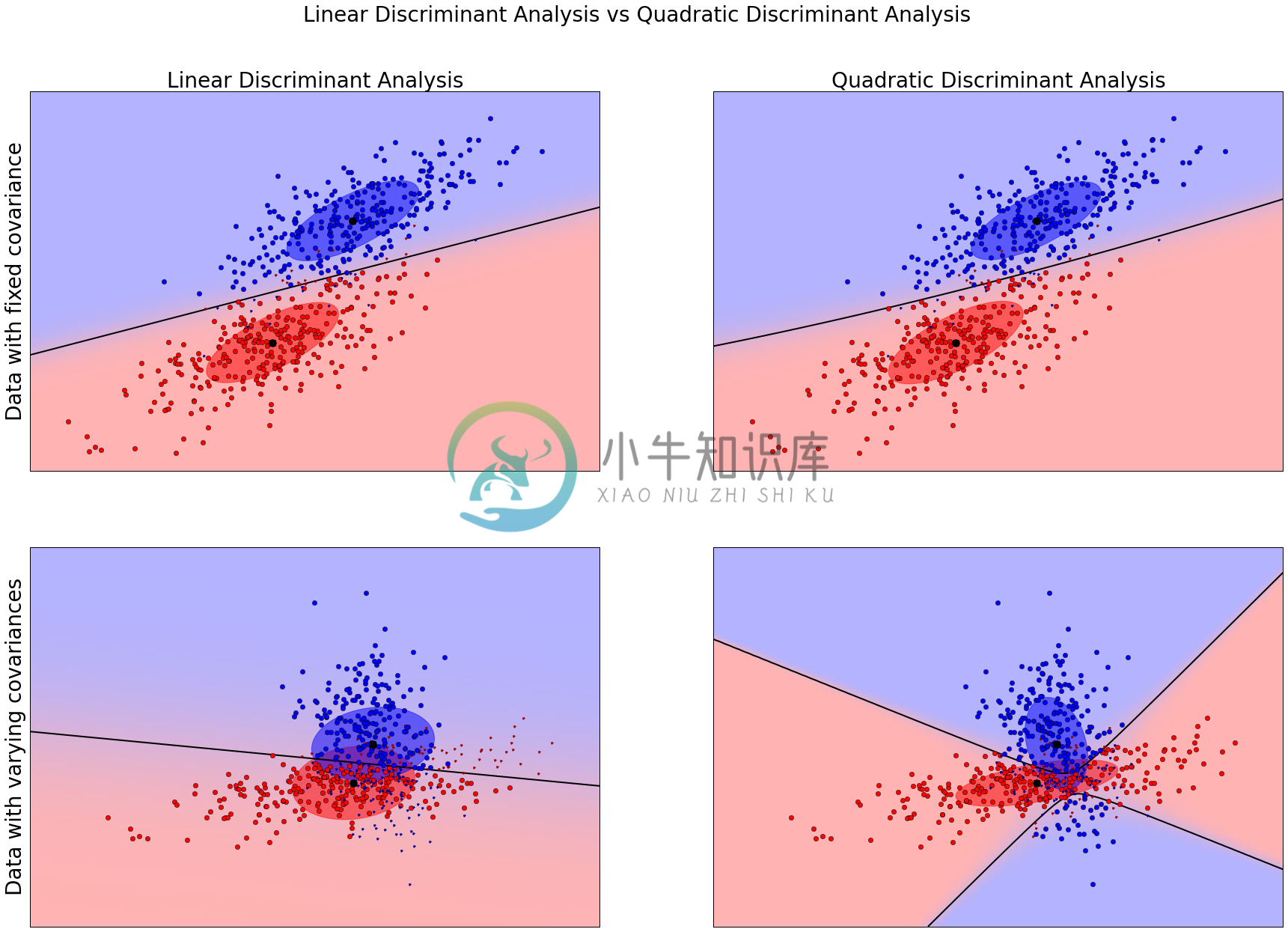
    差异落在X资料的产生np.dot(np.random.randn(n, dim), C) 与 np.dot(np.random.randn(n, dim), C.T)的不同。np.dot(np.random.randn(n, dim), C)会产生300x2之矩阵，其乱数产生的范围可交由C矩阵来控制。在dataset_fixed_cov()中，前后300笔资料产生之范围皆由C来调控。我们可以在最下方的结果图示看到上排影像(相同共变数)的资料分布无论是红色(代表类别1)以及蓝色(代表类别2)其分布形状相似。而下排影像(不同共变数)，分布形状则不同。图示中，横轴及纵轴分别表示第一及第二个特征，读者可以试着将 0.83这个数字减少或是将C.T改成C，看看最后结果图形有了什幺改变？
  1. def dataset_fixed_cov():
  2.     '''Generate 2 Gaussians samples with the same covariance matrix'''
  3.     n, dim = 300, 2
  4.     np.random.seed(0)
  5.     C = np.array([[0., -0.23], [0.83, .23]])
  6.     X = np.r_[np.dot(np.random.randn(n, dim), C),
  7.               np.dot(np.random.randn(n, dim), C) + np.array([1, 1])] #利用 + np.array([1, 1]) 产生类别间的差异
  8.     y = np.hstack((np.zeros(n), np.ones(n))) #产生300个零及300个1并连接起来
  9.     return X, y
  11. def dataset_cov():
  12.     '''Generate 2 Gaussians samples with different covariance matrices'''
  13.     n, dim = 300, 2
  14.     np.random.seed(0)
  15.     C = np.array([[0., -1.], [2.5, .7]]) * 2.
  16.     X = np.r_[np.dot(np.random.randn(n, dim), C),
  17.               np.dot(np.random.randn(n, dim), C.T) + np.array([1, 4])]
  18.     y = np.hstack((np.zeros(n), np.ones(n)))
  19.     return X, y

(二)绘图函式

  1. 找出 True Positive及False Negative 之辨认点
  2. 以红色及蓝色分别表示分类为 0及1的资料点，而以深红跟深蓝来表示误判资料
  3. 以lda.predict_proba()画出分类的机率分布(请参考范例三)

(为了方便在ipython notebook环境下显示，下面函式有经过微调)

  1. def plot_data(lda, X, y, y_pred, fig_index):
  2.     splot = plt.subplot(2, 2, fig_index)
  3.     if fig_index == 1:
  4.         plt.title('Linear Discriminant Analysis',fontsize=28)
  5.         plt.ylabel('Data with fixed covariance',fontsize=28)
  6.     elif fig_index == 2:
  7.         plt.title('Quadratic Discriminant Analysis',fontsize=28)
  8.     elif fig_index == 3:
  9.         plt.ylabel('Data with varying covariances',fontsize=28)
  11.     # 步骤一：找出 True Positive及False postive 之辨认点
  13.     tp = (y == y_pred)  # True Positive
  14.     tp0, tp1 = tp[y == 0], tp[y == 1] #tp0 代表分类为0且列为 True Positive之资料点
  15.     X0, X1 = X[y == 0], X[y == 1]
  16.     X0_tp, X0_fp = X0[tp0], X0[~tp0]
  17.     X1_tp, X1_fp = X1[tp1], X1[~tp1]
  19.     # 步骤二：以红蓝来画出分类资料，以深红跟深蓝来表示误判资料
  21.     # class 0: dots
  22.     plt.plot(X0_tp[:, 0], X0_tp[:, 1], 'o', color='red')
  23.     plt.plot(X0_fp[:, 0], X0_fp[:, 1], '.', color='#990000')  # dark red
  25.     # class 1: dots
  26.     plt.plot(X1_tp[:, 0], X1_tp[:, 1], 'o', color='blue')
  27.     plt.plot(X1_fp[:, 0], X1_fp[:, 1], '.', color='#000099')  # dark blue
  29.     #步骤三：画出分类的机率分布(请参考范例三)
  30.     # class 0 and 1 : areas
  31.     nx, ny = 200, 100
  32.     x_min, x_max = plt.xlim()
  33.     y_min, y_max = plt.ylim()
  34.     xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx),
  35.                          np.linspace(y_min, y_max, ny))
  36.     Z = lda.predict_proba(np.c_[xx.ravel(), yy.ravel()])
  37.     Z = Z[:, 1].reshape(xx.shape)
  38.     plt.pcolormesh(xx, yy, Z, cmap='red_blue_classes',
  39.                    norm=colors.Normalize(0., 1.))
  40.     plt.contour(xx, yy, Z, [0.5], linewidths=2., colors='k')
  42.     # means
  43.     plt.plot(lda.means_[0][0], lda.means_[0][1],
  44.              'o', color='black', markersize=10)
  45.     plt.plot(lda.means_[1][0], lda.means_[1][1],
  46.              'o', color='black', markersize=10)
  48.     return splot
  1. def plot_ellipse(splot, mean, cov, color):
  2.     v, w = linalg.eigh(cov)
  3.     u = w[0] / linalg.norm(w[0])
  4.     angle = np.arctan(u[1] / u[0])
  5.     angle = 180 * angle / np.pi  # convert to degrees
  6.     # filled Gaussian at 2 standard deviation
  7.     ell = mpl.patches.Ellipse(mean, 2 * v[0] ** 0.5, 2 * v[1] ** 0.5,
  8.                               180 + angle, color=color)
  9.     ell.set_clip_box(splot.bbox)
  10.     ell.set_alpha(0.5)
  11.     splot.add_artist(ell)
  12.     splot.set_xticks(())
  13.     splot.set_yticks(())

(三)测试资料并绘图

  1. def plot_lda_cov(lda, splot):
  2.     plot_ellipse(splot, lda.means_[0], lda.covariance_, 'red')
  3.     plot_ellipse(splot, lda.means_[1], lda.covariance_, 'blue')
  6. def plot_qda_cov(qda, splot):
  7.     plot_ellipse(splot, qda.means_[0], qda.covariances_[0], 'red')
  8.     plot_ellipse(splot, qda.means_[1], qda.covariances_[1], 'blue')
  10. ###############################################################################
  11. figure = plt.figure(figsize=(30,20), dpi=300)
  12. for i, (X, y) in enumerate([dataset_fixed_cov(), dataset_cov()]):
  13.     # Linear Discriminant Analysis
  14.     lda = LinearDiscriminantAnalysis(solver="svd", store_covariance=True)
  15.     y_pred = lda.fit(X, y).predict(X)
  16.     splot = plot_data(lda, X, y, y_pred, fig_index=2 * i + 1)
  17.     plot_lda_cov(lda, splot)
  18.     plt.axis('tight')
  20.     # Quadratic Discriminant Analysis
  21.     qda = QuadraticDiscriminantAnalysis(store_covariances=True)
  22.     y_pred = qda.fit(X, y).predict(X)
  23.     splot = plot_data(qda, X, y, y_pred, fig_index=2 * i + 2)
  24.     plot_qda_cov(qda, splot)
  25.     plt.axis('tight')
  26. plt.suptitle('Linear Discriminant Analysis vs Quadratic Discriminant Analysis',fontsize=28)
  27. plt.show()

png

Python source code: plot_lda_qda.py

http://scikit-learn.org/stable/_downloads/plot_lda_qda.py

  1. print(__doc__)
  3. from scipy import linalg
  4. import numpy as np
  5. import matplotlib.pyplot as plt
  6. import matplotlib as mpl
  7. from matplotlib import colors
  9. from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
  10. from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
  12. ###############################################################################
  13. # colormap
  14. cmap = colors.LinearSegmentedColormap(
  15.     'red_blue_classes',
  16.     {'red': [(0, 1, 1), (1, 0.7, 0.7)],
  17.      'green': [(0, 0.7, 0.7), (1, 0.7, 0.7)],
  18.      'blue': [(0, 0.7, 0.7), (1, 1, 1)]})
  19. plt.cm.register_cmap(cmap=cmap)
  22. ###############################################################################
  23. # generate datasets
  24. def dataset_fixed_cov():
  25.     '''Generate 2 Gaussians samples with the same covariance matrix'''
  26.     n, dim = 300, 2
  27.     np.random.seed(0)
  28.     C = np.array([[0., -0.23], [0.83, .23]])
  29.     X = np.r_[np.dot(np.random.randn(n, dim), C),
  30.               np.dot(np.random.randn(n, dim), C) + np.array([1, 1])]
  31.     y = np.hstack((np.zeros(n), np.ones(n)))
  32.     return X, y
  35. def dataset_cov():
  36.     '''Generate 2 Gaussians samples with different covariance matrices'''
  37.     n, dim = 300, 2
  38.     np.random.seed(0)
  39.     C = np.array([[0., -1.], [2.5, .7]]) * 2.
  40.     X = np.r_[np.dot(np.random.randn(n, dim), C),
  41.               np.dot(np.random.randn(n, dim), C.T) + np.array([1, 4])]
  42.     y = np.hstack((np.zeros(n), np.ones(n)))
  43.     return X, y
  46. ###############################################################################
  47. # plot functions
  48. def plot_data(lda, X, y, y_pred, fig_index):
  49.     splot = plt.subplot(2, 2, fig_index)
  50.     if fig_index == 1:
  51.         plt.title('Linear Discriminant Analysis')
  52.         plt.ylabel('Data with fixed covariance')
  53.     elif fig_index == 2:
  54.         plt.title('Quadratic Discriminant Analysis')
  55.     elif fig_index == 3:
  56.         plt.ylabel('Data with varying covariances')
  58.     tp = (y == y_pred)  # True Positive
  59.     tp0, tp1 = tp[y == 0], tp[y == 1]
  60.     X0, X1 = X[y == 0], X[y == 1]
  61.     X0_tp, X0_fp = X0[tp0], X0[~tp0]
  62.     X1_tp, X1_fp = X1[tp1], X1[~tp1]
  64.     # class 0: dots
  65.     plt.plot(X0_tp[:, 0], X0_tp[:, 1], 'o', color='red')
  66.     plt.plot(X0_fp[:, 0], X0_fp[:, 1], '.', color='#990000')  # dark red
  68.     # class 1: dots
  69.     plt.plot(X1_tp[:, 0], X1_tp[:, 1], 'o', color='blue')
  70.     plt.plot(X1_fp[:, 0], X1_fp[:, 1], '.', color='#000099')  # dark blue
  72.     # class 0 and 1 : areas
  73.     nx, ny = 200, 100
  74.     x_min, x_max = plt.xlim()
  75.     y_min, y_max = plt.ylim()
  76.     xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx),
  77.                          np.linspace(y_min, y_max, ny))
  78.     Z = lda.predict_proba(np.c_[xx.ravel(), yy.ravel()])
  79.     Z = Z[:, 1].reshape(xx.shape)
  80.     plt.pcolormesh(xx, yy, Z, cmap='red_blue_classes',
  81.                    norm=colors.Normalize(0., 1.))
  82.     plt.contour(xx, yy, Z, [0.5], linewidths=2., colors='k')
  84.     # means
  85.     plt.plot(lda.means_[0][0], lda.means_[0][1],
  86.              'o', color='black', markersize=10)
  87.     plt.plot(lda.means_[1][0], lda.means_[1][1],
  88.              'o', color='black', markersize=10)
  90.     return splot
  93. def plot_ellipse(splot, mean, cov, color):
  94.     v, w = linalg.eigh(cov)
  95.     u = w[0] / linalg.norm(w[0])
  96.     angle = np.arctan(u[1] / u[0])
  97.     angle = 180 * angle / np.pi  # convert to degrees
  98.     # filled Gaussian at 2 standard deviation
  99.     ell = mpl.patches.Ellipse(mean, 2 * v[0] ** 0.5, 2 * v[1] ** 0.5,
  100.                               180 + angle, color=color)
  101.     ell.set_clip_box(splot.bbox)
  102.     ell.set_alpha(0.5)
  103.     splot.add_artist(ell)
  104.     splot.set_xticks(())
  105.     splot.set_yticks(())
  108. def plot_lda_cov(lda, splot):
  109.     plot_ellipse(splot, lda.means_[0], lda.covariance_, 'red')
  110.     plot_ellipse(splot, lda.means_[1], lda.covariance_, 'blue')
  113. def plot_qda_cov(qda, splot):
  114.     plot_ellipse(splot, qda.means_[0], qda.covariances_[0], 'red')
  115.     plot_ellipse(splot, qda.means_[1], qda.covariances_[1], 'blue')
  117. ###############################################################################
  118. for i, (X, y) in enumerate([dataset_fixed_cov(), dataset_cov()]):
  119.     # Linear Discriminant Analysis
  120.     lda = LinearDiscriminantAnalysis(solver="svd", store_covariance=True)
  121.     y_pred = lda.fit(X, y).predict(X)
  122.     splot = plot_data(lda, X, y, y_pred, fig_index=2 * i + 1)
  123.     plot_lda_cov(lda, splot)
  124.     plt.axis('tight')
  126.     # Quadratic Discriminant Analysis
  127.     qda = QuadraticDiscriminantAnalysis(store_covariances=True)
  128.     y_pred = qda.fit(X, y).predict(X)
  129.     splot = plot_data(qda, X, y, y_pred, fig_index=2 * i + 2)
  130.     plot_qda_cov(qda, splot)
  131.     plt.axis('tight')
  132. plt.suptitle('Linear Discriminant Analysis vs Quadratic Discriminant Analysis')
  133. plt.show()
免责声明： 以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。
@小牛知识库 xnip.cn