数据结构_Advanced
优质
小牛编辑
163浏览
2023-12-01
树状数组
树状数组是一种用于维护前缀信息的数据结构
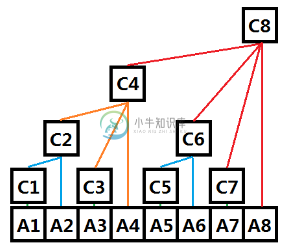
树状数组
C在物理空间上是连续的;对于数组中的两个位置
C[x], C[y],若满足y = x + 2^k(其中k表示x二进制中末尾 0 的个数),则定义C[x], C[y]为一组父子关系;4 的二进制为 100,则 k = 2 所以 4 是 4 + 2^2 = 8 的孩子 5 的二进制位 101,则 k = 0 所以 5 是 5 + 2^0 = 6 的孩子由以上定义,可知奇数下标的位置一定是叶子节点
C[i] 的直观含义
C[i]实际上表示原数组中一段区间内的某个统计意义(区间和、区间积、区间最值等等);- 该区间为
[i-2^k+1, i],是一个闭区间; - 以区间和为例
1=(001) C[1]=A[1]; 2=(010) C[2]=A[1]+A[2]; 3=(011) C[3]=A[3]; 4=(100) C[4]=A[1]+A[2]+A[3]+A[4]; 5=(101) C[5]=A[5]; 6=(110) C[6]=A[5]+A[6]; 7=(111) C[7]=A[7]; 8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
树状数组的构建(以区间和问题为例)
LeetCode - 307. 区域和检索 - 数组可修改
问题描述
给定一个数组,支持两种操作:
1.查询区间和
2.修改某个元素的值
示例:
Given nums = [1, 3, 5]
sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8- 构建树状数组的过程即初始化数组
C的过程 - 基本操作:
lowbit(x)——求 2^k,其中 k 表示 x 二进制位中后缀 0 的个数updateC(x, delta)——更新 C 数组中 A[x] 的祖先- 如果是初始化阶段 delta = A[i],
- 如果是更新 A[i],则 delta = new_val - A[i]
sumPrefix(x)——求前缀区间 [1, x] 的和update(i, val)——更新 A[i] = val,同时也会更新所有 A[i] 的祖先sumRange(lo, hi)——求范围 [lo, hi] 的区间和
C++
class NumArray {
int n;
vector<int> A;
vector<int> C;
// 求 2^k,其中 k 表示 x 二进制位中后缀 0 的个数
int lowbit(int x) {
return x & (-x);
}
// 更新 C 数组,对 A[x] 的每个祖先都加上 delta:
// 如果是初始化阶段 delta = A[i],如果是更新 A[i],则 delta = new_val - A[i]
void updateC(int x, int delta) {
for (int i = x; i <= n; i += lowbit(i)) {
C[i] += delta;
}
}
// 求前缀区间 [1, x] 的和
int sumPrefix(int x) {
int res = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
res += C[i];
}
return res;
}
public:
// 初始化
NumArray(vector<int> nums) {
n = nums.size();
A.resize(n + 1, 0);
C.resize(n + 1, 0);
for (int i = 1; i <= n; i++) {
A[i] = nums[i - 1]; // 树状数组的内部默认从 1 开始计数
updateC(i, A[i]);
}
}
// 将 A[i] 的值更新为 val
void update(int i, int val) {
i++; // 树状数组的内部默认从 1 开始计数,如果外部默认从 0 开始计数,则需要 +1;
updateC(i, val - A[i]); // 更新 A[i] 的所有祖先节点,加上 val 与 A[i] 的差即可
A[i] = val;
}
// 求范围 [lo, hi] 的区间和
int sumRange(int lo, int hi) {
lo++; hi++; // 树状数组的内部默认从 1 开始计数,如果外部默认从 0 开始计数,则需要 +1;
return sumPrefix(hi) - sumPrefix(lo - 1);
}
};
void solve() {
vector<int> nums{1, 3, 5};
auto na = NumArray(nums);
int ret;
ret = na.sumRange(0, 2);
na.update(1, 2);
ret = na.sumRange(0, 2);
}树状数组的特点
- 线段树不能解决的问题,树状数组也无法解决;
- 树状数组和线段树的时间复杂度相同:初始化
O(n),查询和修改O(logn);但实际效率要高于线段树; - 直接维护前缀信息也能解决查询问题,但是修改的时间复杂度会比较高;
相关问题
- 665. 二维区域和检索 - 矩阵不可变 - LintCode
- 817. 二维区域和检索 - 矩阵可变 - LintCode
- 249. 统计前面比自己小的数的个数 - LintCode
- 248. 统计比给定整数小的数的个数 - LintCode
- 532. 逆序对 - LintCode
相关阅读
- 夜深人静写算法(三)- 树状数组 - CSDN博客
数据结构设计
LRU 缓存
LeetCode/146. LRU缓存机制
思路
- 双向链表 + haspmap
- 数据除了被保存在链表中,同时也保存在 map 中;前者用于记录数据的顺序结构,后者以实现
O(1)的访问。
- 数据除了被保存在链表中,同时也保存在 map 中;前者用于记录数据的顺序结构,后者以实现
- 更新过程:
- 新数据插入到链表头部
- 每当缓存命中(即缓存数据被访问),则将数据移到链表头部
- 当链表满的时候,将链表尾部的数据丢弃
- 操作:
put(key, value):如果 key 在 hash_map 中存在,则先重置对应的 value 值,然后获取对应的节点,将节点从链表移除,并移动到链表的头部;若果 key 在 hash_map 不存在,则新建一个节点,并将节点放到链表的头部。当 Cache 存满的时候,将链表最后一个节点删除。get(key):如果 key 在 hash_map 中存在,则把对应的节点放到链表头部,并返回对应的value值;如果不存在,则返回-1。
C++(AC)
// 缓存节点(双端队列)
struct CacheNode {
int key;
int value;
CacheNode *pre, *next;
CacheNode(int k, int v) : key(k), value(v), pre(nullptr), next(nullptr) {}
};
class LRUCache {
int size = 0;
CacheNode* head = nullptr;
CacheNode* tail = nullptr;
unordered_map<int, CacheNode*> dp; // hash_map
void remove(CacheNode *node) {
if (node != head) { // 修改后序节点是需判断是否头结点
node->pre->next = node->next;
}
else {
head = node->next;
}
if (node != tail) { // 修改前序节点是需判断是否尾结点
node->next->pre = node->pre;
}
else {
tail = node->pre;
}
// remove 时不销毁该节点
//delete node;
//node = nullptr;
}
void setHead(CacheNode *node) {
node->next = head;
node->pre = nullptr;
if (head != nullptr) {
head->pre = node;
}
head = node;
if (tail == nullptr) {
tail = head;
}
}
public:
LRUCache(int capacity) : size(capacity) { }
int get(int key) {
auto it = dp.find(key);
if (it != dp.end()) {
auto node = dp[key];
// 如果命中了,把该节点移动到头部
remove(node);
setHead(node);
return node->value;
}
return -1;
}
void put(int key, int value) {
auto it = dp.find(key);
if (it != dp.end()) {
auto node = dp[key];
node->value = value; // 更新
remove(node);
setHead(node);
}
else {
auto node = new CacheNode(key, value);
setHead(node);
dp[key] = node;
// 关键:判断容量
//if (dp.size() >= size) { // 若先删除节点,则为 >=
if (dp.size() > size) { // 若先存入 dp,则为 >
auto it = dp.find(tail->key);
remove(tail);
// 这里才销毁内存(即使不销毁也能过 LeetCode)
delete it->second;
it->second = nullptr;
dp.erase(it); // 先销毁,在移除
}
}
}
};
