数据结构与算法 - 分治

优质

小牛编辑

138浏览

2023-12-01

分治和回溯其实本质上就是递归，只不过它是递归的其中一个细分类。可以认为分治和回溯最后就是一种特殊的递归或者是较为复杂的递归即可。

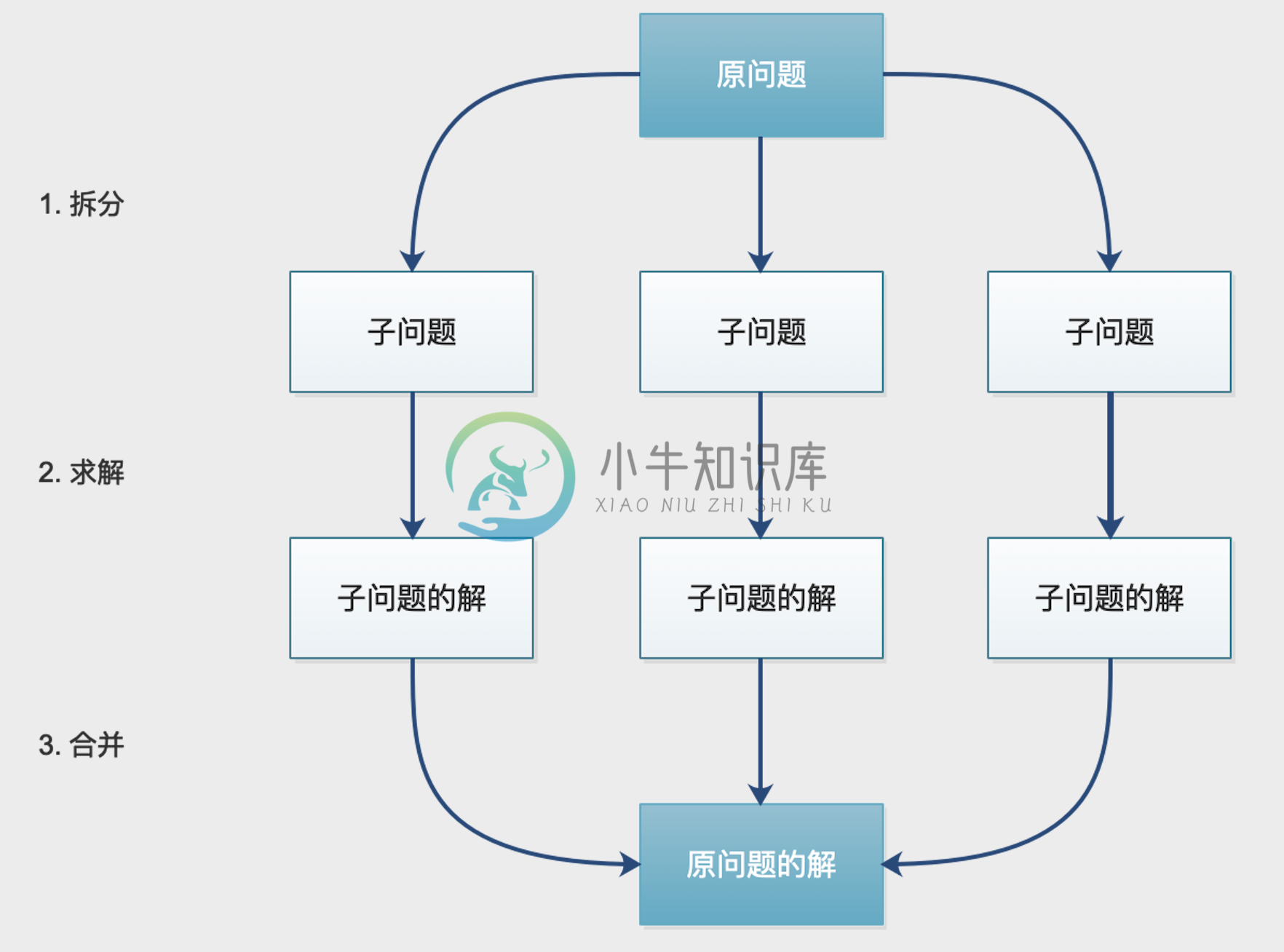
分治算法，即分而治之（divide and conquer，D&C），把一个复杂问题分成两个或更多的相同或相似子问题，直到最后子问题可以简单地直接求解，最后将子问题的解合并为原问题的解。

分治法的核心思想就是，将原问题分解成小问题来求解，只要遵循三个步骤即可：分解 -> 解决 -> 合并 **

分解(Divide)：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题。
解决(Conquer)：递归地求解出子问题。如果子问题的规模足够小，则停止递归，直接求解
合并(Combine)：将子问题的解组合成原问题的解

理解了思想后，就开始用代码来实现吧。

归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。归并排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

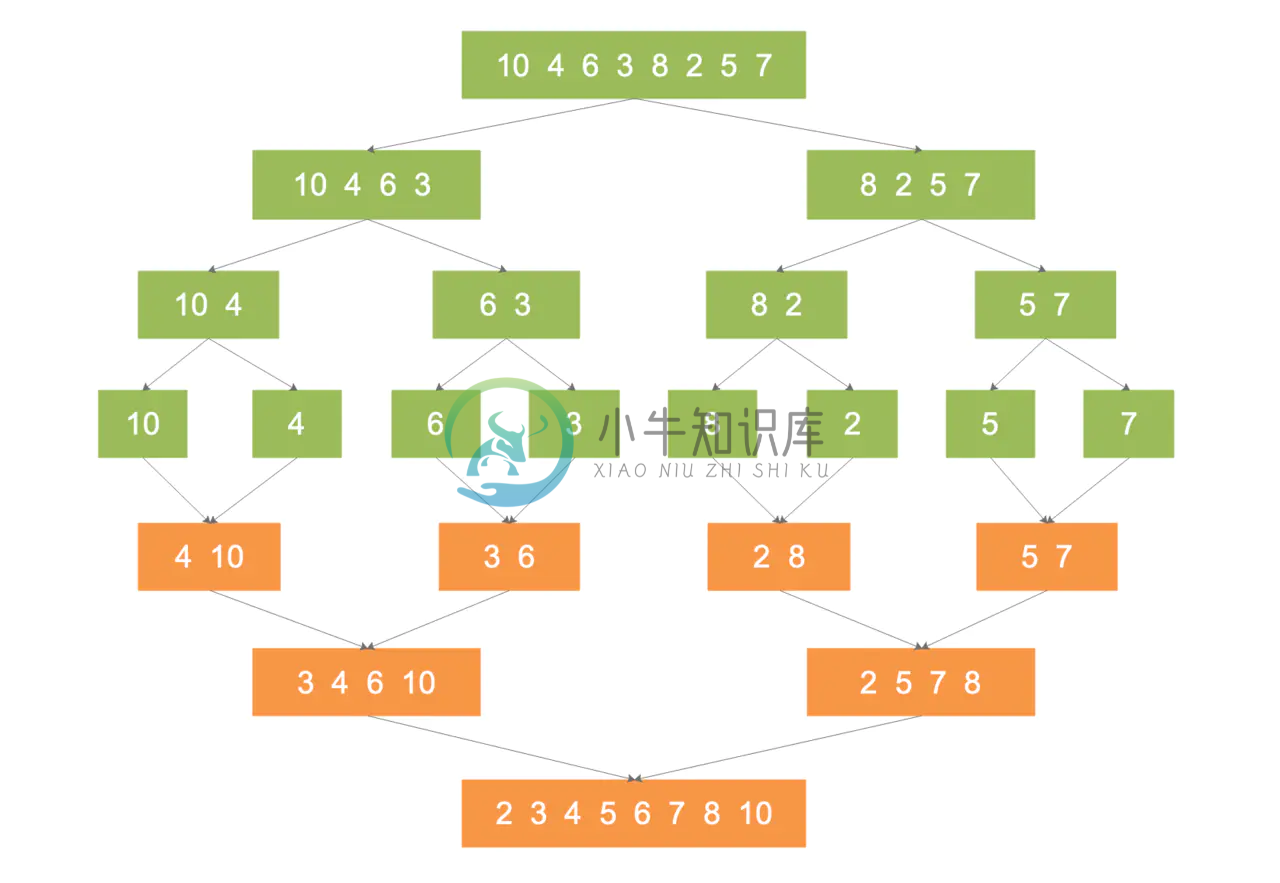
现在有一个待排序的序列：[10, 4, 6, 3, 8, 2, 5, 7]

先对序列进行分解，把该序列一分为二，直到无法拆分为止。整个拆分过程如下：

然后对分解出的序列进行两两排序与合并：

10, 4 排序合并后：4, 10 6, 3 排序合并后：3, 6 8, 2 排序合并后：2, 8 5, 7 排序合并后：5, 7 ……

整个归并排序完整过程如下：

  /**
   1. 先将数划分为两个数组left和right（即把数组mid从中间分开）
   2. 再分别对数组left、right重复步骤1的操作，逐步划分，直到不能再划分为止(每个子数组只剩下一个元素)

   */
  function merge(left, right) {
    let tmp = []
    while (left.length && right.length) {
      if (left[0] < right[0]) {
        tmp.push(left.shift())
      } else {
        tmp.push(right.shift())
      }
    }
    return tmp.concat(left, right)
  }

  function mergeSort(arr) {
    if (arr.length === 1) {
      return arr
    }


    let mid = Math.floor(arr.length / 2)

    let left = arr.slice(0, mid)
    let right = arr.slice(mid)

    return merge(mergeSort(left), mergeSort(right))
  }

  console.log(mergeSort([10, 4, 6, 3, 8, 2, 5, 7]))
  // [2, 3, 4, 5, 6, 7, 8, 10]

二分查找

二分查找是典型的分治算法的应用。需要注意的是，二分查找的前提是查找的数列是有序的。

二分查找又称折半查找

优点是比较次数少，查找速度快，平均性能好；
缺点是要求待查表为有序表，且插入删除困难。

因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；
否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。
重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

算法流程： （1）选择一个标志 i 将集合分为二个子集合。（2）判断标志 L(i) 是否能与要查找的值 des 相等，相等则直接返回。（3）否则判断 L(i) 与 des 的大小。（4）基于判断的结果决定下步是向左查找还是向右查找。（5）递归继续上面的步骤。通过二分查找的流程可以看出，二分查找是将原有序数列划分为左右两个子序列，然后在对两个子序列中的其中一个在进行划分，直至查找成功。

  /**
   * @param arr   有序数组（升序
   * @param low   低位
   * @param high  高位
   * @param key   要查找的数字
   * @returns {(number|undefined)|number}  返回查元的索引值，未找到返回-1
   */
  function binary(arr, key, low, high) {
    if (low <= high) {
      if (arr[low] === key) {
        return low
      }

      if (arr[high] === key) {
        return high
      }

      /**
       Math.ceil(4.5) 5 向下取整
       Math.foor(4.5) 4 向下取整
       */

      let mid = Math.ceil((high + low) / 2)   // 分解成子问题，以 mid 为准分成左右表

      if (arr[mid] === key) {
        return mid                            // 子问题足够小，停止递归，直接求解，返回元素索引

      } else if (arr[mid] > key) {            // 第一次 arr[3]> 12 ? 左表
        return binary(key, arr, low, mid - 1) // 递归地求解出子问题1

      } else {
        // 右表
        return binary(key, arr, mid + 1, high) // 递归地求解出子问题2
      }
    }
    return -1
  }

  let arr = [3, 5, 6, 7, 9, 12, 15]
  console.log( binary(arr, 12, 0, arr.length - 1)) //5

二分搜索
归并排序
快速排序
汉诺塔
大整数乘法
Strassen矩阵乘法
棋盘覆盖
线性时间选择
最接近点对问题
循环赛日程表

参考经典优化算法之分治法（Divide-and-Conquer Algorithm）浅谈什么是分治算法从生活出发了解什么是分治算法