数据结构与算法 - 递归算法

优质

小牛编辑

152浏览

2023-12-01

从前有座山
山里有座庙
庙里有个老和尚和小和尚
老和尚对小和尚说: 从前有座山返回1

从前有座山，山里有个庙，庙里有个和尚讲故事……这是一个古老的童谣，每个人都知道下面一句说了什么，但还要不厌其烦的说下去。犹如我们的人性，陷入一种循环，不可逃脱，无法自拔。

所以在我们现实生活中，很多时候也有所谓的重复性，而这种重复性用计算机解决的话，就能够省很多事情。如果用一部电影来类比的话，那《盗梦空间》就是找到这种所谓的归去来兮的感觉。电影的主线情节就是从飞机开始，再到城市，再往下不断地递归，到最后在一个雪山的屋子里面。

向下进入到不同梦境中；向上又回到原来一层
通过声音同步回到上一层
每一层的环境和周围的人都是一份拷贝、主角等几个人穿越不同层级的梦境（发生和携带变化）

主角的团队可以穿越梦境，把自已所携带的东西带到梦境里，且把变化可以携带回来，而这样主角团队就类似于函数里面的参数，同时还会一些全局变量。

这里更加强调的是通过现实中盗梦空间这样一个跳跃的含义，来说明递归它整个发生和现实中怎么联系一起的。

那么在计算机中，递归是算法中一种非常重要的思想，应用也很广，小到阶乘，再在工作中用到的比如统计文件夹大小。在前端开发中如树型菜单、递归组件。也是面试官很喜欢的考点。

简单地说，就是如果在 函数中存在着调用函数本身 的情况，这种现象就叫递归。

例如求和问题：若要求解 S = 1 + 2 + 3 + 4 + …. + 100 的值，通过循环的方式代码如下：

let sum = 0;
for (int i = 1; i <= 100; i++) {
    sum = sum + i;
}

通过递归方式是如何求解呢？由 1 + 2 + 3 + 4 + …. + 100 可以分解为 ( 1 + 2 + 3 + 4 + …. + 99) + 100 可以看出 S = S + 100，可以得出 S = S + n。通过递归的方式代码如下：

  function sum(n) {
    if (n === 1) { // 结束条件
      return 1
    } else {
      return sum(n - 1) + n // 调用函数本身
    }
  }

函数的调用模型可以参考之前的C笔记 https://www.yuque.com/ueumd/clang/mkfmt1

对于很多人把问题分析清楚了，写出上在代码并不很难，但是程序的执行过程又是什么样呢？

在我看来分析问题与程序执行过程一样重要，两者缺一不可，只会分析问题，很容易写出有BUG的程序，同时也不易深入理解，只理解递归执行过程，不会分析问题，那就是纸上谈兵，实际上也什么都没学到。

其实递归函数和普通函数的调用并没有什么区别，所以先理解普通函数的调用，再理解递归就不难了。

普通函数调用

嵌套调用


 function C(num) {
    console.log('function C', num)
  }
  function B(num) {
    C(num-1)
    console.log('function B', num)
  }

  function A(num) {
    B(num-1)
    console.log('function A', num)
  }
  function main() {
    A(3)
    console.log('function main')
  }
  main(4)
  /**
   function C 1
   function B 2
   function A 3
   function main
   */

我们在执行main方法时，main调用函数A，A再调用B，B再调用C，C打印出" function C"。此时C执行完毕返回至B继续执行，打印出" function B"，然后B执行完毕返回至A，A打印" function A"，再返回到main打印" function main"，执行完毕，执行结果如下所示

  /**
   function C
   function B
   function A
   function main
   */

可以看出来，每次调用一次函数，都是等它彻底执行完毕之后，才会返回去继续执行。同时在函数同步调用的时候，先执行的函数最后才执行完毕。可以看出是一个栈，先进后出。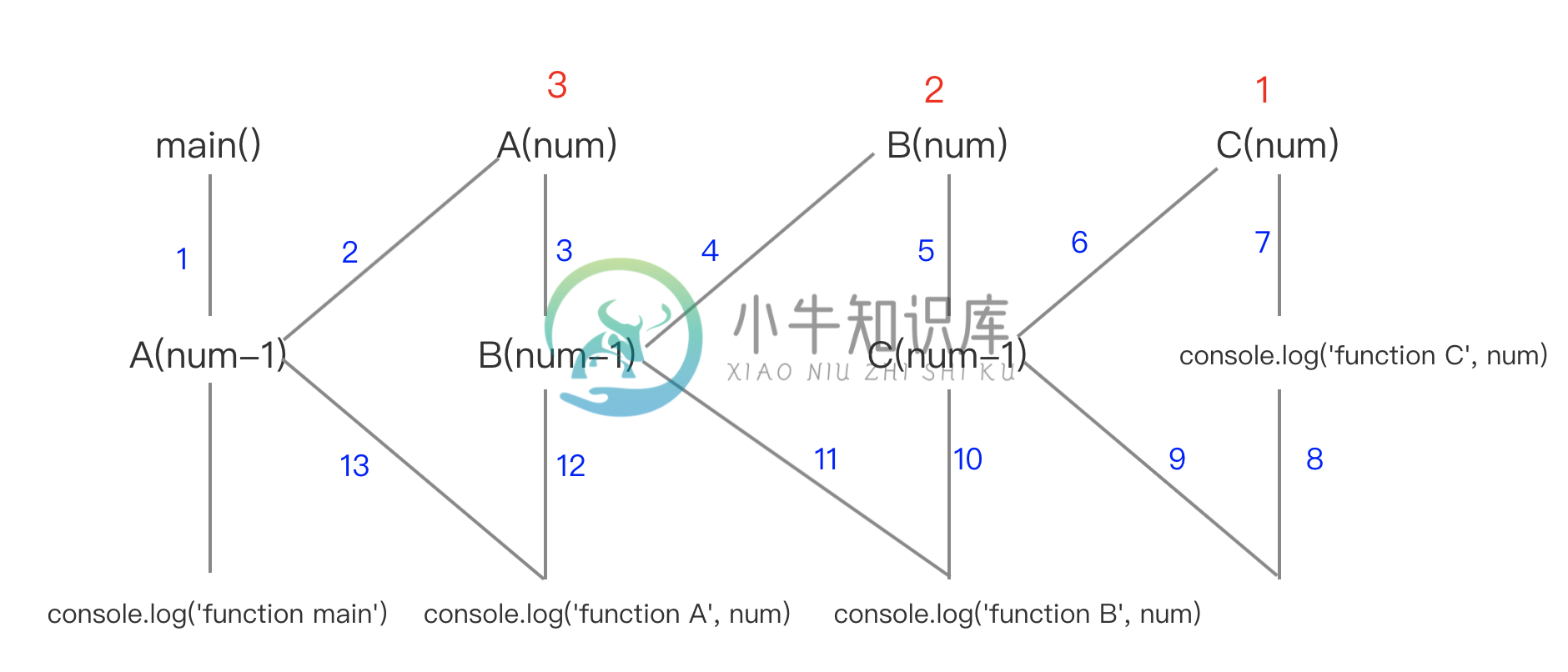

递归函数调用


  // 递归函数调用
  function test(a) {
    if (a === 1) { // 函数终止调用的条件，非常重要

      console.log("a = ", a)

      return         //终止函数调用
    }

    // 函数调用自身
    test(a - 1)

    console.log("a = ", a)
  }

  function main2() {
    test(3)
    console.log("main")
  }

  main2()
  /**
   a =  1
   a =  2
   a =  3
   main
   */

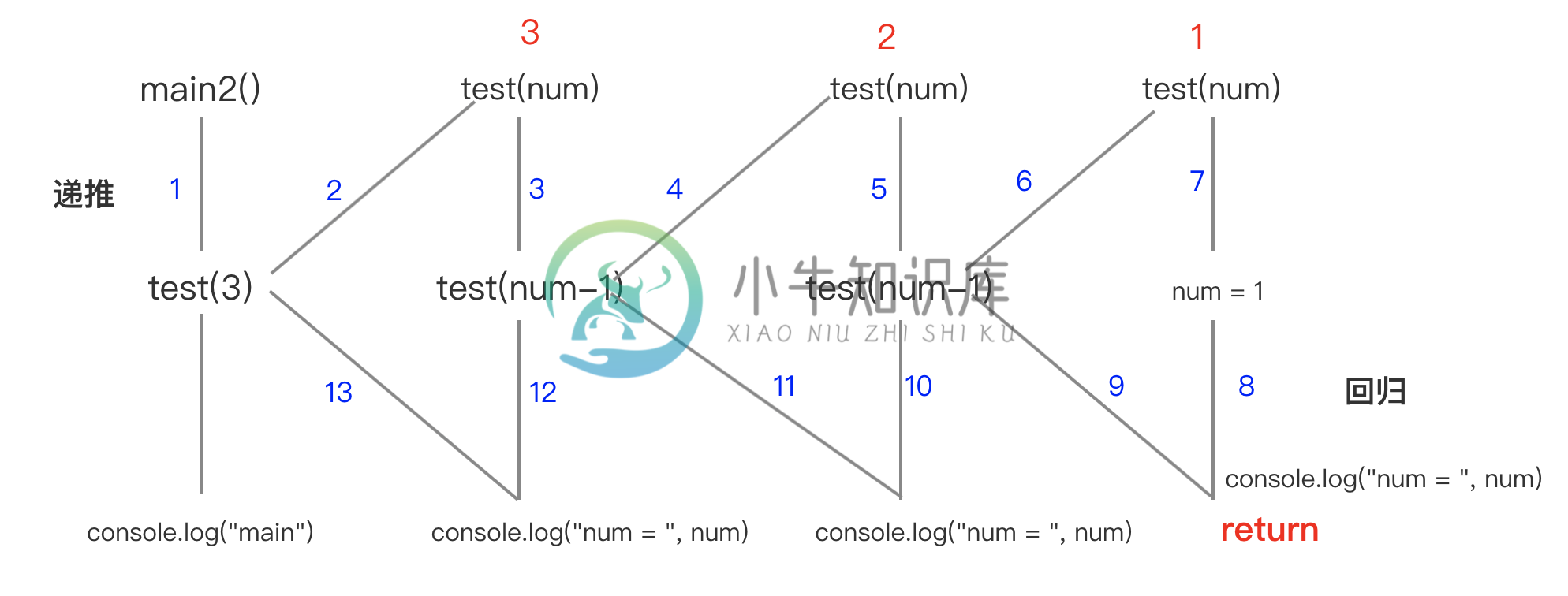当递归进入到最内层的时候，即结束条件，递归就结束了，就开始逐层退出了，也就是逐层执行 return 语句。

num 的值为 1 时达到最内层，打印num的值为1，执行 return 语句。
执行完test(1) 后，就可以返回上一层，执行test(2)，此时num=2，对打印结果为2
以此类推，当得到 test(3) 的调用结果后，就可以返回最顶层。

每一个递归函数都应该只进行有限次的递归调用，否则它就会进入死胡同，永远也不能退出。

要想让递归函数逐层进入再逐层退出，需要解决两个方面的问题：

存在限制条件，当符合这个条件时递归便不再继续。对于 test()，当形参 num 等于1时，递归就结束了。
每次递归调用之后越来越接近这个限制条件。对于 test()，每次递归调用的实参为 num- 1，这会使得形参 n 的值逐渐减小，越来越趋近于1。