数据结构与算法 - 图

优质

小牛编辑

129浏览

2023-12-01

图是一种比线性表和树更复杂的数据结构，在图中，结点之间的关系是任意的，任意两个数据元素之间都可能相关。

图是一种 多对多 的数据结构。

Gravph(V, E)

V - vertex：点
- 度 - 入度和出度
- 点与点之间：连通与否
E - edge: 边
- 有向边和无向（单线线）
- 权重（边长）

无向图(边没有方向)
有向图(边有方向)

图是由顶点和边组成的：(可以无边，但至少包含一个顶点)

一组顶点：通常用 V(vertex) 表示顶点集合
一组边：通常用 E(edge) 表示边的集合

图可以分为有向图和无向图，在图中：

(v, w) 表示无向边，即 v 和 w 是互通的
表示有向边，该边始于 v，终于 w

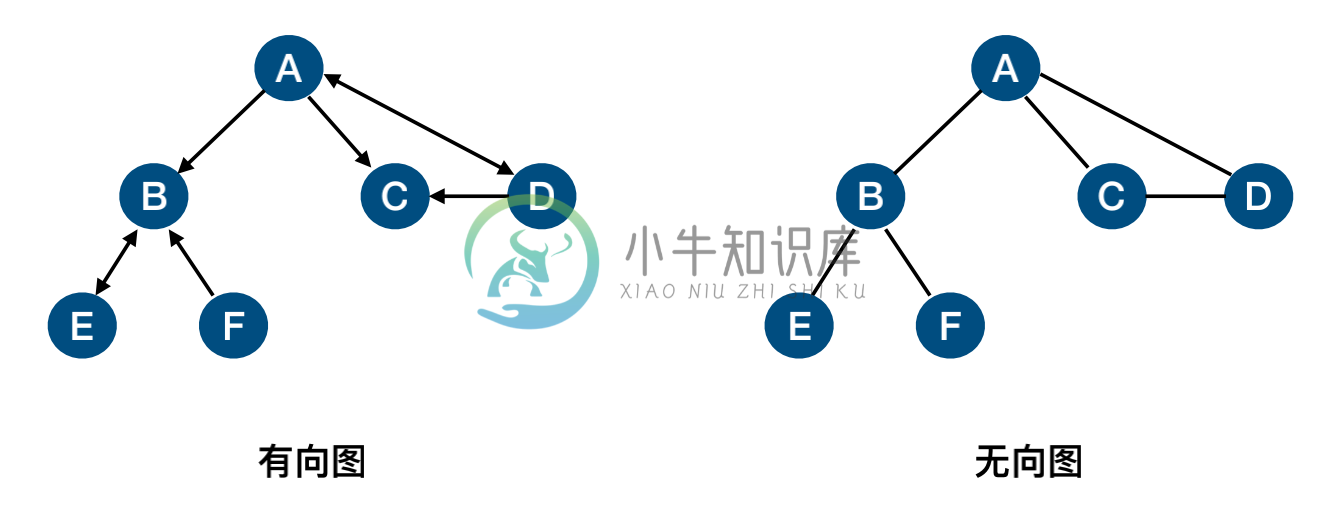
邻接矩阵
邻接表

邻接矩阵

图的邻接矩阵（Adjacency Matrix）存储方式是用两个数组来表示图。

一个一维数组存储图中顶点信息 [A, B, C, D, E, F]
一个二维数组（称邻接矩阵）存储图中的边或弧的信息

邻接矩阵中的 0 表示边不存在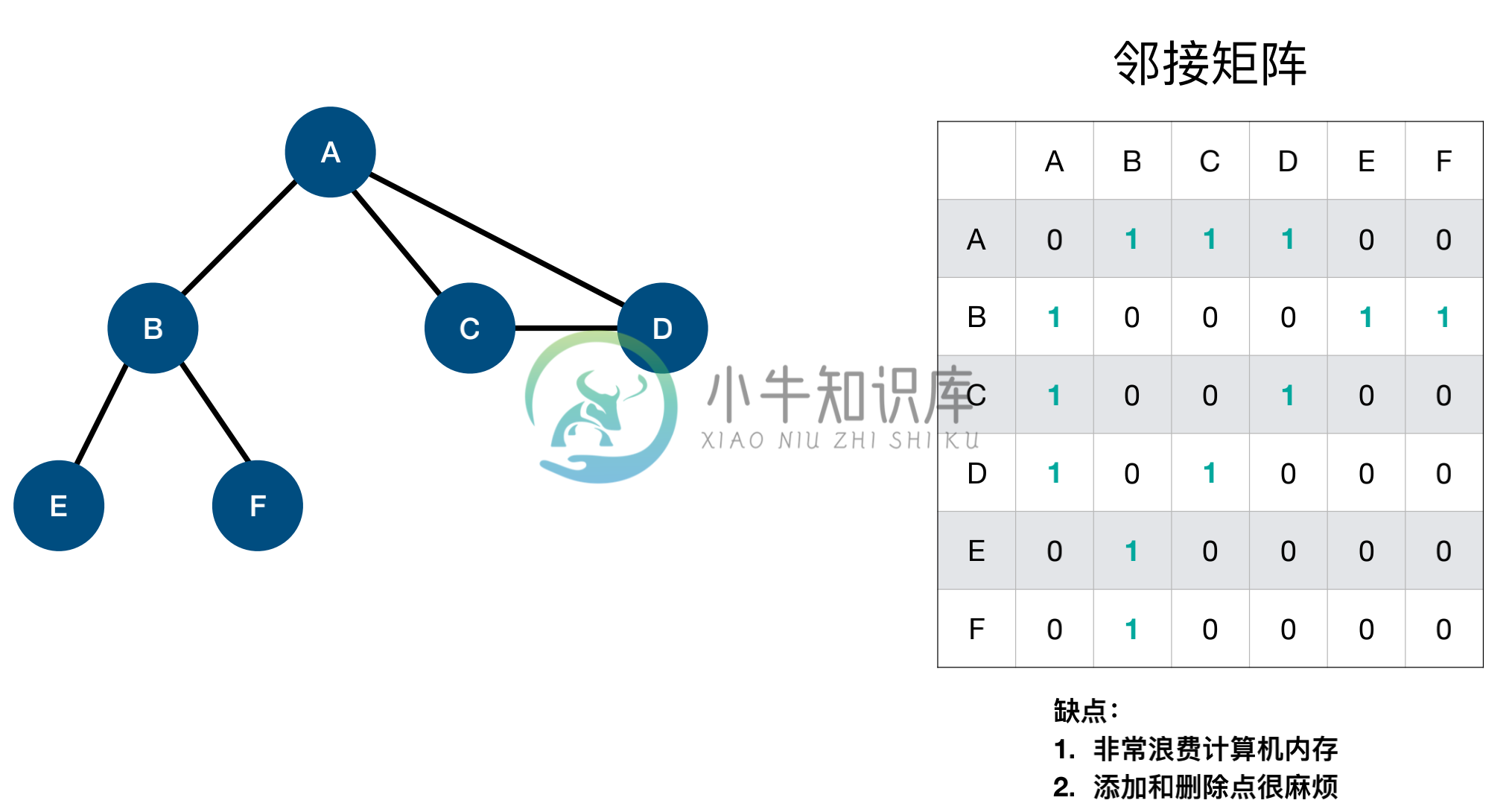

优点
1. 直观、简单、好理解
2. 方便检查任一对顶点间是否存在边
3. 方便找任一顶点的所有“邻接点”
4. 方便计算任一顶点的“度”（“入度”与“出度”）
缺点
1. 浪费空间—适合于稠密图
2. 浪费时间—统计稀疏图一共有多少条边

邻接表

邻接表是一种将数组与链表相结合的存储方法。其具体实现为：

将图中顶点用一个一维数组存储
每个顶点Vi的所有邻接点用一个单链表来存储

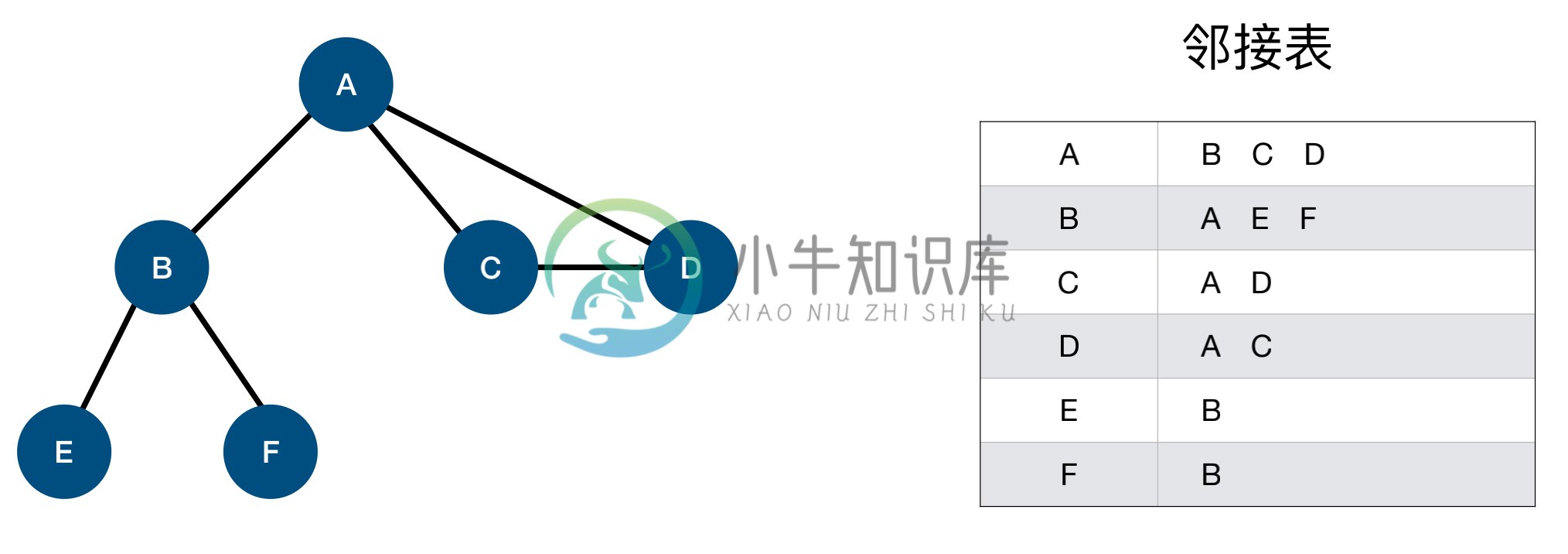
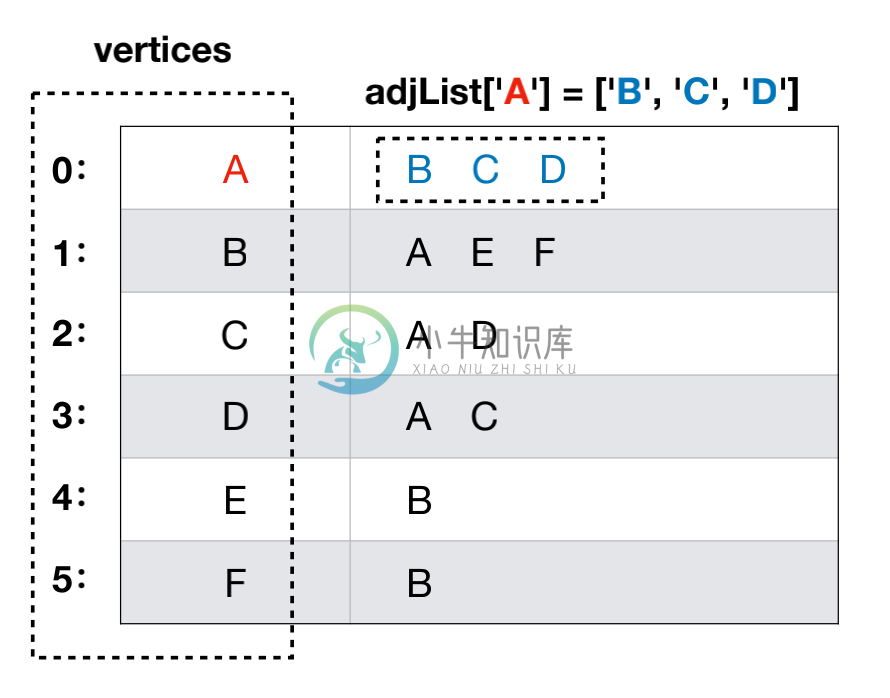
代码实现一个邻接表

<meta charset="UTF-8">
<script type="module">
  /**
   一个图G=(V, E)由以下兀素组成：
   V: 一组顶点
   E: 一组边，连接V中的顶点

   深度优先搜索（Depth-First Search，DFS)：
   桟，通过将顶点存入桟中，顶点是沿着路径被探索的，存在新的相邻顶点就去访问

   广度优先搜索（Breadth-First Search，BFS) ：
   队列，通过将顶点存入队列中，最先入队列的顶点先被探索
   */

  /**
   * 邻接表
   */
  class Graph {
    constructor() {
      // 存储顶点
      this.vertices = []

      // 存储边
      this.adjList = new Map()

      // 边数
      this.edges = 0
    }

    // 添加顶点
    addVertex(v) {
      // 添加顶点
      this.vertices.push(v)

      // 顶点对应的边，先置为空数组 A = []
      this.adjList.set(v, [])
    }

    // 添加边
    addEdge(v, e) {

      // 获取顶点 再加边
      this.adjList.get(v).push(e)

      // 无向的 所以互相添加
      this.adjList.get(e).push(v)

      // 边数加1
      this.edges ++
    }

    toString() {
      return this.vertices.reduce((r, v, i) => {
        return this.adjList.get(v).reduce((r, w, i) => {
          return r + `${w} `
        }, `${r}\n${v} => `)
      }, '')
    }

    /**
     * 广度优先搜索
     * @param v          顶点
     * @param callback   回调函数
     * @returns {{distances: Array, predecessors: Array}}
     */
    bfs (v, callback) {

      const read = []                         // 存入读取过的节点

      const distances = []                    // 距离

      const predecessors = []                 // 前溯点

      const addJlist = this.adjList           // 邻接表

      // 正在读取的节点 bfs 方法接受一点顶点作为算法的起始点, 起始顶点是必要的
      let pending = [v || this.vertices[0]]

      const readVertices = vertices => {
        vertices.forEach(key => {
          // 队列 先进先出
          read.push(key)
          pending.shift()

          // 使用BFS寻找最短路径
          distances[key] = distances[key] || 0
          predecessors[key] = predecessors[key] || null

          addJlist.get(key).forEach(v => {
            if (!pending.includes(v) && !read.includes(v)) {
              pending.push(v)
              distances[v] = distances[key] + 1
              predecessors[v] = key
            }
          })

          if (callback) callback(key)
          if (pending.length) readVertices(pending)
        })
      }

      readVertices(pending)

      return { distances, predecessors }
    }

    /**
     * 顶点到其他顶点的路径
     * @param fromVertex
     */
    distance(fromVertex) {
      const vertices = this.vertices
      const { distances, predecessors } = this.bfs(fromVertex)
      vertices.forEach(toVertex => {
        if (!!distances[toVertex]) {
          let preVertex = predecessors[toVertex]
          let slug = ''
          while (fromVertex !== preVertex) {
            slug = `${preVertex} - ${slug}`
            preVertex = predecessors[preVertex]
          }
          slug = `${fromVertex} - ${slug}${toVertex}`
          console.log(slug)
        }
      })
    }

    /**
     * 深度优先搜索
     * @param callback
     * @returns {{readTimes: *, predecessors: *, finishedTimes: *}}
     */
    dfs2 (callback) {
      const read = []
      const adjList = this.adjList
      const readVertices = vertices => {
        vertices.forEach(key => {
          if (read.includes(key)) return false
          read.push(key)
          if (callback) callback(key)
          if(read.length !== vertices.length) {
            readVertices(adjList.get(key))
          }
        })
      }
      readVertices([...adjList.keys()])
    }

    /**
     * 深度优先搜索
     * @param callback
     * @returns {{readTimes: *, predecessors: *, finishedTimes: *}}
     */
    dfs(callback) {
      let readTimer = 0
      const read = []
      const readTimes = []

      const finishedTimes = []
      const predecessors = []
      const adjList = this.adjList

      const readVertices = (vertices, predecessor) => { // 当前节点  前溯点
        vertices.forEach(key => {
          readTimer++
          if (adjList.get(key).every(v => read.includes(v)) && !finishedTimes[key]) {
            finishedTimes[key] = readTimer
          }
          if (read.includes(key)) return false
          readTimes[key] = readTimer
          read.push(key)
          if (callback) callback(key)
          predecessors[key] = predecessors[key] || predecessor || null
          if (read.length !== this.vertices.length) {
            readVertices(adjList.get(key), key)
          }
        })
      }
      readVertices([...adjList.keys()])
      return { readTimes, finishedTimes, predecessors }
    }
  }

  window.graph = new Graph()

  // 添加顶点
  ;['A', 'B', 'C', 'D', 'E', 'F'].forEach(v => graph.addVertex(v))

  // 添加边
  graph.addEdge('A', 'B')
  graph.addEdge('A', 'C')
  graph.addEdge('A', 'D')

  graph.addEdge('B', 'E')
  graph.addEdge('B', 'F')

  graph.addEdge('C', 'D')


  console.log('print:', graph)


  console.log('\n 打印邻接表：\n ')
  console.log(graph.toString())
  /*
   A => B C D
   B => A E F
   C => A D
   D => A C
   E => B
   F => B
   */

  let o = graph.bfs(graph.vertices[0], (v) => {
    console.log('访问了节点： ' + v)
  })
  /*
  访问了节点： A
  访问了节点： B
  访问了节点： C
  访问了节点： D
  访问了节点： E
  访问了节点： F
  */

  console.log('距离：', o.distances)
  // [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2]

  console.log('前溯点：', o.predecessors)
  // [A: null, B: "A", C: "A", D: "A", E: "B", F: "B"]



  console.log('\n 顶点到其他点的距离：\n ')
  graph.distance(graph.vertices[0])
 /*
  A - B
  A - C
  A - D
  A - B - E
  A - B - F
  */



  console.log('\n 深度优先搜索：\n ')

  graph.dfs((v) => {
    console.log('访问了节点： ' + v)
  })

  /*
  访问了节点： A
  访问了节点： B
  访问了节点： E
  访问了节点： F
  访问了节点： C
  访问了节点： D
  */

</script>

图的遍历

有两种算法可以对图进行遍历：

广度优先搜索（Breadth-First Search,BFS）
深度优先搜索（Depth-First Search,DFS）

图遍历可以用来寻找特定的顶点或者是寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环等。

图遍历算法的思想是必须追踪每个第一次访问的节点，并且追踪有哪些节点还没有被完全探索，对于两种图遍历算法，都需要明确指出第一个被访问的节点。

广度优先搜索算法和深度优先搜索算法基本上是相同的，只有一点不同，那就是待访问顶点列表的数据结构。

算法	数据结构	描述
广度优先搜索	队列（先进先出）	通过将顶点存入队列，最先入队列的顶点先被探索
深度优先搜索	栈（先进后出）	通过将顶点存入队列，最先入队列的顶点先被探索

广度优先搜索（Breadth-First Search, BFS）

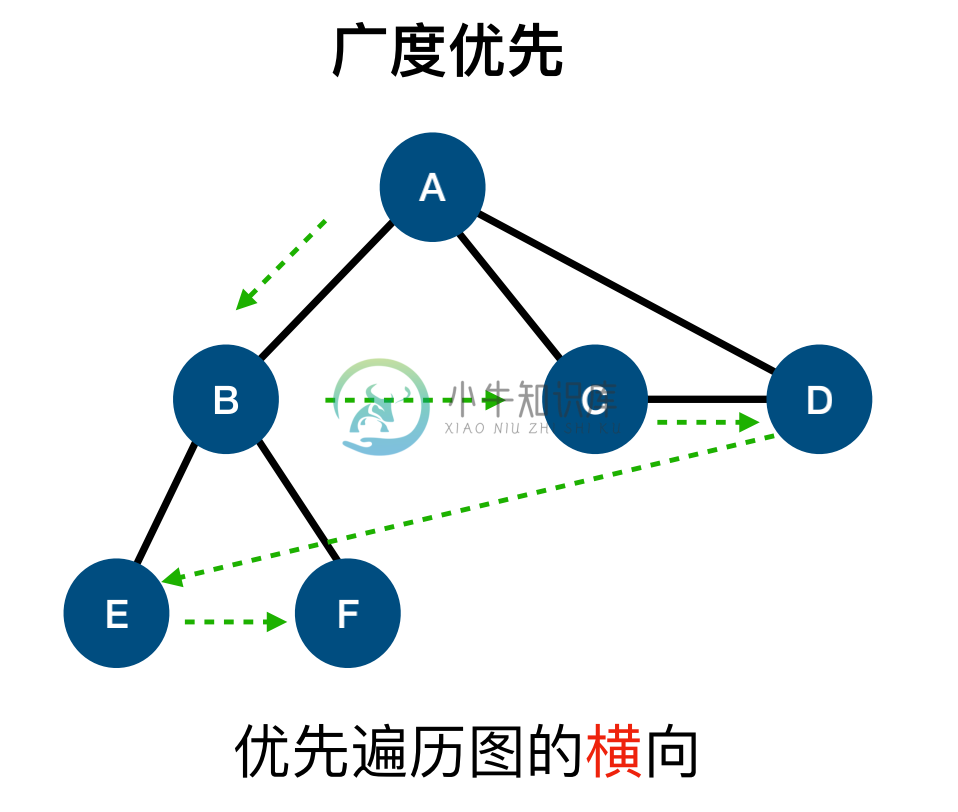
使用 BFS 寻找最短路径 使用 BFS 寻找最短路径** 我们可以用该算法做更多事情，而不只是输出被访问顶点的顺序。例如，考虑如何来解决下面的问题。给定一个图G和源顶点v，找出每个顶点u,u和v之间最短的路径（以边的数量计）

对于给定顶点v，广度优化算法会访问所有与其距离为1的顶点，接着是距离为2的顶点，以此类推。所以，可以用广度优先算法来解决这个问题。

我们可以修改bfs方法以返回给我们一些信息：

从v到u的距离d[u]，如A-> B 为 1，A->E为2

前溯点pred[u], 用来推导出从v到其他每个顶点u的最短路径。

/**
   * 广度优先搜索
   * @param v          顶点
   * @param callback   回调函数
   * @returns \{\{distances: Array, predecessors: Array\}\}
   */
  bfs (v, callback) {

    const read = []                         // 存入读取过的节点

    const distances = []                    // 距离

    const predecessors = []                 // 前溯点

    const addJlist = this.adjList           // 邻接表

    // 正在读取的节点 bfs 方法接受一点顶点作为算法的起始点, 起始顶点是必要的
    let pending = [v || this.vertices[0]]

    const readVertices = vertices => {
      vertices.forEach(key => {
        // 队列 先进先出
        read.push(key)
        pending.shift()

        // 使用BFS寻找最短路径
        distances[key] = distances[key] || 0
        predecessors[key] = predecessors[key] || null

        addJlist.get(key).forEach(v => {
          if (!pending.includes(v) && !read.includes(v)) {
            pending.push(v)
            distances[v] = distances[key] + 1
            predecessors[v] = key
          }
        })

        if (callback) callback(key)
        if (pending.length) readVertices(pending)
      })
    }

    readVertices(pending)

    return { distances, predecessors }
  }

let o = graph.bfs(graph.vertices[0], (v) => {
    console.log('访问了节点： ' + v)
  })
  /*
  访问了节点： A
  访问了节点： B
  访问了节点： C
  访问了节点： D
  访问了节点： E
  访问了节点： F
  */

  console.log('距离：', o.distances)
  // [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2]

  console.log('前溯点：', o.predecessors)
  // [A: null, B: "A", C: "A", D: "A", E: "B", F: "B"]

补充知识点：

看到上面距离的结果时，这个距离明明返回的是数组啊，lentgh属是0，怎么会是下面这种形式，然后访问 distances['B'] 得到 1。

distances:    [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2]
predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B"]

其实这里只是一个的A，C，D, E, F只是distances数组的一个属性而已，数组本来就是Object对象，如下面

let dis =[]

dis.A = 0
dis.B = 1
dis.C = 2

// dis：[A: 0, B: 1, C: 2]

dis['C'] //2
delete dis['B'] // true

// dis [A: 0, C: 2]

通过前溯数组，我们可以用下面这段代码来构建从顶点A到其他顶点的路径：

 /**
     * 顶点到其他顶点的路径
     * @param fromVertex
     */
    distance(fromVertex) {
      const vertices = this.vertices
      const { distances, predecessors } = this.bfs(fromVertex)
      vertices.forEach(toVertex => {
        if (!!distances[toVertex]) {
          let preVertex = predecessors[toVertex]
          let slug = ''
          while (fromVertex !== preVertex) {
            slug = `${preVertex} - ${slug}`
            preVertex = predecessors[preVertex]
          }
          slug = `${fromVertex} - ${slug}${toVertex}`
          console.log(slug)
        }
      })
    }


console.log('\n 顶点到其他点的距离：\n ')
  graph.distance(graph.vertices[0])
 /*
  A - B
  A - C
  A - D
  A - B - E
  A - B - F
  */

深度优先搜索（Depth-First Search,DFS）

/**
     * 深度优先搜索
     * @param callback
     * @returns {{readTimes: *, predecessors: *, finishedTimes: *}}
     */
    dfs(callback) {
      let readTimer = 0
      const read = []
      const readTimes = []

      const finishedTimes = []
      const predecessors = []
      const adjList = this.adjList

      const readVertices = (vertices, predecessor) => { // 当前节点  前溯点
        vertices.forEach(key => {
          readTimer++
          if (adjList.get(key).every(v => read.includes(v)) && !finishedTimes[key]) {
            finishedTimes[key] = readTimer
          }
          if (read.includes(key)) return false
          readTimes[key] = readTimer
          read.push(key)
          if (callback) callback(key)
          predecessors[key] = predecessors[key] || predecessor || null
          if (read.length !== this.vertices.length) {
            readVertices(adjList.get(key), key)
          }
        })
      }
      readVertices([...adjList.keys()])
      return { readTimes, finishedTimes, predecessors }
    }

新手推荐学习红点工厂 Skipper老师的 Javascript数据结构。Skipper老师上课思路清晰，简单易懂。

参考学习JavaScript数据结构与算法为什么我要放弃javaScript数据结构与算法（第九章）—— 图蚂蚁保险体验技术图形算法（邻接矩阵）初学者应该了解的数据结构： Graph 数据结构与算法：图和图算法(一)