数据结构与算法 - 跳表

优质

小牛编辑

137浏览

2023-12-01

也称为跳跃表(Skip List)是一种基于【有序链表】的扩展，简称【跳表】。存储的数据是有序的。所以跳表对标的是平衡树（AVL Tree）和二分查找，是一种插入/删除/搜索都是O(log n)的数据结构。

它最大的优势是原理简单、容易实现、方便扩展、效率更高。

定义

增加了向前指针的链表叫作跳表。跳表全称叫做跳跃表，简称跳表。
跳表是一个随机化的数据结构，实质就是一种可以进行二分查找的有序链表。
跳表在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。
跳表不仅能提高搜索性能，同时也可以提高插入和删除操作的性能。

时间复杂度

查找、插入、删除均为O(logn)，最坏为O(n)

空间复杂度

O(n)

实践

Redis、LevelDB

性能

和红黑树、AVL树不相上下

如何给有序的链表加速？

极客大学覃超老师的讲解

1. 添加第一级索引

next 指向next的next。步长+2，比如我们查找7 和 8

查找7，先从第一级索引 1 4 7，直接找到7
查找8，先从第一级索引 1 4 7，8大于7，再往后找到9，8小于9。那么在7和9之间，再回到原始链表里查找

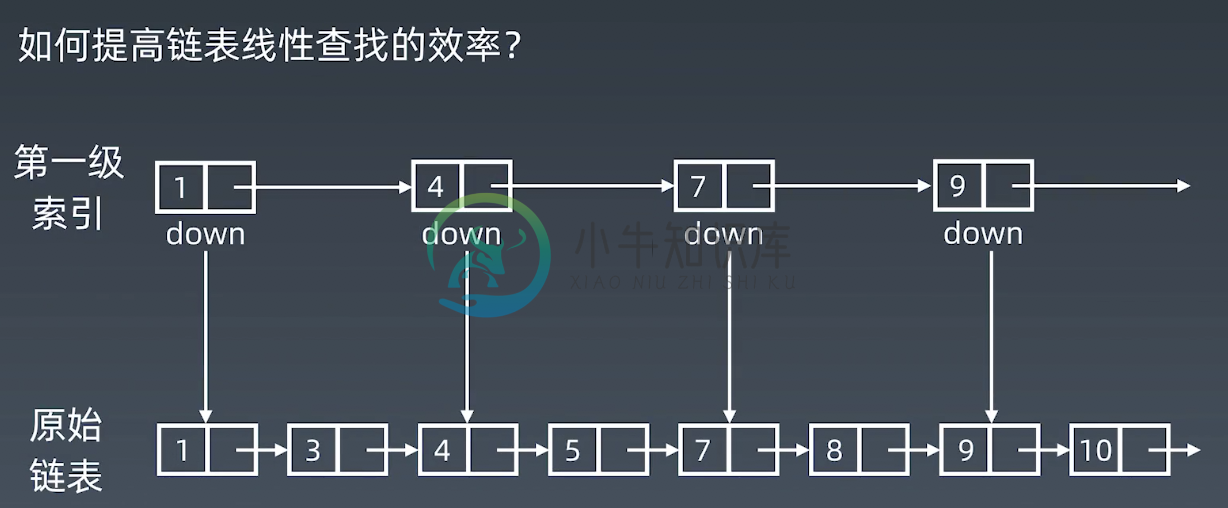
2. 添加第一级索引

如何进一步提高链表的查找效率？步长+4

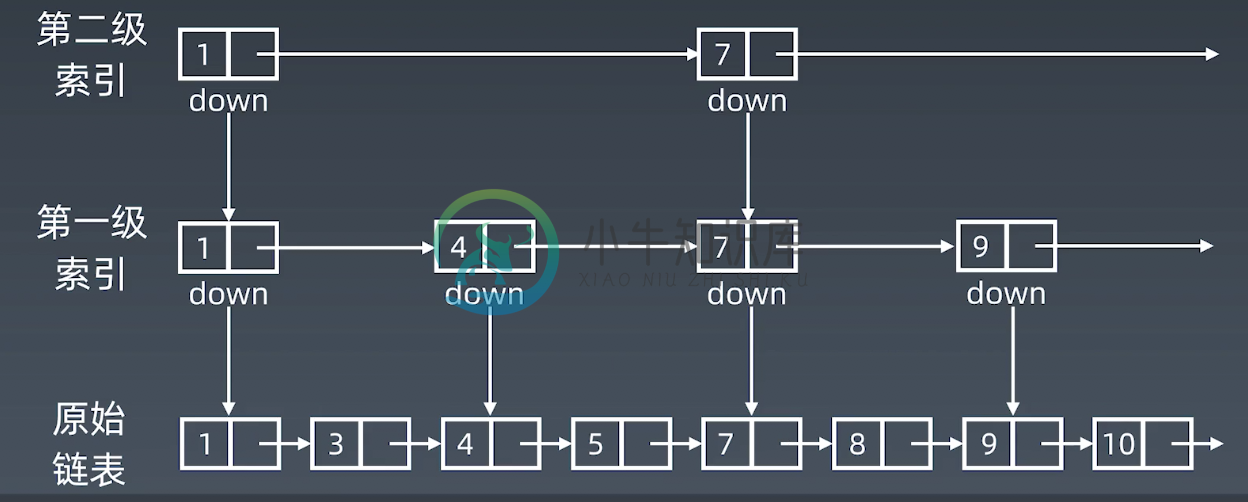
3. 多级索引

由比类推我们可以添加多级索引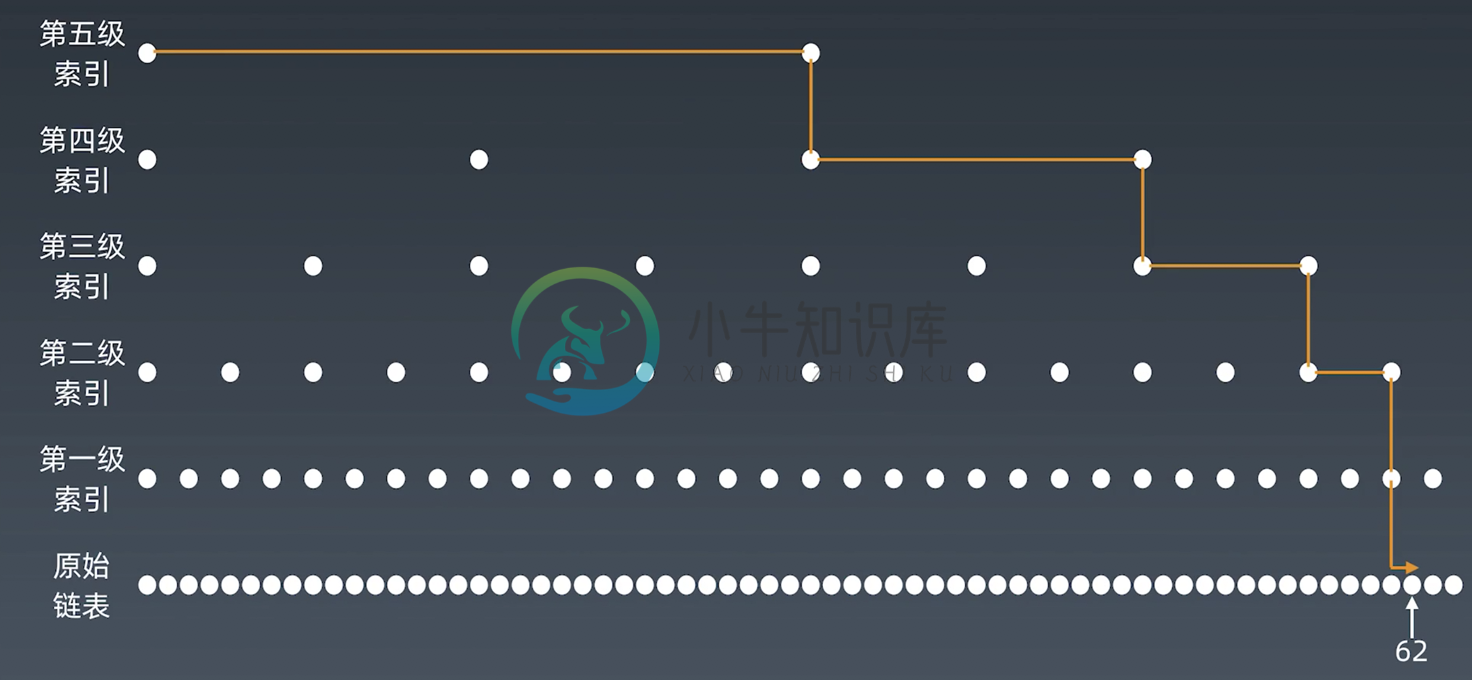

跳表查询的时间复杂度分析

n/2、n/4、n/8、第K级索引结节点的个数就是n/(2^k)。假设索引有h级，最高级的索引有2个结点。n(2^h) = 2，从而乾坤湾得 h = log2(n)-1。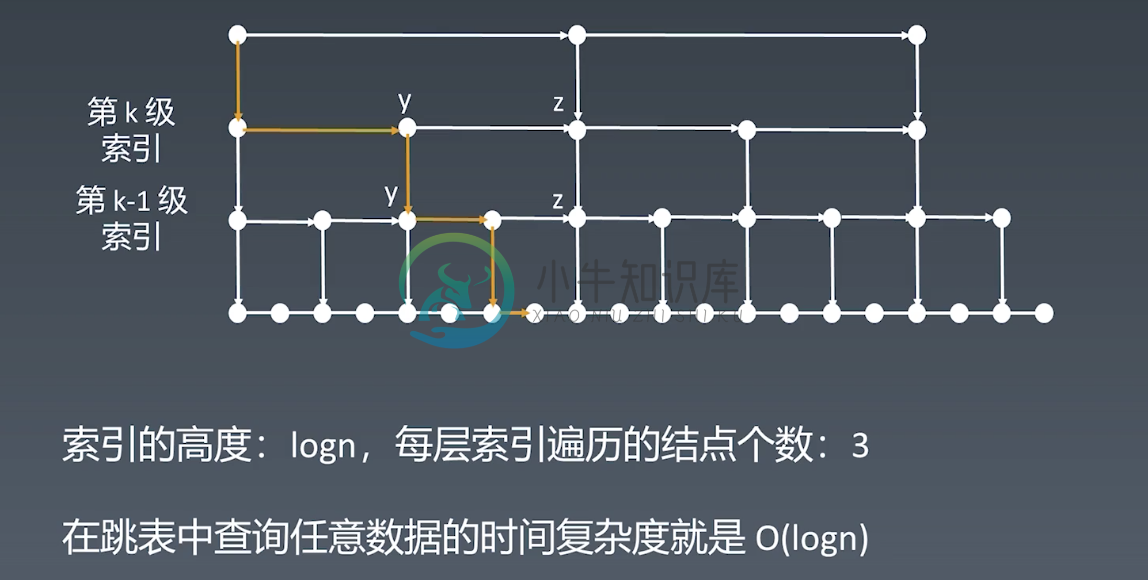

代码实现

代码来自 Alex660/Algorithms-and-data-structures

/**
 * 跳表索引默认最大级数
 */
const MAX_LEVEL = 16;
/**
 * 随机生成索引层数概率因子
 */
const SKIPLIST_P = 0.5;
/**
 * Node 类
 * @param {*} data - 存放类每个节点的数据
 * @param {number} maxLevel - 当前节点处于整个跳表索引的级数
 * @param {array} forwards - 当前层当前节点的下一个节点，如链表的 next 指针
 */
class Node {
    constructor (data = -1,maxLevel = 0,forwards = new Array(MAX_LEVEL)){
        this.data = data;
        this.maxLevel = maxLevel;
        this.forwards = forwards;
    }
}
/**
 * 跳表 类
 * 跳表中存储的是正整数，并且存储的是不重复的。
 */
class SkipList {
    constructor() {
        // 带头链表
        this.head = new Node();
        // 当前跳表索引的总级数
        this.levelCount = 1;
    }
    /**
     * 静态方法：随机生成 1~MAX_LEVEL 之间的索引级数
     * 配合概率因子SKIPLIST_P，使得跳表插入新元素时，每一层索引节点数约等于上一级索引节点数的2倍
     */
    static randomLevel() {
        let level = 1;
        while (Math.random() < SKIPLIST_P && level < MAX_LEVEL) {
            level++;
        }
        return level;
    }
    /**
     * 查找返回跳表里面的某个数据节点，没有返回 null
     * @param val - 需要查找的数据
     * @returns {*}
     */
    find(val) {
        if(!val) return null;
        let p = this.head;
        let levelCount = this.levelCount;
        // 从顶层开始查找，找到前一节点
        // i--，依次移动到下一层级查找前一节点
        for(let i = levelCount - 1;i >= 0;i--){
            while(p.forwards[i] != null && p.forwards[i].data < val){
                // 每层都找到一个当前节点的前一个节点，如链表的pre 指针 
                p = p.forwards[i];
            }
        }
        // 回到第一层，即原始链表
        if(p.forwards[0] !== undefined && p.forwards[0].data === val) {
            return p.forwards[0];
        }
        return null;
    }
    /**
     * 向跳表里插入数据
     * @param val - 需要插入的数据
     */
    insert(val) {
        // 随机层数
        const level = SkipList.randomLevel();
        // 创建新节点
        const newNode = new Node(val,level);
        // 每一层小于插入节点的前一个节点数组
        const update = new Array(level).fill(new Node());
        // 当前节点默认为头节点
        let p = this.head;
        // 寻找每一层需要插入节点的前一个节点
        for(let i = level - 1;i >= 0;i--){
            while(p.forwards[i] !== undefined && p.forwards[i].data < val) {
                p = p.forwards[i];
            }
            update[i] = p;
        }
        // 插入节点
        // 将每一层节点和后面节点相关联
        // 其实就是链表的插入操作(参考当前目录链表一节)
        for(let i = 0;i < level;i++){
            newNode.forwards[i] = update[i].forwards[i];
            update[i].forwards[i] = newNode;
        }
        // 更新层高[添加后有可能多了n层]
        if(this.levelCount < level) this.levelCount = level;
    }
    /**
     * 移除跳表里的某个数据节点
     * @param val - 需要删除的数据
     * 和插入方法同理，先找到每层需要删除节点数据的前一个节点
     * 然后就是执行链表的删除操作(参考当前目录链表一节)
     */
    remove(val) {
        const update = new Node();
        let p = this.head;
        let levelCount = this.levelCount;
        for(let i = levelCount - 1;i >= 0;--i){
            while(p.forwards[i] !== undefined && p.forwards[i].data < val) {
                p = p.forwards[i];
            }
            update[i] = p;
        }
        if(p.forwards[0] !== undefined && p.forwards[0].data === val) {
            for(let i = levelCount - 1;i >= 0;i--){
                if(update[i].forwards[i] !== undefined && update[i].forwards[i].data === val) {
                    update[i].forwards[i] = update[i].forwards[i].forwards[i];
                }
            }
        }
        // 同样更新层高[删除后有可能少了n层]
        while(this.levelCount > 1 && this.head.forwards[this.levelCount] === undefined) {
            this.levelCount--;
        }
    }
    // 打印跳表里的所有数据
    printRes() {
        let p = this.head;
        while(p.forwards[0] !== undefined) {
            console.log(p.forwards[0].data + ' ');
            p = p.forwards[0];
        }
    }
}
// 测试
let test = () => {
    let list = new SkipList();
    // 顺序插入
    for (let i = 1; i <= 10; i++) {
        list.insert(i);
    }
    // 输出
    // 1，2，3，4，5，6，7，8，9，10 
    list.printRes();
    // 查找
    //
    // {
    //  data: 8
    //  maxLevel: 1
    //  forwards: (16) [Node, empty × 15]
    // }
    list.find(8)
    // 删除
    list.remove(8)
    // 输出
    // 1，2，3，4，5，6，7，9，10
    list.printRes()
}
test();

相关文章：Redis源码学习之跳表