数据结构与算法 - 树、二叉搜索树
树是一种非线性的数据结构,以分层的方式存储数据,它对于存储需要快速查找的数据非常有用。 树是一种一对多的数据结构。树又有很多子集,比如:二叉树、二叉搜索树、2-3树、红黑树等等。
现实例子就是公司的组织架构,总裁为树的最顶端叫根节点,各部门按照领导人区分为子树。 在计算机科学中,HTML结构就是典型的树结构 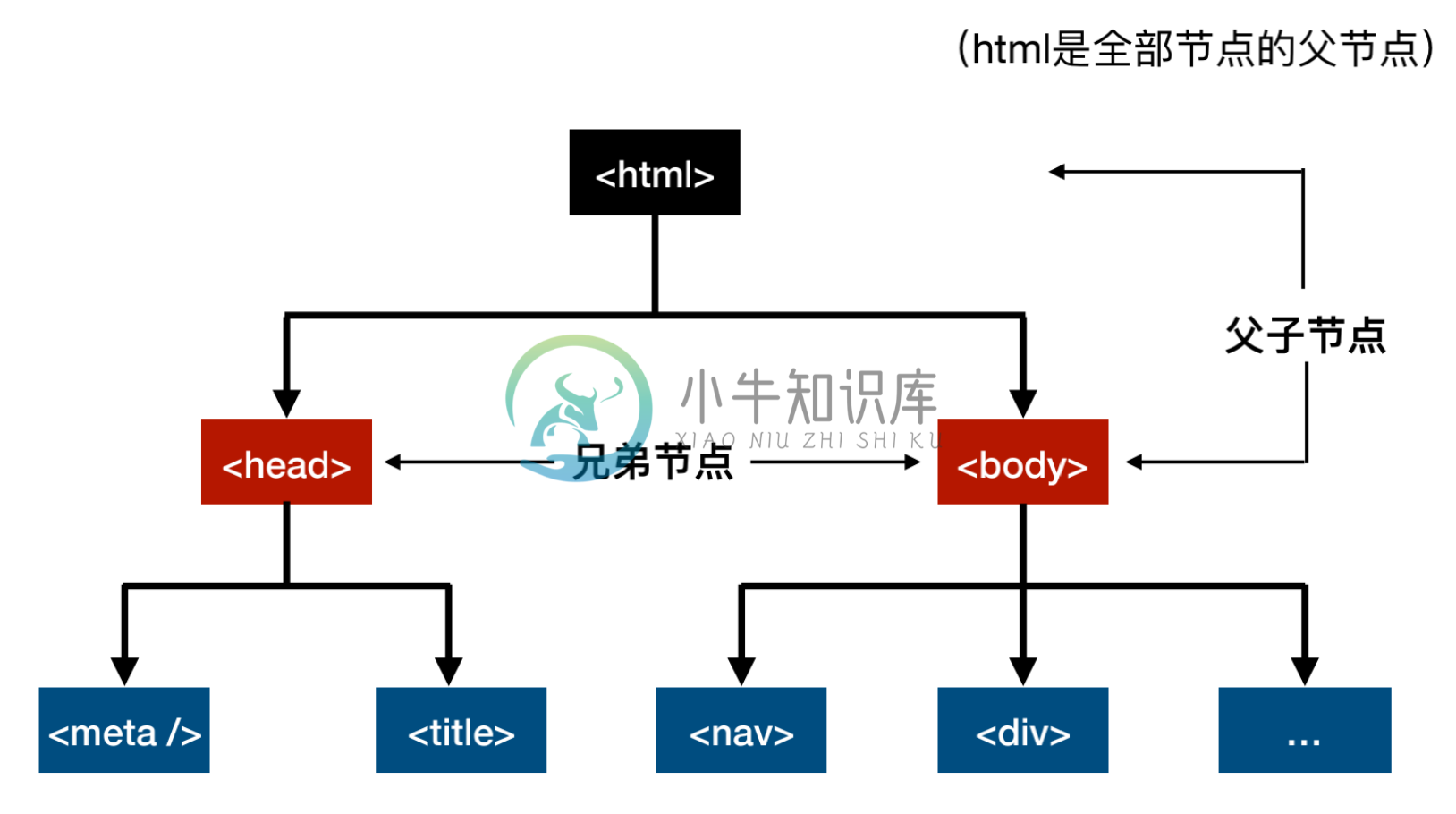
树的节点可以有0个或多个子节点。当一棵树(的所有节点)最多只能有两个子节点时,这样的树被称为二叉树。 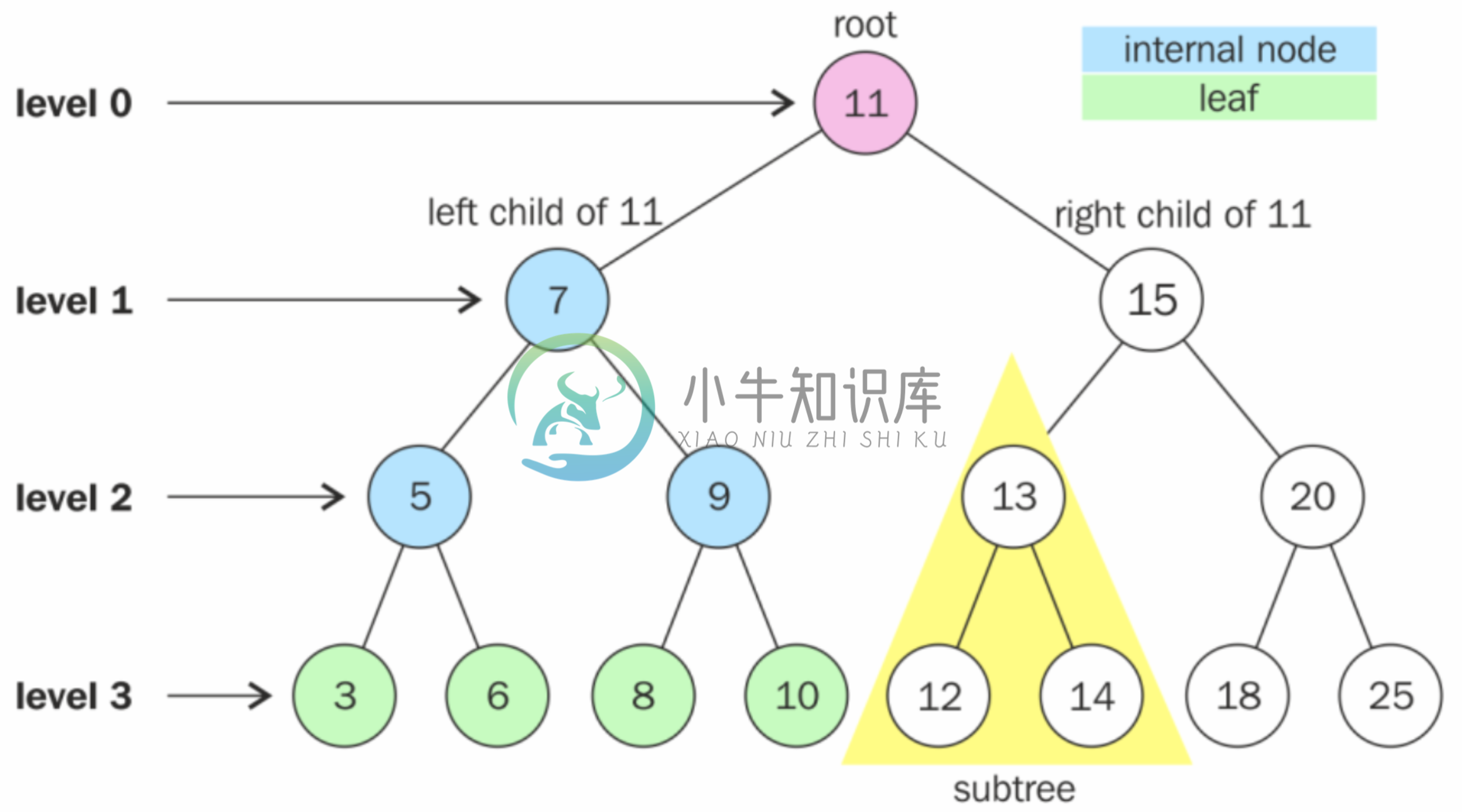
结点(root):指树中的一个元素; 叶子:度为0的结点,也称为终端结点; 层(levle):根在第一层,以此类推; 结点的度:指结点拥有的子树的个数,二叉树的度不大于2; 数的度:指树中的最大结点度数;如上图25 高度:叶子节点的高度为1,根节点高度最高;
取决于二叉树节点的组织方式,一棵二叉树又可以分为:
- 完满二叉树(Full binary tree):除去叶节点,每个节点都有两个子节点。
- 完全二叉树(Complete binary tree):除了最深一层之外,其余所有层的节点都必须有两个子节点。
- 完美二叉树(Perfect binary tree):满足完全二叉树性质,即满二叉树,树的叶子节点均在最后一,

完满二叉树、完全二叉树与完美二叉树并不总是互斥的:
- 完美二叉树 必然是 完满二叉树和完全二叉树
- 完美的二叉树正好有 2 的 k 次方 减 1 个节点,其中 k 是树的最深一层(从1开始)
- 深度为k的二叉树最多有2k-1个结点,2^k-1,如上图完美二叉树,深度为3,2^3-1=7。
- 完全二叉树并不总是完满二叉树。
- 正如上面的完全二叉树例子,最右侧的灰色节点是它父子点仅有的一个子节点。如果移除掉它,这棵树就既是完全二叉树,也是完满二叉树。(译者注:其实有了那个灰色节点的话,这颗树不能算是完全二叉树的,因为完满二叉树需要左对齐)
- 完满二叉树并不一定是完全二叉树与完美二叉树。
二叉树遍历原理
二叉树的遍历:是指从根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点被访问一次且仅被访问一次。 这里有两个关键词:访问和次序。
二叉树的遍历次序不同于线性结构,最多也就是从头到尾、循环和双向等简单的遍历方式。树的结点之间不存在唯一的前驱和后继关系,在访问一个结点后,下一个被访问的结点面临着不同的选择。
二叉树遍历方法
二叉树的遍历方式可以有很多,如果我们限制从左到右的顺序,就主要分为四种:
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
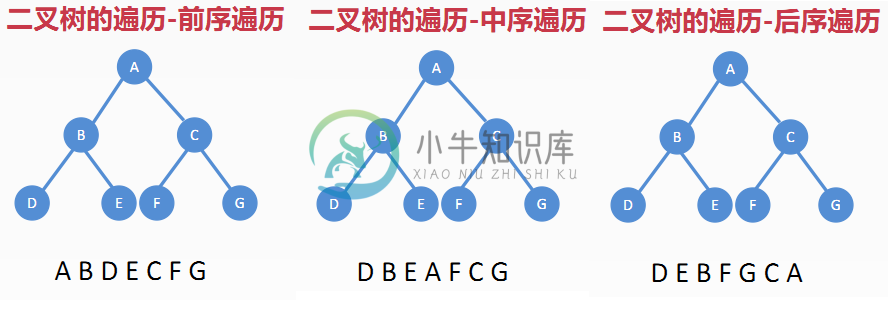
| 前序遍历 | 中序遍历 | 后序遍历 |
|---|---|---|
| 1. 访问根节点 | 1. 中序遍历左子树 | 1. 后序遍历左子树 |
| 2. 前序遍历左子树 | 2. 访问根节点 | 1. 后序遍历右子树 |
| 3. 前序遍历右子树 | 3. 中序遍历右子树 | 1. 访问根节点 |
一句话总结:
- 先序 (根->左->右)
- 中序 (左->根->右)
- 后序 (左->右->根)
前序遍历
若二叉树为空,则空操作返回,否则,然后,再前树。 如下图遍历顺序为:A B D G H C E I F。 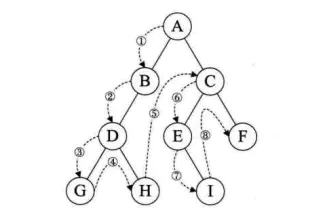
中序遍历
若二叉树为空,则空操作返回,否则从,中序遍历根结点左子树,然后访问根结点,最后中序遍历右子树。 如下图遍历顺序为:G D H B A E I C F。 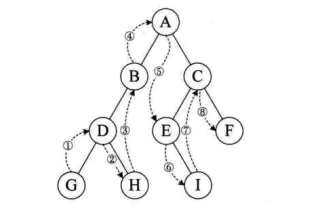
后序遍历
若二叉树为空,则空操作返回,,最后是访问根结点,如下图遍历顺序为:G H D B I E F C A。 
层序遍历
若二叉树为空,则空操作返回,否则从树的第一层开始,也就是从根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。 如下图遍历顺序为:A B C D E F G H I。 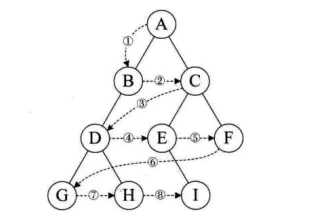
定义
- 二叉搜索树 (BST, Binary Search Tree), 也称二叉排序树或二叉查找树。只允许你在值,在。
- 二叉搜索树是一颗二叉树,可以为空;
特点
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
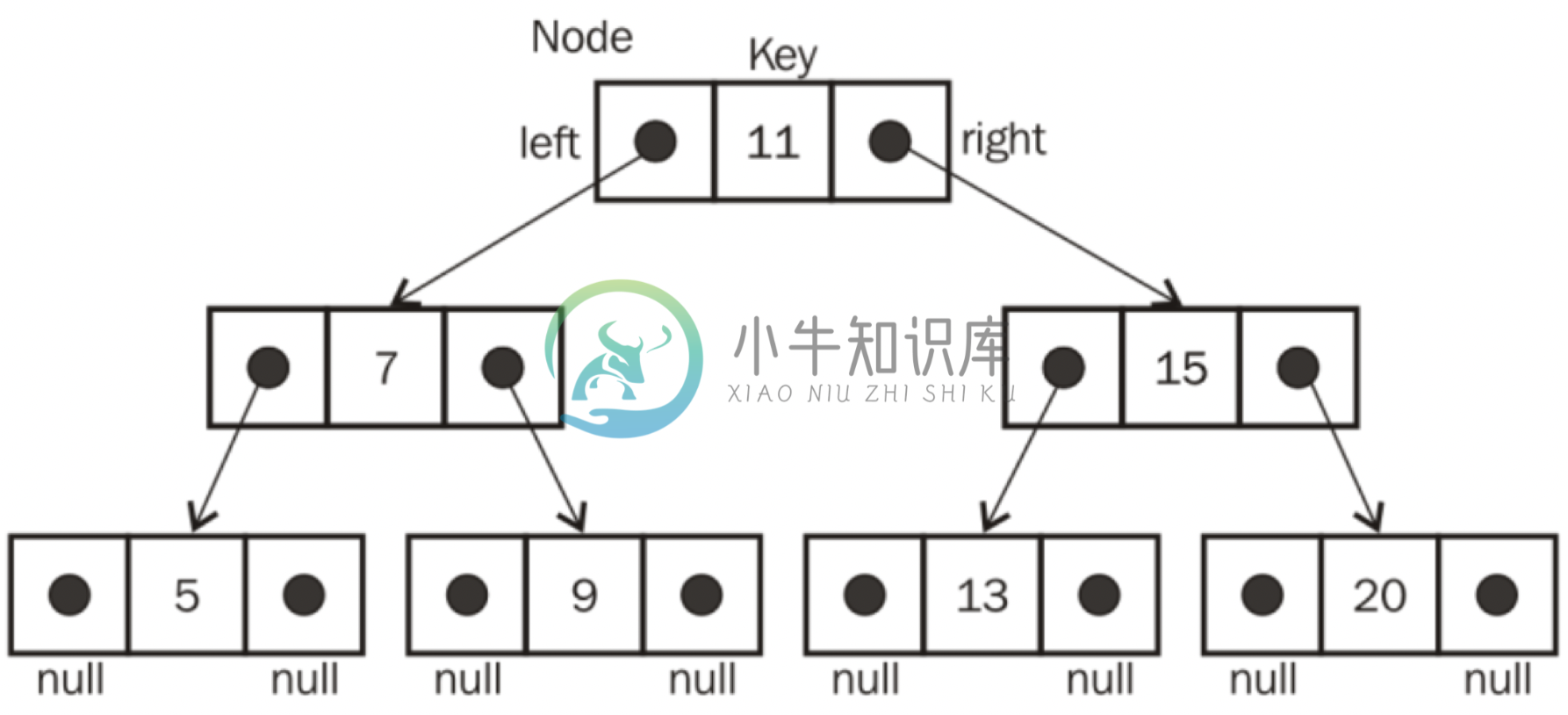
实现
<meta charset="UTF-8">
<script>
class Node {
constructor(key) {
this.key = key
this.left = null
this.right = null
}
}
class BinarySearchTree {
constructor() {
this.root = null
}
insert(key) {
let newNode = new Node(key)
if (this.root === null) {
this.root = newNode
} else {
this.insertNode(this.root, newNode)
}
}
/**
* 左边子树小于右边子树的值
* @param node
* @param newNode
*/
insertNode(node, newNode) {
// 准备向左子树插入数据
if (newNode.key < node.key) {
if (node.left === null) {
node.left = newNode
} else {
// 子树上有内容递归
this.insertNode(node.left, newNode)
}
} else {
// 准备向右子树插入数据
if (node.right === null) {
node.right = newNode
} else {
this.insertNode(node.right, newNode)
}
}
}
search(key) {
let node = this.root
while (node !== null) {
if (node.key > key) { // 根节点大于key 左子树
node = node.left
} else if (node.key < key) { // 根节点小于key 右子树
node = node.right
} else {
// 找到(包含root)
return true
}
}
// 未找到
return false
}
getRoot() {
return this.root
}
/**
* 最大的节点: 根节点 右子树上
*/
maxNode() {
let node = this.root
if (node) {
while (node && node.right !== null) {
node = node.right
}
return node
}
return null
}
/**
* 最小节点: 根节点 左子树上
*/
minNode() {
let node = this.root
if (node) {
while (node && node.left !== null) {
node = node.left
}
return node
}
return null
}
/**
移除节点的实现情况比较复杂,它会有三种不同的情况:
1. 需要移除的节点是一个叶子节点
2. 需要移除的节点包含一个子节点
3. 需要移除的节点包含两个子节点
和实现搜索指定节点一元,要移除某个节点,必须先找到它所在的位置,因此移除方法的实现中部分代码和上面相同:
*/
remove(key) {
this.removeNode(this.root, key)
}
removeNode(node, key) {
if (node === null) {
return null
}
if (key < node.key) {
node.left = this.removeNode(node.left, key)
return node
} else if (key > node.key) {
node.right = this.removeNode(node.right, key)
return node
} else {
//需要移除的节点是一个叶子节点
if (node.left === null && node.right === null) {
node = null
return node
}
//需要移除的节点包含一个子节点
if (node.left === null) {
node = node.right
return node
} else if (node.right === null) {
node = node.left
return node
}
//需要移除的节点包含两个子节点
let aux = this.minNode(node.right)
node.key = aux.key
node.right = this.removeNode(node.right, aux.key)
return node
}
}
/**
* 先序遍历 根 左 右
*/
preOrderTraversal(cb) {
this.preOrderTraversalNode(this.root, cb)
}
preOrderTraversalNode(node, cb) {
if (node !== null) {
cb(node.key)
// 递归算法
this.preOrderTraversalNode(node.left, cb)
this.preOrderTraversalNode(node.right, cb)
}
}
/**
非递归遍历(利用栈:将遍历到的结点都依次存入栈中,拿结果时从栈中访问)
1. 初始化一个栈,将根节点压入栈中;
2. 当栈为非空时,循环执行步骤3到4,否则执行结束;
3. 从队列取得一个结点(取的是栈中最后一个结点),将该值放入结果数组;
4. 若该结点的右子树为非空,则将该结点的右子树入栈,若该结点的左子树为非空,则将该结点的左子树入栈;
(注意:先将右结点压入栈中,后压入左结点,从栈中取得时候是取最后一个入栈的结点,而先序遍历要先遍历左子树,后遍历右子树)
*/
ptn() {
let result = []
let stack = []
stack.push(this.root)
while (stack.length) {
let node = stack.pop()
result.push(node.key)
if (node.right) stack.push(node.right)
if (node.left) stack.push(node.left)
}
return result
}
/**
* 中序遍历 左 根 右
*/
inOrderTraversal(cb) {
this.inOrderTraversalNode(this.root, cb)
}
inOrderTraversalNode(node, cb) {
if (node !== null) {
this.inOrderTraversalNode(node.left, cb)
cb(node.key)
this.inOrderTraversalNode(node.right, cb)
}
}
// 左 根 右
itn(node) {
let result = []
let stack = []
while (stack.length || node) {
if (node) {
stack.push(node)
node = node.left
} else {
node = stack.pop()
result.push(node.key)
node = node.right
}
}
return result
}
/**
* 后序遍历 左 右 根
*/
postOrderTraversal(cb) {
this.postOrderTraversalNode(this.root, cb)
}
postOrderTraversalNode(node, cb) {
if (node !== null) {
this.postOrderTraversalNode(node.left, cb)
this.postOrderTraversalNode(node.right, cb)
cb(node.key)
}
}
// 层遍历
bfs() {
let result = []
let stack = [this.root]
let count = 0; // 用来记录执行到第一层
let bfs2 = function () {
let node = stack[count];
if (node) {
result.push(node.key);
if (node.left) stack.push(node.left);
if (node.right) stack.push(node.right);
count++;
bfs2();
}
}
bfs2()
return result
}
// 非递归算法
bfs2(node) {
let result = [];
let queue = [];
queue.push(node);
let pointer = 0;
while (pointer < queue.length) {
let node = queue[pointer++]; // // 这里不使用 shift 方法(复杂度高),用一个指针代替
result.push(node.ke);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
return result;
}
/**
翻转二叉树
4
/ \
2 7
/ \ / \
1 3 6 9
4
/ \
7 2
/ \ / \
9 6 3 1
*/
invertTree(node = this.root) {
if (node === null) {
return
}
this.invertTree(node.left)
this.invertTree(node.right)
this.exchange(node)
}
exchange(node) {
let temp = node.left
node.left = node.right
node.right = temp
}
}
/**
11,7,15,5,3,9,8,10,13,12,14,20,18,25,6
先序遍历: 11,7,5,3,6,9,8,10,15,13,12,14,20,18,25
中序遍历: 3,5,6,7,8,9,10,11,12,13,14,15,18,20,25
后序遍历: 3,6,5,8,10,9,7,12,14,13,18,25,20,15,11
*/
var tree = new BinarySearchTree()
tree.insert(11)
tree.insert(7)
tree.insert(15)
tree.insert(5)
tree.insert(3)
tree.insert(9)
tree.insert(8)
tree.insert(10)
tree.insert(13)
tree.insert(12)
tree.insert(14)
tree.insert(20)
tree.insert(18)
tree.insert(25)
tree.insert(6)
let res = ''
function print(node) {
res += node + ' '
// console.log(node)
}
tree.preOrderTraversal(print) //先序遍历11,7,5,3,6,9,8,10,15,13,12,14,20,18,25
console.log(res)
res = ''
tree.inOrderTraversal(print) //3 5 6 7 8 9 10 11 12 13 14 15 18 20 25
console.log(res)
res = ''
tree.postOrderTraversal(print) //3 6 5 8 10 9 7 12 14 13 18 25 20 15 11
console.log(res)
res = ''
let result = tree.ptn()
console.log('1111111', result)
console.log(tree.itn(tree.root))
console.log(tree.bfs())
tree.invertTree()
</script>

