JavaScript数据结构与算法之二叉树遍历算法详解【先序、中序、后序】

本文实例讲述了JavaScript数据结构与算法之二叉树遍历算法。分享给大家供大家参考，具体如下：

javascript数据结构与算法--二叉树遍历（先序）

先序遍历先访问根节点， 然后以同样方式访问左子树和右子树

代码如下：

/*
 *二叉树中，相对较小的值保存在左节点上，较大的值保存在右节点中
 *
 *
 * */
/*用来生成一个节点*/
function Node(data, left, right) {
  this.data = data;//节点存储的数据
  this.left = left;
  this.right = right;
  this.show = show;
}
function show() {
  return this.data;
}
/*用来生成一个二叉树*/
function BST() {
  this.root = null;
  this.insert = insert;
}
/*将数据插入二叉树
 （1）设根节点为当前节点。
 （2）如果待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点；反
 之，执行第4步。
 （3）如果当前节点的左节点为null，就将新的节点插入这个位置，退出循环；反之，继续
 执行下一次循环。
 （4）设新的当前节点为原节点的右节点。
 （5）如果当前节点的右节点为null，就将新的节点插入这个位置，退出循环；反之，继续
 执行下一次循环。
 * */
function insert(data) {
  var n = new Node(data, null, null);
  if (this.root == null) {
    this.root = n;
  }
  else {
    var current = this.root;
    var parent;
    while (true) {
      parent = current;
      if (data < current.data) {
        current = current.left;//待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点
        if (current == null) {//如果当前节点的左节点为null，就将新的节点插入这个位置，退出循环；反之，继续执行下一次while循环。
          parent.left = n;
          break;
        }
      }
      else {
        current = current.right;//待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点
        if (current == null) {
          parent.right = n;
          break;
        }
      }
    }
  }
}
/*先序遍历
 *用递归的方法
 */
function preOrder(node) {
  if (!(node == null)) {
    console.log(node.show() + " ");
    preOrder(node.left);
    preOrder(node.right);
  }
}
/* 测试代码 */
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
console.log("先序遍历: ");
preOrder(nums.root);

运行结果：

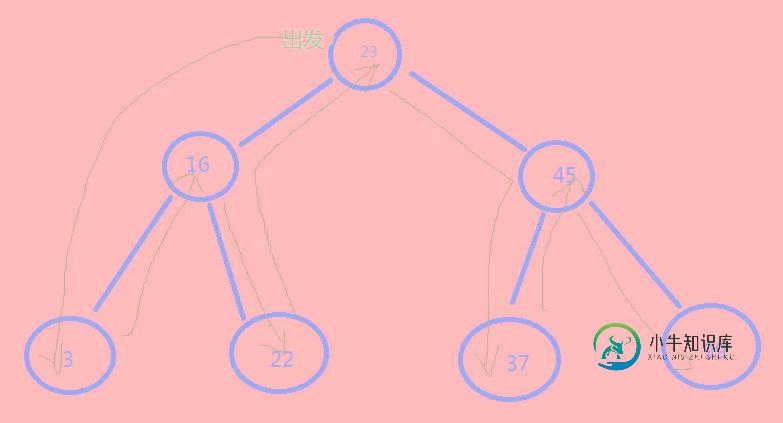
javascript数据结构与算法--二叉树遍历（中序）

中序遍历按照节点上的键值，以升序访问BST上的所有节点

代码如下：

/*
 *二叉树中，相对较小的值保存在左节点上，较大的值保存在右节点中
 *
 *
 * */
/*用来生成一个节点*/
function Node(data, left, right) {
  this.data = data;//节点存储的数据
  this.left = left;
  this.right = right;
  this.show = show;
}
function show() {
  return this.data;
}
/*用来生成一个二叉树*/
function BST() {
  this.root = null;
  this.insert = insert;
}
/*将数据插入二叉树
 （1）设根节点为当前节点。
 （2）如果待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点；反
 之，执行第4步。
 （3）如果当前节点的左节点为null，就将新的节点插入这个位置，退出循环；反之，继续
 执行下一次循环。
 （4）设新的当前节点为原节点的右节点。
 （5）如果当前节点的右节点为null，就将新的节点插入这个位置，退出循环；反之，继续
 执行下一次循环。
 * */
function insert(data) {
  var n = new Node(data, null, null);
  if (this.root == null) {
    this.root = n;
  }
  else {
    var current = this.root;
    var parent;
    while (true) {
      parent = current;
      if (data < current.data) {
        current = current.left;//待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点
        if (current == null) {//如果当前节点的左节点为null，就将新的节点插入这个位置，退出循环；反之，继续执行下一次while循环。
          parent.left = n;
          break;
        }
      }
      else {
        current = current.right;//待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点
        if (current == null) {
          parent.right = n;
          break;
        }
      }
    }
  }
}
/*中序遍历
*用递归的方法
*/
function inOrder(node) {
  if (!(node == null)) {
    inOrder(node.left);
    console.log(node.show() + " ");
    inOrder(node.right);
  }
}
/* 测试代码 */
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
console.log("中序遍历: ");
inOrder(nums.root);

运行结果：

javascript数据结构与算法--二叉树遍历（后序）

后序遍历先访问叶子节点，从左子树到右子树，再到根节点。

/*
 *二叉树中，相对较小的值保存在左节点上，较大的值保存在右节点中
 *
 *
 * */
/*用来生成一个节点*/
function Node(data, left, right) {
  this.data = data;//节点存储的数据
  this.left = left;
  this.right = right;
  this.show = show;
}
function show() {
  return this.data;
}
/*用来生成一个二叉树*/
function BST() {
  this.root = null;
  this.insert = insert;
}
/*将数据插入二叉树
 （1）设根节点为当前节点。
 （2）如果待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点；反
 之，执行第4步。
 （3）如果当前节点的左节点为null，就将新的节点插入这个位置，退出循环；反之，继续
 执行下一次循环。
 （4）设新的当前节点为原节点的右节点。
 （5）如果当前节点的右节点为null，就将新的节点插入这个位置，退出循环；反之，继续
 执行下一次循环。
 * */
function insert(data) {
  var n = new Node(data, null, null);
  if (this.root == null) {
    this.root = n;
  }
  else {
    var current = this.root;
    var parent;
    while (true) {
      parent = current;
      if (data < current.data) {
        current = current.left;//待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点
        if (current == null) {//如果当前节点的左节点为null，就将新的节点插入这个位置，退出循环；反之，继续执行下一次while循环。
          parent.left = n;
          break;
        }
      }
      else {
        current = current.right;//待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点
        if (current == null) {
          parent.right = n;
          break;
        }
      }
    }
  }
}
/*后序遍历
 *用递归的方法
 */
function postOrder(node) {
  if (!(node == null)) {
    postOrder(node.left);
    postOrder(node.right);
    console.log(node.show() + " ");
  }
}
/* 测试代码 */
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
console.log("后序遍历: ");
postOrder(nums.root);

运行结果：

感兴趣的朋友可以使用在线HTML/CSS/JavaScript代码运行工具：http://tools.jb51.net/code/HtmlJsRun测试上述代码运行效果。

更多关于JavaScript相关内容感兴趣的读者可查看本站专题：《JavaScript数学运算用法总结》、《JavaScript数据结构与算法技巧总结》、《JavaScript数组操作技巧总结》、《JavaScript排序算法总结》、《JavaScript遍历算法与技巧总结》、《JavaScript查找算法技巧总结》及《JavaScript错误与调试技巧总结》

希望本文所述对大家JavaScript程序设计有所帮助。