数据结构
- 数据结构相关基本是现场面试中出现频率最高的问题。
- 因为现场面试的时间限制,更难的问题需要大量的思考时间,所以一般只要求需要阐述思路(比如动态规划);
- 而数据结构相关的问题,因为有很强的先验知识,通常要求手写代码。
- 本专题只收录基础数据结构相关问题,不包括高级数据结构及数据结构的设计,比如线段树或者 LRU 缓存,这些问题可以参考数据结构_Advanced。
二叉树的深度
二叉树的深度 - 牛客
C++
class Solution {
public:
int TreeDepth(TreeNode* root) {
if (root == NULL) return 0;
return max(TreeDepth(root->left), TreeDepth(root->right)) + 1;
}
};二叉树的宽度
思路
- 层序遍历(队列)
C++
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
if (root == nullptr)
return 0;
queue<TreeNode*> Q;
Q.push(root);
int ans = 1;
while(!Q.empty()) {
int cur_w = Q.size(); // 当前层的宽度
ans = max(ans, cur_w);
for (int i=0; i<cur_w; i++) {
auto p = Q.front();
Q.pop();
if (p->left)
Q.push(p->left);
if (p->right)
Q.push(p->right);
}
}
return ans;
}
};二叉树最大宽度(LeetCode)
LeetCode - 662. 二叉树最大宽度
问题描述
给定一个二叉树,编写一个函数来获取这个树的最大宽度。
树的宽度是所有层中的最大宽度。
这个二叉树与满二叉树(full binary tree)结构相同,但一些节点为空。
每一层的宽度被定义为两个端点(该层最左和最右的非空节点,两端点间的null节点也计入长度)之间的长度。
示例 1:
输入:
1
/ \
3 2
/ \ \
5 3 9
输出: 4
解释: 最大值出现在树的第 3 层,宽度为 4 (5,3,null,9)。
示例 2:
输入:
1
/
3
/ \
5 3
输出: 2
解释: 最大值出现在树的第 3 层,宽度为 2 (5,3)。思路
- 本题在二叉树宽度的基础上加入了满二叉树的性质,即每层都有 2 ^ (n-1)个节点。某节点的左孩子的标号是2n, 右节点的标号是2n + 1。
- 注:如果在循环中会增删容器中的元素,则不应该在
for循环中使用size()方法,该方法的返回值会根据容器的内容动态改变。
C++
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
if (root == nullptr)
return 0;
deque<pair<TreeNode*, int>> Q; // 记录节点及其在满二叉树中的位置
Q.push_back({ root, 1 });
int ans = 0;
while (!Q.empty()) {
int cur_n = Q.size();
int cur_w = Q.back().second - Q.front().second + 1; // 当前层的宽度
ans = max(ans, cur_w);
//for (int i = 0; i<Q.size(); i++) { // err: Q.size() 会动态改变
for (int i = 0; i<cur_n; i++) {
auto p = Q.front();
Q.pop_front();
if (p.first->left != nullptr)
Q.push_back({ p.first->left, p.second * 2 });
if (p.first->right != nullptr)
Q.push_back({ p.first->right, p.second * 2 + 1 });
}
}
return ans;
}
};二叉树中的最长路径
思路
- 基于二叉树的深度
- 对任一子树而言,则经过该节点的一条最长路径为其
左子树的深度 + 右子树的深度 + 1 - 遍历树中每个节点的最长路径,其中最大的即为整个树的最长路径
为什么最长路径不一定是经过根节点的那条路径?
判断平衡二叉树 TODO
判断树 B 是否为树 A 的子结构
树的子结构 - 牛客
题目描述
输入两棵二叉树A,B,判断B是不是A的子结构。
约定空树不是任意一个树的子结构。- 图示
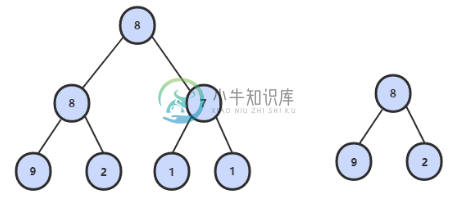
思路
- 递归
- 有两个递归的点:一、递归寻找树 A 中与树 B 根节点相同的子节点;二、递归判断子结构是否相同
Code(递归)
class Solution {
public:
bool HasSubtree(TreeNode* p1, TreeNode* p2) {
if (p1 == nullptr || p2 == nullptr) // 约定空树不是任意一个树的子结构
return false;
return isSubTree(p1, p2) // 判断子结构是否相同
|| HasSubtree(p1->left, p2) // 递归寻找树 A 中与树 B 根节点相同的子节点
|| HasSubtree(p1->right, p2);
}
bool isSubTree(TreeNode* p1, TreeNode* p2) {
if (p2 == nullptr) return true; // 注意这两个判断的顺序
if (p1 == nullptr) return false;
if (p1->val == p2->val)
return isSubTree(p1->left, p2->left) // 递归判断左右子树
&& isSubTree(p1->right, p2->right);
else
return false;
}
};利用前序和中序重建二叉树
重建二叉树 - 牛客
题目描述
根据二叉树的前序遍历和中序遍历的结果,重建出该二叉树。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。思路
前序遍历的第一个值为根节点的值,使用这个值将中序遍历结果分成两部分,左部分为左子树的中序遍历结果,右部分为右子树的中序遍历的结果。
根据左右子树的长度,可以从前序遍历的结果中划分出左右子树的前序遍历结果
接下来就是递归过程
注意:必须序列中的值不重复才可以这么做
示例
前序 1,2,4,7,3,5,6,8 中序 4,7,2,1,5,3,8,6 第一层 根节点 1 根据根节点的值(不重复),划分中序: {4,7,2} 和 {5,3,8,6} 根据左右子树的长度,划分前序: {2,4,7} 和 {3,5,6,8} 从而得到左右子树的前序和中序 左子树的前序和中序:{2,4,7}、{4,7,2} 右子树的前序和中序:{3,5,6,8}、{5,3,8,6} 第二层 左子树的根节点 2 右子树的根节点 3 ...
Code(Python)
C++ 版本 > 题解-剑指Offer/重建二叉树
# class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: # 返回构造的TreeNode根节点 def reConstructBinaryTree(self, pre, tin): if len(pre) < 1: return None
root = TreeNode(pre[0])
index = tin.index(root.val) # 注意值不重复,才可以这么做
root.left = self.reConstructBinaryTree(pre[1: 1+index], tin[:index])
root.right = self.reConstructBinaryTree(pre[1+index:], tin[index+1:])
return root
## 二叉树的序列化与反序列化
> [序列化二叉树](https://www.nowcoder.com/practice/cf7e25aa97c04cc1a68c8f040e71fb84?tpId=13&tqId=11214&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking) - NowCoder
**题目描述**请实现两个函数,分别用来序列化和反序列化二叉树。 接口如下:
char* Serialize(TreeNode *root);
TreeNode* Deserialize(char *str);空节点用 '#' 表示,节点之间用空格分开
- 比如中序遍历就是一个二叉树序列化
- 反序列化要求能够通过序列化的结果还原二叉树
**思路**
- 前序遍历
**Code**
```C++
class Solution {
stringstream ss_fw;
stringstream ss_bw;
public:
char* Serialize(TreeNode *root) {
dfs_fw(root);
char ret[1024];
return strcpy(ret, ss_fw.str().c_str());
// return (char*)ss.str().c_str(); // 会出问题,原因未知
}
void dfs_fw(TreeNode *node) {
if (node == nullptr) {
ss_fw << "#";
return;
}
ss_fw << node->val;
ss_fw << " ";
dfs_fw(node->left);
ss_fw << " ";
dfs_fw(node->right);
}
TreeNode* Deserialize(char *str) {
if (strlen(str) < 1) return nullptr;
ss_bw << str;
return dfs_bw();
}
TreeNode* dfs_bw() {
if (ss_bw.eof())
return nullptr;
string val; // 因为 "#",用 int 或 char 接收都会有问题
ss_bw >> val;
if (val == "#")
return nullptr;
TreeNode* node = new TreeNode{ stoi(val) };
node->left = dfs_bw();
node->right = dfs_bw();
return node;
}
};最近公共祖先
《剑指 Offer》 7.2 案例二
问题描述
给定一棵树的根节点 root,和其中的两个节点 p1 和 p2,求它们的最小公共父节点。如果树是二叉搜索树
- 找到第一个满足
p1 < root < p2的根节点,即为它们的最小公共父节点; - 如果寻找的过程中,没有这样的
root,那么p1和p2的最小公共父节点必是它们之一,此时遍历到p1或p2就返回。
如果树的节点中保存有指向父节点的指针
- 问题等价于求两个链表的第一个公共节点
如果只是普通的二叉树
236. 二叉树的最近公共祖先 - LeetCode
利用两个辅助链表/数组,保存分别到
p1和p2的路径;则
p1和p2的最小公共父节点就是这两个链表的最后一个公共节点C++
class Solution { bool getPath(TreeNode* root, TreeNode* p, deque<TreeNode*>& path) { if (root == nullptr) return false; path.push_back(root); if (p == root) return true; bool found = false; if (!found) found = getPath(root->left, p, path); if (!found) found = getPath(root->right, p, path); if (!found) path.pop_back(); return found; } public: TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { deque<TreeNode*> path_p; auto found_p = getPath(root, p, path_p); deque<TreeNode*> path_q; auto found_q = getPath(root, q, path_q); TreeNode* ret = root; if (found_p && found_q) { auto it_p = path_p.begin(); auto it_q = path_q.begin(); while (it_p != path_p.end() && it_q != path_q.end()) { if (*it_p != *it_q) return ret; ret = *it_p; it_p++, it_q++; } return ret; } return nullptr; } };
获取节点的路径
二叉树
// 未测试
#include <deque>
bool getPath(TreeNode* root, TreeNode* p, deque<TreeNode*>& path) {
if (root == nullptr)
return false;
path.push_back(root);
if (p == root)
return true;
bool found = false;
if (!found)
found = getPath(root->left, p, path);
if (!found)
found = getPath(root->right, p, path);
if (!found)
path.pop_back();
return found;
}非二叉树
// 未测试
#include <deque>
struct TreeNode {
int val;
std::vector<TreeNode*> children;
};
bool getPath(const TreeNode* root, const TreeNode* p, deque<const TreeNode*>& path) {
if (root == nullptr)
return false;
path.push_back(root);
if (root == p)
return true;
bool found = false;
auto i = root->children.begin(); // 顺序遍历每个子节点
while (!found && i < root->children.end()) {
found = GetNodePath(*i, p, path);
++i;
}
if (!found) // 如果没有找到就,说明当前节点不在路径内,弹出
path.pop_back();
return found;
}旋转链表(Rotate List)
LeetCode/61. 旋转链表
问题描述
给定一个链表,旋转链表,将链表每个节点向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL
示例 2:
输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL思路
- 双指针
l, r记录两个位置,其中l指向倒数第k+1个节点,r指向最后一个非空节点; - 然后将
r指向头结点h,h指向l的下一个节点,最后断开l与下一个节点; - 注意
k可能大于链表的长度,此时可能需要遍历两次链表
代码 1
- 比较直观的写法,代码量稍大
# class ListNode: # def __init__(self, x): # self.val = x # self.next = None
class Solution: def rotateRight(self, h, k): """ :type h: ListNode :type k: int :rtype: ListNode """ if not h or k == 0: return h
n = 1 # 记录链表的长度,因为只遍历到最后一个非空节点,所以从 1 开始
l = h
r = h # tail
while r.next is not None and k > 0:
k -= 1
n += 1
r = r.next
# print(k, n)
if k > 0:
k -= 1 # 这里要先减 1,因为 n 是从 1 开始计数的
k = k % n
r = h
while k > 0:
k -= 1
r = r.next
# 找到倒数第 k 个节点
while r.next is not None:
l = l.next
r = r.next
r.next = h
h = l.next
l.next = None
return h
**代码 2**
- 代码量少一点,但是遍历的长度要多一点。
```python
class Solution:
def rotateRight(self, h, k):
"""
:type h: ListNode
:type k: int
:rtype: ListNode
"""
if not h or k == 0:
return h
n = 1 # 记录链表的长度,因为只遍历到最后一个非空节点,所以从 1 开始
r = h # tail
while r.next is not None:
n += 1
r = r.next
r.next = h # 构成环
k %= n
t = n - k
while t > 0:
r = r.next
t -= 1
h = r.next
r.next = None # 断开 链表
return h反转链表
反转链表 - 牛客
题目描述
输入一个链表,反转链表后,输出新链表的表头。- 要求:不使用额外空间
思路
- 辅助图示思考
Code(迭代)
class Solution {
public:
ListNode * ReverseList(ListNode* head) {
if (head == nullptr)
return nullptr;
ListNode* cur = head; // 当前节点
ListNode* pre = nullptr; // 前一个节点
ListNode* nxt = cur->next; // 下一个节点
cur->next = nullptr; // 断开当前节点及下一个节点(容易忽略的一步)
while (nxt != nullptr) {
pre = cur; // 把前一个节点指向当前节点
cur = nxt; // 当前节点向后移动
nxt = nxt->next; // 下一个节点向后移动
cur->next = pre; // 当前节点的下一个节点指向前一个节点
}
return cur;
}
};Code(递归)
class Solution {
public:
ListNode * ReverseList(ListNode* head) {
if (head == nullptr || head->next == nullptr)
return head;
auto nxt = head->next;
head->next = nullptr; // 断开当前节点及下一个节点
auto new_head = ReverseList(nxt);
nxt->next = head;
return new_head;
}
};合并排序链表
合并两个排序的链表 - 牛客
问题描述
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。迭代
class Solution {
public:
ListNode* Merge(ListNode* p1, ListNode* p2) {
if (p1 == nullptr) return p2;
if (p2 == nullptr) return p1;
// 选择头节点
ListNode* head = nullptr;
if (p1->val <= p2->val) {
head = p1;
p1 = p1->next;
} else {
head = p2;
p2 = p2->next;
}
auto cur = head;
while (p1 && p2) {
if (p1->val <= p2->val) {
cur->next = p1;
p1 = p1->next;
} else {
cur->next = p2;
p2 = p2->next;
}
cur = cur->next;
}
// 别忘了拼接剩余部分
// if (p1) cur->next = p1;
// if (p2) cur->next = p2;
if (p1) {
cur->next = p1;
} else if (p2) {
cur->next = p2;
} else {
cur->next = nullptr;
}
return head;
}
};递归
class Solution {
public:
ListNode* Merge(ListNode* p1, ListNode* p2){
if (!p1) return p2;
if (!p2) return p1;
if (p1->val <= p2->val) {
p1->next = Merge(p1->next, p2);
return p1;
} else {
p2->next = Merge(p1, p2->next);
return p2;
}
}
};两个链表的第一个公共节点
思路 1
先求出两个链表的长度
l1和l2,然后让长的链表先走|l1-l2|步,此时两个指针距离第一个公共节点的距离相同,再走相同的步数即可在第一个公共节点相遇时间复杂度
O(m + n)代码(未测试)
ListNode* FindFirstCommonNode(ListNode *pHead1, ListNode *pHead2) { ListNode *back1 = nullptr; int l1 = GetListLength(pHead1, back1); // 返回链表的长度及尾节点指针 ListNode *back2 = nullptr; int l2 = GetListLength(pHead2, back2); if (back1 != back2) // 没有公共节点 return nullptr; ListNode *p1 = pHead1; ListNode *p2 = pHead2; if (l1 > l2) { int d = l1 - l2; while (d--) p1 = p1->next; while (p1 != p2) { p1 = p1->next; p2 = p2->next; } } else { int d = l2 - l1; while (d--) p2 = p2->next; while (p1 != p2) { p1 = p1->next; p2 = p2->next; } } return p1;
思路 2
两个指针同时开始遍历,
当其中一个指针到达尾节点时,转到另一个链表继续遍历;
当另一个指针也到达尾节点时,也转到另一个链表继续遍历;
此时两个指针距离第一个公共节点的距离相同,再走相同的步数即可在第一个公共节点相遇
时间复杂度
O(m + n)代码(未测试)
ListNode* FindFirstCommonNode(ListNode *pHead1, ListNode *pHead2) { ListNode *back1 = nullptr; GetListLength(pHead1, back1); // 获取尾节点指针 ListNode *back2 = nullptr; GetListLength(pHead2, back2); if (back1 != back2) // 没有公共节点 return nullptr; ListNode *p1 = pHead1; ListNode *p2 = pHead2; while(p1!=p2){ p1 = (p1==NULL ? pHead2 : p1->next); // 游标到达尾部后,转到另一条链表 p2 = (p2==NULL ? pHead1 : p2->next); } return p1;
链表排序
链表快排
LeetCode/148. 排序链表
问题描述
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5思路
- 与数组快排几乎一致,只是 partition 操作需要从左向右遍历;
- 因为涉及指针,还是用 C++ 写比较方便;
- 另外 LeetCode 讨论区反映 Python 可能会超时;
- 时间复杂度:最好
O(NlogN),最坏O(N^2)
代码 1 - 只交换节点内的值
- 参考数组快排中的写法,这里选取第一个元素作为枢纽
/**
- Definition for singly-linked list.
- struct ListNode {
- int val;
- ListNode *next;
- ListNode(int x) : val(x), next(NULL) {}
- }; */
class Solution {
void qsort(ListNode* lo, ListNode* hi) {
if (lo == hi || lo->next == hi) // 至少有一个元素
return;
auto mid = partition(lo, hi);
qsort(lo, mid);
qsort(mid->next, hi);
}
ListNode* partition(ListNode* lo, ListNode* hi) { // 链表范围为 [lo, hi)
int key = lo->val; // 以 low 作为枢纽
auto mid = lo;
for (auto i=lo->next; i != hi; i = i->next) {
if (i->val < key) {
mid = mid->next;
swap(i->val, mid->val); // 交换节点内的值
}
}
swap(lo->val, mid->val); // 交换 low 与 mid
return mid;
}public: ListNode sortList(ListNode head) { if (head == nullptr || head->next == nullptr) return head;
qsort(head, nullptr); // 传入首尾区间,是一个半开区间
return head;
}};
**代码 2 - 交换节点**
- ~~需要要重写 `swap`,而且注意,因为是链表,所以传入的节点应该是需要交换节点的前置节点~~
- 依然选择第一个节点作为枢纽;然后把小于枢纽的节点放到一个链中,不小于枢纽的及节点放到另一个链中,最后拼接两条链以及枢纽。
```C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
void qsort(ListNode* pre, ListNode* lo, ListNode* hi) { // 链表范围为 [lo, hi), pre 为 lo 的前置节点
if (lo == hi || lo->next == hi) // 至少有一个元素
return;
auto mid = partition(pre, lo, hi);
qsort(pre, pre->next, mid); // qsort(pre, lo, mid);
qsort(mid, mid->next, hi);
}
ListNode* partition(ListNode* pre, ListNode* lo, ListNode* hi) {
int key = lo->val;
auto mid = lo; // 不是必须的,直接使用 lo 也可以
ListNode ll(0), rr(0); // 创建两个新链表
auto l = &ll, r = &rr; // ListNode *l = &ll, *r = &rr;
for (auto i=lo->next; i != hi; i = i->next) { // i 从 lo 的下一个节点开始遍历,因为 lo 是枢纽不参与遍历
if (i->val < key) {
l = l->next = i; // python 中不能这么写
} else {
r = r->next = i; // python 中不能这么写
}
}
// 拼接
r->next = hi;
l->next = mid; // 这里的 mid 实际上就是 lo,即 l->next = lo
mid->next = rr.next;
pre->next = ll.next;
return mid; // 返回中枢
}
public:
ListNode* sortList(ListNode* head) {
if(head == nullptr || head->next == nullptr)
return head;
ListNode pre(0); // 设置一个新的头结点
pre.next = head;
qsort(&pre, head, nullptr);
return pre.next;
}
};链表归并
LeetCode/148. 排序链表
问题描述
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5思路
- 用快慢指针的方法找到链表中间节点,然后递归的对两个子链表排序,把两个排好序的子链表合并成一条有序的链表
- 归并排序比较适合链表,它可以保证了最好和最坏时间复杂度都是
O(NlogN),而且它在数组排序中广受诟病的空间复杂度在链表排序中也从O(n)降到了O(1)- 因为链表快排中只能使用第一个节点作为枢纽,所以不能保证时间复杂度
- 还是使用 C++
- 时间复杂度:最好/最坏
O(NlogN)
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
ListNode* merge(ListNode *h1, ListNode *h2) { // 排序两个链表
if (h1 == nullptr) return h2;
if (h2 == nullptr) return h1;
ListNode* h; // 合并后的头结点
if (h1->val < h2->val) {
h = h1;
h1 = h1->next;
} else {
h = h2;
h2 = h2->next;
}
ListNode* p = h;
while (h1 && h2) {
if (h1->val < h2->val) {
p->next = h1;
h1 = h1->next;
} else {
p->next = h2;
h2 = h2->next;
}
p = p->next;
}
if (h1) p->next = h1;
if (h2) p->next = h2;
return h;
}
public:
ListNode* sortList(ListNode* h) {
if (h == nullptr || h->next == nullptr)
return h;
auto f = h, s = h; // 快慢指针 fast & slow
while (f->next && f->next->next) {
f = f->next->next;
s = s->next;
}
f = s->next; // 中间节点
s->next = nullptr; // 断开
h = sortList(h); // 前半段排序
f = sortList(f); // 后半段排序
return merge(h, f);
}
};链表插入排序
LeetCode/147. 对链表进行插入排序
注意:以下代码在148. 排序链表也能 AC(要求时间复杂度
O(NlogN))
问题描述
对链表进行插入排序。
插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
重复直到所有输入数据插入完为止。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5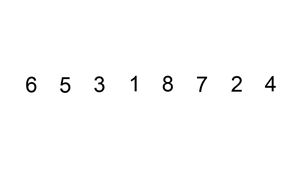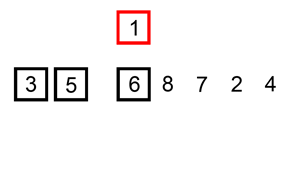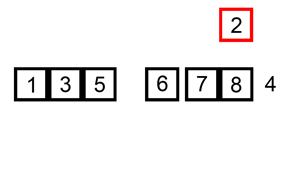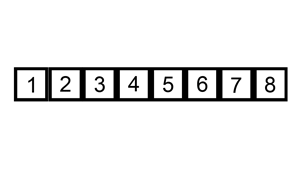
- 插入排序的动画演示如上。从第一个元素开始,该链表可以被认为已经部分排序(用黑色表示)。 每次迭代时,从输入数据中移除一个元素(用红色表示),并原地将其插入到已排好序的链表中。
思路
- 见代码注释
- 时间复杂度:最好/最坏
O(N^2)
代码 1 - 非原地
实际上,对链表来说,不存在是否原地的问题,不像数组
这里所谓的非原地是相对数组而言的,因此下面的代码只针对链表,不适用于数组。
class Solution { public: ListNode* insertionSortList(ListNode* h) { if (h == nullptr || h->next == nullptr) return h; // 因为是链表,所以可以重新开一个新的链表来保存排序好的部分; // 不存在空间上的问题,这一点不像数组 auto H = new ListNode(0); auto pre = H; auto cur = h; ListNode* nxt; while (cur) { while (pre->next && pre->next->val < cur->val) { pre = pre->next; } nxt = cur->next; // 记录下一个要遍历的节点 // 把 cur 插入 pre 和 pre->next 之间 cur->next = pre->next; pre->next = cur; // 重新下一轮 pre = H; cur = nxt; } h = H->next; delete H; return h; } };
代码 2 - 原地
即不使用新链表,逻辑与数组一致;
此时链表拼接的逻辑会复杂一些
class Solution { public: ListNode* insertionSortList(ListNode* h) { if (h == nullptr || h->next == nullptr) return h; auto beg = new ListNode(0); beg->next = h; auto end = h; // (beg, end] 指示排好序的部分 auto p = h->next; // 当前待排序的节点 while (p) { auto pre = beg; auto cur = beg->next; // p 将插入到 pre 和 cur 之间 while (cur != p && p->val >= cur->val) { cur = cur->next; pre = pre->next; } if (cur == p) { end = p; } else { end->next = p->next; p->next = cur; pre->next = p; } p = end->next; } h = beg->next; delete beg; return h; } };
链表选择排序
LeetCode/147. 对链表进行插入排序
注意:以下代码在148. 排序链表也能 AC(要求时间复杂度
O(NlogN))
思路
- 见代码注释
- 时间复杂度:最好/最坏
O(N^2)
C++
class Solution {
public:
ListNode* sortList(ListNode* h) {
if (h == nullptr || h->next == nullptr)
return h;
auto H = new ListNode(0); // 为了操作方便,添加一个头结点
H->next = h;
auto s = h; // 指向已经排好序的尾部
ListNode* m; // 指向未排序部分的最小节点 min
ListNode* p; // 迭代器
while (s->next) {
m = s;
p = s->next;
while (p) { // 寻找剩余部分的最小节点
if (p->val < m->val)
m = p;
p = p->next;
}
swap(s->val, m->val); // 交换节点内的值
s = s->next;
}
h = H->next;
delete H;
return h;
}
};链表冒泡排序
LeetCode/147. 对链表进行插入排序
思路
- 见代码注释
- 时间复杂度:最好
O(N),最坏O(N^2)
C++
以下代码不能 AC 148. 排序链表
class Solution { public: ListNode* insertionSortList(ListNode* h) { if (h == nullptr || h->next == nullptr) return h; ListNode* q = nullptr; // 开始时指向尾节点 ListNode* p; // 迭代器 bool changed = true; while (q != h->next && changed) { changed = false; p = h; // 把大的元素“冒泡”到尾部去 while (p->next && p->next != p) { if (p->val > p->next->val) { // 如果已经有序,则退出循环 swap(p->val, p->next->val); changed = true; } p = p->next; } q = p; } return h; } };
二分查找
搜索二维矩阵 1
LeetCode - 74. 搜索二维矩阵
问题描述
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
示例 1:
输入:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 3
输出: true思路
- 当做一维有序数组二分查找
C++
class Solution {
public:
bool searchMatrix(vector<vector<int>>& M, int t) {
if (M.size() < 1 || M[0].size() < 1)
return false;
int m = M.size();
int n = M[0].size();
int lo = 0;
int hi = m * n;
while (lo + 1 < hi) {
int mid = lo + (hi - lo) / 2;
if (M[mid / n][mid % n] > t) {
hi = mid;
} else {
lo = mid;
}
}
return M[lo / n][lo % n] == t;
}
};搜索二维矩阵 2
LeetCode - 240. 搜索二维矩阵 II
思路
- 1)从右上角开始查找,时间复杂度
O(M+N) - 2)每一行二分查找,时间复杂度
O(MlogN)
class Solution {
public:
bool searchMatrix(vector<vector<int>>& M, int t) {
if (M.size() < 1 || M[0].size() < 1)
return false;
auto m = M.size();
auto n = M[0].size();
int row = 0;
int col = n - 1;
while(row <= m - 1 && col >= 0) {
if (M[row][col] < t)
row++;
else if (M[row][col] > t)
col--;
else
return true;
}
return false;
}
};打印二维数组
回形打印
蛇形打印
堆的调整(自上而下)
用两个栈模拟队列
用两个栈实现队列 - 牛客
题目描述
用两个栈来实现一个队列,完成队列的 Push 和 Pop 操作。思路
- 假设
stack_in用于处理入栈操作,stack_out用于处理出栈操作 stack_in按栈的方式正常处理入栈数据;- 关键在于出栈操作
- 当
stack_out为空时,需要先将每个stack_in中的数据出栈后压入stack_out - 反之,每次弹出
stack_out栈顶元素即可
- 当
Code(C++)
class Solution {
stack<int> stack_in;
stack<int> stack_out;
public:
void push(int node) {
stack_in.push(node);
}
int pop() {
if(stack_out.size() <= 0) {
while (stack_in.size() > 0) {
auto tmp = stack_in.top();
stack_in.pop();
stack_out.push(tmp);
}
}
auto ret = stack_out.top();
stack_out.pop();
return ret;
}
};
