10.1 斐波那契数列

题目链接

NowCoder

题目描述

求斐波那契数列的第 n 项，n <= 39。

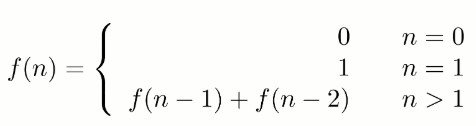
解题思路

如果使用递归求解，会重复计算一些子问题。例如，计算 f(4) 需要计算 f(3) 和 f(2)，计算 f(3) 需要计算 f(2) 和 f(1)，可以看到 f(2) 被重复计算了。

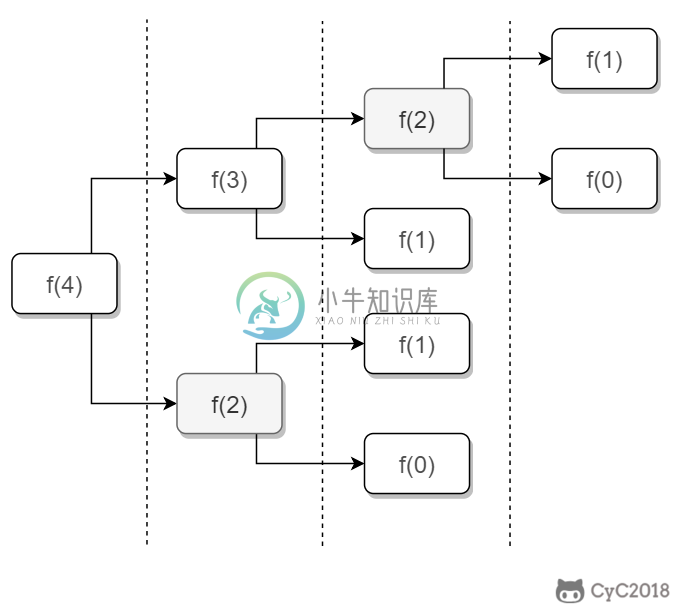
递归是将一个问题划分成多个子问题求解，动态规划也是如此，但是动态规划会把子问题的解缓存起来，从而避免重复求解子问题。

// java
public int Fibonacci(int n) {
    if (n <= 1)="" return="" n;="" int[]="" fib="new" int[n="" +="" 1];="" fib[1]="1;" for="" (int="" i="2;" 

考虑到第 i 项只与第 i-1 和第 i-2 项有关，因此只需要存储前两项的值就能求解第 i 项，从而将空间复杂度由 O(N) 降低为 O(1)。
// java
public int Fibonacci(int n) {
    if (n <= 1)="" return="" n;="" int="" pre2="0," pre1="1;" fib="0;" for="" (int="" i="2;" 

由于待求解的 n 小于 40，因此可以将前 40 项的结果先进行计算，之后就能以 O(1) 时间复杂度得到第 n 项的值。
// java
public class Solution {

    private int[] fib = new int[40];

    public Solution() {
        fib[1] = 1;
        for (int i = 2; i < fib.length; i++)
            fib[i] = fib[i - 1] + fib[i - 2];
    }

    public int Fibonacci(int n) {
        return fib[n];
    }
}