二分搜索树深度优先遍历

精华

小牛编辑

139浏览

2023-03-14

二分搜索树遍历分为两大类，深度优先遍历和层序遍历。

深度优先遍历分为三种：先序遍历（preorder tree walk）、中序遍历（inorder tree walk）、后序遍历（postorder tree walk），分别为：

1、前序遍历：先访问当前节点，再依次递归访问左右子树。
2、中序遍历：先递归访问左子树，再访问自身，再递归访问右子树。
3、后序遍历：先递归访问左右子树，再访问自身节点。

前序遍历结果图示：

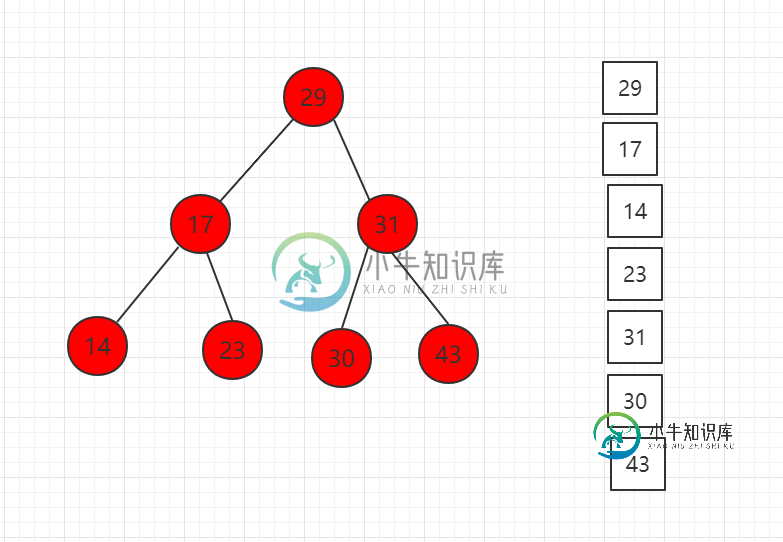
对应代码示例：

...
// 对以node为根的二叉搜索树进行前序遍历, 递归算法
private void preOrder (Node node ) {

if ( node != null ) {
System. out. println (node. key ) ;
preOrder (node. left ) ;
preOrder (node. right ) ;
}
}
...

中序遍历结果图示：

对应代码示例：

...
// 对以node为根的二叉搜索树进行中序遍历, 递归算法
private void inOrder (Node node ) {

if ( node != null ) {
inOrder (node. left ) ;
System. out. println (node. key ) ;
inOrder (node. right ) ;
}
}
...

后序遍历结果图示：

对应代码示例：

...
// 对以node为根的二叉搜索树进行后序遍历, 递归算法
private void postOrder (Node node ) {

if ( node != null ) {
postOrder (node. left ) ;
postOrder (node. right ) ;
System. out. println (node. key ) ;
}
}
...

Java 实例代码

src/binary/Traverse.java 文件代码：

package binary ;

/**
* 优先遍历
*/

public class Traverse < Key extends Comparable <Key >, Value > {

// 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
private class Node {
private Key key ;
private Value value ;
private Node left, right ;

public Node ( Key key, Value value ) {
this. key = key ;
this. value = value ;
left = right = null ;
}
}

private Node root ; // 根节点
private int count ; // 树种的节点个数

// 构造函数, 默认构造一棵空二分搜索树
public Traverse ( ) {
root = null ;
count = 0 ;
}

// 返回二分搜索树的节点个数
public int size ( ) {
return count ;
}

// 返回二分搜索树是否为空
public boolean isEmpty ( ) {
return count == 0 ;
}

// 向二分搜索树中插入一个新的(key, value)数据对
public void insert ( Key key, Value value ) {
root = insert (root, key, value ) ;
}

// 查看二分搜索树中是否存在键key
public boolean contain ( Key key ) {
return contain (root, key ) ;
}

// 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
public Value search ( Key key ) {
return search ( root , key ) ;
}

// 二分搜索树的前序遍历
public void preOrder ( ) {
preOrder (root ) ;
}

// 二分搜索树的中序遍历
public void inOrder ( ) {
inOrder (root ) ;
}

// 二分搜索树的后序遍历
public void postOrder ( ) {
postOrder (root ) ;
}

//********************
//* 二分搜索树的辅助函数
//********************

// 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
// 返回插入新节点后的二分搜索树的根
private Node insert (Node node, Key key, Value value ) {

if ( node == null ) {
count ++;
return new Node (key, value ) ;
}

if ( key. compareTo (node. key ) == 0 )
node. value = value ;
else if ( key. compareTo (node. key ) < 0 )
node. left = insert ( node. left , key, value ) ;
else // key > node->key
node. right = insert ( node. right, key, value ) ;

return node ;
}

// 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
private boolean contain (Node node, Key key ) {

if ( node == null )
return false ;

if ( key. compareTo (node. key ) == 0 )
return true ;
else if ( key. compareTo (node. key ) < 0 )
return contain ( node. left , key ) ;
else // key > node->key
return contain ( node. right , key ) ;
}

// 在以node为根的二分搜索树中查找key所对应的value, 递归算法
// 若value不存在, 则返回NULL
private Value search (Node node, Key key ) {

if ( node == null )
return null ;

if ( key. compareTo (node. key ) == 0 )
return node. value ;
else if ( key. compareTo (node. key ) < 0 )
return search ( node. left , key ) ;
else // key > node->key
return search ( node. right, key ) ;
}

// 对以node为根的二叉搜索树进行前序遍历, 递归算法
private void preOrder (Node node ) {

if ( node != null ) {
System. out. println (node. key ) ;
preOrder (node. left ) ;
preOrder (node. right ) ;
}
}

// 对以node为根的二叉搜索树进行中序遍历, 递归算法
private void inOrder (Node node ) {

if ( node != null ) {
inOrder (node. left ) ;
System. out. println (node. key ) ;
inOrder (node. right ) ;
}
}

// 对以node为根的二叉搜索树进行后序遍历, 递归算法
private void postOrder (Node node ) {

if ( node != null ) {
postOrder (node. left ) ;
postOrder (node. right ) ;
System. out. println (node. key ) ;
}
}
}