BF算法(串模式匹配算法)
精华
小牛编辑
280浏览
2023-03-14
串的模式匹配算法,通俗地理解,是一种用来判断两个串之间是否具有"主串与子串"关系的算法。
主串与子串:如果串 A(如 "shujujiegou")中包含有串 B(如 "ju"),则称串 A 为主串,串 B 为子串。主串与子串之间的关系可简单理解为一个串 "包含" 另一个串的关系。
实现串的模式匹配的算法主要有以下两种:
本节,先来学习 普通模式匹配(BF)算法的实现。
例如,使用普通模式匹配算法判断串 A("abcac")是否为串 B("ababcabacabab")子串的判断过程如下:
首先,将串 A 与串 B 的首字符对齐,然后逐个判断相对的字符是否相等,如图 1 所示:
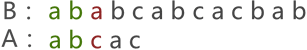
图 1 串的第一次模式匹配示意图
图 1 中,由于串 A 与串 B 的第 3 个字符匹配失败,因此需要将串 A 后移一个字符的位置,继续同串 B 匹配,如图 2 所示:
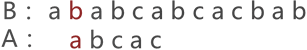
图 2 串的第二次模式匹配示意图
图 2 中可以看到,两串匹配失败,串 A 继续向后移动一个字符的位置,如图 3 所示:
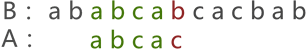
图 3 串的第三次模式匹配示意图
图 3 中,两串的模式匹配失败,串 A 继续移动,一直移动至图 4 的位置才匹配成功:

图 4 串模式匹配成功示意图
由此,串 A 与串 B 以供经历了 6 次匹配的过程才成功,通过整个模式匹配的过程,证明了串 A 是串 B 的子串(串 B 是串 A 的主串)。
接下来,我们要编写代码实现两个串的模式匹配(图 1 ~图 4)。
BF 算法最坏情况的时间复杂度为
主串与子串:如果串 A(如 "shujujiegou")中包含有串 B(如 "ju"),则称串 A 为主串,串 B 为子串。主串与子串之间的关系可简单理解为一个串 "包含" 另一个串的关系。
实现串的模式匹配的算法主要有以下两种:
- 普通的模式匹配算法;
- 快速模式匹配算法;
本节,先来学习 普通模式匹配(BF)算法的实现。
BF算法原理
普通模式匹配算法,其实现过程没有任何技巧,就是简单粗暴地拿一个串同另一个串中的字符一一比对,得到最终结果。例如,使用普通模式匹配算法判断串 A("abcac")是否为串 B("ababcabacabab")子串的判断过程如下:
首先,将串 A 与串 B 的首字符对齐,然后逐个判断相对的字符是否相等,如图 1 所示:
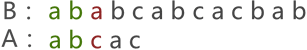
图 1 串的第一次模式匹配示意图
图 1 中,由于串 A 与串 B 的第 3 个字符匹配失败,因此需要将串 A 后移一个字符的位置,继续同串 B 匹配,如图 2 所示:
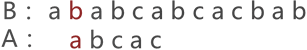
图 2 串的第二次模式匹配示意图
图 2 中可以看到,两串匹配失败,串 A 继续向后移动一个字符的位置,如图 3 所示:
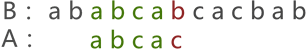
图 3 串的第三次模式匹配示意图
图 3 中,两串的模式匹配失败,串 A 继续移动,一直移动至图 4 的位置才匹配成功:

图 4 串模式匹配成功示意图
由此,串 A 与串 B 以供经历了 6 次匹配的过程才成功,通过整个模式匹配的过程,证明了串 A 是串 B 的子串(串 B 是串 A 的主串)。
接下来,我们要编写代码实现两个串的模式匹配(图 1 ~图 4)。
BF算法实现
BF 算法的实现思想是:将用户指定的两个串 A 和串 B,使用串的定长 顺序存储结构存储起来,然后循环实现两个串的模式匹配过程,C 语言实现代码如下:
#include <stdio.h>
#include <string.h>
//串普通模式匹配算法的实现函数,其中 B是伪主串,A是伪子串
int mate(char * B,char *A){
int i=0,j=0;
while (i<strlen(B) && j<strlen(A)) {
if (B[i]==A[j]) {
i++;
j++;
}else{
i=i-j+1;
j=0;
}
}
//跳出循环有两种可能,i=strlen(B)说明已经遍历完主串,匹配失败;j=strlen(A),说明子串遍历完成,在主串中成功匹配
if (j==strlen(A)) {
return i-strlen(A)+1;
}
//运行到此,为i==strlen(B)的情况
return 0;
}
int main() {
int number=mate("ababcabcacbab", "abcac");
printf("%d",number);
return 0;
} 程序运行结果:
6
注意,在实现过程中,我们借助 i-strlen(A)+1 就可以得到成功模式匹配所用的次数,也就是串 A 移动的总次数。BF算法时间复杂度
该算法最理想的时间复杂度O(n),n 表示串 A 的长度,即第一次匹配就成功。
BF 算法最坏情况的时间复杂度为
O(n*m),n 为串 A 的长度,m 为串 B 的长度。例如,串 B 为 "0000000001",而串 A 为 "01",这种情况下,两个串每次匹配,都必须匹配至串 A 的最末尾才能判断匹配失败,因此运行了 n*m 次。
