Javascript中的广度优先搜索遍历
BFS在访问子顶点之前先访问邻居顶点,并且在搜索过程中使用队列。以下是BFS的工作方式-
访问相邻的未访问顶点。将其标记为已访问。显示它。将其插入队列。
如果找不到相邻的顶点,请从队列中删除第一个顶点。
重复规则1和规则2,直到队列为空。
让我们看一下BFS遍历如何工作的图示:
|
步
|
遍历
|
描述
|
|---|---|---|
|
1
|
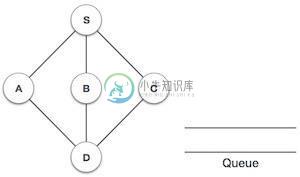
|
初始化队列。
|
|
2
|

|
我们首先访问
S(起始节点)并将其标记为已访问。
|
|
3
|

|
然后,我们看到一个来自
S的未访问的相邻节点
。在此示例中,我们有三个节点,但按字母顺序选择
A,将其标记为已访问并排队。
|
|
4
|

|
接下来,S中未访问的相邻节点是B,我们将其标记为已访问并对其进行排队。 |
|
5
|

|
接下来,S中未访问的相邻节点是C,我们将其标记为已访问并将其排队。 |
|
6
|

|
现在,
S不再有未访问的相邻节点。所以,我们出队,并找到
一个。
|
|
7
|

|
在
A中,我们将
D 作为未访问的相邻节点。我们将其标记为已访问并入队。
|
在这一阶段,我们没有未标记(未访问)的节点。但是按照算法,我们继续进行出队以获取所有未访问的节点。清空队列后,程序结束。
让我们看一下如何在JavaScript中实现它。
示例
BFS(node) {
//创建一个队列并在其中添加我们的初始节点
let q = new Queue(this.nodes.length);
let explored = new Set();
q.enqueue(node);
//将第一个节点标记为已探索。
add(node);
//我们将继续直到队列变空
while (!q.isEmpty()) {
let t = q.dequeue();
//记录从队列中出来的每个元素
console.log(t);
//1.在edges对象中,我们搜索该节点直接连接到的节点。
//2.我们过滤掉已经探索过的节点。
//3.然后,我们将每个未探索的节点标记为已探索,并将其添加到队列中。
this.edges[t]
.filter(n => !explored.has(n))
.forEach(n => {
explored.add(n);
q.enqueue(n);
});
}
}
您可以使用-测试此功能
示例
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C");
g.addEdge("A", "B");
g.addEdge("A", "D");
g.addEdge("D", "E");
g.addEdge("E", "F");
g.addEdge("B", "G");
g.BFS("A");
输出结果
这将给出输出-
A C B D G E F
-
主要内容:深度优先搜索(简称“深搜”或DFS),广度优先搜索,总结前边介绍了有关图的 4 种存储方式,本节介绍如何对存储的图中的顶点进行遍历。常用的遍历方式有两种: 深度优先搜索和 广度优先搜索。 深度优先搜索(简称“深搜”或DFS) 图 1 无向图 深度优先搜索的过程类似于树的先序遍历,首先从例子中体会深度优先搜索。例如图 1 是一个无向图,采用深度优先算法遍历这个图的过程为: 首先任意找一个未被遍历过的顶点,例如从 V1 开始,由于 V1 率先访问过了,所以
-
我正在研究BFS算法,我有一个关于如何将相邻节点插入队列的问题。 例如,假设我们正在处理一个无向图,我们希望执行BFS来输出图的内容,那么我们如何知道在从队列中取出一个初始节点后,相邻节点以什么顺序插入到队列中呢?还有,有没有办法修改邻居节点插入队列的方式? 任何帮助都将不胜感激,谢谢。
-
我有一个无向连通图。我使用邻接矩阵实现了它,它是一个2维数组。 据我所知,DFS在兄弟节点之前访问子节点。BFS先于孩子探望兄弟姐妹。 这两个我是这样实现的: 如果让我执行一个从D到E的DFS,是D、C、a、E还是D、E。我以为DFS和BFS必须访问每个节点,在这种情况下B不能访问。我不知道我应该如何改变我目前的方法来满足这些要求。
-
本文向大家介绍什么是广度优先搜索?相关面试题,主要包含被问及什么是广度优先搜索?时的应答技巧和注意事项,需要的朋友参考一下 类似树的按层遍历,其过程为:首先访问初始点Vi,并将其标记为已访问过,接着访问Vi的所有未被访问过可到达的邻接点Vi1、Vi2……Vit,并均标记为已访问过,然后再按照Vi1、Vi2……Vit的次序,访问每一个顶点的所有未被访问过的邻接点,并均标记为已访问过,依此类推,直到图
-
在继续使用其他图算法之前,让我们分析广度优先搜索算法的运行时性能。首先要观察的是,对于图中的每个顶点 $$|V|$$ 最多执行一次 while 循环。因为一个顶点必须是白色,才能被检查和添加到队列。这给出了用于 while 循环的 $$O(V)$$。嵌套在 while 内部的 for 循环对于图中的每个边执行最多一次,$$|E|$$。原因是每个顶点最多被出列一次,并且仅当节点 u 出队时,我们才检
-
通过构建图,我们现在可以将注意力转向我们将使用的算法来找到字梯问题的最短解。我们将使用的图算法称为“宽度优先搜索”算法。宽度优先搜索(BFS)是用于搜索图的最简单的算法之一。它也作为几个其他重要的图算法的原型,我们将在以后研究。 给定图 G 和起始顶点 s,广度优先搜索通过探索图中的边以找到 G 中的所有顶点,其中存在从 s 开始的路径。通过广度优先搜索,它找到和 s 相距 k 的所有顶点,然后找

