12.9 HTML 画布几何变换

到现在为止，你在画布中绘制的所有元素都是按照它应该出现的样子绘制的。例如，矩形是按照fillRect方法定义的位置和尺寸绘制的，并且它是用水平和垂直的线条绘制的，平淡无奇。但是，如果你想要画一些奇特的图形呢？如果想要旋转一个矩形呢？如果想要缩放图形呢？2D渲染上下文的变形功能能够帮助你实现所有这样的操作。它们支持的功能是非常强大的。

平移

最基本的操作就是平移，即将2D渲染上下文的原点从一个位置移动到另一个位置。在画布中进行平移使用的是translate方法时，实际上它移动的是2D渲染上下文的坐标原点，而不是所绘制的对象（参见图1）。

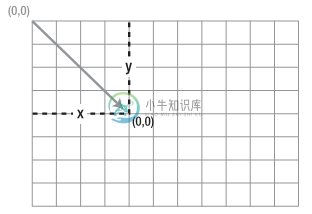
Translate方法的调用方式如下：

context.translate(150, 150); 

两个参数是（x，y）坐标值，表示把2D渲染上下文的原点移动多远．一定要注意，将来你所指定（x，y）坐标值会加上原点的平移，原点最初的默认值是(0，0)。例如，如果执行两次与上面例子完全相同的平移，那么实际上是将原点在x轴方向移动300个单位(0+150+150)，在y轴方向也移动300个单位(0+150+150)。

通过移动2D渲染上下文的原点，画布中的所有对象都将移动相应的距离：

context.fillRect(150, 150, 100, 100);
    context.translate(150, 150);
    context.fillStyle = "rgb(255, 0, 0)";
    context.fillRect(150, 150, 100, 100); 

一般情况下，第二次调用fillRect时，所绘制的正方形的原点坐标是(150，150)，但是由于执行了一次平移，这个正方形的原点现在变成(300，300)（参见图2）。

一定要理解这其中的原理。红色正方形的原点仍然为(150，150)，它只是看上去又平移了150像素，这是因为在黑色正方形绘制之后，2D渲染上下文的原点已经平移了150像素。如果你希望红色正方形仍然出现在点(150，150)原来的位置（即黑色正方形所在位置），那么可以直接将它的原点设为(0,0)：

context.translate(150, 150);
    context.fillStyle = "rgb(255, 0, 0)";
    context.fillRect(0, 0, 100, 100); 

这是因为你已经将2D渲染上下文移动到位置(150，150)，所以从现在开始，所有在点(0,0)绘制的图形实际上都显示在点(150，150)上。

注意：每一种变形方法，包括平移，都会影响方法执行后所绘制的所有元素。这是因为它们都是直接在2D渲染上下文上操作的，而不是只针对所绘制的图形，这与你修改了fillStyle等属性的效果一样，新的颜色会影响后来绘制的所有元素。

缩放

另一个变形方法就是缩放(scale)，顾名思义，它是调整2D渲染上下文的尺寸。它与平移的区别在于（x，y）参数是缩放倍数，而不是像素值。

 context.scale(2, 2); 
    context.fillRect(0, 0, 100, 100); 

这个例子将2D渲染上下文的x和y方向都乘以2。通俗地说，2D渲染上下文及其绘制的所有对象现在都变成2倍尺寸（参见图3）。

单独使用scale将使所有绘图内容变大，而且它也会使一些对象被画在一些不恰当的位置上。例如，放大2倍实际上意味着现在1个像素变成2个像素．所以如果你绘制了一个x为150像素的图形，现在它看起来像是变成x为300像素了。如果这不符合你的要求，或者你只想要缩放一个图形，可以组合使用scale和translate方法。

 context.save();
    context.translate(150, 150);
    context.scale(2, 2);
    context.fillRect(0, 0, 100, 100); 

在这个例子中，首先保存画布的状态，再将原点平移到(150，150)。然后，将画布放大两倍，在位置(0，0)绘制一个正方形。因为已经将2D渲染上下文平移到(150，150)，所以这个正方形会被绘制在正确的位置，并同时放大两倍（参见图4）。

问题是，从现在开始绘制的其他图形都将平移150像素并在两个方向同时放大两倍。幸好，你已经完成了前面一半的工作：在执行变形之前保存了绘图状态。剩下一半工作是恢复之前保存的绘图状态。

context.restore();
    context.fillRect(0, 0, 100, 100); 

在恢复绘图状态之后，后面绘制的所有图形都不会出现变形效果(参见图5)。

旋转

如果要我选择一个最喜欢的变形功能，我肯定会选择rotate方法。到现在为止，我们介绍的变形方法的共同特点是它们都很容易调用。rotate方法也不例外，你只需要传入以弧度为单位的2D渲染上下文旋转角度值即可：

context.rotate(0.7854); // Rotate 45 degrees (Math.PI/4) 
    context.fillRect(0, 0, 100, 100); 

然而，这个旋转的结果可能并不是你所期望的。为什么正方形会旋转到浏览器边界以外呢？（参见图6）。

出现这种结果，是因为rotate方法是把2D渲染上下文绕其原点(0,0)进行旋转的，在前面这个例子中，原点是屏幕的左上角。因此，你所绘制的正方形本身是不会旋转的，它现在实际上是以45度角绘制到画布中。图7可以帮助理解这一点。

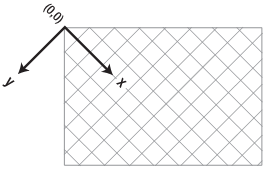
当然，如果你只想旋转所要绘制的图形，那么这样肯定不行。这时，仍然还需要使用translate方法。要实现所期望的效果，需要将2D渲染上下文的原点平移到正在绘制的图形的中心。然后，再对画布执行一次旋转，接着在当前位置绘制图形。这个过程描述起来有些复杂，所以让我们用示例代码来演示这个过程：

context.translate(200, 200); // Translate to centre of square 
    context.rotate(0.7854); // Rotate 45 degrees
    context.fillRect(-50, -50, 100, 100); // Draw a square with the centre at the point of rotation 

这样你会得到一个旋转45度角的有趣正方形，它正位于你想要的位置（参见图8）。

注意：执行变形的顺序是极为重要的。例如，如果在执行平移之前将画布旋转45度，那么你会在45度角上进行平移。WHATWG规范中有一个例子指出，如果一个缩放变形操作先将你给制的任何图形的宽度放大2倍，随后再旋转90度，那么当你绘制一个宽度是高度2倍的矩形时，这个缩放变形操作会把你所绘制的矩形变成一个正方形。仔细想想，你就能明白它的意思，它强调了考虑变形顺序的必要性。如果绘图时出现错误，那么请先检查顺序！

变换矩阵

现目前为止，你所使用的所有变形方法都会影响一个东西，那就是变换矩阵。我们不讨论一些非必要的细节（这些细节信息并不重要），变换矩阵就是一组数字，它们各自描述一个稍后将会介绍的特定变形类型。矩阵分成多个列和行。在画布中，你使用的是一个3x3矩阵——3列和3行（参见图9）。

你可以忽略最后一行，因为你不需要也不能修改它的值．最重要的是第一行和第二行，其中包含的数字值对应画布中使用的a至f。你可以看到，图9中每一个数字值都对应一种特定的变形。例如，a表示在x轴的缩放倍数，f表示在y轴的平移。

现在，在学习如何手动处理变换矩阵之前，我先说明一下这个矩阵的默认值。一个新的2D渲染上下文将包含一个全新的变换矩阵，即单位矩阵(identity matrix)（参见图10）。

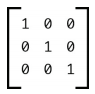
除了左上角至右下角的主对角线以外，这个特殊矩阵的每个值都设置为0。这样设置的唯一原因是它更适合进行计算，但是可以确定的是，单位矩阵表示完全未执行过变形。全面理解单位矩阵的含义并不是很重要，重要的是要知道变换矩阵中的默认值是什么。

操作变换矩阵

本节要介绍的最后两个方法是transform和setTransform。它们能够帮助我们操作2D渲染上下文的变换矩阵。 我们已经了解了足够多的基本概念，所以现在让我们使用transform执行一个平移和缩放，然后再绘制一个正方形，以此说明它的作用：

context.transform(2, 0, 0, 2, 150, 150);
    context.fillRect(0, 0, 100, 100); 

transform方法有6个参数，分别对应变换矩阵的每一个值，第一个表示a，最后一个表f。在这个例子中，你想将画布的尺寸放大2倍，所以将第1个和第4个参数设置为2，即a和d——分别对应x轴缩放和y轴缩放。 可以理解。而如果要平移画布原点呢？没错：你需要设置第5个和第6个参数，即e和f——分别对应x轴平移和y轴平移（参见图11）。

希望你现在已经理解了它的使用方法，手动操作变换矩阵其实并不复杂。只要理解每一个值的意义，就能够执行正确的操作。现在让我们用变换矩阵执行一些更高级的变形——旋转！

不使用rotate方法执行旋转变形似乎有些复杂，但是如果你听我讲下去，很快就能明白这样做的意义：

context.setTransform(1, 0, 0, 1, 0, 0); // Identity matrix 
    var xScale = Math.cos(0.7854); 
    var ySkew = -Math.sin(0.7854);
    var xSkew = Math.sin(0.7854);
    var yScale = Math.cos(0.7854);
    var xTrans = 200;
    var yTrans = 200;
    context.transform(xScale, ySkew, xSkew, yScale, xTrans, yTrans);
    context.fillRect(-50, -50, 100, 100); 

首先，你需要调用setTransform方法。这是第二个操作变换矩阵的方法，它的作用是将矩阵重置为单位矩阵，然后按照6个参数执行变形。在这个例子中，使用它来重置变换矩阵，从而保证你操作的是一个原始状态的变换矩阵。然后，为一些变量赋值，它们是调用transform方法所使用的参数。有了这些作为参数的变量，就能够使整个过程变得更加简洁和清晰，而且更容易理解。

需要指出的是，transform方法实际上是将现有的变换矩阵乘以你所指定的值，而不是直接设置变换矩阵的值．这意味着其中会有一个累积效应．如果你多次调用transform，那么每一次变形都是应用到前一个变形所得到的变换矩阵。我承认这有一些复杂，但是我希望它能够帮助你理解变形的工作方式。

你可能注意到了，我们又一次使用到Math对象。在这个例子中，使用它来返回一些必要值，缩放和倾斜变形将使用这些值来生成旋转效果。因为掌握这一点非常重要，所以在此重复一遍：使用变换矩阵进行旋转是倾斜和缩放的组合效果。

注意：我们还会在本书中使用正弦和余弦等三角函数，如果你希望学习更多关于它们的使用方法和作用，我强烈建议你找些书来复习一下这些函数。 但是，我们无法在这里逐一解释每一个概念．变换矩阵的维基百科页面包含更丰富的信息：https://en.wikipedia.org/wiki/Transformation_matrix。

最后，将所有代码编写出来，你会得到下面的结果：一个漂亮的旋转后的正方形（参见图12）。

这些旋转效果完全是你从零开始做出来的，根本没用rotate方法！一般而言，这三个核心的变形方法在大多数时间都能够满足要求，但是即便不满足要求，理解变换矩阵也能够帮助你解决问题。

$(document).ready(function () { var canvas2 = $("#canvas2"); var context2 = canvas2.get(0).getContext("2d"); context2.fillRect(150, 150, 100, 100); context2.translate(150, 150); context2.fillStyle = "rgb(255, 0, 0)"; context2.fillRect(150, 150, 100, 100); var canvas3 = $("#canvas3"); var context3 = canvas3.get(0).getContext("2d"); context3.scale(2, 2); context3.fillRect(0, 0, 100, 100); var canvas4 = $("#canvas4"); var context4 = canvas4.get(0).getContext("2d"); context4.save(); context4.translate(150, 150); context4.scale(2, 2); context4.fillRect(0, 0, 100, 100); var canvas5 = $("#canvas5"); var context5 = canvas5.get(0).getContext("2d"); context5.save(); context5.translate(150, 150); context5.scale(2, 2); context5.fillRect(0, 0, 100, 100); context5.restore(); context5.fillRect(0, 0, 100, 100); var canvas6 = $("#canvas6"); var context6 = canvas6.get(0).getContext("2d"); context6.rotate(0.7854); // Rotate 45 degrees (Math.PI/4) context6.fillRect(0, 0, 100, 100); var canvas8 = $("#canvas8"); var context8 = canvas8.get(0).getContext("2d"); context8.translate(200, 200); // Translate to centre of square context8.rotate(0.7854); // Rotate 45 degrees context8.fillRect(-50, -50, 100, 100); // Draw a square with the centre at the point of rotation var canvas11 = $("#canvas11"); var context11 = canvas11.get(0).getContext("2d"); context11.transform(2, 0, 0, 2, 150, 150); context11.fillRect(0, 0, 100, 100); var canvas12 = $("#canvas12"); var context12 = canvas12.get(0).getContext("2d"); context12.setTransform(1, 0, 0, 1, 0, 0); // Identity matrix var xScale = Math.cos(0.7854); var ySkew = -Math.sin(0.7854); var xSkew = Math.sin(0.7854); var yScale = Math.cos(0.7854); var xTrans = 200; var yTrans = 200; context12.transform(xScale, ySkew, xSkew, yScale, xTrans, yTrans); context12.fillRect(-50, -50, 100, 100); });