12.23 HTML Canvas动画 - 圆周运动
形状不一定始终沿着直线运动。如果你需要的动画效果是沿着圆周运动,例如,沿着圆形轨道运行(如图1所示)该如何实现呢?这是完全可以实现的,并且不需要使用太多代码,这里需要使用三角函数的相关知识,可能需要你稍微动一下脑筋。
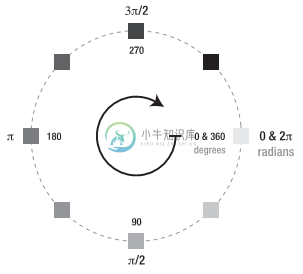
概念非常简单:将一个形状放在圆周的边缘处(它的周长上),以圆周的任意位置作为起点。但为了简单起见,可以将形状放在周长上角度为0弧度的位置,该位置位于右手边(如图1所示)。在每次动画循环中,只需要增加位于圆周上的形状的角度,就可以使形状沿着圆周运动。这非常简单,接下来我们具体讨论如何实现。
1.三角函数
需要解决的问题是:如何计算位于圆周上的形状的(x,y)坐标值(如图2所示)。这听上去也许很深奥,但需要解决的问题其实很简单。当然,只有用正确的方式来考虑需要解决的问题,才会觉得它容易。
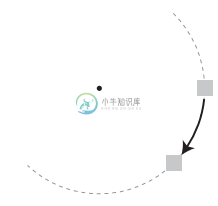
在解决问题之前,首先需要知道圆的实际大小。可以选择任意大小的圆周,毕竟,这里只是示例,所以实际大小并不重要。重要的是可以通过半径(从圆心到圆周的长度)来描述圆的大小。如果画出运动轨道所在圆周的半径,那么你会发现形状移动的角度遵循一种有趣的模式(如图3所示)。
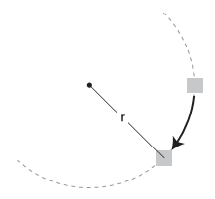
如果你认真地看或者稍微思考一下,也许就会发现这种模式。如果幸运的话,你会发现三角形的边存在一些规律。如果没有发现规律,也不要紧。如果你是第一次接触这种问题,那么稍微发挥一下想象力就可以了。图4中有这里要讨论的三角形。
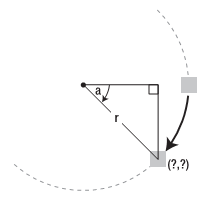
圆周中包含了一个三角形。但它有何用处呢?这个三角形能够提供一些准确的信息,帮助你计算形状沿圆周移动到新位置处的(x,y)坐标值。更具体地说,现在得到了一个三角形和两个角度(沿圆周转动的角度和三角形的90度直角),接下来可以构造一些基本三角形来计算你需要的值。这也体现了数学的重要作用。但是,在真正解决问题之前,我还要简要解释一下三角函数的原理。
三角函数的基本要点是:如果已知一个三角形的一个角是90度,并且已知另外一个角,那么就可以计算三角形的边长之间的比值。然后,可以通过该比值来计算边的长度,边的长度单位是任意的,本示例中边的单位是像素。因此,你需要知道三角形的哪条边是需要计算的长度,因为它们分别对应着不同的三角函数规则。这三条边分别是斜边(最长的边)、邻边(与除直角以外的已知角相邻的边)和对边(与已知角相对的边)。图5详细标注了这些边。
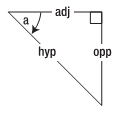
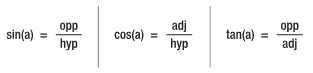
要计算边之间的比值,需要用3种三角函数:正弦函数(sin)、余弦函数(cos)或正切函数(tan)。正弦函数是对边与斜边的比值,余孩函数是邻边与斜边的比值,正切函数是对边与邻边的比值(如图6所示)。你也许听过把这些函数叫做SOH-CAH-TOA,其实这就是代表正弦-对边-斜边、余弦-邻边-斜边、正切-对边-邻边。通过把三角形中的已知角代入正确的函数,可以计算出所需的比值来。
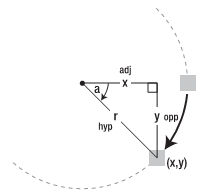
在此,我们需要知道三角形的邻边和对边的长度,它们分别代表x和y的位置(如图7所示)。要计算这些边的长度,首先需要在对应的三角函数中通过已知角计算比值。在JavaScript中,可以使用Math对象来计算这些比值:
var angle = 45; var adjRatio = Math.cos(angle*(Math.PI/180)); // CAH var oppRatio = Math.sin(angle*(Math.PI/180)); // SOH
你会注意到,Math对象的cos和sin方法中执行了一些简单的计算过程。这种计算是为了将角从角度转换为弧度,因为JavaScript使用的单位是弧度。如果你在开始就使用弧度制,就不需要做任何转换了。
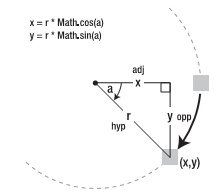
得到这些比值仅仅完成了一半的工作量。另外一半工作才是最终我们需要得到的答案,将这些比值与斜边(因为它是半径,所以长度已知)的长度相比较,如图8所示。最终的答案可以由半径乘以该比值得到,即:
var radius = 50; var x = radius * adjRatio; var y = radius * oppRatio;
2.综合运用
既然你能够计算位于圆周上某个角度的形状对应的(x,y)坐标值,那么把这些结果综合应用于当前的示例就非常简单了。第一步是更新Shape类,并向其中添加几个新属性:
var Shape = function(x, y, width, height) {
this.x = x; this.y = y;
this.width = width;
this.height = height;
this.radius = Math.random()*30;
this.angle = 0;
}; 这两个属性用于设置起始角度和计算圆周的随机半径(介于0~30之间)。倒数第二步是使用以下代码替换动画循环中的现有代码,从而更新形状:
var x = tmpShape.x+(tmpShape.radius*Math.cos(tmpShape.angle*(Math.PI/180)));
var y = tmpShape.y+(tmpShape.radius*Math.sin(tmpShape.angle*(Math.PI/180)));
tmpShape.angle += 5;
if (tmpShape.angle > 360) {
tmpShape.angle = 0;
};前两行代码没有什么新内容,它们分别用于计算位于圆周上当前角度的形状所对应的x和y值,其中圆周是通过半径来定义的。 这里的x和y值能够提供坐标值(假设圆周中心的坐标为(0,0)),因此,当将x和y值添加到形状中对应的点(x,y)时,就可以把形状移动到正确的位置。 注意,形状对象中定义的点(x,y)现在引用的是圆周的中心——形状围绕它旋转的点,而不是形状的起点。 最后几行代码用于在每个动画循环中增加角的度数,如果角度超过360度(一个完整的圆),则将角度重新设置为0度。
最后,将新的x和y变量添加到fillRect方法中:
context.fillRect(x, y, tmpShape.width, tmpShape.height);
如果一切运行正常,点击Start启动动画,就可以出现各个形状沿着不同的圆周轨迹运动(如图9所示)。 我们可以在此例基础上进一步实现经典的太阳系(公转/自传)模型。
本节需要一些基础的几何知识,可能有些难度,以下是完整的代码供你参考。
var canvas = $("#myCanvas");
var context = canvas.get(0).getContext("2d");
var canvasWidth = canvas.width();
var canvasHeight = canvas.height();
var playAnimation = true;
var startButton = $("#startAnimation");
var stopButton = $("#stopAnimation");
startButton.hide();
startButton.click(function() {
$(this).hide();
stopButton.show();
playAnimation = true;
animate();
});
stopButton.click(function() {
$(this).hide();
startButton.show();
playAnimation = false;
});
var Shape = function(x, y, width, height) {
this.x = x;
this.y = y;
this.width = width;
this.height = height;
this.radius = Math.random()*30;
this.angle = 0;
};
var shapes = new Array();
for (var i = 0; i < 10; i++) {
var x = Math.random()*250;
var y = Math.random()*250;
var width = height = Math.random()*30;
shapes.push(new Shape(x, y, width, height));
};
function animate() {
context.clearRect(0, 0, canvasWidth, canvasHeight);
var shapesLength = shapes.length;
for (var i = 0; i 360) {
tmpShape.angle = 0;
};
context.fillRect(x, y, tmpShape.width, tmpShape.height);
};
if (playAnimation) {
setTimeout(animate, 33);
};
};
animate();
