【LeetCode】33~154. 4 道「搜索旋转排序数组」题

本文涉及 4 道「搜索旋转排序数组」题：

• LeetCode 33 题：搜索旋转排序数组
• LeetCode 81 题：搜索旋转排序数组-ii
• LeetCode 153 题：寻找旋转排序数组中的最小值
• LeetCode 154 题：寻找旋转排序数组中的最小值-ii

可以分为 3 类：

• 33、81 题：搜索特定值
• 153、154 题：搜索最小值
• 81、154 题：包含重复元素

33. 搜索旋转排序数组

题目要求时间复杂度 $O(logn)$，显然应该使用二分查找。二分查找的过程就是不断收缩左右边界，而怎么缩小区间是关键。

如果数组「未旋转」，在数组中查找一个特定元素 target 的过程为：

• 若 target == nums[mid]，直接返回
• 若 target < nums[mid]，则 target 位于左侧区间 [left,mid) 中。令 right = mid-1，在左侧区间查找
• 若 target > nums[mid]，则 target 位于右侧区间 (mid,right] 中。令 left = mid+1，在右侧区间查找

但是这道题，由于数组「被旋转」，所以左侧或者右侧区间不一定是连续的。在这种情况下，如何判断 target 位于哪个区间？

根据旋转数组的特性，当元素不重复时，如果 nums[i] <= nums[j]，说明区间 [i,j] 是「连续递增」的。

i、j 可以重合，所以这里使用的比较运算符是「小于等于」

因此，在旋转排序数组中查找一个特定元素时：

• 若 target == nums[mid]，直接返回
• 若 nums[left] <= nums[mid]，说明左侧区间 [left,mid]「连续递增」。此时：
  • 若 nums[left] <= target <= nums[mid]，说明 target 位于左侧。令 right = mid-1，在左侧区间查找
  • 否则，令 left = mid+1，在右侧区间查找
• 否则，说明右侧区间 [mid,right]「连续递增」。此时：
  • 若 nums[mid] <= target <= nums[right]，说明 target 位于右侧区间。令 left = mid+1，在右侧区间查找
  • 否则，令 right = mid-1，在左侧区间查找
• 注意：区间收缩时不包含 mid，也就是说，实际收缩后的区间是 [left,mid) 或者 (mid,right]

可以很容易地写出代码：

func search(nums []int, target int) int {
	left, right, mid := 0, len(nums)-1, 0
	for left <= right { // 等号：考虑 left==right，即只有一个元素的情况
		mid = (left + right) / 2
		if nums[mid] == target {
			return mid
		}
		// [left,mid] 连续递增
		if nums[left] <= nums[mid] { // 等号：考虑 left==mid，即只有一个元素的情况
			if nums[left] <= target && target < nums[mid] { // 加等号，因为 left 可能是 target；mid 已经比较过了，加不加都无所谓
				right = mid - 1 // 在左侧 [left,mid) 查找
			} else {
				left = mid + 1
			}
		} else { // [mid,right] 连续递增
			if nums[mid] < target && target <= nums[right] { // 加等号，因为 right 可能是 target；mid 已经比较过了，加不加都无所谓
				left = mid + 1 // 在右侧 (mid,right] 查找
			} else {
				right = mid - 1
			}
		}
	}
	return -1
}

// ...
        // mid > 0 防止越界
        if mid > 0 && nums[left] <= nums[mid-1] { // [left,mid-1] 递增
            if nums[left] <= target && target <= nums[mid-1] {
                right = mid - 1
            } else {
                left = mid + 1
            }
        } else { // [mid+1,right] 递增
            // mid < n-1 防止越界
            if mid < n-1 && nums[mid+1] <= target && target <= nums[right] {
                left = mid + 1
            } else {
                right = mid - 1
            }
        }
// ...

        if mid > left && nums[left] <= nums[mid-1] { // [left,mid-1] 递增
            // ...
        } else {
            if mid < right && nums[mid+1] <= target && target <= nums[right] {
                // ...
            }
        }

81. 搜索旋转排序数组-ii

这道题是 33 题的升级版，元素可以重复。当 nums[left] == nums[mid] 时，无法判断 target 位于左侧还是右侧，此时无法缩小区间，退化为顺序查找。

顺序查找的一种方法是直接遍历 [left,right] 每一项：

if nums[left] == nums[mid] {
    for i := left; i <= right; i++ { 
        if nums[i] == target {
            return i
        }
}

另一种方法是令 left++，去掉一个干扰项，本质上还是顺序查找：

if nums[left] == nums[mid] {
    left++
    continue
}

直接将这几行代码加到 33 题的代码中就可以了：

func search(nums []int, target int) bool {
	left, right, mid := 0, len(nums)-1, 0
	for left <= right {
		mid = (left + right) / 2
		if nums[mid] == target {
			return true
		}
+		if nums[left] == nums[mid] {
+			left++
+			continue
+		}
		if nums[left] <= nums[mid] {
			if nums[left] <= target && target < nums[mid] {
				right = mid - 1
			} else {
				left = mid + 1
			}
		} else {
			if nums[mid] < target && target <= nums[right] {
				left = mid + 1				} else {
				right = mid - 1
			}
		}
	}
	return false
}

if nums[right] == nums[mid] {
    right--
    continue
}

[1,3,1,1,1]
1

if nums[left] == nums[mid] && nums[mid] == nums[right] {
    left++
}

153. 搜索旋转排序数组中的最小值

如果数组没有翻转，即 nums[left] <= nums[right]，则 nums[left] 就是最小值，直接返回。

如果数组翻转，需要找到数组中第二部分的第一个元素：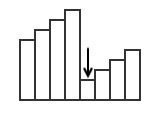

下面讨论数组翻转的情况下，如何收缩区间以找到这个元素：

• 若 nums[left] <= nums[mid]，说明区间 [left,mid] 连续递增，则最小元素一定不在这个区间里，可以直接排除。因此，令 left = mid+1，在 [mid+1,right] 继续查找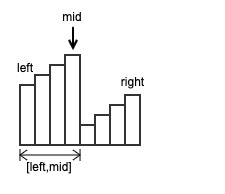
  
• 否则，说明区间 [left,mid] 不连续，则最小元素一定在这个区间里。因此，令 right = mid，在 [left,mid] 继续查找
• [left,right] 表示当前搜索的区间。注意 right 更新时会被设为 mid 而不是 mid-1，因为 mid 无法被排除。这一点和「33 题 查找特定元素」是不同的

代码如下：

func findMin (nums []int) int {
    left, right := 0, len(nums)-1
    for left <= right { // 实际上是不会跳出循环，当 left==right 时直接返回
        if nums[left] <= nums[right] { // 如果 [left,right] 递增，直接返回
            return nums[left]
        }
        mid := left + (right-left)>>1
        if nums[left] <= nums[mid] { // [left,mid] 连续递增，则在 [mid+1,right] 查找
            left = mid + 1
        }else {
            right = mid // [left,mid] 不连续，在 [left,mid] 查找
        }
    }
    return -1
}

C++ 版本：

int findmin(int array[], int count) {
  int left = 0, right = count - 1;
  while (left <= right) {
    if (array[left] <= array[right]) {
      return array[left];
    }
    int mid = (left + right) / 2;
    if (array[left] <= array[mid])
      left = mid + 1;
    else
      right = mid;
  }
  return -1;
}

154. 搜索旋转排序数组中的最小值-ii

这道题是 153 题的升级版，元素可以重复。和 81 题一样，当 nums[left] == nums[mid] 时，退化为顺序查找。

81 题提供了两种方法：

• 一种是直接遍历 [left,right] 每一项
• 另一种是 left++，跳过一个干扰项

154 题可以使用第一种方法直接修改 153 题的代码，代码略。

对于第二种方法，由于本题是查找「下界」而不是特定元素，当区间中只有一个元素时，有 nums[left] == nums[mid]，这里如果 left++，那么会跳过正确答案。

一种解决办法是：保证进入循环后，[left,right] 中至少有两个元素。代码如下（注释部分就是和 153 题不同的地方）：

func findMin(nums []int) int {
    left, right := 0, len(nums)-1
    for left < right { // <= 换成 <，保证进入循环后，[left,right] 中至少两个元素
        if nums[left] < nums[right] { // <= 换成 <，nums[left]==nums[right] 时无法判断 [left,right] 递增
            return nums[left]
        }
        mid := left+(right-left)>>1
        if nums[left] == nums[mid] { // 去掉一个干扰项
            left++
            continue
        }
        if nums[left] < nums[mid] { // 这里也不需要 <= 了
            left = mid+1
        } else {
            right = mid
        }
    }
    return nums[left] // 循环结束后，[left,right] 只有一个元素，直接返回
}

另一种解决办法是：当区间中只有一个元素时，直接返回 nums[left]。代码如下：

func findMin (nums []int) int {
    left, right := 0, len(nums)-1
    for left <= right { // 实际上不会跳出循环，同 153 题
        if nums[left] < nums[right] || left == right { // 这里增加一个判断条件
            return nums[left]
        }
        mid := left + (right-left)>>1
        if nums[left] < nums[mid] {
            left = mid + 1
        } else if nums[left] == nums[mid] {
            left++
        } else {
            right = mid
        }
    }
    return -1
}

总结

在旋转排序数组中进行二分查找时，无论是搜索特定值，还是搜索最小值，都需要在左右两个区间里，找到「连续递增」的那个区间。

判断区间是否「连续递增」，只需比较区间边界值：如果 nums[left] <= nums[mid]，则区间 [left,mid] 连续递增；反之，区间 [mid,right] 连续递增。但是上述判断仅适用于数组中不含重复元素的情况，如果数组中包含重复元素，那么在 nums[left]==nums[mid] 时将退化为线性查找。

找到「连续递增」的区间后，问题就变得简单了许多：

• 33 题，查找特定值：只需要判断目标值在「连续递增」区间内还是区间外。比如当区间 [left,mid] 连续递增时，若目标值位于该区间内，则 right = mid-1；若目标值位于该区间外，则 left = mid+1。如果是区间 [mid,right] 连续递增，也可以用类似的方法收缩区间
• 153 题，查找最小值：只需要排除左侧或者右侧的一段「连续区间」，使得 [left,right] 不连续，就可以找到最小值