【LeetCode】77 组合(n 个元素中选择 k 个)
问题描述
这道题是 LeetCode 77 题。
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
解法一:回溯法
递归 k 层。每层选取一个数,然后递归地选取 k-1 个数,直到选够 k 个数为止。设每层的数字区间为 [start, end],则这一层可以选择 [start, end-(k-1)] 的任何一个数 i,只要给下一层留出 k-1 个数即可。下一层的数字区间为 [i+1, end]。
时间复杂度:$O(k×C_n^k)$。 空间复杂度:$O(k×C^k_n)$,保存最终结果所需的空间。
时间复杂度推导:
将递归过程想象成一棵树,那么第一层递归有 $n$ 个节点,第二层递归有 $(n-1)+(n-2)+…+1$ 个节点,…,最后一层递归有 $C_n^k$ 个节点。实际的节点总数很难计算,但是一共 k 层,每层节点数都比最后一层少,所以时间复杂度可以表示为 $O(k×C_n^k)$。
这种方法得到的组合是字典序升序的。
代码:
var res [][]int
func combine(n int, k int) [][]int {
res = nil
solve(1, n, k, nil)
return res
}
func solve(start, end, k int, cur []int) {
if k == 0 {
res = append(res, copy(cur))
return
}
for i := start; i <= end-(k-1); i++ { // 从 start 开始;保证 i+1~end 至少有 k-1 个数
solve(i+1, end, k-1, append(cur, i))
}
}
func copy (nums []int) []int {
res := make([]int ,len(nums))
for i, v := range nums {
res[i] = v
}
return res
}
回溯法基本框架
func solve(start, end, k, cur) {
// 遍历当前层的所有选择
for i := all_choice {
// 选择 i
cur = append(cur, i)
// 进入下一层 solve
solve(i+1, end, k-1, cur)
// 取消选择 i,回溯
cur = cur[:len(cur)-1]
}
}
解法二:下一个组合
参考 LeetCode 31题 - 下一个排列,我们可以定义“下一个组合”:从 n 个数字序列中选择 k 个数字,从小到大组合,组成下一个字典序更大的组合。
以 1,2,3,4,5 为例,选择 3 个元素组成一个组合,依次为:
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 5
2 4 5
3 4 5
可以看到有这样的关系:123 < 124 < 125 < ... < 345。
如何得到这样的组合顺序?我们可以采用和求“下一个排列”类似的思路:
- 我们希望下一个数比当前数大,因此需要从未选择的数字中,用一个更大的数字替换已选择的数字。在上面的例子中,
1 2 3→1 2 4是用4替换3,1 2 4→1 2 5是用5替换4…- 肯定是「未选择的」数字,这样才能得到一个不同的组合
- 我们还希望下一个数增加的幅度尽可能的小,因此:
- 在未选择的数字中,使用尽可能小的数字 $b$ 替换已选择数字的尽可能低位的数字 $a$,满足 $b > a$
- 将 $b$ 后面的所有数字依次替换为比 $b$ 大的数。比如
1 4 5的下一个组合是2 3 4,相当于先用2替换1得到2 4 5,再用比2大的3 4替换4 5得到2 3 4
算法过程:
- 开一个数组,其下标表示第 1 到 n 个数,数组元素的值为 1 表示其代表的数被选中,为 0 则没选中
- 初始化,将数组前 n 个元素置 1,表示第一个组合为前 n 个数。
1 1 1 0 0 - 然后从右到左扫描数组,找到第一个连续的
1 0,将其交换为0 1。这表示用一个更大的数替换掉和它相邻的比它小的数 - 将上一步
0 1右边的所有的“1”都移动到0 1右侧区间的最左端。比如1 1 0 0 1,经过步骤 3 变为1 0 1 0 1,经过步骤 4 变为1 0 1 1 0,表示1 2 5的下一个组合是1 3 4 - 当 n 个“1”全部移动到最右端时,就得到了最后一个组合。
0 0 1 1 1
这种方法得到的组合是字典序升序的。
时间复杂度:$O(n×C^k_n)$。需要求 $C^k_n$ 个“下一个组合”,每求一个需要 $O(n)$。
空间复杂度:$O(n)$,需要开一个数组,不算保存结果所需的空间。
代码:
func combine(n int, k int) [][]int {
if n == 0 || k == 0 {
return nil
}
res = nil
nums := make([]int, n)
for i := 0; i < k; i++ {
nums[i] = 1
}
for {
tmp := make([]int, 0)
for i, v := range nums {
if v == 1 {
tmp = append(tmp, i+1)
}
}
res = append(res, tmp)
if !nextCombination(nums) {
break
}
}
return res
}
func nextCombination(nums []int) bool {
i := len(nums) - 2
for i >= 0 { // 从右往左找第一个 10
if nums[i] == 1 && nums[i+1] == 0 {
break
}
i--
}
if i < 0 { // 最后一个排列
return false
}
nums[i], nums[i+1] = nums[i+1], nums[i] // 10 交换为 01
for c, i := i+1, i+1; i < len(nums); i++ { // 把 i+1 后面的 1 全部移动到 [i+1:] 左端
if nums[i] == 1 {
nums[i] = 0 // 注意这两个赋值语句的顺序不能颠倒
nums[c] = 1
c++
}
}
return true
}
解法三:01 转换法
这个解法的过程和“下一个组合”非常像,相当于“下一个组合”的“镜像版”,但是其原理却完全不同(见附录)。算法过程如下:
- 开一个数组,其下标表示第 1 到 n 个数,数组元素的值为 1 表示其代表的数被选中,为 0 则没选中
- 初始化,将数组前 n 个元素置 1,表示第一个组合为前 n 个数。
1 1 1 0 0 - 然后从左到右扫描数组,找到第一个连续的
1 0,将其交换为0 1 - 将上一步
0 1左边的所有的“1”都移动到数组的最左端 - 当 n 个“1”全部移动到最右端时,就得到了最后一个组合。
0 0 1 1 1
例如求5中选3的组合:
1 1 1 0 0 //1,2,3
1 1 0 1 0 //1,2,4
1 0 1 1 0 //1,3,4
0 1 1 1 0 //2,3,4
1 1 0 0 1 //1,2,5
1 0 1 0 1 //1,3,5
0 1 1 0 1 //2,3,5
1 0 0 1 1 //1,4,5
0 1 0 1 1 //2,4,5
0 0 1 1 1 //3,4,5
注意:这种方法得到的组合不是字典序升序的。
时间复杂度:$O(n×C^k_n)$。
空间复杂度:$O(n)$,不算保存结果所需的空间。
代码只需微调“下一个组合”的代码:
func combine(n int, k int) [][]int {
if n == 0 || k == 0 {
return nil
}
res = nil
nums := make([]int, n)
for i := 0; i < k; i++ {
nums[i] = 1
}
for {
tmp := make([]int, 0)
for i, v := range nums {
if v == 1 {
tmp = append(tmp, i+1)
}
}
res = append(res, tmp)
if !nextCombination2(nums) {
break
}
}
return res
}
func nextCombination2(nums []int) bool {
i := 0
for i < len(nums)-1 { // 从左往右找第一个 10
if nums[i] == 1 && nums[i+1] == 0 {
break
}
i++
}
if i >= len(nums)-1 { // 最后一个排列
return false
}
nums[i], nums[i+1] = nums[i+1], nums[i] // 10 交换为 01
for c, j := 0, 0; j < i; j++ { // 把 i 前面的 1 全部移动到数组最左端
if nums[j] == 1 {
nums[j] = 0 // 注意这两个赋值语句的顺序不能颠倒
nums[c] = 1
c++
}
}
return true
}
解法四:迭代法
LeetCode 78 题的解法三-逐个枚举法:将空集作为默认子集,然后逐个枚举集合中的元素。每新增一个元素,就在之前的所有子集中追加这个元素,得到新增的子集。代码的外层循环是所有元素,内层循环是当前的结果集。
78 题需要保留所有长度的组合,而本题只需保留长度为 k 的组合。因此一种方法是在 78 题代码的基础上,过滤最终结果集,只保留长度为 k 的组合。不过这种方法需要保留所有长度为 1~k 的结果集,空间复杂度太大。
我们可以换一种思路:先找出长度为 1 的所有组合,再找出长度为 2 的所有组合,直到找到长度为 k 的所有组合。代码的外层循环是 1~k,表示长度;中间循环是当前的结果集;内层循环是某个特定集合可以添加的所有候选元素。这种方法只需保留当前长度的结果集。
这种方法得到的组合是字典序升序的。
时间复杂度:$O(k×C_n^k)$。同解法一的推导。
空间复杂度:$O(k×C^k_n)$,保存最终结果所需的空间。
解法四相当于解法一的迭代版本,虽然这两个解法的时间复杂度/空间复杂度一样,但解法一需要维护一个 $O(k)$ 的调用栈,所以按道理是解法四运行速度更快。但实测发现恰恰相反,猜想是因为解法四需要频繁地开辟数组空间导致。
代码:
func combine(n int, k int) [][]int {
if n == 0 || k == 0 {
return nil
}
res := [][]int{[]int{}}
for l := 1; l <= k; l++ { // 遍历所有长度
size := len(res)
for i := 0; i < size; i++ { // 遍历所有集合
item := res[i]
start := 1 // 剩余元素的起始位置
if len(item) > 0 {
start = item[len(item)-1] + 1
}
end := n - (k - l) // 剩余元素的结束位置,保证下一轮有 k - l 个候选元素
for t := start; t <= end; t++ { // 遍历所有的剩余元素
newSub = append(copy(item), t)
res = append(res, newSub)
}
}
res = res[size:] // 只保留当前长度的结果集
}
return res
}
解法五:递推法
这种方法和解法三类似,都是利用求组合数的递推公式:$C^k_n =C_{n-1}^{k-1}+C_{n-1}^{k}$。
这里用递归实现。先在 n 个元素中任选一个特殊元素,则“n 个元素中选择 k 个元素”的所有结果可以分为两种,包含特殊元素,或不包含特殊元素。
- 若包含特殊元素,则再从 n-1 个元素中选出 k-1 个元素的组合,即 $C_{n-1}^{k-1}$
- 否则,从 n-1 个元素中选出 m 个元素,即 $C_{n-1}^k$
为了简单起见,选择最后一个元素 n 作为特殊元素。重复上述过程,直到 k==0,表明找到了一个新的组合。
注意:这种方法得到的组合不是字典序升序的。
时间复杂度:$O(k×C_n^k)$。递归树为最大深度为 k、共 $C_n^k$ 个叶节点的二叉树。
空间复杂度:$O(k×C^k_n)$,保存最终结果所需的空间。
代码:
func combine(n int, k int) [][]int {
if n == 0 || k == 0 {
return nil
}
res = nil
dfs(n, k, nil)
return res
}
func dfs(n, k int, nums []int) {
if n < k || k == 0 { // 非法情况,或找够了 k 个数
if k == 0 {
tmp := make([]int, len(nums))
copy(tmp, nums)
res = append(res, tmp)
}
return
}
dfs(n-1, k, nums) // C(k, n-1)
dfs(n-1, k-1, append(nums, n)) // C(k-1, n-1)
return
}
解法六:动态规划法
解法五使用递归找到所有的解,递归的时候是从大到小,不断分解的过程,那我们只需将这个过程反过来,从小到大,不断合并,就能得到动态规划的解法。
根据 $C^k_n =C_{n-1}^{k-1}+C_{n-1}^{k}$,从 n 个元素中选择 k 个元素的所有结果,相当于「从 n-1 个元素中选出 k-1 个元素的所有结果分别再加上第 n 个元素」+「从 n-1 个元素中选出 m 个元素的所有结果」。
如下图所示,求 $C_5^3$ 需要知道 $C_4^3$ 与 $C_4^2$ 的值,求 $C_4^3$ 需要知道 $C_3^3$ 与 $C_3^2$ 的值… 即每个位置的值,是其正上方与左上方两个位置的值的并集,左上方位置的每个结果需要先加上第 n 个元素。
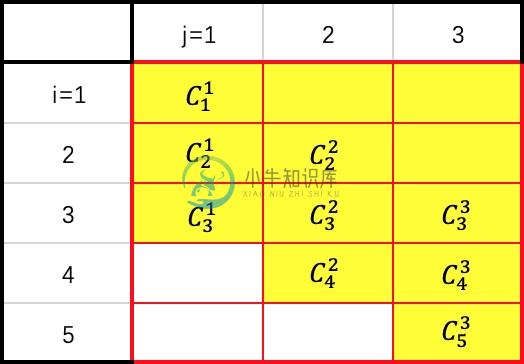
定义状态 P[i,j] 表示从前 i 个元素中选择 j 个元素的结果集。i 从 1~n,j 从 1~k 遍历,更新每个位置的值即可。由于更新每一行的时候只需要知道前一行的值,所以可以只申请一个一维数组,j 从 k~1 反向遍历,这是动态规划常见的优化空间复杂度的方法,数组大小从 $O(n×k)$ 降为 $O(k)$。
边界情况:j==1,即 i 个元素中选 1 个。C(i,1)=C(i-1,1)+C(i-1,0),C(i-1,0) 的解相当于是一个空集。因此可以将 P[0] 初始化为只包含一个空数组,表示 C(i,0)=1。这样可以统一处理每个 j 的情况。
这种方法得到的组合是字典序升序的。
时间复杂度:$O(n×k)$。
空间复杂度:$O(k×C_n^k)$,保存最终结果所需的空间。
func combine(n int, k int) [][]int {
if n == 0 || k == 0 {
return nil
}
type Results = [][]int
P := make([]Results, k+1)
P[0] = Results{[]int{}} // 初始化 P[0],包含一个空集
for i := 1; i <= n; i++ {
for j := k; j >= 1; j-- { // 一个隐含条件是 i >= j。如果 i < j,这个 for 循环不会执行,P[j-1] 是空集
for _, v := range P[j-1] { // 遍历左上方每个结果,P[j-1] 相当于 C(i-1, j-1)
item := copy(v) // 这里需要复制一下,否则切片可能被修改
item = append(item, i) // 左上方每个结果先新增当前元素
P[j] = append(P[j], item) // 然后合并左上方和上方的结果,P[j] 相当于 C(i-1, j)
}
}
}
return P[k]
}
附:01 转换法原理
求组合数的递推公式
求组合数 $C_n^m$ 一共有两种方式:
- 直接计算:$C^m_n = \frac{n!}{m!×(n-m)!}=\frac{A_n^m}{A_m}$
- 递推公式:$C^m_n =C_{n-1}^{m-1}+C_{n-1}^{m}$
递推公式的推导:先在 n 个元素中任选一个特殊元素,则“n 个元素中选择 m 个元素”的所有结果可以分为两种,包含特殊元素,或不包含特殊元素。
- 若包含特殊元素,则再从 n-1 个元素中选出 m-1 个元素的组合,即 $C_{n-1}^{m-1}$
- 否则,从 n-1 个元素中选出 m 个元素,即 $C_{n-1}^m$
递推公式举例:
\(\begin{equation} \begin{aligned} C_5^3 &= C_4^3 + C_4^2 \\ &= (C^3_3 + C^2_3) + (C_3^2 + C_3^1) \\ &= (C^3_3 + C^2_3 + C^1_3) + (C_3^1 + C^2_2 + C_3^1) \\ &= (C^3_3 + C^1_3 + C^1_2 + C^1_3) + (C_3^1 + C^2_2 + C_3^1) \\ &= ... \end{aligned} \end{equation}\)
01 转换法原理
01 转换法实际上是对递推公式的模拟。我们使用一个大小为 n 的数组,模拟在 n 个元素中选择 m 个元素过程。约定:
- 起始状态:数组前 $m$ 个数为 1,后 $n-m$ 个数为 0。
1 1 ... 1 0 0 ... 0 - 结束状态:数组后 $m$ 个数为 1,前 $n-m$ 个数为 0。
0 0 ... 0 1 1 ... 1
求 $C_n^m$,就是让数组从起始状态一步步变为结束状态。根据递推公式,该问题可以分解为两个子问题:
- 首先求 $C^{m}_{n-1}$,使其从起始状态变为结束状态:
- 起始状态:
{1 1 1 ... 1} 0 ... 0 | 0 - 结束状态:
0 ... 0 {1 1 1 ... 1} | 0 - 括号里是 $m$ 个 1,竖线左边有 $n-m-1$ 个 0
- 起始状态:
- 然后求 $C^{m-1}_{n-1}$,使其从起始状态变为结束状态:
- 起始状态:
{1 1 ... 1} 0 ... 0 | 1 - 结束状态:
0 ... 0 {1 1 ... 1} | 1 - 括号里是 $m-1$ 个 1,竖线左边有 $n-m$ 个 0
- 起始状态:
- 以此类推,只要当前子问题还没有到结束状态,就继续分解子问题
也就是说,在最后一个 1 移动到数组末尾之前,执行的是 $C^m_{n-1}$ ;当最后一个 1 移动到数组末尾后,将所有 1 重置到数组最前面,这时执行的是 $C^{m-1}_{n-1}$。
以 $C_5^3$ 为例:
1 1 1 0 0 - 开始求 C(3,4)
1 1 0 1 0
1 0 1 1 0
0 1 1 1 0 - 求得 C(3,4)
1 1 0 0 1 - 开始求 C(2,4)
1 0 1 0 1 - - - 开始求 C(2,3)
0 1 1 0 1 - - - 求得 C(2,3)
1 0 0 1 1 - - - 开始求 C(1,3) -> 开始求 C(1,2)
0 1 0 1 1 - - - 求得 C(1,2) -> 求得 C(1,3)
0 0 1 1 1 - 求得 C(2,4)

