【LeetCode】72 最短编辑距离

这道题是 LeetCode 72 题。

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数。你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

动态规划

解决两个字符串的动态规划问题，一般都是用两个指针 i,j 分别指向两个字符串的最后，然后一步步往前走，缩小问题的规模。

定义状态：dp[i][j] 表示 s1、s2 长度为 i、j 的子串的最短编辑距离，即 s1[0~i-1] → s2[0~j-1]。

状态转移方程：

• 若 s1[i]==s2[j]，则 dp[i+1][j+1]=dp[i][j]
• 否则，dp[i+1][j+1]= 以下三个的最小值：
  • dp[i][j+1]+1，相当于先删除 s1[i]，然后将 s1[0~i-1] 转为 s2[0~j]
  • dp[i][j]+1，相当于先替换 s1[i] 为 s2[j]，然后将 s1[0~i-1] 转为 s2[0~j-1]
  • dp[i+1][j]+1，相当于先将 s1[0~i] 转为 s2[0~j-1]，然后再插入 s2[j]

初始化：dp[0][j]=j, dp[i][0]=i。

更新过程：按行或按列更新。

可视化：以 horse 到 ros 为例，其更新过程如下图所示。根据状态转移方程，每更新一个位置，可能需要用到左、左上、上三个位置的值。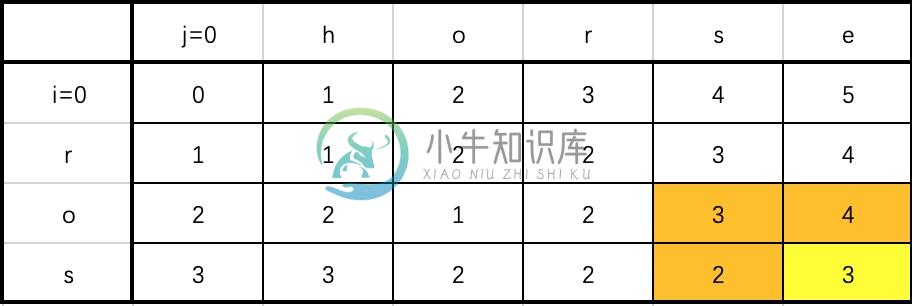

时间复杂度：$O(MN)$。
空间复杂度：$O(MN)$。

代码：

C++:

int minDistance(string word1, string word2) {
    int dp[word1.length()+1][word2.length()+1]; // dp[i][j] => w1, w2 长度为 i, j 的编辑距离
    for (int i = 0; i <= word1.length(); i++) dp[i][0] = i;
    for (int i = 0; i <= word2.length(); i++) dp[0][i] = i;
    for (int i = 1; i <= word1.length(); i++) {
        for (int j = 1; j <= word2.length(); j++) {
            if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
            else dp[i][j] = min(dp[i-1][j-1], min(dp[i][j-1], dp[i-1][j]))+1;
        }
    }
    return dp[word1.length()][word2.length()];
}

Go:

func minDistance(word1 string, word2 string) int {
	dp := make([][]int, len(word1)+1)
	for i, _ := range dp {
		dp[i] = make([]int, len(word2)+1)
	}

	for i := 0; i <= len(word1); i++ {
		dp[i][0] = i
	}
	for i := 0; i <= len(word2); i++ {
		dp[0][i] = i
	}

	for i := 0; i < len(word1); i++ {
		for j := 0; j < len(word2); j++ {
			if word1[i] == word2[j] {
				dp[i+1][j+1] = dp[i][j]
			} else {
				dp[i+1][j+1] = min(dp[i][j+1]+1, dp[i][j]+1)
				dp[i+1][j+1] = min(dp[i+1][j+1], dp[i+1][j]+1)
			}
		}
	}

	return dp[len(word1)][len(word2)]
}

func min(a, b int) int {
	if a > b {
		return b
	}
	return a
}

优化空间复杂度

既然 DP Table 每个位置的值只依赖于它附近 3 个位置的值，因此空间复杂度可以优化为 O(N)。这里需要用一个临时变量保存左上角的值，也就是 dp[i-1][j-1] 在上一轮的值。代码如下：

int minDistance(string word1, string word2) {
    if (word1.length() < word2.length()) swap(word1, word2);
    int dp [word2.length()+1];
    int tmp = 0; // 相当于二维数组的 dp[i-1][j-1]
    for (int i = 0; i <= word2.length(); i++) dp[i] = i;
    for (int i = 1; i <= word1.length(); i++) {
        dp[0] = i; // j 从 1 开始，故手动设置 dp[0]
        tmp = i-1; // dp[i][0] = i，故 dp[i-1][0] = i-1
        for (int j = 1; j <= word2.length(); j++) {
            int _tmp = dp[j];
            if (word1[i-1] == word2[j-1]) dp[j] = tmp;
            else dp[j] = min(tmp, min(dp[j-1], dp[j]))+1;
            tmp = _tmp;
        }
    }
    return dp[word2.length()];
}