登录
目录
当前位置： 首页 > 文档资料 > 文章推荐 2 >

【LeetCode】31、46、47 下一个排列、全排列

优质
小牛编辑
136浏览
2023-12-01

下一个排列

问题描述

这道题是 LeetCode 31题。

“下一个排列”的定义是：给定数字序列的字典序中下一个更大的排列。如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

我们可以将该问题形式化地描述为：给定若干个数字，将其组合为一个整数。如何将这些数字重新排列，以得到下一个更大的整数。如 123 下一个更大的数为 132。如果没有更大的整数，则输出最小的整数。

以 1,2,3,4,5,6 为例，其排列依次为：

123456
123465
123546
...
654321

可以看到有这样的关系：123456 < 123465 < 123546 < ... < 54321。

算法推导

如何得到这样的排列顺序？这是本文的重点。我们可以这样来分析：

  1. 我们希望下一个数比当前数大，这样才满足“下一个排列”的定义。因此只需要将后面的「大数」与前面的「小数」交换，就能得到一个更大的数。比如 123456，将 5 和 6 交换就能得到一个更大的数 123465。
  2. 我们还希望下一个数增加的幅度尽可能的小，这样才满足“下一个排列与当前排列紧邻“的要求。为了满足这个要求，我们需要：
    1. 在尽可能靠右的低位进行交换，需要从后向前查找
    2. 将一个尽可能小的「大数」与前面的「小数」交换。比如 123465，下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换
    3. 将「大数」换到前面后，需要将「大数」后面的所有数重置为升序，升序排列就是最小的排列。以 123465 为例：首先按照上一步，交换 5 和 4，得到 123564；然后需要将 5 之后的数重置为升序，得到 123546。显然 123546 比 123564 更小，123546 就是 123465 的下一个排列

以上就是求“下一个排列”的分析过程。

算法过程

标准的“下一个排列”算法可以描述为：

  1. 从后向前查找第一个相邻升序的元素对 (i,j)，满足 A[i] < A[j]。此时 [j,end) 必然是降序
  2. 在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
  3. 将 A[i] 与 A[k] 交换
  4. 可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序
  5. 如果在步骤 1 找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到步骤 4

该方法支持数据重复，且在 C++ STL 中被采用。

代码

func nextPermutation(nums []int) {
	if len(nums) <= 1 {
		return
	}

	i, j, k := len(nums)-2, len(nums)-1, len(nums)-1

	// find: A[i]<A[j]
	for i >= 0 && nums[i] >= nums[j] {
		i--
		j--
	}

	if i >= 0 { // 不是最后一个排列
		// find: A[i]<A[k]
		for nums[i] >= nums[k] {
			k--
		}
		// swap A[i], A[k]
		nums[i], nums[k] = nums[k], nums[i]
	}

	// reverse A[j:end]
	for i, j := j, len(nums)-1; i < j; i, j = i+1, j-1 {
		nums[i], nums[j] = nums[j], nums[i]
	}
}

可视化

以求 12385764 的下一个排列为例：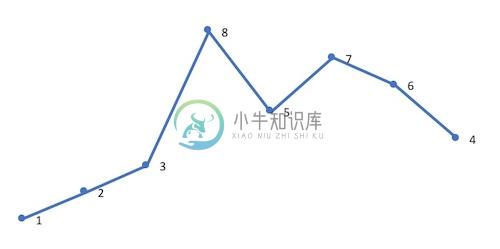
-w347

首先从后向前查找第一个相邻升序的元素对 (i,j)。这里 i=4，j=5，对应的值为 5，7：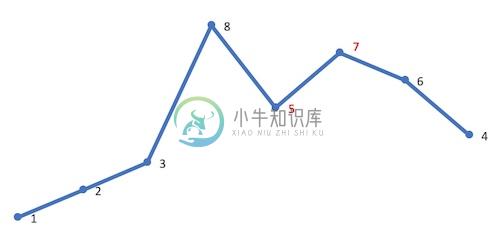
-w382

然后在 [j,end) 从后向前查找第一个大于 A[i] 的值 A[k]。这里 A[i] 是 5，故 A[k] 是 6：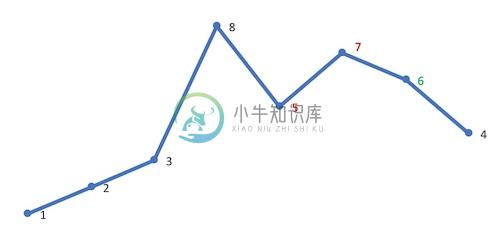
-w391

将 A[i] 与 A[k] 交换。这里交换 5、6：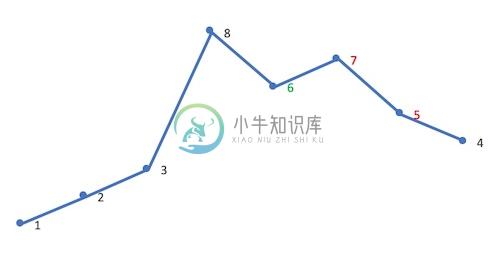
-w340

这时 [j,end) 必然是降序，逆置 [j,end)，使其升序。这里逆置 [7,5,4]：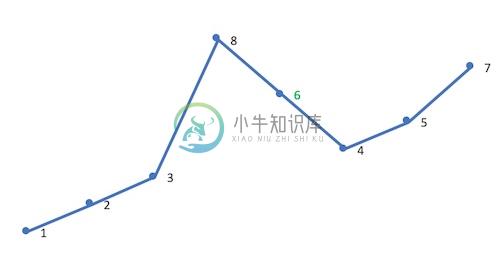
-w339

因此，12385764 的下一个排列就是 12386457。

最后再可视化地对比一下这两个相邻的排列（橙色是蓝色的下一个排列）：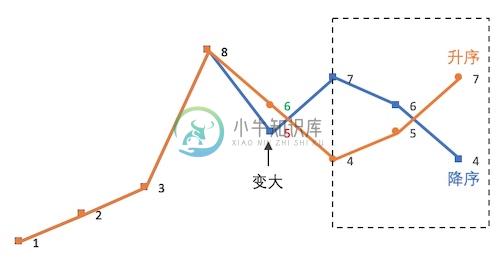
-w342

全排列

问题描述

这道题是 LeetCode 46题。

给定一个没有重复数字的序列，返回其所有可能的全排列。比如序列 [1,2,3]，其全排列为：

[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

解法一：下一个排列

可以不断求下一个排列，直到找到 $n!$ 个排列（前提是没有重复元素）。如果序列中包含重复元素，那么判断条件需要改为“直到下一个排列和第一个排列相同”。

时间复杂度：$O(n×n!)$。需要求 $n!$ 次下一个排列，每求一个需要 $O(n)$。
空间复杂度：$O(n×n!)$。需要保存 $n!$ 个解，每个解所需的空间为 $n$。如果不算保存结果所需的空间，那么空间复杂度为 $O(1)$。

这种方法得到的全排列是字典序升序的。

代码：

func permute(nums []int) [][]int {
	if len(nums) == 0 {
		return nil
	}
	res := [][]int{}
	cnt := 1
	for i := 1; i <= len(nums); i++ {
		cnt *= i
	}
	for i := 0; i < cnt; i++ {
		res = append(res, copyNums(nums))
		nextPermutation(nums)
	}
	return res
}

func nextPermutation(nums []int) {
	if len(nums) <= 1 {
		return
	}

	i, j, k := len(nums)-2, len(nums)-1, len(nums)-1

	// find: A[i]<A[j]
	for i >= 0 && nums[i] >= nums[j] {
		i--
		j--
	}

	if i >= 0 {
		// find: A[i]<A[k]
		for nums[i] >= nums[k] {
			k--
		}
		nums[i], nums[k] = nums[k], nums[i]
	}

	// reverse A[j:end]
	for i, j := j, len(nums)-1; i < j; i, j = i+1, j-1 {
		nums[i], nums[j] = nums[j], nums[i]
	}
}

func copyNums(nums []int) []int {
	tmp := make([]int, len(nums))
	copy(tmp, nums)
	return tmp
}

解法二：回溯遍历法

如果序列元素个数已知，可以手写 n 层循环，求所有元素的全排列。以 3 个元素为例，只需要手写 3 层循环：

length := 3
for i := 0; i < length; i++ {
    for j := 0; j < length; j++ {
        for k := 0; k < length; k++ {
            if i, j, k 都不相同 {
                addToResults([]int{a[i], a[j], a[k]})
            }
        }
    }
}

如果序列元素个数 $n$ 未知，可以利用递归实现回溯过程。递归时，每次选择一个元素加入到当前排列中，然后进入下一层，选择下一个元素。如果已经选择了 $n$ 个元素，那么就得到了一个新的排列。

需要一个数组来标记每个元素是否被使用。在每一层中，需要遍历序列中的每一个元素。如果该元素未被使用，则选择该元素，然后进入下一层；返回当前层时，取消选择该元素（回溯），继续选择下一个可用元素。

时间复杂度：$O(n^n)$，实际是 $T(n+n^2+…+n^n)$。
空间复杂度：$O(n×n!)$。需要保存 $n!$ 个解，每个解所需的空间为 $n$。如果不算保存结果所需的空间，那么空间复杂度为 $O(n)$，即递归的深度。

这种方法得到的全排列是字典序升序的。

代码：

var res [][]int
var flag []bool

func permute(nums []int) [][]int {
	if len(nums) == 0 {
		return nil
	}
	res = [][]int{}
	flag = make([]bool, len(nums))
	dfs(nums, []int{})
	return res
}

func dfs(nums, cur []int) {
	if len(cur) == len(nums) {
		res = append(res, copyNums(cur))
		return
	}
	for i := 0; i < len(nums); i++ {
		if flag[i] == false {
			flag[i] = true
			dfs(nums, append(cur, nums[i]))
			flag[i] = false // 回溯
		}
	}
}

解法三：回溯交换法

这种方法的思路最为简单：一个长为 $n$ 的字符串 s，它的所有排列，相当于每个 s[i] 作为第一个元素，然后剩下的 n-1 个字符的所有排列。

时间复杂度：$O(\sum_{k = 1}^{n}{A_n^k})$。
空间复杂度：$O(n×n!)$。需要保存 $n!$ 个解，每个解所需的空间为 $n$。如果不算保存结果所需的空间，那么空间复杂度为 $O(n)$，即递归的深度。

时间复杂度推导

第一层循环 $n$ 次，第二层循环 $n-1$ 次，…，第 n 层循环 1 次。如果将递归过程想象成一棵树，那么第一层递归有 $n$ 个节点，第二层递归有 $n×(n-1)$ 个节点，…，最后一层递归有 $n!$ 个节点。循环的总次数就是树的节点总数： $T(n + n×(n-1) + n×(n-1)×(n-2) + … + n!) = O(\sum_{k = 1}^{n}{A_n^k})$

注意：这种方法得到的全排列不是字典序升序的。

代码要注意：从第一个元素开始交换而不是从第二个元素开始，保证当前序列的每个元素都可以作为开头元素。

实现上有两种方式。一种是每当递归到最后一层时，新增一个结果，这需要使用全局变量保存所有结果。

var res [][]int

func permute(nums []int) [][]int {
	if len(nums) == 0 {
		return nil
	}
	res = [][]int{}
	dfs(nums, 0)
	return res
}

func dfs(nums []int, start int) {
	if start == len(nums)-1 { // 到最后一层再保存结果
		res = append(res, copyNums(nums))
		return
	}
	for i := start; i < len(nums); i++ { // i 从 start 开始
		nums[start], nums[i] = nums[i], nums[start] // 交换
		dfs(nums, start+1)
		nums[start], nums[i] = nums[i], nums[start] // 换回原来的位置，回溯
	}
}

另一种是分治法的思路。对于 n 个字符的全排列，先选出某个字符 s[i]，然后求解子问题 剩下的 n-1 个字符的全排列。然后在子问题每个解的开头加上选出的字符 s[i]，就是当前问题的解了。

func permute(nums []int) [][]int {
	if len(nums) <= 1 {
		return [][]int{nums}
	}
	res := [][]int{}
	for i := 0; i < len(nums); i++ {
		nums[0], nums[i] = nums[i], nums[0] // 将 i 换到第一个位置
		subres := permute(nums[1:])         // 求剩余 n-1 个元素的全排列
		for _, v := range subres {          // n-1 个元素的排列，前面加上 s[0]，得到 n 个元素的排列
			res = append(res, append([]int{nums[0]}, v...))
		}
		nums[0], nums[i] = nums[i], nums[0] // 恢复之前的次序
	}
	return res
}

三种解法对比

解法一、二均能得到按字典序升序的全排列，解法三则不能。

从 LeetCode 实际执行结果来看，三种解法的时间、空间复杂度均不相上下。

全排列（包含重复元素）

如何去重？

这道题是 LeetCode 47题。

如果序列中包含重复元素，上述三种解法该如何修改？

对于解法一，按照下一个排列的规则，当到达最后一个排列后，再下一个排列就是第一个排列。因此只需要不断取下一个排列，直到与第一个排列相等时终止。比较两个排列是否相等需要 $O(n)$，因此时间复杂度变为 $O(n^2 ×n!)$。代码略。

对于解法二和解法三，需要在每层递归中不重复选择相同的元素。有两种方法：

  • 方法一：将原数组排序，每层递归中，相邻的相同元素，只选择第一个（或只选择最后一个）
  • 方法二：是使用一个哈希表记录本轮递归过程中已经选择过的元素，不再重复选择，这种方法对空间复杂度的影响是 $O(n)$

解法一：下一个排列

略。

解法二：回溯遍历法

解法二使用排序或哈希表均可去重。这里以排序为例：将原数组排序，每层递归中，相邻的相同元素，只选择最后一个。

时间复杂度：不变，$O(n^n)$。
空间复杂度：不变，$O(n)$。

var res [][]int
var flag []bool

func permuteUnique(nums []int) [][]int {
	if len(nums) == 0 {
		return nil
	}
+	sort.Ints(nums) // 先排序
	res = [][]int{}
	flag = make([]bool, len(nums))
	dfs(nums, []int{})
	return res
}

func dfs(nums, cur []int) {
	if len(cur) == len(nums) {
		res = append(res, copyNums(cur))
		return
	}
	for i := 0; i < len(nums); i++ {
+		if i < len(nums)-1 && flag[i+1] == false && nums[i] == nums[i+1] { // 相同的元素，选择最后一个
+			continue
+		}
		if flag[i] == false {
			flag[i] = true
			cur = append(cur, nums[i])
			dfs(nums, cur)
			flag[i] = false
			cur = cur[:len(cur)-1]
		}
	}
}

解法三：回溯交换法

解法三只能使用哈希表去重，因为它会修改原数组的顺序。使用一个哈希表记录本轮递归过程中已经选择过的元素，不再重复选择。

时间复杂度：不变，$O(\sum_{k = 1}^{n}{A_n^k})$。
空间复杂度：从 $O(n)$ 变为 $O(n^2)$。

var res [][]int

func permuteUnique(nums []int) [][]int {
	if len(nums) == 0 {
		return nil
	}
+	sort.Ints(nums) // 先排序
	res = [][]int{}
	dfs(nums, 0)
	return res
}

func dfs(nums []int, start int) {
	if start == len(nums)-1 {
		res = append(res, copyNums(nums))
		return
	}
+	selected := map[int]bool{}
	for i := start; i < len(nums); i++ {
+		if _, ok := selected[nums[i]]; ok { // 已经选择过的就不再选择
+			continue
+		}
+		selected[nums[i]] = true
		nums[start], nums[i] = nums[i], nums[start]
		dfs(nums, start+1)
		nums[start], nums[i] = nums[i], nums[start]
	}
}
免责声明： 以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。
@小牛知识库 xnip.cn