javascript中将多个排序序列合并为一个排序序列的算法

Question

注意：我不想使用任何库。试图解决https://icpc.kattis.com/problems/stacking

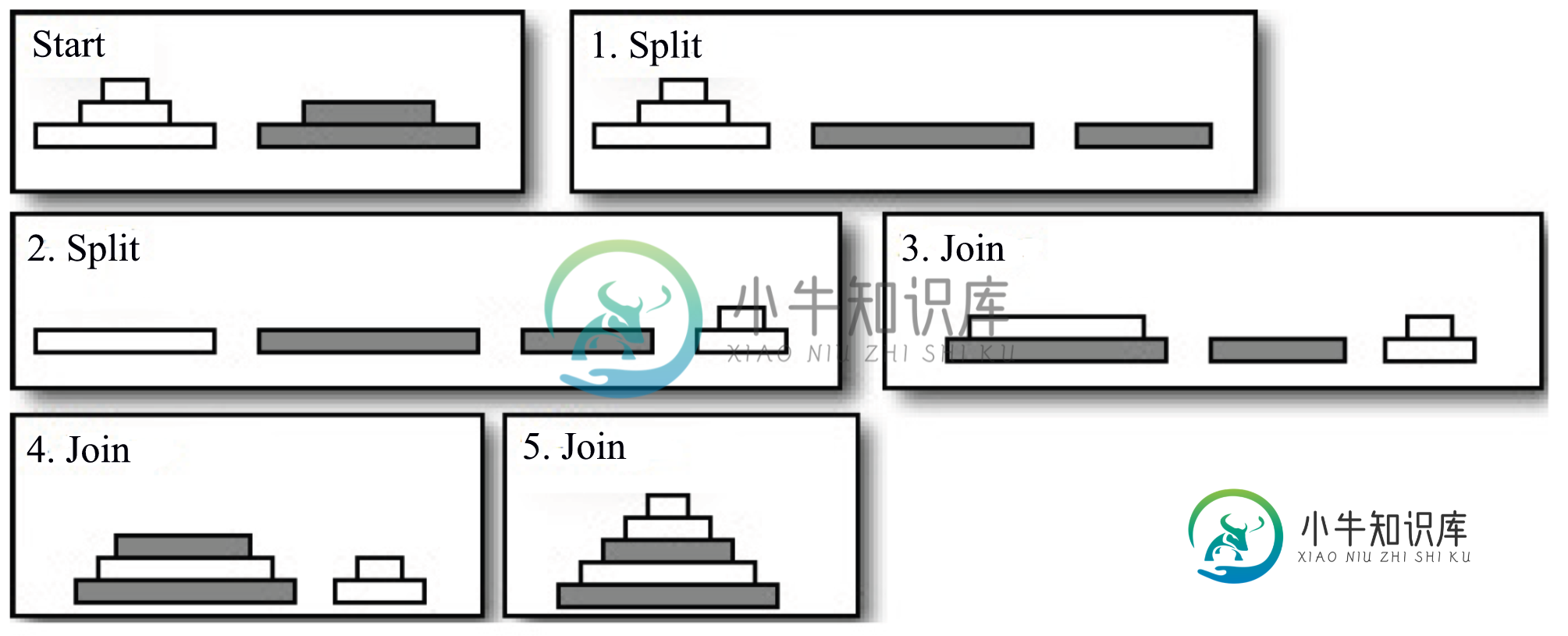
在以下条件下，合并排序数组所需的最小操作数是多少：

拆分：可以将单个堆栈拆分为两个堆栈，方法是将堆栈的任何顶部提起并放在一边，形成一个新堆栈。

连接：两个堆栈可以通过将一个放在另一个上面来连接。仅当顶部堆叠的底板不大于底部堆叠的顶板时，才允许这样做，也就是说，必须正确订购连接的堆叠。

Answer 1

只需将它们添加到一个大数组中并进行排序。

您可以使用堆，将每个序列的第一个元素添加到堆中，弹出最低的元素（这是您的第一个合并元素），从弹出的元素序列中添加下一个元素，然后继续，直到所有序列都结束。

不过，将它们添加到一个大数组中并对其进行排序要容易得多。

Answer 2

简单的方法是连接所有的k序列，并对结果进行排序。但是如果每个序列都有n元素，那么代价将是O（k*n*log（k*n））。太多了！

相反，您可以使用优先级队列或堆。这样地：

var sorted = [];
var pq = new MinPriorityQueue(function(a, b) {
  return a.number < b.number;
});
var indices = new Array(k).fill(0);
for (var i=0; i<k; ++i) if (sequences[i].length > 0) {
  pq.insert({number: sequences[i][0], sequence: i});
}
while (!pq.empty()) {
  var min = pq.findAndDeleteMin();
  sorted.push(min.number);
  ++indices[min.sequence];
  if (indices[min.sequence] < sequences[i].length) pq.insert({
    number: sequences[i][indices[min.sequence]],
    sequence: min.sequence
  });
}

优先级队列最多同时包含k个元素，每个序列一个元素。继续提取最小的元素，并在该序列中插入以下元素。

因此，成本将为：

• k*n插入到k元素堆中：O（k*n）
• k*n在k元素堆中删除：O（k*n*log（k））
• 每个数字的各种常量运算：O（k*n）

所以只有O（k*n*log（k））

Answer 3

这个问题已经解决了一个多世纪，可以追溯到赫尔曼·霍勒瑞斯（Hermann Hollerith）和庞切卡（punchcards）。巨大的Punchcard集合，例如人口普查产生的Punchcard集合，通过将它们划分为批次，对每个批次进行排序，然后合并排序的批次，即所谓的“合并排序”。你在1950年代科幻电影中看到的那些磁带机很可能是将多个分类的磁带合并到一个磁带上。

你需要的所有算法都可以在https://en.wikipedia.org/wiki/Merge_algorithm.在JS中写这一点很简单。更多信息可在问题N路合并算法中获得。也可以看到这个问题，这是一个几乎完全重复的问题，尽管我不确定任何答案都很好。

天真的康卡特和度假村方法甚至不能作为问题的答案。有些天真的从任何输入中获取下一个最小值的方法要好得多，但不是最优的，因为找到下一个输入以获取值所需的时间比必要的时间要多。这就是为什么使用“最小堆”或“优先级队列”的最佳解决方案。

这是一个真正简单的版本，我没有要求优化，除了能够看到它在做什么：

const data = [[1, 3, 5], [2, 4]];    

// Merge an array or pre-sorted arrays, based on the given sort criteria.
function merge(arrays, sortFunc) {
  let result = [], next;
   
  // Add an 'index' property to each array to keep track of where we are in it.
  arrays.forEach(array => array.index = 0);
 
  // Find the next array to pull from.
  // Just sort the list of arrays by their current value and take the first one.     
  function findNext() {
    return arrays.filter(array => array.index < array.length)
      .sort((a, b) => sortFunc(a[a.index], b[b.index]))[0];
  }

  // This is the heart of the algorithm.
  while (next = findNext()) result.push(next[next.index++]);

  return result;
}

function arithAscending(a, b) { return a - b; }

console.log(merge(data, arithAscending));