登录
目录
当前位置： 首页 > 文档资料 > 文章推荐 2 >

【数据结构】线段树原理及其实现

优质
小牛编辑
124浏览
2023-12-01

问题引入

给定一个长度为 $n$ 的序列，需要频繁地求其中某个区间的最值，以及更新某个区间的所有值。

最朴素的算法是遍历地查询与插入，则查询的时间复杂度 $O(q×n)$，$q$ 为查询的个数。在数据量大、查询次数多的时候，效率是很低的。

另一种思路是使用一个 $O(n^2)$ 的数组，a[i][j] 表示区间 [i,j] 的最小值。这样查询操作的复杂度为 O(1)，相当于用空间换时间。但是修改某个区间的值较麻烦，空间复杂度较大。

线段树可以解决这类需要维护区间信息的问题。线段树可以在 $O(logn)$ 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

线段树简介

以序列 {5,9,7,4,6,1} 为例，一共 6 个元素。构成的线段树是这样的：

每个节点代表一个区间，节点的值是该区间的最小值，比如根节点表示区间 [0,5] 内的最小值是 1。每个节点的左孩子是该节点所代表的的区间的左半部分，右孩子是右半部分。

线段树的每个节点可以储存不同的值，例如区间内的最大值、最小值、区间的求和等等。上图示例中，线段树节点保存的是最小值。

可以看到，线段树有以下几个特点：

  • 它是一棵近似于完全二叉树的平衡二叉树
  • 每个非叶节点一定有两个子节点
  • 每个叶子节点对应数组中的一个元素

构建线段树

显然，可以通过递归来构建一棵线段树。如果区间左右下标相等，说明这是一个叶子节点，创建新节点并返回。否则，先递归构建左半区，再构建右半区，然后将当前节点的值设为左右子树的最小值。

时间复杂度：O(n)，需要创建 n 个节点。 空间复杂度：O(n)，同上。

线段树的节点定义与构建线段树的代码如下（以最小值为例）：

type SegmentTreeNode struct {
	start int
	end   int
	min   int
	left  *SegmentTreeNode
	right *SegmentTreeNode
}

func BuildSegmentTree(nums []int, left, right int) *SegmentTreeNode {
	if left > right {
		return nil
	}
	root := &SegmentTreeNode{left, right, nums[left], nil, nil} // 根据节点区间的左边界值初始化
	if left == right {
		return root
	}
	mid := (left + right) / 2
	root.left = BuildSegmentTree(nums, left, mid)
	root.right = BuildSegmentTree(nums, mid+1, right)
	root.min = min(root.left.min, root.right.min)
	return root
}

单点更新

更新序列中的一个节点，同时将这种变化体现到线段树上。只需要递归地找到这个叶子节点，更新值，然后依次向上返回，更新沿途每个节点的值即可。

时间复杂度：$O(logn)$

代码：

func (root *SegmentTreeNode) Modify(index, value int) {
	if root.start == root.end && root.start == index { // 找到被改动的叶子节点
		root.min = value
		return
	}
	mid := (root.start + root.end) / 2
	if index <= mid {
		root.left.Modify(index, value)
		root.min = min(root.right.min, root.left.min)
	} else {
		root.right.Modify(index, value)
		root.min = min(root.left.min, root.right.min)
	}
}

区间查询

构建好线段树以后，如何查找某个区间的最小值？思想是从线段树中选出若干个区间，使它们合并后恰好涵盖整个查询区间；整个查询区间的最小值，就是这些小区间的最小值的最小值。

一般地，如果要查询的区间是 $[l, r]$，则可以将其拆成最多为 $O(logn)$ 个极大的区间，合并这些区间即可求出 $[l, r]$ 的答案。

设查询区间为 [start, end]，线段树的当前节点为 root。查询区间和当前节点代表的区间有以下三种情况：

  1. 查询区间包含当前区间，即 start <= root.start && root.end <= end，则直接返回当前区间的最小值
  2. 查询区间与当前区间无交集，即 start > root.end || end < root.start，返回无穷大
  3. 查询区间与当前区间有交集，则分别地查询当前区间的左右子树，返回左右子树的最小值

时间复杂度：$O(logn)$

代码：

func (root *SegmentTreeNode) Query(start, end int) int {
	if start <= root.start && end >= root.end {
		return root.min
	}
	if start > root.end || end < root.start {
		return math.MaxInt64
	}
	return min(root.left.Query(start, end), root.right.Query(start, end))
}

区间更新

区间更新是指对某个长度为 m 的区间内的全部元素执行相同的操作。

简单的方法是执行 m 次单点更新，时间复杂度为 $O(mlogn)$。另一种方法是先递归地更新左子树和更新右子树，然后再更新当前节点。这种方法需要递归地更新 m 个叶节点，因此其时间复杂度相比于 $O(mlogn)$ 并没有太大的优化。这两种方法在 m 很大的时候耗时都无法接受。

线段树引入了延迟标记的概念，能够在 $O(logn)$ 的时间内完成区间的更新。简而言之，在更新某个区间的所有值时，并没有立刻更新每个叶节点的值，而是将更新操作暂存在这个区间所对应的父节点上，之后特定的时机再将操作下传给子节点。

还是以序列 {5,9,7,4,6,1} 为例，假设我们要将区间 [0,2] 的 3 个元素的值都加 2，则其线段树的变化如下所示：

也就是说，对区间 [0,2] 的修改并没有下传到值为 5、9、7 的三个叶节点上，而是先暂存在父节点的 mark 字段里，只更新父节点的值。这个 mark 字段，就是“延迟标记”。这里我们对 [0,2] 的每个元素加 2，那么父节点保存的区间最小值自然也要加 2。

有了延迟标记，另一个问题就是什么时候下传延迟标记？答案是在访问任何节点的子节点的时候，“访问”既包括区间更新时的访问，也包括区间查询时的访问。

在访问任何节点的子节点之前，如果当前节点有延迟标记，那么要先将延迟标记下传给左右子节点，清除当前节点的延迟标记，再去访问它的子节点。这样能保证每次访问某个节点时，该节点已经按照之前的所有更新操作修改过了，该节点的值是最新的。

如下图所示，当我们试图访问表示 [0,1] 区间的节点时，会先将其父节点的延迟标记下传：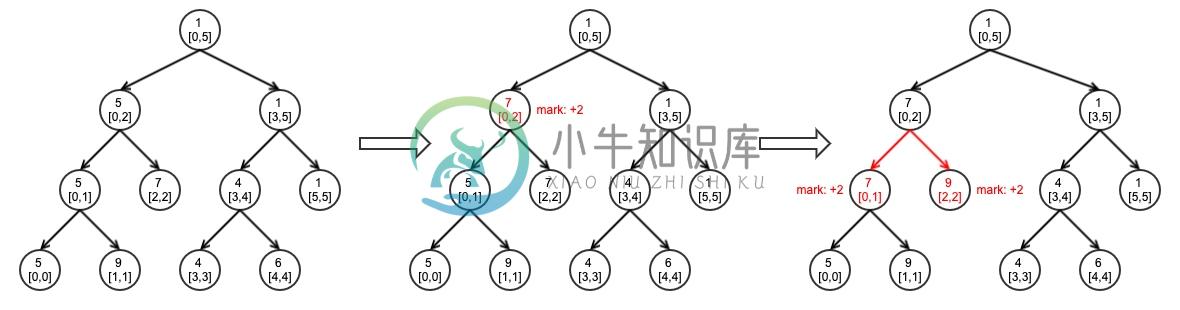

增加延迟标记后的代码如下：

// 区间更新
func (root *SegmentTreeNode) Update(start, end, delta int) {
	if start <= root.start && end >= root.end {
		root.mark += delta
		root.min += delta
		return
	}
	if start > root.end || end < root.start {
		return
	}
	if root.mark != 0 { // 如果当前节点的延迟标记不为空，下发到左右子节点
		root.left.mark += root.mark
		root.left.min += root.mark
		root.right.mark += root.mark
		root.right.min += root.mark
		root.mark = 0 // 清空当前节点的延迟标记
	}
	root.left.Update(start, end, delta)
	root.right.Update(start, end, delta)
	root.min = min(root.left.min, root.right.min)
}

// 区间查询
func (root *SegmentTreeNode) Query(start, end int) int {
	if start <= root.start && end >= root.end {
		return root.min
	}
	if start > root.end || end < root.start {
		return math.MaxInt64
	}
	// 增加了如下判断
	if root.mark != 0 { // 如果当前节点的延迟标记不为空，下发到左右子节点
		root.left.mark += root.mark
		root.left.min += root.mark
		root.right.mark += root.mark
		root.right.min += root.mark
		root.mark = 0 // 清空当前节点的延迟标记
	}
	return min(root.left.Query(start, end), root.right.Query(start, end))
}

有了区间更新后，就不再需要单点更新了。单点更新就相当于是区间更新的特例。

使用数组存储线段树

由上面的示意图可知，线段树是一棵类似于完全二叉树的平衡二叉树。这种树的存储密度较高，因此可以使用数组来存储树。

使用数组存储树时，下标 0 作为根节点。对于下标为 i 的节点，其左右孩子的下标分别为 2i+1、2i+2。

对于长度为 $n$ 的序列，可以直接申请一个大小为 2n+1 的数组。推导过程如下：

  • 该线段树一共有 $n$ 个结点，高度为 $h=\lceil logn\rceil$。除了最后一层外，线段树的 1 ~ h-1 层构成了一棵满二叉树。
  • 高为 $h$ 的满二叉树的节点总数为 $2^h-1$。故线段树的节点数 $n$ 与高度 $h$ 有如下关系：$2^{h-1}-1 < n <= 2^h-1$。不等式左右分别乘 2，有 $2^h-2<2n$，即 $2^h-1 < 2n+1$。
  • 因此 2n+1 个节点能够存储高为 $h$ 的满二叉树。

也可以直接申请一个大小为 4n 的数组来存储线段树。这样可以保存第 $h+1$ 层的所有无用的叶节点。推导过程同上：$2^{h-1}-1 < n => 2^{h+1}-1<4n+3$。

代码略。

完整代码

type SegmentTreeNode struct {
	start int
	end   int
	min   int
	mark  int // 延迟标记，表示区间内的所有值的变化量
	left  *SegmentTreeNode
	right *SegmentTreeNode
}

func BuildSegmentTree(nums []int, left, right int) *SegmentTreeNode {
	if left > right {
		return nil
	}
	root := &SegmentTreeNode{left, right, nums[left], 0, nil, nil} // 根据节点区间的左边界值初始化
	if left == right {
		return root
	}
	mid := (left + right) / 2
	root.left = BuildSegmentTree(nums, left, mid)
	root.right = BuildSegmentTree(nums, mid+1, right)
	root.min = min(root.left.min, root.right.min)
	return root
}

func (root *SegmentTreeNode) Update(start, end, delta int) {
	if start <= root.start && end >= root.end {
		root.mark += delta
		root.min += delta
		return
	}
	if start > root.end || end < root.start {
		return
	}
	root.PushDown()
	root.left.Update(start, end, delta)
	root.right.Update(start, end, delta)
	root.min = min(root.left.min, root.right.min)
}

func (root *SegmentTreeNode) Query(start, end int) int {
	if start <= root.start && end >= root.end {
		return root.min
	}
	if start > root.end || end < root.start {
		return math.MaxInt64
	}
	root.PushDown()
	return min(root.left.Query(start, end), root.right.Query(start, end))
}

func (root *SegmentTreeNode) PushDown() {
	if root.mark != 0 { // 如果当前节点的延迟标记不为空，下发到左右子节点
		root.left.mark += root.mark
		root.left.min += root.mark
		root.right.mark += root.mark
		root.right.min += root.mark
		root.mark = 0 // 清空当前节点的延迟标记
	}
}

测试：

func main() {
	list := []int{5, 9, 7, 4, 6, 1}
	root := BuildSegmentTree(list, 0, len(list)-1)
	fmt.Println(root.Query(-1, 2)) // 区间 [-1,2] 的最小值为 5
	fmt.Println(root.Query(3, 1))  // 非法区间，返回 MaxInt64
	root.Update(0, 0, -5)          // 相当于 list[0] -= 5
	fmt.Println(root.Query(0, 1))  // 区间 [0,1] 的最小值为 0
}

总结

什么时候用线段树：如果问题可以转化为一系列区间操作。比如：

  • 查找区间的最大值、最小值、和
  • 对区间的一个点的值进行修改
  • 对区间的一段值进行统一的修改

什么时候不能用线段树：如果需要删除或者增加区间中的元素，区间大小将发生变化，线段树需要重新构建。此时无法使用线段树。

参考资料：

免责声明： 以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。
@小牛知识库 xnip.cn