【LeetCode】一个模板通杀所有「二分查找」问题
本文涉及到的 LeetCode 题目:
个人笔记
- 建议使用左闭右开的模板,需要注意的细节更少
// 返回第一个满足 x >= target 的 x 的下标
// 也相当于按升序插入 target 的位置
// 不存在满足此条件的 x 时,返回 len(nums),即 target 应该插入在 nums 末尾
func LowerBound(nums []int, target int) int {
left, right := 0, len(nums)
for left < right {
mid := left+(right-left)>>1
if nums[mid] >= target { // find first x >= target
right = mid // 下界是在左侧,所以应该往左缩小区间,因此调 right
} else {
left = mid+1
}
}
return left
}
引言
二分查找有很多应用场景。可以说,只要问题对应的函数图像在给定区间是单调的,那就可以使用二分查找在这个区间搜索目标值。
二分查找的题目类型有:
- 查找特定值
- 查找第一个大于等于特定值的元素
- 查找最后一个小于等于特定值的元素
- …
二分查找说简单也简单,说难也难。说简单是因为,它无非就是一个循环里嵌套了两三个 if/else。说难是因为,它有很多细节,而且每个细节都不能出错:
left、right要初始化为0、n-1还是0、n?- 循环的判定条件是
left < right还是left <= right? if的判定条件应该怎么写?if的判定条件为真时,应当更新left还是right?- 更新
left、right时,mid要不要±1? - …
可以看到,二分查找不仅有很多类型,还有很多细节。以前每次做二分查找问题的时候,我都会重新推导一遍代码,但是由于细节很多,难免出错。有没有一个通用的模板,能够一劳永逸地解决所有二分查找问题呢?
本文首先从「找下界」入手,引出通用的二分查找模板;然后在不同类型的二分查找中套用这个模板,验证其适用性;最后对比了「闭区间」和「左闭右开」两种写法,说明了这两种写法其实是同一种思路。
本文希望通过最自然、最容易理解的方式来描述思路。理解了本文的内容后,我们可以直接「写」出模板,而不需要「背」会模板,且无论哪种写法都能信手拈来。
找下界
问题定义
给定一个升序排列的数组,我们将满足 x ≥ target 的第一个元素定义为「下界」。给定一个目标值 target,要求返回其下界的下标。如果下界不存在,返回数组长度。
比如:对于数组 [0,1,2,3,4],当 target=3 时,返回下标 3;当 target=5 时,返回下标 5。
C++ STL 中的 lower_bound() 函数就实现了这个功能。
思路描述
对于数组 [1,2,3,5,5,5,6,7,9],令 target=5,则满足 x ≥ target 的下界的下标应该是 3,如下图所示: 
可以看到,从这个位置将数组分为左右两部分,左侧的元素都「小于」target,右侧的元素都「大于等于」target: 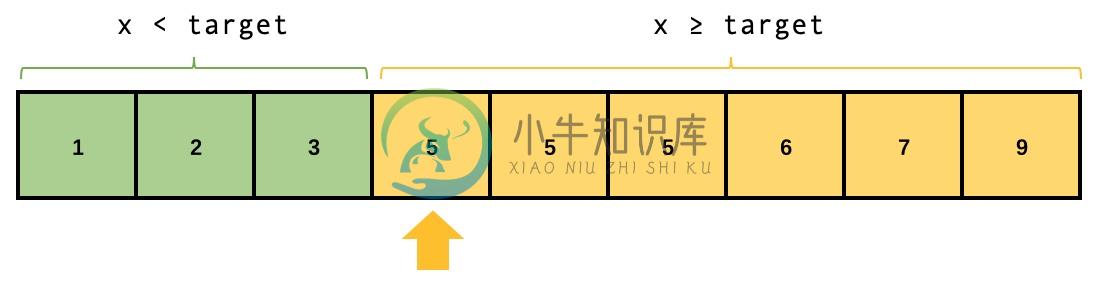
接下来,我们使用「闭区间」的写法来描述思路。先定义几个变量:
- 区间范围为
[left,right],left、right是区间的左右边界的下标 mid是[left,right]的中间位置- 初始时,
left、right分别指向数组的第一个和最后一个元素 - 当
left > right时,表示区间为空
如果我们在二分查找的过程中,不断右移 left,左移 right,使得所有「小于」target 的元素都在 left 左侧,所有「大于等于」target 的元素都在 right 右侧,那么当区间为空时,left 就是要查找的下界: 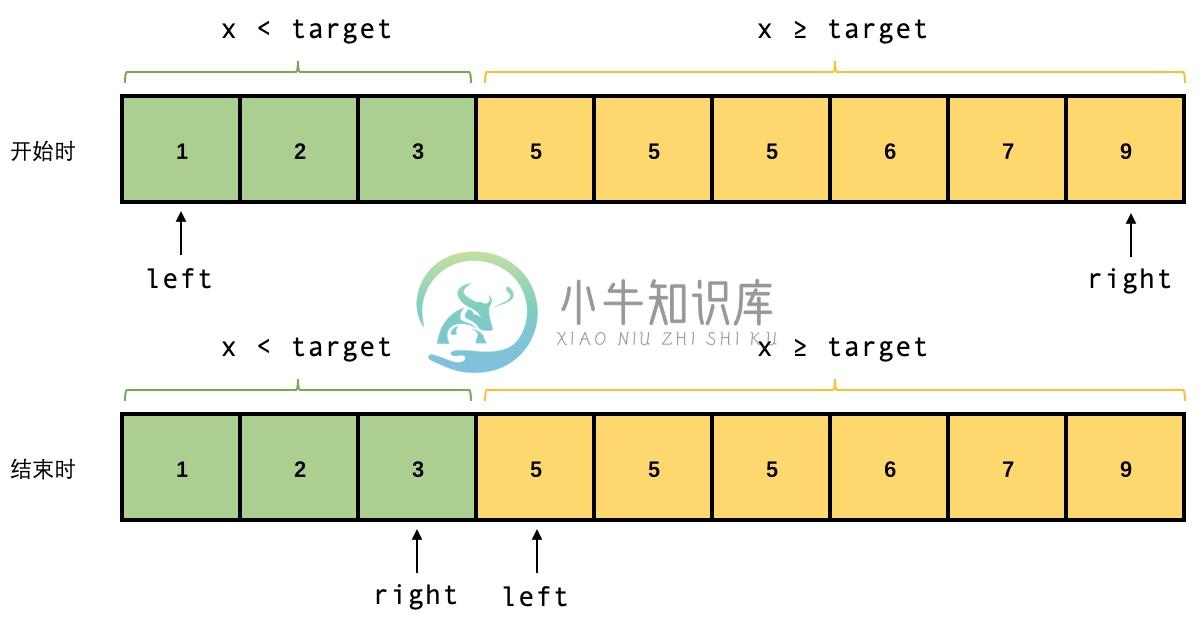
根据上述思路,算法步骤如下:
- 若
nums[mid] >= target,说明[mid,right]区间的所有元素均「大于等于」target,因此right左移,有right = mid-1 - 否则,说明
[left,mid]区间的所有元素均「小于」target,因此left右移,有left = mid+1 - 重复上述步骤,直到区间为空,表示找到了下界,返回
left。因此循环条件为left <= right,表示“区间不为空” - 注意,上述两个赋值语句均跳过了中间元素
mid
上面示例的查找过程如下: 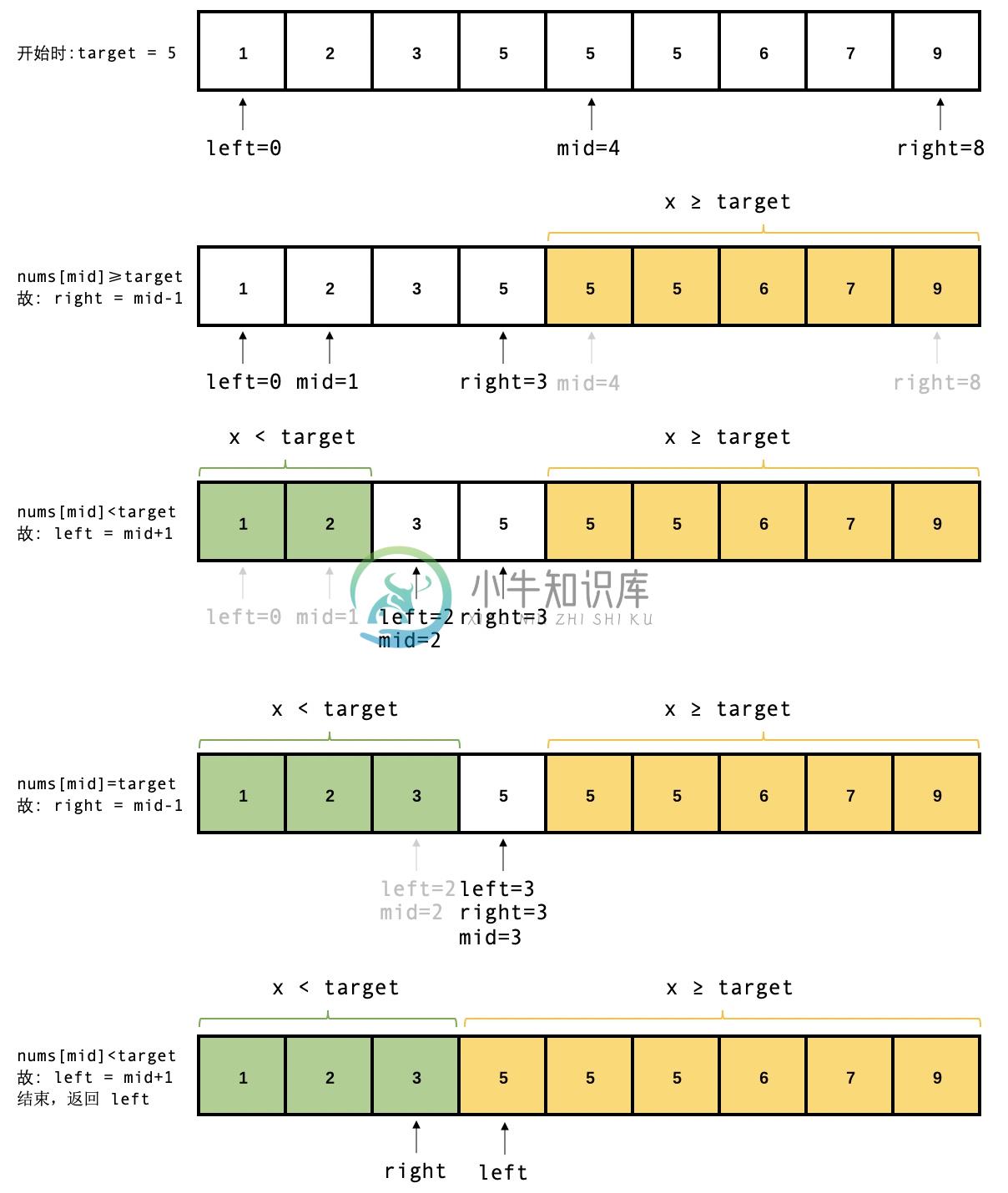
模板代码
// 查找满足 x ≥ target 的下界的下标
func LowerBound(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left) >> 1
if nums[mid] >= target { // 这里的比较运算符与题目要求一致
right = mid - 1
} else {
left = mid + 1
}
}
return left // 返回下界的下标
}
当区间为空时,left 指向第一个「大于等于」target 的元素,因此要返回 left。若下界不存在,有 left == n。「下界」实际上就是按顺序插入 target 的位置。
上面的代码中,if 的判定条件和给定的比较规则是一致的:要找满足 x >= target 的第一个元素,所以是 if nums[m] >= target。如果要找满足 x > target 的第一个元素,那么只需改为 if nums[m] > target。if 为真时更新 right。
最后注意一些细节:
left、right的初值为0、n-1,表示「闭区间」- 循环的判定条件是
left <= right,表示区间不为空 - 更新
left和right时均跳过了中间元素mid
无论是找下界、还是找上界、还是找特定值,都可以套用这个模板代码。接下来,我们看看如何使用这一个模板,通杀所有二分查找问题。
找上界
定义满足 x ≤ target 的最后一个元素为「上界」。给定一个 target,要求返回升序数组中上界的下标。比如:对于数组 [0,1,2,3,4],当 target=3 时,返回下标 2;当 target=5 时,返回下标 4。
根据上界和下界的定义,我们可以发现:上界和「互补的」下界是相邻的,并且 上界 = 下界 - 1。比如 x ≤ target 的上界和 x > target 的下界相邻。因此,所有找上界的问题,都可以转换为「互补的」找下界的问题。
对于本题而言,要找 x ≤ target 的上界,首先套用上文的模板代码,实现找 x > target 的下界的函数:
// 查找满足 x > target 的下界的下标
func LowerBound(nums []int, target int) int {
// ...
if nums[mid] > target { // 只需将这里改为 >
// ...
}
然后将下界的下标减一,就是我们要找的上界:
// 查找满足 x ≤ target 的上界的下标
func UpperBound(nums []int, target int) int {
return LowerBound(nums, target)-1
}
或者,我们可以直接将 LowerBound 代码中的返回语句改为 left-1 或者 right,就能得到一个纯净的、无依赖的 UpperBound:
func UpperBound(nums []int, target int) int {
// ...
if nums[mid] > target { // 这里是 >
// ...
return right // 或者返回 left-1
}
可以看到,找下界的模板代码略作修改,就能用来查找上界了!
查找指定值第一次出现的位置
查找满足 x == target 的第一个元素,如果不存在,返回 -1。
只需要先查找满足 x >= target 的下界,然后再判断下界与 target 是否相等。只需在模板代码中增加一个判断:
func searchFirst(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left) >> 1
if nums[mid] >= target {
right = mid - 1
} else {
left = mid + 1
}
}
+ if left >= len(nums) || nums[left] != target { // 判断一下是否越界,或者不相等
+ return -1
+ }
return left
}
查找指定值最后一次出现的位置
查找满足 x == target 的最后一个元素,如果不存在,返回 -1。
只需要先查找满足 x <= target 的上界,然后再判断上界与 target 是否相等。上文中已经描述了如何将查找上界转化为查找下界,直接调用模板代码:
func searchLast(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left) >> 1
if nums[mid] > target { // 这里是 > 而不是 >=
right = mid - 1
} else {
left = mid + 1
}
}
if right < 0 || nums[right] != target { // 判断一下是否越界,或者不相等
return -1
}
return right // 这里返回 right 而不是 left
}
这两道题对应于 LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置。有了上面两个函数,题解代码仅需一行:
func searchRange(nums []int, target int) []int {
return []int{searchFirst(nums, target), searchLast(nums, target)}
}
查找指定值的位置
这是最基本的二分查找问题,对应于 LeetCode 35. 搜索插入位置:给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
之所以把这道题放在最后面说,是因为这道题完完全全就是找下界的题目!模板代码一行都不需要改:
func searchInsert(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left+(right-left)>>1
if nums[mid] >= target {
right = mid-1
} else {
left = mid+1
}
}
return left
}
target 按顺序插入的位置,就是满足 x ≥ target 的第一个元素的位置。由于可以返回任意一个等于目标值的位置,所以这里还可以增加一个判断,当 nums[mid] == target 时直接返回。代码略。
总结:模板代码
二分查找无论是找下界、还是找上界、还是找特定值,都可以套用「找下界」的模板代码:
- 循环条件为
left <= right,表示闭区间不为空 if的判定条件和给定的比较规则是一致的:比如要找满足x >= target的第一个元素,就令if nums[m] >= target;要找满足x > target的第一个元素,就令if nums[m] > targetif为真时,更新right:right = mid - 1;否则left = mid + 1- 当循环结束时,
left就指向下界,right指向「互补条件」的上界
对比:左闭右开的写法
两者对比
上面我们采用了「闭区间」的写法,这种情况下:
- 区间范围是
[left,right] - 循环条件是「小于等于」,表示
[left,right]不为空 right的初值为「最大值」left、right分别需要「±1」,才能使新区间不包含mid- 区间为空时,
left指向下界,right指向互补条件的上界 - 如果需要下界,只能返回
left
另一种常见的写法是「左闭右开」,比如 C++ 标准库 <algorithm> 中就采用了这种写法,带来的变化是:
- 区间范围是
[left, right) - 循环条件变为「小于」,表示
[left,right)不为空 right的初值为「最大值+1」right直接赋值为mid,不需要-1就能使新区间不包含mid- 区间为空时,
left、right都指向下界(它们重合) - 如果需要下界,可以返回任意一个!
模板代码
func LowerBound(nums []int, target int) int {
left, right := 0, len(nums) // 3. 下标的最大值为 n-1,故 right 初值为 n,即「最大值+1」
for left < right { // 2. 循环条件为「小于」
mid := left + (right-left) >> 1
if nums[mid] >= target {
right = mid // 4. right 不需要 -1
} else {
left = mid + 1
}
}
return left // 6. 返回 left、right 均可以
}
补充说明
有人认为「左闭右开」这种写法的优点是:
- 当区间为空时,「左闭右开」是
left == right,而「闭区间」是left > right,前者更为直观。比如:0 ≤ a < 0和0 ≤ a ≤ -1,前者更符合人类直觉 - 另外在这种情况下,返回
left和right均可,因为它们重合。而「闭区间」只能返回first
但在我看来,无论哪种写法,只要理解了思路,就都能很容易地将它们写出来。至于更喜欢哪种写法,就见仁见智了。
总结
本文主要介绍了一种通用的二分查找下界的模板代码,理解其原理后,不需要背模板,也可以自然地将代码写出来。
本文得出了以下结论:
- 二分查找无论是找下界、还是找上界、还是找特定值,都可以套用同一个模板代码
- 上界和下界是相邻的,因此找上界可以转换为「互补的」找下界的问题,从而套用本文的模板
- 「左闭右开」和「闭区间」的写法本质上都是相同的原理,只要理解了本文的内容,选择哪种写法都没有问题
在后续的文章中,我们将继续使用这个模板,解决更多的实际问题,请阅读:在实际问题中运用二分查找模板代码。

