9.2. 分析和解读数据
分析和解读数据
错误检查
试验开始之后的短时间内(几个小时或者1天),我们应该通过实时观察「试验概况」与「指标详情」页面,来检查试验数据是否表现正常,也就是检查是否有程序错误。如果包括原始版本在内的任一版本没有数据显示或者和正常数据相比有很大的、异常的差异,说明试验可能在集成环节出现问题,或者存在程序错误。这时需要停止试验,重新检查调试。
置信区间的解读
若短时间内的数据正常,试验应继续运行至预定的结束时间,然后就可以分析和解读试验数据,进而做出决策了。一般而言,这个试验时段大概是至少1-2个周,这样才能得出较为准确的结果。
我们主要通过某个指标的试验版本(均值)变化值以及置信区间来判断,在这个指标上,试验版本是否比对照版本(原始版本)表现得更好。
如果置信区间同为正或同为负,说明试验结果是统计显著的。如果置信区间为一正一负,说明试验结果是非统计显著的。
统计显著和效果显著
统计显著说明当前的样本容量条件下已经检测出试验版本和对照版本的差异。如果这个差异(变化)是正的,是不是说我们就可以下结论试验版本比对照版本好,应该发布该试验版本了呢?
以表格中 Case1 到 Case5 这 5 个试验版本的试验数据为例,Case1, Case2 和 Case3 结果都是统计显著的,Case4 和 Case5 是非统计显著的,我们还能做进一步的判断吗?
| 均值(变化) | 95% 置信区间 | 结果解读 | |
|---|---|---|---|
| Case1 | +8.0% | [+6.4%, +9.6%] | 统计显著 |
| Case2 | +4.0% | [+2.0%, +6.0%] | 统计显著 |
| Case3 | +3.0% | [+1.5%, +4.5%] | 统计显著 |
| Case4 | +2.5% | [-0.6%, +5.6%] | 非统计显著 |
| Case5 | +1.0% | [-1.0%, +3.0%] | 非统计显著 |
这里我们应该区分两个不同的概念:统计显著和效果显著。统计显著不等于真实效果显著,它只说明当前的统计功效下检测出了试验版本和对照版本的差异,但是这个差异有可能是非常小的,在实际应用中微不足道的。
因此,试验版本的结果只有兼备统计显著和效果显著两个特征,该版本才是可用的,值得发布的。这里,我们需要引入一个“最小重要变化”的概念来帮助我们判断和决策。最小重要变化是一个最小的可接受的效果标准,检测到的效果差异只有在此标准之上,我们才认为它是有实际价值的。这个标准通常由指标的具体意义和我们的优化需求来确定,例如 1% 或者 5%。
通过下面的图示我们看一下怎么应用最小重要变化这个标准来对试验数据做进一步的判断。 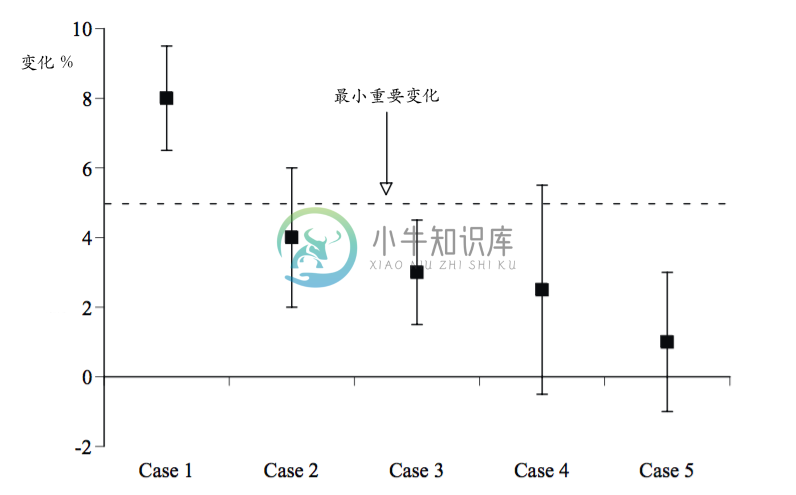 最小重要变化 δ 为 5% 的情况下,我们可以做如下判断:
最小重要变化 δ 为 5% 的情况下,我们可以做如下判断:
- Case1 的整个置信区间都在最小重要变化之上,它是效果显著的;
- Case2 的置信区间跨越了最小重要变化,它的效果是否显著是不确定的;
- Case3 的整个置信区间都在最小重要变化之下,它的效果是不显著的;
- Case4 的置信区间跨越了最小重要变化,它的效果是否显著是不确定的;
- Case5 的整个置信区间都在最小重要变化之下,它的效果是不显著的;
简而言之,在置信区间为正的情况下,只有其下限大于最小重要变化(而不是0),试验版本才是效果显著的。
最后试验数据的解读结果总结如下:
| 均值(变化) | 95% 置信区间 | 结果解读 | |
|---|---|---|---|
| Case1 | +8.0% | [+6.4%, +9.6%] | 统计显著,效果显著 |
| Case2 | +4.0% | [+2.0%, +6.0%] | 统计显著,效果不确定 |
| Case3 | +3.0% | [+1.5%, +4.5%] | 统计显著,效果不显著 |
| Case4 | +2.5% | [-0.6%, +5.6%] | 非统计显著,效果不确定 |
| Case5 | +1.0% | [-1.0%, +3.0%] | 非统计显著,效果不显著 |
只有 Case1 是有实际效果的可用版本。
解读非统计显著
前面我们提到,如果置信区间为一正一负,说明试验结果是非统计显著的。非统计显著说明当前收集的样本数据和试验的原假设(试验版本和对照版本没有差异)是一致的,注意,这并不意味着原假设是正确的。
以上面例子中的 Case4 为例,置信区间包含了 0(原假设),说明样本数据和原假设不冲突;但是,它同样包含了 5.6%,也就是说,版本的差异可能是 0,也可能是 5.6%,或者置信区间内的其他值。
也就是说,非统计显著只能说明当前的统计功效较小,不足以检测出试验版本和对照版本的真正差异。这个差异有可能很小,所以当前的样本容量即使较大也检测不出来;差异也有可能较大,但是因为样本容量较小,或者方差较大,导致统计功效小,同样检测不出来。
因此,在非统计显著的情况下,我们同样需要对实际效果做进一步的解读,这个手段依然是置信区间和最小重要变化。
上面的例子中,最小重要变化为 5% 的情况下,Case4 和 Case5 都是非统计显著,它们的效果如下:
- Case4 的置信区间跨越了最小重要变化,它的效果是否显著是不确定的;
- Case5 的整个置信区间都在最小重要变化之下,它的效果是不显著的;
| 均值(变化) | 95% 置信区间 | 结果解读 | |
|---|---|---|---|
| Case4 | +2.5% | [-0.6%, +5.6%] | 非统计显著,效果不确定 |
| Case5 | +1.0% | [-1.0%, +3.0%] | 非统计显著,效果不显著 |
根据效果可做如下判断:
- Case4 情况下我们不能得出可用的结论;
- Case5 情况下可以下结论版本差异很小,应维持原假设;
对于 Case4 这种情况我们应该怎么办呢?前面说了,差异可能较大,但是统计功效较小,我们不能下结论版本是否存在重要差异。
因为试验的统计功效取决于样本容量大小、样本数据的方差和试验方式等因素,我们可以通过这几方面的数据来决定下一步的对策:
- 如果试验已经充分进行(足够的时间,足够的样本容量),说明样本的方差较大,试验难以检测出版本差异,这种情况下我们可以重新设计和进行新的试验,改进统计功效;
- 如果试验进行的时间不够(如不到 7 天),或者样本容量可能不够(根据 APP 用户数大致判断),可以继续进行试验到足够时间和用户数,随着试验的进行,样本方差可能会减少,置信区间会进一步收敛;
统计功效的计算和解读
统计功效的作用是用来在置信区间的基础之上做进一步的判断。在统计显著和非统计显著这两种情况下统计功效的计算方式和解读稍有不同。
非统计显著时的统计功效
非统计显著时我们很可能做出决策——维持原假设,这样我们可能会犯第 II 类错误(取伪错误,原假设为假时未拒绝原假设,这个错误概率记为 β),我们要尽量减少这类错误 β 的概率,最好在 20% 以下。
统计功效 power = 1 - β,是指版本差异(效果)为某个指定值时,通过显著性检验能正确地把差异检验出来的概率。非统计显著情况下,我们取最小重要变化 δ 为指定值,计算针对此效果的统计功效。因为效果越大,统计功效越大;如果最小效果的统计功效足够,说明其他更大效果的统计功效也都是足够的
只要统计功效足够大,就保证了我们犯第 II 类错误的概率足够小。如果 power > 80%,说明原假设为假(存在大于 δ 的差异)时,我们做出正确判断(拒绝原假设)的可能是足够大的,只有不到 20% 的概率可能出错。
下面我们看看不同情况下怎么解读统计功效。
我们先看 Case5 这种情况(非统计显著、效果不显著),前面说过,这种情况基本可以下结论维持原假设了。不过,我们还可以通过统计功效对它进行进一步的检验。如果统计功效是 60%,说明功效一般,我们犯错的概率还是比较大;如果统计功效是 80%,说明功效足够,我们犯错的概率较小,我们之所以得到非统计显著的结果,是因为真实差异确实很小,而不是因为统计功效不够,因此,我们可以放心地维持原假设。
对于 Case4 这种情况(非统计显著、效果不确定),我们可以通过统计功效辅助决策下一步的行动:下结论拒绝原假设还是继续试验一段时间然后再观察结果。如果统计功效大于 80%,说明试验已经充分进行(足够的时间,足够的样本容量),很可能样本的方差较大,试验难以检测出版本差异,这种情况下我们可以重新设计和进行新的试验,改进统计功效。如果统计功效很小(如 30%),很可能是样本容量可能不够,可以继续进行试验到足够时间和用户数。
统计显著时的统计功效
统计显著的情况下,我们取置信区间的最小边界值(Case1 就是 6.4%)为指定值,计算针对此效果的统计功效。
为什么要用最小边界值为指定值呢?因为置信区间是对真实差异的一个区间估计,而最小边界值是其中绝对值最小的值,如果该效果的统计功效足够,说明置信区间内的其他更大效果的检测所需的统计功效也都是足够的。
在统计显著的情况下,统计功效主要用来针对 Case1 这种效果显著的情况来进行进一步的深入判断。因为是用最小边界值的到的统计功效,所以我们降低对它的功效要求。一般来说,该功效大于 50% (功效一般)我们就可以认为功效满足要求了;如果小于 50%,我们有理由怀疑统计功效不足导致置信区间的精度不够,为了得到更放心的结果,建议继续试验和观察。

