9.4. A/B 测试的统计学原理

A/B 测试的统计学原理

了解一些统计学知识对正确地进行 A/B 测试和研判试验结果是很有帮助的，本篇文章深入介绍了 AppAdhoc 平台上进行 A/B 测试的原理和背后的统计学依据。完全理解本文中提到的数学计算需要您掌握概率方面的一点基础知识。

统计学在 A/B 测试中的作用

A/B 测试是一种对比试验(下文中对比试验特指 AppAdhoc 平台上的 A/B 测试)，而试验就是从总体中抽取一些样本进行数据统计，进而得出对总体参数的一个评估。可以看出，做试验并从试验数据中得出有效结论的科学基础是统计学。

统计学的基本概念

• 总体：是客观存在的、具有某一共同性质的许多个体组成的整体； 总体是我们的研究对象，在对比试验中，总体就是网站/APP的所有用户。
• 样本：所谓样本就是按照一定的概率从总体中抽取并作为总体代表的一部分总体单位的集合体； 样本是我们的试验对象，在对比试验中缺省的对照版本和测试版本的用户都是样本。
• 参数：用来描述总体特征的概括性数字度量，称为参数，如总体平均数(μ)；在对比试验中总体参数就是所有用户的某个优化指标的平均值。
• 统计量：用来描述样本特征的概括性数字度量，称为统计量，如样本平均数(x)；在对比试验中统计量就是测试版本用户的某个优化指标的统计平均值。
• 均值：变量值的算数平均数。
• 方差：各变量值与其算术平均数离差平方的算术平均数。标准差是方差的平方根。
• 正态分布：是一种应用非常广泛的概率分布，它是下面介绍的假设检验等统计推断方法的数学理论基础。

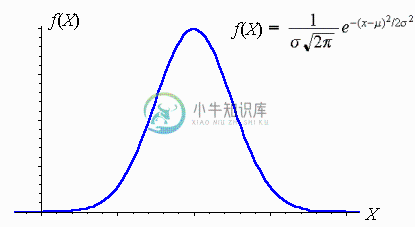
所以，对比试验的工作原理就是统计对照版本和测试版本两个样本的数据（样本数量，样本平均数和方差等），通过以正态分布为基础的统计学公式进行计算，衡量测试版本的总体参数(均值)是否比对照版本的总体参数有确定性的提升。

抽样

抽样是指按照随机原则，以一定概率从总体中抽取一定容量的单位作为样本进行调查，根据样本统计量对总体参数作出具有一定可靠程度的估计与推断。

抽样最重要的问题是抽取的样本是否能够代表总体。如果样本没有代表性，那么以样本的统计量数据来对总体参数进行估计就没有逻辑基础。

AppAdhoc 试验引擎的用户流量分割算法根据用户特征对用户进行聚类，把用户分为具有相同代表性的多个小组，然后通过随机抽样的方式得到测试版本的用户群（样本），保证了样本的代表性。

参数估计

参数估计是一种统计推断方法，用样本统计量去估计总体参数。 总体的统计指标在一定范围内以一定的概率取各种数值，从而形成一个概率分布，但是这个概率分布可能是未知的。 当总体分布类型已知（通常是正态分布），仅需对分布的未知参数进行估计的问题称为参数估计。

用来估计总体参数的统计量的名称称为估计量，如样本均值；估计量的具体数值称为估计值。参数估计方法有点估计与区间估计两种方法。

用样本估计量的值直接作为总体参数的估计值称为点估计。例如在对比试验中，缺省对照版本的优化指标均值就是对缺省版本总体的优化指标均值的一个点估计。

我们必须认识到，点估计是有误差的，样本均值不能完全代表总体均值。 在一些比较粗糙的 A/B 测试方式中，试验者得到对照版本和测试版本的均值之后，直接比较它们的大小，由此得出哪个版本更优的结论，这样的做法误差是非常大的，结论的可靠性没有保障。

点估计只能给出总体参数的一个大概值，但不能给出估计的精度。区间估计就是在点估计的基础上，给出总体参数的一个概率范围。区间估计的几个要素是点估计值、方差、样本大小以及估计的置信水平。 专业的 A/B 调试工具会通过结合这些要素的统计学公式来对结果进行科学地评估，而不是简单粗糙地比较点估计值的大小。

假设检验

从 A/B 测试的试验原理来看，它是统计学上假设检验(显著性检验)的一种形式。

假设检验(中的参数检验)是先对总体的参数提出某种假设，然后利用样本数据判断假设是否成立的过程。逻辑上运用反证法，统计上依据小概率思想。

小概率思想是指小概率事件（显著性水平 p < 0.05）在一次试验中基本上不会发生。反证法是指先提出假设，再用适当的统计方法确定假设成立的可能性大小；如可能性小，则认为假设不成立。

具体到对比试验，就是假设测试版本的总体参数（优化指标均值）等于对照版本的总体参数，然后利用这两个版本的样本数据来判断这个假设是否成立。

假设检验的基本概念

• 统计假设：是对总体参数(包括总体均值μ等)的具体数值所作的陈述。
• 原假设：是试验者想收集证据予以反对的假设 ,又称“零假设”，记为 H0； 对比试验中的原假设就是测试版本的总体均值等于对照版本的总体均值。
• 备择假设：也称“研究假设”，是试验者想收集证据予以支持的假设，记为 H1； 对比试验中的备择假设就是测试版本的总体均值不等于对照版本的总体均值。
• 双侧检验与单侧检验：如果备择假设没有特定的方向性，并含有符号“≠”，这样的称为双侧检验。如果备择假设具有特定的方向性，并含有符号 “>” 或 “<” 的假设检验，称为单侧检验。

提出假设

原假设和备择假设是一个完备事件组，而且相互对立。在一项假设检验中，原假设和备择假设必有一个成立，而且只有一个成立。 在对比试验中，因为我们试验的目的是通过反证法证明测试版本和对照版本有明显的不同（提升），所以我们的原假设是测试版本的总体均值等于对照版本的总体均值。

假设检验的两类错误

• 第 I 类错误(弃真错误)：原假设为真时拒绝原假设；第 I 类错误的概率记为 α(alpha)。
• 第 II 类错误(取伪错误)：原假设为假时未拒绝原假设。第 II 类错误的概率记为 β(Beta)。

α 是一个概率值，表示原假设为真时, 拒绝原假设的概率，也称为抽样分布的拒绝域。在这两类错误中，相对更加严重的是第 I 类错误，所以 α 的取值应尽可能小。常用的 α 值有 0.01，0.05，0.10， 由试验者事先确定。对比试验中使用的 α 值是 0.05(5%)，这是显著性检验中最常用的小概率标准值。

显著性水平 p(p-value)

显著性水平 p是指在原假设为真的条件下，样本数据拒绝原假设这样一个事件发生的概率。例如，我们根据某次假设检验的样本数据计算得出显著性水平 p = 0.04；这个值意味着如果原假设为真，我们通过抽样得到这样一个样本数据的可能性只有 4%。

那么，0.04 这个概率或者说显著性水平到底是大还是小，够还是不够用来拒绝原假设呢？这就需要把 p 和我们采用的第 I 类错误的小概率标准 α 来比较确定。假设检验的决策规则：

• 若 p ≤ α，那么拒绝原假设；
• 若 p > α，那么不能拒绝原假设。

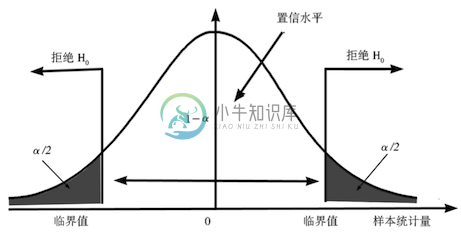
如果 α 取 0.05 而 p = 0.04，说明如果原假设为真，则此次试验发生了小概率事件。根据小概率事件不会发生的判断依据，我们可以反证认为原假设不成立。

显著性水平 p 的计算公式取决于假设检验的具体方式，将在下文的 t 检验部分介绍。

统计显著性 (Significance)

在假设检验中，如果样本数据拒绝原假设，我们说检验的结果是显著的；反之，我们则说结果是不显著的。一项检验在统计上是“显著的”，意思是指这样的样本数据不是偶然得到的，即不是抽样的随机波动造成的，而是由内在的影响因素导致。

t 检验

常用的假设检验方法有 z 检验、t 检验和卡方检验等，不同的方法有不同的适用条件和检验目标。t 检验(Student's t test)是用 t 分布理论来推断两个平均数差异的显著性水平。

我们的对比试验是用对照版本和测试版本两个样本的数据来对这两个总体是否存在差异进行检验，所以适合使用 t 检验方法中的独立双样本检验。

为了简化，对比试验忽略了样本大小在 30 以下的小样本情况（视为结果不显著），按大样本检验公式进行 p-value 的计算。

首先通过 t 检验公式计算出检验统计量 Z 的值：

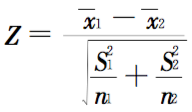
• x1：样本 1 均值；x2：样本 2 均值；
• S1：样本 1 标准差；S2：样本 2 标准差；
• n1：样本 1 大小；n2：样本 2 大小；

然后通过 t 分布（大样本情况下近似正态分布）的公式计算得出和 Z 值对应的 p 值。

p 值算出来之后，我们就可以根据 p 值按照前面介绍的假设检验决策规则来判断这两个样本均值的差异是否显著了。

小结

下面我们以 AppAdhoc 后台 Demo APP 的试验 page_order02 为例来走一遍对比试验的整个过程，从统计假设检验的角度来看看 AppAdhoc 是怎么处理试验数据并得出结论的。

page_order02 这个试验的目的是测试不同页面顺序对购买点击的影响，它设计了一个具有不同页面顺序的测试版本 experiment_1_page_order02 和对照版本 CONTROL-page_order02 进行对比， 每个版本的用户流量分配都是 7% 的用户，通过 buy_success 优化指标来衡量试验的结果。

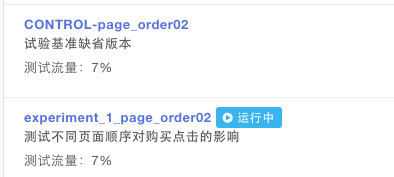
试验开始之后，AppAdhoc 试验引擎通过抽样把两个具有相同代表性的用户群体（样本）分配到这两个版本。试验运行一段时间之后 buy_success 指标有如下数据（方差数据未在表格中显示）：

总体和样本

此试验中，总体就是应用的所有用户，涉及到两个样本：CONTROL-page_order02 的 33771 个用户和 experiment_1_page_order02 的 34190 个用户。

原假设

在此试验条件下，假设检验的原假设就是：experiment_1_page_order02 版本的 buy_success 指标的总体均值等于 CONTROL-page_order02 版本的 buy_success 指标的总体均值。也就是说，如果应用采用新的页面顺序，所有用户的 buy_success 指标的均值相比原页面顺序下的均值没有差异。

如果原假设不成立，说明 experiment_1_page_order02 和 CONTROL-page_order02 这两个样本不是来自同一个总体；换句话说，采用新页面顺序的所有用户的表现和采用原页面顺序的所有用户的表现是有本质区别的。因为这两个样本的代表性是相同的，唯一的区别在于页面顺序， 所以我们可以推断得出页面顺序的改变是有效果的，试验的目的就达到了。

p-value 的计算

接着要做的就是根据这两个样本的数据按照前面介绍的 t 检验的公式来计算原假设的显著性水平 p 值。

• x1：CONTROL-page_order02 版本的 buy_success 均值 (23.01)；
• x2：experiment_1_page_order02 版本的 buy_success 均值 (22.11)；
• S1：CONTROL-page_order02 版本的 buy_success 标准差 (53.21)；
• S2：experiment_1_page_order02 版本的 buy_success 标准差 (50.21)；
• n1：CONTROL-page_order02 版本的样本大小/用户数 (33771)；
• n2：experiment_1_page_order02 版本的样本大小/用户数 (34190)；

通过上面介绍的t检验大样本检验公式计算得出 Z = 2.28，然后根据正态分布公式由 Z 值计算得出 p-value = 0.01。

0.01 < 0.05，根据决策规则我们可以下结论此次检验的统计显著性是“显著”，即原假设不成立，改变页面顺序显著地影响了购买点击。

测试结果的好坏

现在我们知道初步的试验结果了，这次试验是具有统计显著性的，我们可以继续研读试验的数据，得出进一步的结论。 如果结果不显著，说明样本数量可能还不够，应该等待试验继续运行；如果试验已经充分运行，说明结论是原假设不能被拒绝，我们不能确定改变页面顺序会显著地影响购买点击。

我们接着看两个版本（样本）的均值，experiment_1_page_order02 的均值 22.11 比 CONTROL-page_order02 的均值 23.01 小，变化（提升）是 -3.90%。 我们现在更清楚了，测试版本的 buy_success 指标均值下降了，页面顺序的改动对购买点击有负面的影响，我们不应该发布这个版本。

OK，至此我们可以得出明确的结论了：检验结果显著，测试版本和对照版本有明显不同，但是提升效果是负面的。

置信区间

好吧，事还没完。我们知道测试结果好坏之后，还可以更深入地查看它大概好了多少，或者差了多少。

experiment_1_page_order02 的均值 22.11 和 CONTROL-page_order02 的均值 23.01 都是点估计，所以来自这两个均值比较得到的变化百分值 -3.90% 也是点估计，它是有误差的。 前面的参数估计部分已经提到了，我们需要区间估计的方法来得到一个概率范围，这才是比较准确的描述。

置信区间（Confidence interval）就是用来对一个概率样本的总体参数的进行区间估计的样本均值范围。置信区间展现了这个均值范围包含总体参数的概率，这个概率称为置信水平。

置信水平代表了估计的可靠度，一般来说，我们使用 95% 的置信水平来进行区间估计。简单地讲，置信区间就是我们想要找到的这么一个均值区间范围，此区间有 95% 的可能性包含真实的总体均值。

根据统计学的中心极限定理，样本均值的抽样分布呈正态分布。因此，通过相关的公式我们可以计算出两个总体均值差的95%置信区间。

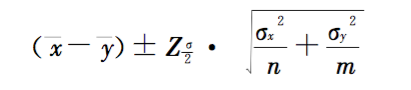
结果为：[-0.9 - 0.778, -0.9 + 0.778]

即区间 [-1.678, -0.122] 有 95% 的可能性包含两个总体均值之差。

为了更直观，我们把这个总体均值差的置信区间转换为相比对照版本均值的变化的百分比置信区间：

[变化1,变化2]

变化1 = -1.678 / 23.01 = -0.073 (-7.3%)

变化2 = -0.122 / 23.01 = -0.005 (-0.5%)

变化百分比形式的置信区间为：[-7.3%, -0.5%]

最后，我们可以这么评价试验的结果：测试版本不如对照版本，有 95% 的可能性差了 0.5% 到 7.3% 之间。

参考资料

《应用统计学》

《生物统计学基础》