4.3.1 树的基础
一、树的介绍
1.树的定义
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
(01) 每个节点有零个或多个子节点;
(02) 没有父节点的节点称为根节点;
(03) 每一个非根节点有且只有一个父节点;
(04) 除了根节点外,每个子节点可以分为多个不相交的子树。
2.树的基本术语
若一个结点有子树,那么该结点称为子树根的"双亲",子树的根是该结点的"孩子"。有相同双亲的结点互为"兄弟"。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
结点的度:结点拥有的子树的数目。
叶子:度为零的结点。
分支结点:度不为零的结点。
树的度:树中结点的最大的度。
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1。
树的高度:树中结点的最大层次。
无序树:如果树中结点的各子树之间的次序是不重要的,可以交换位置。
有序树:如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
二、二叉树的介绍
1.二叉树的定义
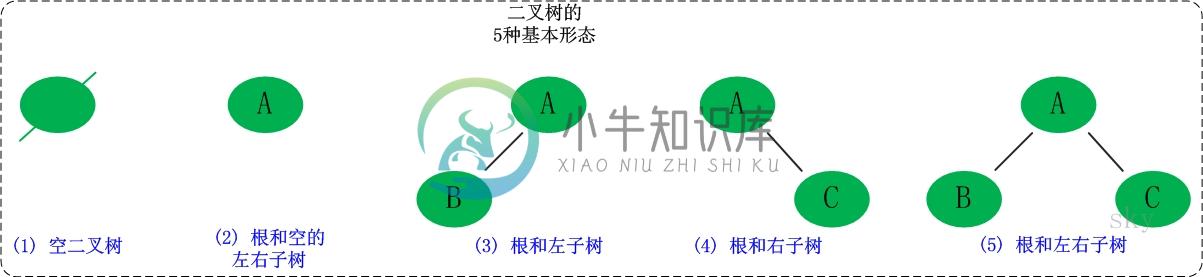
二叉树是每个节点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
2. 二叉树的性质
二叉树有以下几个性质:
性质1:二叉树第i层上的结点数目最多为$2^{i-1}$ (i≥1)。
性质2:深度为k的二叉树至多有$2^k - 1$个结点(k≥1)。
性质3:包含n个结点的二叉树的高度至少为$log_2(n+1)$。
性质4:在任意一棵二叉树中,若叶子结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
2.1 性质1:二叉树第i层上的结点数目最多为$2^{i-1}$(i≥1)
证明:下面用"数学归纳法"进行证明。
(01) 当i=1时,第i层的节点数目为1。因为第1层上只有一个根结点,所以命题成立。
(02) 假设当i>1,第i层的节点数目为$2^{i-1}$。这个是根据(01)推断出来的!
下面根据这个假设,推断出"第(i+1)层的节点数目为$2^{i}$"即可。
由于二叉树的每个结点至多有两个孩子,故"第(i+1)层上的结点数目" 最多是 "第i层的结点数目的2倍"。即,第(i+1)层上的结点数目最大值=2×$2^{i-1}$=$2^{i}$。
故假设成立,原命题得证!
2.2 性质2:深度为k的二叉树至多有$2^{k}-1$个结点(k≥1)
证明:在具有相同深度的二叉树中,当每一层都含有最大结点数时,其树中结点数最多。利用"性质1"可知,深度为k的二叉树的结点数至多为:
$ 2^0+2^1+…+2^{k-1}=2^k-1$
故原命题得证!
2.3 性质3:包含n个结点的二叉树的高度至少为$log_2(n+1)$
证明:根据"性质2"可知,高度为h的二叉树最多有$2^{h}-1$个结点。反之,对于包含n个节点的二叉树的高度至少为$log_2(n+1)$。
2.4 性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
证明:因为二叉树中所有结点的度数均不大于2,所以结点总数(记为n)="0度结点数(n0)" + "1度结点数(n1)" + "2度结点数(n2)"。由此,得到等式一。
(等式一) n=n0+n1+n2
另一方面,0度结点没有孩子,1度结点有一个孩子,2度结点有两个孩子,故二叉树中孩子结点总数是:n1+2n2。此外,只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。
(等式二) n=n1+2n2+1
由(等式一)和(等式二)计算得到:n0=n2+1。原命题得证!
3. 满二叉树,完全二叉树和二叉查找树
3.1 满二叉树
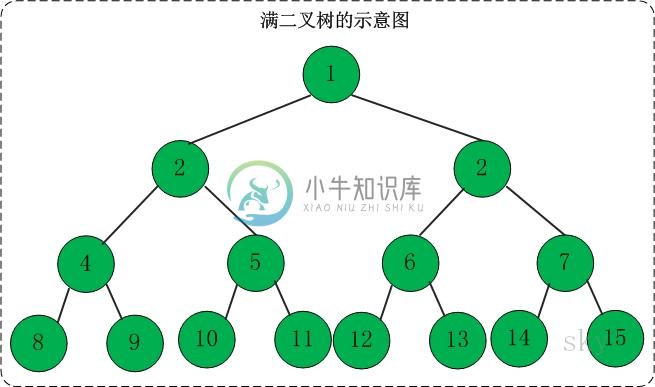
定义:高度为h,并且由$2^{h}-1$个结点的二叉树,被称为满二叉树。
3.2 完全二叉树
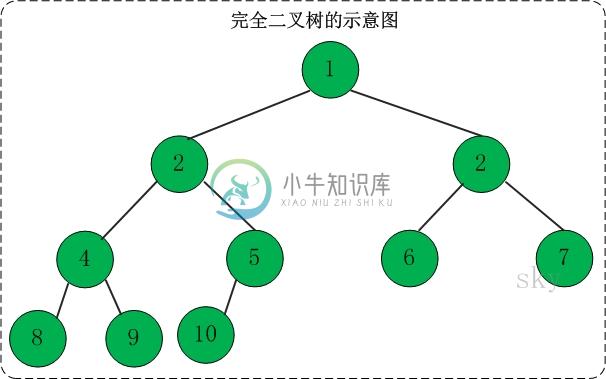
定义:一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
特点:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树。
3.3 二叉查找树
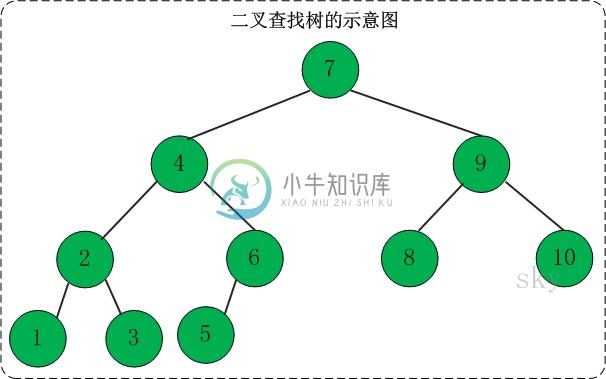
定义:二叉查找树(Binary Search Tree),又被称为二叉搜索树。设x为二叉查找树中的一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
在二叉查找树中:
(01) 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(02) 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点(no duplicate nodes)。
三、二叉查找树的Java实现
1.二叉查找树节点的定义
public class BSTree<T extends Comparable<T>> {
private BSTNode<T> mRoot; // 根结点
public class BSTNode<T extends Comparable<T>> {
T key; // 关键字(键值)
BSTNode<T> left; // 左孩子
BSTNode<T> right; // 右孩子
BSTNode<T> parent; // 父结点
public BSTNode(T key, BSTNode<T> parent, BSTNode<T> left, BSTNode<T> right) {
this.key = key;
this.parent = parent;
this.left = left;
this.right = right;
}
}
......
}
BSTree是二叉树,它保含了二叉树的根节点mRoot;mRoot是BSTNode类型,而BSTNode是二叉查找树的节点,它是BSTree的内部类。BSTNode包含二叉查找树的几个基本信息:
(01) key -- 它是关键字,是用来对二叉查找树的节点进行排序的。
(02) left -- 它指向当前节点的左孩子。
(03) right -- 它指向当前节点的右孩子。
(04) parent -- 它指向当前节点的父结点。
2.遍历
这里讲解前序遍历、中序遍历、后序遍历3种方式。
2.1 前序遍历
若二叉树非空,则执行以下操作:
(01) 访问根结点;
(02) 先序遍历左子树;
(03) 先序遍历右子树。
前序遍历代码
private void preOrder(BSTNode<T> tree) {
if(tree != null) {
System.out.print(tree.key+" ");
preOrder(tree.left);
preOrder(tree.right);
}
}
public void preOrder() {
preOrder(mRoot);
}
2.2 中序遍历
若二叉树非空,则执行以下操作:
(01) 中序遍历左子树;
(02) 访问根结点;
(03) 中序遍历右子树。
中序遍历代码
private void inOrder(BSTNode<T> tree) {
if(tree != null) {
inOrder(tree.left);
System.out.print(tree.key+" ");
inOrder(tree.right);
}
}
public void inOrder() {
inOrder(mRoot);
}
2.3 后序遍历
若二叉树非空,则执行以下操作:
(01) 后序遍历左子树;
(02) 后序遍历右子树;
(03) 访问根结点。
后序遍历代码
private void postOrder(BSTNode<T> tree) {
if(tree != null)
{
postOrder(tree.left);
postOrder(tree.right);
System.out.print(tree.key+" ");
}
}
public void postOrder() {
postOrder(mRoot);
}
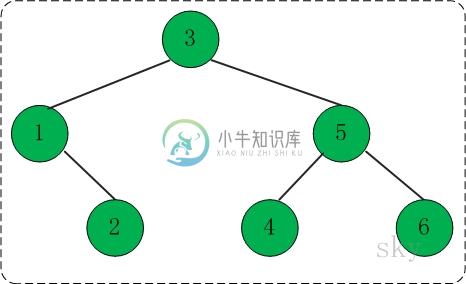
看看下面这颗树的各种遍历方式:
对于上面的二叉树而言,
(01) 前序遍历结果: 3 1 2 5 4 6
(02) 中序遍历结果: 1 2 3 4 5 6
(03) 后序遍历结果: 2 1 4 6 5 3
3. 查找
递归版本的代码
/*
* (递归实现)查找"二叉树x"中键值为key的节点
*/
private BSTNode<T> search(BSTNode<T> x, T key) {
if (x==null)
return x;
int cmp = key.compareTo(x.key);
if (cmp < 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
}
public BSTNode<T> search(T key) {
return search(mRoot, key);
}
非递归版本的代码
/*
* (非递归实现)查找"二叉树x"中键值为key的节点
*/
private BSTNode<T> iterativeSearch(BSTNode<T> x, T key) {
while (x!=null) {
int cmp = key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else
return x;
}
return x;
}
public BSTNode<T> iterativeSearch(T key) {
return iterativeSearch(mRoot, key);
}
4. 最大值和最小值
查找最大值的代码
/*
* 查找最大结点:返回tree为根结点的二叉树的最大结点。
*/
private BSTNode<T> maximum(BSTNode<T> tree) {
if (tree == null)
return null;
while(tree.right != null)
tree = tree.right;
return tree;
}
public T maximum() {
BSTNode<T> p = maximum(mRoot);
if (p != null)
return p.key;
return null;
}
查找最小值的代码
/*
* 查找最小结点:返回tree为根结点的二叉树的最小结点。
*/
private BSTNode<T> minimum(BSTNode<T> tree) {
if (tree == null)
return null;
while(tree.left != null)
tree = tree.left;
return tree;
}
public T minimum() {
BSTNode<T> p = minimum(mRoot);
if (p != null)
return p.key;
return null;
}
5. 前驱和后继
节点的前驱:是该节点的左子树中的最大节点。
节点的后继:是该节点的右子树中的最小节点。
查找前驱节点的代码
/*
* 找结点(x)的前驱结点。即,查找"二叉树中数据值小于该结点"的"最大结点"。
*/
public BSTNode<T> predecessor(BSTNode<T> x) {
// 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
if (x.left != null)
return maximum(x.left);
// 如果x没有左孩子。则x有以下两种可能:
// (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。
// (02) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。
BSTNode<T> y = x.parent;
while ((y!=null) && (x==y.left)) {//满足条件,不断往上追溯,直到找到右祖先结点
x = y;
y = y.parent;
}
return y;
}
查找后继节点的代码
/*
* 找结点(x)的后继结点。即,查找"二叉树中数据值大于该结点"的"最小结点"。
*/
public BSTNode<T> successor(BSTNode<T> x) {
// 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
if (x.right != null)
return minimum(x.right);
// 如果x没有右孩子。则x有以下两种可能:
// (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。
// (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。
BSTNode<T> y = x.parent;
while ((y!=null) && (x==y.right)) {//满足条件,不断往上追溯,直到找到右祖先结点
x = y;
y = y.parent;
}
return y;
}
6. 插入
插入节点的代码
/*
* 将结点插入到二叉树中
*
* 参数说明:
* tree 二叉树的
* z 插入的结点
*/
private void insert(BSTree<T> bst, BSTNode<T> z) {
int cmp;
BSTNode<T> y = null;
BSTNode<T> x = bst.mRoot;
// 查找z的插入位置
while (x != null) {
y = x;
cmp = z.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else
x = x.right;
}
z.parent = y;
if (y==null)
bst.mRoot = z;
else {
cmp = z.key.compareTo(y.key);
if (cmp < 0)
y.left = z;
else
y.right = z;
}
}
/*
* 新建结点(key),并将其插入到二叉树中
*
* 参数说明:
* tree 二叉树的根结点
* key 插入结点的键值
*/
public void insert(T key) {
BSTNode<T> z=new BSTNode<T>(key,null,null,null);
// 如果新建结点失败,则返回。
if (z != null)
insert(this, z);
}
注:本文实现的二叉查找树是允许插入相同键值的节点的。
7. 删除
删除节点的代码
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* bst 二叉树
* z 删除的结点
*/
private BSTNode<T> remove(BSTree<T> bst, BSTNode<T> z) {
BSTNode<T> x=null;
BSTNode<T> y=null;
if ((z.left == null) || (z.right == null) )
y = z;
else
y = successor(z);
if (y.left != null)
x = y.left;
else
x = y.right;
if (x != null)
x.parent = y.parent;
if (y.parent == null)
bst.mRoot = x;
else if (y == y.parent.left)
y.parent.left = x;
else
y.parent.right = x;
if (y != z)
z.key = y.key;
return y;
}
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* tree 二叉树的根结点
* z 删除的结点
*/
public void remove(T key) {
BSTNode<T> z, node;
if ((z = search(mRoot, key)) != null)
if ( (node = remove(this, z)) != null)
node = null;
}
8. 打印
打印二叉查找树的代码
/*
* 打印"二叉查找树"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
private void print(BSTNode<T> tree, T key, int direction) {
if(tree != null) {
if(direction==0) // tree是根节点
System.out.printf("%2d is root\n", tree.key);
else // tree是分支节点
System.out.printf("%2d is %2d's %6s child\n", tree.key, key, direction==1?"right" : "left");
print(tree.left, tree.key, -1);
print(tree.right,tree.key, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
9. 销毁
销毁二叉查找树的代码
/*
* 销毁二叉树
*/
private void destroy(BSTNode<T> tree) {
if (tree==null)
return ;
if (tree.left != null)
destroy(tree.left);
if (tree.right != null)
destroy(tree.right);
tree=null;
}
public void clear() {
destroy(mRoot);
mRoot = null;
}
四、树的深度/广度优先遍历
树的深度优先遍历需要用到额外的数据结构--->栈;而广度优先遍历需要队列来辅助;这里以二叉树为例来实现。
import java.util.ArrayDeque;
public class BinaryTree {
static class TreeNode{
int value;
TreeNode left;
TreeNode right;
public TreeNode(int value){
this.value=value;
}
}
TreeNode root;
public BinaryTree(int[] array){
root=makeBinaryTreeByArray(array,1);
}
/**
* 采用递归的方式创建一颗二叉树
* 传入的是二叉树的数组表示法
* 构造后是二叉树的二叉链表表示法
*/
public static TreeNode makeBinaryTreeByArray(int[] array,int index){
if(index<array.length){
int value=array[index];
if(value!=0){
TreeNode t=new TreeNode(value);
array[index]=0;
t.left=makeBinaryTreeByArray(array,index*2);
t.right=makeBinaryTreeByArray(array,index*2+1);
return t;
}
}
return null;
}
/**
* 深度优先遍历,相当于先根遍历
* 采用非递归实现
* 需要辅助数据结构:栈
*/
public void depthOrderTraversal(){
if(root==null){
System.out.println("empty tree");
return;
}
ArrayDeque<TreeNode> stack=new ArrayDeque<TreeNode>();
stack.push(root);
while(stack.isEmpty()==false){
TreeNode node=stack.pop();
System.out.print(node.value+" ");
if(node.right!=null){
stack.push(node.right);
}
if(node.left!=null){
stack.push(node.left);
}
}
System.out.print("\n");
}
/**
* 广度优先遍历
* 采用非递归实现
* 需要辅助数据结构:队列
*/
public void levelOrderTraversal(){
if(root==null){
System.out.println("empty tree");
return;
}
ArrayDeque<TreeNode> queue=new ArrayDeque<TreeNode>();
queue.add(root);
while(queue.isEmpty()==false){
TreeNode node=queue.remove();
System.out.print(node.value+" ");
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
System.out.print("\n");
}
/**
* 13
* / \
* 65 5
* / \ \
* 97 25 37
* / /\ /
* 22 4 28 32
*/
public static void main(String[] args) {
int[] arr={0,13,65,5,97,25,0,37,22,0,4,28,0,0,32,0};
BinaryTree tree=new BinaryTree(arr);
tree.depthOrderTraversal();
tree.levelOrderTraversal();
}
}