1.27 提升

提升(Boosting)

1. 提升

到目前为止，我们已经了解了如何在已经选择了数据表示的情况下解决分类（和其他）问题。我们现在讨论一个称为boost的过程，它最初是由Rob Schapire发现的，后来由Schapire和Yoav Freund进一步开发，它自动选择特性表示。我们采用了一种基于优化的视角，这与Freund和Schapire最初的解释和论证有些不同，但这有助于我们的方法的理解：

• $(1)$选择模型表达，
• $(2)$选择损失，
• $(3)$最小化损失函数。

在阐明这个问题之前，我们先对我们要做的事情有一点直觉。粗略地说，提升的思想是用一个弱学习算法——任何一个只要比随机选择好一点的分类学习算法——然后把它转换成一个比随机选择好很多的强分类器。为了对此建立一些直觉，考虑一个的数字识别案例，在这个案例中，我们希望区分$0$和$1$，我们接收到的图像必须进行分类。那么一个自然的弱学习器可能会取图像的中间像素，如果它是有颜色的，就把图像称为$1$，如果它是空白的，就把图像称为$0$。这个分类器可能远远不够完美，但它可能比随机分类器要好。提升过程通过收集这些弱分类器，然后对它们的贡献进行加权，从而形成一个比任何单个分类器精度都高得多的分类器。

考虑到这一点，让我们来阐明这个问题。我们对提升的理解是在无限维空间中采用坐标下降法，虽然听起来很复杂，但其实该方法并不像听上去那么难。首先，假设我们有原始标签为$y \in{-1,1}$的输入示例$x \in \mathbb{R}^{n}$，该示例在二分类中很常见。我们还假设我们有无穷多个特征函数$\phi{j} : \mathbb{R}^{n} \rightarrow{-1,1}$以及无穷向量$\theta=\left[ \begin{array}{lll}{\theta{1}} & {\theta_{2}} & {\cdots}\end{array}\right]^{T}$，然而我们总假设只有有限数量的非零元素。我们使用的分类器如下：

$$h{\theta}(x)=\operatorname{sign}\left(\sum{j=1}^{\infty} \theta{j} \phi{j}(x)\right)$$

这里让我们随便使用下符号，并定义$\theta^{T} \phi(x)=\sum{j=1}^{\infty} \theta{j} \phi_{j}(x)$。

在提升中，我们通常称特征$\phi_{j}$为弱假设。给定一个训练集$\left(x^{(1)}, y^{(1)}\right), \ldots,\left(x^{(m)}, y^{(m)}\right)$，我们称一个向量$p=\left(p^{(1)}, \ldots, p^{(m)}\right)$为样本中的一个分布，如果对于所有$i$以及下式成立时有$p^{(i)} \geq 0$。

$$\sum_{i=1}^{m} p^{(i)}=1$$

然后我们称一个弱学习器具有边界$\gamma>0$，如果对于任意在第$m$个训练样本的分布$p$存在一个弱假设$\phi_j$，使得：

$$\sum{i=1}^{m} p^{(i)} 1\left{y^{(i)} \neq \phi{j}\left(x^{(i)}\right)\right} \leq \frac{1}{2}-\gamma \qquad\qquad(1)$$

译者注：实际该式左边就是第j个弱学习器在测试集上分类错误的期望也就是说，我们假设有一些分类器比对数据集的随机猜测稍微好一些。弱学习算法的存在只是一个假设，但令人惊讶的是，我们可以将任何弱学习算法转换成一个具有完美精度的算法。

在更一般的情况下，我们假设我们采用了一个弱学习器算法，该算法以训练示例上的一个分布（权重）$p$作为输入，并返回一个性能略好于随机选择的分类器。我们将展示了在给定弱学习算法的条件下，boost如何返回在训练数据上具有完美精度的分类器。（诚然，我们希望分类器能够很好地推广到测试集数据中，但目前我们忽略了这个问题。)

1.1 提升算法

粗略地说，boost首先在数据集中为每个训练示例分配相等的权重。然后，它接收到一个弱假设，该弱假设在当前训练实例的权重下分类性能良好，并将其合并到当前的分类模型中。然后对训练实例进行权重调整，在分类出错的例子上分配更高的权重，使弱学习算法集中于对这些例子进行分类的处理，而没有分类错误的例子上分配更低的权重。这种在训练数据上重复调整权重，使其虽然加上了一个学习能力较差的学习器，但是该学习器在当前分类器表现不佳的示例上做得很好，这样总体来说就产生了性能较好的分类器。

该算法对分类问题的指数损失进行坐标下降法，目标为：

$$J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \exp \left(-y^{(i)} \theta^{T} \phi\left(x^{(i)}\right)\right)$$

我们首先展示如何使用坐标下降法更新计算得到损失函数$J(\theta)$的准确形式。坐标下降迭代法如下：

(i) 选择一个坐标$j \in \mathbb{N}$

(ii) 更新$\theta_j$为：

$$\theta{j}=\underset{\theta{j}}{\operatorname{argmin}} J(\theta)$$

对于所有$k\neq j$不相同时留下$\theta_k$。

我们迭代上面的过程直到收敛。

在提升的情况下，由于自然指数函数分析很方便，坐标更新的推导并不困难。现在我们展示如何进行更新。假设我们想要更新坐标$k$。定义：

$$w^{(i)}=\exp \left(-y^{(i)} \sum{j \neq k} \theta{j} \phi_{j}\left(x^{(i)}\right)\right)$$

为权重，并注意优化坐标$k$达到相应的最小化：

$$\sum{i=1}^{m} w^{(i)} \exp \left(-y^{(i)} \phi{k}\left(x^{(i)}\right) \alpha\right)$$

在$\alpha=\theta_k$时。现在定义：

$$W^{+} :=\sum{i : y^{(i)} \phi{k}\left(x^{(i)}\right)=1} w^{(i)} \text { and } W^{-} :=\sum{i : y^{(i)}\phi{k}\left(x^{(i)}\right)=-1} w^{(i)}$$

为了实例权值之和使得$\phi_k$分别分类正确和错误。找出$\theta_k$与对下面的式子进行的选择相同：

$$\alpha=\underset{\alpha}{\arg \min }\left{W^{+} e^{-\alpha}+W^{-} e^{\alpha}\right}=\frac{1}{2} \log \frac{W^{+}}{W^{-}}$$

为了得到最终的等式，我们求导并将其设为零。我们得到$-W^{+} e^{-\alpha}+W^{-} e^{\alpha}=0$。即$W^{-} e^{2 \alpha}=W^{+}$或$\alpha=\frac{1}{2} \log \frac{W^{+}}{W^{-}}$。

剩下的就是选择特定的坐标来执行坐标下降。我们假设已经使用了如图$1$所示的弱学习器算法，在第$t$次迭代时使用具有分布$p$的训练集作为输入，并返回一个具有边缘分布$(1)$的弱假设$\phit$。我们提出总提升算法如图$2$所示。它在迭代$t=1,2,3, \ldots$中进行计算。我们通过弱学习算法在$t$时刻返回的$\left{\phi{1}, \dots, \phi_{t}\right}$来表示假设集。

2 提升的收敛性

我们现在认为，提升程序达到$0$训练误差，我们也提供了收敛速度为零。为此，我们提出了一个保证取得提升的引理。

引理 2.1 令：

$$J\left(\theta^{(t)}\right)=\frac{1}{m} \sum{i=1}^{m} \exp \left(-y^{(i)} \sum{\tau=1}^{t} \theta{\tau} \phi{\tau}\left(x^{(i)}\right)\right)$$

则：

$$J\left(\theta^{(t)}\right) \leq \sqrt{1-4 \gamma^{2}} J\left(\theta^{(t-1)}\right)$$

由于引理的证明是有点复杂的，而不是本节笔记的中心——尽管知道该算法会收敛是很重要的！——我们把证明推迟到附录A.1。让我们描述一下它如何保证增强过程收敛到一个训练误差为零的分类器。

我们在$\theta^{(0)}=\overrightarrow{0}$处初始化过程，以便初始经验损失为$J\left(\theta^{(0)}\right)=1$。现在,我们注意到对于任何$\theta$，误分类误差满足：

$$1\left{\operatorname{sign}\left(\theta^{T} \phi(x)\right) \neq y\right}=1\left{y \theta^{T} \phi(x) \leq 0\right} \leq \exp \left(-y \theta^{T} \phi(x)\right)$$

因为对于所有$z\ge 0$有$e^z\ge 1$。由此可知，误分类错误率具有上界：

$$\frac{1}{m} \sum_{i=1}^{m} 1\left{\operatorname{sign}\left(\theta^{T} \phi\left(x^{(i)}\right)\right) \neq y^{(i)}\right} \leq J(\theta)$$

因此如果$J(\theta)<\frac{1}{m}$，则向量$\theta$在训练样本中没有错误。经过$t$次提升迭代，得到经验风险满足：

$$J\left(\theta^{(t)}\right) \leq\left(1-4 \gamma^{2}\right)^{\frac{t}{2}} J\left(\theta^{(0)}\right)=\left(1-4 \gamma^{2}\right)^{\frac{t}{2}}$$

为了找出多少次迭代才能保证$J\left(\theta^{(t)}\right)<\frac{1}{m}$。我们对$J\left(\theta^{(t)}\right)<1 / m$取对数：

$$\frac{t}{2} \log \left(1-4 \gamma^{2}\right)<\log \frac{1}{m}, \quad \text { or } \quad t>\frac{2 \log m}{-\log \left(1-4 \gamma^{2}\right)}$$

用一阶泰勒展开，得到$\log \left(1-4 \gamma^{2}\right) \leq-4 \gamma^{2}$，我们看到，如果我们使用提升的轮数——我们使用弱分类器的数量——满足下面的条件：

$$t>\frac{\log m}{2 \gamma^{2}} \geq \frac{2 \log m}{-\log \left(1-4 \gamma^{2}\right)}$$

则$J\left(\theta^{(t)}\right)<\frac{1}{m}$。

3 实现弱学习器(Implementing weak-learners)

增强算法的一个主要优点是，它们可以自动从原始数据中为我们生成特性。此外，由于弱假设总是返回${1,1}$中的值，所以在使用学习算法时不需要将特征标准化，使其具有相似的尺度，这在实践中会产生很大的差异。此外。虽然这不是理论上易于理解，许多类型的弱学习器程序中引入非线性智能分类器，可以产生比到目前为止我们已经看到的更多的表达模型的简单线性模型形式$\theta^Tx$。

3.1 决策树桩(Decision stumps)

有很多策略对应学习能力差的弱学习器，这里我们只关注其中一种，即决策树桩。为了具体说明这个方法，让我们假设输入变量$x \in \mathbb{R}^{n}$是实值的。决策树桩是一个函数$f$，它由阈值$s$和索引$j\in{1,2,\dots, n}$确定，然后返回：

$$\phi{j, s}(x)=\operatorname{sign}\left(x{j}-s\right)=\left{\begin{array}{ll}{1} & {\text { if } x_{j} \geq s} \ {-1} & {\text { otherwise }}\end{array}\right. \qquad\qquad(2)$$

正如我们现在所描述的，这些分类器非常简单，我们甚至可以有效地将它们用于加权数据集。

事实上，一个决策树桩弱学习器的计算过程如下。我们从一个分布开始——权重$p^{(1)}, \ldots, p^{(m)}$组成的集合中所有元素之和为$1$——在训练集上。我们希望选择公式$(2)$中的一个决策残差来最小化训练集上的误差，也就是说，我们希望找到一个阈值$s \in \mathbb{R}$和索引$j$，使得：

$$\widehat{\operatorname{Err}}\left(\phi{j, s}, p\right)=\sum{i=1}^{m} p^{(i)} 1\left{\phi{j, s}\left(x^{(i)}\right) \neq y^{(i)}\right}=\sum{i=1}^{m} p^{(i)} 1\left{y^{(i)}\left(x_{j}^{(i)}-s\right) \leq 0\right}\qquad\qquad(3)$$

达到最小。简单来说，这可能是一个低效的计算，但是一个更智能的过程允许我们在大约$O(nmlogm)$时间内解决这个问题。为每一个特征$j=1,2, \dots, n$，我们对原始输入特性进行排序：

$$x{j}^{\left(i{1}\right)} \geq x{j}^{\left(i{2}\right)} \geq \cdots \geq x{j}^{\left(i{m}\right)}$$

由于决策残差的误差仅能改变$s$的值，所以决策残差只能改变$x_{j}^{(i)}$的值 一点巧妙的推导使我们能够计算：

$$\sum{i=1}^{m} p^{(i)} 1\left{y^{(i)}\left(x{j}^{(i)}-s\right) \leq 0\right}=\sum{k=1}^{m} p^{\left(i{k}\right)} 1\left{y^{\left(i{k}\right)}\left(x{j}^{\left(i_{k}\right)}-s\right) \leq 0\right}$$

以排序的顺序递增地修改和，这是有效的，在我们已经对值排序之后，这将花费$O(m)$的时间 （这里我们不详细描述算法，留给感兴趣的读者来推导。）因此，对每个$n$个输入特性执行这种计算需要总时间$O(nmlogm)$ 我们可以选择指标$j$和阈值$s$来给出误差公式$(3)$的最佳决策残差。

需要注意的一个非常重要的问题是，通过翻转重新排序的决策树桩的符号$\phi{j, s}$，我们实现误差$1-\widehat{\operatorname{Err}}\left(\phi{j, s}, p\right)$，即下式的误差：

$$\widehat{\operatorname{Err}}\left(-\phi{j, s}, p\right)=1-\widehat{\operatorname{Err}}\left(\phi{j, s}, p\right)$$

（你应该让自己相信这是真的。）因此，跟踪在所有阈值上$1-\widehat{\operatorname{Err}}\left(\phi{j, s}, p\right)$的最小值也是很重要的，因为这个可能比$\widehat{\operatorname{Err}}\left(\phi{j, s}, p\right)$小。这样可以给出一个更好的弱学习器。对我们的弱学习者使用这个过程（图1）给出了基本的，但非常有用的提升分类器。

3.2 例子

现在，我们给出一个示例，展示对简单数据集进行提升的行为。特别地，我们考虑一个数据点为$x \in \mathbb{R}^{2}$的问题，其中最优分类器是：

$$y=\left{\begin{array}{ll}{1} & {\text { if } x{1}<.6 \text { and } x{2}<.6} \ {-1} & {\text { otherwise }}\end{array}\right.\qquad\qquad(4)$$

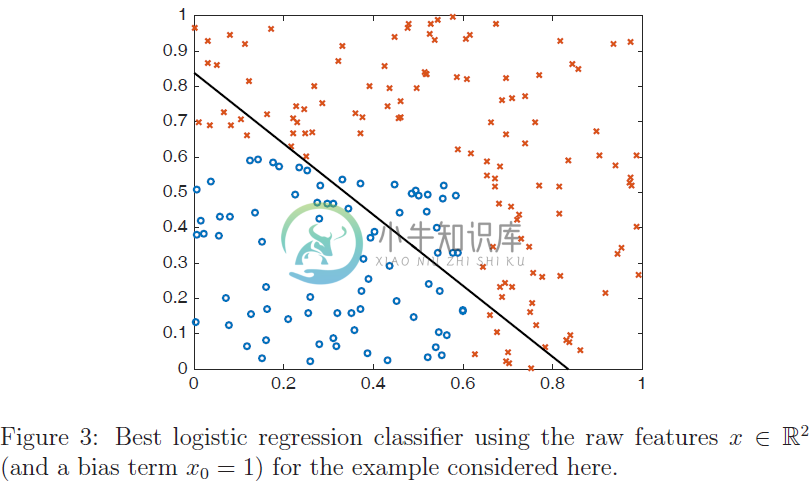
这是一个简单的非线性决策规则，但标准线性分类器（如logistic回归）是不可能学习的。在图$3$中，我们展示了logistic回归学习的最佳决策线，其中正例为圆圈，负例为X。很明显，logistic回归对数据的拟合不是特别好。

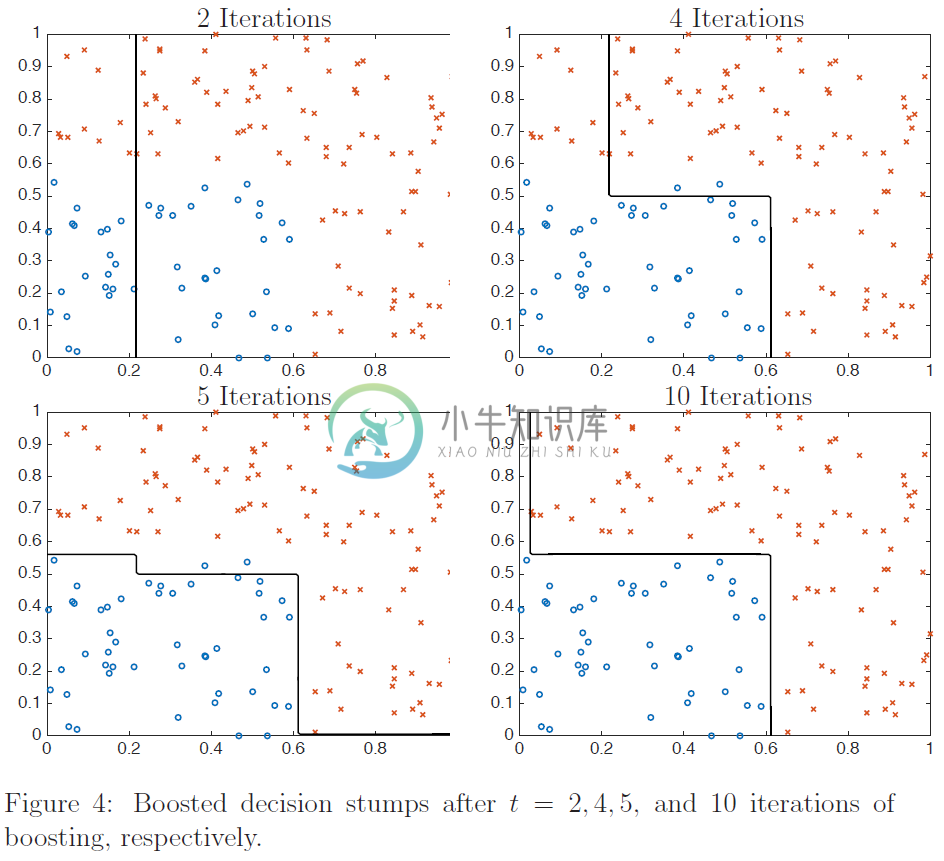
然而，对于简单的非线性分类问题$(4)$，使用提升决策树桩可以获得更好的拟合效果。图$4$显示了经过不同次数的提升迭代之后我们学习到的增强分类器，使用的训练集大小为$m = 150$。从图中可以看出，第一个决策残差是将特征$x1$的阈值设为$s \approx .23$，即对于$s \approx .23$有$\phi(x)=\operatorname{sign}\left(x{1}-s\right)$。

3.3 其他策略

在基本的增强决策树桩思想上有大量的变化。首先，我们不要求输入特性$xj$是实值的。有时可能是分类的值，也就是说对于一些$k$，有$x{j} \in{1,2, \ldots, k}$。在这种情况下，自然决策障碍就是下面的形式：

$$\phi{j}(x)=\left{\begin{array}{ll}{1} & {\text { if } x{j}=l} \ {-1} & {\text { otherwise }}\end{array}\right.$$

如果$x{j} \in C$，对于在标签下某些集合$C \subset{1, \ldots, k}$，与变量设定为$\phi{j}(x)=1$一样。

另一种自然的变种是提升决策树，在这种树中，我们考虑的不是针对弱学习者的单一层次决策，而是特征的组合或决策树。谷歌可以帮助您找到关于这类问题的示例和信息。

A 附录

A.1 引理2.1的证明

现在我们返回来证明进展引理。我们通过直接展示$t$时刻权重与$t-1$时刻权重之间的关系来证明这个结果。我们尤其注意到这一点：

$$J\left(\theta^{(t)}\right)=\min {\alpha}\left{W{t}^{+} e^{-\alpha}+W{t}^{-} e^{\alpha}\right}=2 \sqrt{W{t}^{+} W_{t}^{-}}$$

以及：

$$J\left(\theta^{(t-1)}\right)=\frac{1}{m} \sum{i=1}^{m} \exp \left(-y^{(i)} \sum{\tau=1}^{t-1} \theta{\tau} \phi{\tau}\left(x^{(i)}\right)\right)=W{t}^{+}+W{t}^{-}$$

我们通过弱学习假设知道：

$$\sum{i=1}^{m} p^{(i)} 1\left{y^{(i)} \neq \phi{t}\left(x^{(i)}\right)\right} \leq \frac{1}{2}-\gamma, \quad \text { or } \frac{1}{W{t}^{+}+W{t}^{-}}\underbrace{\sum{i : y^{(i)} \phi{t}\left(x^{(i)}\right)=-1} w^{(i)}}{=W{t}^{-}}\le\frac 12-\gamma$$

重写这个表达式注意到右边的和就是$W_{t}^{-}$，我们有：

$$W{t}^{-} \leq\left(\frac{1}{2}-\gamma\right)\left(W{t}^{+}+W{t}^{-}\right), \quad \text { or } \quad W{t}^{+} \geq \frac{1+2 \gamma}{1-2 \gamma} W_{t}^{-}$$

通过在最小化定义$J\left(\theta^{(t)}\right)$中使用$\alpha=\frac{1}{2} \log \frac{1+2 \gamma}{1-2 \gamma}$，我们可以得到下式：

$$\begin{aligned} J\left(\theta^{(t)}\right) & \leq W{t}^{+} \sqrt{\frac{1-2 \gamma}{1+2 \gamma}}+W{t}^{-} \sqrt{\frac{1+2 \gamma}{1-2 \gamma}} \ &=W{t}^{+} \sqrt{\frac{1-2 \gamma}{1+2 \gamma}}+W{t}^{-}(1-2 \gamma+2 \gamma) \sqrt{\frac{1+2 \gamma}{1-2 \gamma}} \ & \leq W{t}^{+} \sqrt{\frac{1-2 \gamma}{1+2 \gamma}}+W{t}^{-}(1-2 \gamma) \sqrt{\frac{1+2 \gamma}{1-2 \gamma}}+2 \gamma \frac{1-2 \gamma}{1-2 \gamma} \sqrt{\frac{1+2 \gamma}{1-2 \gamma}} W{t}^{+} \ &=W{t}^{+}\left[\sqrt{\frac{1-2 \gamma}{1+2 \gamma}}+2 \gamma \sqrt{\frac{1-2 \gamma}{1+2 \gamma}}\right]+W_{t}^{-} \sqrt{1-4 \gamma^{2}} \end{aligned}$$

其中我们使用了$W{t}^{-} \leq \frac{1-2 \gamma}{1+2 \gamma} W{t}^{+}$。做一些代数运算，我们看到最后的表达式等于：

$$\sqrt{1-4 \gamma^{2}}\left(W{t}^{+}+W{t}^{-}\right)$$

即$J\left(\theta^{(t)}\right) \leq \sqrt{1-4 \gamma^{2}} J\left(\theta^{(t-1)}\right)$。