1.19 集成学习

现在要讲的方法可以来整合训练模型的输出。这里要用到偏差-方差(Bias-Variance)分析，以及决策树的样本来探讨一下每一种方法所做的妥协权衡。

要理解为什么从继承方法推导收益函数(benefit)，首先会议一些基本的概率论内容。加入我们有n个独立同分布(independent, identically distributed,缩写为i.i.d.) 的随机变量$X_i$，其中的$0\le i<n$。假如对所有的$X_i$有$Var(X_i)=\sigma^2$。然后就可以得到均值(mean)的方差(variance)是:

$$Var(\bar x)=Var(\frac{1}{n}\sum_iX_i)=\frac{\sigma^2}{n}$$

现在就去掉了独立性假设(所以变量就只是同分布的，即i.d.)，然后我们说变量$X_i$是通过一个因子(factor)$\rho$而相关联的，可以得到:

$$\begin{aligned} Var(\bar X) &= Var (\frac{1}{n}\sumiX_i) & \quad\text{(1)}\ &= \frac{1}{n^2}\sum{ij}Cov(X_i,X_j) & \quad\text{(2)}\ &= \frac{n\sigma^2}{n^2} +\frac{n(n-1)\rho\sigma^2}{n^2} & \quad\text{(3)}\ &= \rho\sigma^2+ \frac{1-\rho}{n}\sigma^2& \quad\text{(4)}\ \end{aligned}$$

在第3步中用到了皮尔逊相关系数(pearson correlation coefficient)的定义$P_{X,Y}=\frac{Cov(X,Y)}{\sigma_x\sigma_y}$，而其中的$Cov(X,X)=Var(X)$。

现在如果我们设想每个随机变量都是一个给定模型的误差，就可以看到用到的模型的数目在增长(导致第二项消失)，另外模型间的相关性在降低(使得第一项消失并且得到一个独立同分布的定义)，最终导致了集成方法误差的方差的总体降低。

有好几种方法能够生成去除先关的模型(de-correlated models)，包括:

• 使用不同算法
• 使用不同训练集
• 自助聚合(Bagging)
• Boosting

前两个方法很直接，就是需要大规模的额外工作。接下来讲一下后两种技术，boosting和bagging，以及在决策树情境下这两者的使用。

1 袋装(Bagging)

1.1 自助(Bootstrap)

Bagging这个词的意思是"Boostrap Aggregation"的缩写(可以直接翻译成 自助聚合)，是一个方差降低(variance reduction)的集成学习方法(ensembling method)。Bootstrap这个方法是传统统计中用于测量某个估计器(比如均值mean)的不确定性的。

加入我们有一个真实的群体$P$，想要对其计算一个估计器，然后又一个从$P$中取样得到的训练集$S$，$S\sim P$。虽然可以通过对$S$计算估计器(estimator)来找到一个近似，但还是不知道对应真实值的误差是多少。这需要我们多次从$P$中进行独立采样得到多个训练集$S_1,S_2,...$。

可是如果我们假设$S=P$，就可以生成一个Bootstrap集合$Z$，从$S$中进行有放回的采样($Z\sim S,|Z|=|S|$)。实际上我们看医生称很多这样的样本$Z_1,Z_2,...,Z_M$。然后就可以看一下各个Bootstrap集合上估计的方差(variability)来得到对误差(error)的衡量。

1.2 聚合 (Aggregation)

现在回到集成学习的方法上，我们取得每个$Z_m$，然后对每个都训练一个机器学习模型$G_m$，然后定义一个聚合预测器(aggregate predictor):

$$G(X)=\sum_m\frac{G_m(x)}{M}$$

这样上面的过程就叫做袋装(Bagging)。回到等式$(4)$，就有了$M$个相关联的预测器的方差是:

$$Var(\bar X)=\rho\sigma^2+\frac{1-\rho}{M}\sigma^2$$

通过袋装可以得到比简单在$S$上训练更低相关的预测器(predictors)。虽然每个独立的预测器的偏差(bias)都增长了，由于每个Bootstrap集合都没有全部的训练样本可用，但实践中方差的降低带来的优势远超过偏差增加的劣势。另外要注意增加预测器个数$M$并不会引起额外的过拟合，这是由于$\rho$对$M$不敏感，因此总体上方差依然会降低。

袋装的另一个优势就是包外估计(out-of-bag estimation)。可以证明每个Bootstrap的样本都只包含大概$\frac{2}{3}$的$S$，因此可以用额外的$\frac{1}{3}$来对误差(error)进行估计，叫做包外误差(out-of-bag error)。在极端情况下，$M\rightarrow \infty$，包外误差就会等价于留一法交叉验证(leave-one-out cross-validation)。

1.3 袋装决策树 (Bagging+Decision Trees)

回想一下完全生长的决策树是高方差低偏差的模型，因此Bagging的降低方差的效果很适合与上述方法相结合。袋装还允许处理缺失特征:如果一个特征丢失了，排除在树中使用该特征的树。如果特定特征是很重要的预测器，它们虽然不会被包含在全部树内，也还是会在大部分树内。

袋装决策树的一个缺点是失去了单独决策树中继承来的可解释性。有一种叫做变量重要性衡量(variable importance measure)的方法可以来对洞察力(insight)进行一定的恢复。对每个特征，在集成学习中查找每一个用到这个特征的分割，然后在所有分割上将损失函数的降低平均分摊。要注意这和衡量确实这个特征导致的性能下降多少不同，因为其他特征可能是相关的，也可以替补。

袋装决策树的最后一个重要的内容就是一种叫做随机森林(random forests)的方法。如果我们的训练集有一个很强的预测器，然后袋装树就会总是用这个特征来切分并且最终相关。使用随机森林，就可以只允许特征的一个自己来用在每一个切分上。这样就可以得到一个对相关性(correlation)$\rho$的下降(decrease)，最终能导致方差的降低。在此要强调的是这也会导致偏差(bias)的增高因为特征空间的约束，但就和常规的袋装决策树一样这个通常并不会带来什么问题。最后，即便是强大的预测器也不会在每一个树中都出现(假设树有足够的数目以及每个切分都对特征有充分的约束)，这就能对缺失的预测器有更好地控制了。

1.4 本节概要

总结来看，对于决策树来说，袋装发的主要优势是:

• 降低了方差(随机森林更能显著)
• 更好的精度
• 自由验证集
• 支持缺失值

当然也有一些缺点，包括:

• 偏差增大(随机森林里面这种增大更严重)
• 难以解释
• 依然缺乏加性
• 更昂贵(估计是计算成本)

2 推进法(Boosting)

2.1 直观理解 (Intuition)

上文所讲的袋装法(Bagging)是一种将地方插的技术，而这次要讲的推进发(Boosting)则是降低偏差的(bias-reduction)。因此我们想要高偏差低方差的模型，也就是弱学习模型(weak learners)。考虑到在介绍决策树的时候做的解释，可以将决策树在进行预测之前只允许进行一次决策，就能使之成为弱学习模型;这样就成了决策树桩(decision stumps)。

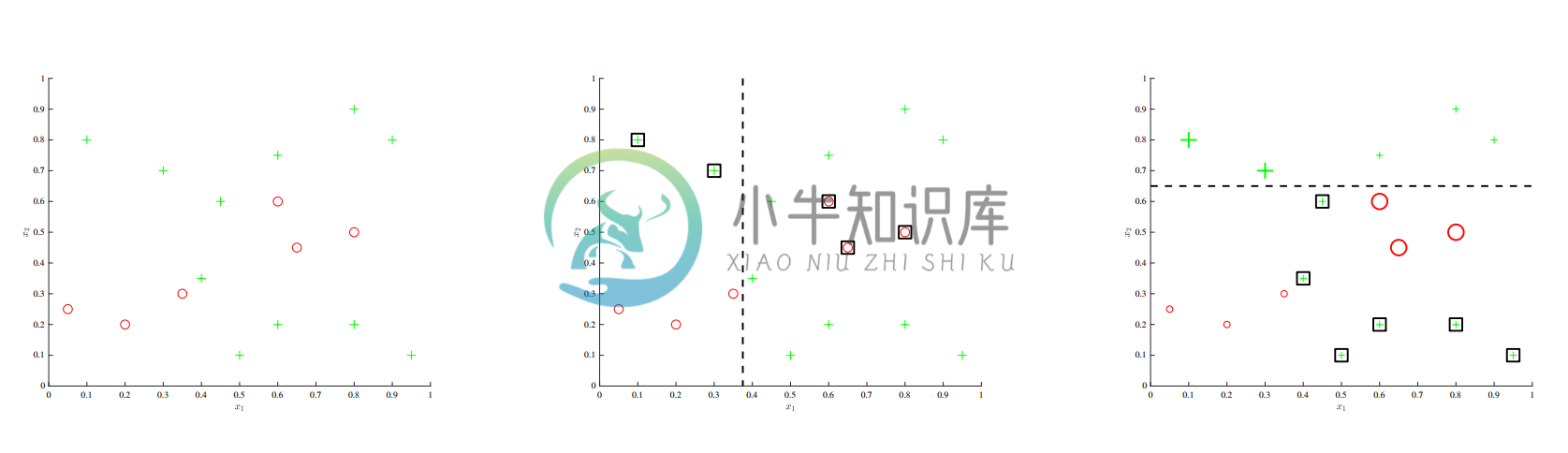
上面的例子可以用于直观理解一下推进法(Boosting)背后的思想。开始时是左边的数据及，然后进行单词决策树桩的训练，如中间图所示。关键思想是接下来要看那些样品被分类错了，然后增加他们和其他正确分类的样品相比的相对权重。然后在训练一个新的决策树桩，这个就会更倾向于将这些特殊值(hard negatives)进行正确的分类。然后继续这样，逐渐在每一步中对样品重新评估权重，最后输出的就是一系列这些弱学习模型(weak learners)的结合，就是一个集成分类器(classier)了。

2.2 Adaboost 算法

简单介绍了直观理解之后，接下来看一种最流行的推进法(boosting)算法:Adaboost，过程如下所示:

每个样本的权重开始的时候都是偶数(begin out even)，误分类样本会在每一步被进一步更新权重，以累积的形式(in a cumulative fashion)。最终得到的累加分类器是对所有弱学习模型(weak learners)的总和(summation)，权重是加权误差(weighted error)的负对数概率(negative log-odds)。

由于最终求和，还可以看到这个集成学习的方法允许对加性项目建模，整体上增强了最终模型的兼容性(以及方差)。每个新的弱学习模型都不再与之前序列中的模型独立，这就意味着增加$M$就会导致增加过拟合的风险。

Adaboost中用到的确切权重似乎第一眼看上去很随意，但实际上可以被证明是经过良好调节的。接下来的章节我们将要通过一个更通用的模块来对此进行了解，Adaboost只是其中一个特例。

2.3 正向累加建模(Forward Stagewise Additive Modeling)

这个算法如下所示，也是一个集成学习方法:

闭合检查(close inspection)表明对目前的学习问题进行了很少的假设，主要的就都是集成学习算法的可加性本质以及在一个给定步骤后之前所有的权重和参数的固定。这次还是要用到弱分类器$G(x)$，虽然这时候我们会用参数$\gamma$来进行参数化。在每一步我们都是要找到下一个若学习模型的参数和权重来使得当前的集成学习算法能够最适合剩余的误差。

作为这个算法的集中实现，使用平方损失函数就等价于将单个分类器拟合到残差$yi-f{m-1}(x_i)$。另外还可以证明的是Adaboost是这个公式的一个特例，具体来说是在二分类的分类问题和指数损失函数的情况下的特例:

$$L(y,\hat y)=\exp(-y\hat y)$$

关于Adaboost和正向累加建模的更多联系，感兴趣的读者可以去参考10.4 统计学习的要素(Elements of Statistical Learning)。

2.4 梯度推进法 (Gradient Boosting)

一般来说，在正向累加建模中出现的最小化问题写出一个闭合形式的解总是容易的。包括xgboost在内的高性能方法都可以将这个问题转换成数值优化问题。

这样做的最显著办法就是对损失函数取积分然后运行梯度下降法。不过复杂的地方在于我们被限制在只能在模型类内进行上述步骤，只能增加参数化的弱学习模型$G(x,\gamma)$,而不能在输入空间内进行任意移动。

在梯度推进法中，我们改为计算每个样本点对应当前预测期的梯度(通常就是一个决策树桩):

$$g_i=\frac{\partial L(y,f(x_i))}{\partial f(x_i)}$$

然后可以训练一个新的回归分类器来匹配这个梯度并且用来进行梯度步骤.在正向累加建模中，这就得到了:

$$\gammai =\arg \min\gamma \sum^N_{i=1}(g_i-G(x_i;\gamma))^2$$

2.5 本节概要

总结一下，推进法的主要优势有:

• 降低偏差(bias)
• 更好的精度
• 可加性建模

当然也有缺陷:

• 方差增长了
• 容易过拟合

更多推进法背后的理论，推荐阅读John Duchi的补充材料。