1.26 损失函数
损失函数
1. 二分类
在二分类问题中,目标$y$只能取两个值。在本节笔记中,我们将展示如何建模这个问题,通过令$y \in{-1,+1}$,这里如果这个例子是正类的一个元素,我们说$y$是$1$,如果这个例子是负类的一个元素,我们说$y = - 1$。和往常一样,我们假设我们的输入特征$x \in \mathbb{R}^{n}$。
和我们处理监督学习问题的标准方法一样,我们首先为我们的假设类选择一个表示(我们试图学习的内容),然后选择一个损失函数,我们将使其最小化。在二分类问题中,通常使用假设类的形式为$h_{\theta}(x)=\theta^{T} x$比较方便,当出现一个新例子$x$,我们把它归类为正例或负例取决于$\theta^{T} x$的符号,也就是说,我们预测如下的式子:
$$\operatorname{sign}\left(h_{\theta}(x)\right)=\operatorname{sign}\left(\theta^{T} x\right) \text { where } \operatorname{sign}(t)=\left{\begin{array}{ll}{1} & {\text { if } t>0} \ {0} & {\text { if } t=0} \ {-1} & {\text { if } t<0}\end{array}\right.$$
那么在一个二元分类问题中,参数为$\theta$的假设函数$h_\theta$分类一个特定的例子$(x,y)$是否正确可以通过下式来判断:
$$\operatorname{sign}\left(\theta^{T} x\right)=y \quad \text { or equivalently } \quad y \theta^{T} x>0 \qquad\qquad(1)$$
式$(1)$中$y \theta^{T} x$的值在二分类问题中是一个非常重要的量。重要到我们称下式的值
$$y \theta^{T} x$$
为例子$(x,y)$的边界(margin)。尽管不总是这样,但是人们通常会将$h_{\theta}(x)=x^{T} \theta$的值解释为对参数向量$\theta$为点$x$分配标签的置信度的度量。标签的判别标准是:如果$x^{T} \theta$非常负(或非常正),则我们更坚信标签$y$是负例(正例)。
既然选择了数据的表示形式,就必须选择损失函数。直观上,我们想要选择一些这样的损失函数,即对于我们的训练数据$\left{\left(x^{(i)}, y^{(i)}\right)\right}_{i=1}^{m}$来说,参数$\theta$的选择让边界$y^{(i)} \theta^{T} x^{(i)}$对于每一个训练样本都非常大。让我们修正一个假设的例子$(x,y)$,令$z=y x^{T} \theta$代表边界,并且设$\varphi : \mathbb{R} \rightarrow \mathbb{R}$为损失函数——也就是说,例子$(x, y)$的损失在边界$z=y x^{T} \theta$上是$\varphi(z)=\varphi\left(y x^{T} \theta\right)$。对于任何特定的损失函数,我们最小化的经验风险是:
$$J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \varphi\left(y^{(i)} \theta^{T} x^{(i)}\right)\qquad\qquad(2)$$
考虑我们想要的行为:我们希望$y^{(i)} \theta^{T} x^{(i)}$对于每个训练样本$i=1, \ldots, m$都是正的,我们应该惩罚那些$\theta$,它们使得训练数据中经常出现$y^{(i)} \theta^{T} x^{(i)} 0$(边界是正的)我们的损失$\varphi(z)$小,而如果$z < 0$(边界是负的)则$\varphi(z)$大。也许最自然的这种损失是$0-1$损失,由下式得出:
$$\varphi_{\mathrm{zo}}(z)=\left{\begin{array}{ll}{1} & {\text { if } z \leq 0} \ {0} & {\text { if } z>0}\end{array}\right.$$
在这种情况下,损失$J(\theta)$是简单的参数$\theta$在训练集上使得结果错误(误分类)的平均数量。不幸的是,损失函数$\phi_{zo}$是不连续、非凸的(为什么会出现这种情况的解释有点超出本课程的范围了),甚至更令人烦恼的是,使其最小化是一个$NP$难问题。因此,我们更愿意选择具有图$1$中所示形状的损失。也就是说,我们基本上总是使用满足下面条件的损失:
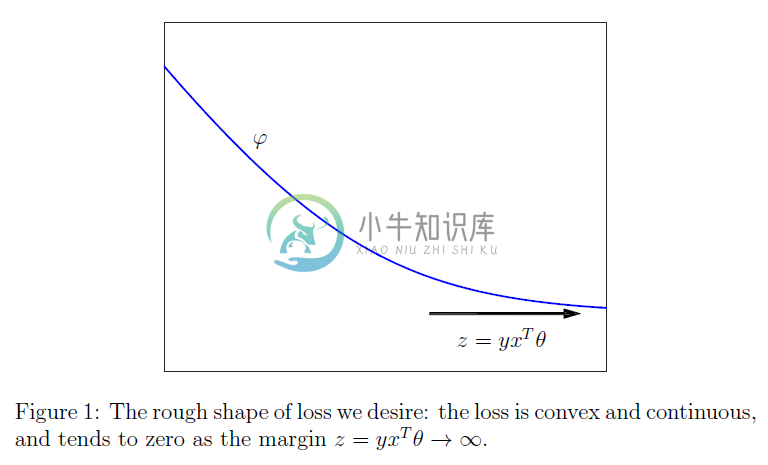
$$\varphi(z) \rightarrow 0 \text { as } z \rightarrow \infty, \quad \text { while } \varphi(z) \rightarrow \infty \text { as } z \rightarrow-\infty$$
下面来一些不同的例子,这里有三个损失函数,我们将会在这门课或现在或以后上看到,这些损失函数都是在机器学习中很常用的。
(i) logistic损失函数:
$$\varphi_{\text { logistic }}(z)=\log \left(1+e^{-z}\right)$$
(ii) 铰链损失函数(hinge loss):
$$\varphi{\text { hinge }}(z)=[1-z]{+}=\max {1-z, 0}$$
(iii) 指数损失函数:
$$\varphi_{\exp }(z)=e^{-z}$$
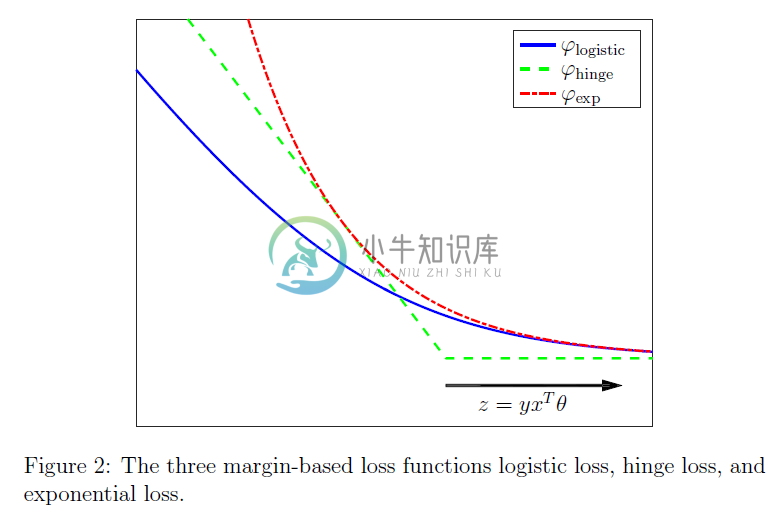
在图$2$中,我们画出了这些损失相对于边界$z=y x^{T} \theta$的图像,注意随着边界增长,每个损失函数都趋于零,并且每个损失函数往往随着边界负向增长而趋近$+\infin$。不同的损失函数将产生不同的机器学习过程;特别要指出,logistic损失$\varphi{\text { logistic }}$对应于逻辑回归问题,铰链损失$\varphi{\text { hinge }}$产生所谓的支持向量机,以及指数损失产生的经典的提升版本,这两个我们以后将更深入地探讨。
2. 逻辑回归
有了这一背景知识,我们现在对Andrew Ng课堂笔记中的逻辑回归给出了一个补充的观点。当我们使用二分标签$y \in{-1,1}$时,可以更简洁地编写逻辑回归算法。特别地,我们使用Logistic损失:
$$\varphi_{\text { logistic }}\left(y x^{T} \theta\right)=\log \left(1+\exp \left(-y x^{T} \theta\right)\right)$$
和逻辑回归算法对应于选择$\theta$来最小化下面的式子:
$$J(\theta)=\frac{1}{m} \sum{i=1}^{m} \varphi{\text {logistic}}\left(y^{(i)} \theta^{T} x^{(i)}\right)=\frac{1}{m} \sum_{i=1}^{m} \log \left(1+\exp \left(-y^{(i)} \theta^{T} x^{(i)}\right)\right)$$
粗略地,我们希望选择$\theta$最小化平均logistic损失,即产生的一个$\theta$对于大多数(甚至全部)训练样本,都可以使得$y^{(i)} \theta^{T} x^{(i)}>0$。
2.1 概率解释
与线性回归(最小二乘)类似,逻辑回归也可以用概率解释。为此,我们定义sigmoid函数(也常称为逻辑函数):
$$g(z)=\frac{1}{1+e^{-z}}$$
如图$3$所示。特别的,sigmoid函数满足:
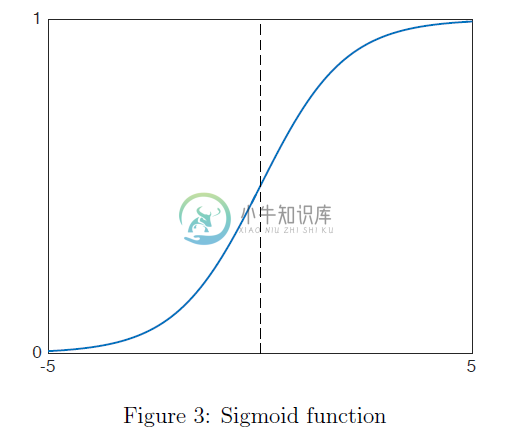
$$g(z)+g(-z)=\frac{1}{1+e^{-z}}+\frac{1}{1+e^{z}}=\frac{e^{z}}{1+e^{z}}+\frac{1}{1+e^{z}}=1$$
因此我们可以用它来定义一个概率模型进行二分类。特别的,对于$y \in{-1,1}$,我们将分类的逻辑模型定义为:
$$p(Y=y | x ; \theta)=g\left(y x^{T} \theta\right)=\frac{1}{1+e^{-y x^{T} \theta}}$$
对于积分,我们看到如果边界$y x^{T} \theta$很大——比如超过$5$等——则$p(Y=y | x ; \theta)=g\left(y x^{T} \theta\right) \approx 1$,也就是说,我们给标签为$y$的事件分配了接近$1$的概率。相反地,如果$y x^{T} \theta$很小,则$p(Y=y | x ; \theta) \approx 0$。
通过将假设类重新定义为:
$$h_{\theta}(x)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta^{T} x}}$$
然后我们得到训练数据的似然函数是:
$$L(\theta)=\prod{i=1}^{m} p\left(Y=y^{(i)} | x^{(i)} ; \theta\right)=\prod{i=1}^{m} h_{\theta}\left(y^{(i)} x^{(i)}\right)$$
对数似然函数的精确解是:
$$\ell(\theta)=\sum{i=1}^{m} \log h{\theta}\left(y^{(i)} x^{(i)}\right)=-\sum_{i=1}^{m} \log \left(1+e^{-y^{(i)} \theta^{T} x^{(i)}}\right)=-m J(\theta)$$
其中$J(\theta)$是来自等式$(3)$的准确的逻辑回归损失。也就是说,逻辑模型中的最大似然$(4)$是和平均逻辑损失同样最小化了,我们又一次得到了逻辑回归。
2.2 梯度下降法
逻辑回归的最后一部分是拟合实际模型。通常情况下,我们考虑基于梯度下降的过程来执行这种最小化。考虑到这一点,我们现在展示如何对逻辑损失求导。对于函数$\varphi_{\text { logistic }}(z)=\log \left(1+e^{-z}\right)$我们有一维导数:
$$\frac{d}{d z} \varphi{\text { logistic }}(z)=\varphi{\text { logistic }}^{\prime}(z)=\frac{1}{1+e^{-z}} \cdot \frac{d}{d z} e^{-z}=-\frac{e^{-z}}{1+e^{-z}}=-\frac{1}{1+e^{z}}=-g(-z)$$
其中$g$是sigmoid函数。然后我们应用链式法则来找出单独的训练样本$(x, y)$的结果,我们有
$$\frac{\partial}{\partial \theta{k}} \varphi{\text {logistic}}\left(y x^{T} \theta\right)=-g\left(-y x^{T} \theta\right) \frac{\partial}{\partial \theta{k}}\left(y x^{T} \theta\right)=-g\left(-y x^{T} \theta\right) y x{k}$$
因此,随机梯度下降最小化$J(\theta)$算法对于$t=1,2, \ldots$,$\alpha_t$为在时间$t$时刻的步长,执行以下迭代:
- 随机均匀的从$i \in{1, \ldots, m}$中选择一个样本
- 执行梯度更新:
$$\begin{aligned} \theta^{(t+1)} &=\theta^{(t)}-\alpha{t} \cdot \nabla{\theta} \varphi{\text { logistic }}\left(y^{(i)} x^{(i)^{T}} \theta^{(t)}\right) \ &=\theta^{(t)}+\alpha{t} g\left(-y^{(i)} x^{(i)^{T}} \theta^{(t)}\right) y^{(i)} x^{(i)}=\theta^{(t)}+\alpha{t} h{\theta^{(t)}}\left(-y^{(i)} x^{(i)}\right) y^{(i)} x^{(i)} \end{aligned}$$
这个更新是很直观的:如果当前的假设$h{\theta^{(t)}}$为不正确的标签$-y^{(i)}$分配接近$1$的概率,则我们通过将$\theta$朝着$y^{(i)} x^{(i)}$方向移动来尽量减少损失。相反,如果当前的假设$h{\theta^{(t)}}$为不正确的标签$-y^{(i)}$分配接近$0$的概率,则更新实际上什么也不做。

