1.18 决策树

接下来就要讲决策树了，这是一类很简单但很灵活的算法。首先要考虑决策树所具有的非线性/基于区域(region-based)的本质，然后要定义和对比基于区域算则的损失函数，最后总结一下这类方法的具体优势和不足。讲完了这些基本内容之后，接下来再讲解通过决策树而实现的各种集成学习方法，这些技术很适合这些场景。

1 非线性(Non-linearity)

决策树是我们要讲到的第一种内在非线性的机器学习技术(inherently non-linear machine learning techniques)，与之形成对比的就是支持向量机(SVMs)和通用线性模型(GLMs)这些方法。严格来说，如果一个方法满足下面的特性就称之为线性方法：对于一个输入$x\in R^n$（截距项 intercept term $x_0=1$），只生成如下形式的假设函数(hypothesis functions)h:

$$h(x)=\theta^Tx$$

其中的$\theta\in R^n$。不能简化成上面的形式的假设函数(hypothesis functions)就都是非线性的(non-linear)，如果一个方法产生的是非线性假设函数，那么这个方法也就是非线性的。之前我们已经看到过，对一个线性方法核化(kernelization)就是一种通过特征映射$\phi(x)$来实现非线性假设函数的方法。

决策树算法则可以直接产生非线性假设函数，不用去先生成合适的特征映射。接下来这个例子很振奋人心(加拿大风格的)，假设要构建一个分类器，给定一个时间和一个地点，要来预测附近能不能滑雪。为了简单起见，时间就用一年中的月份来表示，而地点就用纬度(latitude)来表示(北纬南纬，-90°表示南极，0°表示迟到，90°表示南极)。

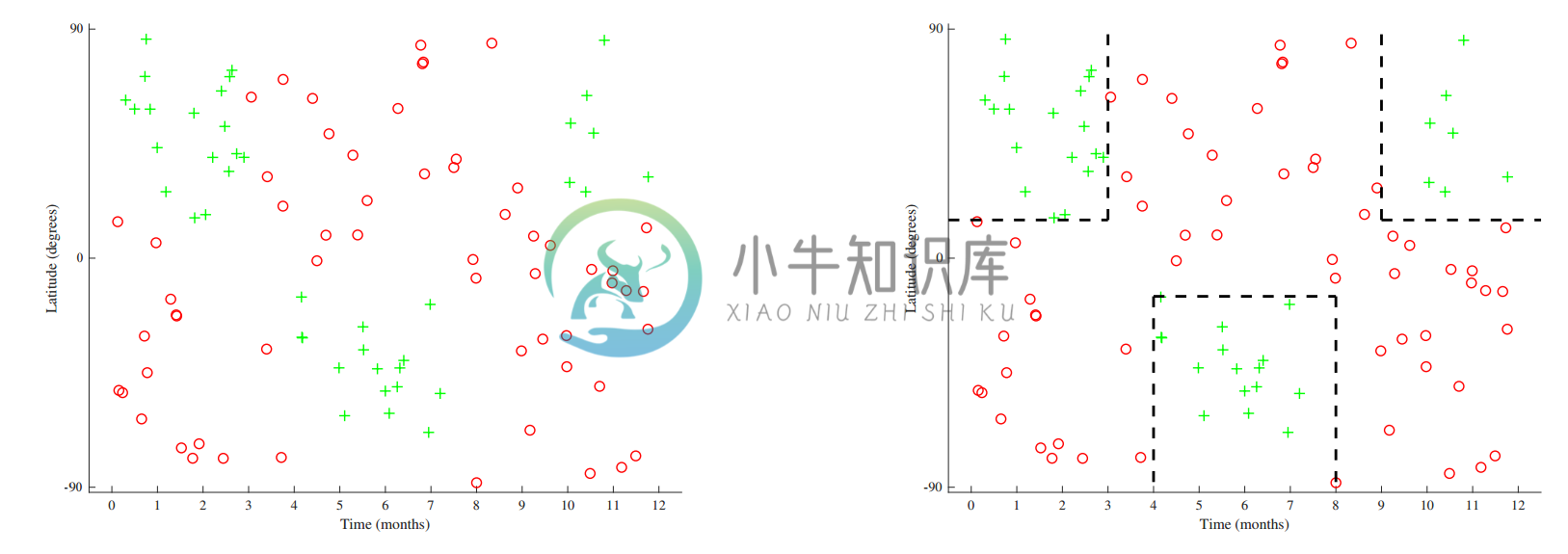
有代表性的数据结构如上图左侧所示。不能划分一个简单的线性便捷来正确区分数据集。不过可以很明显可以发现数据集中的空间中有可以鼓励出来的不同区域，一种划分方式如上图中右侧所示。上面这个分区过程(partitioning)开通过对输入空间$x$分割成不相连接的自己(或者区域)$R_i$:

$$\begin{aligned} X&= \bigcup ^n_{i=0} R_i\ s.t.\qquad R_i \bigcap R_j&= \not{0} \quad\text{for}\quad i \ne j \end{aligned}$$

其中$n\in Z^+$。

2 区域选择(Selecting Regions)

通常来说，选择最有区域是很难的(intractable)。决策树会生通过贪心法，从头到尾，递归分区(greedy, top-down, recursive partitioning) 成一种近似的解决方案。这个方法是从头到尾(top-down) 是因为是从原始输入空间$X$开始，先利用单一特征为阈值切分成两个子区域。然后对两个子区域选择一个再利用一个新阈值来进行分区。然后以递归模式来持续对模型的训练，总是选择一个叶节点(leaf node)，一个特征(feature)，以及一个阈值(threshold)来生成新的分割(split)。严格来说，给定一个父区域$R_p$，一个特征索引$j$以及一个阈值$t\in R$，就可以得到两个子区域$R_1,R_2$，如下所示:

$$\begin{aligned} R_1 &= { X|X_j<t,X\in R_p}\ R_2 &= { X|X_j \ge t,X\in R_p}\ \end{aligned}$$

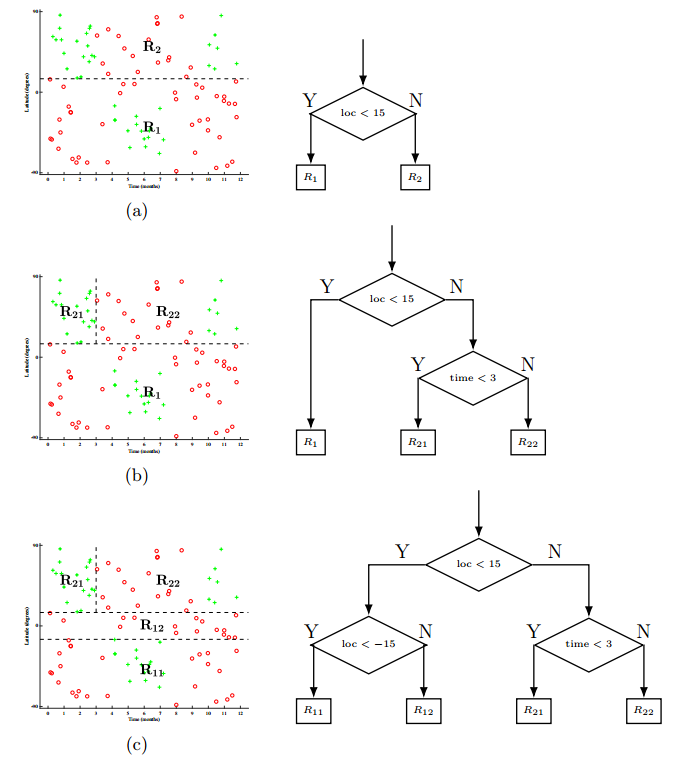
下面就着滑雪数据集来应用上面这样的过程。在步骤a当中，将输入空间$\mathcal{X}$根据地理位置特征切分，阈值设置的是$15$，然后得到了子区域$R1,R_2$。在步骤b，选择一个子区域(例子中选的是$R_2$)来递归进行同样的操作，选择时间特征，阈值设为$3$，然后生成了二级子区域$R{21},R{22}$。在步骤c，对剩下的叶节点($R_1,R{21},R_{22}$)任选一饿，然后继续上面的过程，知道遇到了一个给定的停止条件(stop criterion，这个稍后再介绍)，然后再预测每个节点上的主要类别。

3 定义损失函数(Defining a Loss Function)

这时候很自然的一个问题就是怎么去选择分割。首先要定义损失函数$L$，这个函数是在区域$R$上的一个集合函数(set function)。对一个父区域切分成两个子区域$R_1,R_2$之后，可以计算福区域的损失函数$L(R_p)$，也可以计算子区域的基数加权(cardinality-weighted)损失函数$\frac{|R_1|L(R_1)+|R_2|L(R_2)}{|R_1|+|R_2|}$。在贪心分区框架(greedy partitioning framework)下，我们想要选择能够最大化损失函数减少量(decrease)的叶区域/特征和阈值:

$$L(R_p)-\frac{|R_1|L(R_1)+|R_2|L(R_2)}{|R_1|+|R_2|}$$

对一个分类问题，我们感兴趣的是误分类损失函数(misclassification loss) $L_{misclass}$。对于一个区域$R$，设$\hat p_c$是归于类别$c$的$R$中样本的分区。在$R$上的误分类损失函数可以写为:

$$L_{misclass}(R)=1-\max_c(\hat p_c)$$

这个可以理解为在预测区域$R$上的主要类别中发生错误分类的样本个数。虽然误分类损失函数是我们关心的最终值，但这个指标的对类别概率的变化并不敏感。举个例子，如下图所示的二值化分类。我们明确描述了父区域$R_p$，也描述了每个区域上的正负值的个数。

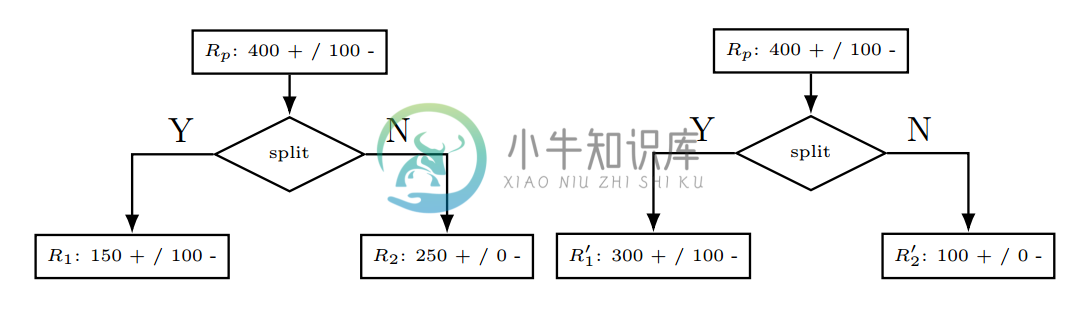
第一个切分就是讲搜有的正值分割开来，但要注意到:

$$L(R_p)=\frac{|R_1|L(R_1)+|R_2|L(R_2)}{|R_1|+|R_2|}=\frac{|R_1'|L(R_1')+|R_2'|L(R_2')}{|R_1'|+|R_2'|}=100$$

这样不仅能使两个切分的损失函数相同，还能使得任意一个分割都不会降低在父区域上的损失函数。(Thus, not only can we not only are the losses of the two splits identical, but neither of the splits decrease the loss over that of the parent.)

因此我们有兴趣去定义一个更敏感的损失函数。前面已经给出过一些损失函数了，这里要用到的是交叉熵(cross-entropy) 损失函数$L_{cross}$:

$$L_{cross}(R)=-\sum_c \hat p_c \log_2 \hat p_c$$

如果$\hat p_c=0$，则$\hat p_c \log_2 \hat p_c\equiv 0$。从信息论角度来看，交叉熵要衡量的是给定已知分布的情况下要确定输出所需要的位数(number of bits)。更进一步说，从父区域到子区域的损失函数降低也就是信息增益(information gain)。

要理解交叉熵损失函数比误分类损失函数相对更敏感，我们来看一下对同样一个二值化分类案例这两种损失函数的投图。从这些案例中，我们能够对损失函数进行简化，使之仅依赖一个区域$R_i$中正值分区的样本$\hat p_i$:

$$\begin{aligned} L{misclass}(R)= L{misclass}(\hat p)=1-\max(\hat p,1-\hat p)\ L{cross}(R)=L{cross}(\hat p)=- \hat p\log \hat p -(1-\hat p)\log(1-\hat p)\ \end{aligned}$$

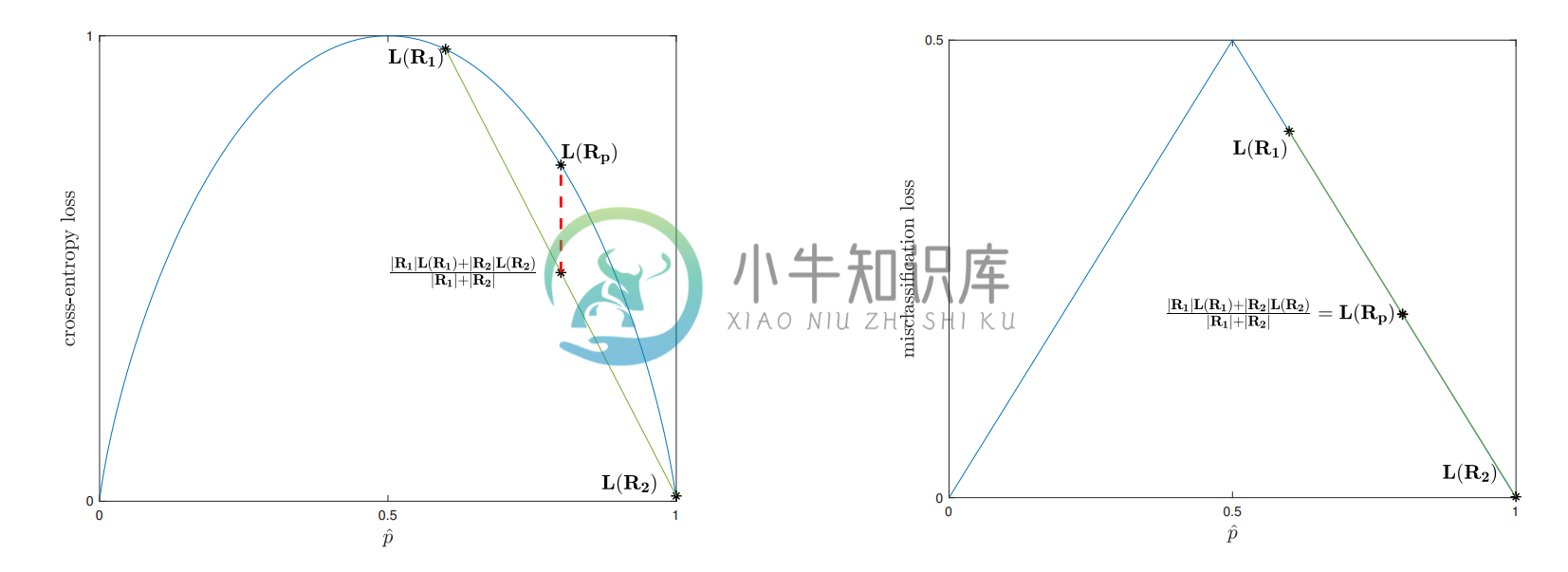
上图左侧中看到的是交叉熵损失函数在$\hat p$上的投图。从前文中样本中的第一个分割得到的区域$(R_p,R_1,R_2)$然后也对其损失函数进行了投图。交叉熵损失函数是严格的凹函数(concave)，可以从投图中明显看出(证明起来也很容易)只要$\hat p_1 \ne \hat p_2$以及两个子区域都是非空的，则子区域损失函数的加权和总会小于父区域。

误分类损失函数，则不是严格凹函数，因此也不能保证子区域损失函数的加权和能够比父区域的小，如上图右侧所示，虽然有同样的分区方案。由于这一点额外的敏感性，交叉熵损失函数（或者与之密切相关的基尼损失函数(Gini loss)）用于用于分类的生长决策树(growing decision trees)。

在谈论其他内容之前，我们先简单介绍一些决策树的回归设定。对每个数据点$x_i$，我们现在有了一个关联值(associated value)也就是我们要去预测的$y_i\in R$。大部分树的生长过程都是相同的，区别只是在对于一个区域$R$的最终预测是所有值的平均：

$$\hat y =\frac{\sum_{i\in R}y_i}{|R|}$$

然后在这个例子中直接使用平方损失函数(squared loss) 来选择切分:

$$L{squared}(R)=\frac{\sum{i\in R}(y_i -\hat y)^2}{|R|}$$

4 其他考虑(Other Considerations)

决策树的流行很大一部分是由于其好解释也好理解，另外就是高度的可解释性：我们可以看到生成的阈值集合来理解为什么模型做出了具体的预测。不过这还不仅仅是全部，接下来我们要讲到一些额外的优点。

4.1 分类变量(Categorical Variables)

决策树的一大优点就是很适合用于处理分类变量。例如在滑雪数据集里面的地点就可以替代城任意的分类数据(Northern Hemisphere, Southern Hemisphere, 或者 Equator （也就是$loc in{N,S,E}$）。相比独热编码(one-hot encoding)或者类似的预处理步骤来讲数据转换到定量特征，这些方法对于之前见过的其他算法来说是必要的，但对于决策树算法来说，可以直接探测子集成员。本章第2节中的最终树形可以写成如下的形式:

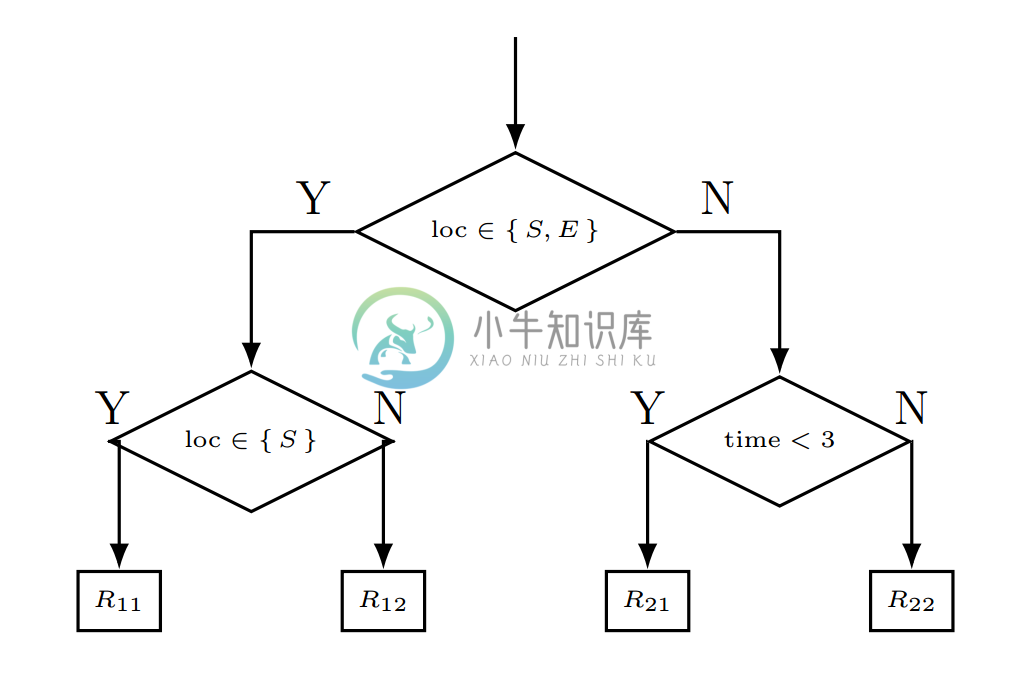
需要注意的就是要留神避免变量有太多的分类。对于一个分类集合$S$，我们的潜在问题集合及就是幂集合(power set)$P(S)$，基数(cardinality)为$2^{|S|}$。因此分类类别太多了就可能是问题选择的计算变得很难。对于二值化分类来说优化倒是可能的，虽然即便这时候也应该考虑将特征重新格式化成定量的而不是使用大规模的潜在阈值然后任它们严重过拟合。

4.2 规范化(Regularization)

在第2节中我们顺便提到了各种停止条件(stopping criteria)来决定是否终止一个树的生长。最简单的判断条件就是让树"完全"生长:一直继续分类知道叶区域包含的只有单个的训练样本点。这个方法会导致高方差和低偏差的模型，因此我们改用其他的各种启发式的方法来规范化。下面是一些常用方法:

• 最小叶规模(Minimum Leaf Size) —— 直到基数(cardinality)落到一个固定的阈值内才停止切割$R$。
• 最大深度(Maximum Depth) —— 如果到达$R$已经经过了超过一个固定估值的阈值，就停止切割$R$。
• 最大节点数(Maximum Number of Nodes) —— 如果一个树到达了超过一个的叶节点阈值就停止。

一种启发式方法是在切分之后使用损失函数的最小降低发。这是一个有问题的方法，因为对决策树的贪心的每次单特正的方法可能意味着损失掉高阶互动(higher order interactions)。如果我们需要对多个特征设置阈值来达到一个良好的分割，就可能没办法在初始分割的损失上达到一个好的降低(decrease)，因此就可能过早停止(prematurely terminate)。一种更好的方法是将树完全生长出来，然后修剪掉那些最小程度上减少错误分类或平方误差的节点，就跟在验证集上进行判断的方法一样。

4.3 运行(Runtime)

我们简短地来看一下决策树的运行。为了易于分析，考虑一个有$n$个样本，$f$个特征，决策树深度为$d$的二值化分类问题。在测试的时候，对一个数据点我们会贯穿(traverse)整个树直到到达一个叶节点(leaf node)然后输出预测，运算时间是$O(d)$。要注意这里的书是平衡的$d=O(\log n)$，因此测试时间的运算还挺快的。

在训练的时候，我们要注意每个数据节点都只会在最多$O(d)$节点中出现。通过排序和对中间值的智能获取，就可以在每个节点对每个数据点的每一个特征构建一个分摊时间为$O(1)$的运算。因此总的运行时间就是$O(nfd)$-鉴于数据矩阵规模是$nf$，这是一个比较快的运行速度了。

4.4 加性结构缺失(Lack of Additive Structure)

决策树的一个重要缺陷就是不能轻易捕获加性结构。例如如下图作图所示，简单的分裂便捷形式$x_1+x_2$只能用于对很多分类模型进行近似，每个分类都可能每次产生一个$x_1$或者$x_2$。而下图右侧的线性模型则直接推导出了这个边界。

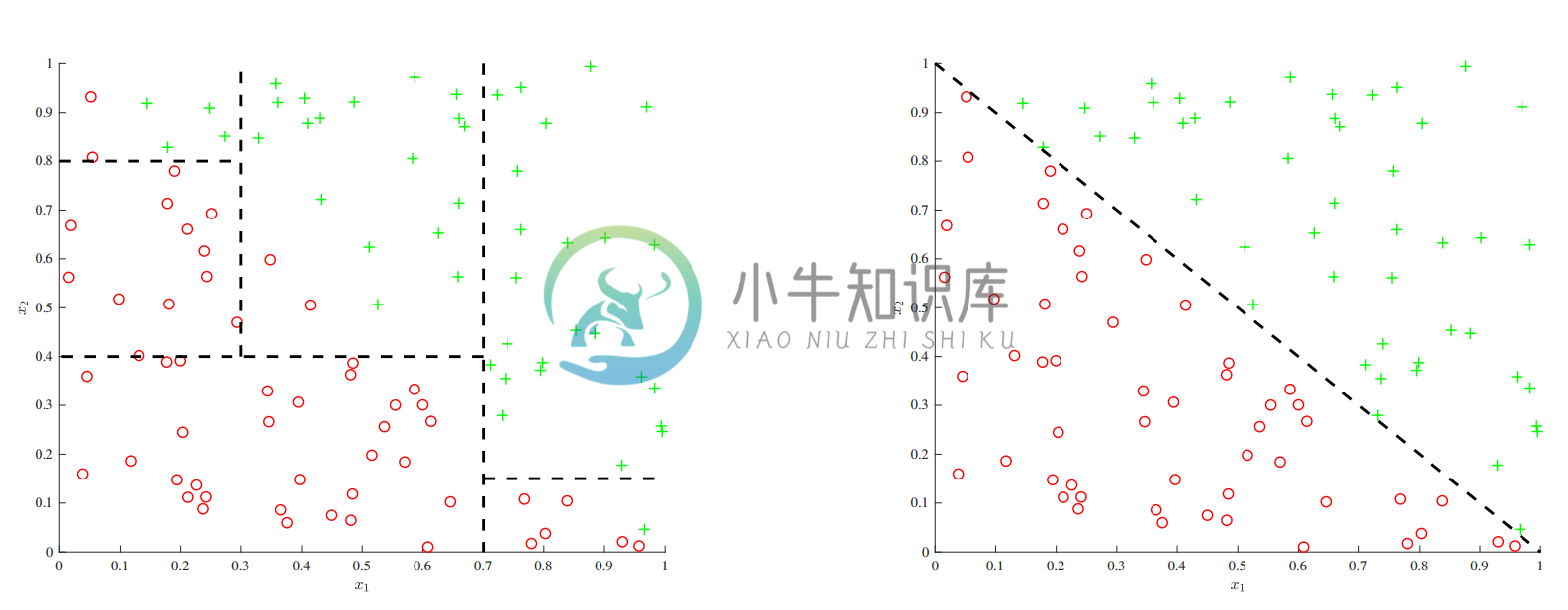
要让决策边界同时从多个特征中寻找因子，还需要很多的工作，随着未来变量的增加，可解释性就会降低，这也是个缺陷。

5 本章概要

总结一下，本节关于决策树的有点是:

• 好解释
• 解释性好
• 分类变量支持的好
• 速度快

缺陷则包括:

• 方差大
• 对加性模型建模很差

很不幸，这些问题都使得单独使用决策树会在整体上导致较低的预测精度。解决这个问题的常见（也是可行）的办法就是通过集成学习(ensembling methods)——留在下一章再讲了。