1.20 凸优化1

凸优化概述

1. 介绍

在很多时候，我们进行机器学习算法时希望优化某些函数的值。即，给定一个函数$f:R^n\rightarrow R$，我们想求出使函数$f(x)$最小化（或最大化）的原像$x\in R^n$。我们已经看过几个包含优化问题的机器学习算法的例子，如：最小二乘算法、逻辑回归算法和支持向量机算法，它们都可以构造出优化问题。

在一般情况下，很多案例的结果表明，想要找到一个函数的全局最优值是一项非常困难的任务。然而，对于一类特殊的优化问题——凸优化问题， 我们可以在很多情况下有效地找到全局最优解。在这里，有效率既有实际意义，也有理论意义：它意味着我们可以在合理的时间内解决任何现实世界的问题，它意味着理论上我们可以在一定的时间内解决该问题，而时间的多少只取决于问题的多项式大小。（译者注：即算法的时间复杂度是多项式级别$O(n^k)$，其中$k$代表多项式中的最高次数）

这部分笔记和随附课程的目的是对凸优化领域做一个非常简要的概述。这里的大部分材料（包括一些数字）都是基于斯蒂芬·博伊德(Stephen Boyd)和利文·范登伯格(lieven Vandenberghe)的著作《凸优化》（凸优化[1]注：参考资料[1]见文章最下方在网上免费提供下载）以及斯蒂芬·博伊德(Stephen Boyd)在斯坦福教授的课程EE364。如果你对进一步研究凸优化感兴趣，这两种方法都是很好的资源。

2. 凸集

我们从凸集的概念开始研究凸优化问题。

定义2.1 我们定义一个集合是凸的，当且仅当任意$x,y\in C$ 且 $\theta\in R, 0\le\theta\le 1$,

$$\theta x + (1-\theta)y\in C$$

实际上，这意味着如果我们在集合$C$中取任意两个元素，在这两个元素之间画一条直线，那么这条直线上的每一点都属于$C$。图$1$显示了一个示例的一个凸和一个非凸集。其中点$\theta x +(1-\theta) y$被称作点集$x,y$的凸性组合(convex combination)。

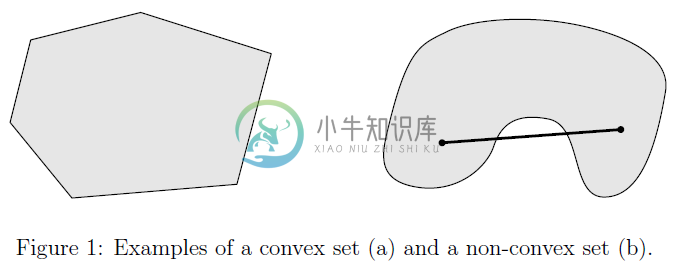
2.1 凸集的实例

• 全集$R^n$ 是一个凸集 （译者注：即$n$维向量空间或线性空间中所有元素组成的集合）。 因为以下结论显而易见：任意$x,y\in R^n$，则$\theta x +(1-\theta) y\in R^n$。（译者注：$n$维向量空间对加法和数乘封闭，显然其线性组合也封闭）

• 非负的象限$R^n_+$组成的集合 是一个凸集。$R^n$中所有非负的元素组成非负象限：$R^n+={x:x_i\ge 0\quad\forall i=1,\dots,n }$。为了证明$R^n+$是一个凸集，只要给定任意$x,y\in R^n_+$，并且$0\le\theta\le 1$，

$$(\theta x +(1-\theta) y)_i = \theta x_i + (1 - \theta)y_i\ge 0\quad\forall i$$

• 范数球是一个凸集。设$\parallel\cdot\parallel$是$R^n$中的一个范数（例如，欧几里得范数，即二范数$\parallel x\parallel2=\sqrt{\sum{i=1}^nx_i^2}$）。则集合${x:\parallel x\parallel\le 1}$是一个凸集。为了证明这个结论，假设$x,y\in R^n$，其中$\parallel x\parallel\le 1,\parallel y\parallel\le 1,0\le\theta\le 1$，则：

$$\parallel \theta x +(1-\theta) y\parallel\le \parallel\theta x\parallel+\parallel(1-\theta) y\parallel = \theta\parallel x\parallel+(1-\theta)\parallel y\parallel\le 1$$

我们用了三角不等式和范数的正同质性(positive homogeneity)。

• 仿射子空间和多面体 是一个凸集。给定一个矩阵$A\in R^{m\times n}$和一个向量$b\in R^m$，一个仿射子空间可以表示成一个集合${x\in R^n:Ax=b}$（注意如果$b$无法通过$A$列向量的线性组合得到时，结果可能是空集）。类似的，一个多面体（同样，也可能是空集）是这样一个集合${x\in R^n:Ax\preceq b}$，其中‘$\preceq$’代表分量不等式(componentwise inequality)（也就是，$Ax$得到的向量中的所有元素都小于等于$b$向量对应位置的元素）$^1$。为了证明仿射子空间和多面体是凸集，首先考虑$x,y\in R^n$，这样可得$Ax=Ay=b$。则对于$0\le\theta\le 1$，有：

1 类似的，对于两个向量$x,y\in R^n$，$x\succeq y$代表，向量$x$中的每一个元素都大于等于向量$y$对应位置的元素。注意有时候文中使用符号‘$\le$’和‘$\ge$’代替了符号‘$\preceq$’和‘$\succeq$’，则符号的实际意义必须根据上下文来确定（也就是如果等式两边都是向量的时候，文中使用的是常规的不等号‘$\le$’和‘$\ge$’，则我们自己心中要知道用后两个符号‘$\preceq$’和‘$\succeq$’的意义代替之）

$$A(\theta x +(1-\theta) y) = \theta Ax + (1-\theta)Ay=\theta b + (1-\theta)b=b$$

类似的，对于$x,y\in R^n$，满足$Ax\le b$以及$Ay\le b,0\le\theta\le 1$，则：

$$A(\theta x +(1-\theta) y) = \theta Ax + (1-\theta)Ay\le\theta b + (1-\theta)b=b$$

• 凸集之间的交集还是凸集。假设$C_1,C_2,\dots,C_k$都是凸集，则它们的交集：

$$\bigcap_{i=1}^kC_i={x:x\in C_i\quad\forall i=1,\dots,k}$$

同样也是凸集。为了证明这个结论，考虑$x,y\in \bigcap_{i=1}^k C_i$以及$0\le\theta\le 1$，则：

$$\theta x +(1-\theta) y\in C_i\quad\forall i=1,\cdots,k$$

因此，根据凸集的定义可得：

$$\theta x +(1-\theta) y\in\bigcap_{i=1}^kC_i$$

然而要注意在通常情况下，凸集之间的并集并不是一个凸集。

• 半正定矩阵是一个凸集。所有对称半正定矩阵的集合，常称为半正定锥，记作$S^n+$，其是一个凸集（通常情况下，$S^n\subset R^{n\times n}$代表$n\times n$对称矩阵的集合）。回忆一个概念，我们说一个矩阵$A\in R^{n\times n}$是对称半正定矩阵，当且仅当该矩阵满足$A=A^T$，并且给定任意一个$n$维向量$x\in R^n$，满足$x^TAx\ge 0$。现在考虑两个对称半正定矩阵$A,B\in S^n+$，并且有$0\le\theta\le 1$。给定任意$n$维向量$x\in R^n$，则：

$$x^T(\theta A +(1-\theta) B)x=\theta x^TAx+(1-\theta)x^TBx\ge 0$$

同样的逻辑可以用来证明所有正定、负定和半负定矩阵的集合也是凸集。

3. 凸函数

凸优化的一个核心要素是凸函数的概念。

定义 $3.1$ 我们称一个函数$f:R^n\rightarrow R$是一个凸函数，需要满足其定义域（记作$\mathcal{D}(f)$）是一个凸集，同时给定任意$x,y\in \mathcal{D}(f)$以及$\theta\in R,0\le\theta\le 1$，满足：

$$f(\theta x +(1-\theta) y)\le \theta f(x)+(1-\theta)f(y)$$

（译者注：注意这里函数的凸凹性和我们本科《高等数学》上册里面微分中值定理与导数应用章节中曲线的凸凹性是相反的，不过这里定义的凸凹的方向在机器学习中更常见）

直观地，考虑这个定义的方法是如果我们在凸函数的图上取任意两点并在两点之间画一条直线，那么函数在这两点之间的部分就会在这条直线下面。这种情况如图$2^2$所示。

2 不要太担心$f$的定义域是凸集的要求，这个要求仅仅是在技术上保证$f(\theta x +(1-\theta) y)$有定义（如果定义域$\mathcal{D}(f)$不是凸集，则即使$x,y\in\mathcal{D}(f)$，$f(\theta x +(1-\theta) y)$也有可能没有意义）

如果在定义$3.1$的基础上增加严格的不等的条件$x\ne y$和$0<\theta<1$，则可以说一个函数是严格凸函数。如果$f$是凸函数则我们可以得到$-f$是凹函数， 同理如果$f$是严格凸函数则$-f$是严格凹函数。

3.1 凸性的一阶条件

假设函数$f:R^n\rightarrow R$可微（即其梯度$^3\nabla_xf(x)$在函数$f$的定义域内处处存在）。则$f$是一个凸函数，只要满足$\mathcal{D}(f)$是一个凸集，同时对所有的$x,y\in\mathcal{D}(f)$，有：

3 回忆一下梯度定义为$\nabla_xf(x)\in R^n,(\nabla_xf(x))_i=\frac{\partial f(x)}{\partial x_i}$。有关梯度和海森函数的知识，请参阅前面关于线性代数的部分的章节笔记。

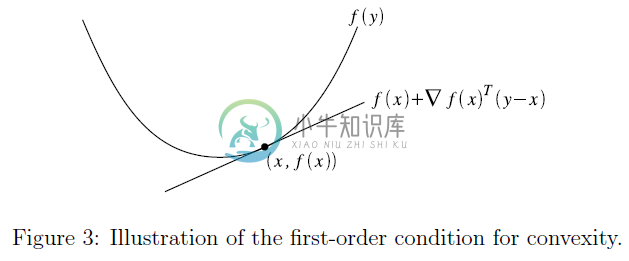
$$f(y)\ge f(x)+\nabla_xf(x)^T(y-x)$$

函数$f(x)+\nabla_xf(x)^T(y-x)$称为函数$f(x)$在点$x$处的一阶近似(first-order approximation)。 直觉上来说，这个函数可以近似的认为是函数$f$在点$x$处的切线。凸性的一阶条件就是阐明了，$f$是凸函数当且仅当该函数的切线是一个全局下估计(global underestimator)。换句话说，如果我们根据函数的特性在任意一点绘制该函数的切线，那么这条直线上的每一点将低于函数$f$在相应位置的点。

与凸性的定义类似，当严格不等条件成立时$f$是严格凸函数，当不等式符号颠倒时$f$是凹函数，当颠倒的不等式的严格不等条件成立时$f$是严格凹函数。

3.2 凸性的二阶条件

假设函数$f:R^n\rightarrow R$二阶可微（即其海森矩阵$^4\nabla_x^2f(x)$在函数$f$的定义域内处处存在）。则$f$是一个凸函数，只要满足$\mathcal{D}(f)$是一个凸集，同时对所有的$x,y\in\mathcal{D}(f)$，有：

4 回忆一下海森矩阵定义为$\nablax^2f(x)\in R^{n\times n},(\nabla_x^2f(x)){ij}=\frac{\partial^2 f(x)}{\partial x_i\partial x_j}$

$$\nabla_x^2f(x)\succeq 0$$

当符号“$\succeq$”在这里与矩阵结合使用时，指的是半正定矩阵，而不是分量不等式(componentwise inequality)$^5$。在一维中，这等价于二阶导数$f''(x)$总是非负的（即函数始终为绝对的非负值(positive non-negative)）。

5 与对称矩阵$X\in S^n$类似，$X\preceq 0$代表$X$是负定矩阵。对于向量不等式来说，有时可以用符号‘$\le$’和‘$\ge$’代替符号‘$\preceq$’和‘$\succeq$’。尽管这里的符号类似向量的符号，但是意义非常不一样。特别的，矩阵$X\succeq 0$并不意味着对于所有矩阵的元素下标$i,j$都有元素$X_{ij}\ge 0$

同样，与凸性的定义以及一阶条件类似，如果海森矩阵是正定的，则函数$f$是严格凸函数，如果是半负定则函数是凹函数，是负定则函数是严格凹函数。

3.3 Jensen不等式

假设我们从凸函数的基本定义中的不等式开始：

$$f(\theta x +(1-\theta) y)\le \theta f(x)+(1-\theta)f(y)\quad 其中\quad 0\le\theta\le 1$$

使用归纳法，这可以相当容易地扩展到多个点的凸组合：

$$f(\sum{i=1}^k\theta_ix_i)\le\sum{i=1}^k\thetaif(x_i)\quad 其中\quad\sum{i=1}^k\theta_i=1,\theta_i\ge 0\quad\forall i$$

事实上，这也可以推广到无穷和或积分。在后一种情况下，不等式可以写成：

$$f(\int p(x)xdx)\le\int p(x)f(x)dx\quad 其中\quad\int p(x)dx=1,p(x)\ge0\quad\forall x$$

由于$p(x)$积分为$1$，通常把它看作概率密度，在这种情况下，前面的方程可以用期望来表示：

$$f(E[x])\le E[f(x)]$$

最后一个不等式叫做Jensen不等式，后面的课上会讲到。$^6$

6 事实上，这四个方程有时都被称为Jensen不等式，因为它们都是等价的。但是，对于这门课，我们将使用该术语来具体指这里给出的最后一个不等式。

3.4 水平集

凸函数产生一种特别重要的凸集称为 $\alpha-sublevel$集。 给出了凸函数$f:R^n\rightarrow R$和一个实数$\alpha\in R$，$\alpha-sublevel$集被定义为：

$${x\in\mathcal{D}(f):f(x)\le\alpha}$$

换句话说，$\alpha-sublevel$集是所有满足$f(x)\le\alpha$的点$x$的集合。

为了证明这是一个凸集，考虑任意$x,y\in\mathcal{D}(f)$，并且$f(x)\le\alpha,f(y)\le\alpha$，则：

$$f(\theta x +(1-\theta) y)\le \theta f(x)+(1-\theta)f(y)\le\theta\alpha+(1-\theta)\alpha=\alpha$$

3.5 凸函数判断的实例

我们从几个单变量凸函数的简单例子开始，然后继续讨论多元函数。

• 指数函数是凸函数。有函数$f:R\rightarrow R$，任意$a\in R$使得$f(x)=e^{ax}$。为了证明$f$是凸函数，我们可以简单的考虑二阶导数$f''(x)=a^2e^{ax}$，对于所有$x$都是正的。

• 负对数函数是凸函数。函数$f:R\rightarrow R,f(x)=-logx$，有定义域$\mathcal{D}(f)=R{++}$（这里的$R{++}$代表严格正实数的集合${x:x>0}$）。则对于所有的$x$都满足$f''(x)=1/x^2>0$。

• 仿射函数。函数$f:R\rightarrow R,f(x)=b^Tx+c$，满足$b\in R^n,c\in R$。在这种情况下对于所有的$x$，该函数的海森矩阵$\nabla^2_xf(x)=0$。应为零矩阵即是半正定也是半负定矩阵，因此函数$f$即是凸函数，也是凹函数。事实上，这种形式的仿射函数是唯一既凸又凹的函数。

• 二次函数。函数$f:R\rightarrow R,f(x)=\frac12x^TAx+b^Tx+c$，系数的对称矩阵为$A\in S^n,b\in R^n$以及$c\in R$。在先前线性代数笔记中，我们展示了这个函数的海森函数为：

$$\nabla^2_xf(x)=A$$

因此，函数$f$的凸性或非凸性完全取决于A是否为半正定矩阵：如果$A$为半正定，则函数为凸函数（严格凸、凹、严格凹函数同样类比）；如果$A$是不定的矩阵，那么$f$既不是凸函数也不是凹函数。

注意，平方欧几里得范数$f(x) = \parallel x\parallel^2_2=x^Tx$是二次函数的一个特例，其中$a = I, b = 0, c = 0$，因此它是一个严格凸函数。

• 范数函数是凸函数。函数$f:R\rightarrow R$为$R^n$上的某个范数。然后根据三角不等式和正范数的同质性，对于$x,y\in R^n,0\le\theta\le 1$，有：

$$f(\theta x +(1-\theta) y)\le f(\theta x)+f((1-\theta)y) =\theta f(x)+(1-\theta)f(y)$$

这是一个凸函数的例子，由于范数不是处处可微的（例如，$1$范数，$\parallel x\parallel1 = \sum{i=1}^n|x_i|$，在任意$x_i = 0$的点上都是不可微的），因此无法根据二阶或一阶条件证明凸性。

• 凸函数的非负加权和是凸函数。令$f_1,f_2,\dots,f_k$是凸函数，并且有$w_1,w_2,\dots,w_k$都是非负实数，则：

$$f(x) = \sum_{i=1}^kw_if_i(x)$$

是一个凸函数，因为：

$$\begin{aligned} f(\theta x +(1-\theta) y)&=\sum{i=1}^kw_if_i(\theta x +(1-\theta) y) \ &\le\sum{i=1}^kwi(\theta f_i(x))+(1-\theta)f_i(y)) \ &=\theta\sum{i=1}^kwif_i(x)+(1-\theta)\sum{i=1}^kw_if_i(y) \ &=\theta f(x) + (1-\theta)f(x) \end{aligned}$$

4 凸优化问题

利用凸函数和集合的定义，我们现在可以考虑凸优化问题。 正式的定义为：一个凸优化问题在一个最优化问题中的形式如下：

$$minimize\quad f(x) \ subject\quad to\quad x\in C$$

其中$f$为凸函数，$C$为凸集，$x$为优化变量。然而，由于这样写可能有点不清楚，我们通常把它写成

$$\begin{aligned} minimize\quad &f(x) \ subject\quad to\quad &g_i(x)\le 0,\quad i=1,\cdots,m \ &h_i(x)=0,\quad i=1,\cdots,p \end{aligned}$$

其中$f$为凸函数，$g_i$为凸函数，$h_i$为仿射函数，$x$为优化变量。

注意这些不等式的方向很重要：凸函数$g_i$必须小于零。这是因为$g_i$的$0-sublevel$集是一个凸集，所以可行域，是许多凸集的交集，其也是凸集（回忆前面讲过的仿射子空间也是凸集）。如果我们要求某些凸函数$g_i$的不等式为$g_i\ge 0$，那么可行域将不再是一个凸集，我们用来求解这些问题的算法也不再保证能找到全局最优解。还要注意，只有仿射函数才允许为等式约束。直觉上来说，你可以认为一个等式约束$h_i= 0$等价于两个不等式约束$h_i\le 0$和$h_i\ge 0$。然而，当且仅当$h_i$同时为凸函数和凹函数时，这两个约束条件才都是有效的，因此$h_i$一定是仿射函数。

优化问题的最优值表示成$p^$（有时表示为$f^$），并且其等于目标函数在可行域$^7$内的最小可能值。

7 数学专业的学生可能会注意到，下面出现的最小值更应该用符号$inf$。这里我们不需要担心这些技术问题，为了简单起见，我们使用符号$min$。

$$p^* = min{f(x):g_i(x)\le 0,i=1,\dots,m,h_i(x)=0,i=1,\dots,p}$$

当问题是不可行（即可行域是空的）时或无下界（即存在这样的可行点使得$f(x)\rightarrow -\infin$）时，我们允许$p^$取值为$+\infin$和$-\infin$。当$f(x^)=p^$时，我们称$x^$是一个最优点(optimal point)。 注意，即使最优值是有限的，也可以有多个最优点。

4.1 凸问题的全局最优性

在说明凸问题中的全局最优性结果之前，让我们正式定义局部最优和全局最优的概念。直观地说，如果一个函数目标值附近没有令该函数值较低的可行点，则该可行点 （译者注：即该函数目标值的原像） 被称为局部最优。 类似地，如果一个函数的全局都没有比目标值更低的可行点，则该可行点称为全局最优。 为了更形式化一点，我们给出了以下两个定义。

定义$4.1$ 如果在可行域（即，满足优化问题的约束条件）内存在某些$R > 0$的数，使得所有可行点$z$，当满足$\parallel x-z\parallel_2\le R$时，均可以得到$f(x)\le f(z)$，则我们称点$x$是局部最优的。

定义$4.2$ 如果在可行域所有可行点$z$，都满足$f(x)\le f(z)$，则我们称点$x$是全局最优的。

现在我们来讨论凸优化问题的关键元素，它们的大部作用都来自于此。其核心思想是对于一个凸优化问题，所有局部最优点都是全局最优的。

让我们用反证法来快速证明这个性质。假设$x$是局部最优点而不是全局最优点，即，存在这样一个可行点$y$使得$f(x)>f(y)$。根据局部最优性的定义，不存在$\parallel x-z\parallel_2\le R$和$f(z) < f(x)$的可行点$z$。现在假设我们选择这个点

$$z = \theta y +(1-\theta)x\quad有\quad\theta=\frac{R}{2\parallel x-y\parallel_2}$$

则：

$$\begin{aligned} \parallel x-z\parallel_2 &= \parallel x-(\frac{R}{2\parallel x-y\parallel_2}y+(1-\frac{R}{2\parallel x-y\parallel_2})x)\parallel_2 \ &= \parallel \frac{R}{2\parallel x-y\parallel_2}(x-y)\parallel_2 \ &= \frac R2\le R \end{aligned}$$

另外，通过$f$的凸性，我们可得：

$$f(z)=f(\theta y +(1-\theta)x)\le\theta f(y)+(1-\theta)f(x)< f(x)$$

此外，由于可行域的集合是凸集，同时$x$和$y$都是可行的，因此$z =\theta y +(1-\theta)$也会是可行的。因此，$z$是一个可行点，满足$\parallel x-z\parallel_2\le R$以及$f(z) < f(x)$。这与我们的假设相矛盾，表明$x$不可能是局部最优的。

4.2 凸问题的特殊情况

由于各种原因，通常考虑一般凸规划公式的特殊情况比较方便。对于这些特殊情况，我们通常可以设计出非常高效的算法来解决非常大的问题，正因为如此，当人们使用凸优化技术时，你可能会看到这些特殊情况。

• 线性规划。 如果目标函数$f$和不等式约束$g_i$都是仿射函数，那么凸优化问题就是一个线性规划(linear program,LP) 问题。换句话说，这些问题都有如下形式：

$$\begin{aligned} minimize\quad &c^Tx+d \ subject\quad to\quad &Gx\preceq h \ &Ax=b \end{aligned}$$

其中，$x\in R^n$是优化变量，$c\in R^n,d\in R,G\in R^{m\times n},h\in R^m,A\in R^{p\times n},b\in R^p$这些变量根据具体问题具体定义，符号‘$\preceq$’代表（多维向量中）各个元素不相等。

• 二次规划。 如果不等式约束（跟线性规划）一样是仿射的，而目标函数$f$是凸二次函数，则凸优化问题是一个二次规划(quadratic program,QP) 问题。换句话说，这些问题都有如下形式：

$$\begin{aligned} minimize\quad &\frac 12x^TPx+c^Tx+d \ subject\quad to\quad &Gx\preceq h \ &Ax=b \end{aligned}$$

其中，$x\in R^n$是优化变量，$c\in R^n,d\in R,G\in R^{m\times n},h\in R^m,A\in R^{p\times n},b\in R^p$这些变量根据具体问题具体定义，但是这里我们还有一个对称半正定矩阵$P\in R^n_+$

• 二次约束二次规划。 如果目标函数$f$和不等式约束条件$g_i$都是凸二次函数，那么凸优化问题就是一个二次约束的二次规划(quadratically constrained quadratic program,QCQP)问题，形式如下：

$$\begin{aligned} minimize\quad &\frac 12x^TPx+c^Tx+d \ subject\quad to\quad &\frac 12x^TQ_ix+r_i^Tx+s_i\le 0,\quad i=1,\dots,m \ &Ax=b \end{aligned}$$

跟二次规划一样，其中的$x\in R^n$是优化变量，并且有$c\in R^n,d\in R,A\in R^{p\times n},b\in R^p,P\in R^n+$，与之不同的是这里还有$Q_i\in S^n+,r_i\in R^n,s_i\in R$，其中$i=1,...,m$。

• 半定规划。 最后一个示例比前面的示例更复杂，所以如果一开始不太理解也不要担心。但是，半定规划在机器学习许多领域的研究中正变得越来越流行，所以你可能在以后的某个时候会遇到这些问题，所以提前了解半定规划的内容还是比较好的。我们说一个凸优化问题是半定规划(SDP) 的，则其形式如下所示：

$$\begin{aligned} minimize\quad &tr(CX) \ subject\quad to\quad &tr(A_iX)=b_i,\quad i=1,\cdots,p \ &X\succeq 0 \end{aligned}$$

其中对称矩阵$X\in S^n$是优化变量，对称矩阵$C,A_1,\cdots,A_p\in S^n$根据具体问题具体定义，限制条件$X\succeq 0$意味着$X$是一个半正定矩阵。以上这些看起来和我们之前看到的问题有点不同，因为优化变量现在是一个矩阵而不是向量。如果你好奇为什么这样的公式可能有用，你应该看看更高级的课程或关于凸优化的书。

从定义可以明显看出，二次规划比线性规划更具有一般性（因为线性规划只是$P = 0$时的二次规划的特殊情况），同样，二次约束二次规划比二次规划更具有一般性。然而，不明显的是，半定规划实际上比以前的所有类型都更一般，也就是说，任何二次约束二次规划（以及任何二次规划或线性规划）都可以表示为半定规划。在本文当中，我们不会进一步讨论这种关系，但是这个结论可能会让你对半定规划为何有用有一个小小的概念。

4.3 实例

到目前为止，我们已经讨论了凸优化背后大量枯燥的数学以及形式化的定义。接下来，我们终于可以进入有趣的部分：使用这些技术来解决实际问题。我们在课堂上已经遇到过一些这样的优化问题，而且几乎在每个领域，都有很多情况需要人们应用凸优化来解决一些问题。

• 支持向量机(SVM)。 支持向量机分类器是凸优化方法在机器学习中最常见的应用之一。如课堂上所讨论的，寻找支持向量分类器（在松弛变量的情况下）可以表示为如下所示的优化问题：

$$\begin{aligned} minimize \quad & \frac 12 \parallel w\parallel2 ^2+C\sum^m{i=1}\xi_i \ subject\quad to \quad& y^{(i)}(w^Tx^{(i)}+b) \geq1-\xi_i,\quad &i=1,...,m\ & \xi_i \geq 0, &i=1,...,m \end{aligned}$$

其中$w\in R^n,\xi\in R^m,b\in R$是优化变量，$C\in R,x^{(i)},y^{(i)},i=1,\cdots,m$根据具体问题具体定义。这是一个二次规划的例子，我们下面通过将问题转换成上一节中描述的形式来展示它。特别的，当我们定义$k=m+n+1$时，则优化变量为：

$$x\in R^k=\left[ \begin{matrix} w \ \xi \ b \end{matrix} \right]$$

然后定义矩阵：

$$P\in R^{k\times k}=\left[ \begin{matrix} I&0&0 \ 0&0&0 \ 0&0&0 \end{matrix} \right],\quad c\in R^k=\left[ \begin{matrix} 0 \ C\cdot 1 \ 0 \end{matrix} \right], \ G\in R^{2m\times k}=\left[ \begin{matrix} -diag(y)X&-I&-y \ 0&-I&0 \end{matrix} \right],\quad h\in R^{2m}=\left[ \begin{matrix} -1 \ 0 \end{matrix} \right]$$

其中$I$是单位矩阵，$1$是所有元素都是$1$的向量，$X$和$y$跟课程中定义的一样：

$$X\in R^{m\times n}=\left[ \begin{matrix} x^{(1)T} \ x^{(2)T} \ \vdots \ x^{(m)T} \end{matrix} \right],\quad y\in R^m=\left[ \begin{matrix} y^{(1)} \ y^{(2)} \ \vdots \ y^{(m)} \end{matrix} \right]$$

你有理由相信在使用上述定义的矩阵时，上一节描述的二次规划与SVM优化问题是等价的。事实上，这里很容易看到支持向量机优化问题的二次优化目标项以及线性约束项，所以我们通常不需要把它化为标准形式“证明”它是一个二次规划(QP)问题，只有在遇到的现成解决方案中要求输入必须为标准形式时，我们才会这样做。

• 约束最小二乘法。 在课堂上，我们也遇到了最小二乘问题，在这个问题中，我们想要在已知某些矩阵$A\in R^{m\times n}$以及$b\in R^m$时最小化$\parallel Ax=b\parallel_2^2$。正如我们所看到的，这个特殊的问题可以通过正规方程得到解析解。但是，假设我们还希望将解决方案中的$x$限制在一些预定义的范围内。换句话说，假设我们要解最优化如下的问题：

$$\begin{aligned} minimize\quad&\frac 12\parallel Ax-b\parallel_2^2 \ subject\quad to\quad &l\preceq x\preceq\mu \end{aligned}$$

$x$是优化变量，$A\in R^{m\times n},b\in R^m,l\in R^n$根据具体问题具体定义。这看起来像是一个简单的附加约束，但事实证明，这个问题将不再存在一个解析解。但是，你应该相信这个优化问题是一个二次规划问题，它的矩阵由如下式子定义：

$$P\in R^{n\times n}=\frac 12A^TA,\quad c\in R^n=-b^TA,\quad d\in R=\frac 12b^Tb, \ G\in R^{2n\times 2n}=\left[ \begin{matrix} -I&0 \ 0&I \end{matrix} \right],\quad h\in R^{2n}=\left[ \begin{matrix} -l \ u \end{matrix} \right]$$

• 最大似然逻辑回归。 作业一要求你需要证明逻辑回归模型中数据的对数似然函数是凹的。逻辑回归的对数似然函数如下：

$$l(\theta)=\sum_{i=1}^n {y^{(i)}lng(\theta^Tx^{(i)})+(1-y^{(i)})ln(1-g(\theta^Tx^{(i)}))}$$

其中$g(z)$表示逻辑回归函数$g(z) = 1/(1 + e^{-z})$，求出最大似然估计是使对数似然最大化的任务（或者等价的最小化负对数似然函数，其是一个凸函数），即：

$$minimize\quad -l(\theta)$$

优化变量为$\theta\in R^n$，并且没有约束。

与前两个示例不同，将这个问题转化为标准形式优化问题并不容易。尽管如此，你们在作业中已经看到这是一个凹函数，这意味着你们可以非常有效地使用一些算法，如：牛顿法来找到全局最优解。

4.4 实现:使用CVX实现线性SVM

利用CVX、Sedumi、CPLEX、MOSEK等现有软件包可以解决许多凸优化问题。因此，在许多情况下，一旦你确定了凸优化问题，就不必担心如何实现算法来解决它，而这一点这对于快速原型开发特别有用。$^8$

8 然而，根据优化问题的不同，这些现成的凸优化求解器会比最佳实现慢得多；因此，有时你可能不得不使用更定制的解决方案或实现自己的解决方案。

在这些软件包中，我们以CVX[2]注：参考资料[2]见文章最下方为例。CVX是一种自由的基于matlab的求解一般凸优化问题的软件包;它可以解决多种凸优化问题，如LP、QP、QCQP、SDP等。作为一个例子，我们通过使用习题集1中的数据为二分类问题实现一个线性SVM分类器来结束本节。对于使用其他非线性内核的一般设置，也可以使用CVX求解对偶公式。

% load data
load q1x.dat
load q1y.dat
% define variables
X = q1x;
y = 2*(q1y-0.5);
C = 1;
m = size(q1x,1);
n = size(q1x,2);
% train svm using cvx
cvx_begin
variables w(n) b xi(m)
minimize 1/2*sum(w.*w) + C*sum(xi)
y.*(X*w + b) >= 1 - xi;
xi >= 0;
cvx_end
% visualize
xp = linspace(min(X(:,1)), max(X(:,1)), 100);
yp = - (w(1)*xp + b)/w(2);
yp1 = - (w(1)*xp + b - 1)/w(2); % margin boundary for support vectors for y=1
yp0 = - (w(1)*xp + b + 1)/w(2); % margin boundary for support vectors for y=0
idx0 = find(q1y==0);
idx1 = find(q1y==1);
plot(q1x(idx0, 1), q1x(idx0, 2), ’rx’); hold on

plot(q1x(idx1, 1), q1x(idx1, 2), ’go’);
plot(xp, yp, ’-b’, xp, yp1, ’--g’, xp, yp0, ’--r’);
hold off
title(sprintf(’decision boundary for a linear SVM classifier with C=%g’, C));

参考资料

[1] Stephen Boyd and Lieven Vandenberghe. Convex Optimization. Cambridge UP, 2004. Online: http://www.stanford.edu/~boyd/cvxbook/

[2] M. Grant and S. Boyd. CVX: Matlab software for disciplined convex programming (web page and software). http://cvxr.com/, September 2008.