CSS Matrix 2D

2D Transform Methods

概念

matrix可以代替：偏移量（translate）,缩放（scale），斜切（skew），旋转（rotate）四大功能。任意一个通过以上四个功能实现的形状改变的效果都能使用matrix来实现。

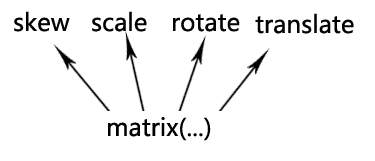
理解

matrix的六个参数用字母表示如下：

selector {
    transform: matrix(a, b, c, d, e, f);
}

矩阵：

2D 的转换是由一个 3*3 的矩阵表示的，前两行代表转换的值，分别是 a b c d e f，要注意是竖着排的，第一行代表 x 轴发生的变化，第二行代表 y 轴发生的变化，第三行代表 z 轴发生的变化，因为这里是 2D 不涉及 z 轴，所以这里是 0 0 1。

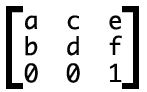
1. e和f 代表着偏移量translate，x和y轴

2. a和d 代表着缩放比例scale,x 和y轴

3. b和c 代表着斜切skew（具体参数和角度关系为, b-->tanθ y轴 c-->tanθ x轴 ,我们具体操作的时候还是要使用小数的）

4. abcd 中的ad代表缩放(scale),bc代表者斜切(skew); abcd四个参数代表着旋转。旋转可以用缩放和斜切一起用来得到, 两者联系在于这个角度θ。具体如下： matrix(cosθ,sinθ,-sinθ,cosθ,0,0)

变换公式

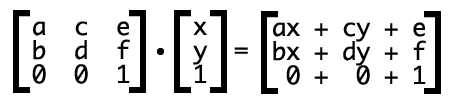
• ax+cy+e表示变换后的水平坐标
• bx+dy+f表示变换后的垂直位置

平移

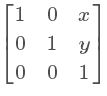
所以translate(x,y)也可以写成matrix(1,0,0,1,x,y)

缩放

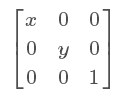
所以scale(x,y)也可以写成matrix(x,0,0,y,0,0)

旋转

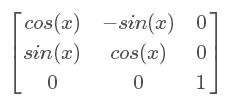
所以rotate(x)也可以写成matrix(cos(x),-sin(x),sin(x),cos(x),0,0)

变形

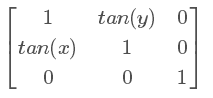
所以skew(x,y)也可以写成matrix(1,tan(y),tan(x) ,1,0,0)

示例

创建一个宽高为 200px 的div，div 里面有一个红色的点，位置是{x:181px y:50px}。

倘若将这个div 向右平移 10px，x 轴向下平移 20px，旋转37°，x轴缩放 1.5 倍，y 轴缩放 2 倍：

transform: translate(10px, 20px) rotate(37deg) scale(1.5, 2);

通过矩阵转换

那么红色点的变化后的位置在哪里呢？

既然我们知道矩阵可以对向量进行转换那么我们只要把上面的信息转换成矩阵信息，通过矩阵信息可以将我们的原始坐标转换到新的坐标。

缩放 scale(x, y)

缩放对应的是矩阵中的 a 和 d，x 轴的缩放比例对应 a，y 轴的缩放比例对应 d。

transform: scale(x,y);

a=x d=y

所以 scale(1.5, 2) 对应的矩阵是：

transform: matrix(1.5, 0, 0, 2, 0, 0);

如果一个没有元素没有被缩放，默认a=1 d=1。

平移 translate(10, 20)

平移对应的是矩阵中的 e 和 f，平移的 x 和y 分别对应 e 和 f。

transform: translate(10, 20)

e=10 f=20

对应：

transform: matrix(a, b, c, d,10, 20);

结合缩放：

transform: matrix(1.5 0, 0, 2, 10, 20);

平移只会影响 e 和 f 值。

旋转 rotate(θdeg)

旋转影响的是a/b/c/d四个值，分别是什么呢？

transform: rotate(θdeg)

a=cosθ

b=sinθ

c=-sinθ

d=cosθ

如果要计算 30° 的sin值：

首先我们要将 30° 转换为弧度，传递给三角函数计算。用 JS 计算就是下面的样子了。

// 弧度和角度的转换公式：弧度=π/180×角度 

const radian = Math.PI / 180 * 30 // 算出弧度

const sin = Math.sin(radian) // 计算 sinθ
const cos = Math.cos(radian) // 计算 cosθ

console.log(sin, cos) // 输出 ≈ 0.5, 0.866

这样我们算出了 sin 和 cos，分别是 0.5 和 0.866

如果我们不考虑缩放和偏移，只旋转30°，矩阵应该表示为

transform: rotate(30deg)

a=0.866

b=0.5

c=-0.5

d=0.866

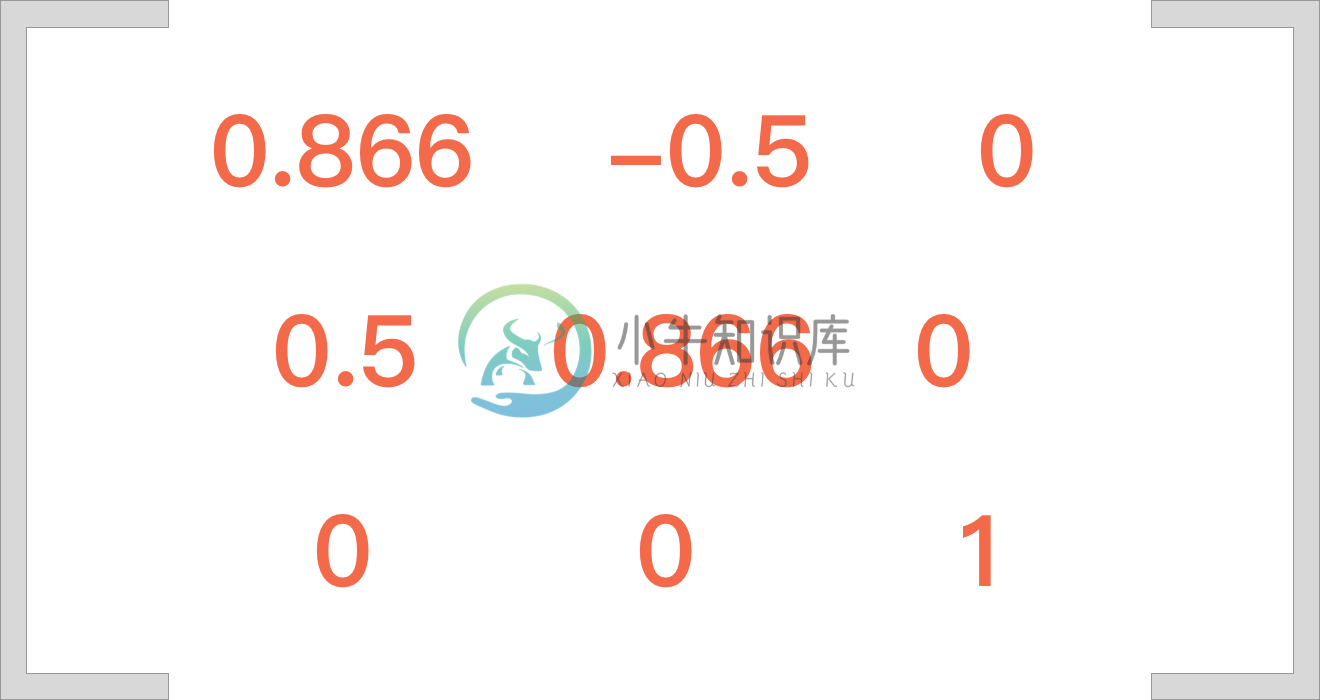
transform: matrix(0.866, 0.5, -0.5, 0.866, 0, 0);

偏移 skew(20deg, 30deg)

上面的题目中没有出现出现偏移值，偏移值也是由两个参数组成，x 轴和 y 轴，分别对应矩阵中的 c 和 b。是 x 对应 c，y 对应 b， 这个对应并不是相等，需要对 skew 的 x 值 和 y 值进行 tan 运算。

transform: skew(20deg, 30deg);

b=tan30°  

c=tan20°

注意 y 对应的是 b，x 对应的是 c。

transform: matrix(a, tan(30deg), tan(20deg), d, e, f)

使用 JS 来算出 tan20 和 tan30

// 先创建一个方法，直接返回角度的tan值
function tan (deg) {
    const radian = Math.PI / 180 * deg
    return Math.tan(radian)
}

const b = tan(30)
const c = tan(20)
console.log(b, c) // 输出 ≈ 0.577, 0.364
b=0.577 c=0.364

transform: matrix(1, 0.577, 0.364, 1, 0, 0)

旋转+缩放+偏移+位移

如果我们既要旋转又要缩放又要偏移，我们需要将旋转和缩放和偏移和位移多个矩阵相乘，要按照transform里面rotate/scale/skew/translate所写的顺序相乘。

这里我们先考虑旋转和缩放，需要将旋转的矩阵和缩放的矩阵相乘。

这里我用小写字母代表第一个矩阵中的值，大写字母代表第二个矩阵里的值

将我们的已经得到的矩阵带入到公式

得出：

transform: rotate(30) scale(1.5 2);

转换为 matrix 表示为：

transform: matrix(1.299, 0.75, -1, 1.732, 0, 0);

找到这次转换的矩阵

div 的transform 值如下:

transform: translate(10px, 20px) rotate(37deg) scale(1.5, 2);

translate(10px, 20px)

x 平移 10px，y 平移 20px，所以 e=10，f=20。

rotate(37deg)

sin37° ≈ 0.6

cos37° ≈ 0.8

根据 a 对应 cos , b 对应 sin，c 对应 -sin，d 对应 cos 的值

得到：

a=0.8，b=0.6，c=-0.6，d=0.8

scale(1.5, 2)

x 轴缩放 1.5，y 轴缩放 2，所以 a=1.5，d=2

结合

transform: translate(10px, 20px) rotate(37deg) scale(1.5, 2);

我们使用 位移矩阵 旋转矩阵 缩放矩阵（根据transform中的变换类型书写的顺序）

可以使用矩阵计算器进行计算

从左往右依次计算

所以最终得到矩阵

matrix(1.2, 0.9, -1.2 1.6, 10, 20)

如何对一个坐标进行矩阵变换

我们已经知道了这个矩阵，如何通过矩阵对一个坐标进行变化，找到这个坐标变化后的位置呢？

我们用之前得出的变换矩阵去乘以这一个坐标组成的3*1（三排一列）矩阵。

上面已经介绍过如何进行矩阵乘法了，这里在介绍一遍

上图中左右两个矩阵颜色相同的位置相乘后相加，每一行都进行这样的计算：

得到一个3*1的矩阵，第一行是转换后的 x 值，第二行是转换后的 y 值，第三行是转换后的 z 值（2d不考虑z值）。

前面讲到，矩阵的第一行影响 x，第二行影响 y，也体现在这个地方。

假设我们的坐标是(50, 80)，这里还没有针对我们提出的问题上面的点进行计算。

我们把坐标写成矩阵的形式，设置 z 轴是1：

然后进行乘法计算：

通过我们计算出来的矩阵变换得到新的位置(46, 172)

继续刚刚问题

坐标是需要基于一个坐标系存在的，我们需要找到正确的坐标系才能算出准确的坐标。

在 CSS transform 中，有个属性是 transform-origin，来设置变换所基于的点，默认是transform-origin: 50% 50%，基于中间元素的中心点。我们需要以这个点建立坐标系。

在网页中，坐标系是 x 轴向右，y 轴向下。

转换前：

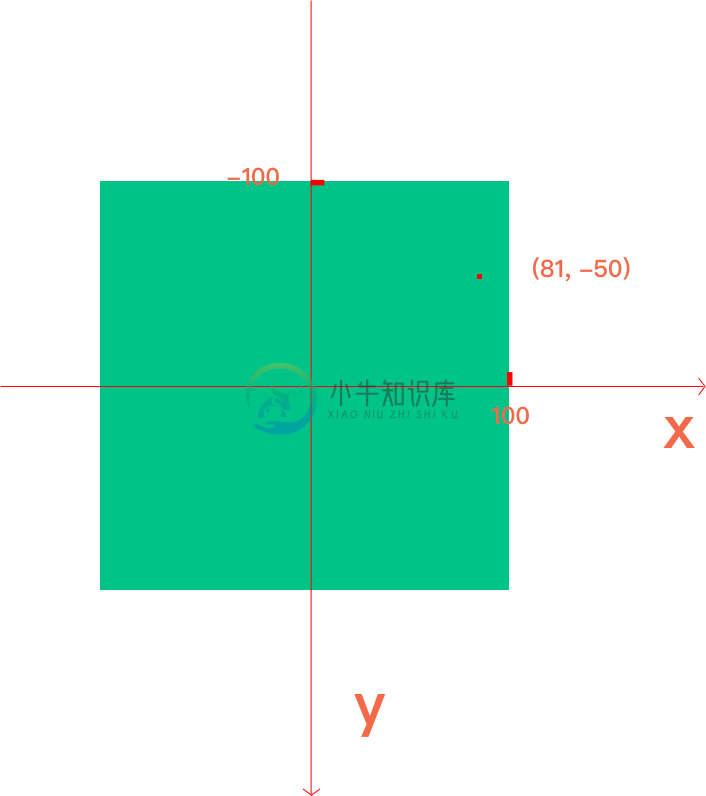
转换后：

根据题目我们知道，这个点相对于绿色div左上角的坐标是(181, 50) 绿色div的宽高为200 基于绿色div中心点建立的坐标系，这个点的坐标是(81, -50)

将坐标代入公式进行计算：

得到坐标约为(167, 13)

再将这个坐标转换成页面坐标系(267,113)

最终我们得到了这个点在经过转换后的坐标