第 7 章 集合数据模型
集合(简称为“集”)是最为基础的数学数据模型。数学中的每种概念,从树到实数,都可以表示为一类特殊的集合。在本书中,我们已经见识过以概率空间中事件的形式出现的集。词典抽象数据类型就是一种集合,可以对其执行插入、删除和查找这些特殊操作。因此,说集合也是计算机科学中的基础模型应该不会让人惊讶。在本章中,我们要了解与集合有关的基本定义,并考虑有效实现集合操作的算法。
7.1 本章主要内容
本章将涵盖以下主题。
集合论的基本定义以及集合的基本运算(7.2节和7.3节)。
3种最常用于实现集合的数据结构:链表、特征向量和散列表。我们将比较这些数据结构在支持各种集合运算时的效率(7.4节~7.6节)。
作为有序对集合的关系和函数(7.7节)。
表示关系和函数的数据结构(7.8节和7.9节)。
特殊类型的二元关系,如偏序关系和等价关系(7.10节)。
无限集(7.11节)。
7.2 基本定义
在数学中,术语“集合”是没有明确定义的。就像几何中的“点”和“线”那样,集合也是由其属性定义的。具体地说,有只适用于集合的成员概念。当S 为集合,而x 为任意事物时,我们可以提出如下问题:“x 是否为集合S 的成员?”集合S 就是由所有属于S 的成员的元素x 组成的。以下几点总结了与集合有关的一些重要概念。
1. 表达式x∈S 意味着元素x 是集合S 的成员。
2. 如果x1,x1,…,xn 都是集合S 的成员,就可以写为
S={x1,x2,…,xn}
在这里,每个x 都是不同的,在集合中任一元素都是不能重复出现的。然而,集合中各成员的顺序是无关紧要的。
3. 空集记为 ∅,表示没有任何成员的集合。也就是说,不管x 是什么,x∈∅都为假。
示例 7.1
设S={1,3,…,6},也就是说,S 是只含有整数成员1、3、6的集合。我们可以说1∈S,3∈S和6∈S。不过,命题2∈S 为假,说其他任何内容是S 的成员的命题也都为假。
集合还能以其他集合作为成员。例如,设T={{1,2},3,∅}。那么T 就有3个成员。第一个成员是集合{1,2},也就是说,含有1和2作为成员的集合。第二个成员是整数3。第三个成员是空集。下列命题是真命题:{1,2}∈T,3∈T,以及∅∈T。不过,1∈T 为假。也就是说,1是T 的成员的成员,但这不意味着1是T 本身的成员。
7.2.1 原子
在正式的集合论中,除了集合别无他物。不过,在非正式的集合论中,以及在基于集合的数据结构和算法中,可以放心地假设存在某些原子。原子是非集合元素。原子可以是集合的成员,但没有什么可以是原子的成员。谨记,空集就像原子那样是没有成员的。不过,空集是集合,而不是原子。
我们一般会假设整数和小写字母都是原子。在谈论数据结构时,使用复杂的数据类型作为原子的类型通常是很方便的。因此,原子可以是看上去不那么像“原子”的结构体或数组。
集合与表
虽然表的表示法(x1,x2,…,xn)与集合的表示法{x1,x2,…,xn}非常相似,但它们之间存在很大区别。首先,集合中元素的次序是无关紧要的。写为{1,2}的集合也可以写作{2,1}。相反,表(1,2)与表(2,1)就不是一回事。
其次,表中元素是可以重复的。例如,表(1,2,2)有3个元素,第一个是1,第二个是2,第三个也是2。集合{1,2,2}是不存在的。元素(比如这里的2)作为成员在集合中出现的次数不能超过一次。上述集合要有意义的话,它就与{1,2}或{2,1}(也就是只含有1和2这两个成员,不含其他成员的集合)相同。
有时候会提到多重集或无序单位组(bag),就是允许其中元素出现多次的集合。例如,我们可以说出现一次1和两次2的多重集。不过多重集与表是不同的,因为多重集中的元素也是没有次序的。
7.2.2 通过抽象对集合的定义
枚举集合的成员不是定义集合的唯一方式。通常,更方便的做法是,从某集合S 与元素的某属性P 开始,然后定义S 中具有属性P 的元素为集合。这一操作对应的表示法称为抽象,就是
{x |x ∈S 且P (x )}
或者说“S 中元素x 的集合都是具有属性P 的x ”。
上述表达式称为集合形成法(set former)。集合形成法中的变量x 是对应某一表达式的,我们也可以用
{y |y ∈S 且P (y )}
来表示同一集合。
示例 7.2
设S 是示例7.1中的集合{1,3,6}。设P (x )是属性“x 为奇数”,则
{x |x ∈S 且x 为奇数}
是定义集合{1,3}的另一种方式。也就是说,我们接受S 中的元素1和3,因为它们是奇数,而6不是奇数,所以我们拒绝了它。
再举个例子,考虑源自示例7.1的集合T={{1,2},3,∅},那么
{A|A∈T 且A 为集合}
就表示集合{{1,2},∅{。
7.2.3 集合的相等性
一定不能将集合的实际组成与其表示形式相混淆。两个集合相等,也就是说,如果它们刚好有相同的成员,那么它们其实是相同的集合。因此,大多数集合有很多不同的表示方式,包括以某种次序直接枚举集合中的元素,以及使用抽象的表示。
示例 7.3
集合{1,2}是有且只有1和2这两个成员的集合。我们可以按照任一次序表示这两个元素,所以{1,2}={2,1}。还有其他很多通过抽象表示该集合的方式,例如
{x|x∈{1,2,3}且x<3}
就等于集合{1,2}。
7.2.4 无限集
我们不介意假设集合都是有限的,也就是说,存在某个整数n,使得集合刚好具有n个成员。例如,集合{1,3,6}具有3个成员。还有一些集合是无限的,意味着没有具体的整数能表示该集合中元素的个数。我们熟悉的无限集包括下列几种。
1. N,非负整数集。
2. Z,整数集。
3. R,实数集。
4. C,复数集。
通过抽象,可以根据这些集合创建其他的有限集。
示例 7.4
集合形成法
{x|x∈Z且x<3}
表示由所有负整数以及0、1和2组成的集合,而集合形成法
{x|x∈Z且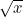 ∈Z}
∈Z}
表示的是完全平方的整数集合,也就是{0,1,4,9,16,…}。
再看一个例子,设P (x )是“x 为质数”(即x>1,且x 只能被1和它本身整除)这一属性。那么质数集就可以表示为
{x|x∈N且P (x )}
这一表达式表示的是无限集{2,3,5,7,11,…}。
无限集有一些微妙而有趣的属性我们将在7.11节中再来讨论这一问题。
7.2.5 习题
1. 集合{{a,b },{a },{b,c }}的成员都有哪些?
2. 写出以下集合的集合形成法表达式。
(a) 大于1000的整数集合。
(b) 偶整数的集合。
3. 用两种不同的表示方式分别表示下列各集合,一种使用抽象,另一种不使用抽象。
(a) {a,b,c}
(b) {0,1,5}
罗素悖论
有人也许想知道,为什么抽象操作要求我们指明另一个集合,然后必须从该集合中选出构成新集合的元素。为什么不能直接使用{x |P (x )}这样的表达式,例如,用
{x |x 是蓝色的}
来定义由所有蓝色事物组成的集合呢?原因在于,如果用这种概括方式来定义集合,就会让我们陷入一种由数学家伯特兰·罗素(Bertrand Russell)发现的名为罗素悖论(Russell Paradox)的逻辑矛盾之中。我们在听说镇上的理发师只给不自己剃胡子的人剃胡子时,就已经接触到这一悖论了。如果他给自己剃胡子,就不该给自己剃胡子;而如果他不给自己剃胡子,就可以给自己剃胡子。引发这种矛盾的原因是“只给不自己剃胡子的人剃胡子”这一说法,尽管看起来很合理,但其实是说不通的。
要理解罗素悖论是如何关系到集合的,先假设可以用{x|P(x)}的形式对任意属性P 定义集合。接着设属性P(x)是“x 不是x 的成员”。也就是说,设P 属性在集合x 不是其本身成员的情况下适用于该集合。令S 为集合
S={x|x不是x 的成员}
现在问,“S 是否为它本身的成员?”
情况1:假设S 不是S 的成员。那么P(S)为真,S 就是集合{x|x不是x 的成员}的成员。不过该集合就是S,所以通过假设S 不是它本身的成员,我们证明了S 其实是它本身的成员。因此,不能有S 不是它本身成员的结论。
情况2:假设S 是它本身的成员。那么S 就不是集合{x|x不是x 的成员}的成员。不过该集合也就是S,这样就得出了S 不是它本身成员的结论。
因此,当我们假设P(S )为假时,就证明了它为真,而当我们假设P(S )为真时,我们又证明了它为假。因为不管怎样都会得出矛盾,这样就只能把责任归咎于这一表示方法。也就是说,真正的问题在于按照这样的方式定义集合S 是行不通的。
罗素悖论另一个有趣的推论是假设存在“所有元素的集合”也是行不通的。如果存在这样的“全集”,
比方说U,那么就可以说 {x|x∈U 且x 不是x 的成员}
而且再次得到了罗素悖论。这样就不得不完全放弃抽象。但是抽象操作十分实用,不容放弃。
7.3 集合的运算
有一些操作集合的特殊运算,比如并集和交集。大家可能熟悉其中很多运算,但我们在此将回顾一些最重要的运算,在下一节中我们将讨论这些运算的一些实现。
7.3.1 并集、交集和差集
也许结合集合最常用的方式就是进行以下3种运算。
1. 两个集合S 和T 的并集,记作S ∪T,表示含有集合S 或集合T 中或同在二者之中的元素的集合。
2. 两个集合S 和T 的交集,记作S ∩T,表示含有同在集合S 和集合T 中的元素的集合。
3. 两个集合S 和T 的差集,记作S-T,表示含有在集合S 中但不在集合T 中的元素的集合。
示例 7.5
设S 是集合{1,2,3},T是集合{3,4,5},那么
S ∪T={1,2,3,4,5},S ∩T={3},而S-T={1,2}。
也就是说,S ∪T 包含了出现在S 或T 中的所有元素。虽然3同时出现在S 和T 中,但是S ∪T 中当然只能出现一个3,因为元素在一个集合中不能出现多次。S ∩T 只含3,因为没有其他元素同时出现在S 和T 中。最后S-T 含有1和2,因为这两个元素出现在S 中而未出现在T 中。元素3没有出现在S-T 中,因为虽然它在S 中出现了,但它也出现在T 中了。
当集合S 和T 是概率空间中的事件时,并集、交集和差集就有了一层含义。S∪T 就是S 发生或T 发生(或都发生)的事件。S ∩T 就是S 和T 都发生的事件。S-T 是S 发生但T 不发生的事件。不过,如果S 是表示整个概率空间的集合,那么S-T 就是“T 不发生”这一事件,也就是T 的补集。
7.3.2 文氏图
将涉及集合的运算看作称为文氏图(Venn diagrams)的图片通常是很有用的。图7-1中的文氏图表示S 和T 这两个集合,它们在图中表示为两个椭圆。这两个椭圆将整个平面分为4个区域,我们分别用数字1到4标记这4个区域。

图 7-1 表示对应基本集合运算的文氏图的区域
1. 区域1表示既不在S 中也不在T 中的元素。
2. 区域2表示S-T,那些在S 中但不在T 中的元素。
3. 区域3表示S ∩T,那些既在S 中也在T 中的元素。
4. 区域4表示T-S,那些在T 中但不在S 中的元素。
5. 区域2、3、4结合在一起表示S ∪T,那些在S 中或在T 中,或同在二者之中的元素。
代数是什么?
可以想到,术语“代数”指的是解决单词问题,求出多项式的根,以及高中代数课程中涵盖的其他问题。不过,对数学家来说,术语“代数”指的是存在可用于构建表达式的操作数和运算符的任一种系统。为了让代数变得有趣而实用,通常会有一些特殊常量和法则,让我们可以将一个表达式变形为另一个“等价的”表达式。
最常见的代数的操作数是整数、实数或是复数,或是表示这些类型中某一种类型的值的变量,而运算符则是普通算术运算符——加号、减号、乘号、除号。常数0和1是特殊的,而且满足x+0=x 这样的法则。在处理算术表达式时,可以使用诸如分配律这样的法则,让我们用a×b(a+c )这样的等价表达式来替代形如a×b+a+c 的表达式。请注意,通过这种变形,可以减少一次算术运算。对表达式进行这种代数变换的目的通常是找出与原表达式等价,但求值所需时间更少的表达式。
纵观全书,我们会遇到各种类型的代数。8.7节介绍了关系代数,是对我们在此讨论的集合代数的一般化;10.5节谈论了描述字符串模式的正则表达式代数;12.8节介绍了逻辑类型的布尔代数。
尽管我们已经说明了图7-1中的区域1具有有限的范围,不过应该记住的是,该区域表示的是S和T之外的一切。因此,该区域并非集合。如果该区域是集合,那么将其与S和T进行并集运算,就会得到“全集”,而根据罗素悖论可知这种“全集”是不存在的。不过,通常可以将不在文氏图明确表示的任一集合中的元素画为一个区域,就像我们在图7-1中所做的。
7.3.3 并集、交集和差集的代数法则
人们可以仿照诸如+和*这样的算术运算代数来定义集合代数,在集合代数中,运算符就是并集、交集和差集,而操作数就是集合或表示集合的变量。一旦可以构建R ∪((S ∩T )-U )这样的复杂表达式,就可以询问两个表达式是否等价。也就是说,不管用什么集合替换作为操作数的变量,它们总是表示相同的集合。通过将一个表达式替换为等价的表达式,有时能简化涉及集合的表达式,使其能更高效地求值。
接下来的内容中,我们将列出用于并集、交集和差集的最重要的代数法则,也就是断言一个表达式与另一个表达式等价的命题。符号≡用于表示表达式的相等性。
在多种代数法则中,一方面是在并集、交集和差集之间有着一种相似性,另一方面是与整数的加法、乘法和减法相似。不过,我们将指出那些与普通算术不存在相似性的法则。
(a) 并集的交换律:(S∪T )≡(T∪S )。也就是说,在并集运算中,两个集合中哪个出现在前面都是没关系的。这一法则成立的原因很简单。如果x 在S 中,或x 在T 中,或同在两者之中,就有元素x 在S∪T 中。而这正好就是x 在T∪S 中所要满足的条件。
(b) 并集的结合律:(S∪(T∪R ))≡(S∪T )∪R )。也就是说,3个集合的并集既可以写为首先求前两个集合的并集,也可以写为首先求后两个集合的并集,不管哪种情况,结果都是一样的。我们可以像验证交换律那样,通过论证当且仅当元素在右边的集合中时才在左边的集合中,从而验证结合律。直观的理由就是两个集合中含有的,都正好是那些出现在S、T 或R 中,或任意两者之中,或同在三者之中的那些元素。
并集的交换律和结合律一起告诉我们,可以按照任意次序为一系列集合求并集。结果总是同一个元素集合,也就是出现在需要求并集的一个或多个集合中的那些元素组成的集合。这一论证就像我们在2.4节中表示加法时用到的,而加法运算中也存在交换律和结合律。那时我们证明过用所有方法组合求和算式都会得到相同的结果。
(c) 交集的交换律:(S∩T )≡(T∩S )。直觉上讲,元素x 在集合S ∩T 和T ∩S 中刚好是在相同的情况下,也就是当x 在S 中而且x 在T 中时。
(d) 交集的结合律:(S ∩(T ∩R ))≡(S ∩T )∩R )。直觉上讲,元素x 在所述的这两个集合中,刚好是当元素x 同在S、T 和R 这3个集合中时。就像加法或并集运算那样,对任意一些集合的交集运算也可以按照我们选择的方式进行组合,而且结果都是相同的,特别要指出的是,结果就是同时出现在所有集合中的那些元素。
(e) 交集对并集的分配律:就像我们所了解的乘法对加法的分配律,即a×(b+c)=a×b+a×c 那样,法则
(S ∩(T∪R ))≡((S ∩T )∪(S ∩R ))
对集合而言也成立。直觉上讲,元素x要分别在这两个集合中,刚好是当x 在S 中,并且至少在T 和R 其中一个之中时。同样,利用并集和交集的交换律,可以从右边起分配交集,就像
((T∪R ) ∩S )≡((T ∩S )∪(R ∩S ))
(f) 并集对交集的分配律:同样,
(S∪(T ∩R ))≡((S∪T )∩(S∪R ))
是成立的。左右两边都是包含在S 中或同时在T 和R 中的元素x 的集合。请注意,将并集运算替换为加法,并将交集运算替代为乘法,这样形成的算术运算法则为假;也就是说,a+b×c 在一般情况下是不等于(a+b)×(a+c)的。这一法则就是集合运算与算术运算相似性被打破的情况之一。就像在(e)法则中那样,我们可以利用并集的交换律得到等价法则
((T ∩R )∪S )≡((T∪S )∩(R∪S ))
示例 7.6
设S={1,2,3},T={3,4,5},R={1,4,6}。那么
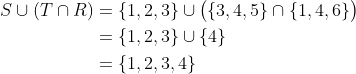
另一方面
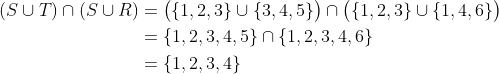
因此,并集对交集的分配律在这种情况下是成立的。当然,这并没有证明这一法则在一般情况下是成立的,不过我们在规则(f)中给出的直觉论证应该是有说服力的。
(g) 并集和差集的结合律:(S-(T∪R ))≡((S-T )-R )。两边所包含的元素x,刚好都是在S 中,而既不在T 中,也不在R 中。请注意,这条法则与算术法则a-(b+c)=(a-b)-c 是相似的。
(h) 差集对并集的分配律:((S∪T )-R )≡((S-T )∪(T-R ))。两边集合中的元素x,都不在R 中,但要么在S 中,或在T 中,或同在S 和T 两者之中。这一法则在算术运算中并没有相似法则,(a+b)-c=(a-c)+(b-c)是不成立的,除非c=0。
(i) 空集是并集的单位元(identity):也就是说,(S∪∅)≡S,而根据并集的交换律,有(∅∪S)≡S。粗略地讲,只有在元素x 在S 中时,它才可能在S∪∅中,因为x 不可能在∅中。请注意,交集是没有单位元的。可以想象一下,包含“所有元素”的“集合”可以作为交集的单位元,因为集合S 与该“集合”的交集肯定是S。不过,正如在介绍罗素悖论时提过的,不可能存在“具有所有元素的集合”。
(j) 并集的幂等律。将某运算符应用到同一个值的两个副本上,如果得到的结果还是该值,就说该运算符是幂等的。可知有(S∪S)≡S。也就是说,在(S∪S)中的元素x,刚好也就是在S 中的元素x。该法则在算术运算中也没有相似法则,因为(S∩S)≡S 一般情况下不等于a。
(k) 交集的幂等律。同样地,我们有(S∩S)≡S。
还有一些与对空集的运算有关的法则,如下所示。
(l) (S-S )≡∅。
(m) (∅S )≡∅。
(n) (∅∩S )≡∅,而且根据交集的交换律,有(S∩∅)≡∅。
7.3.4 利用文氏图证明相等性
图7-2用文氏图表示了交集对并集的分配律。该图展示了3个集合S、T 和R,它们将平面分为8个区域,分别用数字1到8标记。这些区域对应着元素与这3个集合间8种可能存在的(在或不在集合中)关系。

图 7-2 表示交集对并集分配律的文氏图:S ∩(T∪R )由区域3、5和6组成,(S ∩T )∪(S ∩R )也是由这些区域组成
我们可以利用该图记录各子表达式的值。例如,T∪R 是区域3、4、5、6、7、8。因为S 是区域2、3、5、6,所以S ∩(T∪R )就是区域3、5、6。同样,S ∩T 是区域3、6,而S ∩R 是区域5、6。这样一来,(S ∩T )∪(S ∩R )是同样的区域3、5、6,这就证明了
(S ∩(T∪R ))≡((S ∩T )∪(S ∩R ))
一般来说,通过从每个区域考虑一个具有代表性的元素,并验证它要么同在等式两边描述的集合中,要么都不在这两个集合中,我们可以证明相等性。这一方法与我们在第12章中证明命题逻辑的代数法则时用到的真值表方法是非常近似的。
7.3.5 利用变形证明相等性
另一种证明两个表达式相等的方式,是使用我们见过的代数法则将一个表达式变形为另一个表达式。我们将在第12章中更为正式地讲解如何处理表达式,现在只要注意到可以进行下列操作即可。
1. 用任一表达式替换相等关系中的任一变量,要替换所有在该相等关系中出现的该变量。相等关系仍然成立。
2. 设E 是某相等关系中的子表达式,用已知与E 等价的表达式F 替代E 。相等关系仍然成立。
此外,还可以直接写下任何表述为法则的相等关系,并假设这种相等关系是成立的。
示例 7.7
我们要证明相等关系(S-(S∪R ))≡∅。首先使用法则(g),并集和差集的结合律,也就是
(S-(T∪R ))≡((S-T )-R )
我们用S 替换相等关系中出现的两个T,就得到新的相等关系
(S-(S∪R ))≡((S-S )-R )
根据规则(l),(S-S )≡∅。因此,可以用∅替换上面的(S-S ),得到
(S-(S∪R ))≡(∅-R )
用R 替代法则(m)中的S,就有∅-R≡∅。因此可用∅替换∅-R,从而得到(S-(S∪R ))≡∅。
7.3.6 子集关系
集合间也有一系列的比较运算符,它们与数字间的比较运算符相似。如果S 和T 都是集合,当S 中的各成员也都是T 的成员时,就说S⊆T。我们可以用多种方式表示这种关系:“S 是T 的子集”、“T 是S 的超集”、“S 包含于T ”、“T 包含S ”。
如果S⊆T,而且T 中至少有一个元素不是S 中的成员,就说S⊂T。这一关系可以说成是“S 是T 的真子集”、“T 是S 的真超集”、“S 真包含于T ”、“T 真包含S ”。
就像“小于”关系那样,也可以反转这种比较的方向,S⊃T 等同于T⊂S,而S⊆T 等同于T⊆S。
示例 7.8
以下比较关系都是成立的。
1. {1,2}⊆{1,2,3}
2. {1,2}⊂{1,2,3}
3. {1,2}⊆{1,2}
请注意,集合永远是自身的子集,但从不可能是自身的真子集,所以{1,2}⊂{1,2}是不成立的。
还有一些涉及子集运算符和我们见过的其他运算符的代数法则,下面列出了一些。
(o) 对任一集合S,∅⊆S
(p) 如果S⊆T,那么
(i) (S∪R )≡T,
(ii) (S ∩R )≡S,且
(iii) (S-T )≡∅。
7.3.7 通过证明则包含关系对相等性加以证明
当且仅当S⊆T 且T⊆S 时,则有两个集合S 和T 相等。因为,如果S 中的每个元素都是T 的元素,而且反之亦然,那么S 和T 刚好有着相同的成员,因此这两者就是相等的。反过来讲,如果S 和T 有着相同的成员,那么肯定有S⊆T 和T⊆S 都成立。这一规则与这样一条算术规则类似,就是当且仅当a≤b 和b≤a 都成立时有a=b。
通过证明某一集合中的每个元素都包含在另一个集合中,可以证明两个表达式E 和F 的相等性。也就是说,我们
1. 考虑E 中的任意元素x,并证明它也在F 中,然后
2. 考虑F 中的任意元素x,并证明它也在E 中。
请注意,要证明E ≡F,两个方向的证明都是必要的。
示例 7.9
现在来证明并集和差集的结合律,
(S-(T∪R ))≡((S-T )-R )
首先假设x 在左边的表达式中,一系列的步骤如图7-3所示。请注意,在第(4)和第(5)步中,我们反向使用了并集的定义。也就是说,(3)告诉我们x 不在T∪R 中。如果x 在T 中,(3)就是不对的,所以可以得出x 不在T 中的结论。同样,x 不在R 中。
| 步骤 | 原因 |
|---|---|---|
1) | x 在S-(T∪R )中 | 给定 |
2) | x 在S 中 | -的定义,以及(1) |
3) | x 不在T∪R 中 | -的定义,以及(1) |
4) | x 不在T 中 | ∪的定义,以及(3) |
5) | x 不在R 中 | ∪的定义,以及(3) |
6) | x 在S-T 中 | -的定义,以及(2)和(4) |
7) | x 在(S-T )-R 中 | -的定义,以及(6)和(5) |
图 7-3 并集和差集的结合律的一半证明
这还没完,我们必须从假设x 在(S-T )-R 中开始,并证明它在S-(T∪R )中。证明步骤如图7-4所示。
| 步骤 | 原因 |
|---|---|---|
1) | x 在(S-T )-R 中 | 给定 |
2) | x 在S-T 中 | -的定义,以及(1) |
3) | x 不在R 中 | -的定义,以及(1) |
4) | x 在S 中 | -的定义,以及(2) |
5) | x 不在T 中 | -的定义,以及(2) |
6) | x 不在T∪R 中 | ∪的定义,以及(3)和(5) |
7) | x 在S-(T∪R )中 | 的定义,以及(4)和(6) |
图 7-4 并集和差集的结合律的另一半证明
示例 7.10
再举个例子,证明(p)法则的一部分,如果S⊆T,那么S∪R≡T。首先假设x 在S∪T 中。我们根据并集的定义可知,只可能存在下列情况之一
1. x 在S 中;
2. x 在T 中。
在情况(1)中,因为假设有S⊆T,所以可知x 在T 中。在情况(2)中,直接就可以看出x 在T 中。因此,在任一情况下x 都在T 中,这样就完成了证明的第一半——命题(S∪T )⊆T。
再来假设x 在T 中。那么根据并集的定义就有x 在S∪T 中。因此,T⊆(S∪T ),这就是证明的第二半。这样就可以得出,如果S⊆T,那么S∪T ≡T。
7.3.8 集合的幂集
如果S 是任一集合,那么S 的幂集就是指由S 的所有子集组成的集合。我们将用P(S )表示S 的幂集,虽然有时也会使用2S 这样的表示法。
示例 7.11
设S={1,2,3}。那么
P(S )={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}
也就是说,P(S )是含有8个成员的集合,每个成员本身都是一个集合。空集也在P(S )中,因为显然有 ∅⊆S 。单元素集——由S 中的一个元素构成的集合,即{1}、{2}、{3}——也在P(S )中。同 样,从3个成员中任选两个组成的3个集合在P(S )中,而S 本身也是P(S )的成员。
再举一个例子,P(∅)={∅}因为∅⊆S,而除空集之外,没有任何集合S可以满足S⊆∅。请注意,{∅}是包含空集的集合,它和空集是不一样的。特别要指出的是,{∅}含有一个成员,也就是∅,而空集是不含任何成员的。
7.3.9 幂集的大小
如果S 有n 个成员,那么P(S )有2n个成员。在示例7.11中,我们看到有3个成员的集合的幂集共有23=8个成员。此外,20=1,而且我们看到,包含0个元素的空集的幂集刚好有1个元素。
设S={a1,a2,…,an},其中a1,a2,…,an 是任意n 个元素。现在要通过对n 的归纳证明,P(S)有2n个成员。
依据。如果n=0,那么S 就是∅。我们之前已经得出P(∅)有一个成员的结论。因为20=1,所以我们证明了依据情况。
归纳。假设当S={a1,a2,…,an}时,P(S)有2n个成员。设an+1是一个不同于S 中任一元素的新元素,并设T=S∪{an+1},该集合是个具有n+1个元素的集合。现在,T 的子集要么含有an+1这一成员,要么不含这一成员。我们来依次考虑这两种情况。
1. 不包含an+1的T 的子集,也是S 的子集,因此在P(S )中。而根据归纳假设,正好有2n个这样的集合。
2. 如果R 是包含an+1的T 的子集,设Q=R-{an+1},也就是说,Q 是将an+1删除后的R。那么Q 是S 的子集。根据归纳假设,刚好有2n个可能存在的集合Q,而每一个都与唯一的集合R(也就是Q∪{an+1})对应。
我们得出T 刚好有2×2n,也就是2n+1个子集,其中有一半也是S 的子集,而另一半则是由S 的各子集分别加上新元素an+1形成的。因此,归纳步骤得到证明,给定任一具有n 个元素的集合S 都有2n个子集的条件,就证明了具有n+1个元素的任一集合T 都有2n+1个子集。
7.3.10 习题
1. 在图7-2中,我们证明了两个表达式对应着区域集合{3,5,6}。不过,每个区域都可以表示为涉及S、T 和R,以及并集、交集和差集运算符的表达式。写出对应以下各区域的两种不同的表达式。
(a) 区域6。
(b) 区域2和区域8。
(c) 区域2、区域4和区域8。
2. 使用文氏图证明以下代数法则。对于相等关系中涉及的每个子表达式,指出它所表示的区域集合。
(a) (S∪(T ∩R ))≡((S∪T )∩(S∪R ))
(b) (S∪T )-R )≡((S-R )∪(T-R ))
(c) (S -(T∪R ))≡((S-T )-R )
3. 通过证明每一边对另一边的包含关系,证明习题2中的各相等关系。
4. 假设S⊆T,通过证明两边互为另一边的子集,证明如下相等关系:
(a) (S∪T )≡S
(b) (S-T )≡∅
5. * 假设没有集合是其他集合的子集,那么包含n 个集合的文氏图可将平面分割成多少个区域?假设n 个集合中有一个是另一个的子集,但没有其他的包含关系。那么有些区域就将是空的。例如,在图7-1中,如果S⊆T,那么区域2就将为空,因为没有在S 中而不在T 中的元素。一般而言,共有多少个非空区域?
6. 证明,如果S⊆T,那么P (S )⊆P (T )。
7. * 在C语言中,我们可以用元素为链表表头的链表来表示成员为集合的集合S,这些元素对应的链表都表示S 的成员之一。编写C语言程序,接受表示集合的元素构成的表,即表中元素各不相同的表,并返回给定集合的幂集。大家编写的程序的运行时间是多少?提示:利用对“含n 个元素的集合的幂集中有2n个成员”这一命题的归纳证明,得出创建幂集的递归算法。如果脑筋灵活点,就会使用同一个表作为若干集合的相同部分,从而避免复制表示幂集成员的表,这样既能节省时间,又能节省空间。
8. 证明
(a) P (S )∪P (T )⊆P (S∪T )
(b) P (S∩T )⊆P (S )∩P (T )
如果将这里的包含关系替换为相等关系,那(a)或(b)是否还成立?
9. P (P (P (∅)))是什么?
10. * 如果从∅开始,应用幂集运算符n 次,那么得到的集合中有多少个成员?例如,习题(9)就是n=3的情况。
7.4 集合的链表实现
我们已经在6.4节中看到过如何用链表数据结构实现词典操作插入、删除和查找。同时还看到,如果集合有n 个元素,那么这些操作的期望运行时间都是O(n)。这一运行时间不如5.8节中使用平衡二叉查找树实现词典操作平均为O(logn)的运行时间那样理想。另一方面,正如在7.6节中将要看到的,用来表示词典的散列表数据结构是以词典的链表表示为基础的,而它一般要比二叉查找树快。
7.4.1 并集、交集和差集
尽管具体技巧与我们应用在词典操作上的有所不同,但使用链表数据结构还是对诸如并集这样的基本集合运算有利的。特别要说明的是,为表排序可以显著改善并集、交集和差集运算的运行时间。而我们在6.4节中看到的,排序只能对词典操作的运行时间带来比较小的改善。
首先,看看在用未排序表表示集合时会出现什么问题。在这种情况下,要对大小分别为n 和m 的集合进行并集、交集或差集运算,就需要O(mn )的时间。例如,要创建表示集合S 与集合T 的并集的表U,首先要将表示S 的表复制到一开始为空表的U 中。然后对T 中的各个元素加以检验,看看它们是否也在S 中。如果不在,就将该元素添加到U 中。图7-5简要描述了这一思路。
(1) copy S to U; (2) for (each x in T) (3) if (!lookup(x, S)) (4) insert(x,U);
图 7-5 为用未排序表表示的集合求并集的伪代码概要
假设S 含有n 个成员,而T 含有m 个成员。那么第(1)行将S 复制到U 中的操作可以在O(n)时间内完成。如果从第(3)行得知x 不在S 中,那么只要执行第(4)行的插入即可。因为x 只可以在表示T的表中出现一次,所以可知x 还不在U 中。因此,将x 放在表示U 的表的前端是没问题的,并且第(4)行可以在O(1)时间内完成。第(2)行至第(4)行的for循环要迭代m 次,而且其循环体要花费O(n)的时间。因此,第(2)行至第(4)行的运行时间就是O(mn),它主导了第(1)行的O(n)时间。
还有与之类似的实现交集和差集运算的算法,所花的时间也都是O(mn)。我们在此将这些算法留给读者来设计。
7.4.2 使用已排序表的并集、交集和差集
当表示集合的表已经排序时,执行并集、交集和差集运算就要快得多。其实,大家会发现,即便这些表一开始没有排过序,在执行这些集合运算之前先给表排序都是值得的。例如,考虑一下S∪T 的计算,其中S 和T 都是用已排序表表示的。这一过程就和2.8节的归并算法类似。区别之一在于,在当前位于两表开头位置的最小元素相同时,只需要给出该元素的一个副本即可,而不用像归并那样必须给出两个副本。另一个区别在于,我们不能从表示用来求并集的集合S 和T 的表中直接删除元素,因为不应该在构建S 和T 的并集时对S 或T 造成破坏。我们必须为所有 元素创建副本,用以形成二者的并集。
假设类型LIST和CELL是像之前那样,通过宏
DefCell(int, CELL, LIST);
定义的。函数setUnion如图7-6所示。在第(1)行要利用辅助函数assemble(x,L,M)创建一个新单元,在第(2)行将元素x 放入该单元,并在第(3)行调用setUnion求表L和M的并集。然后,assemble会返回对应x 的单元,后面跟着对L 和M 应用setUnion后得到的表。请注意,assemble和setUnion这两个函数是相互递归的,每一个都会调用另一个。
函数setUnion会从两个给定的已排序表中选出最小的元素,并将选定的元素与两个表其余的部分一起传给assemble。对setUnion来说有6种情况,具体取决于两个表中有没有一个为NULL,如果没有,就要看两个表中哪个表表头位置的元素先于另一个。
1. 如果两个表都为NULL,setUnion就直接返回NULL,结束递归过程。这种情况就是图7-6中的第(5)行和第(6)行。
2. 如果L为NULL而M 不是,那么在第(7)行和第(8)行,通过从M 中取出第一个元素,后面跟上NULL表与M 尾部的“并集”,就组成了这两个表的并集。请注意,在这种情况下,对setUnion的成功调用会使M 被复制下来。
3. 如果M 为NULL而L 不是,那么在第(9)行和第(10)行,要完成的工作是相反的,用L 的第一个元素合L 的尾部组成答案。
4. 如果L 和M 的第一个元素是相同的,那么在第(11)行和第(12)行,就创建该元素的一个副本,表示为L->element,加上L 的尾部和M 的尾部,一起构成答案。
5. 如果L 的第一个元素先于M,那么在第(13)行和第(14)行,我们会用该最小元素,L 的尾部,以及整个表M 一起组成答案。
6. 对称地,在第(15)行和第(16)行,如果最小元素在M 中,我们就用该元素、整个表L,以及M 的尾部组成答案。
LIST setUnion(LIST L, LIST M);
LIST assemble(int x, LIST L, LIST M);
/* 由 assemble 函数生成的表,其表头元素为 x 且
尾部为表 L 和表 M 并集中所含元素 */
LIST assemble(int x, LIST L, LIST M)
{
LIST first;
(1) first = (LIST) malloc(sizeof(struct CELL));
(2) first->element = x;
(3) first->next = setUnion(L, M);
(4) return first;
}
/* setUnion 返回的表是 L 和 M 的并集 */
LIST setUnion(LIST L, LIST M)
{
(5) if (L == NULL && M == NULL)
(6) return NULL;
(7) else if (L == NULL) /* M 在这里不能为 NULL */
(8) return assemble(M->element, NULL, M->next);
(9) else if (M == NULL) /* L 在这里不能为 NULL */
(10) return assemble(L->element, L->next, NULL);
/* 如果到了这里,L 和 M 都不能为 NULL */
(11) else if (L->element == M->element)
(12) return assemble(L->element, L->next, M->next);
(13) else if (L->element < M->element)
(14) return assemble(L->element, L->next, M);
(15) else /* 这里有 M->element < L->element */
(16) return assemble(M->element, L, M->next);
}
图 7-6 为用已排序表表示的集合计算并集
示例 7.12
假设集合S 是{1,3,6},T 是{5,3}。表示这两个集合的已排序表分别是L=(1,3,6)和M=(3,5)。调用setUnion(L,M)求并集。因为L 的第一个元素是1,先于M 的第一个元素3,所以情况(5)适用,因此我们用1,L 的尾部,称其为L1=(3,6),以及M 组成要计算的并集。函数assemble(1,L,M)会在第(3)行调用setUnion(L,M),结果就是第一个元素1与等于并集的尾部组成的表。
对setUnion的这一调用是情况(4),也就是两个开头元素相等的情况,这里都是3。因此,我们用元素3的一个副本,加上L1的尾部和M 的尾部,组成要计算的并集。这些尾部分别是只有元素6组成的L2,以及只由元素5组成的M1。接下来的调用是setUnion(L2,M1),这是情况(6)的实例。因此我们将5加到并集中,并调用setUnion(L2,NULL)。这是情况(3),为并集生成6,并调用setUnion(NULL,NULL)。这里就遇到了情况(1),递归就终止了。对setUnion首次调用的结果就是表(1,3,5,6)。图7-7详细展示了这一套示例数据产生的调用与返回。

图 7-7 示例7.12对应的调用合返回序列
请注意,setUnion生成的表总是已排序的。通过看到哪种情况适用,可以知道该算法为何起作用,表L 或M 中的各元素,要么通过成为对assemble调用中的第一个参数,从而被复制到输出中,要么留在作为参数被传递给对setUnion的递归调用的表中。
7.4.3 并集运算的运行时间
如果对分别具有n 个和m 个元素的集合调用setUnion,那么setUnion所花的时间就是O(m+n)。想明白为什么,要注意到对assemble的调用会花O(1)的时间为输出表创建一个单元,然后对剩下的表调用setUnion。因此,图7-6中对assemble的调用,可以视为要花O(1)的时间,再加上对长度之和为比L 和M 长度之和少1,或在情况(4)下比L 和M 长度之和少2的两个表调用setUnion所花的时间。此外,setUnion中的所有工作,除了对assemble的调用之外,所花时间都是O(1)。
多变量函数的大O
正如在6.9节中指出的,我们为单变量函数定义的大O概念自然也可以应用于多变量函数。如果存在常数c 和a1、…、ak,使得对i=1、…、k,只要xi ≥ai,就有f (x1,…,xk )≤cg (x1,…,xk ),就说f (x1,…,xk )是O(g(x1,…,xk ))。特别要说的是,虽然当m 和n 其中一个为0而另一个大于0时会有m+n 大于mn,但通过选择常数c、a1和a2都等于1,仍然可以说m+n 是O(mn)。
接下来,在总长度为m+n 的两个表调用setUnion,这最多会造成m+n 次对setUnion的递归调用,以及同样次数的对assemble的调用。除去递归调用花的时间,每次调用所花的时间为O(1)。因此,求并集所花的时间为O(m+n),也就是说,与两个集合的大小之和成比例。
这一时间比为用未排序表表示的集合求并集所需的时间O(mn)要少。其实,如果表示集合的表是未排序的,可以在O(n logn+m logm)的时间内为这两个表排序,接着再对已排序的表求并集。因为n logn 主导了n,而m logm 主导了m,所以可以将排序与求并集的总时间支出表示为O(n logn+m logm)。这一表达式可能比O(mn)大,但只要n 与m 的值很接近,也就是说,只要两个集合的大小近似相同,它就比O(mn)小。因此,在求并集之前先排序是说得通的。
7.4.4 交集和差集
图7-6概述了求并集的算法思路,这一思路也适用于求交集和差集的运算:当集合用已排序表表示时,交集和差集运算也能以线性时间执行。对交集而言,只有当元素同时出现在两个集合中,也就是像之前的情况(4)那样时,才会把元素复制到输出中。如果有一个表为NULL,在交集中就不会有任何元素了,因此情况(1)、(2)、(3)就可以被替换为返回NULL的操作。在情况(4)中,我们将两个表表头的元素复制到交集中。而在情况(5)和情况(6)中,两个表的表头元素是不同的,这样较小的元素就不可能都出现在两个表中,因此就不用向交集中添加任何内容,而是要将较小的元素从其所在表中弹出,并对剩下部分求交集。
想知道为什么这样能行,可以举个例子,假设a 是在表L 的表头,b 是在表M 的表头,并且有a<b。那么a 就不可能出现在已排序表M 中,因此可以排除a 同时出现在两个表中的可能。不过,b 可能出现在表L 中在a 之后的某个位置,这样一来就仍然有可能用到来自M 的b。因此,我们需要继续对L 的尾部与整个表M 求交集。相反,如果b 小于a,就要对整个表L 与M 的尾部求交集。计算交集的C语言代码如图7-8所示。还需要修改assemble,用对intersection的调用替代对setUnion的调用。我们将这一修改以及为已排序表求差集的程序留作本节习题。
LIST intersection(LIST L, LIST M)
{
if (L == NULL || M == NULL)
return NULL;
else if (L->element == M->element)
return assemble(L->element, L->next, M->next);
else if (L->element < M->element)
return intersection(L->next, M);
else /* 这里有 M->element < L->element */
return intersection(L, M->next);
}
图 7-8 为用已排序表表示的集合计算交集,这里需要新版本的assemble函数
7.4.5 习题
1. 编写C语言程序,为用未排序表表示的集合求(a)并集;(b)交集;(c)差集。
2. 修改图7-6中的程序,使其为用已排序表表示的集合求(a)交集;(b)差集。
3. 图7-6中的assemble和setUnion函数不会改变原来的表,也就是说,它们会创建元素的副本,而非使用给定表本身的单元。大家能否通过在求并集的过程中销毁给定的表来简化程序?
4. * 通过对作为参数给定的两个表的长度之和进行归纳,证明图7-6中的setUnion函数会返回给定表的并集。
5. * 两个集合S 和T 的对称差是(S-T )∪(T-S ),也就是说,刚好只出现在S 或T 其中一个之中的元素。编写程序,为用已排序表表示的两个集合求对称差。大家的程序应该像图7-6中那样只传递一次表,而不要调用求并集与求差集的程序。
6. * 我们对图7-6中的程序进行了非正式的分析,论证了如果两个表的总长度为n,就会有O(n)次对setUnion和assemble的调用,而且每次调用花的时间是O(1)加上递归调用所花的时间。我们可以将这一论证过程正式化,设TU (n)是setUnion对总长度为n 的两个表的运行时间,TA(n)是assemble对总长度为n 的两个表的运行时间。分别写出TU 与TA 相互以对方定义自身的递归规则。进行替换,消去TA,为TU 建立常规的递推关系。为该递推关系求解。这是否证明了setUnion所花时间为O(n)?
7.5 集合的特征向量实现
很多时候,我们遇到的一些集合是要称为“全集”1的某个小集合U 的各子集。例如,扑克牌型就是由全部52张扑克牌组成的集合的子集。当我们关注的集合是某个小集合U 的各子集时,存在一种比7.4节中讨论的表实现有效得多的集合实现方式。我们以某种方式为U 中的元素排定次序,这样一来,U 中的每个元素都可以与一个唯一的“位置”相关联,这一位置是从0到n-1的整数,其中n 是U 中元素的个数。
1当然,U 不可能是真正的全集,我们用罗素悖论论证过这种所有集合的集合是不存在的。
接着,给定一个包含于U 的集合S,就可以用由0和1组成的特征向量表示S,其规则是,对U 中的每个元素x,如果x 在S 中,对应x 的位置上就是1,而如果x 不在S 中,对应的位置上就是0。
示例 7.13
设U 是一副扑克牌组成的集合。我们可以用任何方式为扑克牌排定次序,不过比较合理的模式是先按照它们的花色:梅花、方块、红桃和黑桃。然后,在同一花色中,按照A、2、3、…、10、J、Q、K这样的顺序排列。例如,梅花A的位置就是0,梅花K的位置是12,方块A的位置是13,而黑桃J的位置是49。红桃同花大顺(即红桃10、J、Q、K、A)是由以下特征向量表示的
0000000000000000000000000010000000011110000000000000
第一个1在位置26处,表示红桃A,而其他4个1则是在35到38这4个位置,它们分别表示红桃10、J、Q和K。
所有梅花花色的牌组成的集合是由以下特征向量表示的
1111111111111000000000000000000000000000000000000000
而所有花牌(即各花色的J、Q、K)组成的集合则是由以下特征向量表示的
0000000000111000000000011100000000001110000000000111
7.5.1 集合的数组实现
要表示某n 元素全集各子集的特征向量,可以使用具有如下类型的布尔数组:
typedef BOOLEAN USET[n];
我们在1.6节中描述过BOOLEAN类型。要将对应位置i 的元素插入到声明为USET类型的集合S 中,只需要执行
S[i] = TRUE;
同样,要从S 中删除对应位置i 的元素,就要
S[i] = FALSE;
如果要查找该元素,只需返回值S [i ]即可,该值就告诉了我们第i 个元素是否出现在S 中。
请注意,当集合用特征向量表示时,词典操作插入、删除和查找各需O(1)的时间。这一技巧的唯一缺点是,所有被表示的集合都必须是某个全集U 的子集。此外,该全集必须很小,否则,数组就会变得很大,要存储数组就不方便了。事实上,因为我们通常一定要将表示集合的数组中所有元素初始化为TRUE或FALSE,而初始化U 的任一子集(即便是∅)所花的时间都肯定与U 的大小成比例。如果U 中有大量的元素,那么初始化集合所花的时间可能会主导所有其他操作的开销。
如果两个集合同为某n 元素普通全集的子集,它们分别由特征向量S 和T 表示,要构成这两个集合的并集,可以定义另一个特征向量R 来表示特征向量S 和T 的按位OR:
对 0≤i≤n,R[i] = S[i] || T[i]
同样,要让R 表示S 和T 的交集,就只要对S 和T 的特征向量按位AND:
对 0≤i≤n,R[i] = S[i] && T[i]
最后,可以按照如下方式让R 表示S 和T 的差集S-T:
对 0≤i≤n,R[i] = S[i] && !T[i]
如果恰当地定义类型BOOLEAN,表示特征向量的数组及对这些数组执行的布尔运算都可以用C语言中的按位运算符实现。不过,这些代码都是与机器相关的,所以在这里不会展示任何细节。特征向量有一种可移植但更耗费空间的实现,可以用合适大小的int类型数组实现,而这是一种我们假设过的BOOLEAN类型的定义。
示例 7.14
考虑一下苹果品种的集合。这里的全集由图7-9所示的6个品种构成,其排列次序表示了它们在特征向量中的位置。
| 品种 | 颜色 | 成熟期 |
|---|---|---|---|
0) | 美味(Delicious) | 红 | 晚熟 |
1) | 格兰尼·史密斯(Granny Smith) | 绿 | 早熟 |
2) | 格拉文施泰因(Gravenstein) | 红 | 早熟 |
3) | 乔纳森(Jonathan) | 红 | 早熟 |
4) | 旭苹果(McIntosh) | 红 | 晚熟 |
5) | 翠玉苹果(Pippin) | 绿 | 晚熟 |
图 7-9 某些苹果品种的特征
红苹果的集合是由特征向量
Red=01110
表示的,而早熟苹果的集合是由特征向量
Early=011100
表示的。因此,由红色或早熟的苹果品种构成的集合,即Red ∪Early,是由特征向量111110表示的。请注意,这一向量为1的位置,是表示Red 的特征向量101110中为1的位置,或是表示Early 的特征向量011100中为1的位置,或是两者中都为1的位置。
通过在101110和011100都为1的位置放置1,可以得到表示Red ∩Early(早熟红苹果的集合)的特征向量。得到的向量是001100,表示苹果品种的集合{格拉文施泰因·乔纳森}。而晚熟红苹果的集合,也就是
Red-Early
可以用向量100010表示。该集合为{美味,旭苹果}。
请注意,使用特征变量求并集、交集和差集所花的时间与向量的长度是成正比的。这一长度与待运算集合的大小没有直接关系,而是等于所选择全集的大小。如果待运算集合占据全集中相当可观的一部分元素,那么求并集、交集和差集的时间也和待运算集合的大小成比例。这一时间要优于已排序表的O(n logn)时间,且大大优于未排序表的O(n2)时间。不过,特征向量也有个缺点,假如所涉及集合的大小远小于全集的大小,这些运算的运行时间就要远大于所涉及集合的大小。
7.5.2 习题
1. 给出如下扑克牌集合的特征向量。为了方便起见,大家可以使用0k表示k个连续的0,用1k表示k个连续的1。
(a) 皮诺奇勒牌堆(使用4种花色的9、10、J、Q、K和A各两张)中的扑克牌。
(b) 红色扑克牌。
(c) 红桃J、黑桃J和红桃K。
2. 使用按位运算符,编写C语言程序计算两个扑克牌集合的(a)并集;(b)差集,其中第一个集合是用单词a 1和a 2表示的,而第二个集合则是由b 1和b 2表示的。
3. * 假设要表示元素包含于某小型全集U 的无序单位组(多重集)。该如何将特征向量法推广到无序单位组的表示呢?说明要如何对这样表示的无序单位组执行(a)插入,(b)删除;(c)查找操作。请注意,无序单位组的lookup (x )返回的是x 在无序单位组中出现的次数。
7.6 散列
在可以使用词典的特征向量表示时,我们可以直接访问表示元素的位置,也就是访问数组中以该元素的值为下标的位置。不过,正如前面提到过的,不能让全集的大小太大,否则数组长度就会超出计算机可用内存的容纳能力了。就算计算机内存能容纳这个数组,初始化数组所需的时间也太长了。例如,假设要存储真正的英文词典,并假设我们愿意忽略10个字母以上的单词。仍会有2610+269+…+26个可能存在的单词,这大约是超过1014个单词,每个可能的单词都需要数组的一个位置。
不过,不管什么时候,英语语言中一般只有100万个单词,所以之前所说的数组中只有一亿分之一的数据项为TRUE。我们也许可以缩减该书组,使得很多可能存在的单词共享一个数据项。例如,假设指定头100万个单词存放在数组的第一个单元中,而接下来的100万个可能存在的单词存放在第二个单元中,以此类推,直到第100万个单元。这种安排有两个问题。
(1) 在单元中只放入TRUE已经不够了,因为我们没法知道这100万个可能的单词中到底有哪些实际出现在词典中,也不知道任意一组中是否有多个单词出现。
(2) 比方说,如果头100万个可能的单词包含了所有的短单词,就可以预期有超过平均数的词典内单词落入这一组可能存在的单词中。要注意到,我们的安排是数组单元数要和词典中的单词数相当,这样就可以预期平均每个单元要表示一个单词,但英语中肯定有好几千个单词是在第一组中的,这样就包含了所有不超过5个字母的单词,以及部分6个字母的单词。
要解决问题(1),就需要在数组的每个单元中列出该组中出现在词典里的所有单词。也就是说,该数组单元成了容纳这些单词的链表的表头。要解决问题(2),需要注意如何为潜在的单词分组。一定要合理分配各组中的元素,使得不大可能出现(虽然从不会不出现)某一组中有很多元素的情况,虽然这种情况不太可能不出现。请注意,如果在一组中有大量的元素,而且我们又用链表来表示组,那么在成员众多的组中查找元素就会非常缓慢。
7.6.1 散列表数据结构
我们现在已经从特征向量这种使用范围有限但很有价值的数据结构,演变到了对任意词典都很有用而且对很多其他用户来说也很实用的散列表数据结构。2散列表的词典操作速度平均可达O(1)的水平,而且与构建词典所用全集大小没有关系。图7-10中展示了散列表的图片,不过,我们只给出了x 所在的那一组对应的链表。
2虽然有的情况下用特征向量也是可行的,但我们通常还是会优先选择用散列表来表示。
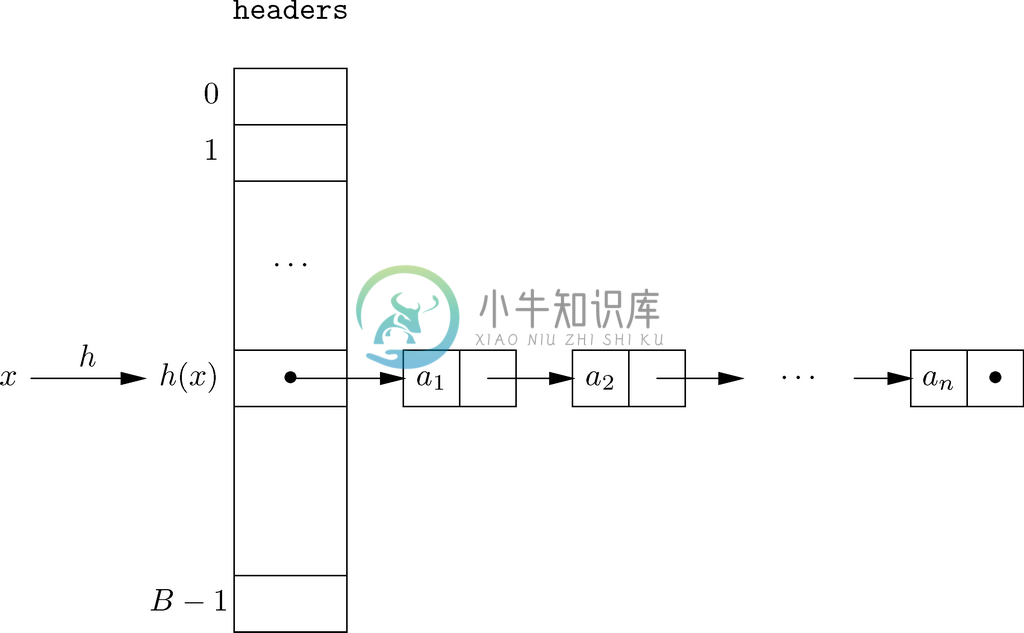
图 7-10 散列表
散列函数接受元素x 作为参数,并生成0到B-1之间的某个整数值,其中B 是散列表中散列表元(bucket)的数量。值h (x )就是我们放置元素x 的散列表元的位置。因此,这些散列表元与我们之前非正式讨论中谈论过的单词“组”是对应的,而散列函数是用来决定某个给定元素应该属于哪个散列表元的。
使用何种散列函数更合适取决于元素的类型。例如
1. 如果元素是整数,就可以令h (x )为x %B,也就是x 除以B 的余数。这一数字总是在所要求的0到B-1这一范围内。
2. 如果元素是字符串,就可以取元素x=a1a2…ak,其中每个ai 都是一个字符,并计算y=a1+a2+…+ak,因为在C语言中char类型是个小整数。这样,我们就得到与字符串x 中所有字符等价的整数的和y。如果用y 除以B,并取余数,就得到了在0到B-1这一范围内的散列表元号。
重点在于散列函数会“混杂”该元素。也就是说,h 会混杂元素要落入的散列表元,这样一来这些元素大约就是会平均落入所有的散列表元中。即便元素本身相当有规律,比如是连续整数,或者只有一个位置不同的连续字符串,这种公平分配也一定会发生。
每个散列表元都是由链表组成的,该链表存储着散列函数发送给该散列表元的集合中的所有元素。要找到元素x,就要计算h (x ),得到散列表元号。如果x 在,它肯定就在h (x )对应的散列表元中,这样我们可以沿着该散列表元对应的链表查找x。实际上,散列表让我们使用了较慢的集合的表实现,不过,通过将集合分为B 个散列表元,让我们在查找表时平均只需要查找整个集合的1/B。如果让B 差不多和集合的大小一样大,那么平均每个散列表元中就只有一个元素,这样查找元素平均只需要O(1)的时间了,就像在集合的特征向量表示中那样。
示例 7.15
假设我们要存储某字符串集合,每个字符串都以空字符结尾,而且最多只含32个字符。我们要使用上述第(2)条中提到的散列函数,其中B=5,也就是说,是有5个散列表元的散列表。要计算每个元素的散列值,就要求出每个字符串中直到空字符为止(但不包括空字符)各字符的整数值之和。以下定义给了我们想要的类型。
(1) #define B 5
(2) typedef char ETYPE[32];
(3) DefCell(ETYPE, CELL, LIST);
(4) typedef LIST HASHTABLE[B];
第(1)行定义了表示散列表元数量5的常量B。第(2)行定义的ETYPE类型是可容纳32个字符的数组。第(3)行是常见的链表及链表单元的定义,只不过这里的元素是ETYPE类型的,也就是32字符的数组。第(4)行将散列表定义为由B 个链表组成的数组。如果接着定义
HASHTABLE headers;
headers数组有着包含散列表元头部的合适类型。
int h(ETYPE x)
{
int i, sum;
sum = 0;
for (i = 0; x[i] != ’\0’; i++)
sum += x[i];
return sum % B;
}
图 7-11 假设ETYPE是字符数组,为与字符等价的整数求和的散列函数
现在必须定义散列函数h。该函数的代码如图7-11所示。与字符串x 中各字符等价的整数会在变量sum中求和。最后一步会计算这个和除以散列表元数B 得到的余数,并将其作为散列函数h 的值返回。
下面拿一些单词作为例子,并考虑散列函数h 安放这些单词的散列表元。要在散列表中输入7个单词3
3这些单词来自E.E.Cummings的一首同名诗,该诗的下一句是“with up so floating many bells down”。
anyone lived in a pretty how town
要计算h(anyone),就需要搞清楚字符表示的整数值。在常用于表示字符的ASCII码中,小写字母对应的整数值从表示a的97(二进制的1100001)开始,到表示b的98,等等,直到表示z的122。而大写字母对应的整数要比相应小写字母对应的整数小32,也就是从表示A的65(二进制的1000001)到表示Z的90。
因此,与anyone中的字符对应的整数分别是97、110、121、111、110、101。它们的和是650。将这个和除以B,也就是5,得到余数为0。因此,anyone属于散列表元0。通过图7-11中的散列函数,就可以将本例中的7个单词分配到如图7-12所示的散列表元中。
单词 | 和 | 散列表元 |
|---|---|---|
anyone | 650 | 0 |
lived | 532 | 2 |
in | 215 | 0 |
a | 97 | 2 |
pretty | 680 | 0 |
how | 334 | 4 |
town | 456 | 1 |
图 7-12 各个单词、它们的值和它们所在的散列表元
我们看到7个单词中有3个被分配到编号为0的散列表元中,有两个被分配到2号散列表元中,而1号和4号中各有一个单词。这与一般情况相比不那么平均,不过对少量的单词和散列表元来说,我们应该能预见这种不规则的情况。随着单词数变多,这些单词在5个散列表元中的分布就会近似平均了。插入了这7个单词之后的散列表如图7-13所示。
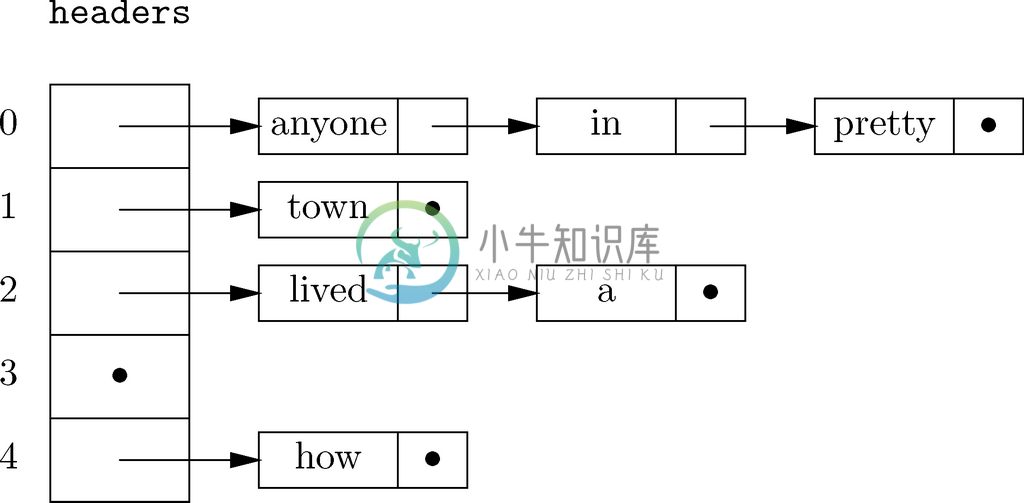
图 7-13 存放7个元素的散列表
7.6.2 词典操作的散列表实现
要在用散列表表示的词典中插入、删除或查找元素x,要经历简单的3步过程。
1. 计算合适的散列表元,也就是h(x)。
2. 利用由表头指针组成的数组,找到与标记为h(x)的散列表元对应的存储元素的表。
3. 对该表执行操作,就像该表表示了整个集合一样。
针对这里的元素是字符串而6.4中的元素是整数这一事实,对6.4节中的算法经过恰当的修改之后,该算法可以用于这里的表操作。举例来讲,我们在图7-14中展示了向散列表插入元素的完整函数。大家可以自行开发delete和lookup函数作为练习。
#include <string.h>
void bucketInsert(ETYPE x, LIST *pL)
{
(1) if ((*pL) == NULL) {
(2) (*pL) = (LIST) malloc(sizeof(struct CELL));
(3) strcpy((*pL)->element, x);
(4) (*pL)->next = NULL;
}
(5) else if (strcmp((*pL)->element, x)) /* x 和 element
是不同的 */
(6) bucketInsert(x, &((*pL)->next));
}
void insert(ETYPE x, HASHTABLE H)
{
(7) bucketInsert(x, &(H[h(x)]));
}
图 7-14 向散列表中插入元素
要理解图7-14,可以注意到函数bucketInsert与图6-5中的函数insert是相似的。在第(1)行,我们进行测试,看看是否已到达表的末端。如果是,就在第(2)行创建一个新单元。不过,在第(3)行,我们不再是把整数存储到新创建的单元中,而是利用标准头文件string.h里的strcpy函数将字符串x复制到该单元的元素字段。
还有,在第(5)行,我们会使用string.h中的strcmp函数测试是否尚未在该表中找到x。当且仅当x 和当前单元的元素相等时,该函数会返回0。因此,只要这一比较的值非0,也就是只要当前元素不是x,我们就会沿着表继续向下。
这里的insert函数只有一行代码,在这行代码中,当我们找到对应适当散列表元h(x)头部的数组元素之后,就会调用bucketInsert。我们假设该散列函数h 是在其他位置定义的。还要记得,类型HASHTABLE意味着H是指向各单元指针组成的数组(即链表数组)。
示例 7.16
假设我们要从图7-13所示的散列表中删除元素in,而使用的散列函数是示例7.15描述的。删除操作的执行方式从根本上讲与图7-14中的insert函数是类似的。我们会计算h (in),其值为0。因此我们前往0号散列表元对应的表头。该散列表元对应的表中第二个单元存放着in,要删除该单元。具体的C语言程序留作本节习题。
7.6.3 散列表操作的运行时间
正如我们通过检视图7-14可以了解的,假设计算h (x )所花的时间是个与存储在散列表中的元素数量无关的常量,4函数insert找到适当散列表元头部所需的时间是O(1)。在这个常数的基础之上,还必须加上平均为O(n/B )的附加时间,其中n 是散列表中的元素数量,而B 则是散列表元的数量。原因在于,bucketInsert要花费与链表长度成比例的时间,而这一长度平均而言肯定是元素总数除以散列表元数,也就是n/B。
4这可能是图7-11所示散列函数的情况,也可能是实践中遇到的大多数散列函数的情况。计算散列表元编号的时间可能取决于元素的类型。例如,更长的字符串可能需要为更多的整数求和,但这一时间与存储的元素数量没关系。
一个有趣的结果就是,如果让B 约等于集合中元素的数量,也就是说,令n 和B 非常接近,则n/B 大约为1,对散列表执行各种词典操作平均花费O(1)的时间,就和我们使用特征向量表示时一样了。如果尝试通过让B 比n 大得多来改善时间,会使多数散列表元为空,而这样做之后找到散列表元头部仍然要花O(1)的时间,因此让B 比n 大很多并不会显著改善运行时间。
还必须考虑到,在某些情况下,可能没法让B 一直与n 很接近。如果该集合增长迅速,那么n 增加了而B 仍然不变,最终n/B 会变得很大。重组散列表是有可能的,只要通过为B 选择一个更大的值,然后将每个元素都插入新的散列表中。完成这一工作需要O(n)的时间,不过这一时间不会大于向先前的散列表中插入n 个元素所需的O(n)时间。请注意,这里的总时间O(n)是执行n 次插入所花的时间,每次插入平均花费时间为O(1)。
7.6.4 习题
1. 继续向图7-13中的散列表填充单词with up so floating many bells down。
2. * 评价一下,下列散列函数在将常用英语单词集合分成大小基本相同的散列表元时,效率有多高。
(a) 使用B=10,并设h (x )是单词长度x 除以10得到的余数。
(b) 使用B=128,并设h (x )是单词x 最后一个字符的整数值。
(c) 使用B=10。求单词x 中各字符对应整数值的和。取求和结果的平方,然后取该结果除以10的余数。
3. 使用与图7-14所示代码相同的假设,编写C语言程序,用于对散列表执行(a)删除;(b)查找操作。
7.7 关系和函数
尽管一般会假设集合中的元素都是原子的,不过在实践中让元素具有某种结构往往是很实用的。例如,在7.6节中我们谈论了长32个字符的字符串元素。另一种可作为元素的重要结构是定长表,它们和C语言的结构体类似。用作集合元素的表称为元组(tuple),表中每个元素称为元组的组分(component)。
元组中组分的数量称为元组的元数(arity)。例如,(a,b)是元数为2的元组,其第一个组分为a,第二个组分为b。元数为k 的元组也称为k 元组。
以具有相同元数(比方说是k)的元组为元素形成的集合称为关系。这一关系的元数就是k。元数为1的元组或关系是一元的。如果元数为2,就是二元的。一般来说,如果元数为k,那么元组或关系就是k 元的。
示例 7.17
关系R={(1,2),(1,3),(2,2)}就是元数为2的关系,也就是二元关系。它的成员分别为(1,2),(1,3)和(2,2),都是元数为2的元组。
在本节中,我们主要考虑二元关系。还有很多非二元关系的重要应用,特别是在表列数据(就像在关系数据库中那样)的表示和操作中。我们将在第8章中进一步讨论该主题。
7.7.1 笛卡儿积
在正式研究二元关系之前,需要定义另一种集合运算。设A 和B 是两个集合,表示为A×B 的A 和B 的积,是指从A中选出第一个组分并从B中选出第二个组分所组成的有序对的集合,也就是
A×B={(a,b)|a∈A且b∈B}
该乘积有时也叫作笛卡儿积,是以法国数学家勒内·笛卡儿的名字命名的。
示例 7.18
回想一下,符号Z约定俗成是表示所有整数的集合的。因此,Z×Z就表示整数有序对的集合。
再举个例子,如果A 是双元素集{1,2},而B是三元素集{a,b,c },那么A×B 就是6元素集{(1,a ),(1,b ),(1,c ),(2,a ),(2,b ),(2,c )}。
请注意,集合的积这一名称是名副其实的,因为如果A 和B 都是有限集,那么A×B 中元素的数量,正好是A 中元素数量乘以B 中元素数量的积。
7.7.2 两个以上集合的笛卡儿积
与算术积不同,笛卡儿积不具备交换律和结合律这些常规属性。很容易找出A×B≠B×A 的例子来推翻交换律。而结合律更是无从说起,(A×B )×C 的成员有序对具有((a,b ),c )的形式,而A×(B×C )的成员有序对则形如(a,(b,c ))。
因为在很多时候需要谈论多元组的集合,所以需要将集合的积的表示法扩展到k 元笛卡儿积。设A1×A2×…×Ak 表示集合A1、A2、…、Ak 的积,也就是说,满足a1∈A1且a2∈A2且…且ak∈Ak的k元组(a1,a2,…,ak )的集合。
示例 7.19
Z×Z×Z表示的是整数三元组(i , j , k )的集合,例如它包含了三元组(1,2,3)。不要把该三元笛卡儿积与表示有序对((1,2),3)的(Z×Z)×Z,或是表示有序对(1,(2,3))的Z×(Z×Z)弄混了。
另一方面,要注意到这3种乘积表达式都可以用由3个整数字段组成的结构体表示。不同之处在于解释结构体类型的方式。因此我们很容易混淆加括号和不加括号的乘积表达式。同样,以下三个C语言类型声明
struct {int f1; int f2; int f3;};
struct {struct {int f1; int f2;}; int f3;};
struct {int f1; struct {int f2; int f3;};};
都是以相似的方式存储的,只是存取字段的表示方式有所区别。
7.7.3 二元关系
二元关系R 是作为集合A 和集合B 笛卡儿积子集的有序对集合。如果关系R 是A×B 的子集,就说R 是A 到B 的关系。而A 就是该关系的定义域(domain),B 就是该关系的值域(range)。如果B 和A 是相同集合,就说R 是A 上的关系,或者说是“定义域”A“上”的关系。
示例 7.20
整数上的算术关系<是Z×Z的子集,由那些满足a 小于b 的有序对(a,b )组成。因此,符号<可被视作集合{(a,b)|(a,b)∈Z×Z,且a 小于b }的名称。然后我们用a< b 作为“(a,b )∈ <”或“(a,b )是关系<的成员”的简略形式。而整数上的其他算术关系,比如>或≤,也可以按照相似的方式定义,而且实数上的算术比较都可以按照相似的方式定义。
再举个例子,考虑示例7.17中的关系R。它的定义域和值域是不确定的。我们知道1和2肯定在其定义域中,因为这两个整数是R 中元组的第一个组分。同样,我们知道R的值域肯定包含2和3。不过,可将R看作是{1,2}到{2,3}的关系,或是将其视作Z到Z的关系,这只是无数选择中的两个例子而已。
7.7.4 关系的中缀表示
正如我们在示例7.20中所表示的,二元关系的中缀表示法是很常用的,所以,像<关系这样本来是有序对的集合,却可以写在关系中各有序对的两个组分之间。这也就是为什么我们通常会看到诸如1<2和4≥4这样的表达式,而不是看到更为学究式的(1,2)∈ <或(4,4)∈≥。
示例 7.21
关系的中缀表示法可以用于任意类型的二元关系。例如,示例7.17中的关系R 就可以写为3个“事实”1R 2、1R 3和2R 2。
声明的及当前的定义域和值域
示例7.20的第二部分强调了一点,就是不能只从看到的表象来断定关系的定义域和值域。作为第一个组分出现的元素组成的集合肯定是定义域的子集,而作为第二个组分的元素组成的集合一定是值域的子集。不过,在定义域或值域中还可能有其他的元素。
当关系不发生改变时,这种差异是不重要的。不过,我们在7.8节和7.9节,以及在第8章的内容中会看到,值会发生改变的关系是非常重要的。例如,我们可能谈论某一关系,其定义域是某门课程中的学生,而值域则是一些整数,表示作业的总分。在开课之前,该关系中是没有有序对的。在第一次作业被评分后,每个学生就各有了一个有序对。随着时间的推移,会有学生弃选这门课程,或是有学生加入该课程,而总分在不断增加。
我们可以将该关系的定义域定义为所有在该大学注册的学生,而将值域定义为整数的集合。当然,不论何时,该关系的值都是这两个集合笛卡儿积的子集。另一方面,不管什么时候,关系都具有当前定义域和当前值域,就是由出现在关系中有序对第一个组分和第二个组分位置的元素分别构成的集合。当我们需要加以区分时,就会将关系本来的定义域和值域称作声明的定义域和值域。当前的定义域和值域分别是声明的定义域和值域的子集。
7.7.5 表示二元关系的图
可以用图来表示定义域为A 且值域为B 的关系R。先为在A 和(或)B 中的每个元素画一个节点。如果aRb,就画一条从a 到b 的箭头(“弧”),我们将在第9章中更详尽地讨论一般图。
示例 7.22
表示示例7.17中关系R 的图如图7-15所示。它有表示1、2、33个元素的3个节点。因为1R 2,所以从节点1到节点2有一条弧。因为1R 3,所以有一条从1到3的弧。而且有2R 2,所以有一条从节点2到它本身的弧。除此之外没有其他的弧,因为R中不再包含其他有序对了。

图 7-15 表示关系{(1,2),(1,3),(2,2)}的图
7.7.6 函数
假设有从定义域A 到值域B 的关系R 具有如此属性:对其定义域A 中个每个成员a 而言,在其值域B 中最多有一个b 满足aRb。这样的R 就被称作从定义域A 到值域B 的偏函数。
如果对A 中每个成员a 来说,都刚好在B 中有一个元素b 满足aRb,就说R 是从A 到B 的全函数。偏函数和全函数之间的区别在于,偏函数可能对其定义域中的某些元素而言无定义,例如,对A 中的某个a,可能在B 中不存在满足aRb 的b。我们会使用术语“函数”来指代偏函数更为一般化的概念,不过,只要偏函数与全函数之间的区别关系重大,我们就会用上“偏”字。
有一种常用的函数表示法,如果b 是满足aRb 的唯一元素,通常就写成R (a)=b。
示例 7.23
设S是由{(a,b)|b=a2}(也就是第二个组分为第一个组分平方的有序对的集合)给出的从Z到Z的全函数。那么S 具有诸如(3,9)、(-4,16)和(0,0)这样的成员。我们可以通过写出S(3)=9、S(-4)=16和S(0)=0来表示S 为平方函数这一事实。
请注意,函数在集合论中的概念与C语言中函数的概念没有太大区别。也就是说,假设s是具有如下声明
int s(int a)
{
return a*a;
}
的C语言函数,它接受一个整数作为参数并返回该整数的平方。我们通常会将s(a)视为与S(a)相同的函数,尽管前者是计算平方的一种方式,而后者只是抽象地定义了求平方的运算。还要注意到,在实际应用中,s(a)总是偏函数,因为出于计算机算术能力的限制,有很多a的值让s(a)不会返回整数。
C语言中也有接受多个参数的函数。接受两个整数参数a和b,并返回一个整数的C语言函数f,就是从Z×Z到Z的函数。同样,如果两个参数分别有着让它们分属集合A 和集合B 的类型,而f返回的是类型C 的某个成员,那么f就是从A×B 到C 的函数。更一般地讲,如果函数f接受分别来自集合A1、A2、…、Ak 的k 个参数,并返回集合B 的某个成员,我们就说f是从A1×A2×…×Ak 到B 的函数。
例如,可以将6.4节中的lookup(x,L)函数视作从Z×L 到{TRIE,FALSE}的函数。这里的L 是整数链表的集合。
函数的多种表示法
从A×B 到C 的函数F 从理论上讲是(A×B)×C 的子集。因此函数F 中的有序对都应该具有((a,b),c)这样的形式,其中a、b、c 分别是集合A、B、C 的成员。使用函数的特别表示法,可以写成F (a,b)=c。
还可将F 视作从A×B 到C 的关系,因为每个函数都是一个关系。使用关系的中缀表示法,((a,b),c)在F 中这一事实也可以写为(a,b)Fc。
在将笛卡儿积扩展到多个集合时,我们可能希望从乘积表达式中删除括号。因此,我们可能将(A×B)×C 视为技术上讲与其不相等的表达式A×B×C。在这种情况下,F 的成员就可以写为(a,b,c)。如果将F 存储为这种三元组的集合,就一定要记住前两个组分一起组成定义域元素,而第三个组分是值域元素。
正式地讲,从定义域A1×A2×…×Ak 到值域B 的函数,就是形如((a1,…,ak),b)的有序对的集合,其中ai 是集合Ai 的成员,b 是集合B 的成员。请注意,该有序对的第一个元素本身也是个k 元组。例如,上面提到的lookup(x,L)函数也可以视作有序对((x,L),t )的集合,其中x是整数,L 是整数链表,而t 要么是TRUE要么是FALSE,具体取决于x 是否在链表L 中。不管函数是用C语言编写的,还是在集合论中正式定义的,都可以将其视为一个从定义域集合接受某个值并生成值域中某个值的容器,如表示函数lookup的图7-16所示。
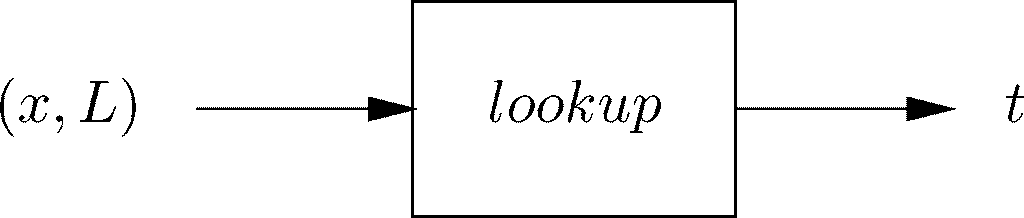
图 7-16 函数将定义域中的元素与值域中唯一的元素关联起来
7.7.7 一一对应
设从定义域A 到值域B 的偏函数F 具有下列属性。
1. 对A 中的每个元素a,在B 中都有一个元素b 满足F(a)=b。
2. 对B 中的每个b,在A 中都存在某个a 满足F(a)=b。
3. 在B 中没有这样的b,使得A 中有两个元素a1和a2满足F(a1)和F(a2)都是b。
这样的F 就称为从A 到B 的一一对应。而这种一一对应也可以用术语双射(bijection)来表示。
属性(1)表示F 是从A 到B 的全函数。属性(2)是表示F 是从A 到B 之上的全函数的条件。一些数学家会使用术语满射(surjection)来表示这种从A 到B 之上的全函数。
属性(2)和属性(3)一起表示F 就像从B 到A 的全函数那样。而具有属性(3)的全函数有时也被称为单射(injection)。
一一对应基本上就是两个方向上的全函数,不过要注意到,F 是否为一一对应不止取决于F 中的有序对,还取决于声明的定义域和值域。例如,可以取任意从A 到B 的一一对应,并通过向A 中增加某个在F 中未提及的新元素e而改变定义域。这样F 就不会是从A∪{e }到B 的一一对应。
示例 7.24
示例7.23中从Z到Z的求平方函数S 就不是一一对应。它确实满足属性(1),因为对每个整数i,都存在某个整数,也就是i 2,满足S(i )=i 2。不过,它不满足属性(2),因为对某些在Z中的b,具体来说就是所有的负整数,在Z中不存在a 使得S(a)=b。S也不满足属性(3),因为存在很多两个不同的a 使S(a)等于同一个b 的例子。例如,S(3)=9,而且S(-3)=9。
要举一一对应的例子,可以考虑定义为P(a)=a+1的从Z到Z的全函数P。也就是说,P 会为任一整数加1。例如,P(5)=6,而且P(-5)=-4。还可以将P 视作由二元组形成的集合{…,(-2,-1),(-1,0),(0,1),(1,2),…},或者是图7-17所示的图。

图 7-17 表示函数P(a)=a+1这一关系的图
我们声明P 是从整数到整数的一一对应。首先,这是个偏函数,因为当为整数a 加上1时,可得到唯一的整数a+1。它是满足属性(1)的,因为对每个整数a,存在某个作为P(a)的整数a+1。属性(2)也得到满足,因为对每个整数b,都存在某个整数,即b-1,满足P(b-1)=b。最后,属性(3)也是满足的,因为对某个整数b 而言,不存在这样两个不同的整数,使得给这两个整数各自加上1后都得到b。
从A 到B 的一一对应是在A 和B 的元素之间构建唯一关联的一种方式。例如,如果双手合十,左手和右手的大拇指触在一起,左手和右手的食指触在一起,等等。我们可以把左手手指集合与右手手指集合之间的这种关联看作一一对应F,定义为F(“左拇指”)=“右拇指”,F(“左食指”)=“右食指”,等等。也可以将这种关联看作F 的逆函数,也就是从右手到左手的函数。总的说来,可以通过调换有序对中组分的次序,反转从A 到B 的一一对应,从而成为从B 到A 的一一对应。
左右手之间存在这种一一对应的结果就是每只手手指的数量是相同的。这似乎是种自然而且直觉上的概念,当一个集合到另一个集合正好存在一一对应时,这两个集合有着相同数量的元素。不过,我们在7.11节中会看到,当集合为无限集时,从这一“元素数量相同”的定义会得出一些惊人的结论。
7.7.8 习题
1. 给出使A×B 不同于B×A 的集合A 和B 的例子。
2. 设R 是由aRb、bRc、cRd、aRc 和bRd 定义的关系。
(a) 画出表示R 的图。
(b) R 是否为函数?
(c) 为R 指出两个可能的定义域,并指出两个可能的值域。
(d) 满足R 是S 上关系(即定义域和值域都可以是S)的最小集合S 是什么?
3. 设T 是树,并设S 是树T 的节点的集合。设R 是节点间的“父子”关系,也就是说,当且仅当c 是p 的子节点时有cRp。回答以下问题,并验证子集的答案。
(a) 不管树T 是什么,R 是否为偏函数?
(b) 不管树T 是什么,R 是否为从S 到S 的全函数?
(c) R 有没有可能是一一对应(即对某树T 而言)?
(d) 表示R 的图是什么样的?
4. 设R 是整数集合{1,2,…,10}上的关系,其中如果a 和b 是不同整数而且有除1之外的公约数,就说aRb。例如,2R 4,6R 9,但是没有2R 3。
(a) 画出表示R 的图。
(b) R是否为函数?为什么?
5. * 虽然我们看到S =(A×B)×C和T=A×(B×C)是不同的集合,但是通过展示出它们之间存在的自然的一一对应,可以证明它们“从根本上讲是相同的”。对S 中的每个((a,b),c)而言,设F(((a,b),c))=(a,(b,c))。证明F 是从S 到T 的一一对应。
6. F(10)=20、10F 20和(10,20)∈F 这3项陈述有何共同之处。
7. *关系R 的逆关系(简称R 的逆)是指满足(a,b)在R中的有序对(b,a)的集合。
(a) 说明如何从表示R 的图得出表示R 的逆的图。
(b) 如果R 是全函数,那么R 的逆是否一定为函数?如果R 是一一对应呢?
8. 证明:当且仅当某关系及其逆关系都是全函数时,该关系是一一对应。
7.8 将函数作为数据来实现
在程序设计语言中,函数通常是由代码实现的,不过当它们的定义域很小时,可以使用相当类似于实现集合的技巧来实现它们。我们在本节中要讨论如何使用链表、特征向量和散列表来实现有限函数。
作为程序的函数与作为数据的函数
尽管7.7节中我们在函数的抽象概念与C语言中实现的函数间作了很强的类比,不过还是应该注意到它们间的重大差别。如果F 是C语言函数,而x 是其定义域集合中的成员,那么F 就告诉了我们如何计算F(x)的值。而同样的程序对任意的值x 都是起作用的。
然而,当我们将函数表示为数据时,首先就需要函数是由有序对的有限集构成。其次,通常这些有序对基本是不可预测的。也就是说,在给定x 的情况下,没什么方便的办法来计算F(x)的值。我们能做的最佳做法就是创建表给出每个满足F(ai )=bi 的有序对
(a1,b1),(a2,b2),…,(an ,bn)
这样的函数事实上是数据,而不是程序,尽管原则上讲可以创建程序,将这样的表存储为该程序的一部分,并在给定x 的情况下从内部表中查找F(x)。不过,更加高效的做法是将该表单独储存为数据,并利用可以处理任一这种函数的通用算法来进行值的查找。
7.8.1 对函数的操作
最常对函数执行的操作与对词典的操作类似。假设F是从定义域集合A到值域集合B的函数。那么我们可以进行下述操作
1. 插入满足F(a)=b 的新有序对(a,b)。唯一的微小区别在于,因为F 一定是函数,所以假如其中已经存在有序对(a,c),那么该有序对肯定会被(a,b)替代。
2. 删除与F(a)关联的值。在这里,我们只需要给出定义域中的值a 即可。如果存在b 满足F(a)=b,有序对(a,b)就会从集合中删除。如果没有这样的有序对,就不会发生任何改变。
3. 查找与F(a)关联的值,也就是说,给定定义域中的值a,返回满足F(a)=b 的值b。如果集合中没有这样的有序对(a,b),就返回某个特殊的值来警告F(a)是未定义的。
示例 7.25
假设F 由有序对{(3,9),(-4,16),(0,0)}组成,也就是说,F(3)=9、F(-4)=16而且F(0)=0。那么lookup(3)会返回9,而lookup(2)则返回一个特殊的值,指示没有值被定义为F(2)。如果F是“求平方”函数,那么值-1可以用来指示不存在的值,因为-1不可能是任何整数真正的平方值。
操作delete(3)会删除有序对(3,9),delete(2)则没有效果。如果执行insert(5,25),那么会在集合F 中添加有序对(5,25),或者说现在有了F (5)=25。如果执行insert(3,10),就会从F 中删除旧的有序对(3,9),并将新的有序对(3,10)添加到F中,这样一来就有了F (3)=10。
7.8.2 函数的链表表示
函数作为有序对集合,可以像其他任何集合那样存储在链表中。定义含有3个字段的单元是很实用的,一个表示定义域的值,另一个表示值域的值,最后一个表示指向下一个单元的指针。例如,我们可以按照如下方式定义单元。
typedef struct CELL *LIST;
struct CELL {
DTYPE domain;
RTYPE range;
LIST next;
};
其中DTYPE是定义域元素的类型,而且RTYPE表示值域元素的类型。那么函数就可以表示为指向链表(第一个单元)的指针。
图7-18中的函数执行操作insert (a,b,L ),假设DTYPE和RTYPE都是32字符的数组。我们查找在domain字段中含有值a的单元。如果找到,就将其range字段置为b。如果到达链表末端,就创建一个新单元,并将(a,b)存储进去。否则,测试该单元中是否含有定义域元素a。如果有,那么就将值域的值改为b,这样就行了。如果定义域中有a 之外的值,就递归地将其插入链表尾部。
如果函数F 中有n 个有序对,那么插入操作平均要花O(n)的时间。同样,用于表示为链表的函数的delete和lookup函数也平均需要O(n)的时间。
typedef char DTYPE[32], RTYPE[32];
void insert(DTYPE a, RTYPE b, LIST *pL)
{
if ((*pL) == NULL) {/* 在表的末端 */
(*pL) = (LIST) malloc(sizeof(struct CELL));
strcpy((*pL)->domain, a);
strcpy((*pL)->range, b);
(*pL)->next = NULL;
}
else if (!strcmp(a, (*pL)->domain)) /* domain 字段是 a,
改变F(a) */
strcpy((*pL)->range, b);
else /* domain 字段不是 a */
insert(a, b, &((*pL)->next));
};
图 7-18 将新事实插入表示为链表的函数中
7.8.3 函数的向量表示
假设声明的定义域是从0到DNUM-1的整数,也可以通过枚举类型来定义。然后我们可以使用特征向量的表示函数,将表示特征向量的类型FUNCT定义为:
typedef RTYPE FUNCT[DNUM];
这是判断该函数为全函数或者RTYPE包含一个可以解释为“值不存在”的值的关键所在。
示例 7.26
假设我们要存储与苹果有关的信息,就像图7-9中的收获期信息,不过现在希望给出具体的收获月份,而不是早熟/晚熟这种二元的选择。通过定义如下枚举类型,我们为定义域和值域中的每个元素都关联了一个整数常量:
enum APPLES {Delicious, GrannySmith, Jonathan, McIntosh, Gravenstein, Pippin};
enum MONTHS {Unknown, Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec};
这一声明将0与标识符Delicious关联,将1与GrannySmith关联,等等。它还将0与Unknown关 联,将1与Jan关联,等等。标识符Unknown表示收获月份是未知的。现在可以声明数组
int Harvest[6];
用该Harvest数组表示图7-19所示的有序对集合。接着数组Harvest就成了图7-20那样,其中数据项Harvest[Delicious]=Oct意味着Harvest[0]=10。
苹果 | 收获月份 |
|---|---|
美味(Delicious) | 十月(Oct) |
格兰尼·史密斯(Granny Smith) | 八月(Aug) |
乔纳森(Jonathan) | 九月(Sep) |
旭苹果(McIntosh) | 十月(Oct) |
格拉文施泰因(Gravenstein) | 九月(Sep) |
翠玉苹果(Pippin) | 十一月(Nov) |
图 7-19 苹果的收获月份

图 7-20 Harvest数组
7.8.4 函数的散列表表示
我们可以将属于某函数的有序对存储在散列表中。关键的是,我们只对定义域的元素应用散列函数,以确定有序对所属的散列表元。形成散列表元的链表单元都有一个表示定义域元素的字段,而另一字段表示对应的值域元素,第三个字段则是将链表中的一个单元链接到下一个单元。下面举个例子,应该就能把这个技巧说清了。
示例 7.27
我们继续使用示例7.26中有关苹果的数据,不过现在要使用实际名称来表示定义域。要表示函数Harvest,我们会使用含5个散列表元的散列表。这里要将APPLES定义为32字符的数组,而MONTHS还是示例7.26中那样的枚举。散列表元是链表,具有表示APPLES类型定义域元素的variety字段、表示int类型(月份)值域元素的harvested字段,以及指向链表中下个元素的链接字段next。
我们会使用与7.6节中图7-11类似的散列函数h。当然,h 只会应用到定义域元素上,也就是说,只会应用到由苹果品种名组成的长32个字符的字符串上。
现在,可以将类型HASHTABLE定义为B个LIST组成的数组。其中B是散列表元的数量,我们已经将其定为5了。所有这些声明都出现在图7-22的开头。然后就可以声明散列表Harvest来表示所需的函数。
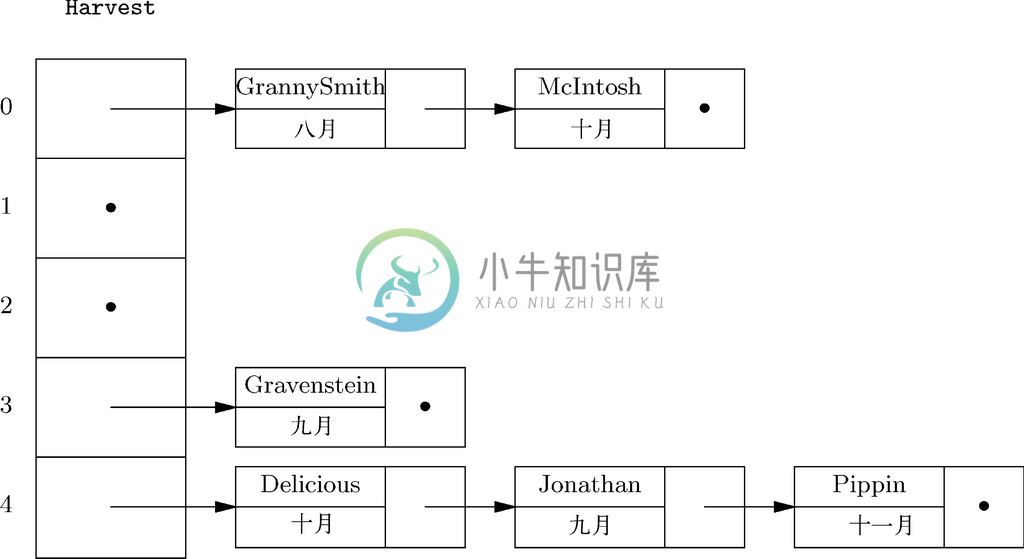
图 7-21 存储在散列表中的苹果品种名称及其收获月份
在插入图7-19中列出的6个苹果品种之后,散列表元中单元的分布如图7-21所示。例如,如果将单词Delicious的9个字符对应的整数值加起来,就得到929。因为929除以5的余数为4,所以美味苹果(Delicious)就属于4号散列表元。而表示该苹果品种的单元将字符串Delicious存放在variety字段中,将月份Oct存放在harvested字段中,最后还有一个指向散列表元中下一个单元的指针。
#include <string.h>
#define B 5
typedef char APPLES[32];
enum MONTHS {Unknown, Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec};
typedef struct CELL *LIST;
struct CELL {
APPLES variety;
int harvested;
LIST next;
};
typedef LIST HASHTABLE[B];
int lookupBucket(APPLES a, LIST L)
{
if (L == NULL)
return Unknown;
if (!strcmp(a, L->variety)) /* 找到 */
return L->harvested;
else /* 未找到 a,检查尾部 */
return lookupBucket(a, L->next);
}
int lookup(APPLES a, HASHTABLE H)
{
return lookupBucket(a, H[h(a)]);
}
图 7-22 用于通过散列表表示的函数的查找
7.8.5 对用散列表表示的函数的操作
要执行插入、删除和查找操作,都要从需要散列的定义域值从而找到散列表元开始。要插入有序对(a,b),就要找到散列表元h(a),并查找它对应的链表。接下来的操作就和图7-18中给出的向链表插入函数有序对的函数一样了。
要执行delete(a),先要找到散列表元h(a),查找具有定义域值a 的单元,要是找到这样的单元,就从链表中删除该单元。而执行lookup(a)操作还是要散列a,然后在散列表元h(a)中查找含有定义域值a 的单元。如果找到这样的单元,就会返回与之对应的值域值。
例如如图7-22所示的函数lookup(a,H)。函数lookupBucket(a,L)会沿着与某散列表元对应的链表L向下查找,并返回值harvested(a),也就是苹果品种a收获的月份。如果这一月份是未定义的,就返回值Unknown。
向量和散列表
示例7.26和示例7.27中看待有关苹果的信息的方式有着根本的区别。在特征向量法中,苹果品种是个固定集,是枚举类型的。当C语言程序正在运行时,是没办法改变苹果名称集合的,而且对一个未出现在枚举集合中的名称执行查找也是没意义的。
另一方面,当我们用散列表来构建同一函数时,是将苹果名称作为字符串,而不是枚举类型的数字。这样一来,就有可能在程序正在运行时对名称集合进行修改了,比方说是为了响应某些与新的苹果品种有关的输入数据。对散列表中未出现的品种执行查找是可行的,而且我们必须有所防备,要加上
Unknown这样一个“月份”,以防出现查找散列表中未提及品种的情况。因此,散列表的灵活性要比特征向量更佳,不过要付出一些速度上的代价。
7.8.6 函数操作的效率
对以我们在本节中讨论过的这3种方式表示的函数执行各种操作所需的时间,与对词典执行同样操作所需的时间是一样的。也就是说,如果函数由n 个有序对组成,那么链表表示下每种操作平均需要O(n)的时间。特征向量法每种操作只需要O(1)的时间,不过,就像词典那样,只有定义域类型的大小比较有限时,才能使用该表示法。而具有B 个散列表元的散列表每种操作的平均时间是O(n /B )。如果有可能让B 接近n,那么就可以达到每种操作平均花费O(1)时间的水平。
7.8.7 习题
1. 模仿图7-18中的insert函数,编写函数,对用链表表示的函数执行(a)删除;(b)查找操作。
2. 编写函数,对用向量表示的函数,也就是由DTYPE类型的整数作为下标的RTYPE类型的数组,执行(a)插入;(b)删除和(c)查找操作。
3. 模仿图7-22中的lookup函数,编写函数,对用散列表表示的函数执行(a)插入;(b)查找操作。
4. 二叉查找树也可用来表示作为数据的函数。为二叉查找树定义合适的数据结构,以存放图7-19中的苹果信息,并使用这些数据结构实现(a)插入;(b)删除;(c)查找操作。
5. 设计一个信息检索系统,记录有关棒球球员击球和击中的信息。所设计的系统应该接受形如Ruth 5 2的三元组,表示Ruth在5次击球中击中了2次。对应Ruth的数据项应该得到适当的更新。大家应该还能查询任意球员的击球次数和击中次数。实现该系统,使得只要执行插入和查找操作的函数使用了合适的子程序和类型,就对任意数据结构都有效。
7.9 二元关系的实现
二元关系的实现与函数的实现有些许差异。回想一下,二元关系与函数都是有序对的集合,不过在函数中,对定义域中的各元素a 来说,最多只能与任一值域元素b 构成一个形如(a,b)的有序对。而二元关系则不同,可以有任意数量的值域元素与某个给定的定义域元素a 相关联。
在本节中,我们首先会考虑二元关系的插入、删除和查找操作的意义。然后看看已经用到的3种实现——链表、特征向量和散列表——是如何一般化到二元关系上的。在第8章中,我们会讨论多元关系的实现。通常,表示多元关系的数据结构,都是构建在表示函数和二元关系的数据结构的基础之上的。
7.9.1 对二元关系的操作
当我们将有序对(a,b)插入二元关系R 中时,并不需要关心R 中是否已经存在某个有序对(a,b),其中c≠b,但向某个函数中插入(a,b)时,就需要关心这个了。原因当然是R 中包含定义域值a 的有序对数量是没有限制的。因此,可以直接将有序对(a,b)插入R 中,就像将元素插入任意集合中那样。
同样,从关系中删除有序对(a,b)也类似于从集合中删除元素:要查找该有序对,如果存在就将其删除。
查找操作可以用多种方式定义。例如,我们可以接受有序对(a,b),并询问该有序对是否在R 中。不过,如果我们因此将对关系的查找操作解释成与刚定义的插入和删除操作那样,与对任意词典的这些操作行为相同,被操作的元素是有序对而不是原子这一事实就只是个小细节,它只能影响到词典中元素的类型。
然而,定义lookup来接受定义域元素a,并返回所有满足(a,b)在二元关系R 中的值域元素b 往往是很实用的。对lookup的这种解释给了我们一种与词典有所区别的抽象数据类型,它有着与词典ADT不同的某些特定用途。
示例 7.28
大多数李子品种需要另一种特定的品种来传粉,没有合适的“传粉者”,这棵李树就不会结果。有少数品种是“自育的”,也就是说它们可以作为自己的传粉者。图7-23展示了李子品种集合上的二元关系。这一关系中的有序对(a,b)表明品种b 是品种a 的传粉者。
将有序对插入该表表示断言某个品种是另一个品种的传粉者。例如,如果培育出新品种,就可能要向该关系中输入与可以给该新品种传粉的品种以及可以被它传粉的品种有关的事实。删除某个有序对,就表示收回某个品种可为另一品种传粉的断言。
品种 | 传粉者 |
|---|---|
美丽(Beauty) | 圣罗莎(Santa Rosa) |
圣罗莎(Santa Rosa) | 圣罗莎(Santa Rosa) |
伯班克(Burbank) | 美丽(Beauty) |
伯班克(Burbank) | 圣罗莎(Santa Rosa) |
澳得罗达(Eldorado) | 圣罗莎(Santa Rosa) |
澳得罗达(Eldorado) | 威克森(Wickson) |
威克森(Wickson) | 圣罗莎(Santa Rosa) |
威克森(Wickson) | 美丽(Beauty) |
图 7-23 某些李子品种的传粉者
对关系更一般的操作
除了对示例7.28中的李子品种进行插入、删除和查找这3种操作可以提供的信息之外,我们可能还需要更多的信息。例如,我们可能想问,“圣罗莎可以为哪些品种传粉?”或者“澳得罗达能否给美丽传粉?”某些数据结构,比如链表,让我们能以执行这3种基本词典操作的速度回答这样的问题,只要不是链表对这些操作很低效。
基于定义域元素的散列表无助于回答给定了值域元素并必须找到对应定义域元素的问题,例如,“圣罗莎可以为哪些品种传粉?”当然,可以对值域元素应用散列函数,不过这样一来就不好回答“什么品种可以给伯班克传粉?”这样的问题了。还可以对定义域元素和值域元素的组合应用散列函数,不过这样一来对哪种类型的查询都不能高效响应了,只能回答一些类似“澳得罗达能否给美丽传粉?”这样的简单问题。
有多种方式能高效地回答所有这些类型的问题。不过,我们要等到第8章谈论关系模型时才会了解到这些技巧。
我们定义的查找操作接受变量a作为参数,查看第一列,寻找所有包含值a的有序对,并返回与之关联的值域值集合。也就是说,询问“哪个品种可以给品种a传粉?”该问题似乎是最可能询问的与该表有关的信息,因为如果我们种植了一棵李树,就必须确认,如果它不是自育的,就应该在附近种植传粉者。例如,如果调用lookup(Burbank),预期答案就是{Beauty,Santa Rosa}。
7.9.2 二元关系的链表实现
如果愿意的话,我们可以将关系中的有序对在链表中链接起来。该链表的单元都含有一个定义域元素、一个值域元素,以及一个指向下一个单元的指针,就像表示函数的链表单元那样。插入和删除操作,就像6.4节中讨论过的针对一般集合的插入和删除那样。唯一的小差别就是这里集合成员的相等性,是通过比较存放定义域元素的字段以及存放值域元素的字段确定的。
这里的查找操作要与我们之前遇到的查找操作有些不同。我们必须沿着链表向下,查找含某个特定定义域值a 的单元,而且必须将与之相关的值域值组成一个链表。下面的示例将会展示对链表进行查找操作的机制。
示例 7.29
假设我们想用链表来实现示例7.28中的李子关系。可以将RVARIETY类型定义为长32个字符的字符串,并将类型为RCELL(relation cell,关系单元)的单元定义为结构体
typedef char PVARIETY[32];
typedef struct RCELL *RLIST;
struct RCELL {
PVARIETY variety;
PVARIETY pollinizer;
RLIST next;
};
我们还需要一个单元容纳一个李子品种和指向下一个单元的指针,以构建某给定品种传粉者的链表,并以此来回应lookup查询。我们将该类型称为PCELL,并定义
typedef struct PCELL *PLIST;
struct PCELL {
PVARIETY pollinizer;
PLIST next;
};
然后可以通过图7-24中的函数定义查找操作。
函数lookup接受定义域元素a 和指向有序对链表第一个单元的指针作为参数。通过调用lookup(a,L),可以对关系R 执行lookup(a)操作,这里的L 是指向表示关系R 的链表第一个单元的指针。第(1)行和第(2)行都很简单。如果链表为空,就返回NULL,因为在空链表中不存在第一个组分为a 的有序对。
PLIST lookup(PVARIETY a, RLIST L)
{
PLIST P;
(1) if (L == NULL)
(2) return NULL;
(3) else if (!strcmp(L->variety, a)) /* L->variety == a */ {
(4) P = (PLIST) malloc(sizeof(struct PCELL));
(5) strcpy(P->pollinizer, L->pollinizer);
(6) P->next = lookup(a, L->next);
(7) return P;
}
else /* a 不是当前数对的定义域值 */
(8) return lookup(a, L->next);
}
图 7-24 在用链表表示的二元关系中进行查找
难题就是在链表第一个单元的定义域字段variety中找到a 的情况。这种情况是在第(3)行检测,在第(4)行至第(7)行得到处理的。我们在第(4)行创建一个PCELL类型的新单元,这将成为我们要返回的PCELL链表中的第一个单元。第(5)行会将相关联的值域值复制到新单元中。然后在第(6)行我们会对链表L 的尾部递归地调用lookup。该调用的返回值是指向得到的链表中第一个单元的指针(如果链表为空则是NULL),它会成为我们在第(4)行中所创建单元的next字段。然后第(7)行要返回指向新创建单元的指针,该单元存放着对应定义域值a 的一个值域值,而且如果存在对应a 的其他值域值,该单元还将链接到存放其他值域值的单元。
最后一种情况是没有在链表L 的第一个单元中找到所需的定义域值a。这时只要在第(8)行对链表L 的尾部调用lookup,并返回该调用返回的任何内容即可。
7.9.3 特征向量法
我们看到,对于集合与函数,可以通过创建以某个“全集”的元素为索引的数组,并在数组中放置合适的值来表示这些集合与函数。对集合来说,合适的数组值就是TRUE和FALSE,而对函数而言,就是那些可以出现在值域中的值,通常还要加上表示“无”的特殊值。
对二元关系来说,可以通过某个较小的声明定义域中的成员作为数组的索引,就像处理函数时那样。不过,不能使用单个值作为数组元素,因为在二元关系中,对于某个给定的定义域值,可能有任意数量的值域值与之对应。最好是把与某给定定义域值相关联的所有值域值存入一个链表,然后将该链表的表头作为数组的元素。
示例 7.30
我们用这种组织方式再来处理李子品种的例子。正如我们在7.8节中指出的,在使用特征向量表示法时,必须让值的集合固定不变,至少要保证定义域值的集合不变,而对链表或散列表的表示而言,就不存在这种限定。因此,必须重新将PVARIETY类型声明为枚举类型
enum PVARIETY {Beauty, SantaRosa, Burbank, Eldorado, Wickson};
我们可以继续使用示例7.29中定义的表示品种链表的PCELL类型,这样就可以将数组定义为
PLIST Pollinizers[5];
也就是说,表示图7-23所示关系的数组,是用该图中提及的品种作为索引的,而与每个品种关联的值,都是指向其传粉者链表第一个单元的指针。图7-25展示了用特征向量法表示出的图7-23中的有序对。
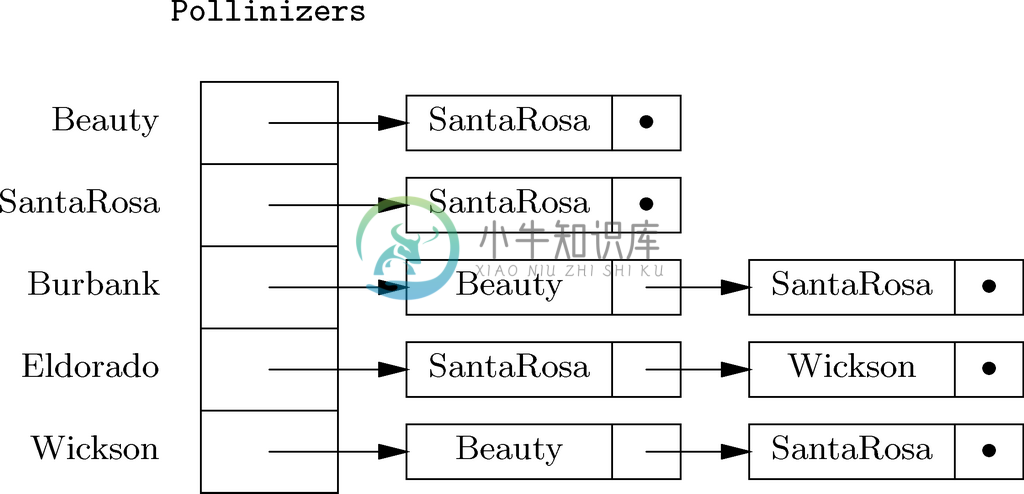
图 7-25 传粉者关系的特征向量表示
要执行有序对的插入和删除,先要找到恰当的数组元素,并从那里开始沿着链表行进。至此,链表的插入和删除操作就很平常了。例如,如果我们确定威克森不能充分给澳得罗达传粉,就可以执行 delete(Eldorado,Wickson)操作。对应Eldorado的链表表头在Pollinizers[Eldorado]中被找到,而且要从那里开始沿着链表向下行进,直到找到存放Wickson的单元并 将其删除。
查找操作更是小菜一碟,只需要返回在合适的数组条目中找到的指针。例如,要对查询lookup(Burbank,Pollinizers)作出回应,只要返回链表Pollinizers[Burbank]就行了。
7.9.4 二元关系的散列表表示
我们可以使用只取决于有序对第一个组分的散列函数,将给定的二元关系R 存储在散列表中。也就是说,有序对(a,b)会被放置在散列表元h(a)中,其中h 是散列函数。请注意,这种安排与针对函数的安排是一模一样的,唯一的差异在于,对二元关系而言,一个散列表元中可能包含多个以给定的值a 作为第一个组分的有序对,而对函数而言,它所含的这种有序对决不会超过一个。
要插入有序对(a,b),就要计算h(a),并对含有该成员的散列表元加以检查,以确保(a,b)尚未出现在其中。如果还没出现,就将(a,b)添加到该散列表元对应链表的末端。要删除(a,b),就要先找到散列表元h(a),然后查找该有序对,如果链表中存在该有序对,就将其删除。
要执行lookup(a),就还是要先找到散列表元h(a),然后沿着该散列表元对应的链表向下行进,收集所有在第一个组分为a 的单元中出现的b。图7-24中为二元关系的链表表示编写的lookup函数也可以用于构成散列表表元的链表。
7.9.5 二元关系操作的运行时间
二元关系3种表示的性能与函数或词典上同样结构的性能差别不大。首先考虑链表表示。尽管还没有编写过用于插入和删除操作的函数,但我们应该能意识到这些函数会行遍整个链表,查找目标有序对,然后在找到它的地方停下。在长度为n的链表上,这样的查找平均会耗费O(n)的时间,因为如果没找到这样的有序对,它肯定是扫描了整个链表,而如果找到了,它平均也要扫描链表的半数单元。
对查找操作来说,图7-24中的检测应该能说服我们,该函数所花的时间是O(1)加上对链表尾部的递归调用耗费的时间。因此,如果链表长度为n,我们会执行n 次调用,总共花费O(n)的时间。
现在考虑一般化的特征向量。操作lookup(a)是最简单的。找到以a 为下标的数组元素,可以在该元素处找到所需的答案——满足有序对(a,b)在该关系中的所有b 组成的链表。我们甚至不必检验这些元素或复制它们。因此,在使用特征向量时,查找操作花的时间为O(1)。
另一方面,插入和删除操作就没那么简单了。要插入(a,b),可以相当容易地找到下标为a的数组元素,不过必须查找整个链表,以确保(a,b)尚未出现在其中。5这样做所需的时间与链表的平均长度成比例,也就是说,与关联某给定定义域值的值域值的平均数量成正比。我们将该参数称为m。另一种看待m 的方式是,它是关系中有序对的总数量n 除以不同定义域值的数量。如果假设任一链表与其他链表被查找的可能都是相同的,则执行插入或删除操作平均需要O(m)的时间。
5也可以在不考虑该有序对是否已经出现的情况下直接插入该有序对,不过这样就会同时带来6.4节中讨论过的允许重复的链表表示所具有的优点和缺点。
最后来考虑散列表。如果在关系中有n 个有序对,并且散列表中有B 的散列表元,就能预期平均每个散列表元中有n/B 个有序对。不过,这里还是要引入参数m。如果存在n/m 个不同的定义域值,那么至多有n/m 个散列表元可以是非空的,因为对应有序对的散列表元只由定义域值决定。因此,不管B 是多少,m 是散列表元平均大小的下界。因为n/B 也是下界,所以执行这3种操作其中之一所花的时间是O(max(m,n/B ))。
示例 7.31
假设有一个含1000个有序对的关系,这些有序对分布到100个定义域值中。那么每个定义域值会有10个值域值与之关联,也就是说m=10。如果使用1000个散列表元,也就是B=1000,那么m 要大于n/B,也就是1,这样就可以预期我们实际可能查找的散列表元(因为表元编号为h(a),其中a 是关系中的某个定义域值)平均含有约10个有序对。事实上,每个散列表元中平均所含有序对数量要略多于这个值,因为不同的定义域值a1和a2在经过散列之后,得到的h(a1)和h(a2)可能恰巧是同一个散列表元。如果选择B=100,那么m=n/B=10,还是可以预期每个可能查找的散列表元含有约10个元素。正如刚刚提到的,实际数字可能要略大于10,因为可能出现两个或多个定义域值散列到同一散列表元的巧合。
7.9.6 习题
1. 使用示例7.29中的数据类型编写函数,接受传粉者的值b 以及由品种-传粉者有序对组成的链表作为参数,并返回由可以被b 传粉的品种组成的链表。
2. 使用示例7.29中的假设,编写用来处理品种-传粉者有序对的(a)插入;(b)删除程序。
3. 为用示例7.30所述的向量数据结构表示的二元关系编写执行(a)插入;(b)删除;(c)查找操作的函数。在插入有序对时,不要忘了检查相同的有序对是否已经出现在该关系中。
4. 设计散列表数据结构,用来表示构成本节中大量示例的传粉者关系。编写执行插入、删除和查找操作的函数。
5. * 通过对链表L的长度进行归纳,证实lookup返回了满足有序对(a,b)在L 中的所有元素b组成的链表,从而证明图7-24中的lookup函数可以正常工作。
6. * 设计数据结构,使其执行插入、删除、查找和反向查找(inverseLookup)操作的平均时间可以达到O(1)的水平。反向查找操作是接受值域元素,并找到与之关联的定义域元素。
7. 在本节以及前面的几节中,我们定义了一些具有插入、删除和查找操作的新抽象数据类型。不过,这些操作与对词典的同名操作稍有差异。绘制表格,分别记下词典、函数(如7.8节所描述)和关系(如本节所描述)可能的抽象实现,以及支持这些抽象实现的数据结构。对每种实现,给出各操作的运行时间。
对函数和关系的“词典操作”
有序对的集合可以视为集合、函数或是关系。对每种情况来说,我们都已经定义了合适的插入、删除和查找操作。这些操作有着不同的形式。多数情况下,操作会同时取有序对的定义域元素和值域元素。不过,有时候只有定义域元素被用作参数。下表总结了这3种操作在使用中的差异。
有序对集合
函数
关系
插入
定义域和值域
定义域和值域
定义域和值域
删除
定义域和值域
仅定义域
定义域和值域
查找
定义域和值域
仅定义域
仅定义域
7.10 二元关系的一些特殊属性
在本节中,我们将考虑某些实用的二元关系所具备的一些特殊属性。首先要定义一些基本属性:传递性、自反性、对称性与反对称性。这些结合起来就形成了几类常见的二元关系:偏序关系、全序关系和等价关系。
7.10.1 传递性
设R 是定义域D 上的二元关系。如果只要aRb 和bRc 为真,就有aRc 也为真,就说关系R 是传递的。图7-26展示了传递性这种属性。就像它在关系图中出现的那样,只要从a 到b 以及从b 到c 的虚线箭头出现在图中,那么从a 到c 的实线箭头也一定会出现在图中。谨记,传递性与本节中要定义的其他属性一样,都是关于整个集合的属性。只有3个特定的定义域元素满足该属性是不够的,声明的定义域D 中所有的三元组a、b、c 都必须满足。
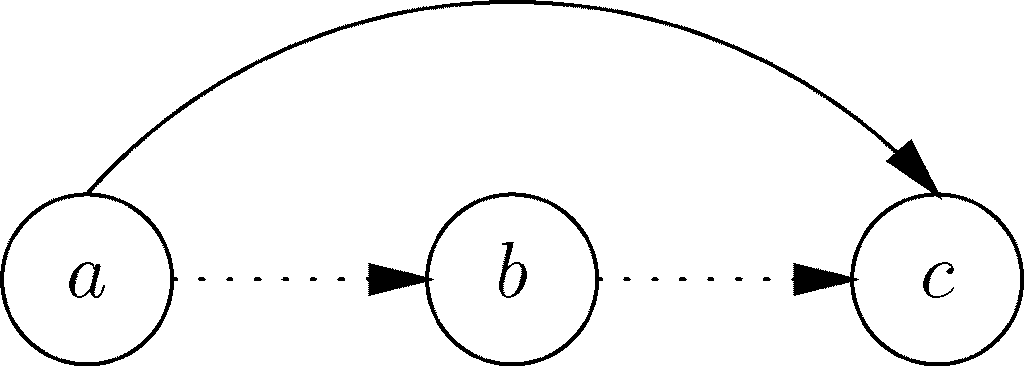
图 7-26 传递性成立的条件要求如果aRb 和bRc 的弧在表示关系的图中出现,那么弧aRc 也要出现
示例 7.32
考虑一下整数集Z上的<关系。也就是说,<是满足a 小于b 的整数有序对(a,b)的集合。关系<是传递的,因为如果a< b且b< c,就可知a< c。同样,整数上的关系≤、>和≥也都是传递的。这4种比较关系在实数集合上也同样具有传递性。
不过,考虑一下整数(或者是实数)上的≠关系。该关系就不具传递性。例如,设a 和c 都是3,并设b 是5。这样a≠b 与b≠c 都为真。如果该关系是传递的,那么应该有a≠c。不过这就是说3≠3,显然是错的。所以可以得出≠是不具传递性的。
再举个传递关系的例子,考虑一下⊆,也就是子集关系。我们也许想将该关系视为所有满足S 为T 的子集的集合有序对(S,T )组成的集合,但想象一下,有这样的集合就会再次将我们引向罗素悖论。不过,假设有“全集”U,就可以设⊆U 是集合有序对的结合
{(S,T )|S⊆T 且T⊆U }
那么⊆U 就是U 的幂集P(U )上的关系,而我们可以将⊆U 当作子集关系。
例如,设U={1,2}。那么⊆{1,2}就是由如图7-27所示的9个(S,T )有序对组成的。因此,⊆U 刚好含有满足第一个组分是第二个组分的子集(不一定是真子集),而且二者皆为{1,2}的子集的那些有序对。
不管全集U 是什么,都很容易检验⊆U是传递的。如果A⊆B 而且B⊆C,那么肯定有A⊆C。原因在于,对A 中的每个x,我们知道x 也在B 中,因为A⊆B。因为x 在B 中,我们知道x 也在C 中,因为B⊆C。因此A 中的每个元素也都是C 中的元素。所以A⊆C。
S | T |
|---|---|
∅ | ∅ |
∅ | {1} |
∅ | {2} |
∅ | {1,2} |
{1} | {1} |
{1} | {1,2} |
{2} | {2} |
{2} | {1,2} |
{1,2} | {1,2} |
图 7-27 关系⊆{1,2}中的有序对
7.10.2 自反性
有些二元关系R 还具有这样的属性,就是对声明的定义域中的每个元素a,R 中都包含有序对(a,b),也就是都有aRa。如果这样的话,就说R 是自反的。图7-28展示了某自反关系的图,其声明的定义域中每个元素上都有个循环。该图中除了这些循环外还可能有其他的箭头。不过,当前定义域中每个元素都有循环是不够的,必须是声明定义域中每个元素都有循环才行。
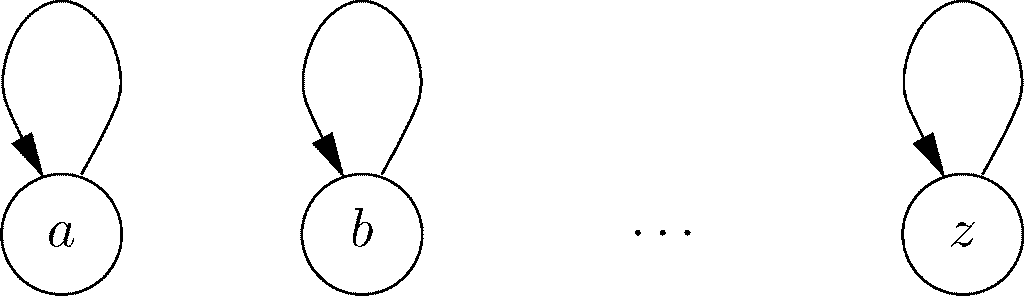
图 7-28 自反关系R 对其声明定义域中每个元素x 来说都有xRx
示例 7.33
实数集合上的关系≥就是自反的。对每个实数a 而言,都有a≥a。同样,≤是自反的,而这两种关系在整数集合上也是自反的。不过,<和>就不是自反的,因为至少有一个a 的值可以使a>a 和a< a 不成立,其实,对所有的a 来说,a>a 和a< a 都是不成立的。
示例7.32中定义的子集关系⊆U 也是自反的,因为对任意集合A 而言,都有A⊆A。不过,有着相似定义,包含满足T⊆U 和S⊆T 的有序对(S,T )的关系⊆U ——表示S 是T 的真子集的关系——就不是自反的。原因在于,A⊂A 对某些A(事实上是对所有的A)来说不成立。
7.10.3 对称性与反对称性
设R 是某二元关系。正如7.7节的习题(7)所定义的那样,R 的逆是指将R 中各有序对的组分调换位置后形成的新有序对组成的集合。也就是说,R 的逆,记作R-1,就是
{(b,a)|(a,b)∈R }
例如,>是<的逆,因为刚好当b< a 时有a>b。同样,≥是≤的逆。

图 7-29 对称性要求如果aRb,就也有bRa
如果R 是它自己的逆,就说它是对称的。也就是说,如果只要aRb,就也有bRa,就说R 是对称的。图7-29展示了在表示关系的图中对称性是什么样的。如果出现了向前的弧,就肯定还要有向后的弧。
如果只有a=b 在时才有aRb 和bRa 都为真,我们就说R 是反对称的。请注意,在反对称关系中,都不必有aRa 对任意特定a 来说为真。不过,反对称关系也可以是自反的。图7-30展示了在关系图中反对称的条件是怎样的。

图 7-30 反对称关系不能具有涉及两个元素的循环,不过单一元素上的循环是可以出现的
示例 7.34
整数集或实数集上的≤关系就是反对称的,因为,如果a≤b 且b≤a,就肯定有a=b。关系<也是反对称的,因为在任何条件下a< b 和b< a都不可能同时成立。同样,≥和>是反对称的,示例7.32中讨论的子集关系⊆U 也是。
不过,要注意到≤不是对称的。例如,3≤5,但5≤3是不成立的。同样,上一段中提到的其他几种关系也都不是对称的。
整数上的≠关系就是对称关系的一个例子。也就是说,如果a≠b,就一定有b≠a。
属性定义中的陷阱
正如前文已经指出的,属性的定义都是针对一般情况的,适用于定义域中的所有元素。例如,要让声明定义域D 上的某关系R 是自反的,就需要对每个a∈D 都有aRa。aRa 对某个a 成立是不够的,而且说某个关系对某些元素自反而对另一些元素不自反也是说不通的。就算D 中只有一个a 让aRa 不成立,也说明R 不是自反的。因此,自反性可能取决于定义域,而且取决于关系R。
还有,像传递性——若aRb 且bRc,则aRc ——这样的条件具有“若A 则B ”的形式。请记住,要满足这样的命题,既可以让B 为真,也可以令A 为假。因此,对某个给定的三元组a、b 和c,只要aRb 为假,或bRc 为假,或aRc 为真,就满足传递性的条件。最极端的情况是,空关系是传递的、对称的而且反对称的,因为“若”的条件从不能满足。不过,空关系不是自反的,除非声明的定义域为∅。
7.10.4 偏序和全序
偏序是传递且反对称的二元关系。如果除了传递性和反对称性之外,某关系能让每个定义域元素对都是可比的,就说该关系是全序关系。也就是说,如果R 是全序的,而且a 和b 是其定义域中的任意两个元素,则要么aRb 为真,要么bRa 为真。请注意,每个全序关系都是自反的,因为可以设a 和b 是相同的元素,这样可比性的要求就告诉我们有aRa。
示例 7.35
整数或实数上的算术比较≤和≥都是全序关系,因此也都是偏序关系。请注意,对任意的a 和b 来说,要么a≤b,要么b≤a,不过当a=b 时刚好两者都成立。
算术比较<和>都是偏序关系而非全序关系。尽管它们是反对称的,不过不是自反的,也就是说a< a 和a>a 都不成立。
对应某个全集U 的2U 上的子集关系⊆U 和⊆U 都是偏序关系。我们已经知道,它们是传递且反对称的。不过,只要U 中至少有两个成员,这些关系就不是全序关系,因为这样一来就有不可比的元素了。例如,设U={1,2}。那么{1}和{2}都是U 的子集,但这两个集合之间谁也不是谁的子集。
大家可将全序关系R 视作一个如图7-31所示的线性元素序列,其中只要对不同的元素a 和b 有aRb,a 就出现在这条线上b 的左侧。例如,如果R 是整数上的≤关系,那么轴上的元素就是…,-2,-1,0,1,2,…。如果R 是实数上的≤关系,那么这些点就对应实数轴上的点,就像这根轴是把无限长的尺子那样,如果实数x 非负,那么x 就是在0标记右侧x 个单元处,而如果x 为负,那么它就在0标记左侧-x 个单元处。
如果R 是偏序关系而非全序关系,还可以将定义域中的元素画成这样:如果aRb,那么a 在b 的左边。不过,因为可能存在不可比的元素,所以不一定能做到把所有元素画在一条轴上从而使关系R 意味着“在左边”。

图 7-31 表示a1,a2,a3,…,an上的全序关系的图
示例 7.36
图7-32展示了偏序关系⊆{1,2,3}。我们已经将该关系绘成了简化图(reducedgraph),在图中省略了可由传递性指出的弧。也就是说要有S⊆{1,2,3}T,就要满足以下任一条件。
1. S=T。
2. 存在从S 到T 的弧。
3. 从S 到T 之间有一条由两条或多条弧构成的路径。
例如,我们知道∅⊆{1,2,3}{1,3},因为存在路径从∅到{1}再到{1,3}。
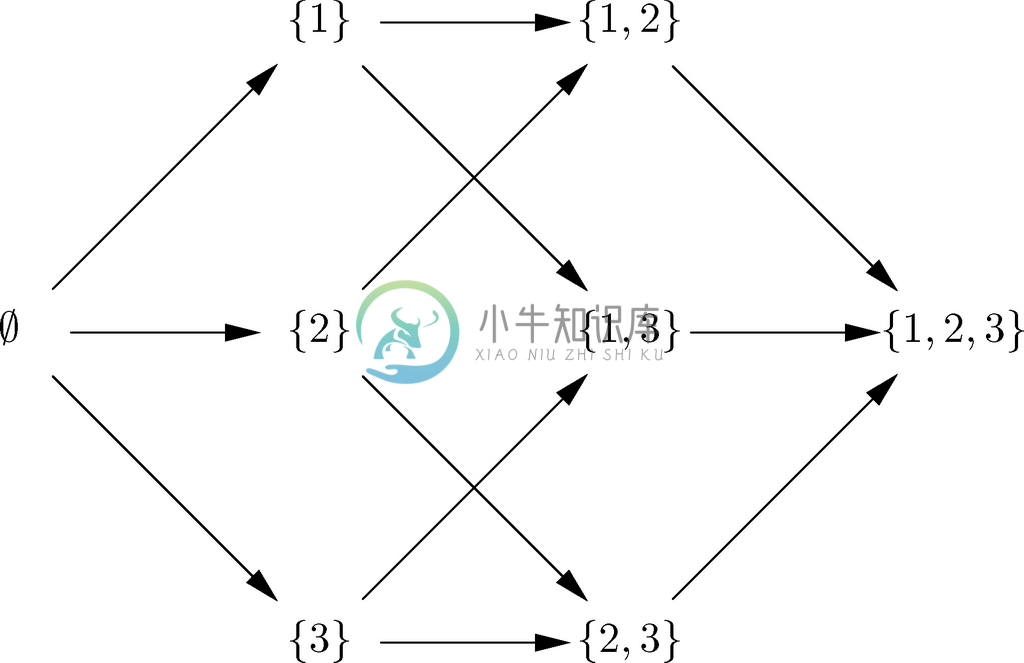
图 7-32 表示偏序关系⊆{1,2,3}的简化图
7.10.5 等价关系
等价关系是自反、对称且传递的二元关系。这种关系与之前的示例中看到的偏序关系和全序关系差别很大。事实上,偏序关系从不可能是等价关系,除非在声明的定义域为空,或者声明定义域中只有一个元素a而且该关系是{(a,a)}这样一些微不足道的情况下。
示例 7.37
像整数上的≤这样的关系就不是等价关系。虽然它是传递且自反的,但它不是对称的。如果a≤b,除非a=b,否则是不会有b≤a 的。
举个等价关系的例子,设R 是由那些满足a-b 是3的整数倍的整数有序对(a,b)组成的。比如,3R9,因为3-9=-6=3×(-2)。还有5R(-4),因为5-(-4)=9=3×3。不过,(1,2)就不在R 中,或者可以说“1R2不成立”,因为1-2=-1,它不是3的整数倍。可以按照如下方式展示R 是等价关系。
1. R 是自反的,由于对任意整数a 都有aRa,这是因为a-a 为0,是3的整数倍。
2. R 是对称的。如果a-b 是3的整数倍,比方说是3c,其中c 为某整数,那么b-a 就是-3c,因此也是3的整数倍。
3. R 是传递的。假设aRb 而且bRc,也就是说,a-b 是3的倍数,比方说是3d,而b-c 也是3的倍数,比方说是3e。那么
a-c=(a-b)+(b-c)=3d+3e=3(d+e)
因此a-c 也是3的倍数。由aRb 和bRc 得出aRc,这表示R 是传递的。
再举个例子,设S 是世界城市的集合,而T 是由aTb 定义的关系,其中a 和b 是由公路相连的,也就是说,可以从a 驾车到达b。因此,有序对(多伦多,纽约)是在T 中,不过(檀香山,安克雷奇)就不在T 中。可以说T 是等价关系。
T 是自反的,因为每个城市都是连接到它自己的。T 也是对称的,因为如果a 连接到b,那么b 也连接到a。T 还是传递的,因为如果a 连接到b,且b 连接到c,那么a 是连接到c 的,如果没有更短路径的话,可以通过b 从a 行驶到c。
7.10.6 等价类
另一种看待等价关系的方式是,它将子集的定义域分成了等价类。如果R是定义域D上的等价关系,那么可以将D 分为等价类,使得下列命题成立。
1. 每个定义域元素刚好在一个等价类中。
2. 如果aRb,那么a 和b 在相同的等价类中。
3. 如果aRb 不成立,那么a 和b 在不同的等价类中。
示例 7.38
考虑示例7.37中的关系R,其中当a-b 是3的倍数时有aRb。一个等价类是刚好被3整除的整数的集合,也就是除以3余数为0的那些整数的集合。该类为{…,-3,0,3,6,…}。第二个是除以3时余数为1的整数的集合,也就是{…-2,1,4,7,…}。最后一个类是除以3时余数为2的整数的集合,该类为{…,-1,2,5,8,…}。这些类将整数集划分成3个不相交的集合,如图7-33所示。
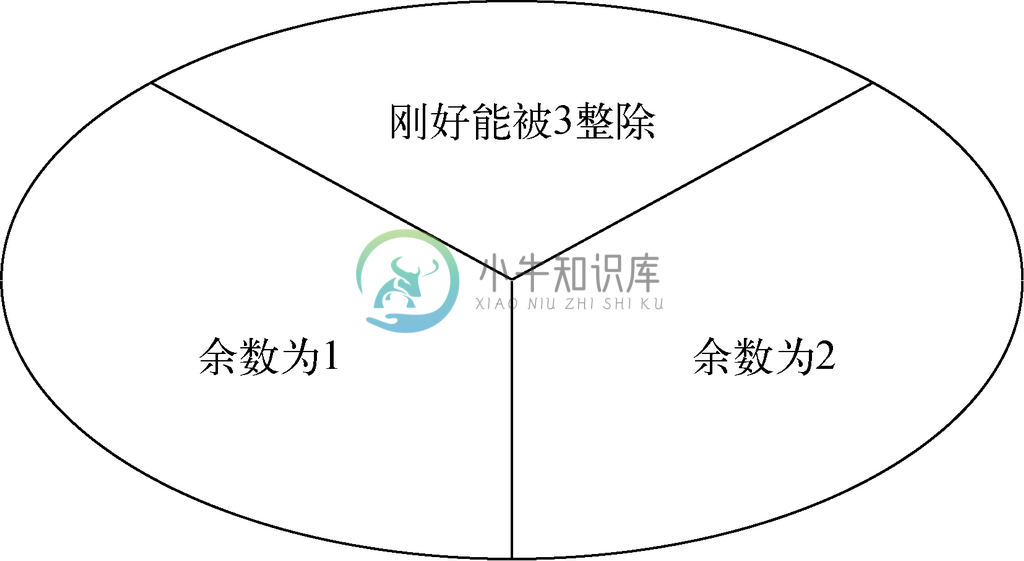
图 7-33 整数上的关系“差能被3整除”相应的等价类
请注意,当两个整数除以3的余数相同时,它们的差就能被3整除。例如,14=3×4+2而5=3×1+2,因此14-5=3×4-3×1+2-2=3×3,于是可知14R 5。另一方面,如果两个整数除以3的余数不同,它们的差就肯定不能被3整除。因此,来自不同等价类的整数(比如5和7)之间,就不具备R 关系。
要为等价关系R 构建等价类,设class(a)是满足aRb 的元素b 的集合。例如,如果等价关系是示例7.37中我们称为R 的那个,那么class(4)就是除以3时余数为1的整数的集合,也就是说class(4)={…,-2,1,4,7,…}。
请注意,如果让a 对定义域的各元素而言是不同的,通常会多次得到同样的类。其实,当有aRb 时,就有class(a)=class(b)。要知道为什么,可以假设c 在class(a)中。则根据类的定义有aRc。因为给定了aRb,根据对称性有bRa。而根据传递性,由bRa 和aRc 可以得出bRc。而bRc 就说明c 在class(b)中。因此,class(a)中的每个元素都在class(b)中。因为同样的推理告诉我们,只要aRb,那么class(b)中的每个元素也都在class(a)中,所以我们可以得出结论:class(a)和class(b)是相同的。
不过,如果class(a)和class(b)不同,则这些类不可能有相同的元素。作相反的假设,那么就肯定有某个c 同时在class(a)和class(b)中。而根据之前的假设,知道有aRc 和bRc。根据对称性,有cRb。根据传递性,可由aRc 和cRb 得到aRb。不过我们刚证明了,只要aRb 成立,则class(a)和class(b)是相同的。而这里假设这些类是不同的,因此就得出了矛盾。所以,假设的出现在class(a)和class(b)的交集中的元素c 不可能存在。
还要看到:每个定义域元素都在某个等价类中。特别要说的是,a 总是在class(a)中,因为自反性告诉我们有aRa。
我们现在就可以得出结论,等价关系将其定义域划分为不相交的等价类,而且将每个元素刚好放在一个类中。示例7.38就展示了这一现象。
7.10.7 关系的闭包
对二元关系的常见运算还有一种,就是取某个不具有自反性(或对称性、传递性)的集合,在为其添加尽可能少的有序对后使得新形成的关系具有自反性(或对称性、传递性)。得到的关系就称为原关系的自反(或对称、传递)闭包。
示例 7.39
我们在图7-32中讨论过简化图。虽然表示的是传递关系⊆{1,2,3},但是只画出了与该关系中有序对的某个子集对应的弧。不过通过应用传递法则推断出新的有序对,直到不能推断出新的有序对,就可以重建完整的关系。例如,我们看到存在有序对({1},{1,3})和({1,3},{1,2,3})相对应的弧,因此传递法则就告诉我们有序对({1},{1,2,3})也肯定在该关系中。而该有序对与有序对(∅,{1})一起,又说明(∅,{1,2,3})也在该关系中。除此之外,还必须加上“自反的”有序对(S,S ),其中S是{1,2,3}的各个子集。这样一来,就重建了关系⊆{1,2,3}中的所有有序对。
另一种实用的闭包运算是拓扑排序,我们接受某个偏序,并向其添加元组,直到它成为全序。尽管二元关系的传递闭包是唯一的,但常常有多个全序包含某一给定的偏序。我们将在第9章中了解到一种特别高效的拓扑排序算法。现在,先考虑一个展示拓扑排序实用性的例子。
示例 7.40
人们常将生产过程中必须执行的一系列任务表示为一套必须服从的“优先级”。举个简单的例子,在给左脚穿鞋之前必须先给左脚穿上袜子,而在穿上右脚的鞋之前要先穿上右脚的袜子。不过,这其中没有其他必须遵守的优先级了。我们可以用由两个有序对(左袜,左鞋)和(右袜,右鞋)组成的集合来表示这些优先级。该集合是个偏序。
可以将该集合扩展为6个不同的全序。其中一个全序是先穿好左脚的鞋袜,该关系是含以下
10个有序对的集合。
(左袜,左袜) (左袜,左鞋) (左袜,右袜) (左袜,右鞋)
(左鞋,左鞋) (左鞋,右袜) (左鞋,右鞋)
(右袜,右袜) (右袜,右鞋)
(右鞋,右鞋)
可将该全序视作如下线性排列
左袜→左鞋→右袜→右鞋
先穿好右脚的鞋袜有着与之相似的过程。
由原始的偏序还可以得到其他4种全序,其中我们要先穿袜子再穿鞋,它们可由以下线性排 列表示:
左袜→右袜→左鞋→右鞋
左袜→右袜→右鞋→左鞋
右袜→左袜→左鞋→右鞋
右袜→左袜→右鞋→左鞋
闭包的第三种形式是找到含有某给定关系的最小等价关系。例如,公路图表示的关系是由公路路段直接连接而不含中间城市的城市对组成的。要确定由公路连接的城市,可以利用自反性、传递性和对称性推断出由某些基础道路序列连接的城市对。闭包的这种形式称为找出图中的“连通分支”(connected component),我们将在第9章讨论一种解决该问题的高效算法。
7.10.8 习题
1. 给出对某一声明定义域自反,但对另一声明定义域不自反的关系。请记住,对作为某关系R 可能的定义域的D 而言,D 必须包含出现在R 的有序对中的每个元素,但它还可以包含更多的元素。
2. **关系⊆{1,2,3}中有多少个有序对?考虑一般的情况,如果U 有n 个元素,那么⊆U 中有多少个有序对?提示:试着从元素较少的情况猜测该函数,比如含两个元素的情况下有9个有序对,如图7-27所示。然后通过归纳证明自己的猜测是正确的。
3. 考虑定义域在4字母字符串上的二元关系R,它是由sRt 定义的,其中t 是由字符串s 的字母向左循环移动一位形成的。也就是说,abcdRbcda,其中a、b、c、d 都是单独的字母。确定R 是否为(a)自反的;(b)对称的;(c)传递的;(d)偏序,和(或)(e)等价关系。为每种情况给出简要论证或是反例。
4. 考虑习题(3)中的4字母字符串定义域。设S 是应用0次或多次R 组成的二元关系。因此,abcdSabcd,abcdSbcda,abcdScdab,且abcdSdabc。换句话说,字符串与它经过任意循环位移后形成的字符串具有S 关系。对关系S 回答习题(3)中提出的5个问题,并且每种情况都要给出论证。
5. * 以下“证明”有何错误?
(非)定理:如果二元关系R 是对称且传递的,那么R 是自反的。
(非)证明:设x 是R 定义域中的某个成员,取某个满足xRy 的y。根据对称性,有yRx。而根据传递性,xRy 和yRx 可以得出xRx。因为x 是R 定义域的任一成员,所以证明了xRx 对R 定义域中的每个元素都成立,也就“证明”了R 是自反的。
6. 给出声明定义域为{1,2,3},具有如下属性的二元关系的例子。
(a) 自反且传递,但不对称。
(b) 自反且对称,但不传递。
(c) 对称且传递,但不自反。
(d) 对称且反对称。
(e) 自反,传递,而且是全函数。
(f) 反对称,而且是一一对应。
7. * 如果为关系⊆U 使用简化图,其中集合U 有n 个元素,那么与使用完全图相比要节省多少条弧?
8. 当U 只有一个元素时,(a)⊆U 和(b)⊂U 是否为偏序或全序?当U 中没有元素时呢?
9. * 从n=1开始,通过对n 的归纳证明,如果有n 个有序对a0Ra1、a1Ra2、…、an-1Ran,而且如果R 是传递的关系,那么有a0Ran 。也就是要证明,如果表示传递关系的图中存在任一路径,就存在一条从该路径开头到该路径结尾的弧。
10. 找出包含有序对(a,b)、(a,c)、(d,e)和(b,f )的最小等价关系。
11. 设R 是整数集上满足如下条件的关系,若a 和b 是互不相同的而且有除了1之外的公约数,则aRb。确定R 是否为(a)自反的;(b)对称的;(c)传递的;(d)偏序和(或)(e)等价关系。
12. 存在某树T 所有节点上的关系RT,其中当且仅当在树T 中a 是b 的祖先时有aRTb,针对该关系重复习题(11)中的练习。
13. 存在某树T 所有节点上的关系ST,其中当且仅当在树T中a在b的左侧时有aSTb,针对该关系重复习题(12)中的练习。
7.11 无限集
人们在计算机程序中要实现的所有集合都是有限的,如果这些集合不是有限的,就没法将它们存储在计算机的内存中。而在数学中,很多集合(比如整数集或实数集)都是无限的。这些观点似乎直观清晰,不过有限集和无限集到底有何区别呢?
有限集和无限集之间的区别是相当令人惊讶的。有限集的元素数量与它任一真子集的元素数量都不同。回想一下,在7.7节中,我们说过可以利用两个集合间一一对应的存在得出它们是等势的(equipotent),也就是说,它们有着相同数量的成员。
如果取一个如S={1,2,3,4}这样的有限集及其任意真子集,如T={1,2,3},那么在这两个集合间没办法找到一一对应。例如,可以把S 中的4映射到T 中的3,把S 中的3映射到T中的2,把S 中的2映射到T 中的1,但接着就找不出T 中的成员来和S 中的1相关联。其他建立从S 到T 的一一对应的尝试也一定同样失败。
大家直观上可能会认为这一点对任意集合来说都应该成立,一个集合在丢掉其中一个或多个元素后怎么可能还具有相同的元素数呢?考虑一下自然数(非负整数)集N和N去掉0后得到的真子集,称该集合为N-{0},{1,2,3,…}。那么考虑一下从N到N-{0}的一一对应F,其中F (0)=1,F (1)=2,一般来讲,F (i )=i+1。
惊人的是,F 是从N到N-{0}的一一对应。对N中的每个i,至多有一个 j 满足F(i )=j,所以F 是个函数。其实,刚好就有一个这样的j,即i+1,使得一一对应的定义中的条件(1)(见7.7节)得到满足。对N-{0}中的每个 j,存在某个i 满足F(i )=j,也就是,i=j-1。因此一一对应的定义中的条件(2)也得到满足。最后,在N中不存在两个不同的数字i1和i2使得F(i1)和F(i2)都为 j,因为那样的话i1+1和i2+1都为 j,这样一来就得出i1=i2,进而就得出F 是N与其真子集N-{0}之间一一对应的结论。
无限酒店
为了帮助大家理解从0开始和从1开始有着同样多的数字,可以想象一家酒店,它有着无限个房间,分别编号为0、1、2,等等。对任意整数而言,都存在一个以该整数作为房号的房间。在某一特定时间,每个房间里都会有一名顾客。一只袋鼠来到前台开房间。前台接待告诉它:“我们这里不接待袋鼠。”等一下,这跑题了。事实上,前台接待按照如下方式给袋鼠腾出了房间。他让0号房间的客人住进1号房,让1号房的客人住进2号房,等等。所有的旧客都还是有一间房可住,而现在0号房是空房了,而这只袋鼠就住进了0号房。这种“戏法”之所以能奏效,是因为从1开始编号的房间与从0开始编号的房间其实是同样多的房间。
7.11.1 无限集的正式定义
数学家们认可的定义是,无限集是指自身与其至少一个真子集之间存在一一对应的集合。在一些极端例子下,无限集和其某个真子集之间可以存在一一对应关系。
示例 7.41
自然数集合与偶自然数集合是等势的。设F(i )=2i。那么F 就是一一对应,它将0映射到0,1映射到2,2映射到4,3映射到6,而一般来讲,就是将每个自然数映射到一个唯一的自然数,它的两倍。
同样,Z和N是同样大小的集合,也就是说,非负整数和负整数一起,与非负整数是一样多的。设对所有的i ≥0,有F (i )=2i,并设对所有的i <0,有F (i )=-2i -1。那么0映射到0,1映射到2,-1映射到1,2映射到4,-2映射到3,等等。每个整数都被映射到一个唯一的非负整数,其中负整数映射为奇数,而非负整数则映射为偶数。
更让人咋舌的是,自然数对组成的集合与N本身也是等势的。要知道这样的一一对应是如何构建起来的,可以考虑一下图7-34,其中展示了N×N中的有序对分布在一个无限的方阵中。我们根据有序对中组分的和来确定它们的次序,而对那些组分的和相等的有序对,则根据其第一个组分的大小确定次序。这一次序始于(0,0)、(0,1)、(1,0)、(0,2)、(1,1)、(2,0)、(0,3)、(1,2),等等,如图7-34所示。
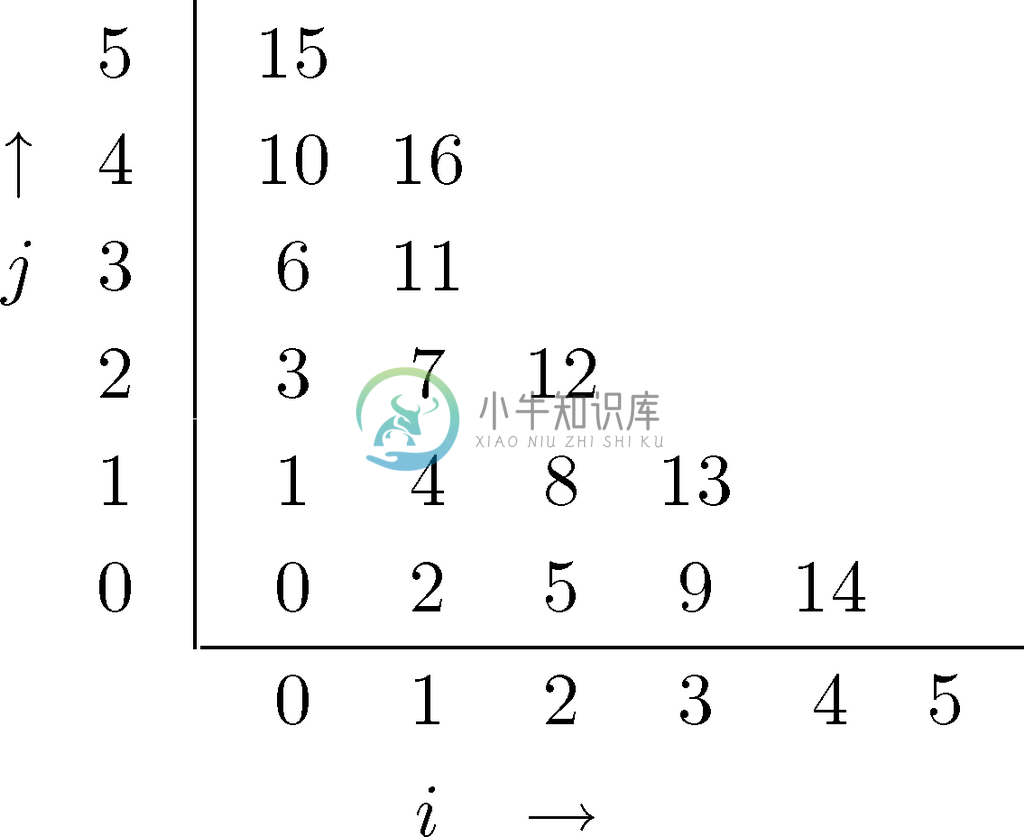
图 7-34 为自然数对排序
现在,这些自然数对有了先后次序。原因在于,对任意自然数对(i , j ),和比其小的自然数对的数量是有限的,而和相同情况下值i更小的自然数对的数量也是有限的。其实,我们可以计算自然数对(i , j )在这一次序中的位置,就是(i+j )(i+j+1)/2+i。也就是说,我们的一一对应是将自然数对(i , j )与唯一的自然数(i+j )(i+j+1)/2+i 关联起来。
请注意,一定要谨慎选择为有序对排序的方式。假设在图7-34中按行排序,那么永远都没法到达第二行或更高行的自然数对,因为每一行中都有无数个自然数对。同样,按列排序也是行不通的。
集合不是有限的,就是无限的
乍一看,可能会出现不那么有限和不那么无限的事物。例如,当谈论链表时,对链表的长度未作限制。而只要在程序的执行中创建了链表,它就具有了有限的长度。因此,可以作出如下区分。
1. 每个链表的长度都是有限的,也就是说,它的单元数是有限的。
2. 链表的长度可能是任何非负整数,而链表可能长度的集合是无限的。
无限集的正式定义是很有意思的,不过这一定义可能不符合我们对无限集的直觉认识。例如,我们可能觉得无限集是对每个整数n 而言,包含至少n 个元素的集合。好在可以证明这一属性是每个由正式定义可知无限的集合都具备的,这一证明过程又要用到归纳法。
命题S(n)。如果I 是有限集,那么I具有一个含n 个元素的子集。
依据。设n=0,显然有∅⊆1。
归纳。假设对某个n≥0有S(n)。要证明I有一个含n+1个元素的子集。根据归纳假设,I 有一个含n 个元素的子集T。根据无限集的正式定义,存在某个真子集J⊂I,以及从I 到J 的一一对应f。设a 是I-J 中的元素,因为J 是个真子集,所以a 肯定是存在的。
考虑R,T 在 f 下的镜像,也就是说,若T={b1,…,bn},则R={f (b1),…,f (bn)}。因为f是一一对应,则f (b1),…,f (bn)各不相同,所以R 的大小也为n。因为f 是从I 到J 的,所以每个f (bk)都在J 中,也就是说R⊆J。因此,a 不可能在R 中。这样一来,R∪{a}就是I 含n+1个元素的子集,这证明了S(n+1)。
集合的基数
如果存在从S 到T 的一一对应,就定义两个集合S 和T 是等势的(大小相等)。等势是在任意由集合组成的集合上的等价关系,我们将这一点留作本节习题。集合S 所属的等价类就称作S 的基数。例如,空集属于它自身的等价类,可以用基数0来标识该类。含有集合{a}(其中a 为任意元素)的类是基数1,而含集合{a,b }的类是基数2,等等。
含N的类是“整数的基数”,通常称为阿列夫零(aleph-0),而该类中的集合都是可数集。实数的集合属于另一个通常被称为连续统的等价类。其实,不同的无限基数有无数个。
7.11.2 可数集与不可数集
由示例7.41,我们可能会认为所有无限集都是等势的。我们已经看到整数的集合Z以及非负整数的集合N是同样大小的,还有一些直觉上讲“似乎”比N小的集合也与它大小相同。因为我们在示例7.41中看到,自然数对是与N等势的,而非负有理数也是与自然数等势的,因为有理数是由其分子和分母组成的自然数对。同样,可以证明(非负和负)有理数与整数是等势的,因此也就与自然数是等势的。
对任意集合S 而言,如果存在从S 到N的一一对应,就说该集合是可数的。这里用到术语“可数的”是说得通的,因为S 肯定有一个与0对应的元素,一个与1对应的元素,等等,所以可以“数”S 的成员。我们之前说过的,整数、有理数、偶数,以及自然数对的集合,都是可数集。还有很多其他的可数集,我们在这里把对合适的一一对应的探索留作练习。
不过,也存在不可数的无限集。特别要指出的是,实数就是不可数的。其实,可以证明从0到1之间的实数要比自然数多。论证的关键在于,0到1之间的实数都可以表示为无限长度的小数。我们为小数点右侧的位标记上0、1等编号,如果从0到1之间的实数是可数的,那么可以将它们标记为r0、r1,等等,然后就可以将这些实数排列在一个无限的方阵表格中,如图7-35所示。在假设的从0到1的所有实数的排列中,π/10被分配到第0行,5/9被分配到第1行,5/8被分配到第2行,4/33被分配到第3行,等等。
不过,可以证明图7-35并不能真正表示0到1这个范围内所有实数的列表。我们的证明是被称为对角化的一类过程,要使用表的对角线创造出一个不可能在该实数列表中的值。假设创造一个新实数r,其十进制表示为0.a0a1a2。第i 位的值ai,取决于对角线上的第i 个数字,也就是在第i 个实数的第i 位找到的值。如果该值是0到4,就设ai=8。如果对角线上第i个位置是5到9,那么ai=1。
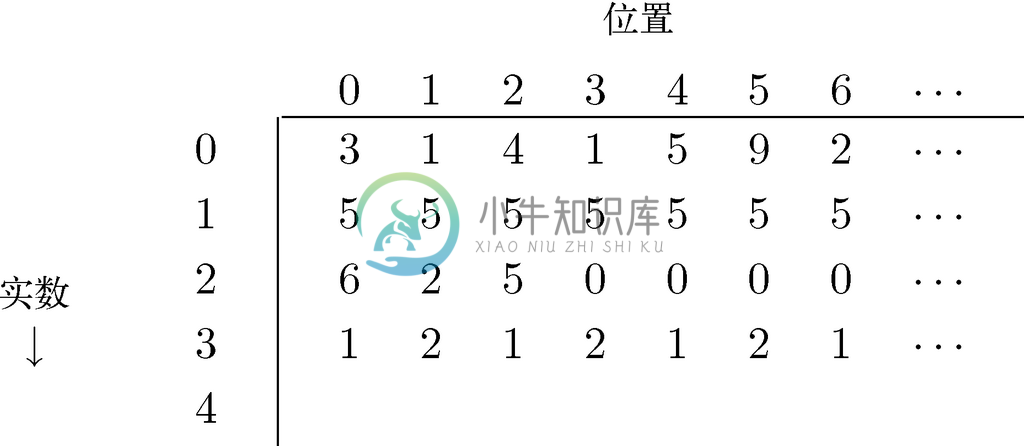
图 7-35 假设实数是可数的,表示实数的假想表格
示例 7.42
给定如图7-35所示的部分表格,我们的实数r是从0.8118…开始的。要知道原因,请注意,0号实数0号位置的值是3,所以a0=8。1号实数1号位置的值是5,所以a1=1。接下来,2号实数2号位置的值是5而3号实数3号位置的值是2,所以接下来的两位数字是18。
我们的主张是,即便假设所有从0到1的实数都在该表中,r也不会出现在这一假想的实数列表中。假设r 是rj,与第 j 行关联的实数。考虑r 与rj 的差d。r 的十进制展开第 j 位数字为aj,我们知道该值是具体选择的,从而与rj 第 j 个位置的数字存在至少为4至多为8的差。因此,第 j 个位置对d 的贡献在4/10j+1到9/10j+1之间。
第 j 位之后的所有位置对 d 的贡献加起来不会超过1/10j+1,因为这就是r 和r 那些位置上一个全为0而另一个全为9时的差。因此,j 及 j 之后的各个位置对d 的贡献在3/10j+1到9/10j+1之间。
最后,在第 j 位之前的位置中,r 和rj 要么是相同的,在这种情况下,前j-1位对d的贡献为0;要么就是r 和r 之间至少存在1/10j 的区别。不管哪种情况,我们都可以看到d 不会为0。因此,r 和rj 不可能是同一个实数。
这样就可以得出r 不在该实数列表中的结论。因此,我们假设的这种从非负实数到从0到1之间实数的一一对应其实不是一对一的。这样就证明了,在0到1的范围内至少存在一个实数r 不与任何整数相关联。
7.11.3 习题
1. 证明等势是一种等价关系。提示:难点在于传递性,要证明如果存在从S 到T 的一一对应f,而且存在从T 到R 的一一对应g,就存在从S 到R 的一一对应。该函数是f 和g 的复合函数,也就是将S 中的x 变为R 中的g(f (x))的函数。
2. 在图7-34所示的有序对次序中,编号为100的有序对是哪个?
3. * 证明以下集合是可数的(在它们和自然数之间存在一一对应)。
(a) 完全平方数的集合。
(b) 自然数三元组(i,j,k)的集合。
(c) 2的乘方的集合。
(d) 自然数有限集组成的集合。
4. ** 证明自然数的幂集P(N)与实数有着相同的基数,也就是说,存在从P(N)到0至1这一范围的实数的一一对应。请注意,这一结论与习题3的(d)小题并不矛盾,因为现在讨论的是整数的有限集和无限集,而我们只能为有限集计数。提示:以下构造几乎能行得通了,不过还需要进行修正。考虑一下任意自然数集合的特征向量。该向量是有限的0和1组成的序列。例如,{0,1}的特征向量是1100…,而含奇数个自然数的集合的特征向量则是010101…。如果在特征向量前加上小数点,就得到了0到1之间的二进制小数,它是表示实数的。因此,每个集合都可以转换为0到1范围内的实数,而且通过将二进制表示转换成特征向量,该范围内的每个实数都可以与一个集合相关联。这种关联不是一一对应的原因在于,某些实数可能会有两种二进制表示。例如,0.11000…和0.10111…都表示实数3/4。不过,这两个二进制小数对应的特征向量表示的是不同的集合,前者表示{0,1},而后者则表示除了1之外的所有整数组成的集合。大家可以修改这种构造以定义一一对应。
5. ** 证明:从0到1范围内的实数组成的有序对到该范围的实数间存在一一对应。提示:要模仿图7-34中的表格是不可能的。不过,我们可以取某个实数对,比方说是(r,s),然后将表示r 和s 的无限小数集合起来,形成唯一的新实数t。t 与r 和s 之间不是以简单的算术表达式相关联的,不过从t,可以唯一地恢复恢复r 和s。大家必须找出一种方式,从r 和s 的十进制展开构建t 的十进制展开。
6. ** 证明:只要集合S包含所有整数大小0,1,…的子集,该集合就是符合“无限集”正式定义的无限集,也就是说,S 与它的一个真子集间存在一一对应。
7.12 小结
大家应该从本章中了解到了以下要点。
集合的概念对数学与计算机科学来说都是基础。
集合的常见运算包括可以用文氏图直观呈现的并集、交集和差集运算。
代数法则可用于处理和简化涉及集合与集合运算的表达式。
链表、特征向量和散列表提供了3种表示集合的基本方式。链表提供了适用于最多集合运算的最佳灵活性,但并非总是最高效的。特征向量对某些集合运算而言有着最快的速度,但只能用于全集规模较小的情况。散列表是通常被选用的方式,兼具表示的经济性与访问的迅速性。
(二元)关系是有序对的集合。函数是对某给定的第一个组分而言至多有一个元组的 关系。
两个集合间的一一对应关系是个函数,它会给第一个集合中的各个元素关联上第二个集合中的唯一元素,反之亦然。
二元关系具有一些重要属性,其中自反性、传递性、对称性和反对称性属于最重要的。
偏序、全序和等价关系是二元关系的重要特例。
无限集是指那些与其某一真子集间存在一一对应关系的集合。
一些无限集是“可数的”,也就是说,它们与整数间存在一一对应的关系。另外一些无限集,比如实数,是不可数的。
在本章中定义的集合和关系上的数据结构与运算还会在本书剩下的部分以多种不同的方式使用。
7.13 参考文献
Halmos [1974]很好地介绍了集合论。散列技术最早是在20世纪50年代诞生的,而Peterson [1957]涵盖了早期的散列技术。Knuth [1973]和Morris [1968]包含了更多有关散列技术的材料。Reingold [1972] 讨论了基本集合运算的计算复杂度。无限集的理论是由 Cantor [1915] 提出的。
Cantor, G. [1915]. “Contributions to the founding of the theory of transfinite numbers,” reprinted by Dover Press, New York.
Halmos, P. R. [1974]. Naive Set Theory, Springer-Verlag, New York.
Knuth, D. E. [1973]. The Art of Computer Programming, Vol. III, Sorting and Searching, Addison-Wesley, Reading, Mass.
Morris, R. [1968]. “Scatter storage techniques,” Comm. ACM 11:1, pp. 35–44.
Peterson, W. W. [1957]. “Addressing for random access storage,” IBM J. Research and Development 1:7, pp. 130–146.
Reingold, E. M. [1972]. “On the optimality of some set algorithms,” J. ACM 19:4,pp. 649–659.

