第 7 章 数据模型范例

下面的章节包括了如何在不同领域使用Neo4j的简单范例。这不是为了给我们完整的范例，而是给我们演示使用节点，关系，图数据模式以及在查询中的数据局部性的可能的方法。

这些范例使用了大量的Cypher查询，要了解更多信息，请参考：cypher-query-lang。

7.1. 在图数据库中的用户角色模型

7.1.1. 得到管理员

7.1.2. 得到一个用户的组成员

7.1.3. 获取所有的用户组

7.1.4. 找到所有用户

这个范例展示了一个角色的等级制度。有趣的是，一棵树是不能足够用于存储这样的结构，下文阐述。

这个范例是 Kemal Erdogan在由撰写的文章 A Model to Represent Directed Acyclic Graphs (DAG) on SQL Databases中的一个实现。这个文章讨论了如何在基于SQL的数据库中存储 directed acyclic graphs(DAGs) 。DAGs很像树结构，但有一点：它们可能通过不同的路径到达相同的节点。从这个来说树结构是被严格限制的，保证他们更容易控制。在我们的这种情况下，它是 "Ali" 和 "Engin"，因为他们是管理员和普通用户因此可以通过他们的组节点到达。现实往往看起来这样而不能被树结构处理。

在文章中一个SQL存储过程提供了一个解决方案。主要的意思就是他们有来自科学家的一些支持，他们能预先计算所有可能的路径。这种方法的优缺点是：

- 提升读性能

- 降低插入性能

- _大量_的空间浪费

- 依赖存储过程

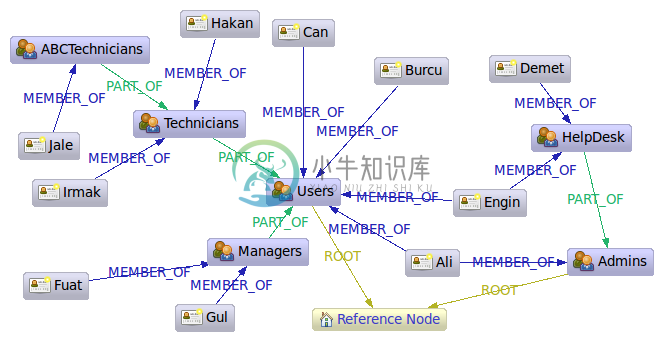
在Neo4j中存储角色是没有价值的。在这种情况下我们使用 PART_OF（绿边）关系来对用户组层次建模而 MEMBER_OF+（蓝边）用来表示组中的成员。我们也把顶级组节点通过关系 +ROOT连接到参考节点（第一个节点）。这提供了一个非常有用的分割方法给我们。Neo4j并没有预先定义关系类型，你可以自由的创建任何关系类型并且赋予他们任何你希望的语义。

现在让我们看下如何从图数据库接收信息。Java代码使用Neo4j遍历相关的API（参考：tutorial-traversal-java-api），查询工具使用cypher-query-lang, Cypher。

7.1.1. 得到管理员

结果是：

结果是从遍历器收集的：

在Cypher中，一个简单的查询如下：

输出结果：

表 . --docbook

7.1.2. 得到一个用户的组成员

使用Neo4j Java遍历API,这个查询像这样：

输出结果：

在Cypher中：

表 . --docbook

7.1.3. 获取所有的用户组

在Java中：

输出结果:

在Cypher中：

表 . --docbook

7.1.4. 找到所有用户

现在，让我们试图找到在系统中属于任何用户组的所有用户。

在Java中：

在Cypher中像这样:

输出结果：

表 . --docbook

使用在Java中比较短的构建和其他查询机制来实现更加复杂语义的查询。

7.2. 在图数据库中的ACL结构模型

这个范例对于在图数据库中控制ACL给了一个通用方法概述，和一个具体查询的简单范例。

7.2.1. 通用方法

在许多场景，一个应用需要控制某些管理对象的安全。这个范例描述了一个管理这些的一个模式，通过在一个图中建立一个对任何管理对象的完整权限结构。这导致产生一个基于位置和管理对象上下文的动态结构。

这个结果是一个很容易正图结构中实现的复杂安全规划。支持权限重载，规则和内容组件，而不用复制数据。

技术

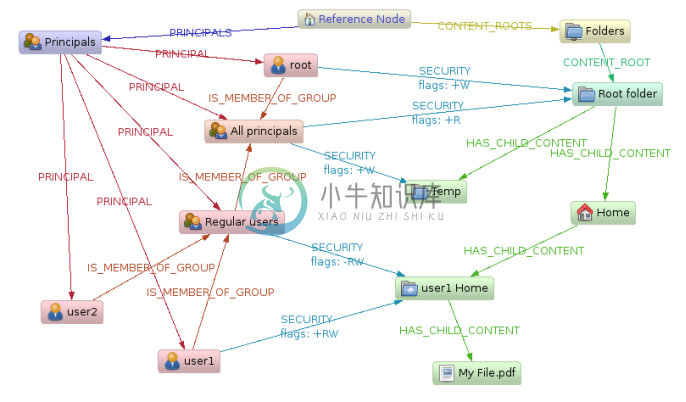
就像范例图布局看到的一样，在这个领域模型中有如下一些要点：

- 管理内容（文件和目录）通过 HAS_CHILD_CONTENT连接

- 主要子树通过 PRINCIPAL关系指出能作为ACL成员的规则

- 规则聚合成组，通过 IS_MEMBER_OF关系连接，我们的规则可以同时属于多个组。

- SECURITY — 一个关系，连接内容组件到规则组件，附带一个可以修改和删除的属性： ("+RW")。

构建ACL

将穿越对于任何给定的ACL管理节点（内容）的有效权限（如读，写，执行）的计算都将遵循一系列被编码的权限遍历的规则。

自顶向下的遍历

这个方案将让你在根内容上面定义一个通用的权限模式，而后提取出指定的子内容节点和指定的规则。

1.从内容节点开始向上移动直到内容根节点以找到它的路径。

2.从一个"所有允许的"有效的乐观权限列表开始（ 111是以BIT位编码表示读写执行情况）。

3.从最上面的内容节点开始，查找在它上面有任何 SECURITY关系的节点。

4.If found, look if the principal in question is part of the end-principal of the SECURITYrelationship.

5.If yes, add the "+" permission modifiers to the existing permission pattern, revoke the "-" permission modifiers from the pattern.

6.If two principal nodes link to the same content node, first apply the more generic prinipals modifiers.

7.Repeat the security modifier search all the way down to the target content node, thus overriding more generic permissions with the set on nodes closer to the target node.

相同的算法也适用于自下而上的方案，基本上只是从目标内容节点向上遍历和在遍历器向上时应用动态安全修饰符。

范例

现在，为了得到访问权限的结果，比如 在文件 "My File.pdf" 上的用户 "user 1" 处于一个自上而下方案中时，在图数据库中的模型应该如下：

1.Traveling upward, we start with "Root folder", and set the permissions to 11initially (only considering Read, Write).

2.There are two SECURITYrelationships to that folder. User 1 is contained in both of them, but "root" is more generic, so apply it first then "All principals" +W+R→ 11.

3."Home" has no SECURITYinstructions, continue.

4."user1 Home" has SECURITY. First apply "Regular Users" (-R-W) → 00, Then "user 1" (+R+W) → 11.

5.The target node "My File.pdf" has no SECURITYmodifiers on it, so the effective permissions for "User 1" on "My File.pdf" are ReadWrite→ 11.

7.2.2. 读取权限范例

在这个范例中，我们将解释一个 directories和 files的树结构。也包括拥有这些文件的用户以及这些用户的角色。角色可以作用于目录或者文件结构上（相对于完整的 rwxUnix权限，这儿我们只考虑 +canRead+），而且可以被继承。一个定义ACL架构的更彻底的范例可以在这找到：如何在SQL中建立基于角色控制的权限系统。

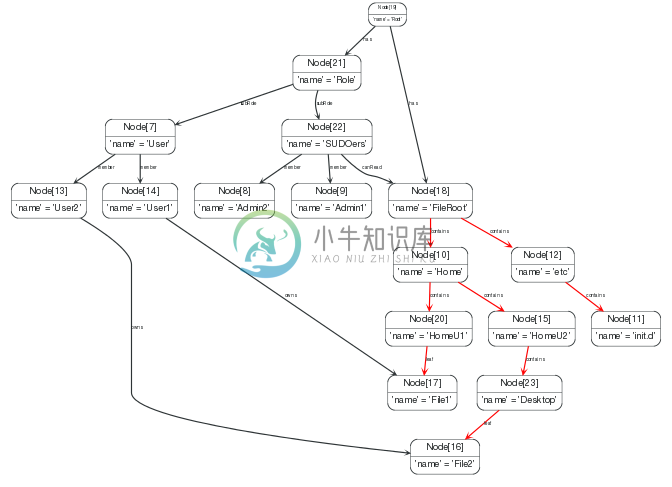
在目录结构中查找所有的文件

为了找到包含正这个结构中的所有文件，我们需要一个可变长度查询，找到跟随了关系 contains的节点，并返回关系 leaf另外一端的节点。

输出结果：

表 . --docbook

谁拥有哪些文件？

如果我们引入了文件的所有权概念，然后我们要求找到我们找到的文件的拥有者 — 通过 owns关系连接到文件节点的。

返回在 FileRoot节点下面的所有文件的拥有者。

表 . --docbook

谁可以访问这个文件？

如果我们现在想检查下哪些有用可以读取所有文件，可以定义我们的ACL如下：

- 根目录授权无法访问。

- 任何用户都被授予了一个角色 canRead，允许访问一个文件的上级目录中任何一个。

为了找到可以读取上面的文件的父文件夹层次结构中的任何部分的用户， Cypher提供了可选的可变长度的路径。

这将返回 file， 拥有 canRead权限的目录，以及 user本身以及他们的 role。

表 . --docbook

这个结果列出了包含 null值的路径片段，它们能通过一些查询来缓解或者只返回真正需要的值。

7.3. 链表

使用图形数据库的强大功能是您可以创建您自己的图形数据结构 — — 喜欢的链接的列表。

此数据结构使用单个节点列表的引用。引用已传出关系到列表，头和传入的关系，从列表中的最后一个元素。如果该列表为空，该引用将指向它自我。就像这样：

Graph

要初始化为空的链接的列表，我们只需创建一个空的节点，并使其链接到本身。

Query

Adding values is done by finding the relationship where the new value should be placed in, and replacing it with a new node, and two relationships to it.

Query

Deleting a value, conversely, is done by finding the node with the value, and the two relationships going in and out from it, and replacing with a new value.

Query

7.4. 超边

假设用户正在不同组的一部分。一个组可以有不同的角色，并且用户可以不同组的一部分。他还可以在不同的组成员除了具有不同的角色。该协会的用户、 组和角色可以称为 HyperEdge。然而，它可以轻松地建模属性图中为捕获此多元的关系，一个节点下面所示的 U1G2R1 节点。

Graph

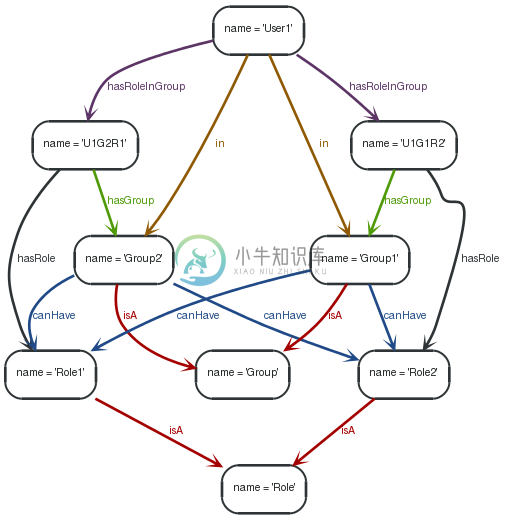
7.4.1. Find Groups

To find out in what roles a user is for a particular groups (here Group2), the following query can traverse this HyperEdge node and provide answers.

Query

The role of User1is returned:

表 . --docbook

7.4.2. Find all groups and roles for a user

Here, find all groups and the roles a user has, sorted by the name of the role.

Query

The groups and roles of User1are returned:

表 . --docbook

7.4.3. Find common groups based on shared roles

Assume a more complicated graph:

1.Two user nodes User1, User2.

2.User1is in Group1, Group2, Group3.

3.User1has Role1, Role2in Group1; Role2, Role3in Group2; Role3, Role4in Group3(hyper edges).

4.User2is in Group1, Group2, Group3.

5.User2has Role2, Role5in Group1; Role3, Role4in Group2; Role5, Role6in Group3(hyper edges).

The graph for this looks like the following (nodes like U1G2R23representing the HyperEdges):

Graph

To return Group1and Group2as User1and User2share at least one common role in these two groups, the query looks like this:

Query

The groups where User1and User2share at least one common role:

表 . --docbook

7.5. 基于社交邻居的朋友查找

Imagine an example graph like the following one:

Graph

To find out the friends of Joe’s friends that are not already his friends, the query looks like this:

Query

This returns a list of friends-of-friends ordered by the number of connections to them, and secondly by their name.

表 . --docbook

7.6. Co-favorited places

Graph

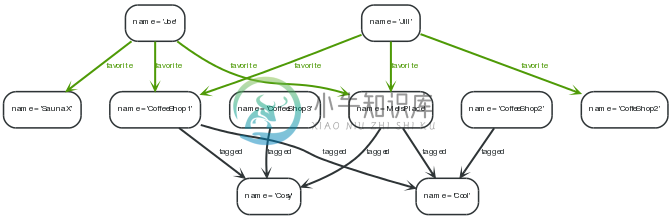
7.6.1. Co-favorited places — users who like x also like y

Find places that people also like who favorite this place:

- Determine who has favorited place x.

- What else have they favorited that is not place x.

Query

The list of places that are favorited by people that favorited the start place.

表 . --docbook

7.6.2. Co-Tagged places — places related through tags

Find places that are tagged with the same tags:

- Determine the tags for place x.

- What else is tagged the same as x that is not x.

Query

This query returns other places than CoffeeShop1 which share the same tags; they are ranked by the number of tags.

表 . --docbook

7.7. Find people based on similar favorites

Graph

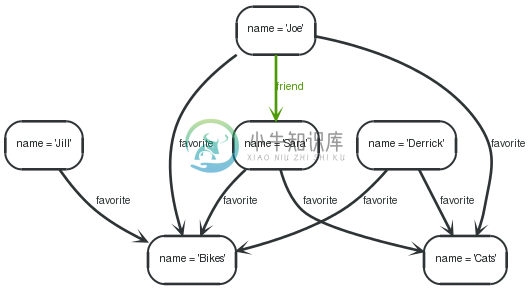
To find out the possible new friends based on them liking similar things as the asking person, use a query like this:

Query

The list of possible friends ranked by them liking similar stuff that are not yet friends is returned.

表 . --docbook

7.8. Find people based on mutual friends and groups

Graph

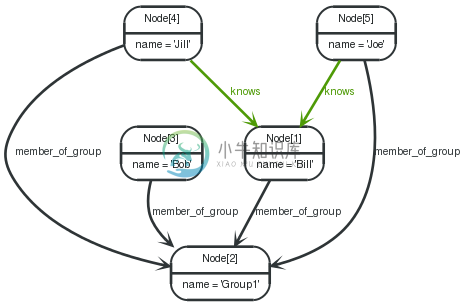
In this scenario, the problem is to determine mutual friends and groups, if any, between persons. If no mutual groups or friends are found, there should be a 0returned.

Query

The question we are asking is — how many unique paths are there between me and Jill, the paths being common group memberships, and common friends. If the paths are mandatory, no results will be returned if me and Bob lack any common friends, and we don’t want that. To make a path optional, you have to make at least one of it’s relationships optional. That makes the whole path optional.

表 . --docbook

7.9. Find friends based on similar tagging

Graph

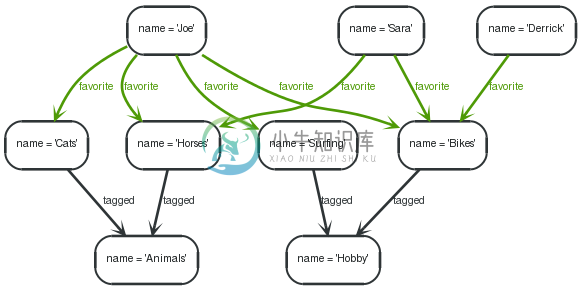
To find people similar to me based on the taggings of their favorited items, one approach could be:

- Determine the tags associated with what I favorite.

- What else is tagged with those tags?

- Who favorites items tagged with the same tags?

- Sort the result by how many of the same things these people like.

Query

The query returns the list of possible friends ranked by them liking similar stuff that are not yet friends.

表 . --docbook

7.10. Multirelational (social) graphs

Graph

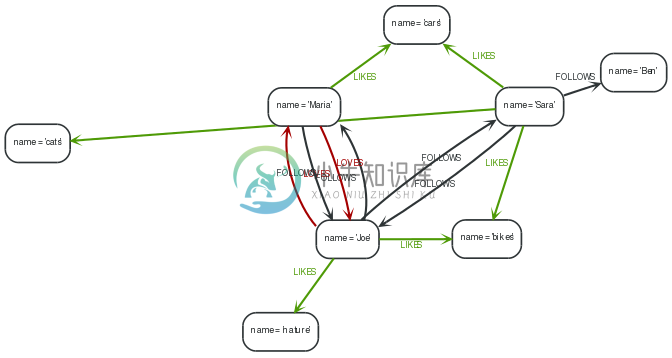
This example shows a multi-relational network between persons and things they like. A multi-relational graph is a graph with more than one kind of relationship between nodes.

Query

The query returns people that FOLLOWSor LOVESJoeback.

表 . --docbook

7.11. Boosting recommendation results

Graph

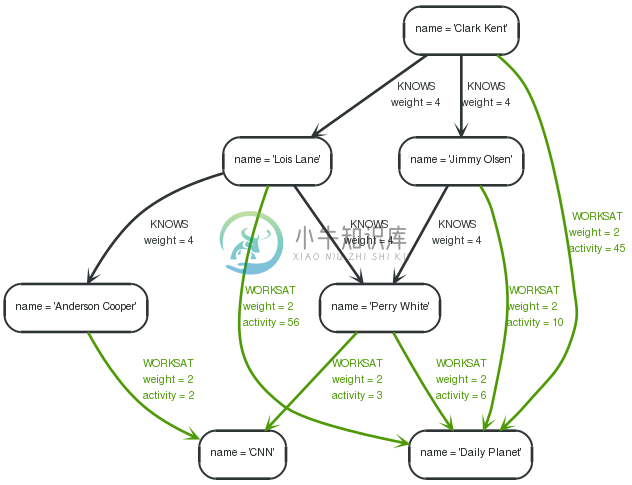
This query finds the recommended friends for the origin that are working at the same place as the origin, or know a person that the origin knows, also, the origin should not already know the target. This recommendation is weighted for the weight of the relationship r2, and boosted with a factor of 2, if there is an activity-property on that relationship

Query

This returns the recommended friends for the origin nodes and their recommendation score.

表 . --docbook

7.12. Calculating the clustering coefficient of a network

Graph

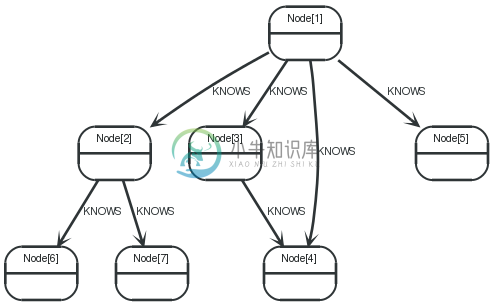
In this example, adapted from Niko Gamulins blog post on Neo4j for Social Network Analysis, the graph in question is showing the 2-hop relationships of a sample person as nodes with KNOWSrelationships.

The clustering coefficientof a selected node is defined as the probability that two randomly selected neighbors are connected to each other. With the number of neighbors as nand the number of mutual connections between the neighbors rthe calculation is:

The number of possible connections between two neighbors is n!/(2!(n-2)!) = 4!/(2!(4-2)!) = 24/4 = 6, where nis the number of neighbors n = 4and the actual number rof connections is 1. Therefore the clustering coefficient of node 1 is 1/6.

nand rare quite simple to retrieve via the following query:

Query

This returns nand rfor the above calculations.

表 . --docbook

7.13. Pretty graphs

7.13.1. Star graph

7.13.2. Wheel graph

7.13.3. Complete graph

7.13.4. Friendship graph

This section is showing how to create some of the named pretty graphs on Wikipedia.

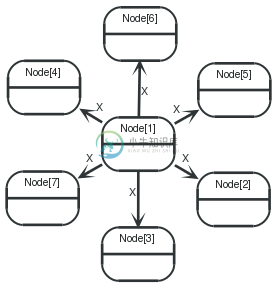
7.13.1. Star graph

The graph is created by first creating a center node, and then once per element in the range, creates a leaf node and connects it to the center.

Query

The query returns the id of the center node.

表 . --docbook

Graph

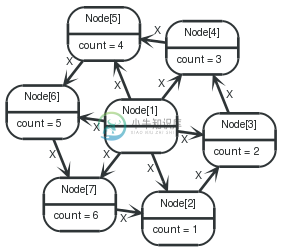
7.13.2. Wheel graph

This graph is created in a number of steps:

- Create a center node.

- Once per element in the range, create a leaf and connect it to the center.

- Select 2 leafs from the center node and connect them.

- Find the minimum and maximum leaf and connect these.

- Return the id of the center node.

Query

The query returns the id of the center node.

表 . --docbook

Graph

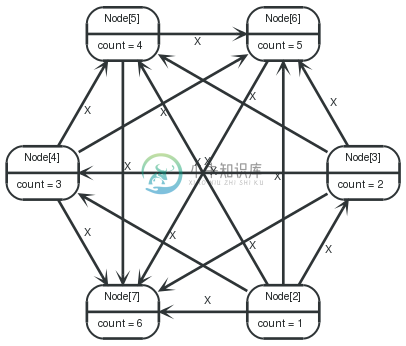
7.13.3. Complete graph

For this graph, a root node is created, and used to hang a number of nodes from. Then, two nodes are selected, hanging from the center, with the requirement that the id of the first is less than the id of the next. This is to prevent double relationships and self relationships. Using said match, relationships between all these nodes are created. Lastly, the center node and all relationships connected to it are removed.

Query

Nothing is returned by this query.

表 . --docbook

Graph

7.13.4. Friendship graph

This query first creates a center node, and then once per element in the range, creates a cycle graph and connects it to the center

Query

The id of the center node is returned by the query.

表 . --docbook

Graph

7.14. A multilevel indexing structure (path tree)

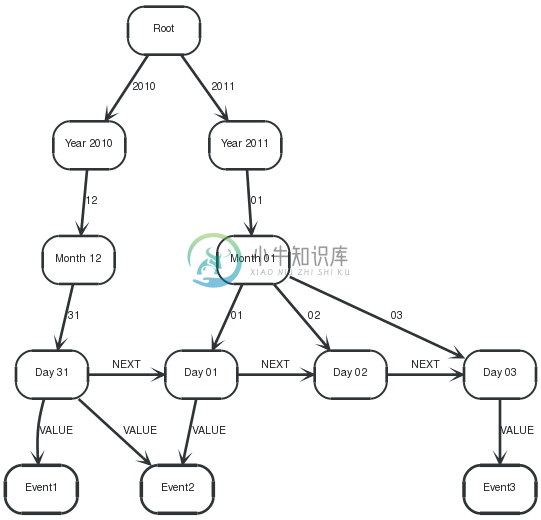
In this example, a multi-level tree structure is used to index event nodes (here Event1, Event2and Event3, in this case with a YEAR-MONTH-DAY granularity, making this a timeline indexing structure. However, this approach should work for a wide range of multi-level ranges.

The structure follows a couple of rules:

- Events can be indexed multiple times by connecting the indexing structure leafs with the events via a VALUErelationship.

- The querying is done in a path-range fashion. That is, the start- and end path from the indexing root to the start and end leafs in the tree are calculated

- Using Cypher, the queries following different strategies can be expressed as path sections and put together using one single query.

The graph below depicts a structure with 3 Events being attached to an index structure at different leafs.

Graph

7.14.1. Return zero range

Here, only the events indexed under one leaf (2010-12-31) are returned. The query only needs one path segment rootPath(color Green) through the index.

Graph

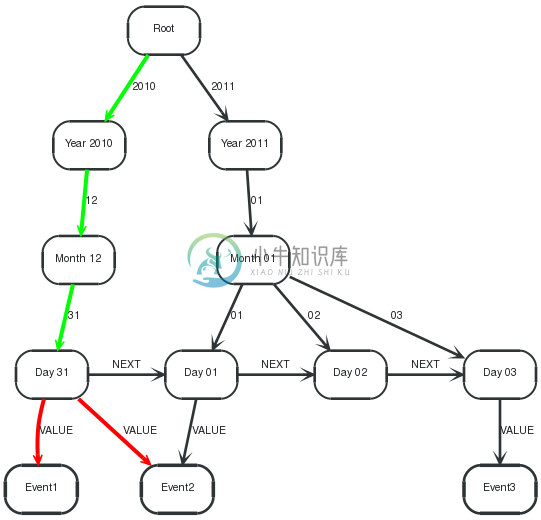
Query

Returning all events on the date 2010-12-31, in this case Event1and Event2

表 . --docbook

7.14.2. Return the full range

In this case, the range goes from the first to the last leaf of the index tree. Here, startPath(color Greenyellow) and endPath(color Green) span up the range, valuePath(color Blue) is then connecting the leafs, and the values can be read from the middlenode, hanging off the values(color Red) path.

Graph

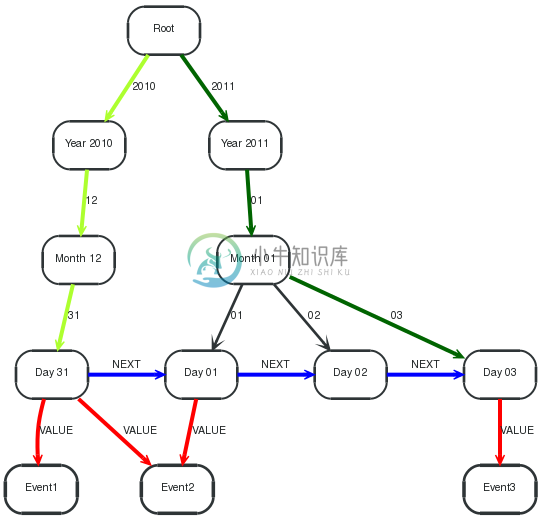
Query

Returning all events between 2010-12-31 and 2011-01-03, in this case all events.

表 . --docbook

7.14.3. Return partly shared path ranges

Here, the query range results in partly shared paths when querying the index, making the introduction of and common path segment commonPath(color Black) necessary, before spanning up startPath(color Greenyellow) and endPath(color Darkgreen) . After that, valuePath(color Blue) connects the leafs and the indexed values are returned off values(color Red) path.

Graph

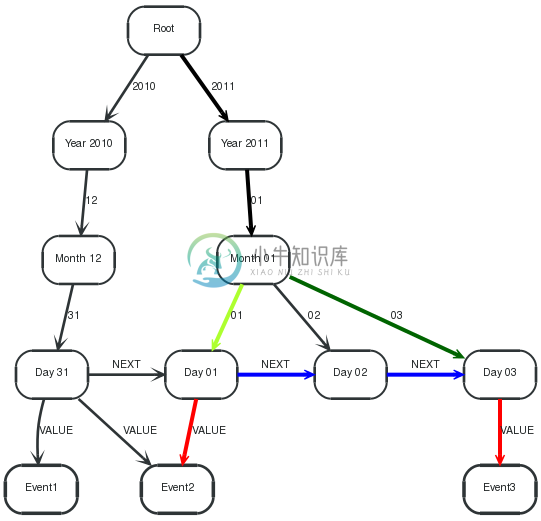
Query

Returning all events between 2011-01-01 and 2011-01-03, in this case Event2and Event3.

表 . --docbook

7.15. Complex similarity computations

7.15.1. Calculate similarities by complex calculations

7.15.1. Calculate similarities by complex calculations

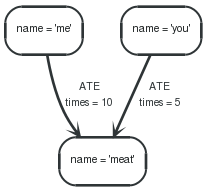
Here, a similarity between two players in a game is calculated by the number of times they have eaten the same food.

Query

The two players and their similarity measure.

表 . --docbook

Graph