第 6 章　表数据模型

优质

小牛编辑

116浏览

2023-12-01

和树一样，表也是计算机程序中最基础的数据模型之一。从某种意义上讲，表就是树的简化形式，因为大家可以将表视为每个左子节点都是叶子节点的二叉树。不过，表还能表示其他一些方面，这些方面与我们之前了解的关于树的那些情况不同。例如，我们将要谈论对表的操作，比如压入和弹出，这是没法用树来模拟的；而且要探讨字符串，这种特殊而重要的表需要它们自己的数据结构。

6.1　本章主要内容

6.2节介绍了与表有关的术语。本章其余部分将介绍以下主题。

表的基本操作（6.3节）。
由链表数据结构（6.4节）和数组数据结构（6.5节）实现的抽象表。
栈：只能从一端插入和删除的表（6.6节）。
队列：从一端插入从另一端删除的表（6.8节）。
字符串和用来表示字符串的特殊数据结构（6.10节）。

此外，我们还将详细研究表的两类应用。

运行时栈，C语言以及其他多种语言用来实现递归函数的方法（6.7节）。
找出两个字符串最长公共子序列的问题，及其通过“动态规划”（或者说填表）算法得出的解决方案（6.9节）。

6.2　基本术语

表是由0个或多个元素组成的有限序列。如果这些元素全是T 类型的，那么就说该类型的表是“T 表”。因此，就有整数表、实数表、结构体表、整数表的表，等等。一般可以预期列表的元素都是某一类型的。不过，因为一种类型可以是多种类型的联合，所以单一“类型”的限制是可以绕开的。

表通常表示为用逗号分隔表中各元素，并用一对圆括号将这些元素括起来，如

(a₁,a₂,…,a_n)

其中a_i 都是表中的元素。

在某些情况下，我们将不会把逗号和括号写出来。特别要说的是，我们将要研究字符串，也就是由字符组成的表。字符串一般不会写上逗号或其他分隔符号，而且不会用括号括起来。字符串的元素通常都是用等宽字体表示的。foo就是由3个字符组成的表，其中第一个字符为f，而第二和第三个字符都是o。

示例 6.1

下面是一些表的例子。

1. 小于20的质数按照从小到大的顺序组成的表：

(2，3，5，7，11，13，17，19)

2. 稀有气体元素按照原子量从小到大的顺序排列组成的表：

(氦，氖，氩，氪，氙，氡)

3. 平年各月天数组成的表：

(31，28，31，30，31，30，31，31，30，31，30，31)

这个例子提醒我们，同一元素可以在某个表中出现多次。

示例 6.2

一行文本是表的另一个例子。组成这行文本的单个字符就是表中的元素，所以该表就是个字符串。该字符串通常会包含若干空字符，而且一行文本的最后一个字符通常是“换行”符。

再举一个例子，文档也可视作表。这种情况下，表中的元素就是文本行。因此，文档就是由表作为元素组成的表，具体说来这些作为元素的表都是字符串。

示例 6.3

n 维空间中的点可以表示为由n 个实数构成的表。例如，单位正方体的顶点可以表示为图6-1所示的三元组。各表中的3个元素表示作为正方体8个角（“顶点”）之一的点的坐标。第一个元素表示x 坐标（水平方向），第二个表示y 坐标（向页内方向），第三个表示z 坐标（垂直方向）。

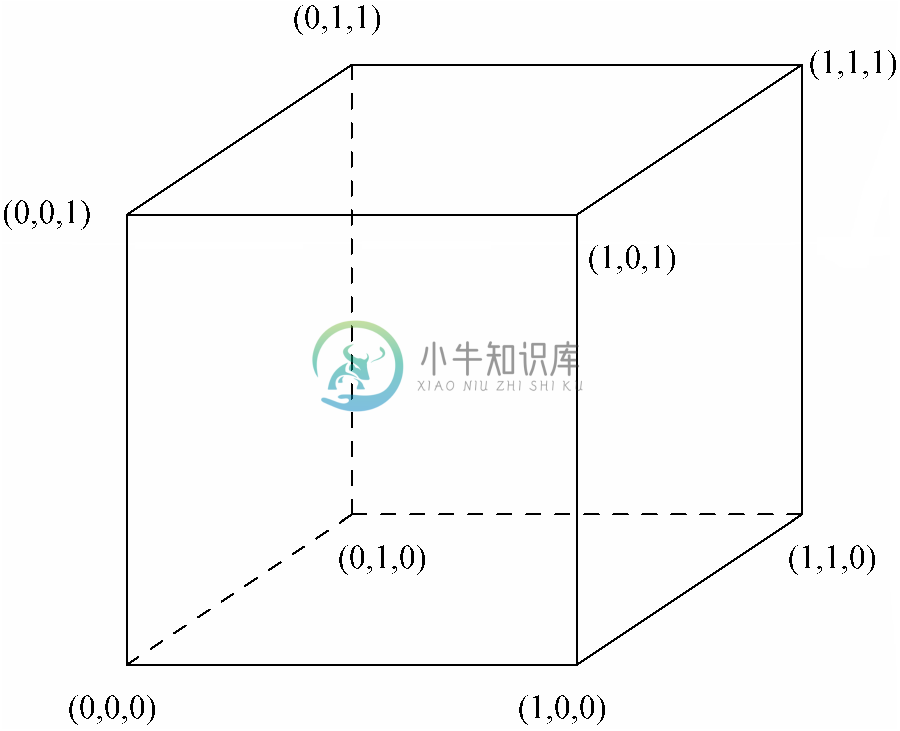
图 6-1　表示为三元组的单位正方体顶点

6.2.1　表的长度

表的长度是指元素在表中出现的次数。如果表中元素数为0，那么就说该表为空表。我们用希腊字母ε（音“伊普西龙”）表示空表。还可以用一对不包含任何内容的圆括号()表示空表。谨记，长度是按位置计算而不是按不同符号计算的，所以在表中出现k 次的某一符号可以为表增加长度k 。

示例 6.4

示例6.1中表(1)的长度是8，而表(2)的长度是6。表(3)的长度为12，因为每个月都要占据一个位置。而表中只有3个元素这一事实对表的长度来说是无关紧要的。

6.2.2　表的部分

如果表非空，那么它就是由称为表头（head）的第一个元素，以及称为尾部（tail）的表中其余部分组成的。例如，示例6.1中表(2)的表头就是“氦”，而该表的尾部则由其余5个元素组成：

(氖，氩，氪，氙，氡)

元素和长度为1的表
谨记，表的表头是个元素，而表的尾部却是表。此外，我们不应该将表的表头（假如为a）与只包含一个元素a 的长度为1的表（通常会写为带括号的(a)）混淆。如果元素a 是T 类型的，那么表(a)就是“T 表”类型的。
如果不能认识到这种区别，就可能在用数据结构实现表时造成编程错误。例如，我们可以用互相链接的单元表示表，这些单元通常是结构体，具有存放T 类型元素的element字段，以及存放指向下一单元的指针的next字段。那么元素a 就是T 类型的，而表(a)则是具有存放着a的element字段和存放着NULL的next字段的单元。

如果有表L=(a₁,a₂,…,a_n)，则对满足1≤i≤j≤n 的i 和 j 来说，(a_i ,a_i+1,…,a_j )是L 的子表。也就是说，子表是由从某个位置i 开始到某个位置j 结束的所有元素组成的。还可以说空表ε 是任何表的子表。

表L=(a₁,a₂,…,a_n)的子序列是指从L 中剔除0个或多个元素后形成的表。剩下的这些元素，也就是构成子序列的这些元素，必须按照与出现在L 中相同的顺序排列，不过子序列的元素在L 中不一定是连续的。请注意，ε 和表L 本身总是L 的子序列，而且L 的子表也是L 的子序列。

示例 6.5

设L 是字符串abc，那么L 的子表有

ε，a，b，c，ab，bc，abc

它们也都是L 的子序列。除此之外，ac也是子序列，但它不是子表。

再举个例子，设L 是字符串abab，那么子表就有

ε，a，b，ab，ba，aba，bab，abab

这些也是L 的子序列。除此之外，L 还有子序列aa，bb，aab，abb。请注意，bba这样的字符串不是L 的子序列。即便L中确实有两个b和一个a，但它们在L 中出现的顺序，不能让我们通过从L 中剔除某些元素构成bba。也就是说，在L 中，第二个b后面是没有a的。

表前缀是指从表的开头开始的任意子表。表后缀则是以表的结尾为末尾的子表。空表ε 是种特殊情况，它是任意表的前缀和后缀。

示例 6.6

表的前缀有ε，a，ab和abc，而它的后缀是ε，c，bc和abc。

Car和Cdr
在Lisp语言中，表头叫作car，而尾部则称为cdr（音“cudder”）。术语“car ”和“cdr ”的名字来源于IBM 709型计算机中机器指令的两个字段，Lisp最早就是在该型计算机上实现的。car表示“contents of the address register”（地址寄存器的内容），而cdr则表示“contents of the decrement register”（减量寄存器的内容）。某种意义上讲，存储字（memory word）可以视为有着element和next字段（分别对应car和cdr）的单元。

6.2.3　表中元素的位置

表中的每个元素都有与之关联的位置。如果有表(a₁,a₂,…,a_n)，而且n≥1，a₁就是第一个元素，a₂就是第二个元素，以此类推，而a_n 则是最后一个元素。还可以说a_i 出现在位置i。除此之外，a_i 是在a_i-1之后，在a_i+1之前。而存放元素a 的位置则称作a 的出现。

表中位置的数量就等于表的长度。同一元素是有可能出现在两个或多个位置的，因此不要把位置和出现在该位置的元素弄混了。例如，示例6.1中的表(3)就有12个位置，其中有7个存放着31，分别是位置1、3、5、7、8、10和12。

6.2.4　习题

1. 针对表(2，7，1，8，2)回答以下问题。

(a) 它的长度是多少？

(b) 它的前缀有哪些？

(d) 它的子表有哪些？

(e) 它有多少个子序列？

(f) 它的表头是什么？

(g) 它的尾部是什么？

(h) 它包含多少个位置？

2. 对字符串banana重复习题1中的练习。

3. ** 在长度为n≥0的表中，最多可能有多少(a)前缀；(b)子表；(c)子序列？而最少又分别可能有多少？

4. 如果表L 尾部的尾部是空表，那么L 的长度为多少？

5. * 胡图写了个由整数表组成的表，不过他省略了括号，结果成了：1，2，3。而这可以表示很多由表组成的表，比如((1),(2,3))。那么在不含空表作为元素的情况下，所有可能的表都有哪些？

6.3　对表的操作

可以对表执行多种不同的操作。第2章中，当我们讨论归并排序时，基本问题就是为表排序，不过我们还需要将表一分为二，再合并两个已排序的表。从形式上讲，为表(a₁,a₂,…,a_n)排序的操作就是将表替换为由其元素的排列组成的表(b₁,b₂,…,b_n)，其中b₁≤b₂≤…≤b_n。这里就像之前一样，≤表示元素的次序关系，比如整数或实数的“小于或等于”，或是字符串的词典次序。合并两个已排序表的操作是用给定的两个表构建一个包含其中相同元素的已排序表。多重性必须得到保持，也就是说，如果某个元素a 在给定的两个表中出现了k 次，那么得出的表中a 也出现k 次。回顾2.8节就能看到对表的这两种操作的示例。

6.3.1　插入、删除和查找

回想一下5.7节，“词典”是可以对其执行插入、删除和查找操作的元素集合。集合与表之间存在一个重要区别。虽然元素在集合中绝不能出现多次，但正如我们所见，元素在表中可出现多次。集合的问题将在第7章中讨论。不过，表可以实现集合，其方式是将集合{a₁,a₂,…,a_n}中的元素以任意次序放置到表中，例如次序(a₁,a₂,…,a_n)，或次序(a_n,a_n-1,…,a₁)。因此，如果一些对表的操作与对集合的词典操作类似，应该不会让人感到奇怪。

1. 可以向表L 中插入元素x。从原则上讲，x 可能出现在表中任何位置，而且x 在L 中出现一次或多次都是没关系的。我们通过在表中增加一次x的出现来插入x。作为一种特例，如果让x 作为新表的表头（这样一来L 就成了尾部），就是将x 压入表L 中。如果L=(a₁,a₂,…,a_n)，那么得到的表就是(x,a₁,a₂,…,a_n)。

2. 可以从表L 中删除元素x。这里，是从L 中删除x 的一次出现。如果x 出现多次，那么就要指出删除哪个x。例如，我们可以总是删除第一个x。如果想要删除所有的x，就要重复删除操作，直到不再剩下x 为止。如果表L 中未出现x，那么删除操作就不会造成任何影响。作为特例，如果是删除了表的表头元素，使表(x,a₁,a₂,…,a_n)变成了(a₁,a₂,…,a_n)，就说是弹出表。

3. 可以在表L 中查找元素x。这一操作会返回TRUE或FALSE，具体取决于x 是否为表中元素。

示例 6.7

设L 为表(1，2，3，2)。如果我们选择压入1，也就是将1插入到表头位置，则insert (1，L )的结果是(1，1，2，3，2)。而若是将1插入到末尾，就得到(1，2，3，2，1)。此外，这个新的1还可以被放置到表L 内部3个位置中的任何一个上。

如果删除表中第一个2，那么deletemax (2，L )的结果是表(1，3，2)。若问lookup (x，L )，则当x为1、2或3时，答案为TRUE，而当x 为其他值时，答案为FALSE。

6.3.2　串接

要串接表L 和表M，就是以L 的元素作为开头部分，后面接上M 的元素形成新表。也就是说，如果L=(a₁,a₂,…,a_n)，而M=(b₁,b₂,…,b_k)，那么L 和M 的串接LM 就是表

(a₁,a₂,…,a_n ,b₁,b₂,…,b_k )

请注意，空表是串接恒等的。也就是说，对任何表L 都有εL=Lε=L。

示例 6.8

如果L 是表(1，2，3)，M 是表(3，1)，那LM 就是表(1，2，3，3，1)。如果L 是字符串dog，而M 是字符串house，那LM 就是字符串doghouse。

6.3.3　表的其他操作

另一类对表的操作是与表的特定位置相关的。例如

(a) first (L )会返回表L 的第一个元素（表头），而first (L )会返回L 的最后一个元素。如果L 是空表，则这两种操作都会导致错误出现。

(b) retrieve (i，L )操作会返回表L 中第i 个位置处的元素。如果L 的长度小于i，就会出错。

除此之外，还有涉及表的长度的操作。常见的包括下列两种。

(d) isEmpty (L )，如果L 为空表则返回TRUE，否则返回FALSE。而isNotEmpty (L )会返回相反的结果。

6.3.4　习题

1. 设L 是表(3，1，4，1，5，9)，回答下列问题。

(a) delete (5，L )的值是多少？

(b) delete (1，L )的值是多少？

(d) 将2压入表L 的结果是什么？

(e) 如果以元素6和表L 执行lookup，会返回什么？

(f) 如果M 是表(6，7，8)，那么LM（L 和M 的串接）的值是多少？ML 的值又是多少？

(g) first (L )是多少？last (L )又是多少？

(h) retrieve (3，L )的结果是多少？

(i) flengh (L )的值是多少？

(j) isEmpty (L )的值是多少？

2. ** 如果L 和M 是表，在什么条件下有LM=ML？

3. ** 设x 是元素而L 是表，那么在什么条件下以下等式为真？

(a) delete (x，insert (x，L ))=L

(b) insert (x，delete (x，L ))=L

(d) last (L )=retrieve (length (L )，L )

6.4　链表数据结构

实现表的最简单方式就是使用链表。每个链表单元都由两个字段构成，一个字段包含着表中的元素，另一个字段则含有指向链表下一单元的指针。简单起见，假设元素都是整数。我们不仅能使用具体的int类型来表示元素的类型，而且能用==、<等标准比较运算符来比较元素。本节习题将会启发读者编写这些函数的变体，使其能处理任意类型的元素，而元素的比较则是由用户定义的函数进行的，比如测试相等性的eq，及测试x 在次序上是否先于y 的lt (x,y )，等等。

接下来，要使用来自1.6节中的宏：

DefCell(int, CELL, LIST);

它可展开为表示单元和表的标准结构体

typedef struct CELL *LIST;
struct CELL {
    int element;
    LIST next;
};

请注意，LIST是指向单元的指针类型。实际上，每个单元的next字段既指向下一个单元，也指向表中剩余的所有部分。

图6-2展示了表示抽象表L=(a₁,a₂,…,a_n)的链表。每个单元都对应一个元素，元素a_i 出现在第i 个单元的element字段。对i=1,2,…,n-1而言，第i 个单元中的指针是指向第i+1个单元的，而最后一个单元中的指针为NULL，表示这是表的末尾。在表之外是个名为L的指针，它指向该表的第一个单元，L是LIST类型的。如果表L 为空，L的值就为NULL。

{%}

图 6-2　表示表L=(a₁,a₂,…,a_n )的链表

表和链表
请记住，表是一种抽象模型，或者说是数学模型。而链表则是种简单的数据结构，这在第1章中提到过。虽然链表是实现表数据模型的一种方式，但正如我们所见，它并非实现表数据模型的唯一方式。无论如何，这是再次记住模型与实现模型的数据结构之间区别的良好时机。

6.4.1　词典操作的链表实现

如果用链表表示词典，那么该如何实现操作？以下对词典的操作是在5.7节中定义的。

1. insert (x，D )，将元素x 插入词典D 中；

2. delete (x，D )，从词典D 中删除元素x；

3. lookup (x，D )，确定元素x 是否在词典D 中。

我们将看到，与之前章节中讨论过的二叉查找树相比，链表是一种更为简单的实现词典的数据结构。不过，在使用链表表示时，词典操作的运行时间不像使用二叉查找树时那么少。在第7章中还将看到一种更佳的表示词典的方式——散列表，它利用对表的词典操作作为子例程。

这里假设我们的词典包含的是整数，而且单元是按照本节开头那样定义的。那么词典的类型就是LIST，也是像本节开头那样定义的。含有元素集合{a₁,a₂,…,a_n}的词典可以用图6-2中的链表表示。还有很多其他的表可以表示这一集合，因为元素的次序在集合中是无关紧要的。

6.4.2　查找

要执行lookup(x，D )，就要对表示D 的表中的每个单元加以检验，看看它是否存放了所需的元素x。如果是，就返回TRUE。如果到达表末仍未发现x，就返回FALSE。一如之前那样，定义的常量TRUE和FALSE表示常数1和0，BOOLEAN则表示定义的类型int。递归函数lookup(x,D)如图6-3所示。

如果表的长度为n，就说图6-3中的函数所花的时间为O(n)。除了结尾的递归调用外，lookup花的时间是O(1)。当调用执行之后，剩余的表的长度要比表L 的长度小1。因此对长度为n 的表执行lookup要花上O(n)的时间应该不会让人感到意外。更加正式地讲，以下递推关系给出了当第二个参数指向的表L 长度为n 时lookup的运行时间。

BOOLEAN lookup(int x, LIST L)
{
    if (L == NULL)
        return FALSE;
    else if (x == L->element)
        return TRUE;
    else
        return lookup(x, L->next);
}

图 6-3　在链表中查找

依据。T₀.=O(1)，因为当L 为NULL时，没有进行递归调用。

归纳。T(n)=T(n-1)+O(1)。

正如我们在第3章中见过很多次，这一递推关系的解是T(n)=O(n)。因为含n 个元素的词典是用长度为n 的表表示的，所以对大小为n 的词典执行查找操作所花的时间也是O(n)。

不幸的是，进行一次成功查找的平均时间也与n 成比例。如果要查找的元素x 确定在D 中，那么x 在表中位置的期望值为(n+1)/2。也就是说，x 会等可能地出现在从第一个元素到第n 个元素中的任一位置。因此，递归调用lookup的次数的期望值是(n+1)/2。因为每次调用所花的时间是O(1)，所以平均成功查找所花的时间为O (n )。当然，如果查找不成功，那么在到达表末并返回FALSE之前，已经进行了全部n 次调用。

6.4.3　删除

从链表中删除元素x 的函数如图6-4所示。第二个参数pL是指向表L 的指针，而不是表L 本身。这里使用了“按引用调用”的风格，因为我们希望delete可以从表中删除含有x 的单元。随着我们沿着表向下移动，pL中存放着一个指针，它指向的是指向“当前”单元的指针。如果在第(2)行发现x 在当前单元C 中，就接着在第(3)行改变指向单元C 的指针，使得它指向该表中紧跟在C 之后的那个单元。如果C 正好在表的末尾，之前指向C 的指针就成了NULL。如果x 不是当前的元素，那么在第(4)行就递归地从表尾删除x。

请注意，如果表为空表，那么第(1)行的测试会使该函数在没有任何动作的情况下返回。这是因为x 不会出现在空表中，而我们不需要采取任何措施来从词典中删除x。如果D 是表示词典的链表，那么调用delete(x,&D)就会初始化从词典D 中删除x 的操作。

     void delete(int x, LIST *pL)
     {
(1)      if ((*pL) != NULL)
(2)          if (x == (*pL)->element)
(3)              (*pL) = (*pL)->next;
             else
(4)              delete(x, &((*pL)->next));
     }

图 6-4　删除元素

如果元素x 没有出现在表示词典D 的链表中，那么就会继续向下运行直到表的末端，为每个元素花上O(1)的时间。分析过程类似对图6-3中lookup函数的分析，这里就将细节留给读者自己来分析吧。因此，如果D 有n 个元素，那么删除不在D 中的元素所花的时间是O(n)。如果x 在词典D 中，那么平均下来，将会在表中接近中点的位置遇到x。因此，平均要查找(n+1)/2个单元，而成功删除操作的运行时间也是O(n)。

6.4.4　插入

向链表中插入元素x 的函数如图6-5所示。要插入x，需要确定x 没有出现在表中。如果它已经在表中，就什么都不用做。如果x 未出现，就必须将其添加到表中。将x 添加到表中的什么位置并不重要，不过图6-5中的函数是将x 添加到表的末尾。在第(1)行检测到末尾的NULL时，就确定x 不在表中。那么，第(2)到第(4)行就会将x 添加到表尾。

如果表非NULL，第(5)行就会检查x 是否在当前单元。如果x 不在这里，第(6)行就会对表的尾部进行递归调用。如果在第(5)行就找到x，那么函数insert就会终止，不进行任何递归调用，而且不会对表L 造成任何改变。调用insert(x,&D)会初始化将x 插入词典D 的操作。

     void insert(int x, LIST *pL)
     {
(1)      if ((*pL) == NULL) {
(2)          (*pL) = (LIST) malloc(sizeof(struct CELL));
(3)          (*pL)->element = x;
(4)          (*pL)->next = NULL;
         }
(5)      else if (x != (*pL)->element)
(6)          insert(x, &((*pL)->next));
     }

图 6-5　元素的插入

与查找和删除的情况一样，如果在表中没有找到x，就会到达表的末端，花费O(n)的时间。如果找到x，那么平均会走过表中一半1的位置，而且平均而言仍会花O(n)的时间。

1在后面的分析中，当说到长度为n的表的中点时，将会使用“一半”或“n/2”这样的说法。严格地说，(n+1)/2要更加精确。

6.4.5　带重复的插入、查找和删除

如果在执行插入操作之前不检查x是否出现在表中，可以让插入操作运行得更快。不过，这样做的后果就是，在表示词典的表中可能有某一元素的多个副本。

要执行词典操作insert (x，D )，只要创建一个新单元，将x放进去，并将该单元压入表示D 的表的开头即可。这一操作花费O(1)的时间。

查找操作就和图6-3中所示的一模一样。唯一的不便就是可能要查找更长的表，因为表示词典D 的表的长度可能会大于D 中的成员数。

重提抽象和实现
大家可能会感到惊讶，我们在表示词典的表中使用了重复，因为抽象数据类型DICTIONARY被定义为集合，而集合是不含重复的。不过，有重复的并不是词典，而实现词典的数据结构可以有重复。但是，即便当x在链表中多次现身，它在链表表示的词典中也只会出现一次。

删除操作稍有区别。在遇到含有元素x 的单元时，我们不能停止对x 的查找，因为表中可能还有x 的其他副本。因此，就算表L 的表头包含x，也必须将x 从L 的尾部删除。这样一来，我们不只要处理更长的表，而且要实现成功的删除操作，就必须查找每个单元，而不像表中不允许出现重复的情况时那样是平均查找表的一半。这些带重复的词典操作的细节就留作本节习题了。

总之，通过允许重复，可以让插入操作变得更快，时间是O(1)而不是O(n)。不过，成功的删除操作需要对整个表进行查找，而不是平均查找一半列表。而且对于查找和删除，必须要处理比不允许重复时更长的表，虽然长多少取决于插入词典中已存在元素的频率有多高。

要选择哪种方法是有点技巧的。显然，如果插入操作占主导地位，就应该允许重复。在极端情况下，如果只插入而从不查找或删除，就能让每次操作具有O(1)（而不是O(n)）的性能。2如果有理由确定从不会插入词典中已存在的元素，就可以使用快速插入和快速删除，那样只要找到待删除元素的一次出现就可以停下了。另一方面，如果有可能插入重复的元素，而且查找或删除又占主导地位，那么在插入x 之前最好还是先检查一下它是否已经存在于表中，就如图6-5所示的insert函数那样。

2如果从来都不管词典中有什么，还干嘛费事往里面插东西呢？

6.4.6　表示词典的已排序表

另一种方案是让表示词典D 的表中的元素一直按照递增次序排好序。然后，如果希望查找元素x，只要行进到x 可能出现的位置就行了，平均而言，也就是表的中间位置。如果遇到大于x 的元素，就说明在后面的部分没希望找到x 了。因此就不用沿着表行进以继续进行失败的查找了。这样做可以节省为2的因数（开销变为一半），不过确切的因数是有些模糊的，因为在表中每遇到一个元素就必须询问按照排序次序x 是否在其之后。不过，在进行插入和删除操作时，在不成功的查找上也能节约同样的开销。

用于已排序表的查找函数如图6-6所示。把图6-4和图6-5所示函数修改为处理已排序表的版本的工作就留作本节习题了。

BOOLEAN lookup(int x, LIST L)
{
    if (L == NULL)
        return FALSE;
    else if (x > L->element)
        return lookup(x, L->next);
    else if (x == L->element)
        return TRUE;
    else /* 这里有 x < L->element，
            因此x 不可能在已排序表 L 中 */
        return FALSE;
}

图 6-6　在已排序表中查找

6.4.7　各种方法的比较

图6-7中的表格表明了对我们讨论过的3种基于表的词典表示，执行3种词典操作各自必须查找的单元数。设词典中有n 个元素，如果不允许重复，这也就是表示词典的表的长度。在允许重复出现时，我们用m 来表示该表的长度。我们知道m≥n，但不知道m 比n 大多少。在用到n/2→n 这样的表示方式时，意思是当查找成功时，平均查找了n/2个单元，而在不成功时，平均查找了n 个单元。而n/2→m 这样的项则表示，在一次成功的查找中，我们在看到要查找的元素之前，平均会看到词典中n/2个元素3，但在失败的查找中，就必须走完整个长度为m 的表，直到到达其末端。

3事实上，因为可能存在重复，所以在看到n/2个不同元素前，可能已经检查了多于n/2个元素。

	插入	删除	查找
无重复	n/2→n	n/2→n	n/2→n
有重复	0	m	n/2→m
已排序	n/2	n/2	n/2

图 6-7　3种用链表表示词典的方法所查找的单元数

请注意，除了有重复情况下的插入操作外，这些运行时间都要比数据结构为二叉查找树时词典操作的平均运行时间长。正如我们在5.8节中所见，在使用二叉查找树时，词典操作平均所花时间为O(logn)。

明智的测试次序
请注意图6-6的程序中3项测试的次序。首先要测试L 不为NULL。我们没有其他的选择，因为如果L 为NULL，则其余两项测试会导致错误。设y 是L->element的值。那么除了最后一个单元外，在每个访问过的单元都有x>y。因为如果有x=y，就是成功完成了查找，而如果x< y，就是没能找到x 而终止。因为首先要测试x>y，而且当且仅当它失败时，我们才需要区分另两种情况。测试的这种次序遵循这样一个基本原则：要首先测试最平常的情况，并因此节约平均要执行的总测试数。
如果访问了k 个单元，就要测试k 次L 是否为NULL，而且要测试k 次x 是否大于y。并且还要测试一次是否有x=y，这样总共要进行2k+1次测试。也就是说，只比图6-3中利用未排序表的lookup函数成功找到元素x 的情况多一次测试。如果未找到该元素，可以预期在图6-6中使用的测试要比在图6-3中使用的测试少得多，因为图6-6中平均只要检查一半单元后就会停止。因此，虽然不管使用已排序表还是使用非排序表，词典操作的大O运行时间都是O(n)，但是如果使用已排序表的话，通常会有常数因子上的轻微优势。

6.4.8　双向链表

在链表中，要从某个单元向表的开头移动不是那么容易的。而双向链表是这样一种数据结构，它让表中向前和向后的移动都非常方便。整数双向链表中的单元包含3个字段：

typdef struct CELL *LIST;
struct CELL {
    LIST previous;
    int element;
    LIST next;
};

多出来的这个字段含有指向表中前一个单元的指针。图6-8展示了表示表L=(a₁,a₂,…,a_n)的双向链表数据结构。

{%}

图 6-8　表示表L=(a₁,a₂,…,a_n)的双向链表

双向列表结构上的词典操作基本与单向链表上的那些操作相同。要了解双向链表的优势，可以考虑只给定指向元素a_i 所在单元的指针时删除该元素的操作。在单向链表中，我们要通过从头开始查找该表来找出前一个单元。而有了双向链表，就可以通过如图6-9所示的一系列指针操作，在O(1)时间里完成这一操作。

     void delete(LIST p, LIST *pL)
     {
         /* p 是指向待删除单元的指针，
           而pL 是指向链表的指针 */
(1)      if (p->next != NULL)
(2)          p->next->previous = p->previous;
(3)      if (p->previous == NULL) /* p 指向第一个单元 */
(4)          (*pL) = p->next;
         else
(5)          p->previous->next = p->next;
     }

图 6-9　从双向链表中删除元素

图6-9中所示的delete(p,pL)函数接受指向待删除单元的指针p，以及指向表L 本身的指针p_L 作为参数。也就是说，pL 是指向表中第一个单元的指针的地址。在图6-9的第(1)行中，我们要检查p 有没有指向最后一个单元。如果没有的话，那么在第(2)行，我们会让接下来那个单元的反向指针指向在p 之前的那个单元。如果p 正好指向第一个单元的话，就让它等于NULL。

第(3)行会测试p 是否为第一个单元。如果是，那么在第(4)行我们会让pL 指向第二个单元。请注意，在这种情况下，第(2)行会让第二个单元的previous字段变为NULL。如果p 不是指向第一个单元，那么在第(5)行我们会让前一个单元的正向指针指向p 之后的那个单元。这样一来，由p 指向的那个单元就顺利地与表分离了，其前一个单元和后一个单元现在是互相指向的。

6.4.9　习题

1. 为(a)图6-4中delete函数，(b)图6-5中insert函数的运行时间建立递推关系。它们的解各是多少？

2. 为使用带重复链表的词典操作插入、查找和删除编写C语言函数。

3. 为如图6-6那样使用已排序表的插入和删除操作编写C语言函数。

4. 编写C语言函数，使其能在双向链表中由p 指向的单元之后的新单元中插入元素x。图6-9是用于删除的相似函数，不过对插入操作来说，我们不需要知道表头L。

5. 如果使用双向链表数据结构，一种选择是不通过指向单元的指针表示表，而通过具有未使用element字段的单元来表示。请注意，这一“表头”单元本身并非表的一部分。该“表头”的next字段指向该表真正的第一个单元，而这第一个单元的previous字段则指向该“表头”单元。然后可以在不知道表头L（正是我们在图6-9中需要知道的）的情况下删除由指针p指向的单元，而不是那个未使用element字段的“表头”。编写C语言函数，使其利用这里描述的格式从双向链表中删除元素。

6. 编写递归函数，实现使用链表数据结构的(a)retrieve (i ,L )；(b)length (L )；(c)last (L )。

7. 扩展下列函数，使其单元可以接受任意类型ETYPE的元素，使用函数eq (x,y )测试x 和y 是否相等，并用lt (x,y )分辨x 是否在ETYPE类型元素的次序下先于y。

(a) 图6-3中的lookup 。

(b) 图6-4中的delete 。

(d) 使用带重复表的insert、delete 和lookup 。

(e) 使用已排序表的insert、delete 和lookup 。

6.5　表基于数组的实现

实现表的另一种常见方式是创建由下列两部分组成的结构体。

1. 存放元素的数组；

2. 记录表中当前元素数量的变量length。

图6-10展示了如何使用数组A[0..MAX-1]表示表(a₀,a₁,…,a_n-1)。元素a₀、a₁、…、a_n-1存储在A[0..n-1]中，而且length=n。

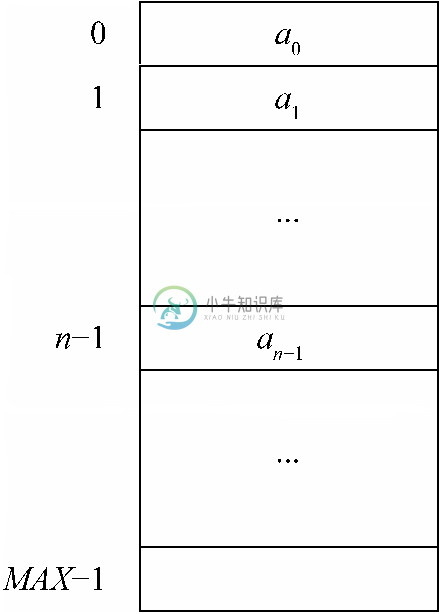
图 6-10　存放表(a₀,a₁,…,a_n-1)的数组A

就像在6.4节中那样，我们假设表中元素都是整数，并邀请读者将这些函数一般化为支持任意类型。表基于数组的实现所使用结构体的声明如下

typedef struct {
    int A[MAX];
    int length;
} LIST;

这里的LIST是包含两个字段的结构体，第一个字段是存储元素的数组A，而第二个则是含有表中当前元素数目的整数变量length。MAX是个用户定义的常量，用于为存储在表中的元素的数目确定边界。

与表的链表表示相比，基于数组的表示从多个方面讲都更方便。不过，它会受到表不能长过数组的限制，这可能导致插入操作失败。在链表表示中，只要有可用的计算机内存，就可以让表增长到尽可能长。

对基于数组的表执行词典操作，所花的时间与对链表表示的表执行这些操作所花的时间基本相同。要插入x，先查找x。如果没找到x，就要检查是否有length< MAX。如果length 不小于MAX，就有出错的情况，因为没法将新元素装入数组中。否则，我们将x 存储在A[length]中，并将length 增加1。要删除x，还是先查找x，如果找到，就将数组A中x 之后的元素都下移一个位置，然后将length 减1。插入和删除的具体函数实现留作本节习题。接下来要介绍查找操作的细节。

6.5.1　线性查找

图6-11是实现查找操作的函数。因为数组A可能很大，所以选择传递指向LIST类型结构体的指针pL作为lookup 的形式参数。在该函数中，结构体的两个字段可以称为pL->A[i]和pL->length。

从i=0开始，第(1)至第(3)行的for循环会依次检查数组的每个位置，直到它到达最后出现的位置，或是找到x。如果找到x，就返回TRUE。如果它检查了表中的每个元素而没有找到x，就会在第(4)行返回FALSE。这种查找方法叫作线性查找或顺序查找。

     BOOLEAN lookup(int x, LIST *pL)
     {
         int i;

(1)      for (i = 0; i < pL->length; i++)
(2)          if (x == pL->A[i])
(3)              return TRUE;
(4)      return FALSE;
     }

图 6-11　通过线性查找进行查找操作函数

不难理解，如果x 在表中，那么在找到x 之前，平均要查找数组A[0..length-1]的一半。因此，设n 为length的值，那么执行一次查找要花O(n)的时间。如果x 未出现，就要查找完整个数组A[0..length-1]，再次需要O(n)的时间。这样的表现，与对用链表表示的表执行查找操作的表现是一样的。

常数因子在实际应用中的重要性
纵观第3章，我们一直在强调运行时间的大O度量的重要性，而且可能给大家留下了这样的印象：大O是唯一的影响因素，或是说任何O(n)算法在执行某项任务时都和其他O(n)算法有着同样的表现。不过在这里，在对哨兵的讨论中，以及其他几节中，我们都会细究隐藏在O(n)之中的常数因子。原因很简单。尽管运行时间的大O度量主导了常数因子，但研究该主题的人都能很快地了解这一点。例如，我们了解到只要n 大到足以产生影响，就要使用具有O(n logn)运行时间的排序。软件性能上的竞争优势，往往源于对具有正确“大O”运行时间的算法中的常数因子的改进，而这种优势通常能决定软件产品的成败。

6.5.2　带哨兵的查找

通过将x 临时插入表的末尾，可以简化图6-11中for循环的代码，并为该程序提速。在表末端的这个x 就叫作哨兵（sentinel）。这项技术最先是在3.6节附注栏内容“更具防御性的程序设计”中提到的，而它在这里有着重要的应用。假设在表的末端始终有一个额外的槽，就可以使用图6-12中的程序查找x。该程序的运行时间仍为O(n)，但比例常数更小，因为图6-12所示程序的循环体和循环测试所需的机器指令数，通常小于图6-11所示程序所需的。

     BOOLEAN lookup(int x, LIST *pL)
     {
         int i;

(1)      pL->A[pL->length] = x;
(2)      i = 0;
(3)      while (x != pL->A[i])
(4)          i++;
(5)      return (i < pL->length);
     }

图 6-12　进行带哨兵查找的函数

第(1)行将哨兵放置在刚好越过该表的位置。请注意，因为length不会发生改变，所以这个x 并非真正是表的一部分。第(3)和第(4)行的循环会增加 i，直到我们找到x。请注意，因为设置了哨兵，所以即便表是空表，还是保证能找到x。在找到x 之后，第(5)行会测试是找到了表中真正出现的x（也就是，i < length），还是找到了哨兵（也就是，i < length）。请注意，如果使用哨兵，就一定要严格保证length 小于MAX，否则就没有位置放置哨兵了。

6.5.3　利用二叉查找对已排序表进行查找

假设表L中的元素a₀、a₁、…、a_n-1已经按照非递减次序排好序。如果该已排序表存储在数组A[0..n-1]中，就可以利用二叉查找技术，从而带来可观的速度提升。我们首先必须找到中间元素的下标m，也就是说m=[(n-1)/2]。4然后将元素x与A[m ]相比较。如果它们相等，就已经找到x 了。如果x< A[m ]，就递归地重复对子表A[0..m-1]的查找。如果x>A[m ]，就递归地重复对子表A[m+1..n-1]的查找。无论何时尝试查找空表，都会报错。图6-13展示了分区过程。

4⌊a⌋表示a 向下取整，就是a 的整数部分。因此⌊6.5⌋=6，而且⌊6⌋=6。而⌈a⌉表示a 向上取整，是大于等于a 的最小整数。例如⌈6.5⌉=7，而⌈6⌉=6。

函数binsearch的代码要将x 放置在如图6-14所示的已排序数组A 中。该函数使用变量low和high表示x 可能出现的区域的下界和上界。如果较低的区域超过了较上的区域，那么就没找到x，此时函数就会终止并返回FALSE。

否则，binsearch会通过mid=⌊(low+high)/2⌋计算该区域的中点。然后该函数会检查区域正中的元素A[mid ]，以确定x 是否在该位置。如果x 不在该位置，而且小于A[mid ]，就继续在中点下方的区域查找，要是x 大于A[mid ]，就继续在中点上方的区域查找。这一思路概括了图6-13所示的划分，其中low 是0，而high 是n-1。

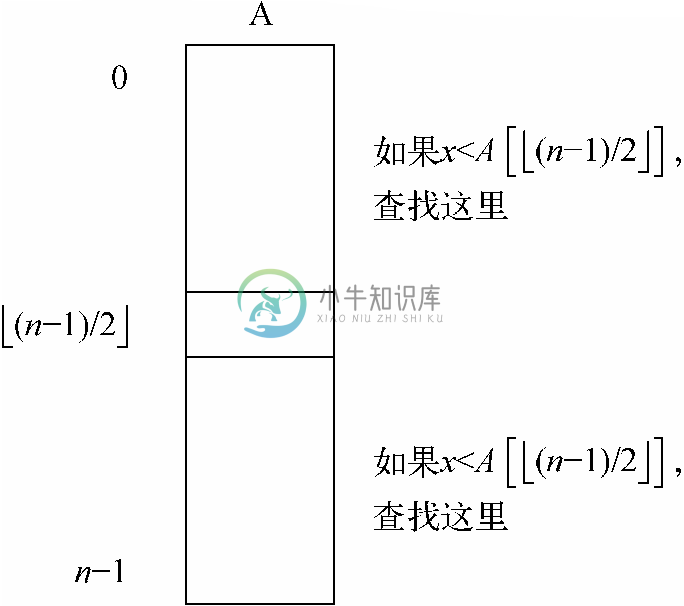
图 6-13　二叉查找将区域一分为二

利用归纳断言“如果x 在数组中，那么它一定出现在A[low..high]这个区域内”，就可以证明函数binsearch的正确性。证明过程要对high-low 的差进行归纳，这留作本节的习题。在每次迭代中，binsearch 要么

1. 在到达第(8)行时找到元素x，要么

2. 在第(5)行或第(7)行，对长度至多为待查找数组A[low..high]长度一半的子表递归调用自身。

     BOOLEAN binsearch(int x, int A[], int low, int high)
     {
         int mid;
(1)      if (low > high)
(2)          return FALSE;
         else {
(3)          mid = (low + high)/2;
(4)          if (x < A[mid])
(5)              return binsearch(x, A, low, mid-1);
(6)          else if (x > A[mid])
(7)              return binsearch(x, A, mid+1, high);
             else /* x == A[mid] */
(8)              return TRUE;
         }
     }

图 6-14　使用二叉查找进行查找操作的函数

由长度为n 的数组开始，在其长度变为1之前，我们最多对有待查找的数组进行log₂n 次分割。于是我们要么在A[mid]找到x，要么在对空表调用该函数后仍未找到x。

想要在具有n 个元素的数组A中寻找x，可以调用binsearch(x,A,0,n-1)。我们知道binsearch最多会调用自身O(logn)次。在每次调用中，都要花费O(1)的时间，再加上递归调用的时间，因此二叉查找的运行时间是O(logn)。这是可与平均花费O(n)时间的线性查找相媲美的查找方式。

6.5.4　习题

1. 编写函数，利用对数组的线性查找进行下列操作：(a)向表L中插入x；(b)从表L中删除x。

2. 使用带哨兵的数组，重复习题(1)的练习。

3. 使用已排序数组，重复习题(1)的练习。

4. 假设表中元素具有任意类型ETYPE，对ETYPE类型来说有函数eq (x,y )区分x 和y 是否相等，还有ly (x, y ) 函数可以区分x 就ETYPE类型元素的次序而言是否先于y，编写以下函数：

(a) 图6-11中的lookup函数；

(b) 图6-12中的lookup函数；

5. ** 设图6-14中的二叉查找算法最多进行k 次探测（也就是在第(3)行求mid的值）时最长数组的长度(high-low+1)为P (k )。例如，P(1)=1，且P(2)=3。写出P (k )的递推关系，再求出自己所写的递推关系的解。它是否说明二叉查找进行的探测次数为O(logn)？

6. * 对low 和high 之差进行归纳，证明：如果x 在区域A[low..high]中，那么图6-14中的二叉查找算法会找到x。

7. 假设数组中可以出现重复的元素，使得插入操作可以在O(1)时间内完成。为这种数据结构编写插入、删除和查找函数。

8. 使用迭代，重新编写二叉查找程序。

9. ** 为对n 个元素的数组进行二叉查找的运行时间建立递推关系，并求解。提示：为了简化问题，可以取T(n)作为对具有n 个或更少元素（而不是像我们常用的方法那样刚好有n 个元素）的数组进行二叉查找的运行时间上界。

10. 在三分查找中，给定从low 到high 的区域，先计算该区域中大约1/3处的位置

first=⌊(2×low+high)/3⌋

并将其与A[second ]相比较。如果x>A[first ]，就计算近似2/3处的位置

second=⌈(low+2×high)/3⌉

并将x与A[second ]进行比较。因此我们将x 隔离在这3个区域的其中一个里，每个区域都不大于low 到high 形成区域的三分之一。编写函数执行三分查找。

11. ** 用三分查找重复习题5。也就是说，要找出三分查找时最多需要k 次探测的最大数组的递推关系并为其求解。二叉查找和三分查找哪种所需的探测次数多？也就是说，对于给定的k，二叉查找和三分查找哪种能处理更大的数组？

6.6　栈

栈是基于表数据模型的抽象数据类型，栈中的所有操作都是在表的一端执行的，而这一端就叫作栈的栈顶。术语“LIFO表”（后入先出表）指的就是栈。

栈的抽象模型与表的抽象模型如出一辙，也就是一列某一类型的元素a₁、a₂、…、a_n 。将栈与一般表区分开来的就是栈可以接受的一些特殊操作。我们将在后面的内容中介绍更加齐全的操作，不过现在，我们注意到最精髓的栈操作就是push（压入）和pop（弹出），其中push (x )是将元素x 放在栈顶，pop 则是从栈中移除最顶端的元素。如果将栈顶写在右端，那么对表（a₁,a₂,…,a_n）应用push (x )操作，就得到表（a₁,a₂,…,a_n ,x）。而弹出表（a₁,a₂,…,a_n）得到的是表（a₁,a₂,…,a_n-1）。弹出空表ε 是不可能的，而且会出错。

示例 6.9

很多编译器首先会把出现在程序中的中缀表达式转换成等价的后缀表达式。例如，表达式(3+4)×2的后缀形式就是34+2×。栈可以用来为后缀表达式求值。由空栈开始，我们从左至右扫描需要求值的后缀表达式。每当遇到一个参数，就将其压入栈中。而在遇到运算符时，就弹出栈两次，并记下弹出的操作数。然后对弹出的两个值（其中第二个值是运算符左边的操作数）应用该运算符，然后将结果压入该栈。图6-15展示了处理后缀表达式34+2×每一步操作之后栈的情况。在完成处理后，求值的结果14留在该栈中。

处理的符号	栈	操作
初始化	ε
3	3	push 3
4	3,4	push 4
+	ε	pop 4;pop 3 计算7=3+4
	7	push 7
2	7,2	push 2
×	ε	pop 2;pop 7 计算14=7×2
	14	push 14

图 6-15　用栈求后缀表达式的值

6.6.1　对栈的操作

之前讨论过的两种抽象数据类型——词典和优先级队列，都拥有一组明确与之关联的操作。栈其实是一些相似的ADT，它们有着相同的底层模型，但各自有着所允许操作集不同的变种。在本节中，我们要讨论栈的通用操作，并展示两种可用来实现栈的数据结构，一种是基于链表的，另一种是基于数组的。

正如之前提到的，在任意一组栈操作中都可以看到push 和pop。为栈ADT选择的操作还有个共性：它们都可以在O(1)时间内实现，而与栈中的元素数量无关。大家可以自行验证一下，对于我们提到的两种数据结构，所有操作都只需要常数时间。

除了push 和pop 外，通常还需要clear 操作将栈初始化为空栈。在示例6.9中，默认假设栈一开始为空，而没有解释它为什么是这样。还有一种操作，就是确定栈当前是否为空的测试。

最后要考虑的操作是确定栈是否“已满”的测试。现在在栈的抽象模型中，没有关于满栈的概念，因为原则上讲，栈是可以随意变长的表。不过，在栈的任何一种实现中，都会有某个无法超越的长度。最常见的例子就是在用数组表示表或栈时。正如在6.5节中看到的，必须假设表的长度不会超过常量MAX，否则insert 函数的实现就没法正常工作了。

我们在自己的栈的实现中将要使用的这一操作的正式定义如下。设S 是ETYPE类型的栈而且x 是ETYPE类型的元素。

1. clear (S )。将栈S 清空。

2. isEmpty (S )。如果S 为空，返回TRUE，否则返回FALSE。

3. isFull (S )。如果S 已满，返回TRUE，否则返回FALSE。

4. pop (S,x )。如果S 为空，返回FALSE；否则，将x 置为栈S 栈顶元素的值，并将该元素从栈S 中删除，然后返回TRUE。

5. push (x,S )。如果S 已满，返回FALSE；否则，将元素x 添加到S 的栈顶，并返回TRUE。

pop 的一个常见变种会假设S 非空。它只接受S 作为参数，并返回被弹出的元素x。而pop 的另一个版本则根本不返回值，它只是将栈顶处的元素删除。同样，我们可以在编写push 时假设S“未满”。在这种情况下，push 不返回任何值。

6.6.2　栈的数组实现

用于表的这种实现也能用于栈。我们将首先讨论基于数组的实现，接着讨论链表表示。在两种情况下，我们都将元素类型定为int。更一般化的工作还是留作本节习题。

图 6-16　表示栈的数组

基于数组的整数栈的声明如下。

typedef struct {
    int A[MAX];
    int top;
} STACK;

在基于数组的实现中，栈既可以向上增长（从较低区域向较高区域），也可以向下增长（从较高区域向较低区域）。在这里我们选择让栈向上增长5，也就是说，栈中最老的元素a₀在位置0，第二老的元素a₁在位置1，而最新插入的元素a_n-1在位置n-1。

5因此“栈顶”在图中是出现在底部的，这是种不凑巧但相当标准的约定。

数组结构体中的top字段指示了栈顶的位置。因此，在图6-16中，top的值为n-1。空栈是通过top=-1来表示的。在这种情况下，数组A的内容是无关紧要的，栈中没有任何元素。

6.6.1节中定义的5种栈操作对应的程序如图6-17所示。我们通过引用传递栈，来避免复制作为函数参数的大数组。

void clear(STACK *pS)
{
    pS->top = -1;
}

BOOLEAN isEmpty(STACK *pS)
{
    return (pS->top < 0);
}

BOOLEAN isFull(STACK *pS)
{
    return (pS->top >= MAX-1);
}

BOOLEAN pop(STACK *pS, int *px)
{
    if (isEmpty(pS))
        return FALSE;
    else {
        (*px) = pS->A[(pS->top)--];
        return TRUE;
    }
}

BOOLEAN push(int x, STACK *pS)
{
    if (isFull(pS))
        return FALSE;
    else {
        pS->A[++(pS->top)] = x;
        return TRUE;
    }
}

图 6-17　用来实现数组上的栈操作的函数

6.6.3　栈的链表实现

与表一样，可以用链表数据结构表示栈。不过，如果栈顶是表的前端就会很方便。这样的话，可以在表的表头压入和弹出，都只用花O(1)的时间。如果必须找到表的端点再压入和弹出，对长度为n 的栈执行这些操作就要花O(n)的时间。而这样一来，栈S＝（a₁,a₂,…,a_n）必须用链表“倒着”表示为：

{%}

在定义表单元时使用过的类型定义宏也可以用于栈。宏

DefCell(int, CELL, STACK);

定义了整数栈，并扩展为

typdef struct CELL *STACK;
struct CELL {
    int element;
    STACK next;
};

对这种表示而言，5种操作可以用图6-18中的函数实现。我们假设malloc从不会用尽空间，这意味着isFull 操作总是会返回FALSE，而且push 操作从不会失败。

void clear(STACK *pS)
{
    (*pS) = NULL;
}

BOOLEAN isEmpty(STACK *pS)
{
    return ((*pS) == NULL);
}

BOOLEAN isFull(STACK *pS)
{
    return FALSE;
}

BOOLEAN pop(STACK *pS, int *px)
{
    if ((*pS) == NULL)
        return FALSE;
    else {
        (*px) = (*pS)->element;
        (*pS) = (*pS)->next;
        return TRUE;
    }
}

BOOLEAN push(int x, STACK *pS)
{
    STACK newCell;

    newCell = (STACK) malloc(sizeof(struct CELL));
    newCell->element = x;
    newCell->next = (*pS);
    (*pS) = newCell;
    return TRUE;
}

图 6-18　链表实现的栈所使用的函数

对用链表实现的栈执行push 和pop 的效果如图6-19所示。

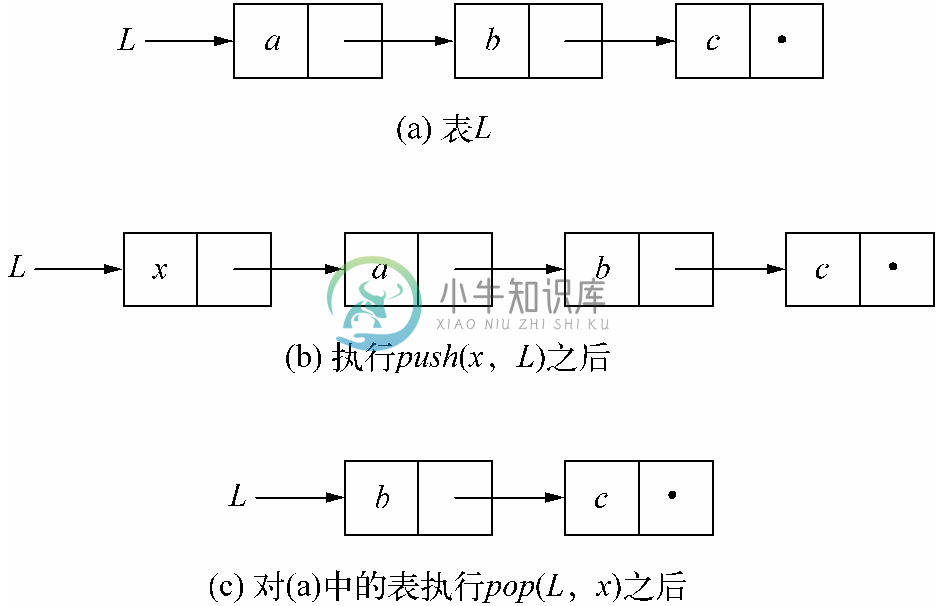
图 6-19　对用链表实现的栈执行压入和弹出操作

6.6.4　习题

1. 由空栈开始，在执行操作序列push (a )、push (b )、pop 、push (c )、push (d )、pop 、push (e )、pop、pop 之后，栈中还剩什么。

2. 只使用本节讨论的5种栈操作操作栈，编写C语言程序，按照图6-9所示的算法，为使用整数操作数及4种常用算术运算符的后缀表达式求值。恰当地定义数据类型STACK，并先后在程序中用上图6-17和图6-18中的函数，以此证实大家编写的程序既可以使用数组实现，也可以使用链表实现。

3. * 怎样用栈为前缀表达式求值？

4. 计算图6-17和图6-18中各函数的运行时间。它们是否全为O(1)？

5. 栈ADT有时会使用top 操作，top (S )会返回栈S（一定要假设该栈非空）的栈顶元素。编写可与本节中定义栈的

(a) 数组数据结构

(b) 链表数据结构

一起使用的top 函数。这两个top 的实现花的时间是否都是O(1)?

6. 模拟栈，计算以下后缀表达式的值：

(a) ab+cd×+e+

(b) abcde++++

7. * 假设从空栈开始，执行一些压入和弹出操作。如果在这些操作之后的栈为(a₁,a₂,…,a_n)，栈顶在右侧，证明：对i=1,2,…,n-1,a_i 是在a_i+1压入之前被压入栈的。

6.7　使用栈实现函数调用

栈的一项重要应用常不为人所见：栈可以用来为程序中多个函数的变量分配计算机内存空间。我们要讨论的是用于C语言的机制，不过相似的机制也几乎用在其他每种程序设计语言中。

要理解问题是什么，可考虑2.7节中简单的递归阶乘函数fact，该函数图6-20所示。fact函数有一个参数n以及一个返回值。随着fact递归地调用自身，不同的调用将会同时处于活动状态。这些调用有着值各不相同的参数n，而且会产生不同的返回值。那这些有着相同名称的不同对象要存放在哪里呢？

           int fact(int n)
           {
(1)            if (n <= 1)
(2)                return 1; /* 依据 */
               else
(3)                return n*fact(n-1); /* 归纳 */
           }

图 6-20　计算n!的递归函数

要回答这一问题，必须先对与程序设计语言相关联的运行时组织（run-time organization）有所了解。运行时组织是一种规划，它将计算机内存细分为不同区域，以存放程序所使用的不同数据项。当程序运行的时候，函数的每次执行称作一次活动（activation）。与每次活动相关联的数据对象都存储在计算机内存中称为该活动的活动记录（activation record）的区块里。这些数据对象包括参数、返回值、返回地址和该函数的局部变量。

图6-21展示了有代表性的运行时内存细分情况。第一个区域含有执行中的程序的对象代码。而接下来的区域包含了用于该程序的静态数据，比如某些常量以及程序使用的外部变量的值。第三个区域是运行时栈，它是向着内存中的高位地址向下增长的。在最高编号内存区域的是堆，该区域是为用malloc动态分配的对象预留的。6

6不要把这里用到的术语“堆”与5.9节中讨论的堆数据结构弄混了。

图 6-21　典型的运行时内存组织

运行时栈中存放着当前处于活跃状态的所有活动的记录。栈是种合适的结构，因为在调用函数时，可以把活动记录压入栈中。任何时候，当前正在执行的活动A₁的记录会在栈顶位置。而正好位于栈顶之下的是调用A₁的A₂的活动记录。在A₂的活动记录之下的，是调用A₂的活动的记录，以此类推。当函数返回时，就弹出栈顶的活动记录，露出调用该活动的函数的活动记录。这正是要做的事情，因为当函数返回时，控制权会传递给调用函数。

示例 6.10

考虑一下如图6-22所示的程序骨架。该程序是非递归的，而且任一函数中一直只有一个活动。当主函数开始执行时，它包含着变量x、y和z对应空间的活动记录会被压入栈中。当函数P在标记为Here的位置被调用时，它的活动记录（含有变量p1和p2对应的空间）会被压入栈中。7当P调用Q时，Q的活动记录被压入栈中。至此，栈的情况如图6-23所示。

7请注意，P的活动记录有两个数据对象，因此它的“类型”与主程序活动记录的“类型”是不同的。不过，我们可以将某程序所有记录类型的形式视作某一记录类型的不同变种，因此维护了栈的元素具有相同类型的观点。

void P();
void Q();

main() {
    int x, y, z;

    P(); /* 这里 */
}

void P();
{
    int p1, p2;

    Q();
}

void Q()
{
    int q1, q2, q3;

            …
}

图 6-22　程序骨架

图 6-23　当函数Q正在执行时的运行时栈

当Q执行完毕时，它的活动记录就会从栈中弹出。此时，P也完成了，所以它的活动记录也会被弹出。最后，main也完成执行，并将它的活动记录弹出栈。现在栈为空栈，而程序也执行完毕了。

示例 6.11

考虑图6-20所示的递归函数fact。同一时间可能有很多fact的活动处于活跃状态，不过每一个活动都有着相同形式的活动记录，即

其中首先装入的是对应参数n的单词，接着是对应返回值的单词，这里表示为fact。返回值直到活动的最后一步，在返回之前才会被装入。

假设调用fact(4)，这样就创建了具有如下形式的活动记录。

随着fact(4)调用fact(3)，接着要将表示该活动的活动记录压入运行时栈，现在该栈就成了：

请注意，这里有两个名为n和两个名为fact的位置。不过这样并不冲突，因为它们属于不同的活动，而且一次只有一个活动记录可以位于栈顶：属于当前正在执行的活动的活动记录。

fact(3)接着会调用fact(2)，而fact(2)又会调用fact(1)。至此，运行时栈如图6-24所示。fact(1)现在不再进行递归调用，而是赋值fact=1。因此，值1被放入顶部活动记录为fact预留的槽中。而其他标记为fact的槽未受影响，如图6-25所示。

图 6-24　fact执行期间的活动记录

图 6-25　fact(1)计算其值之后

接着，fact(1)返回，将对应fact(2)的活动记录暴露在外，并在fact(1)被调用的位置将控制权返回给fact(2)。来自fact(1)的返回值1会乘上fact(2)对应活动记录中n 的值，而该乘积就被放置到该活动记录里fact对应的槽中，正如图6-20中第(3)行所需要的。得到的栈如图6-26所示。

图 6-26　fact(2)计算其值之后

同样，fact(2)接着将控制权返回给fact(3)，而且对应fact(2)的活动记录会被弹出栈。而返回值2会乘上fact(3)对应的n，得出返回值6。然后，fact(3)返回，并将其返回值乘以fact(4)中的n，得到返回值24。运行时栈现在成了：

至此，fact(4)返回到某假设的调用函数，其活动记录（未表示出来）在栈中正位于fact(4)之下。不过，它会接收返回值24作为fact(4)的值，并继续自己的执行。

习题

1. 考虑一下图6-27中的C语言程序。main函数的活动记录含有对应整数i的槽。而sum的活动记录中的重要数据包括：

(a) 参数i；

(b) 返回值；

假设A[i ]的值为10i，给出紧邻每次对sum的调用之前和之后活动记录栈的情况。也就是说，给出紧接在压入sum的活动记录之后，且刚要从栈中弹出一个活动记录之前栈的情况。大家无需每次都给出底层（对应main函数的）活动记录的内容。

     #define MAX 4
     int A[MAX];
     int sum(int i);

     main()
     {
         int i;

(1)      for (i = 0; i < MAX; i++)
(2)          scanf("%d", &A[i]);
(3)      printf("%d\n", sum(0));
     }

     int sum(int i)
     {
(4)          if (i >= MAX)
(5)              return 0;
             else
(6)              return A[i] + sum(i+1);
     }

图 6-27　习题(1)的程序

2. *图6-28所示的delete函数会删除链表中第一次出现的整数x，链表由定义如下的普通单元组成：

delete的活动记录由参数x和pL组成。不过，因为pL是指向表的指针，所以活动记录中第二个参数的值不是指向表中第一个单元的指针，而是另一个指针，它指向的是指向第一个单元的指针。通常，活动记录会存放指向某个单元next字段的指针。在从其他某个函数调用delete(3,&L)，而且L是指向链表(1，2，3，4)第一个单元的指针时，给出栈的序列。

void delete(int x, LIST *pL)
{
    if ((*pL) != NULL)
        if (x == (*pL)->element)
            (*pL) = (*pL)->next;
        else
            delete(x, &((*pL)->next));
}

图 6-28　习题(2)的程序

6.8　队列

另一种基于表数据模型的抽象数据类型是队列。这是一种形式受限的表，它的元素只能从后端插入，并从前端删除。术语“FIFO表”（先入先出表）就是指队列。

对队列的直观想法就是出纳员窗口前的队伍。人们从尾部进入队伍，并在到达队首时接受服务。与栈不同的是，队列是很公平的，人们是按照进入队伍的顺序接受服务的。因此，等待得最久的那个人就是下一个接受服务的人。

6.8.1　对队列的操作

队列使用的抽象模型与表（或栈）使用的抽象模型是相同的，不过对队列执行的操作却是特殊的。队列具有两种特有的操作，入队（enqueue）和出队（dequeue）。enqueue (x )会将x 添加到队列后端，而dequeue 则会从队列前端删除元素。就像栈那样，我们还会需要将其他一些实用操作应用到队列上。

设Q 是元素类型皆为ETYPE的队列，并设x 是ETYPE类型的元素。我们要考虑以下对队列的操作。

1. clear (Q )。将队列Q 置空。

2. dequeue (Q，x )。如果Q 为空，返回FALSE；否则，将x 置为Q 前端元素的值，并将该元素从Q中删除，然后返回TRUE。

3. enqueue (x，Q)。如果Q 已满，返回FALSE；否则，将元素x 添加到Q 的后端，并返回TRUE。

4. isEmpty (Q)。若Q 为空则返回TRUE，否则返回FALSE。

5. isFull (Q)。若Q 已满则返回TRUE，否则返回FALSE。

就像栈那样，我们可以给出更具“信任度”的enqueue 和dequeue，其中enqueue 不会检查队列是否已满，而dequeue 不会检查队列是否为空。enqueue 不再返回值，而dequeue 则只接受Q 作为参数，并返回被请出队列的值。

6.8.2　队列的链表实现

用于队列的一种实用数据结构是基于链表的。首先是由宏给出的单元定义

DefCell(int, CELL, LIST);

一如本章前面的内容，假设队列中的元素都是整数，并请读者自己将我们的函数一般化为处理任意元素类型。

队列的元素将存储到链表的单元中。队列本身是具有两个指针的结构，一个指向前端单元，也就是链表的第一个单元；另一个指向后端单元，也就是链表的最后一个单元。这就是说，有如下定义

typedef struct {
    LIST front, rear;
} QUEUE;

如果队列为空，front就将是NULL，而rear的值就无关紧要了。

更多的抽象数据类型
可以将栈和队列加到5.9节中引入的抽象数据类型表中。我们在6.6节中介绍了栈使用的两种数据结构，并在6.8节中介绍了队列使用的一种数据结构。而6.8节的习题(3)则提到了实现数组的另一种数据结构，“循环数组”。
抽象数据类型
栈
队列
抽象实现
表
表
数据结构
1) 链表
2) 数组
1) 链表
2) 循环数组

抽象数据类型	栈	队列
抽象实现	表	表
数据结构	1) 链表 2) 数组	1) 链表 2) 循环数组

图6-29给出了实现本节所提队列操作的程序。请注意，在使用链表时，就没有“满”队列的概念了，这样一来isFull 总会返回FALSE。不过，如果使用某种基于数组的队列实现，就可能会有满队列。

6.8.3　习题

1. 给出从空队列开始，在执行操作序列enqueue (a )、enqueue (b )、dequeue、enqueue (c )、enqueue (d )、dequeue、enqueue (e )、dequeue 、dequeue 之后剩下的队列。

2. 证明图6-29中的各函数都能在O(1)时间内执行，而不需要考虑队列的长度。

3. * 可以用数组表示队列，只要队列不会增长得太长。为了让操作只花O(1)的时间，必须将数组视为循环的。也就是说，数组A[0..n-1]要被视为A[1]在A[0]之后、A[2]在A[1]之后，以此类推，直到A[n-1]在A[n-2]之后，不过还有A[0]在A[n-1]之后。队列可以用表示队列前端元素和后端元素位置的一对整数front和rear表示。空队列可以表示为在循环的情况下，front 的位置紧邻rear 之后，例如front =23且rear =22，或是front =0且rear =n-1。请注意，因此该队列不是有n 个元素，否则该条件也可以由rear 紧跟front 之后来表示。因此，当该队列有n-1个元素，而不是有n 个元素时，它就已经满了。假设使用循环数组数据结构，为这些队列操作编写函数，不要忘了检查满队列和空队列。

4. * 证明：如果(a₁,a₂,…,a_n)是以a₁为前端的队列，那么对i=1,2,…,n-1而言，a_i 是在a_i+1之前入队的。

void clear(QUEUE *pQ)
{
    pQ->front = NULL;
}

BOOLEAN isEmpty(QUEUE *pQ)
{
    return (pQ->front == NULL);
}

BOOLEAN isFull(QUEUE *pQ)
{
    return FALSE;
}

BOOLEAN dequeue(QUEUE *pQ, int *px)
{
    if (isEmpty(pQ))
        return FALSE;
    else {
        (*px) = pQ->front->element;
        pQ->front = pQ->front->next;
        return TRUE;
    }
}

BOOLEAN enqueue(int x, QUEUE *pQ)
{
    if (isEmpty(pQ)) {
        pQ->front = (LIST) malloc(sizeof(struct CELL));
        pQ->rear = pQ->front;
    }
    else {
        pQ->rear->next = (LIST) malloc(sizeof(struct CELL));
        pQ->rear = pQ->rear->next;
    }
    pQ->rear->element = x;
    pQ->rear->next = NULL;
    return TRUE;
}

图 6-29　实现链表队列操作的例程

6.9　最长公共子序列

本节专门探讨一个与表有关的有趣问题。假设有两个表，而我们想知道这两者之间有何差异。该问题会以很多不同的形式出现，也许最常见的就是两个表分别表示某文本文件的两个版本，并希望确定两个版本有哪几行相同的情况。为简便起见，纵贯本节我们都将假设这些表是字符串。

考虑这一问题的一种实用方式就是将两个文件当作符号序列，x=a₁…a_m 和y=b₁…b_n，其中a_i 表示第一个文件中的第i 行，而b_j 表示第二个文件的第 j 行。因此，像a_i 这样的抽象符号其实也许是个“大”对象，有可能是一整句话。

UNIX命令diff就可以比较两个文本文件的区别。文件x 可能是某程序当前的版本，文件y 则可能是该程序在经过某次细小修改之前的版本。可以使用diff提醒自己在将y 变为x 时进行的修改。对文本文件的常见修改有：

1. 插入一行；

2. 删除一行。

而文本行的修改可以视为删除一行之后紧接着插入一行。

通常，当一个文本文件转化为另一个时，如果对两个文本文件间发生的少量改变加以检验，很容易发现哪些文本行是与哪些行对应的，且很容易看出哪些文本行被删除了以及哪些文本行是新插入的。diff命令作出了这样的假设，用两个表表示两个文本文件，表中元素是文本文件中的文本行，于是可以通过首先找出两个表的最大公共子序列（Longest Common Subsequence，LCS）来确定都有哪些改变。LCS表示那些没有修改过的文本行。

回想一下，子序列是在保留剩余元素次序的前提下从表中删除0个或多个元素得到的。两个表的公共子序列就是同为两者子序列的表，而两个表的最长公共子序列就是两个表公共子序列中最长的那个。

示例 6.12

在下文的内容中，我们可以将a、b或c这样的字符视为表示文本文件中的文本行，或者如果愿意的话，视作其他类型的元素。举例来说，baba及cbba都是abcabba和cbabac的最长公共子序列。可以看到，baba是abcabba的子序列，因为从abcabba中选取位置2、4、5和7就能形成baba。字符串baba也是cbabac的子序列，因为可以选择位置2、3、4和5。同样，cbba是由abcabba的位置3、5、6和7形成的，也是由cbabac的位置1、2、4和5形成的。因此cbba也是这些字符串的公共子序列。我们必须相信，这就是最长公共子序列，也就是说，没有长度为5或更长的公共子序列了。这一事实可由接下来要描述的算法得出。

6.9.1　对LCS计算的递归

我们提供了两个表LCS长度的递归定义。该定义使LCS长度的计算变得很容易，而且，通过检验它构建的表，可以发现一个可能的LCS，而不只是其长度。由该LCS，可以推断出文本文件发生了什么变化，本质上讲，不属于LCS的部分都是变化。

要找出表x 和表y 某个LCS的长度，就需要弄清所有前缀（一个来自x，另一个来自y）对LCS的长度。回想一下，前缀是以表首字母开头的子表，也就是说，cbabac的前缀就是ε、c、cb、cba，等等。假设x=(a₁,a₂,…,a_m )而且y=(b₁,b₂,…,b_n )。对每个i 和每个j，其中i 在0到m 之间，而j 在0到n 之间，都可以要求来自x 的前缀(a₁,…,a_i )和来自y 的前缀(b₁,…,b_j )的LCS。

如果i 或 j 之中有一个为0，那么其中一个前缀就是ε，这样两个前缀唯一可能的公共子序列就是ε。因此，当i 或 j 之中有一个为0时，LCS的长度就是0。这一直观结果可以转化为在LCS计算方式的非正式讨论之后的归纳中依据和规则(1)的正式形式。

现在考虑一下i 和 j 都大于0的情况。最好将LCS视为两个字符串的某些位置间的匹配。也就是说，对LCS的每个元素而言，都可以将该元素在两个字符串中各自所在的位置匹配起来。匹配过的位置必须具有相同的符号，而且匹配过的位置之间的文本行一定不能交叉。

示例 6.13

图6-30a展示了字符串abcabba和cbabac两种可能匹配中对应公共子序列baba的那种，图6-30b则展示了对应cbba的匹配。

{%}

图 6-30　表示为位置间匹配的LCS

因此，我们来考虑前缀(a₁,…,a_i )和(b₁,…,b_j )之间的匹配。存在如下两种情况，具体取决于两个表的最后一个符号是否相等。

(a) 如果a_i ≠b_j，那么匹配中就不可能同时含有a_i 和b_j，因此(a₁,…,a_i )和(b₁,…,b_j )的LCS一定是下列两者之一。

(i) (a₁,…,a_i-1)和(b₁,…,b_j )的LCS；

(ii) (a₁,…,a_i )和(b₁,…,b_j-1)的LCS。

如果已经得出了上述两对前缀的LCS的长度，就可以取其中的较大值作为(a₁,…,a_i )和(b₁,…,b_j )的LCS的长度。这种情况将成为接下来的归纳中正式的规则(2)。

(b) 如果a_i =b_j，就可以匹配a_i 和b_j，而且该匹配将不会妨碍其他任何可能的匹配。因此，(a₁,…,a_i )和(b₁,…,b_j )的LCS的长度，要比(a₁,…,a_i-1)和(b₁,…,b_j-1)的LCS的长度大1。这种情形将成为接下来的归纳中正式的规则(3)。

这些直观结果让我们给出了L( i , j )——(a₁,…,a_i )和(b₁,…,b_j )的LCS的长度——的递归定义。其中利用了对i+j 的和的完全归纳。

依据。如果i+j=，那么i 和 j 都为0，所以LCS是ε。因此L(0,0)=0。

归纳。考虑i 和 j，并假设已经为满足g+h< i+j 的任意g 和h 计算出L(g,h )。有如下3种情况需要考虑。

1. 如果i 或 j 中有一个为0，那么L(i,j)=0。

2. 如果i>0且j>0，而且a_i ≠b_j，那么L(i, j )=max(L(i ,j-1),L(i-1 , j ))。

3. 如果i>0且j>0，而且a_i ≠b_j，那么L(i, j )=1+L(i-1, j-1)。

6.9.2　用于LCS的动态规划算法

我们最终想要的是L(m,n)，即表x 和表y 的LCS的长度。如果根据之前的归纳编写递归程序，它所花的时间是m 和n 的较小者的指数。这一简单的递归算法对n=m=100这样的情况而言要花上太多太多的时间。这一递归表现如此糟糕的原因有些复杂。首先，假设表x 和表y 中的字符间完全没有匹配，并调用L(3,3)。这会带来对L(2,3)和L(3,2)的调用，而这两次调用又都会带来对L(2,2)的调用。因此就要将L(2,2)的工作完成两遍。随着L 的参数变小，L(i , j )的调用次数会迅速增加。如果将调用追踪继续下去，就会发现，L(1,1)被调用了6次，L(0,1)和L(1,0)各被调用了10次，而L(0,0)被调用了20次。

如果构建二维表或二维数组来存储对应不同i 和 j 的L(i, j )，就可以有更佳的表现。如果按照归纳的次序计算这些值，也就是说先从最小的(i+j )的值开始计算，那么在计算L(i, j )时所需的L 的值总是在表中。其实，逐行计算L 要更简单，也就是对i=0，1，2等计算L，而在一行之中，要按列计算L，也就是对j=0，1，2等计算L。在计算L(i, j )时，还是一定能够在表中找到所需的值，而且不需要进行递归调用。这样一来，计算表中每一项都只需要花费O(1)的时间，而要构建二维表表示长度分别为m 和n 的表的LCS，需要花的时间是O(mn)。

图6-31展示了填充该表的C语言代码，是按行处理而非按i+j 的和处理的。假设表x 存储在数组A[1..m]中，而表y 存储在b[1..n]中。请注意，数组中标号为0的元素未被使用，这样做简化了图6-31中的表示法。这里将证明该程序处理长度分别为m 和n 的表的运行时间为O(mn)的工作留作本节习题。8

8严格地讲，我们只讨论了是一个单变量函数的大O表达式。不过，这里要表达的意思应该是明了的。如果T(m,n)是该程序处理长度为m 和n 的表的运行时间，那么存在常数m₀、n₀和c，使得对所有的m≥m₀和n≥n₀，都有T(m,n)≤cmn。

for (j = 0; j <= n; j++)
    L[0][j] = 0;
for (i = 1; i <= m; i++) {
    L[i][0] = 0;
    for (j = 1; j <= n; j++)
        if (a[i] != b[j])
            if (L[i-1][j] >= L[i][j-1])
                L[i][j] = L[i-1][j];
            else
                L[i][j] = L[i][j-1];
        else /* a[i] == b[j] */
            L[i][j] = 1 + L[i-1][j-1];
}

图 6-31　填充LCS表的C语言程序片段

动态规划
术语“动态规划”源自R. E. Bellman在1950年为解决控制系统中的问题所提出的一般理论。而人工智能领域的工作者通常会将这一技术称为备忘（memoing）或制表（tabulation）。

像本例这样的填表技术通常称为动态规划算法（dynamic programming algorithm）。这种情况下，它比重复为相同子问题求解的直接递归实现更高效。

示例 6.14

设x 是表cbabac，y 是表abcabba。图6-32展示了为这两个表构建的二维表。例如，L(6,7)是a₆≠b₇的情况。因此L(6,7)就是它下方和左侧两个项中的较大者。因为这两项分别为4和3，所以我们右上角的项L(6,7)置为4。现在考虑一下L(4,5)。因为a₄和a₅都是符号b，所以在L(4,5)左下的L(3,4)这项上加1。因为该项为2，所以将L(4,5)置为3。

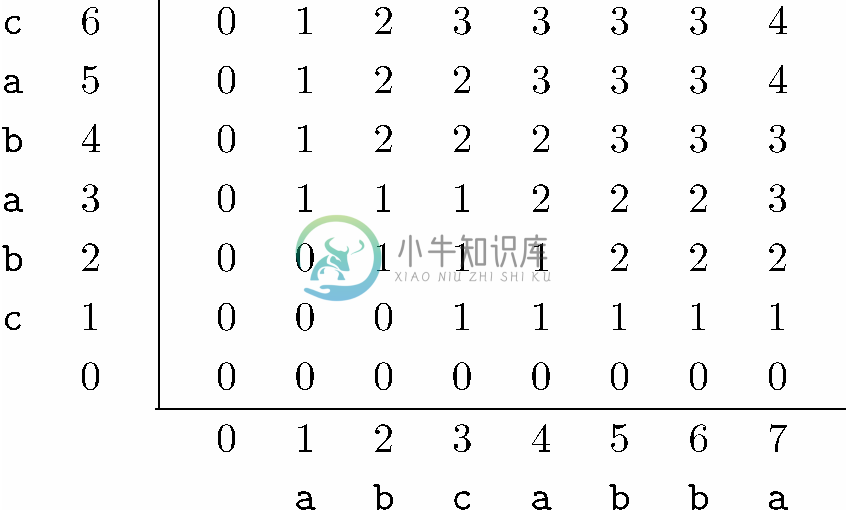
图 6-32　对应cbabac和abcabba最长公共子序列的二维表

6.9.3　LCS的恢复

现在就得到了能给出LCS长度的二维表，不仅能给出问题中两个表的LCS的长度，而且可以给出它们每对前缀的LCS的长度。从这些信息一定能推导出问题中两个表可能的LCS之一。要完成这一工作，就要找到形成LCS之一的匹配元素对。我们会找到一条从右上角开始穿越该二维表的路径，而这一路径将确定一个LCS。

假设这条从右上角开始的路径已经将我们带到了第i 行第j 列，也就是该二维表中对应元素对a_i 和b_j 的点。如果a_i=b_j，L(i , j )就是1+L(i-1, j-1)。因此可以将a_i 和b_j 当作已匹配的元素对，而且我们会把a_i（也是b_j）表示的符号包含在LCS中，并排在目前为止所有已被找到的LCS元素之前。然后将路径向左下移动，也就是说移动到第i-1行第 j-1列。

不过，也可能a_j ≠b_j。如果这样，L(i , j )肯定至少与L(i-1 , j )和L(i , j-1)中的某一个是相等的。如果L(i , j )=L(i-1 , j )，就会把路径向下移动一行，否则，就知道L(i , j )=L(i , j-1)，就会把路径向左移动一列。

遵循这一规则，最终会到达左下角。至此，就已经选定了一个作为LCS的元素序列，而且该LCS本身也是由这些元素组成的表，表中元素的次序与它们被选定的次序是相反的。

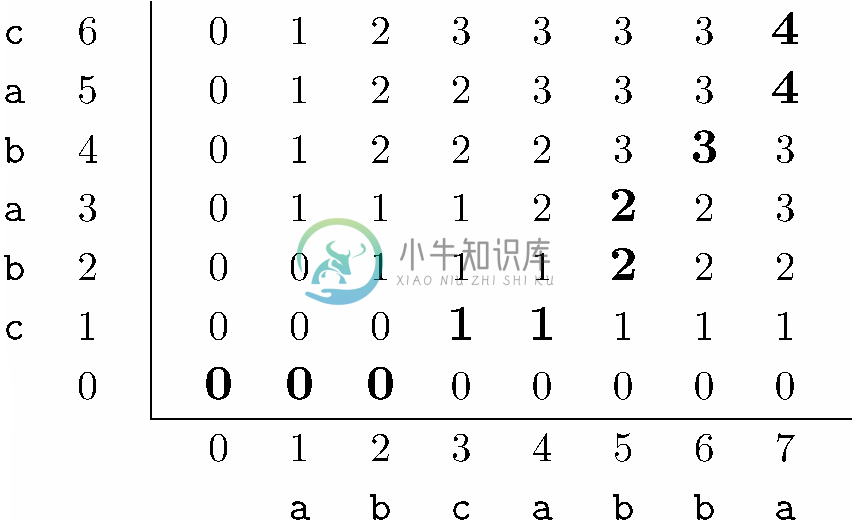
图 6-33　找到最长公共子序列cbba的路径

示例 6.15

图6-33再次展示了图6-32中的二维表，并将路径加粗表示出来。我们从值为4的L(6,7)开始。因为a₆≠b₇，所以立刻向左和向下寻找值4，它至少会在这两个位置中的一个出现。在本例中，4出现在L(6,7)下方，所以我们移动到L(5,7)。现在有a₅≠b₇，都是a。因此a就是该最长公共子序列中最后的符号，于是我们移向左下方，移动到L(4,6)。

因为a₄和b₆都是b，所以将b放入正在成形的LCS中，位于a之前，而我们继续向左下移动，移动至L(3,5)。这里，我们发现a₃≠b₅，不过L(3,5)的值为2，与它下面和左边的项都相等。在这种情况下我们选择向下移动，所以接下来要移动到L(2,5)。在该点会看到a₂=b₅=b，所以我们将b放在正在成形的LCS前头，并继续向左下移动到L(1,4)。

因为a₁≠b₄，L(1,4)只有在它左边的项，而且该项有着与它相同的值1，所以我们移动到L(1,3)。现在有a₁=b₃=c，因此可以将c添加到LCS的前端，并移动到L(0,2)。至此，我们别无选择，只能向左移动到L(0,1)，然后移动到L(0,0)，最终完成了这条路径。得到的LCS由我们发现的4个字符按反序组成，就是cbba。这刚好是我们在示例6.12中提到的两个LCS之一。要得到其他的LCS，可以在L(i , j )与L(i-1 , j )和L(i , j-1)都相等时选择向左移动而非向右移动，并且在L(i-1, j )和L(i , j-1)其中之一等于L(i , j)时，选择向左或向右移动，即便是在a_i =b_j 的情况下（即跳过某些匹配而直接到达其左边的匹配）。

可以证明，这一寻路算法总能找到最大公共子序列。我们要利用对两个表长度之和进行完全归纳加以证明的命题如下。

命题S(k)。如果在第i 行第 j 列，其中i+j=k，而且有L(i , j )=v，我们随后就会在LCS中找到v 个元素。

依据。依据是k=0的情况。如果i+j=0，那么i 和 j 都为0。我们已经完成了路径，并发现LCS不会有更多元素。因为已经知道L(0,0)=0，所以归纳假设对i+j=0成立。

归纳。假定对k 或更小的和的归纳假设成立，并令i+j=k+1。假设我们在值为v 的L(i , j )处。如果a_i=b_j，就找到了匹配并移动到L(i-1, j-1)。因为(i-1）+（j-1)的和小于i+1，所以归纳假设是适用的。因为L(i-1, j-1)一定是v-1，所以我们知道LCS还将找到v-1个元素，再加上已经找到的一个元素，就会给我们v 个元素。这一直观结果证明了这种情况下的归纳假设。

唯一的例外是a_i ≠b_j 的情况。这种情况下，L(i-1, j )或L(i , j-1)，或者这两者，一定具有值v，而且我们要移动到具有值v 的这些位置之一。因为任一情况下行列值的和都是i+j-1，所以归纳假设是适用的，这样就能得出在LCS中找到v 个元素的结论。这样我们又能得出S(k+1)为真的结论。因为已经考虑了所有的情况，所以就完成了证明，并可以说如果在数据项L(i , j )处，就总是在LCS找出L(i , j )个元素。

6.9.4　习题

1. 下列表的LCS的长度各为多少？

(a) banana和cabana

(b) abaacbacab和bacabbcaba

2. * 找到习题1两个小题中两个表的所有LCS。提示：在为习题(1)构建二维表之后，从右上角往回追溯，在遇到有两条或三条不同路径的点时，要顺着每种选择继续移动。

3. ** 假设使用我们最先描述的递归算法而不是推荐的填表程序计算LCS。如果对两个没有共同符号的表调用L(4,4)，要执行多少次对L(1,1)的调用？提示：使用填表（动态规划）算法计算二维表，给出对应所有i 和 j 的L(i , j )的值。将计算结果与4.5节中的帕斯卡三角相比较。这一关系表示了与调用次数的公式有关的哪些信息？

4. ** 假设有表x 和表y，且二者的长度均为n。当n 小到一定程度之后，就最多只有一个字符串是x 和y 的LCS了，虽然该字符串可能出现在x 和/或y 的不同位置。例如，如果n=1，那么LCS只能是ε，除非x 和y 都是同一个符号a，这种情况下a 就是唯一的LCS。那么，让x 和y 可以有两个不同LCS的最小n 值是多少？

5. 证明图6-31所示的程序运行时间为 O(mn) 。

6. 编写C语言程序，接受图6-31所示程序计算出的那种表，并找出LCS在各字符串中的位置。如果该表的规格为m×n，那么这一程序的运行时间是多少？

7. 在6.9节开头，我们表示过LCS的长度是与两个字符串最大位置匹配的大小有关的。

(a*) 通过对k 的归纳证明，如果两个字符串有着长度为k 的公共子序列，那么它们也有着长度为k 的匹配。

(b) 证明：如果两个字符串有长度为k 的匹配，那么它们也有长度为k 的公共子序列。

6.10　字符串的表示

字符串可能是实践过程中最常见的表的形式。表示字符串的方法数不胜数，而且其中一些技巧很难适用于其他类型的表。因此，本节专门介绍一些与字符串有关的特殊问题。

首先，应该意识到存储单个字符串基本不成问题。通常，我们有大量很短的字符串。它们可能形成词典，意味着我们可以随着时间的推移插入和删除字符串，也可能是静态字符串集合，时间再久也不会改变。下面要讲两个典型的例子。

1. 字母索引是一种研究文本的实用工具，它是由文档中使用过所有单词以及这些单词出现的位置构成的表。在大型文档中通常会有成千上万个不同的单词，而单词每出现一次就要被存储一次。这一单词集合是静态的，也就是说，一旦成形就不会改变，除非原有的字母索引中存在错误。

2. 将C语言程序转化为机器代码的编译器必须记录表示程序变量的所有字符串。大型程序可能拥有成百上千的变量名。想想看，分别在两个函数中声明的局部变量i，其实是两个不同的变量，这样就能明白为什么会有如此多的变量了。随着编译器对程序加以扫描，会找到新的变量名，并将其插入变量名集合中。一旦编译器完成了函数的编译，该函数的变量对随后的函数来说便不可用了，因此可以删除掉。

在这两个例子中，都存在很多短字符串。英语中的短单词比比皆是，而程序员则喜欢用i或x这样的字母表示变量。另一方面，不管是在英语文本还是在程序中，单词的长度都是没有限制的。

6.10.1　C语言中的字符串

C语言程序中可能出现字符串常量，而它们会被存储为字符数组，后面跟上名为空字符（null character）且值为0的特殊字符“\0”。不过，在上面提到的应用中，我们需要随着程序运行而创建并存储新字符串的便利。因此，需要能向其中存储任意字符串的数据结构。其中一些可能如下。

1. 使用定长数组存放字符串。比数组短的字符串之后由空字符补齐。而比数组长的字符串不能完整地存储到数组中，它们必须被截断，只将长度与数组长度相等的前缀存储到数组中。

2. 与(1)类似的模式，但假设每一个字符串或被截断字符串的前缀之后都有一个空字符。这种方式简化了字符串的读操作，但它让数组中可以存储的字符串的长度减少了1。

3. 与(1)类似的模式，它不会在字符串后放置空字符，而是用另一个整数length 指示字符串的真实长度。

4. 要避免最大字符串长度的限制，可以将字符串中的字符存储为链表元素，而且可以将多个字符存储在一个单元中。

5. 可以创建大型字符数组，将很多单独的字符串放置其中。而每个字符串就由指向该字符串开头字符在该数组中位置的指针表示。字符串可能以空字符结尾，也可能有与之关联的长度。

6.10.2　定长数组表示

我们来考虑一下上述第(1)类结构，其中字符串是由定长数组表示的。在下面的例子中，我们会创建拥有定长数组作为其中一个字段的结构体。

示例 6.16

考虑一下用来存放索引中某一项，即单个单词以及与其相关的信息的数据结构。我们需要

存放下列内容。

1. 单词本身；

2. 单词出现的次数；

3. 表示文档中文本行的表，该单词会在其中出现一次或多次。

因此可以使用如下结构体：

typedef struct {
    char word[MAX];
    int occurrences;
    LIST lines;
} WORDCELL;

这里的MAX是指单词的最大长度。所有的WORDCELL结构体都包含一个名为word的有MAX个字节的数组，不管要存放的单词到底有多短。

字段occurrence是计算某单词出现次数的计数器，而lines则是指向链表开头的指针。链表中的单元具有由以下宏定义的常规类型：

DefCell(int, CELL, LIST);

每个单元存放着一个整数，表示出现问题中单词的文本行。请注意，如果某个单词在一行中出现若干次，那么occurrence就要比表的长度更大。

在图6-34中，我们看到表示《圣经·创世记》第1章中的单词earth的结构体。假设MAX至少为6。表示行（诗句）号的完整表是(1，2，10，11，12，15，17，20，22，24，25，26，28，29，30)。

{%}

图 6-34　单词earth在《圣经·创世记》第1章中的索引项

整个索引可能是由一系列WORDCELL类型的结构体组成的。例如，这些结构体可以被组织为一棵二叉查找树，有着基于单词字母顺序的<次序。在使用字母索引时，该结构体可以提供相当高的单词访问速度。而随着我们不断扫描文本，找到并列出各单词的出现，它还能让我们高效地创建索引。要使用二叉树结构，就需要在类型WORDCELL中定义表示左子节点和右子节点的字段。我们还可以在原始的WORDCELL类型定义中加入“next”字段，从而将这些结构体排列在链表中。这是一种更简单的结构，不过如果单词数量众多，它的效率就要差不少。我们在第7章中将会看到如何在散列表中排列这些结构体，这基本上是解决这一问题的所有数据结构中性能最佳的。

6.10.3　字符串的链表表示

字符串长度的限制，以及不管字符串有多短都需要分配固定量的空间，这是字符串定长数组实现的两大缺点。不过，C语言和其他语言都允许使用者构建其他更为灵活的数据结构来表示字符串。例如，如果希望字符串长度没有上限，可以使用常规的字符链表存放字符串。也就是，可以声明如下类型：

typedef struct CHARCELL *CHARSTRING;
struct CHARCELL {
    char character;
    CHARSTRING next;
};

在类型WORDCELL中，CHARSTRING成了word字段的类型，如：

typedef {
    CHARSTRING word;
    int occurrences;
    LIST lines;
} WORDCELL;

例如，单词earth可以表示为

{%}

这种模式消除了单词长度的上限，不过在实际应用中，对空间的利用却不是很好。原因在于，假设用1个字节表示字符，并且通常用4个字节表示指向链表下一个单元的指针，那么每个CHARCELL类型的结构体至少要占用5个字节。因此，绝大部分空间是由指针的“系统开销”占用的，只有少部分空间是由字符的“有效负载”使用的。

不过可以更灵活些，将若干字节打包装入每个单元的数据字段。例如，如果在每个单元中放入4个字符，而指针还是消耗4个字节，那么就有一半空间是由“有效负载”使用的，而每单元一个字符的模式只有20%的有效负载。唯一要注意的地方是，必须用某一字符（比如说空字符）作为字符串终止字符，就像存储在数组中的字符串所做的那样。一般而言，如果CPC（Characters Per Cell，每单元字符数）是我们希望在一个单元中放置的字符数，就可以按照如下声明定义单元：

typedef struct CHARCELL *CHARSTRING;
struct CHARCELL {
    char characters[CPC];
    CHARSTRING next;
};

例如，如果CPC=4，就可以将单词earth存储在两个单元中，形如：

{%}

也可以将CPC增加到4以上。这样做的话，指针所占空间的比例进一步下降，这是很好的情况，意味着使用链表的系统开销下降了。另一方面，如果使用非常大的CPC值，就会发现，几乎所有单词都只需要使用一个单元，但是该单元中可能有很多未使用的位置，就像长度为CPC的数组那样。

示例 6.17

假设在所有的字符串中，有30%是长为1到4个字符的字符串，40%是长5到8个字符的，20%是9到12个字符的，还有10%是13到16个字符的。图6-35中的表给出了表示4个范围的单词的链表，在CPC分别为4、8、12和16时所占的字节数。就我们假设的单词出现频率而言，CPC=8的结果最佳，平均要使用15.6个字节。也就是说，每个单元最好用8个字节存放字符，加上存放next指针的4个字节，即每个单元总共要使用12个字节。请注意总空间开销，在加上指向表前端的指针之后，就达到了19.6字节，就不如使用16字节的字符数组那么好了。不过，这种链表模式也可以容纳长度超过16个字符的字符串，虽然这里假设找到这样这种字符串的概率为0。

每单元字符数
范围	概率	4	8	12	16
1-4	0.3	8	12	16	20
5-8	0.4	16	12	16	20
9-12	0.2	24	24	16	20
13-16	0.1	32	24	32	20
平均		16.8	15.6	17.6	20.0

图 6-35　当CPC为不同值时，不同长度范围的字符串使用的字节数

6.10.4　字符串的海量存储

还存在另一种存储大量字符串的方法，它兼具数组存储的优势（低系统开销）与链表存储的优势（因为填充而不浪费空间，且字符串长度无限制）。我们创建一个非常长的字符数组，并将每个字符串都存储到这一数组中。为了区分一个字符串的结束与下一个字符串的开始，需要一个名为端记号（endmarker）的特殊字符。端记号字符不是合法字符串的一部分。尽管选择不打印的字符（比如空字符）是更常见的，不过为了便于识别，在接下来的内容中会使用*作为端记号。

示例 6.18

假设通过

char space[MAX];

声明数组space。然后就可以通过给出指向某单词在space数组中第一个位置的指针来存储该单词了。模仿示例6.16中WORDCELL结构体的WORDCELL结构就是：

typedef struct {
    char *word;
    int occurrences;
    LIST lines;
} WORDCELL;

在图6-36中，我们看到表示《圣经·创世记》的字母索引中单词the的WORDCELL结构体。不过接下来的情况并不是这样。即便接下来的元素中含有beginning、God和created，space数组也不会出现第二个the了。通过增加WORDCELL结构体中对应单词the的occurrences的值，该单词就被记录在列了。随着在这本书中继续向前处理，发现单词更多的重复，space数组中的项就不再像《圣经》原文那样了。

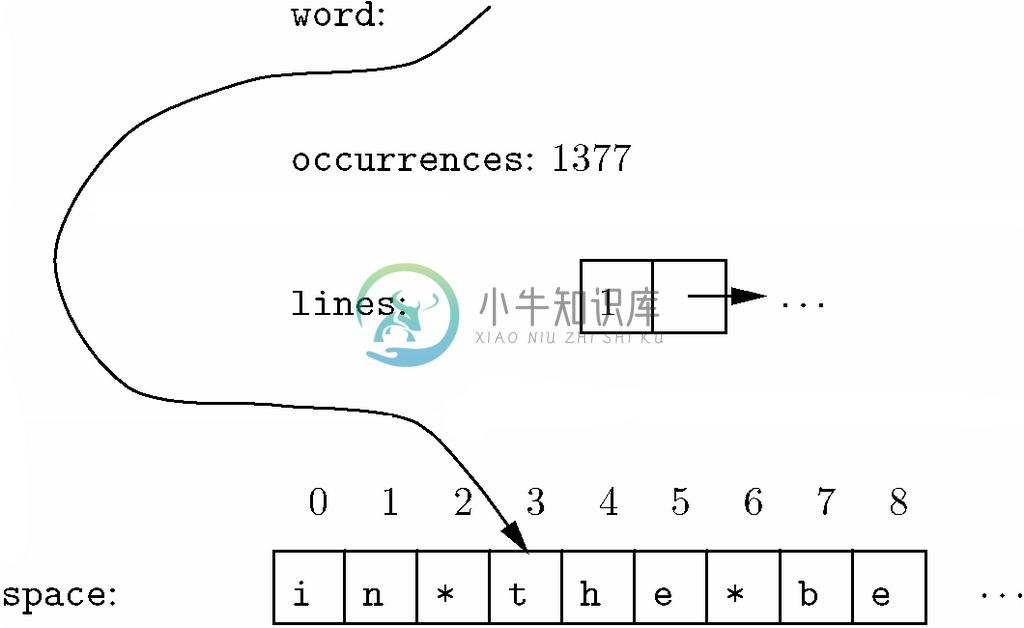
图 6-36　通过字符串空间的索引表示单词

就像示例6.16中那样，示例6.18中的结构体也可以通过添加指向WORDCELL结构体的合适指针字段形成二叉查找树或链表这样的数据结构。函数lt (W₁,W₂)可以按照两个WORDCELL类型结构体W₁和W₂的word字段的词典顺序对二者加以比较。

要使用这样的二叉查找树构建索引，需要使用指针available指向space数组中第一个未被占用的位置。一开始，available指向space[0]。假设对要构建索引的文本进行扫描，并且找到下一个单词，比方说是the。我们现在不知道the是否已经在二叉查找树中，因此要临时将the*添加到available指向的位置以及接下来的3个位置中。记住，这一新添加的单词要占用4个字节。

现在可以在二叉查找树中查找单词the了。如果找到该单词，就在其出现次数的计数器上加1，并将当前行插入表示文本行的表中。如果未找到，就创建含有WORDCELL结构体的各个字段以及左子节点和右子节点指针（都为NULL）的新节点，并将其插入树中合适的位置。我们将新节点的word字段置为available，这样一来它就指向我们这里单词the的副本了。再将occurrences置为1，并创建由当前文本行的组成的表示字段lines的表。最后，必须给available加上4，因为现在已经把单词the永久地加入space数组了。

空间用尽时会发生什么情况？
我们假设了space是足够大的，从而总是有空间容纳新添加的单词。实际情况是，每当添加新的字符时，我们都必须注意当前写入字符的位置一定要小于MAX。
如果想在空间用尽后输入新的单词，就需要准备好在旧块用尽后获得新空间块。并不是创建数组space，而是要定义字符数组类型
typedef char SPACE[MAX];
接着可以按照如下定义创建新数组，其中available指向数组的第一个字符。
available = (char *) malloc(sizeof(SPACE));
只要直接赋值
last = available + MAX;
就能得到该数组的末端了。
然后可以向available指向的数组插入单词。如果没办法再往该数组中装入单词，就可以调用malloc创建另一个字符数组。当然，一定要注意不要让写操作越过数组的末端，而且如果遇到长度大于MAX的字符串，就没办法以这种模式存储单词了。

6.10.5　习题

1. 针对示例6.16中讨论的结构体类型WORDCELL，编写如下程序。

(a) 函数create，要返回指向WORDCELL类型结构体的指针。

(b) 函数insert(WORDCELL *pWC, int line)，接受指向WORDCELL结构体的指针以及行号，在该单词的出现次数上加1，而且如果该行未出现在表示各行的表中，就将其添加进去。

2. 重做示例6.17，假设长度从1到40的单词都等可能出现，也就是10%的单词长度为1至4，10%的为5至8，等等，直到10%的在37到40这个范围内。如果CPC分别为4、8、…、40，分别平均需要多少个字节？

3. * 在示例6.17的模型中，如果从1到n 的所有单词长度都等可能出现，那么CPC为何值（表示为n的函数）时使用的字节数是最少的？如果得不出具体的答案，也可以用大O近似值来表示。

4. * 使用示例6.18中所示结构体的优势之一在于，在两个或多个单词中可以共享space数组的一些部分。例如，在图6-36所示的数组中，有单词he的word字段等于5。对单词all、call、man、mania、maniac、recall、two、woman进行压缩，使其在space数组中占用尽可能少的元素。通过压缩可以节省多少空间？

5. * 另一种存储单词的方法要从space数组中消除端记号字符。并且要为示例6.18中的WORDCELL结构体加入length字段，从而表示出在word字段表示的单词中从第一个字符起共有多少个字符。假设length字段的整数要占用4字节，那么这种模式与示例6.18中的模式相比，是节省了空间还是更耗费空间？如果存储该整数只需要1字节呢？

6. ** 习题5中描述的方案也带来了压缩space数组的可能。现在即便单词之间没有任意一方是另一方的后缀，也可以互相重叠了。使用习题5中的模式，存储习题4表中的单词，需要space数组中多少个单元？

7. 编写程序，接受示例6.18中讨论的两个WORDCELL结构体，并确定哪个结构体中的单词在词典次序上先于另一个。回想一下，示例6.18中单词都是由*终结的。

6.11　小结

本章涵盖了以下要点。

表是一种表示元素序列的重要数据模型。
链表和数组是两种可用于实现表的数据结构。
表是词典抽象数据类型的一种简单实现，不过其效率无法与第5章中的二叉查找树和第7章中的散列表相提并论。
将“哨兵”放置在数组末尾，从而确保找到正在寻找的元素，是一种实用的提高效率的方法。
栈和队列都是特殊类型的表。
栈是实现递归函数的“幕后英雄”。
字符串是表的一种重要特例，而且有若干种特殊的数据结构可以有效地表示字符串，其中包括每单元存储若干字符的链表，以及由很多字符串共享的大型数组。
找出最大公共子序列的问题可以通过“动态规划”技术有效地解决，在动态规划过程中我们会按照合适的次序填充信息表格。

6.12　参考文献

Knuth [1968]仍然是表数据结构的基本来源。尽管很难追溯“表”或“栈”这种非常基础的概念的起源，但最先使用表作为数据模型的程序设计语言是IPL-V（Newell etal. [1961]），不过早期的表处理语言中，只有Lisp（McCarthy etal. [1962]）现在还属于重要语言的范畴。顺便提一句，Lisp表示的是LISt Processing（表处理）。

Aho, Sethi, and Ullman [1986]中详细地讨论了栈在递归程序的运行时实现中的使用。

6.9节描述的最长公共子序列算法源自Wagner and Fischer [1975]。Hunt and Szymanski [1977]则描述了实际应用在UNIX的diff命令中的算法。Aho [1990]全面介绍了若干种涉及字符串匹配的算法。

Bellman [1957]描述了作为抽象技巧的动态规划。Aho, Hopcroft, and Ullman [1983]给出了一系列使用动态规划的算法的示例。

Aho, A. V. [1990]. “Algorithms for finding patterns in strings,” in Handbook of Theoretical Computer Science Vol. A: Algorithms and Complexity (J. Van Leeuwen, ed.), MIT Press, Cambridge, Mass.

Aho, A. V., J. E. Hopcroft, and J. D. Ullman [1983]. Data Structures and Algorithms, Addison-Wesley, Reading, Mass.

Aho, A. V., R. Sethi, and J. D. Ullman [1986]. Compilers: Principles, Techniques, and Tools, Addison-Wesley, Reading, Mass.

Bellman, R. E. [1957]. Dynamic Programming, Princeton University Press, Princeton, NJ.

Hunt, J. W. and T. G. Szymanski [1977]. “A fast algorithm for computing longest common subsequences,” Comm. ACM 20:5, pp. 350–353.

Knuth, D. E. [1968]. The Art of Computer Programming, Vol. I, Fundamental Algorithms, Addison-Wesley, Reading, Mass.

McCarthy, J. et al. [1962]. LISP 1.5 Programmer's Manual, MIT Computation Center and Research Laboratory of Electronics, Cambridge, Mass.

Newell, A., F. M. Tonge, E. A. Feigenbaum, B. F. Green, and G. H. Mealy [1961]. Information Processing Language-V Manual, Prentice-Hall, Englewood Cliffs, New Jersey.

Wagner, R. A. and M. J. Fischer [1975]. “The string to string correction problem,” J. ACM 21:1, pp. 168–173.

第 6 章 表数据模型

6.1 本章主要内容

6.2 基本术语

示例 6.1

示例 6.2

示例 6.3

6.2.1 表的长度

示例 6.4

6.2.2 表的部分

示例 6.5

示例 6.6

6.2.3 表中元素的位置

6.2.4 习题

6.3 对表的操作

6.3.1 插入、删除和查找

示例 6.7

6.3.2 串接

示例 6.8

6.3.3 表的其他操作

6.3.4 习题

6.4 链表数据结构

6.4.1 词典操作的链表实现

6.4.2 查找

6.4.3 删除

6.4.4 插入

6.4.5 带重复的插入、查找和删除

6.4.6 表示词典的已排序表

6.4.7 各种方法的比较

6.4.8 双向链表

6.4.9 习题

6.5 表基于数组的实现

6.5.1 线性查找

6.5.2 带哨兵的查找

6.5.3 利用二叉查找对已排序表进行查找

6.5.4 习题

6.6 栈