第 4 章　组合与概率

优质

小牛编辑

125浏览

2023-12-01

在计算机科学中，我们常需要为事物计数，并度量事件的可能性。计数属于数学中的组合学分支，而度量事件的可能性则属于概率论的范畴。本章要介绍这两个领域的基本原理。我们会了解到一些问题的答案，诸如程序中有多少条执行通路（execution path），或给定通路出现的可能性有多大等。

4.1　本章主要内容

本章给出了一系列越来越复杂的情况，每种情况都通过一个简单的范例问题说明，借此对组合（或“计数”）加以研究，而且会为每个问题推导出用于确定可能结果数量的公式。要研究的问题包括以下几个。

为分配计数（4.2节）。范例问题是：用k 种颜色为n 所房屋粉刷共有多少种不同方式。
为排列计数（4.3节）。范例问题是：确定n 个不同项能构成多少种不同的次序。
为有序选择计数（4.4节），也就是从n 个不同事物中选出k 个，并按次序排列这k 个事物。范例问题是：计算赛马比赛中不同马匹获得前三名的排列方法数。
为n 个事物中的m 个的组合计数（4.5节），也就是从n 个不同对象中选择m 个，而不考虑被选取对象的次序。范例问题是：为可能的扑克牌型计数。
为具有某些重复项的排列计数（4.6节）。范例问题是：计算某些字母多次出现的单词的变位词的数量。
为分发容器中对象（可能具有重复对象）的方法计数（4.7节）。范例问题是：为给小朋友分发水果的方法计数。

本章的后半部分要讨论的是概率论，涵盖以下主题。

基本概念：概率空间、实验、事件、事件概率。
条件概率与事件独立性。这些概念可帮助我们了解，对一次实验结果（比如纸牌的牌面图案）的观察会怎样影响未来事件的概率。
概率推理和方法。通过这些推理和方法，可从与事件的概率及条件概率相关的有限数据中，估算出事件组合的概率。

我们还将讨论概率论在计算机领域的一些应用，包括根据数据进行或然性推理的系统，以及一类“有很大概率”有效但不保证一直有效的算法。

4.2　为分配计数

一种简单却极重要的计数问题是处理一组项，为每一项指定某一组固定值中的某个值。我们需要确定可能有多少种将值分配给项的方式。

示例 4.1

图4-1展示了一个典型的例子，其中有并排4所房屋，而且可将每所房屋粉刷成红、绿、蓝这三种颜色中的一种。在本例中，房屋就是之前所提到的“项”，而颜色就是“值”。图4-1展示了一种可能的颜色分配方式，其中第一所房屋被刷成红色，第二所和第四所被刷成蓝色，而第三所被刷成绿色。

{%}

图 4-1　房屋颜色分配的一种方式

要回答“有多少种不同分配方式”，首先需要定义我们所说的“分配”具有何种含义。在本例中，一种分配方式就是一个具有4个值的表，其中每个值都是从红、绿、蓝这3种颜色中任选其一。接下来要分别用字母R、G 和B 来表示这3种颜色。而当且仅当两个这样的表至少有一个位置不同时，我们称这两个表是不同的。

在这个房屋与颜色的例子中，可以为第一所房屋任选三种颜色之一。不管为第一所房屋选择了什么颜色，在粉刷第二所房屋时还是有这三种选择。因此粉刷前两所房屋的方式有9种，对应着9个不同的字母对，每个字母都是R、G 和B 这三者之一。类似地，对前两所房屋所具有的9种分配方式的每一种而言，都可以为第三所房屋在三种颜色中任选其一。这样一来，前三所房屋的粉刷方式就达到了9×3=27种。最后，这27种分配方式中对应的第四所房屋又都能在三种颜色中任选其一，因此总共有27×3=81种粉刷房屋的方式。

4.2.1　为分配计数的规则

可以对以上示例加以扩展。在一般情形下，有一列n个“项”，比如示例4.1中的房屋；还有一组k个“值”，如示例4.1中的颜色，可以给某个项指定这些值中的任一种。一种分配就是一个含有n个值的表(v₁,v₂,…,v_n)。v₁,v₂,…,v_n中的每一个都是从这k个值中任选其一。这种分配指定了v_i 从v₁到第i 项的值，其中i=1,2,…,n。

当有n个项，而且可以为每一项指定k个值之一时，就会有k_n 种不同的分配。例如，在示例4.1中，一共有n=4项，也就是有4所房屋，而且有k=3个值，也就是有3种颜色。我们就可以计算出总共有81种不同的分配。请注意，就是3₄=81种。可以通过对n 的归纳证明这一一般规则。

命题 S(n)。为n个项中每一项分配k个值中的任一个，共有k_n 种方式。

依据。依据为n=1的情况。如果只有一项，可以为它任选k个值中的一个。因为k₁=k，所以依据得证。

归纳。假设命题S(n)为真，并考虑S(n+1)，也就是为n+1项分别分配k个值之一，共有kⁿ⁺¹种方式。可以将这种分配分解为给第一项选择值，以及针对第一个值的每种选择，为剩下的n项分配值。对每种这样的选择而言，根据归纳假设，剩下的n项有kⁿ 种分配值的方式。所以总分配方式共有k×kⁿ 种，也就是有kⁿ⁺¹种。因此我们证明了S(n+1)，完成了归纳步骤。

图4-2表示了当n+1=4且k=3时，即在示例4.1这个讨论4所房屋和3种颜色的具体例子中，对第一个值的选择以及相应的剩余项分配方式的选择。也就是说，在归纳假设中假定选择3种颜色之一粉刷3所房屋共有27种分配方式。

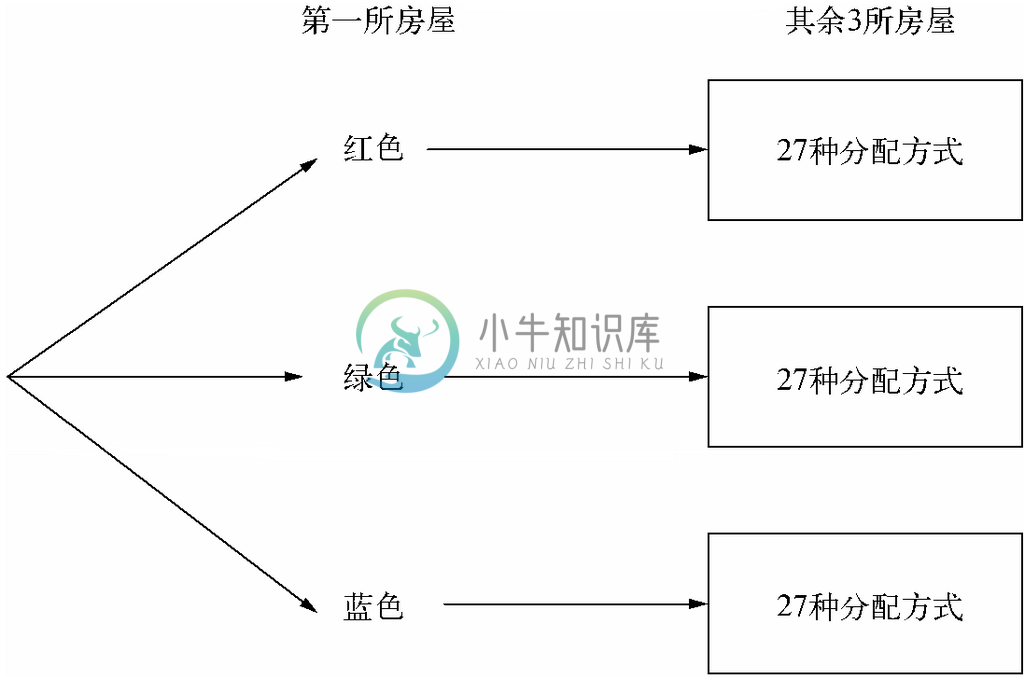
图 4-2　用3种颜色粉刷4所房屋的分配方式数

4.2.2　为位串计数

在计算机系统中，我们常遇到由0和1组成的串，而这些串往往用作对象的名称。例如，我们可能购买具有“64MB主内存”的计算机。每一个字节都有自己的名称，而这个名称是长度为26位的位序列，每一位要么是0，要么是1。这种由0和1组成的表示名称的串就叫作位串。

为什么对64MB的内存来说是26位呢？答案就源自分配计数问题。当我们计算长度为n的位串的数量时，可以将串中的位置视作“项”，而这些位置可能存放0或1这两个值中的一个。因为有两个值，所以有k=2，而为n个项分配二值之一的分配方式共有2ⁿ种。

如果n=26，即考虑长度为26的位串，就可能有2²⁶种位串。2²⁶的精确值为67 108 864。而按照计算机的语法，这个数字会被视为“6 400万”，虽然真实的数字显然要比这个值大上约5%。接下来的附注栏简要介绍了该主题，并试着解释了为2的乘方命名时涉及的一般规则。

K、M和2的乘方
将2的乘方转换成10的乘方有个实用的技巧。我们可以注意到，2¹⁰，也就是1024，与1000是非常接近的。因此，2³⁰，也就是(2¹⁰)³，或者说大概是1000³，即10亿。那么，2³²=4×2³⁰，也就是约40亿。其实，计算机科学家通常都会认可2¹⁰正好是1000的假设，并将2¹⁰说成是1K，其中K表示kilo（千）。例如，我们可将2¹⁵转换成32K，因为
2¹⁵=2⁵×2¹⁰=32×“1000”
而我们将实际值为1 048 576的 2²⁰ 称为1M，或者是1兆，而不是称为1000K或1024K。对 2²⁰到 2²⁹ 这几个2的乘方数，我们会提取出 2²⁰ 这个因子。因此， 2²⁶ 就是 2⁶×2²⁰ ，或者说是64兆。这正是 2²⁶ 字节被称为64兆字节或64 MB的原因。
下表给出了多项10的乘方，以及与其近似相等的2的乘方。
前缀
字母
值
Kilo
K
10³ 或 2¹⁰
Mega
M
10⁶ 或 2²⁰
Giga
G
10⁹ 或 2³⁰
Tera
T
10¹² 或 2⁴⁰
Peta
P
10¹⁵ 或 2⁵⁰
本表格表明对超过 2²⁹ 的2的乘方，我们分别会提取出 2³⁰ 、 2⁴⁰ 或是可以达到的2的任意整十次方作为因子。不管用什么单位度量，剩下的2的乘方会在命名时加上giga-、tera-或peta-这些前缀。例如， 2⁴³ 字节就是8TB。

前缀	字母	值
Kilo	K	10³ 或 2¹⁰
Mega	M	10⁶ 或 2²⁰
Giga	G	10⁹ 或 2³⁰
Tera	T	10¹² 或 2⁴⁰
Peta	P	10¹⁵ 或 2⁵⁰

4.2.3　习题

1. 在下列情形中，分别有多少种粉刷方式?

(a) 3所房屋，每一所可从4种颜色中任选一种。

(b) 5所房屋，每一所可从5种颜色中任选一种。

2. 假设计算机密码由8到10位字母和（或）数字组成。可能有多少种不同的密码？请记住，大写字母和小写字母是不同的。

3. * 考虑如图4-3所示的f函数。f可以返回多少种不同的值？

int f(int x)
{
    int n;

    n = 1;
    if (x%2 == 0) n *= 2;
    if (x%3 == 0) n *= 3;
    if (x%5 == 0) n *= 5;
    if (x%7 == 0) n *= 7;
    if (x%11 == 0) n *= 11;
    if (x%13 == 0) n *= 13;
    if (x%17 == 0) n *= 17;
    if (x%19 == 0) n *= 19;
    return n;
}

图 4-3　f函数

4. 在“好莱坞广场”游戏中，X和O可能以任意组合被放置在井字棋棋盘（一个3×3的矩阵）9个格子的任意一个中（即与普通井字棋玩法不同的是，这里的X和O不必要交替摆放，所以，打个比方，所有的格子都可以放上X）。方阵也可能为空，也就是说，既不含X，也没有O。那么有多少种不同的摆放方法呢？

5. 用10个数字可以组成多少种长度为n的串？其中某个数字可能出现任意次，也可能根本不出现。

6. 用26个小写字母可以组成多少种长度为n的串？其中某个字母可以出现任意次，也可能根本不出现。

7. 根据上文附注栏中所述的规则，将以下内容转换成K、M、G、T或P：(a) 2¹³ (b) 2¹⁷ (c) 2²⁴ (d) 2³⁸ (e) 2⁴⁵ (f) 2⁵⁹。

8. * 将以下10的乘方转换成近似的2的乘方：(a) 10¹² (b) 10¹⁸ (c) 10⁹⁹ 。

4.3　为排列计数

本节中我们将解决另一个基础的计数问题：将给定的n个不同对象排成一列，可以有多少种不同的排列方式？这种排序称为这些对象的排列。我们将用Π(n)表示n个对象的排列数。

关于为排列计数在计算机科学中的重要性，我们来举例说明。假设要为给定的n个对象a₁、a₂、…、a_n排序。如果对这些对象一无所知，那么任何次序都可能是正确的排序次序，因此排序可能的结果数就是Π(n)，也就是n个对象的排列数。我们很快就会看到，这一结果有助于证实：通用的排序算法所需的时间与n logn成正比，并因此可证实3.10节中运行时间为O(n logn)的归并排序算法会快上某个常数因子倍。

排列计数规则还有很多其他应用。例如，我们将在后面的小节中看到的，它在组合与概率这样更为复杂的计数问题中也分量十足。

示例 4.2

为了直观，我们列举一下微量对象的排列。首先，显然有Π(1)=1。也就是说，如果只有一个对象A，就只有一种次序A。

然后考虑有两个对象A 和B 的情况。可以从两个对象中任选其一排列在第一位，而将另一个对象排列在第二位，因此有两种次序：AB 和BA。所以Π(2)=2×1=2 。

接着看看有3个对象A、B 和C 的情况。可以从三者中任选其一排在首位。先考虑选择A 排在第一位的情况，这时候剩下B 和C 这两个对象，它们可以按两个对象的两种次序之一分布，从而完成这一排列。因此可以看出，由A 开头的排列有两种，即ABC 和ACB。

类似地，如果以B 开头，也有两种方式完成这一序列，对应为剩下的对象A 和C 排序的两种方式，因此有序列BAC 和BCA。最后，如果以C 开头，就可以用两种方式为剩下的对象A 和B 排序，从而得到序列CAB 和CBA。ABC、ACB、BAC、BCA、CAB 和CBA 这6个序列就是3个元素可能排成的所有次序了。也就是说，，Π(3)=3×2×1=6。

接下来考虑一下4个对象A、B、C 和D 可以形成多少排列。如果选择A 排在首位，那么跟在A之后的对象B、C 和D 可以按照6种次序中的任意一种排列。类似地，如果将B 排在第一位，那么剩下的A、C 和D 也能按6种次序排列。现在一般模式应该明了了。可以从4个元素中任选一个排在第一位，而对每种选择，都可以按照Π(3)=6种可能方式中的任意一种排列剩余元素。请注意，3个对象的排列数并不取决于这3个元素到底是什么。由此可以得出结论：4个对象的排列数等于4乘以3个对象的排列数。

一般而言，对任意n≥1，有Π(n+1)=(n+1)Π(n)　　　　　　(4.1)

也就是说，要为n+1个对象的排列计数，可以从n+1个对象中任选一个排在首位。然后剩下的n个对象可以有Π(n)种排列方式，如图4-4所示。在我们的例子中，n+1=4，于是有Π(4)=4×Π(3)=4×6=24 。

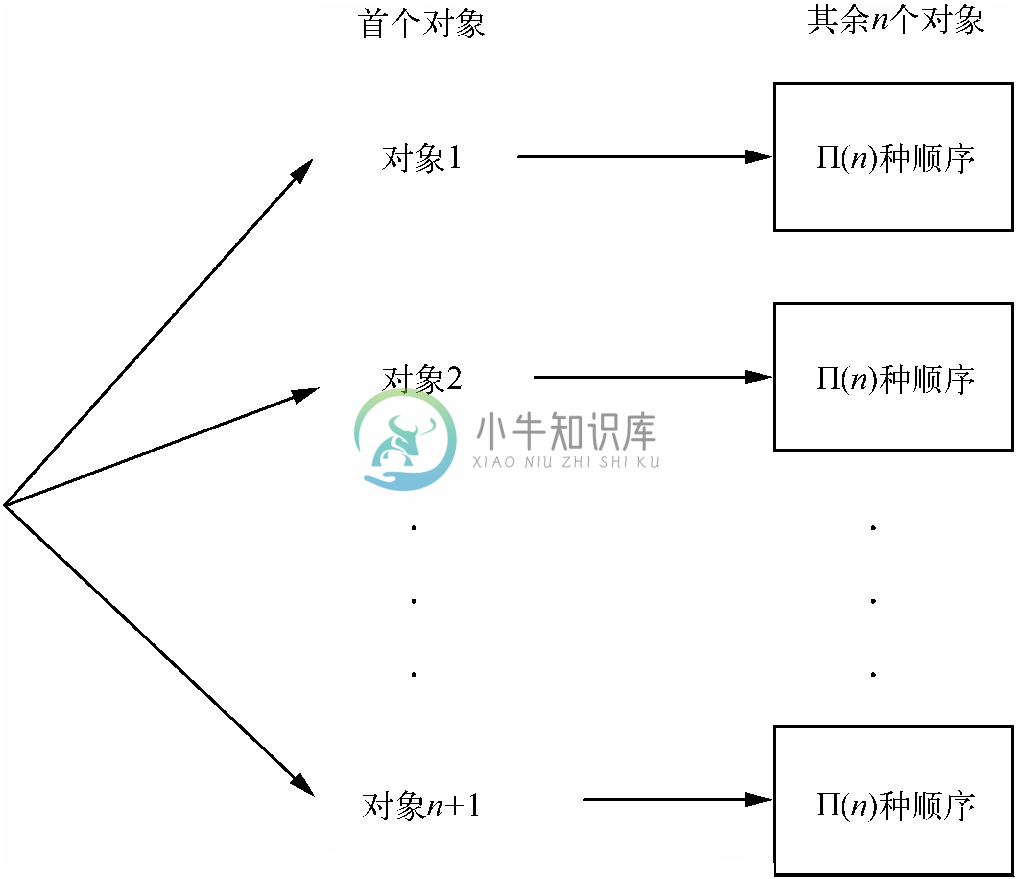
图 4-4　n+1个对象的排列

4.3.1　排列公式

等式(4.1)就是2.5节介绍的阶乘函数定义中的归纳步骤。因此不用为Π(n)等于n!感到惊讶。我们可以通过简单的归纳证明这种等价性。

命题 S(n)。对所有的n≥1，有Π(n)=n!。

依据。对n=1，S(1)表示1个对象有1种排列。我们在示例4.2中已经看出这一点了。

归纳。假设Π(n)=n!。那么要证明的S(n+1)就是Π(n+1)=(n+1)!。由等式(4.1)，有

Π(n+1)=(n+1)×Π(n)

而根据归纳假设，Π(n)=n!。因此，Π(n+1)=(n+1)×n!。因为

n!=n×(n-1)×…×1

所以一定有(n+1)×n!=(n+1)×n×(n-1)×…×1。而后者的积就是(n+1)!，这就证明了S(n+1)为真。

示例 4.3

根据公式Π(n)=n!，可以得出结论：4个对象的排列数是4!=4×3×2×1=24，正如我们在上面所见的。再举个例子，7个对象的排列数就是7!=5040。

4.3.2　排序要花多久

该排列计数公式有个有趣的用途，就是可用来证明，要为n个元素排序，排序算法至少会花上与n logn成正比的某段时间，除非在排序过程中利用到这些元素的某些特殊属性。例如，在后文附注栏有关特例排序算法的介绍中，可以注意到，如果编写只处理较小整数的排序算法，就可以使运行时间比与n logn成正比的值更少。

不过，如果某个排序算法可以处理任意种类的数据，那么只要这些数据可以通过某种“小于”关系进行比较，该算法确定合适次序的唯一方式就是考量两个元素中的一个是否小于另一个。如果某种排序算法对待排序元素的唯一操作是比较二者以确定它们的相对次序，那么这种算法就可称为通用排序算法（general-purpose sorting algorithm）。例如，第2章中介绍的选择排序和归并排序都是这样作出决定的。即便编写的程序是用来处理整数数据的，也可以将其编写得更具一般性，只要将图2-2第(4)行中

if (A[j] < A[small])

这样的比较替换成诸如

if (lessThan(A[j], A[small]))

这类调用布尔值函数的测试即可。

假设有n个不同的元素有待排序。答案（也就是正确的排序次序）可能是这些元素形成的n!种排列中的任意一种。如果用于为任意类型的元素排序的算法能正常工作，它就一定能区分这n!种不同的可能答案。

考虑该算法进行的第一次元素比较，假设是

lessThan(X,Y)

对这n!种可能的排序次序而言，X 要么小于Y，要么不小于Y。因此，这n!种可能的次序会被划分为两组，分别是第一次测试的答案为“是”的组，以及答案为“否”的组。

这两组中的一组必须至少具有n!/2个成员，因为如果两个组的成员都不足n!/2个，总的次序数就少于n!/2+n!/2个，也就是少于n!种次序。而这一次序数量的上限就限制了我们刚好有n!种次序。

现在考虑第二个测试，假设对X 和Y 进行比较的结果是得出如下结论：两组可能的次序中较大的那组会剩下（如果这两组一样大则任取一组）。也就是说，至少会剩余n!/2种次序必须由算法来区分。第二次比较同样有两种可能的结果，而且剩余的次序中至少有一半会与这些结果之一相同。因此，我们会发现，至少有n!/4种次序与前两次测试的结果一致。

可以重复这一论证，直到算法确定正确的排序次序为止。在每一步中，只要将重点放在含有较多一致可能次序的结果上，就至少会留下一半上一步中得到的可能次序。因此，可以看到这样一系列的测试和结果：在第i次测试后，至少有n!/2ⁱ种次序与这些结果相一致。

因为直到每个测试和结果序列最多与一个排序次序一致才会完成排序，所以在完成排序前所进行测试的次数t 要满足

n!/2^t≤1　　　　　　(4.2)

如果对(4.2)式的两边同时取以2为底的对数，就得到log₂n!-t≤0，也就是

t≥log₂(n!)

我们将看到log₂(n!)大约是n log₂n。不过首先要看一个分割可能次序的示例。

示例 4.4

考虑一下图2-2所示的选择排序算法在为给定的3个元素（a,b,c）排序时是如何作出判定的。第一次比较发生在a 和b 之间，如图4-5中的顶端所示，其中方框中表示了进行任何测试前，6种可能的次序全部是一致的。在测试后，abc、acb 和cab 这些次序与结果为“是”（即a< b）的情况一致，而bac、bca 和cab 这些次序与相反的结果（也就是b>a）一致。我们再次在方框中展示了每种情况中的一致序（consistentorder）。

在图2-2所示的算法中，较小元素的下标成了变量small的值。因此，接下来要将c 与a 和b 中的较小者进行比较。请注意，接下来要进行何种测试取决于上一次测试的结果。

在进行第二次判定后，3个元素中最小的那个会被移动到数组的第一个位置，而第三次比较则会确定剩下的两个元素中哪个更大。第三次比较是该算法在为3个元素排序时所要进行的最后一次比较。正如我们在图4-5的底部看到的，有时候判定的结果是确定的。例如，如果已经得到a< b而且c>b，那么c 就是最小的元素，而且最后一次对a 和b 的比较会得出a更小的结论。

{%}

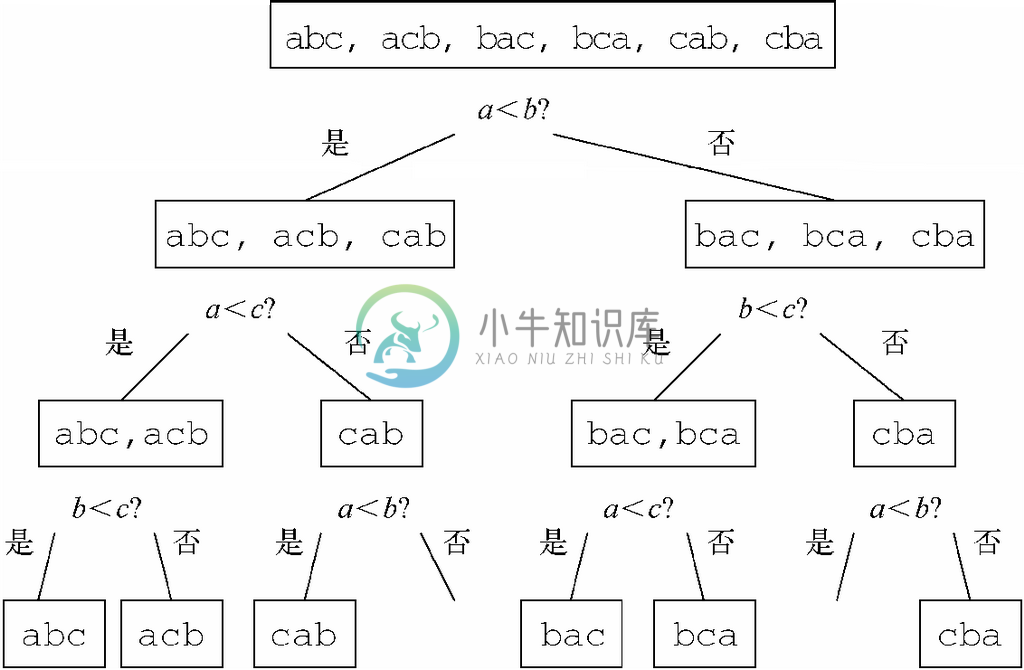
图 4-5　对3个元素进行选择排序的判定树

在本示例中，所有路径都包含3次判定，而且最后至多存在一种一致序，就是正确的排序次序。不含一致序的两条路径从未出现。(4.2)式说明测试次数t一定至少为log₂3!，即log₂6。由于6大于2²且小于2³，所以可知log₂6大于2小于3。所以，为3个元素排序的任意算法至少有某个结果序列必须进行3次测试。因为选择排序只需为3个元素进行3次测试，所以处理3个元素时，它最不济也至少与其他算法一样好。当然，随着元素数量不断变多，选择排序就不那么好了，因为它是种O(n²)的排序算法，而且还存在更佳的算法，比如归并排序。

现在必须要估算log₂n!有多大。因为n!是从1到n这n个整数的积，它肯定要比从n/2到n这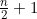 $\frac{n}{2}+1$ 个整数的积大。这 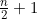$\frac{n}{2}+1$ 个整数的积又至少与n/2个n/2的积，也就是(n/2)^n/2一样大。因此，log₂n!至少是log2((n/2)^n/2)，即 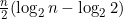$\frac{n}{2}(\log_2n-\log_22)$ ，也就是

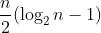
$\frac{n}{2}(\log_2n-1)$

对较大的n来说，这一公式约等于(n log₂n)/2。

更细致的分析将表明常数因子1/2在这里并非必要。也就是说，log₂n!非常接近n log₂n，而非更接近它的一半。

线性时间的专用排序算法
如果对排序算法可以处理的输入加以限制，就可以在一个步骤中将可能的次序分为2个以上的部分，因此会让运行时间少于与n logn成正比的时间。下面讲一个简单例子，如果输入是n个从0到2n-1之间的不同整数，它就能起作用。
(1)  for (i = 0; i  0)
(7)          printf("%d\n", i);
假设输入为长度为n 的数组a。在第(1)行和第(2)行，我们将长度为2n 的数组count初始化为0。接着，在第(3)行和第(4)行中，若x 为第i 个输入元素a[i]的值，则为x的计数加上1。在最后3行代码中，要打印出count[i]为正的各个整数i。因此，要打印那些在输入中至少出现过一次的元素，而之前假设了输入中各元素都是不同的，所以这段代码会将所有的输入元素按照从小到大的顺序打印出来。
分析该算法运行时间很容易。第(1)行和第(2)行是一个会迭代2n次的循环，而且其循环体的运行时间为O(1)。因此，该循环的运行时间为O(n)。同理，第(3)行和第(4)行的循环运行时间也是O(n)，只不过它的迭代次数是n。最后，第(5)行至第(7)行所示循环的循环体运行时间为O(n)，而它会迭代2n次。因此，这3个循环的运行时间均为O(n)，而整个排序算法的运行时间同样是O(n)。请注意，如果给定的输入没有为该算法进行过处理，比如输入中含有超出从0到2n-1范围的整数，那么上面的程序就无法正确排序。

我们只是证实了任意通用排序算法都一定有某些能让它们进行n log₂n或更多次比较的输入。因此，任意通用排序算法在最坏的情况下肯定至少要花上与n logn成正比的时间。其实，可以证明，这一点同样适用于“平均的”输入。也就是说，通用排序算法处理所有输入平均所花的时间一定至少与n logn成正比。因此，归并排序基本上就是我们能做的最佳算法了，因为它处理所有输入都有着这样的大O运行时间。

4.3.3　习题

1. 假设已经为棒球队选择了9名队员。

(a) 可能存在多少种击球次序？

(b) 如果投手必须最后击球，那么可能有多少击球次序？

2. 如果要为4个元素排序，那么图2-2中的选择排序算法要进行多少次比较？这是不是可以达到的最优数字？给出该情况下判定树（具有如图4-5所示样式）最上面的3层。

3. 2.8节介绍的归并排序算法在处理4个元素时要进行多少次比较？这是否为可达到的最优数字？给出该情况下判定树（具有如图4-5所示样式）最上面的3层。

4. * 将n个值分配给n个项的数目多，还是n+1个项的排列数多？请注意：对不同的n来说，答案可能不同。

5. * 将n/2个值分配给n个项的数目是否多于n个项的排列数？

6. ** 说明如何在O(n)时间内为范围在0到n²-1之间的n个整数排序。

4.4　有序选择

有时候我们会希望只从集合中选出某些项，并为它们排定顺序。这里将4.3节中介绍过的为排列计数的函数Π(n)一般化为双参数的函数Π(n,m)，用该函数表示从n个项中选出m项排定次序的方法数，不过对未选定的项来说没有次序可言。因此Π(n)=Π(n,n)。

示例 4.5

赛马比赛会为前三名完成比赛的赛马颁奖。假设有10匹马参赛，那么冠亚季军的排列情况共有多少种呢？

显然，10匹马中的任意一匹都可能赢得比赛。如果给定了获得冠军的马匹，那么剩下的9匹马可以任意排序。因此前两名马匹的选择共有10×9=90种。对每种选择而言，都会剩下8匹赛马，其中任意一匹都可能获得季军。因此，冠亚季军的选择方式共有90×8=720种。图4-6展示了所有可能的选择，重点突出了首先选择3号之后选择1号的情况。

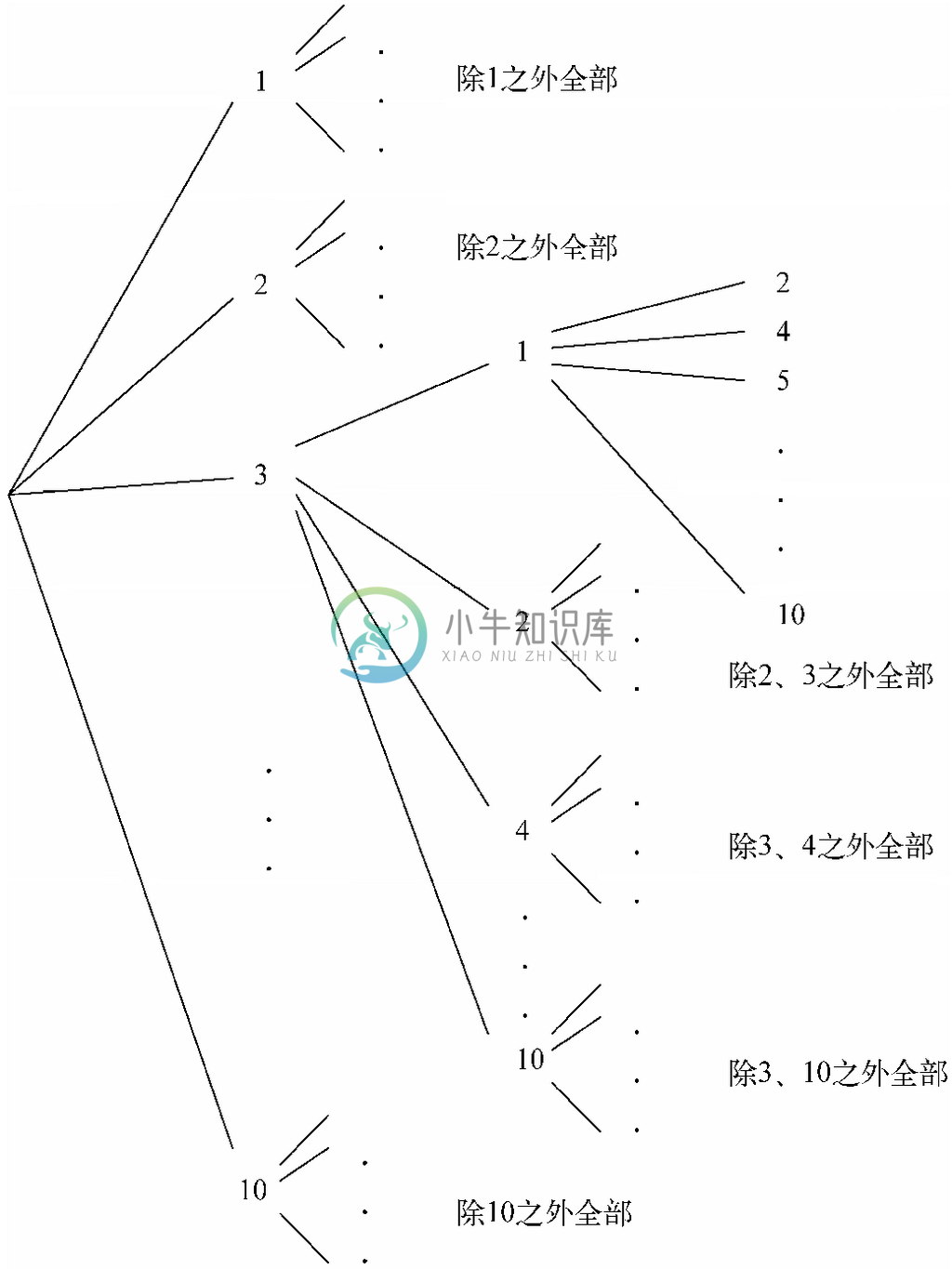
图 4-6　从10项有序地选出3项的情况

4.4.1　无放回选择的一般规则

现在来推导一下Π(n,m)的公式。顺着示例4.5的思路，可知第一次选择时有n种选择。不管第一次作出了怎样的选择，都会剩下n-1个元素有待选择。因此，第二次选择有n-1种不同的方式。前两次选择总共有n(n-1)种方式。类似地，进行第三次选择时还剩n-2个未选取的项，所以第三次选择共有n-2种不同的方式。因此，前三次选择总共可以有n(n-1)(n-2)种方式。

继续用这种方式处理，直到作出m次选择。每次选择都比之前一次的选择少一项。结论就是，从n个项中不放回但有次序地选出m个项，总共有

Π(n,m)=n(n-1)(n-2)…(n-m+1)　　　　　　(4.3)

种不同的方式。也就是说，表达式(4.3)是从n开始依次倒数的m个整数的积。

还可以将(4.3)式写为n!/(n-m)!。也就是

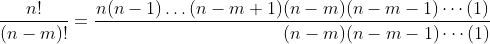
$\frac{n!}{(n-m)!}=\frac{n(n-1)\dots(n-m+1)(n-m)(n-m-1)\cdots(1)}{\qquad\qquad\qquad\qquad\qquad\enskip(n-m)(n-m-1)\cdots(1)}$

分母是从1到n-m这些整数的积。而分子则是从1到n这些整数的积。因为分子和分母中后n-m个因子(n-m)(n-m-1)…(1)是相同的，所以将这些项约去，就得到

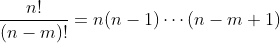
$\frac{n!}{(n-m)!}=n(n-1)\cdots(n-m+1)$

这一公式与(4.3)式是相同的，这样就证实了Π(n,m)=n!/(n-m)!。

示例 4.6

考虑一下示例4.5中的情况，其中n=10且m=3。不难看出，Π(10,3)=10×9×8=720。(4.3)式表示Π(10,3)=10!/7!，或者说是

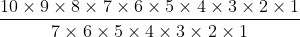
$\frac{10\times9\times8\times7\times6\times5\times4\times3\times2\times1}{7\times6\times5\times4\times3\times2\times1}$

从1到7这些因数同时出现在分子和分母中，因此要约去这些因数。结果就得到8、9、10这三个数字的积，就是10×9×8，正如我们在示例4.5中看到的那样。

有放回选择和无放回选择
示例4.5中考虑的问题与4.2节考虑的分配问题只有细微的差别。如果用房屋和颜色来表示，就可以将选出前三名完成比赛的赛马视为将10匹马（颜色）分配给三个完赛排位（房屋）。唯一的区别是，将多所房屋粉刷成相同颜色是可以的，而说一匹赛马同时获得冠军和季军则很荒唐。因此，用10种颜色之一粉刷3所房屋的方法共有10³或者说是10×10×10种，而从10匹赛马中选择前三名完成比赛的赛马则有10×9×8种方法。
有时候我们会将4.2节进行的这种选择称为有放回选择。也就是说，当为一所房屋选择一种颜色（比如说是红色）后，会将红色“放回”可供选择的颜色池中，然后可以继续为其他房屋再次选择红色。
另一方面，我们在示例4.5中讨论的有序选择被称为无放回选择。这种情况下，如果赛马“硬面包”被选作冠军，那么它就不能被放回含有亚军和季军的马匹池了。类似地，如果赛马“秘书处”被选为第二名，那么它也就不可能再成为获得季军的马匹了。

4.4.2　习题

1. 从26个字母中选出m个字母组成序列，如果不允许同一字母出现一次以上，那么有多少种不同的组合方式？分别计算m=3及m=5的情况。

2. 在一个有200名学生的班级中，我们希望选出一位会长、一位副会长、一位秘书和一位财务主管。选择这4位干部的方式共有多少种？

3. 计算如下阶乘之商：(a)100!/97!(b)200!/195!。

4. “珠玑妙算”（Mastermind）这个游戏要求玩家选择一个由一列4个珠子组成的“密码”，每个珠子都可能是红、绿、蓝、黄、白和黑这6种颜色中的一种。

(a) 总共有多少不同的密码？

(b*) 有两个或多个珠子颜色相同的密码有多少种？提示：这个量是(a)小题的答案与另一个易于计算的量之间的差。

(d*) 不含红色珠子而且至少有两个珠子颜色相同的密码有多少种？

5. * 通过对n 的归纳证明，对1和n 之间的任意m，有Π(n,m)=n!/(n-m)!。

6. * 通过对a-b 的归纳证明，a!/b!=a(a-1)(a-2)…(b+1)。

阶乘之商
请注意，一般而言，只要b< a，a!/b!就是从b+1到a 这些整数的积。通过计算
a×(a-1)×…×(b+1)
来计算阶乘之商，要比分别求出每个阶乘的值然后相除更容易，特别是在b不比a 小很多的情况下。

4.5　无序选择

在很多情况下，我们希望计算出从一组项中进行选择到底有多少种方法，而其中所选项的顺序倒是无关紧要。按照4.4节中赛马结果示例的说法，我们可能想知道前三名完成比赛的赛马是哪三匹，但不关心到底哪匹马赢得了哪个名次。换句话说，就是想知道从n匹赛马中选出3匹作为前三名完成比赛的马匹，方法有多少种。

示例 4.7

再次假设n=10。我们从示例4.5中得知，选择3匹赛马，假设说是A、B和C，分别作为冠亚季军的方式共有720种。然而，我们现在不关心这3匹马完成比赛的具体次序，只是想知道A、B和C这3匹马以某种次序获得了前三名。因此，我们将通过6种不同的方式得到答案“A、B和C是最好的3匹赛马”，分别对应3匹马在前三名中6种不同的排位。可知刚好存在6种方法，因为给3个项排序的方法为Π(3)=3!=6种。如果还有疑问的话，可以参考图4-7所示的这6种方法。

{%}

图 4-7　3匹马完成比赛的6种顺序

对A、B 和C 这3匹马来说成立的情况，对任意一组3匹马来说都成立。在为从10匹马中有序选择出3匹马的情况计数时，每一个3匹马构成的组都会刚好按照它们可能形成的所有次序出现6次。因此，如果只需要计算可能为前三名的3匹马的组合数，就还要在Π(10，3)的基础上除以6。因此，从10匹马中选出3匹作为前三名的马共有720/6=120种不同组合。

示例 4.8

再来考虑一下扑克牌型的数量。在扑克牌游戏中，每名玩家都会分到从52张牌中发出的5张。这里不用考虑分到的5张牌究竟是什么顺序，只关心拿到的这5张牌到底是哪5张。要计算分到的5张牌可能有多少种情况，可以先从计算Π(52，5)开始，也就是从52个对象中有序选择5个对象的情况总数。这一数字是52!/(52-5)!，就是52!/47!，或者说是50×49×48=311 875 200。

不过，就像示例4.7中跑得最快的3匹马总共可能以3!=6种次序出现那样，任意一组5张牌都可能以Π(5)=5!=120种不同的次序出现。因此，要在不考虑选择次序的情况下考虑可能构成的牌型，就必须用有序选择的次数除以120。结果是共有311 875 200/120=2 598 960种不同的牌型。

4.5.1　为组合计数

现在要将示例4.7和示例4.8中介绍的情况一般化，以得出在不考虑选择顺序的情况下计算从n项中选出m项的方法数的公式。这一函数通常可写为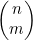 $\begin{pmatrix}n\\m\end{pmatrix}$ ，并说成是“n选m”或是“从n个元素中选取m个元素的组合数”。要计算 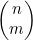$\begin{pmatrix}n\\m\end{pmatrix}$ ，首先要计算Π(n,m)=n!/(n-m)!，也就是从n个事物中有序选择出m个的方法数。然后要根据选出的这m项来为这些有序选择分组。因为这m项可以有Π(m)=m!种不同的次序，所以这些分组中各含m!个成员。要得到无序选择的数目，就必须要用有序选择的数目除以m!，也就是

$\begin{pmatrix}n\\m\end{pmatrix}=\frac{\Pi(n,m)}{\Pi(m)}=\frac{n!}{(n-m)!\timesm!}$ 　　　　　　(4.4)

示例 4.9

回顾一下示例4.8，它用到了公式(4.4)，其中n=52Π，m=5。于是有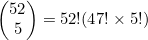 $\begin{pmatrix}52\\5\end{pmatrix}=52!(47!\times5!)$ 。如果将47!与52!中的后47个因数约去，并展开5!，就可以写为

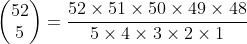
$\begin{pmatrix}52\\5\end{pmatrix}=\frac{52\times51\times50\times49\times48}{5\times4\times3\times2\times1}$

进行简化，就得到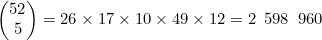 $\begin{pmatrix}52\\5\end{pmatrix}=26\times17\times10\times49\times12=2\enskip598\enskip960$ 。

4.5.2　n 选m 的递归定义

如果递归地考虑从n项中选出m项的方法数，就可以得出计算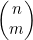 $\begin{pmatrix}n\\m\end{pmatrix}$ 的递归算法。

依据。对任意n≥1，有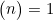 $\begin{pmatrix}n\\0\end{pmatrix}=1$ 。也就是说，从n项中选择0项只有一种方式。此外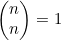， $\begin{pmatrix}n\\n\end{pmatrix}=1$ ，也就是说，从n项中选择n项的唯一方法就是将它们都选上。

归纳。如果0< m< n，那么 $\begin{pmatrix}n\\m\end{pmatrix}=\begin{pmatrix}n-1\\m\end{pmatrix}+\begin{pmatrix}n-1\\m-1\end{pmatrix}$ 。也就是说，如果想从n项中选出m项，可以用以下两种方法中的任一种。

1. 不选取第一个元素，接着从剩下的n-1个元素中选取m个。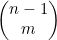 $\begin{pmatrix}n-1\\m\end{pmatrix}$ 这项表示的就是这种情况下可能的选择方法数。

2. 选取第一个元素，然后从剩下的n-1个元素中选取m-1个元素。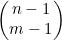 $\begin{pmatrix}n-1\\m-1\end{pmatrix}$ 这项表示的就是这种情况下可能的选择方法数。

顺便提一句，尽管归纳部分的概念应该很明确（先从全选或全不选的最简单情况开始，进而处理选择某些元素的更复杂的情况），不过还是要谨慎起见，说明是对什么量进行归纳。看待这一归纳的方式之一是，将其视为对m和n-m二者中较小的那个与n的积进行完全归纳。那么当该积为0，而且归纳是针对该积的较大值进行时，就会发生依据的情况。我们还必须为归纳过程核实，当0< m< n时，n×min(m,n-m)总大于(n-1)×min(m,n-m-1)以及(n-1)×min(m-1,n-m)。这一验证过程将留作本节的习题。

这种递归关系通常是用帕斯卡三角形（Pascal's triangle）1表示的，如图4-8所示，其中两条边全部由1构成（表示依据），而三角形中每个内部条目都是它左上角和右上角相邻条目之和。那么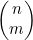 $\begin{pmatrix}n\\m\end{pmatrix}$ 将作为第(n+1)行的第(m+1)个条目被读取。

1又称杨辉三角或贾宪三角。——译者注

{%}

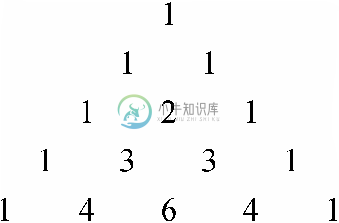
图 4-8　帕斯卡三角形的前几行

示例 4.10

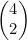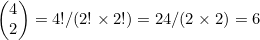考虑一下n=4且m=2的情况。我们在图4-8第5行的第3个条目处找到了 $\begin{pmatrix}4\\2\end{pmatrix}$ 的值。该条目为6，而很容易验证 $\begin{pmatrix}4\\2\end{pmatrix}=4!/(2!\times2!)=24/(2\times2)=6$ 。

通过公式(4.4)或是上述递归这两种方法计算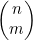 $\begin{pmatrix}n\\m\end{pmatrix}$ ，计算出的自然是相同的值。可以通过诉诸物理推理（physical reasoning）来证实这一点。两种方法计算的都是从n 项中无序选择m 项的方法数，所以一定会得出相同的值。不过，还可以通过对n 的归纳证明这两种方式的等价性。在这里将该证明过程留作本节的习题。

4.5.3　计算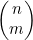 $\begin{pmatrix}n\\m\end{pmatrix}$ 的算法的运行时间

正如在示例4.9中所见，当我们使用公式(4.4)计算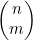 $\begin{pmatrix}n\\m\end{pmatrix}$ 时，可以约去分母中的(n-m)!和分子中n!的后n-m个因数，将 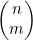$\begin{pmatrix}n\\m\end{pmatrix}$ 表示为

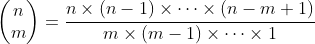$\begin{pmatrix}n\\m\end{pmatrix}=\frac{n\times(n-1)\times\cdots\times(n-m+1)}{m\times(m-1)\times\cdots\times1}$ 　　　　　　(4.5)

如果m 比n 小，那么使用上述公式进行计算要比用公式(4.4)计算更快。大体上讲，图4-9中的C语言代码段就是用来完成这一工作的。

第(1)行将c 初始化为1，c 就成为了结果——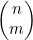 $\begin{pmatrix}n\\m\end{pmatrix}$ 。第(2)行和第(3)行会给c 乘上从n-m+1到n的各个整数。然后，第(4)行和第(5)行会依次从c 除去从2到m 的各个整数。因此，图4-9就实现了(4.5)式中的公式。

(1)      c = 1;
(2)      for (i = n; i > n-m; i--)
(3)          c *= i;
(4)      for (i = 2; i <= m; i++)
(5)          c /= i;

图 4-9　计算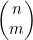 $\begin{pmatrix}n\\m\end{pmatrix}$ 的代码

要计算图4-9的运行时间，只要注意到第(2)～(3)行及第(4)～(5)行这两个循环，每个循环都会迭代m次，而且循环体的运行时间都是O(1)。因此，运行时间是O(m)。

在m接近n而n-m很小的情况下，可以交换m和n-m的角色。也就是说，可以约去n!和m!的因数，得到n(n-1)…(m+1)，并将其除以(n-m)!。该方法给出了(4.5)所示公式的另一种形式，即

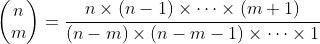$\begin{pmatrix}n\\m\end{pmatrix}=\frac{n\times(n-1)\times\cdots\times(m+1)}{(n-m)\times(n-m-1)\times\cdots\times1}$ 　　　　　　(4.6)

同样，存在与图4-9类似的代码段来实现公式(4.6)，而且所花的时间为O(n-m)。因为要定义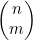 $\begin{pmatrix}n\\m\end{pmatrix}$ 就一定有n-m和m不大于n，所以不管是哪种方式，O(n)都是运行时间的边界。此外，在m接近0或者接近n 时，两种方法中更优方法的运行时间都要大大小于O(n)。

不过，图4-9有个重大缺陷。它先要计算若干整数的积，然后再将其除以相同数量的整数。因为普通的计算机运算只能处理有限大小的整数（通常，一个整数最大可以达到约20亿），所以图4-9第(3)行计算中间结果的过程可能有溢出整数大小限制的风险。即使是在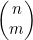 $\begin{pmatrix}n\\m\end{pmatrix}$ 的值足够小，可以在某计算机中表示出来的情况下，也还是可能出现这种情况。

更好的方式是让乘法和除法交替进行。首先乘上n，然后除以m。乘上n-1，再除以m-1，以此类推。这种方法的问题在于，我们没理由相信每一阶段的计算结果都是整数。例如，在示例4.9中，首先要乘上52并除以5，这个结果就已然不是整数了。因此，在进行任何计算前都需要转换为浮点数。在这里将这一修改留作本节的习题。

让 $\begin{pmatrix}n\\m\end{pmatrix}$ 一定得出整数的公式
要看出为什么(4.4)、(4.5)和(4.6)这几个式子中多个因数的商一定是整数可能不容易。唯一的简单论证就是诉诸物理推理。这些公式都是计算从n个事物中选取m个的方法数，而这个数字一定是某个整数。
不借助这些公式的物理意义，而从整数的属性来论证这一事实，要难上很多。其实可以通过仔细分析分子和分母中各质数因子数来证明这一事实。拿示例4.9中的表达式当例子。其中分母中有5这个因数，而分子中有5个因数，由于这些因数是连续的，可知其中必有一个能被5整除，而它正好是中间的那个因数——50。因此，分母中的5肯定会被约去。

现在来考虑计算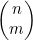 $\begin{pmatrix}n\\m\end{pmatrix}$ 的递归算法。可以通过图4-10所示的简单递归函数来实现这一算法。

图4-10中的函数效率不高，因为它调用choose的次数会呈指数级增长。原因就在于当使用n作为首个参数调用该函数时，往往会在第(6)行用n-1作为首个参数进行两次递归调用。因此，可以预见，当n 增加1时，调用的次数就会翻倍。而且递归调用的确切次数是很难计算的。原因在于第(4)行和第(5)行的依据情况不仅适用于n=1的情况，而对更大的n，会提供值为0或n 的m。

下面要证明一个简单但稍显悲观的上界。设T (n)是当首个参数为n 时图4-10所示程序段的运行时间。可以直接证明T(n)是O(2ⁿ)。假设a是第(1)行到第(5)行，加上第(6)行涉及调用与返回的部分（不含递归调用本身所花的时间）的总运行时间。然后就可以通过对n 的归纳证明下列命题。

         /* 对0 <= m <= n，计算从n 个元素中选择m 个的方法数 */
         int choose(int n, int m)
         {
             int n, m;

(1)          if (m < 0 || m > n) {/* 错误的条件 */
(2)              printf("invalid input\n");
(3)              return 0;
             }
(4)          else if (m == 0 || m == n) /* 依据情况 */
(5)              return 1;
             else /* 归纳 */
(6)              return (choose(n-1, m-1) + choose(n-1, m));
         }

图 4-10　计算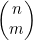 $\begin{pmatrix}n\\m\end{pmatrix}$ 的递归函数

命题 S(n)。如果用第一个参数n以及在0和n之间的第二个参数m调用choose，那么该调用的运行时间T(n)至多为a(2ⁿ-1)。

依据。 n=1。那么一定有m=0或m=1=n。因此，依据情况适用于第(4)行和第(5)行，而且没有进行递归调用。第(1)行到第(5)行的时间都包含在a中，因为S(1)是说T(1)至多为a(2¹-1)=a。

归纳。假设S(n)成立，也就是有T(n)≤a(2ⁿ+1)。要证明S(n+1)成立，假设要以n+1为首个参数调用choose。那么图4-10所示程序段花的时间就是a加上第(6)行两次递归调用的时间。根据归纳假设，每次调用花费的时间至多为(2ⁿ-1)。因此，消耗的总时间最多是：

a+2a(2ⁿ-1)=a(1+2ⁿ⁺¹-2)=a(2ⁿ⁺¹-1)

这一计算过程就证明了S(n+1)成立，并证明了归纳步骤。

因此证明了T(n)≤a(2ⁿ-1)。舍去常数因子及低阶项，就可以得出T(n)是O(2ⁿ)的结论。

奇怪的是，尽管在第3章的分析中，很容易就证明了运行时间的平滑紧上界，但T(n)上的边界O(2ⁿ)虽平滑却不紧凑。合适的平滑紧上界要稍小一些——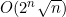 $O(2^n\sqrt{n})$ 。要证明这一事实相当困难，不过在这里要留一个更为简单的事实作为习题来证明，就是图4-10所示程序段的运行时间与它返回的值 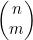$\begin{pmatrix}n\\m\end{pmatrix}$ 成比例。要看到图4-10中的递归算法，效率要比图4-9中的算法低得多。这是一个递归严重不靠谱的例子。

4.5.4　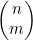 $\begin{pmatrix}n\\m\end{pmatrix}$ 函数的图像

对某个固定的值n 而言，m 的函数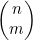 $\begin{pmatrix}n\\m\end{pmatrix}$ 有着不少有意思的属性。对于值比较大的n 来说，如图4-11所示，其图像为一条钟形的曲线。我们很容易看出函数图像是关于中点n/2所在轴线对称的，运用声明 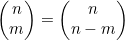$\begin{pmatrix}n\\m\end{pmatrix}=\begin{pmatrix}n\\n-m\end{pmatrix}$ 的公式(4.4)很容易证实这一点。

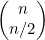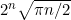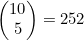最大高度处于中心位置，也就是 $\begin{pmatrix}n\\n/2\end{pmatrix}$ ，大约是 $2^n\sqrt{\pi n/2}$ 。例如，若n=10，这一公式可以得出258.37，而 $\begin{pmatrix}10\\5\end{pmatrix}=252$ 。

该曲线的“厚部”是中点两边各约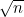 $\sqrt{n}$ 的范围。例如，如果n=10 000，那么对处在4900和5100之间的m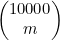， $\begin{pmatrix}10000\\m\end{pmatrix}$ 就接近最大值。而对这个范围之外的m来说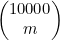， $\begin{pmatrix}10000\\m\end{pmatrix}$ 的值会下降得特别迅速。

{%}

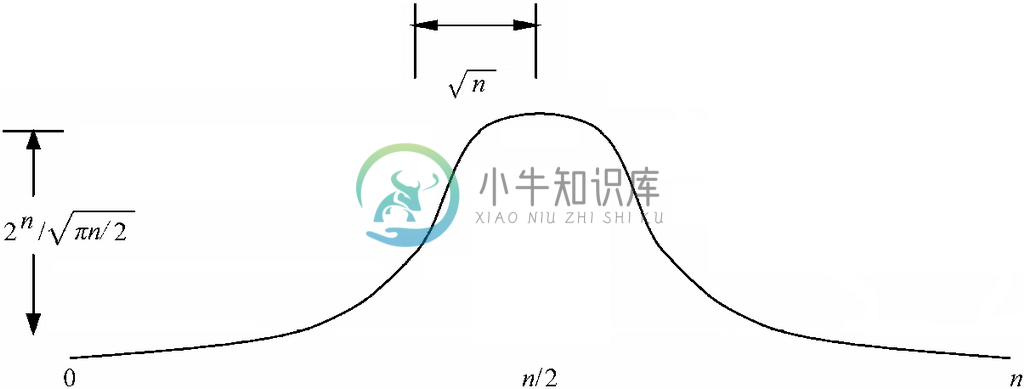
图 4-11　n 为固定值的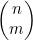 $\begin{pmatrix}n\\m\end{pmatrix}$ 函数

4.5.5　二项式系数

函数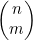 $\begin{pmatrix}n\\m\end{pmatrix}$ 除了可以用来计数外，还能提供二项式系数。在展开二项式的乘方（比如(x+y)ⁿ）时，就会看到这些数字。

在展开(x+y)ⁿ时，会得到2ⁿ个项，其中每一项都是x^my^n-m这样的形式（m是0到n之间的某个整数）。也就是说，对每个因式x+y，都可能从x 和y 中任选其一作为某个特定项的因子。展开式中x^my^n-m的系数是由m个x 和其余n+m个y 组成的项的数量。

示例 4.11

考虑一下n=4的情况，也就是看看(x+y)(x+y)(x+y)(x+y)的积。

总共有16项，其中只有1项是x⁴y⁰（也就是x⁴）。如果从4个因式中都选出x，就能得到这一项。另一方面，有4项是x³y，对应的情况是从4个因式的任意一个中选出y，再从其余3个因式中选出x。对称地，有1项是y⁴，有4项是xy³。

那么有多少项是x²y²呢？如果从两个因式中选取x并从其余两个中选取y，就能得到这样一项。因此，必须要计算从4个因式中选择两个因子的方法数。因为选择两个因子的顺序是不产生影响的，所以这个数字就是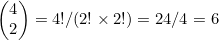 $\begin{pmatrix}4\\2\end{pmatrix}=4!/(2!\times2!)=24/4=6$ 。因此，有6项是x²y²。完整的展开式就是

(x+y)⁴=x⁴+4x³y+6x²y²+4xy³+y⁴

请注意等式右侧各项的系数，(1,4,6,4,1)，正好就是图4-8中帕斯卡三角形的一行。我们会看到，这并非巧合。

示例4.11中用于计算x²y²系数的概念可以推广开来。(x+y)ⁿ展开式中的项x^my^n-m的系数为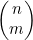 $\begin{pmatrix}n\\m\end{pmatrix}$ 。原因在于，只要从n个因式中选出m个x并选出n-m个y，就可以得到x^my^n-m这一项。从n个因式中选出m个因子的方式有 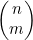$\begin{pmatrix}n\\m\end{pmatrix}$ 种。

在二项式系数和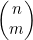 $\begin{pmatrix}n\\m\end{pmatrix}$ 函数之间还有一种有趣的关系。我们已经看出

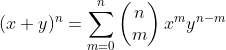
$(x+y)^n=\sum^{n}_{m=0}\begin{pmatrix}n\\m\end{pmatrix}x^my^{n-m}$

令x=y=1，那么有(x+y)ⁿ=2ⁿ。x和y的所有乘方都是1，所以上述等式就成了

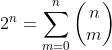
$2^n=\sum^{n}_{m=0}\begin{pmatrix}n\\m\end{pmatrix}$

换句话说，对某个特定的n而言，所有二项式系数的和就是2ⁿ。特别要说的是，每个系数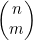 $\begin{pmatrix}n\\m\end{pmatrix}$ 都小于2ⁿ。图4-11就暗示了，对接近n/2的m来说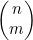， $\begin{pmatrix}n\\m\end{pmatrix}$ 和2ⁿ 特别接近。由于在图4-11中曲线下方的区域表示2ⁿ，因此能看出为什么只有接近中点的一些值会比较大。

4.5.6　习题

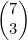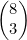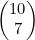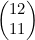1. 计算以下各值：(a) $\begin{pmatrix}7\\3\end{pmatrix}$ ；(b) $\begin{pmatrix}8\\3\end{pmatrix}$ ；(c) $\begin{pmatrix}10\\7\end{pmatrix}$ ；(d) $\begin{pmatrix}12\\11\end{pmatrix}$ 。

2. 从26个小写字母中选出5个不同字母的方法共有多少种？

3. 如下系数各为多少?

(a) (x+y)⁷的展开式中x³y⁴的系数；

(b) (x+y)⁸的展开式中x⁵y³的系数。

4. * 在Real Security公司，计算机密码必须由4位数字（10选4）和6个字母（52选6）组成，字母和数字都可以重复。总共可能有多少种不同的密码组合？提示：首先考虑选择4个存放数字的位置共有多少种方法。

5. * 5个字母组成的双元音序列有多少种？

6. 重新编写图4-9所示的程序片段，从而利用n-m小于n的情况。

7. 重新编写图4-9所示的程序片段，并将其转换成浮点数乘除交替的算法。

8. 证明：如果0≤m≤n，那么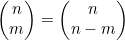 $\begin{pmatrix}n\\m\end{pmatrix}=\begin{pmatrix}n\\n-m\end{pmatrix}$ 。

(a) 借助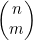 $\begin{pmatrix}n\\m\end{pmatrix}$ 的含义。

(b) 利用(4.4)式。

9. * 通过对n的归纳，证明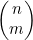 $\begin{pmatrix}n\\m\end{pmatrix}$ 的递归定义正确地定义了 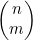$\begin{pmatrix}n\\m\end{pmatrix}$ 等于n!/((n-m)!×m!)。

10. ** 通过对n的归纳，证明图4-10中递归函数choose(n,m)的运行时间最多是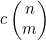 $c\begin{pmatrix}n\\m\end{pmatrix}$ ，其中c为某个常数。

11. * 证明：当0< m< n时，n×min(m,n-m)　总是大于(n-1)×min(m,n-m-1)　和(n-1)×min(m-1,n-m)。

4.6　相同项的次序

在本节中，要处理的是这样一些选择问题，其中含有一些相同项，但不同项出现的次序很重要。而在接下来的4.7节中，则要解决一类类似的选择问题，即有一些相同项，而且项的次序无关紧要。

示例 4.12

构词（anagram）猜谜游戏会给出一列字母，让玩家重新排列字母以构成单词。如果拥有含规范单词的字典，并能生成所有可能的字母序列，就可以通过计算机解决该问题。第10章会介绍判定给定字母序列是否处于字典中的有效方法。不过现在要考虑的是组合问题，可能首先要确定有多少单词需要用字典验证其确实存在。

对有些构词来说，计数很简单。假设有abenst 6个字母，可能会有Π(6)=6!=720种不同的次序，其中之一便是absent，也就是该谜题的“解答”。

不过，构词游戏通常会含有重复的字母。考虑一下谜题eilltt。这些字母就不能构成720种不同的序列。例如，交换两个字母t的位置似乎并不能让单词发生变化。

假设对两个t和两个l加以标记以区分这些字母，分别将其记为t₁、t₂、l₁和l₂。被标记的字母可能有720种次序。然而，这些标记过的l仅在位置上有区别，诸如l₂it₂t₁l₁e和l₁it₂t₁l₂e就并不是真的有区别。因为所有720种次序可以平分为两组，这两组的区别只在于l的下标，所以可以证明：如果将字母串的数量除以2，这些l其实都是相同的。

类似地，在字符串中只有字母t带标记时，可以将只有t的下标不同的字符串配对。例如，lit₁t₂le和lit₂t₁le就是一对。因此，如果再将数目除以2，就可以得到将t和l的标记删除后不同构词串的数量。该数字为360/2=180。即使用eilltt共有180种不同的构词方法。

我们可以将图4-12中的概念一般化为有n个项而且这些项被分为k 组的情形。各组中的成员都是相同的，而不同组的成员则是不同的。在这里假设m_i 是第i 组中的成员项，其中i =1,2,…,k。

示例 4.13

重新考虑示例4.12中用eilltt构词的问题。其中共有6项，也就是说n=6。而分组的数量k 为4，因为有4个不同的字母。这4组中有两组含有一个成员（e 和 i），而另两组则含两个成员。因此可以取i₁=i₂=1，i₃=i₄=2。

如果为这些项加上标记，以使同一组中的成员有所不同，那么会有n!种不同的次序。不过，若第一组中有i₁个成员，那么这些标记过的项可能会以i₁!种不同的次序出现。因此，在从第一组的项上移除标记时，我们要将这些次序分成大小同为i₁!的集合。因此必须将次序数除以i₁!，从而得到从第1组删除标记后的次序数。

类似地，依次从各组中删除标记需要将不同次序的数量除以i₂!、除以i₃!，等等。对那些值为1的i_j!来说，就是除以1!=1，因此没有任何影响。不过，对那些所含项数大于1的分组来说，我们必须除以分组大小的阶乘，这就是示例4.12中的情况。有两组中包含1个以上的元素，而每组的大小都是2，所以就要除以2!两次。可以通过对k的归纳证明该一般规则。

命题 S(k)。如果有n个项，并且分别被分为大小为i₁、i₂、…、i_k的k个组，同一组中的项是相同的，而不同组中的项是不同的，那么这n个项能形成的不同次序的数目为

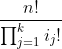$\frac{n!}{\prod^{k}_{j=1}i_j!}$ 　　　　　　(4.7)

依据。如果k=1，那么只有一组无区别的项，不管n有多大都只有一种次序。如果k=1，那么i₁一定为n，而(4.7)式就变成了n!/n!，也就是1。因此，S(1)成立。

归纳。假设S(k)为真，并考虑有k+1个分组时的情况。设最后一组中有m=i_k+1个成员。这些项将会出现在m个位置，而且可以有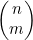 $\begin{pmatrix}n\\m\end{pmatrix}$ 种不同的方式来选择这些位置。一旦选定了m个位置，把最后一组中的哪一项放在这些位置都没关系了，因为这些项都是没有区别的。

在为最后一组选择了位置后，还剩n-m个位置来容纳其余k个组。归纳假设适用，并且表明最后一组的每种位置选择都对应着其余位置中其余元素的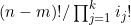 $(n-m)!/\prod^{k}_{j=1}i_j!$ 种不同次序。该式与(4.7)式相比，只是将(4.7)式中n的位置替换成了n-m，因为只剩n-m项有待放置了。因此k+1组项的次序总数为

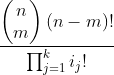$\frac{\begin{pmatrix}n\\m\end{pmatrix}(n-m)!}{\prod^{k}_{j=1}i_j!}$ 　　　　　　(4.8)

如果将(4.8)中的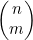 $\begin{pmatrix}n\\m\end{pmatrix}$ 替换成等价的n!((n-m)!m!)，就得到

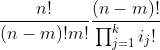$\frac{n!}{(n-m)!m!}\frac{(n-m)!}{\prod^{k}_{j=1}i_j!}$ 　　　　　　(4.9)

可以从(4.8)式的分子和分母中约去(n-m)!。此外，请记住m是i_k+1，是第k+1组中的成员的数目。因此可得到次序数为

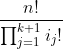
$\frac{n!}{\prod^{k+1}_{j=1}i_j!}$

这正是S(k+1)所给出的式子。

示例 4.14

一位探险家带了两个星期的口粮，其中包括4罐金枪鱼、7罐午餐肉以及3罐黄豆罐头。如果他每天打开一罐罐头，那么他消耗这些口粮的次序共有多少种？这里的14项分成了分别具有4、7和3个相同项的3组。按照(4.7)式，其中n=14，k=3，i₁=4，i₂=7，i₃=3。因此他消耗口粮的次序数为

$\frac{14!}_{4!\times7!\times3!}$

先从分母中的7!开始，可以约去分子14!中最后7个因数。因此就得到

$\frac{14\times13\times12\times11\times10\times9\times8}_{4\times3\times2\times1\times3\times2\times1}$

继续约去分子和分母中的因数，就可以得到结果为120 120。也就是说，消耗这些口粮的方法有逾10万种。可惜每一种听起来都让人没什么胃口。

习题

1. 计算以下单词的字母构词的数量：(a) error；(b) street；(c) allele；(d) Mississippi。

2. 将下列水果排成一线共有多少种方法？

(a) 3个苹果、4个梨和5根香蕉；

(b) 2个苹果、6个梨、3根香蕉和2颗李子。

3. * 将白王、黑王、2个白骑士和1个黑车摆在棋盘上，共有多少种摆法？

4. * 100个人参与到一场彩票游戏中。其中一人可赢得千元大奖，还有5人可以得到50美元储蓄基金的安慰奖。那么总共可能有多少种不同的获奖结果？

5. 写一个简单的公式，用来计算放置n对两两相等的2n个对象的次序数。

4.7　将对象分装入箱

我们要介绍的下一类计数问题涉及对盛装若干对象之容器的选择。这些对象可能相同，也可能不同，不过容器是有区别的。我们必须计算这些装满容器的方法数。

示例 4.15

有凯西、彼得和苏姗3个孩子，我们要将4个苹果分给他们，而不把苹果切开。那么共有多少种分配苹果的方式？

这里的方法数比较少，因此可以直接将其枚举出来。凯西可能得到从0至4个不等的苹果，而不管余下几个苹果，分给彼得和苏姗的方式都只有少数几种。如果设(i,j,k)表示凯西得到i 个苹果、彼得得到j 个苹果而苏姗得到k 个苹果的情况，那么图4-12就展示了全部15种可能的分配方式。每一行对应着分给凯西的苹果数。

(0，0，4)　　(0，1，3)　　(0，2，2)　　(0，3，1)　　(0，4，0)
(1，0，3)　　(1，1，2)　　(1，2，1)　　(1，3，0)
(2，0，2)　　(2，1，1)　　(2，2，0)
(3，0，1)　　(3，1，0)
(4，0，0)

图 4-12　把4个苹果分给3个孩子共有15种方式

为将相同对象分装入箱计数的方法有个诀窍。假设用4个字母A来表示4个苹果，并用两个*来分隔属于不同孩子的苹果。两个*之间的A的数量就表示彼得分到的苹果数，而第二个*之后的A的数量则表示属于苏姗的苹果数。例如，AA*A*A表示（2,1,1）的分配方式，其中凯西分到2个苹果，其余两个孩子各分到1个。而序列AAA*A*则表示（3,1,0）的分配方式，其中凯西得到3个，彼得得到1个，苏姗一个都没有。

因此，每种分发苹果的方式都与由4个A和2个*组成的唯一字符串相关。那么有多少这样的字符串呢？考虑一下组成这种字符串的6个位置。其中任选4个位置用来存放A，另外两个位置用来存放*。正如我们在4.5节中了解到的，从6项中选择4项共有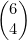 $\begin{pmatrix}6\\4\end{pmatrix}$ 种方法。因为 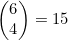$\begin{pmatrix}6\\4\end{pmatrix}=15$ ，所以又一次得出了将4个苹果分给3个孩子的方法共有15种的结论。

4.7.1　装箱问题的一般规则

我们可以按照下列方式将示例4.15介绍的问题一般化。假设给定n个容器，它们对应示例中的3个孩子。同时假设要将m个相同的对象随意地放进这些容器中。那么有多少种分装入箱的方式呢？

这里可以再次考虑A和*组成的字符串。A表示对象，而*表示容器间的边界。如果有n个对象，就有n个A，而如果有m个容器，那么就需要m-1个*来表示分隔不同容器的边界。因此，字符串的长度为n+m-1。

我们可以从这些位置中任选n个存放A，剩下的就是存放*的。因此共有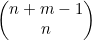 $\begin{pmatrix}n+m-1\\n\end{pmatrix}$ 种由A和 *组成的字符串，那么将对象分装入箱的方式也有这么多种。在示例4.15中，有n=4且m=3，所以就可以得到共有 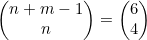$\begin{pmatrix}n+m-1\\n\end{pmatrix}=\begin{pmatrix}6\\4\end{pmatrix}$ 种分配方式的结论。

示例 4.16

在掷骰子游戏中，要掷出3个骰子，其中每个骰子的6个面上都标记了从1到6这6个数字。玩家可以为某个数字赌上1美元。如果这个数字不出现，钱就输掉了。如果该数字出现一次或多次，那么该玩家就可以得到与该数字出现次数等额的美元。

我们可能想要为“结果”计数，不过一开始在“结果”是什么的问题上可能有些疑问。如果将骰子不同的面涂上不同颜色以方便区别，就可将其视为4.2节中那样的计数问题，其中3颗骰子中的每一颗都能分配6个数字中的一个。我们知道，进行这样的分配共有6³=216种方式。

不过，骰子通常是没有区别的，这些数字出现的顺序也是无关紧要的，只有每个数字出现的次数决定了哪个玩家会赢钱，会赢多少钱。例如，掷骰子的结果可能是有两颗是1，而第三颗是6。而6可能出现在第1颗、第2颗或第3颗骰子上，不过出现在哪颗骰子上都是没关系的。

因此，可以把这一问题视为将相同对象分装入箱的问题。“容器”就是1到6这几个数字，而“对象”就是3个骰子。一颗骰子会被“分装”到对应该骰子掷出数字的那个容器。因此，掷骰子游戏总共有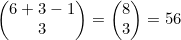 $\begin{pmatrix}6+3-1\\3\end{pmatrix}=\begin{pmatrix}8\\3\end{pmatrix}=56$ 种不同的结果。

4.7.2　分装有区别的对象

我们可以将之前的公式扩展一下，以便处理将可分为k类的n个对象装入m个容器的问题。同一类中的对象是没有区别的，但不同类的对象是不同的。这里用符号a_i 表示第i 类中的成员。因此可以构成由下列对象组成的字符串。

1. 对每个类i，与类中所含成员数量等量的a_i；

2. 用来表示m个容器间的边界的m-1个*。

因此这些字符串的长度是n+m-1，请注意，这些*构成了第k+1个类，而该类包含了m个成员。

我们在4.6节中已经了解过如何为这样的字符串计数。字符串的个数为

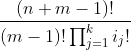
$\frac{(n+m-1)!}{(m-1)!\prod^{k}_{j=1}i_j!}$

其中i_j 表示的是第j 类中的成员数。

示例 4.17

假设有三个苹果、两个梨和一根香蕉要分给凯西、彼得和苏姗。那么“容器”的数量，也就是孩子的数量m=3。共有k=3组，分别有i₁=3、i₂=2和i₃=1个成员。因为总共有6个对象，所以n=6，因此该问题中的字符串的长度为n+m-1=8。这些字符串由3个表示苹果的A、两个表示梨的P、一个表示香蕉的B，以及两个表示边界的*组成。因此，由分发方法数的计算公式可得到共有

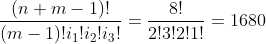
$\frac{(n+m-1)!}{(m-1)!i_1!i_2!i_3!}=\frac{8!}{2!3!2!1!}=1680$

种将这些水果分发给凯西、彼得和苏姗的方式。

计数问题的对比
在本节及之前的4.1到4.5节中，我们已经考虑了6种不同的计数问题。每种问题都可视作为特定的位置分配对象。例如，4.2节介绍的分配问题可以视为给定了n个位置（对应房屋），以及不限量的具有k个不同类型（对应颜色）之一的对象。我们可以顺着3个方向为这些问题分类。
1. 它们是否会放置所有给定的对象？
2. 分配对象的次序是否重要？
3. 所有对象都是不同的，还是说某些对象没有区别？
下表表示了之前各节提到的问题之间的区别。
节
典型问题
是否必须使用所有对象
次序是否重要
是否有相同的对象
4.2
粉刷房屋
否
是
否
4.3
排序
是
是
否
4.4
赛马比赛
否
是
否
4.5
扑克牌型
否
否
是
4.6
构词
是
是
是
4.7
给孩子分苹果
是
否
是
4.2节和4.4节中的问题在上表中体现不出什么区别。它们的区别在于是否放回，正如之前4.4.1节附注栏“有放回选择和无放回选择”中讨论的那样。也就是说，在4.2节中，每种“颜色”都是不限量供应的，可以多次选择同一颜色。而在4.4节中，一匹被选定的“赛马”不能在同一系列的选择中再被选中了。

节	典型问题	是否必须使用所有对象	次序是否重要	是否有相同的对象
4.2	粉刷房屋	否	是	否
4.3	排序	是	是	否
4.4	赛马比赛	否	是	否
4.5	扑克牌型	否	否	是
4.6	构词	是	是	是
4.7	给孩子分苹果	是	否	是

4.7.3　习题

1. 进行下列分配任务分别有多少种方法?

(a) 6个苹果分给4个孩子；

(b) 4个苹果分给6个孩子；

(d) 2个苹果、5个梨和6根香蕉分给3个孩子。

2. 下列情况分别有多少种结果？

(a) 掷4颗无区别的骰子；

(b) 掷5颗无区别的骰子。

3. * 将7个苹果分给3个孩子，并保证每个孩子至少得到一个苹果，共有多少种分发方法？

4. * 假设从国际象棋棋盘的左下角开始向右上角移动，每次向上或向右移动一格，完成这一移动的方式共有多少种？

5. * 将习题(4)一般化。如果有一个由n个方格乘上m个方格组成的矩形，并可以从一个方格向上或向右移动到另一个方格，那么从左下角移动到右上角总共有多少种方法？

4.8　计数规则的组合

组合这一主题能带来无数的挑战，而且很少像本章之前所讨论的那样简单。不过，我们目前所了解到的规则都是最基础，它们都很有价值，能以各种方式结合起来为更加复杂的结构计数。在本节中，我们将了解到3种实用的计数“诀窍”。

1. 将计数表示为一系列选择；

2. 将计数表示为计数的差；

3. 将计数表示为子情况的计数之和。

4.8.1　将计数分解为一系列选择

在为某类分配计数时，有一种实用的方法可以采用，就是将这些待计数的事物描述为一系列的选择，其中每次选择都会细化该类中某个特定成员的描述。在本节中，我们会给出一系列表示某些可能性的示例。

示例 4.18

考虑一下扑克牌型中“对子”（one-pair）的数量。该牌型由一对具有某个秩2的牌，加上3张具有不同秩（而且与之前一对的秩不同）的牌组成。我们可以通过如下步骤描述所有的“对子”牌型。

213个秩分别为A、K、Q、J，以及2到10。

1. 为成对的牌选择秩；

2. 从其余12种秩中为其余3张牌选择3个不同的秩；

3. 为成对的牌选择花色；

4. 为其他3张牌选择花色。

如果将这些数字相乘，将得到“对子”牌型的数量。请注意，牌型中各张牌出现的顺序是无关紧要的，正如之前在示例4.8中讨论过的，而且我们从未尝试过指定次序。

现在，要依次接受这些因素。为成对的那两张牌选择秩的方式有13种。不管选择了哪个秩，都会余下12种。接下来必须从这些秩中选择3个组成剩下的牌型。就像4.5节中讨论过的，这也是一种次序不重要的选择，执行这种选择的方式共有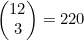 $\begin{pmatrix}12\\3\end{pmatrix}=220$ 种。

现在必须为这对牌选择花色。共有4种花色，而且我们必须从中选择两种。这次又是无序的选择，可以有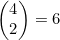 $\begin{pmatrix}4\\2\end{pmatrix}=6$ 种方式。最后，为剩下的3张牌选择花色。每张牌都有4种花色可选，所以又是4.2节中那样的分配问题，进行分配的方式共有4³=64种。

因此，“对子”牌型的总数量为13×220×6×64=1 098 240 种，这一数字在2 598 960种扑克牌型中占了40%以上。

4.8.2　用计数的差来计算计数

另一种实用技巧是，将要计数的内容表示为某个更具一般性的排列类C与C中不满足计数条件的那些事物之间的差。

示例 4.19

还有很多种扑克牌型（两对、三条、铁支和葫芦）可以按照类似示例4.18的方法计数。不过，还有一些其他牌型需要不同的方法来计数。

先来考虑一下同花顺的情况，也就是5张花色相同（同花）而且秩连续（顺子）的牌型。首先，每个顺子都是从A到10这10个秩之一开始的。也就是说，顺子可能是A-2-3-4-5，2-3-4-5-6，3-4-5-6-7，等等，最大的可能是10-J-Q-K-A。一旦秩确定，就只需要指定一种花色来指定该同花顺了。因此，为同花顺计数包含以下两步：

1. 选择顺子的最低秩（10种选择）；

2. 选择花色（4种选择）。

因此，总共有10×4=40种同花顺牌型。

现在来为顺子牌型计数，也就是那些秩连续但又不是同花顺的牌型。先要计算所有具有连续秩的牌型的数量，不考虑它们的花色是否相同，然后再减去40种同花顺牌型。要为秩连续的牌型计数，可以按以下两步进行：

1. 选择最低的秩（10种选择）；

2. 为每个秩指定一种花色（如4.2节介绍的，有4⁵=1024种选择）。

因此，顺子和同花顺牌型的总数是10×1 024=10 240种。减去40种同花顺牌型后，就得出顺子牌型共有10 240-40=10 200种。

接下来，考虑一下同花牌型的数目。这里还是要先将同花顺牌型考虑在内，然后再减去那40种同花顺牌型。可以通过如下方式定义同花牌型。

1. 选择花色（4种选择）；

2. 从13个秩中任选5个，如4.5节介绍的，共有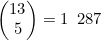 $\begin{pmatrix}13\\5\end{pmatrix}=1\enskip287$ 种方式。

于是可以得出同花牌型共有4×1 287-40=5 108种。·

4.8.3　将计数表示为子情况的和

在面对一些很难直接解决的问题时，就要用到第三种“诀窍”了。可以把为某个类C 计数的问题分解成两个或多个单独的问题，而类C 中的各个成员刚好都能被子问题之一涵盖。

示例 4.20

假设要抛10次硬币，那么8个或8个以上硬币人头面朝上的序列有多少种？如果想知道有多少序列刚好有8个硬币人头面朝上，可以用4.5节介绍的方法来解决。共有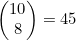 $\begin{pmatrix}10\\8\end{pmatrix}=45$ 种这样的序列。

要解决为8个或8个以上硬币人头面朝上的序列计数的问题，可以将其分解为3个子问题，即分别为刚好有8个硬币人头面朝上、刚好有9个硬币人头面朝上以及10个硬币全部人头面朝上的情况计数。我们已经解决了第一个问题。而9个硬币人头面朝上的序列共有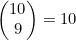 $\begin{pmatrix}10\\9\end{pmatrix}=10$ 种，10个硬币全是人头面朝上的序列共有 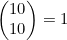$\begin{pmatrix}10\\10\end{pmatrix}=1$ 种。因此，有8个或8个以上硬币人头面朝上的序列共有45+10+1=56种。

示例 4.21

再来考虑一下示例4.16中解决的为掷骰子游戏的结果计数的问题。另一种方法就是根据所出现的不同数字是3个、2个或1个，将该问题分成3个子问题。

(a) 可以用4.5节介绍的技巧计算3个数字皆不同的结果的数量。也就是从一颗骰子6个可能的数字中选出3个，总共有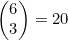 $\begin{pmatrix}6\\3\end{pmatrix}=20$ 种不同的方法。

(b) 接着，要计算两颗骰子是一个数，而另一颗是另一个数的情况有多少种。出现两次的数字有6种选择，每种情况下对应的出现一次的数字有5种选择。所以两颗骰子是一个数而另一颗是另一个数的结果共有6×5=30种。

因此，可能的结果共有20+30+6=56种，这与示例4.16中得到的结论是一样的。

4.8.4　习题

1. * 为以下扑克牌型计数：

(a) 两对；

(b) 三条；

(d) 铁支（四条）。

请注意，在为某种牌型计数时不要将那些更佳的牌型计算在内了。例如，在情况(a)中，要确定两对是不同的，不然就是拿到了铁支牌型，而且要保证第5张牌和这两对的秩不一样，否则就是拿到了葫芦牌型。

2. * 黑杰克由两张牌组成，其中一张是A，而另一张是10分牌，就是10、J、Q或K中的一种。

(a) 在一摞52张扑克牌中，有多少种不同的黑杰克？

(b) 在黑杰克游戏中，有一张牌是暗牌，而另一张是明牌。因此，两张牌的次序是有影响的。在这种情况下，有多少种不同的黑杰克？

3. “什么都不是”（即不是对子或更好）的牌型共有多少种？大家可能要利用示例4.18和示例4.19的结果以及习题(1)的解答。

4. 如果依次抛12枚硬币，那么下列情况各有多少种？

(a) 至少有9枚硬币人头面朝上；

(b) 至多有4枚硬币人头面朝上；

(d) 不到2枚或多于10枚硬币人头面朝上。

5. * 至少有一个数字为1的掷骰子结果共有多少种？

6. * 使用单词little的字母构词，其中两个t不相邻的情况共有多少种？

7. ** 桥牌牌型由52张扑克牌中的13张构成，我们通常会通过“分布”为牌型分类，也就是说，会按照花色为手牌分组。例如，牌型4-3-3-3的分布表示有4张牌是某种花色，而另外3种花色的牌各有3张。牌型5-4-3-1的分布表示各花色的牌分别有5张、4张、3张和1张。为具有如下分布的牌型计数：(a)4-3-3-3；(b)5-4-3-1；(c)4-4-3-2；(d)9-2-2-0。

4.9　概率论简介

概率论在计算机科学领域具有很多用途，其中一种重要应用就是估算平均输入或典型输入情况下的程序运行时间。这种估算对那些最坏情况运行时间远大于平均运行时间的算法来说非常重要。我们很快就会看到这种估算的示例。

概率的另一种用途是在具有不确定性的情况下设计制定决策的算法。例如，可以使用概率论，设计根据可用信息制定最佳医疗诊断的算法，或设计在未来预期需求的基础上分配资源的算法。

4.9.1　概率空间

概率空间是指点的有限集，这些点分别表示某一实验的某种可能结果。每个点x 都与某个称作x 的概率的正实数相关联，而所有点对应概率的和为1。还有无限多个点的概率空间这样的说法，不过这种概念在计算机科学领域鲜有应用，所以这里不需要考虑这些。

通常，概率空间中的点都是等可能的。除非特别声明，否则可以假设概率空间中若干点表示的概率都是相等的。因此，如果概率空间中有n个点，则每个点的概率都是1/n。

示例 4.22

图4-13所示为具有6个点的概率空间。这些点分别被标记为从1到6这6个数字中的一个，而且可将该空间视为表示掷一次骰子这项“实验”的结果。也就是说，骰子6个面中某个面上的数字会出现在最上方，而每个数字出现的概率都是均等的，即都是1/6。

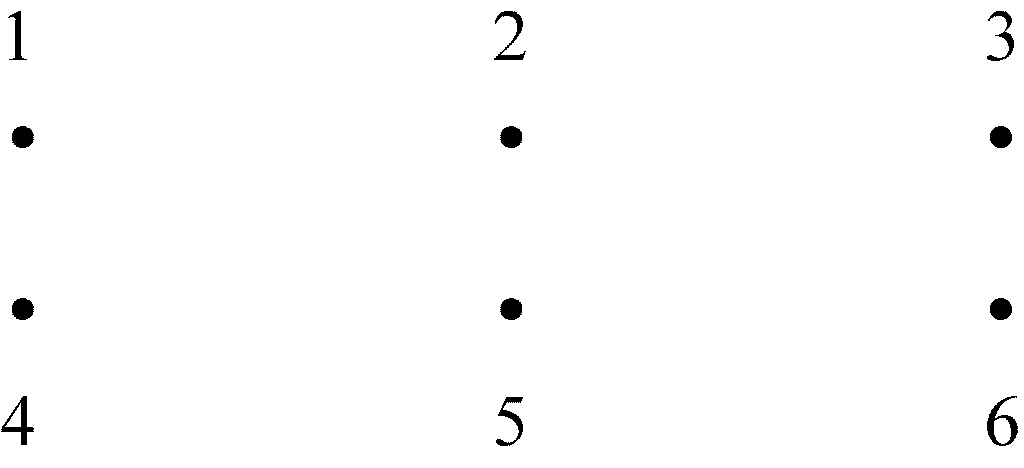
图 4-13　具有6个点的概率空间

概率空间中这些点的任意子集都可称为事件。某个事件E 的概率——记为PROB(E )——就是E 中各点概率之和。如果这些点都是等可能的，就可以用E中点的数目除以整个概率空间中点的数目来计算E的概率。

4.9.2　概率的计算

通常情况下，计算某个事件的概率会涉及组合。我们必须计算事件中点的数量，以及整个概率空间中点的数量。当点是等可能时，这两个计数的比就是该事件的概率。接下来要介绍一系列示例，展示按这种方式计算概率的过程。

无限的概率空间
在某些情况下，可以想象一个具有无数个点的概率空间，其中任何给定的点的概率都可能是无穷的，从而只能将有限的概率与某些点的集合关联起来。举个简单的例子，下图中的正方形表示某个概率空间，而该概率空间中的点是该正方形所在平面上的所有点。
可以假设正方形中任何点被选中的可能性都是相等的，并将这种“实验”视作往该正方形中投掷飞镖，飞镖飞到正方形上任何位置的可能性都是相同的，但肯定不会飞到正方形之外。虽然任何一点被击中的概率都是无穷的，但是该正方形中某个区域的概率等于该区域的面积与整个正方形的面积之比。因此，我们可以计算某些事件的概率。
例如，上图的概率空间中含有一个椭圆形组成的事件E。假设该椭圆区域的面积是整个正方形面积的29%，那么PROB(E )就是0.29。也就是说，如果随机地向该正方形投出飞镖，那么29%的情况下飞镖会落在这个椭圆中。

示例 4.23

图4-14展示了表示掷两颗骰子的概率空间。也就是说，进行的实验是按顺序抛出两颗骰子，并观察它们朝上那面的数字。假设掷骰子的过程是公平的，就有36个等可能的点，或者说是实验结果，所以每个点的概率都是1/36。每个点对应着每颗骰子从6个值中任选其一的分配。例如，（2,3）就表示第一颗骰子为2点，而第二颗骰子为3点的情况。而（3,2）则表示第一颗骰子是3，第二颗是2的情况。

被圈出来的区域表示“吃憋”的事件，也就是两颗骰子的总点数为7或11的情况。这个事件共含有8个点，其中6个是总点数为7的情况，而有两个是总点数为11的情况。投出“吃憋”情况的概率就是8/36，约为22%。

图 4-14　掷两颗骰子的概率空间中的“吃憋”事件

示例 4.24

再来计算一下扑克牌出现对子牌型的概率。我们在示例4.8中已了解到总共有2 598 960种不同的扑克牌型。考虑该公平处理扑克牌型的实验，也就是说，所有牌型出现的可能性都相等。因此，该实验的概率空间总共有2 598 960个点。我们还从示例4.18中得知，这些表示牌型的点中有1 098 240个被分类为对子牌型。假设所有牌型被处理的可能都是均等的，那么“对子”事件的概率就是1 098 240/2 598 960，大约是42%。

示例 4.25

在基诺游戏中，会随机从1到80这些数字中选出20个。而且选取这些数字之前，玩家可以猜测一些数字。这里要专门讲讲这个玩家要猜测5个数字的“5点游戏”。所猜数字与选中的20个数字中有3个、4个或5个吻合的话，玩家就中奖了，而且猜中的数字越多，得到的奖金越丰厚。我们要计算的是玩家在该游戏中正好猜中3个数字的概率。正好猜中4个或5个数字的概率的计算将留作本节的习题。

首先，合适的概率空间包含了表示从1到80中任选20个数字所有可能情况的点。这样的选择总共有

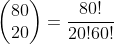
$\begin{pmatrix}80\\20\end{pmatrix}=\frac{80!}{20!60!}$

种，这个数字奇大无比，好在不需要把它写出来。

结果何时是随机的？
在示例中已经假设过某些实验具有“随机的”结果，也就是说，所有可能出现的结果的可能性都是相等的。在一些情况下，这种假设的合理性源自物理学。例如，在投掷公平（未加重）的骰子时，我们假设在物理上不可能控制骰子的某个面比其他面更可能朝上。这在实践中是种有效的假设。同样，我们可以假设公平洗牌的牌堆不会影响结果，而且任何一张牌出现在牌堆中任意位置的可能性都是相同的。
在其他情况下，我们发现一些貌似随机的事物实际上根本不随机，只不过是某个过程原则上可预知但在实践中不可预知的结果。例如，基诺游戏中选出的数字可能是由计算机执行某个特殊算法生成的，而如果没法接触到计算机使用的这些秘密信息，就不可能预测结果。
计算机生成的“随机”序列都是某种被称为随机数生成器的特殊算法的结果。设计这样的算法需要一些专门的数学知识，而这些知识超出了本书的范畴。不过，我们会介绍一种实践中相当好用的随机数生成器——线性同余生成器。
指定常数a≥2，b≥1，x₀≥0，而且a modm>max(a,b,x₀)，便可以通过使用公式
x_n+1=(ax_n+b)modm
生成一列数字x₀，x₁，x₂…。如果选择的a、b、m和x₀很合适，那么得到的数字序列就会显得相当随机，即便它们是通过特定算法由“种子”x₀计算得出的。
随机数生成器生成的序列有很多用途。例如，可以根据上述序列选取基诺游戏中的开奖号码，用上述序列中的每个数除以80，取余数，并加上1，得到1到80间的某个“随机”数。不断这样处理，除去重复的数字，直到选出20个数字。只要没人知道生成算法和种子，这一游戏就可视为是公平的。

现在要计数的情况是从80个数字中选出20个，其中含有玩家所选择5个数字中的3个，以及玩家没有选择的75个数字中的17个。从5个数字中选出3个共有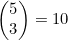 $\begin{pmatrix}5\\3\end{pmatrix}=10$ 种方式，而从剩下的75个数字中选取17个的方式共有 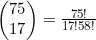$\begin{pmatrix}75\\17\end{pmatrix}=\frac{75!}{17!58!}$ 种。

因此，玩家在5个数字中猜中3个的结果数与总选择数的比就是

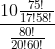
$\frac{10\frac{75!}{17!58!}}{\frac{80!}{20!60!}}$

如果将上下都乘上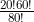 $\frac{20!60!}{80!}$ ，上式就成了

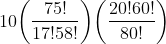
$10\biggl(\frac{75!}{17!58!}\biggr)\biggl(\frac{20!60!}{80!}\biggr)$

可以看到分子和分母中的阶乘项很接近，几乎可以约去。例如，分子中的75!和分母中的80!就可以用分母中80到76这5个数的乘积代替，所以可以简化为

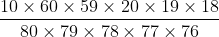
$\frac{10\times60\times59\times20\times19\times18}{80\times79\times78\times77\times76}$

这样就可以对可控数字加以计算了，结果是0.084。也就是说，玩家在5个数字中猜中3个的概率大约为8.4%。

4.9.3　基本关系

本节要审视概率的一些重要属性。首先，如果p 是任一事件的概率，那么

0≤p≤1

也就是说，任何事件都是由0个或更多个点组成，所以它的概率不可能为负值。而且，没有任何事件会由比整个概率空间还多的点构成，所以它的概率不会超过1。

其次，设E 是某个概率空间P 中的事件。那么事件E 的互补事件E 就是P 中不属于事件E 的点的集合。不难看出

PROB(E ) + PROB(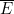 $\overline{E}$ ) = 1

或者换句话说，PROB(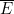 $\overline{E}$ ) = 1 - PROB(E )。原因在于，P 中的每个点，要么在E 中，要么在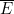 $\overline{E}$ 中，不可能同时在二者之中。

4.9.4　习题

1. 使用图4-14中展示的掷两颗公平骰子的概率空间，给出以下事件的概率。

(a) 掷出的点数为6（即两颗骰子点数之和是6）；

(b) 掷出的点数为10；

(d) 掷出的点数在5到9之间。

2. * 计算以下事件的概率。概率空间是从普通的52张扑克牌堆中按次序取两张牌的所有情况。

(a) 至少有一张牌是A；

(b) 两张牌的秩相同；

(d) 两张牌的秩和花色都相同；

(e) 两张牌要么秩相同要么花色相同；

(f) 第一张牌的秩高于第二张牌的秩。

3. * 将飞镖掷向墙上一英尺见方的区域，击中该方形区域中任何一点的可能性都是相同的。那么在投掷飞镖时

(a) 离中心3英寸以内的概率是多少？

(b) 离边缘3英寸以内的概率是多少？

请注意，在该习题中，概率空间是一个一英尺见方的无限区域，其中所有点都是等可能性的。

4. 计算玩家在基诺5点游戏中猜中如下数字的概率。

(a) 猜中5个数字中的4个；

(b) 猜中全部5个数字。

5. 编写C语言程序实现线性同余随机数生成器。绘制它生成的前100个数字最低有效位各数字出现频率的直方图。该直方图应该具有什么属性？

4.10　条件概率

在本节中，我们将指定数项公式和策略，用来考虑若干事件概率之间的关系。其中一项重要的结论就是独立实验的概念。在独立实验中，一项实验的结果不影响其他实验的结果。我们还将运用一些技巧来计算某些复杂情形下的概率。

这些结论都依赖于“条件概率”的概念。不严谨地说，如果进行一次实验，而且得知事件E 已经发生，那么表示这种结果的点也有可能出现在另一事件F 中。图4-15就展示了这种情况。E 条件下F 的概率就是E 发生前提下F 也发生的概率。

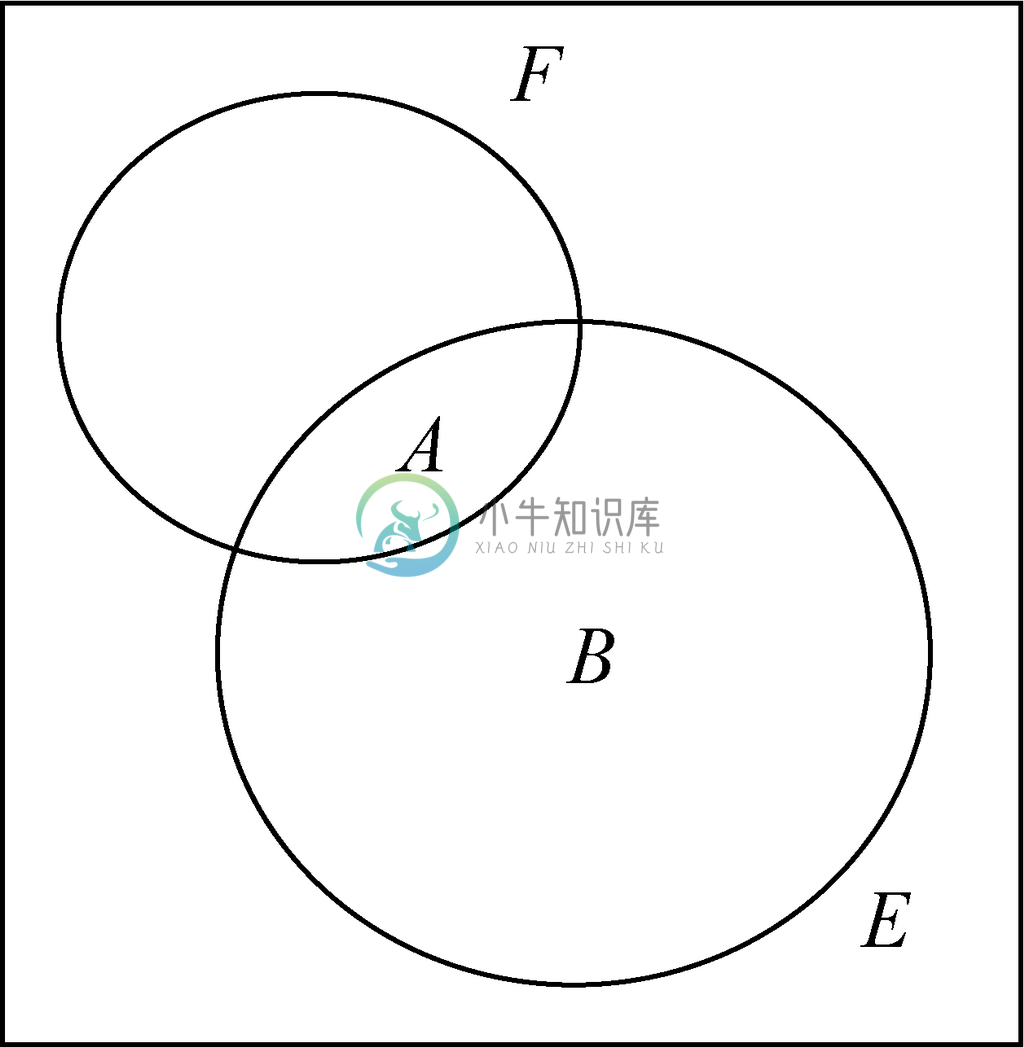
图 4-15　E 条件下F 的概率是结果在A 中的概率除以结果在A 或在B 中的概率

正式地讲，如果E 和F 是某个概率空间中的两个事件，那么E 条件下F 的概率，记作PROB(F |E )，就是同时出现在E 和F 中的所有点的概率之和除以出现在E 中各点的概率之和。在图4-15中，区域A 表示那些同时在E 和F 中的点，B 则表示在E 中而不在F 中的点。如果所有点都是等可能的，那么PROB(F |E )就是A 中点的数量除以A 和B 中点的数量之和。

示例 4.26

考虑图4-14中表示掷两颗骰子的概率空间。设事件E 是第一颗骰子点数为1的6个点，F 是第二颗骰子点数为1的6个点，情形如图4-16所示。既在E 中又在F 中的点只有一个，即点(1，1)。在E 而不在F 中的点共有5个。因此，条件概率PROB(F |E )为1/6。也就是说，在确定第一颗骰子为1的条件下，第二颗骰子为1的概率是1/6。

大家可能会注意到，这一条件概率刚好等于F 本身的概率。也就是说，因为F 占有整个概率空间36个点中的6个点，所以PROB(F )=6/36=1/6。从直观上讲，第二颗骰子掷出1的概率，并不受第一颗骰子已经掷出1这一事实的影响。我们很快就将定义“独立实验”（比如依次掷骰子）的概念，其中一次实验的结果不会对其他实验的结果产生影响。在这样的情况下，如果E 和F 是表示两次实验结果的事件，就可以预期PROB(F |E )=PROB(F )。我们已经看过这一现象的一个例子了。

示例 4.27

假设实验是从有52张扑克的牌堆中按次序取两张牌。在这一不放回选择（如4.4节所述）实验中，点的数目是52×51=2652。假设这种取牌是公平的，所以每个点的可能性都是相同的。

设事件E 是第一张牌为A的情况，F 是第二张牌为A的情况。那么E 中的点共有4×51=204个。也就是说，第一张牌是4张A中的某一张，而第二张牌可以是除去第一次选走的A之外的51张牌中的任意一张。因此，PROB(E )=204/2652=1/13。这一结果是符合大家的直觉的。所有13种秩都是等可能性的，所以可以预期第一张牌出现A的可能是1/13。

同样，事件F 中也有4×51=204个点。可以为第二张牌任选一种A，并在其余51张牌中任选其一作为第一张牌。第一张牌理论上讲要先取得，而这一事实是无关紧要的。因此A出现在第二张的情况共有204种。因此，与E 一样，PROB(F )=1/13。这个结果还是满足A是第二张牌的可能为1/13这一直观感受。

现在来计算PROB(F |E )。在E 的204个点中，第二张牌也为A（也就是点也在F 中）的情况有12个。也就是说，E 中的所有点都表示A为第一张牌的情况。选择A的方式共有4种，对应4种花色的选择。在每种选择中，第二张牌也为A的选择都有3种。因此，根据4.4节介绍的技巧，有序选择两张A的情况共有4×3=12种。

因此，条件概率PROB(F |E )是12/204，或者说是1/17。可以注意到，在本例中，E 条件下F 的概率与F 的概率并不相等。这也是符合直观感受的。当第一张牌取走一张A之后，第二张牌再取到A的概率就下降了。那时候，剩下的51张牌中只有3张A，而3/51=1/17。与之相对的是，如果不知道第一张牌是什么，那么第二张牌就可能是52张牌中4张A中的某一张。

4.10.1　独立实验

正如示例4.23、示例4.26和示例4.27中所介绍的，有时候建立的概率空间会表示两个或多个实验的结果。在最简单的情况下，该共同概率空间中的点是结果的表，每个表代表一项实验的结果。图4-16就给出了两项实验联合起来的概率空间。在实验结果间存在联系的情形中，共同空间中可能会丢失一些点。示例4.27就讨论了这样的情况，其中共同空间表示取两张牌且结果成对，其中不可能取到两张相同的牌。

实验X 独立于序列中前序实验的结果。从直观概念上讲这意味着X 的各种结果都不依赖于前序实验的结果。因此，示例4.26中我们指出掷第二颗骰子是独立于掷第一颗骰子的，而在示例4.27中，我们看到取第二张牌的实验并非独立于取第一张牌的实验，因为取出第一张牌后，就不可能再次取到这张牌了。

在定义独立性时，将着重于两项实验的关系。不过，因为任一实验本身也可能是一个若干实验构成的序列，所以这样的定义有效地涵盖了具有很多实验的情况。首先必须了解表示两项成功实验X₁和X₂的结果的概率空间。

示例 4.28

图4-14展示了一个共同概率空间，其中实验X₁是第一颗骰子，而实验X₂是第二颗骰子。这里每一对结果都是用一个点表示的，而这些点的可能性是相等的，都等于1/36。

在示例4.27中，我们讨论过表示按次序选取两张牌、含52个点的概率空间。该空间由(C,D )这样的牌对组成，其中C 和D 分别是某张扑克牌，而且C≠D。这些点的可能也相同，都是1/2652。

在表示X₁接着X₂的结果的概率空间中，存在表示其中一项实验的结果的事件。也就是说，如果a 是实验X₁可能出现的结果，就有一个事件是由所有表示第一项实验结果为a 的点组成的。这里将该事件称为E_a 。同样，如果b 是实验X₂可能出现的结果，就有一个事件F_b是由所有表示第二项实验结果为b 的点组成的。

示例 4.29

在图4-16中，E是E₁，就是表示第一项实验结果为1的所有点。同样，F是事件F₁，就是那些表示第二项实验结果为1的点。每一行对应着第一项实验6种可能结果中的一种，而每一列则对应第二项实验6种可能结果中的一种。

{%}

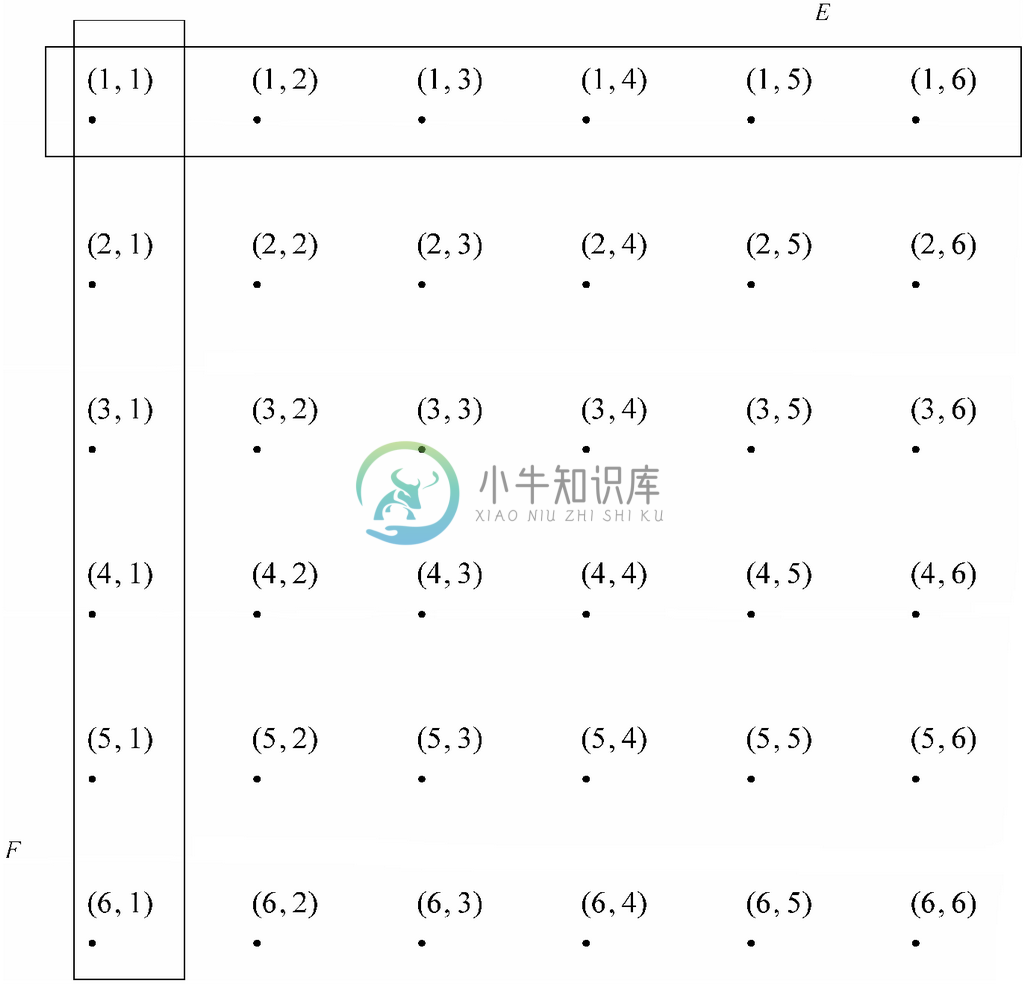
图 4-16　表示第一颗骰子或第二颗骰子点数为1的事件

严格地讲，如果对X₁的所有结果a以及X₂的所有结果b，有PROB(F_b|E_a)=PROB(F_b)，那么就说实验X₂是独立于实验X₁的。也就是说，不管实验X₁的结果是怎样的，实验X₂各结果的条件概率都是相同的，而且都等于实验X₂在整个概率空间中的概率。

示例 4.30

回到图4-16表示掷两颗骰子的概率空间，设a 和b 分别是1到6这些数字中的任意一个。用E_a表示第一颗骰子为a 的事件，F_b表示第二颗骰子是b 的事件。不难注意到，这些事件的概率均为1/6，它们各自排成一行或一列。对任意的a 和b 来说，PROB(F_b|E_a)也是1/6。我们在示例4.26中已经证实这一结论在a=b=1的情况下是成立的，不过同样的论证过程也适用于任意两个结果a和b，因为它们的事件只有一个点是相同的。因此，掷两次骰子是相互独立的。

另一方面，在以扑克牌为例的示例4.27中，就不存在这种独立性。因为，实验X₁是第一张牌的选择，而实验X₂是从剩下的牌中选择第二张牌。考虑诸如F_A♠这样的事件，也就是说，第二张牌为黑桃A的情况。很容易便能得出该事件的概率PROB(FA_A♠这)为1/52的结论。

再来考虑诸如E_3♣，也就是第一张牌为草花3的情况。同在E_3♣和F_A♠中的点只有一个，就是点(3♣,A♠)。而E_3♣中的点共有51个，也就是形如(3♣,C)这样的点，其中C是除了草花3之外的任意一张牌。因此，条件概率PROB(F_A♠|E_3♣)是1/51，而不是1/52，因为这两项实验不是相互独立的。

可以考虑一个更极端的例子，就是第一张牌为黑桃A的事件E_A♠。因为E_A♠和F_A♠中没有相同的点，所以PROB(F_A♠|E_A♠)就是0，而不是1/52。

4.10.2　概率的分配律

有时候，如果先将概率空间划分为几个区域3，就会让概率的计算变得更加容易。也就是说，每个点都只出现在一个区域中。通常，概率空间表示一系列实验的结果，而表示事件的区域则对应其中某一实验可能出现的结果。

3“区域”指的就是“事件”，也就是概率空间的子集。不过，这里使用术语“区域”是为了强调这是将概率空间分为完全覆盖整个区域又不互相重叠的事件。

假设要计算被分为R₁、R₂、…、R_k 这k 个区域的某个具有n个点的概率空间中事件E 的概率。简单起见，假设所有点的概率都是相同的，尽管就算它们的概率不同也不影响结论的成立。设事件E 由m个点组成。设区域R_i 中有r_i 个点（i=1、2、…、k）。最后，设E中处于区域R_i 中的点有e_i 个。请注意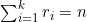， $\sum^{k}_{i=1}r_i=n$ ，而且 $\sum^{k}_{i=1}e_i=m$ 。原因皆在于这些点都会在某个区域中而且只会在一个区域中。

我们知道PROB(E)=m/n，因为m/n 就是E 中的点所占的部分。如果用e_i 的和替代m，就得到

PROB(E) = 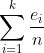$\sum^{k}_{i=1}\frac{e_i}{n}$

接着，在上述和式中每一项的分子和分母中都引入因子r_i 。结果就是

PROB(E) = 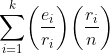$\sum^{k}_{i=1}\biggl(\frac{e_i}{r_i}\biggr)\biggl(\frac{r_i}{n}\biggr)$

现在，请注意r_i /n 就是PROB(R_i )，也就是说，r_i /n是区域R_i 在整个概率空间中所占的部分。此外，e_i /r_i 就是PROB(E /R_i )，即事件R_i 条件下事件E 的概率。换句话说，e_i /r_i 是区域R_i 中也出现在E 中的点的比例。结果就得到以下事件E 概率的计算公式。

PROB(E ) = 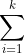$\sum^{k}_{i=1}$ PROB $\bigl(E|R_i\bigr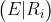)$ PROB(R_i )　　　　　　(4.10)

非正式地讲，E 的概率是各区域的概率乘上E 在相应区域中的概率的总和。

示例 4.31

图4-17表示了(4.10)式的应用方式。图中展示了被垂直划分为R₁、R₂和R₃这3个区域的概率空间。其中事件E 是再度用线勾勒出的。设a 到f 分别是所示6个组中点的数目。

设n=a+b+c+d+e+f。那么有PROB(R₁)=(a+b)/n、PROB(R₂)=(c+d)/n，而且PROB(R₃)=(e+f )/n。而事件E 在这3个区域的条件概率分别是PROB(E |R₂)=a/(a+b)、PROB(E |R₂)=c/(c+d)，而且PROB(E |R₃)=e/(e+f )。现在来评估(4.10)式，就有

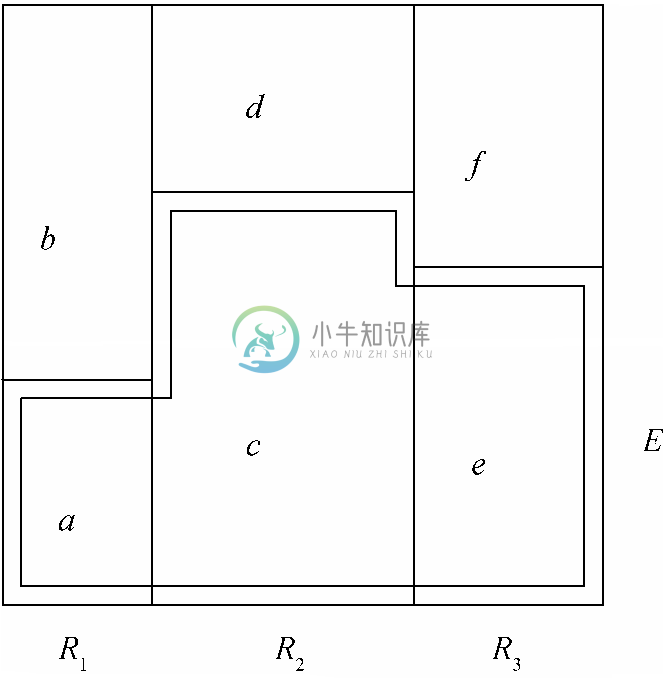
图 4-17　分为区域的概率空间

PROB(E )＝PROB(E |R₁)PROB(R₁)+PROB(E |R₂)PROB(R₂)+PROB(E |R₃)PROB(R₃)

如果将该式用a 到f 的参数表示，就是

PROB(E ) = 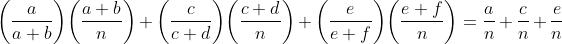$\biggl(\frac{a}{a+b}\biggr)\biggl(\frac{a+b}{n}\biggr)+\biggl(\frac{c}{c+d}\biggr)\biggl(\frac{c+d}{n}\biggr)+\biggl(\frac{e}{e+f}\biggr)\biggl(\frac{e+f}{n}\biggr)=\frac{a}{n}+\frac{c}{n}+\frac{e}{n}$

请注意，直接将标记有a、c、e的3块中点的数目与整个空间的大小相比，也能得到同样的结果。(a+c+e)/n这一分数正是上式给出的E的概率，这一结果证明了(4.10)式。

示例 4.32

现在利用(4.10)式计算事件E“按次序取两张扑克牌均是A”的概率。概率空间是示例4.27中讨论过的那2652个点。这里要将该空间分为R₁、R₂两个区域。

R₁：第一张牌为A的那些点。总共有4×51=204个这样的点，因为第一张牌为A的情况有4种，而每种情况下对应的第二张牌都有51种选择。

R₂：剩下的2448个点。

这种情况下，(4.10)式就成了

PROB(E )＝PROB(E |R₁)PROB(R₁)+PROB(E |R₂)PROB(R₂)

显然PROB(E |R₁)，也就是R₂条件下E 的条件概率，为0。如果第一张牌不为A，那么不可能拿到两张A，因此必须计算PROB(E |R₁)PROB(R₁)，而这个值就是PROB(E )。现在有PROB(R₁)=204/2652=1/13。换句话说，第一张牌拿到A的可能性是1/13。因为总共有13种秩，所以这一概率是说得通的。

现在需要计算PROB(E |R₁)。如果第一张牌是A，那么剩下的51张牌中还剩3张A。因此，PROB(E |R₁)=3/51=1/17。因此可以得出结论：PROB(E )=(1/17)(1/13)=1/221。

示例 4.33

现在用(4.10)式来计算事件E“掷3颗骰子，至少出现一个1点”的概率，就像示例4.16中描述过的掷骰子游戏那样。首先，我们一定要理解，那个例子中描述的“结果”的概念与概率空间中的点并不匹配。在示例4.16中，我们建立的概率空间有56种不同的“结果”，这是骰子出现1到6点的次数。例如，“一个4点、一个5点和一个6点”是一种结果，而“两个3点和一个4点”是另一种结果。然而，这种情况下各种结果的概率并不相同。特别要说的是，3个数字都不同的概率是某个数字出现两次的概率的两倍，是3个骰子数字都相同的概率的6倍。

尽管可以使用点对应示例4.16中那种“结果”的概率空间，不过考虑按顺序掷骰子，从而构建一个包含的点概率相等的概率空间要更为自然。这样一来就有6³=216种不同的结果与按次序掷3次骰子的事件对应，而每个结果的概率均为1/216。

我们可以不使用(4.10)式，而是直接计算至少有一颗骰子为1点的概率。首先，计算没有1出现的情况数。可以为3颗骰子分配2到6之中的任一数字。这样概率空间中不含1的点共有5³=125个，所以有1的点就有216-125=91个。因此，PROB(E )91/216，大约为42%。

上述方法虽然简短，但需要使用些许“技巧”。计算这一概率的另一种方式是“强行”将概率空间分为3个区域，对应出现一个数字、两个不同数字或3个不同数字的情况。设R_i 是具有i 个不同数字的点所在的区域。可以按照下列方式计算各区域的概率。就R₁而言，总共有6个点，也就是3个骰子均为1到6这些点时的情况。就R₃而言，根据4.4节中的规则，从6个数字中选出3个不同的数字共有6×5×4=120种方式。因此R₂中一定是具有剩下的216-6-120=90个点。4各区域的概率分别是PROB(R₁)=6/216=1/36、PROB(R₂)=90/216=5/12、PROB(R₃)=120/216=5/9。

4可以直接计算该数字，用选择会出现两次的点数的6种方式，乘上选择其余骰子点数的5种方式，再乘上选择只出现一次的那个数字所在位置的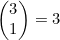 $\begin{pmatrix}3\\1\end{pmatrix}=3$ 种方式。就是6×5×3=90种方式。

接着要计算条件概率。如果出现了6个数字中的3个数字，那么其中一个为1的概率是1/2。如果出现了2个数字，那么至少出现一次1的概率是1/3。如果只有一个数字出现，那么该数字为1的概率是1/6。因此PROB(E |R₁)=1/6、PROB(E |R₂)=1/3，而且PROB(E |R₃)=1/2。将这些概率都代入(4.10)式中，就得到

PROB(E ) = (1/6)(1/36)+(1/3)(5/12)+(1/2)(5/9)
　　　　=1/216+5/36+5/18=91/216

当然，这一分数和直接计算的结果是吻合的。如果能理解直接计算中的那些“诀窍”，那么直接计算的方法是相当容易的。不过，将问题分为若干区域往往是一种更为可靠的保障成功的方式。

4.10.3　独立实验的乘积法则

一类常见的概率问题是求一系列独立实验的一系列结果的概率。在这种情况下，(4.10)式具有了特别简单的形式，表明这一系列结果的概率就是每一结果概率的乘积。

首先，将概率空间等分为k 个区域，就会对所有的i有PROB(R_i )=1/k，因此(4.10)式可以简化为

PROB(E) = 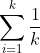$\sum^{k}_{i=1}\frac{1}{k}$ PROB(E |R_i )　　　　　　(4.11)

看待(4.11)式的一种实用方式是将E的概率视为各区域条件下E 的概率的平均值。

现在考虑表示两项独立实验X₁和X₂的结果的概率空间。可以将该空间分为k个区域，每个区域都是点的集合，这些点表示具有某个特定值的X₁的结果，这样每个区域都具有相同的概率1/k。

假设要计算事件E“X₁的结果为a，且X₂的结果为b”的概率，可以使用(4.11)式。如果R_i 不是对应X₁的结果a 的区域，那么PROB(E |R₁)=0。因此，(4.11)式中就只剩下a 区域的项了。如果说该区域为R_a，就得到

PROB(E ) = 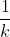$\frac{1}{k}$ PROB(E |R_a)　　　　　　(4.12)

PROB(E |R_a)是什么？它是在X₁的结果为a的条件下，“X₁的结果为a，且X₂的结果为b”的概率。因为给定了X₁的结果为a，所以PROB(E |R_a)是在X₁的结果为a的条件下，X₂的结果为b的概率。又因为X₁和X₂是相互独立的，所以PROB(E |R_a)就是X₂的结果为b的概率。如果X₂可能有m种结果，那么PROB(E |R_a)就是1/m。那么(4.12)式就成了

PROB(E ) = 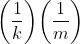$\biggl(\frac{1}{k}\biggr)\biggl(\frac{1}{m}\biggr)$

我们可将上述推理一般化为针对任意数量的实验。想这样做，可以令实验X₁是一系列实验，并通过对独立实验总数量的归纳来证明，有着特定序列的全部结果的概率等于每个结果的概率的乘积。

利用独立性简化计算
如果知道实验是相互独立的，就有很多机会简化概率计算。乘积法则是一个例子。另一个例子就是，只要E 是表示实验X₁特定结果的点集合，F 是另一个独立实验X₂特定结果的点集合，那么就有PROB(E |F )＝PROB(E )。
原则上讲，分辨两项实验是否相互独立是个复杂的任务，涉及对表示实验结果对的概率空间的检测。不过，通常可以借助该情形的物理特性，在不进行这种计算的情况下得出实验互相独立的结论。例如，在依次掷骰子时，不存在物理学上的原因令一次投掷的结果能影响其他投掷的结果，所以它们肯定是独立实验。而从牌堆中取牌则与掷骰子的情况不同。因为取出的牌是无法在随后的过程中被再次取出的，所以不用指望连续取牌是相互独立的事件。事实上，我们已在示例4.29中看到了这种独立性的缺失。

示例 4.34

电话号码后四位为1234的概率是0.0001。每一位号码的选择都是有0到9这10种可能结果的实验。其次，每一位的选择都独立于其他位的选择，因为这里进行的是4.2节中介绍的“有放回的选择”。第一位是1的概率为1/10。同样，第二位是2的概率为1/10，而其他两位的情况也是一样的。所以4位数字依次为1234的概率就是(1/10)⁴=0.0001。

4.10.4　习题

1. 使用图4-14所示的概率空间，给出如下事件对的条件概率。

(a) 在第一颗骰子为奇数的条件下，第二颗骰子是偶数。

(b) 在第二颗骰子至少为3的条件下，第一颗骰子是偶数。

(d) 在两颗骰子点数之和为8的条件下，第二颗骰子是3。

2. 将掷骰子（见示例4.16）游戏的概率空间按照示例4.33所示划分为3个区域，使用这一划分方式与4.10式计算如下概率。

(a) 至少出现两个1点。

(b) 3颗骰子都是1点。

3. 证明：在掷3颗骰子的游戏中，3颗骰子点数均不同的概率，是有两颗骰子出现同一点数的概率的两倍，是3颗骰子点数均相同的概率的6倍。

4. * 通过对n 的归纳证明，如果有n 项实验，而且每一项实验都是相互独立的，那么任一系列结果的概率等于对应实验各项结果概率的乘积。

5. * 证明：如果有PROB(F |E )=PROB(F )，则有PROB(F |E )=PROB(E )。并证明：如果实验X₁独立于实验X₂，那么X₂也独立于X₁。

6. * 考虑从W和L中作出选择组成的长度为7个字母的序列的集合。可以将其视为表示7场4胜制比赛的结果的序列，其中W表示第一支队伍获得1场比赛的胜利，而L表示第二支队伍获胜。哪支队伍先取得4场胜利则赢得这场系列赛（因此，有些比赛可能从未进行过，不过我们需要将其假设结果包含在这些点中，从而获得各点概率相等的概率空间）。

(a) 在某支队伍取得第一场比赛胜利的条件下，该队在这个系列赛中取胜的概率？

(b) 在某支队伍取得前两场比赛胜利的条件下，该队在这个系列赛中取胜的概率？

7. ** 有3个囚犯A、B 和C。他们得知3人中有一个要被枪决，而且狱警知道要枪决谁。A 让狱警告诉他其他两个囚犯中哪个不会被枪决。狱警告诉A，B 不会被枪决。

A 推理要么是他，要么是C 被枪决，所以A 被枪决的概率是1/2。另一方面，对A 进行推理，不管谁被枪决，狱警都知道A 之外的某人不会被枪决，所以他总能回答A 的问题。因此，通过该问题的提问和回答都不能判定A 是否会被枪决，所以A 将被枪决的概率仍是1/3，就像在提出问题之前的概率那样。

那么在经过上述系列事件后，A将被枪决的真实概率是多少？提示：需要构建合适的概率空间，不只要表示囚犯被选中枪决的实验，而且要表示狱警有权选择回答“B ”或“C ”的情况下作出某种选择的实验的概率。

8. * 假设E 是处在被分为R₁、R₂、…、R_k 这k 个区域的空间中的事件。证明：

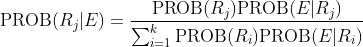
$\text{PROB}(R_j|E)=\frac{\text{PROB}(R_j)\text{PROB}(E|R_j)}{\sum^{k}_{i=1}\text{PROB}(R_i)\text{PROB}(E|R_i)}$

该公式被称为贝叶斯定理（Bayes' Rule）。它给出了在已知E的条件下R_j 的概率的值。针对示例4.31，使用贝叶斯定理计算PROB(R₁|E )、PROB(R₂|E )和PROB(R₃|E )。

4.11　概率推理

概率在计算机领域的一项重要应用就是用在事件预测系统的设计中。其中一个例子就是医疗诊断系统。理想状态下，诊断过程包含执行检测或观察症状，直到检测结果或特定症状的出现与否使医生足以确定患者所患的疾病为止。然而，在实际操作中，诊断很少是确定无疑的。诊断出的只是最为可能的疾病，或者是在进行检测和观察症状的实验条件下，条件概率最大的疾病。

现在来考虑一个特别简单的例子，此例就利用了概率的诊断风格。假设已知当患者出现头痛时，他患流感的概率为50%，也就是

PROB(流感 | 头痛)=0.5

在上式中，我们将“流感”解释为“患者得了流感”这一事件的名称。同样，“头痛”是“患者自称头痛”这一事件的名称。

假设还知道当患者的体温达到或超过38.9摄氏度时，该患者得流感的概率是60%。如果将“发烧”作为“患者体温至少为38.9摄氏度”这一事件的名称，就可以将这一结论写为

PROB(流感 | 发烧)=0.6

现在，考虑如下诊断情形。某患者来看医生，表示自己有头痛的症状。医生为他量了体温，发现他的体温是38.9摄氏度，那么该患者患流感的概率是多少？

这种情形如图4-18所示。其中有“流感”、“头痛”和“发烧”3个事件，将该空间分为8个区域，这里分别用a 到h 这些字母表示这些区域。例如，c就是“患者具有头痛症状而且患了流感，但不发烧”这一事件。

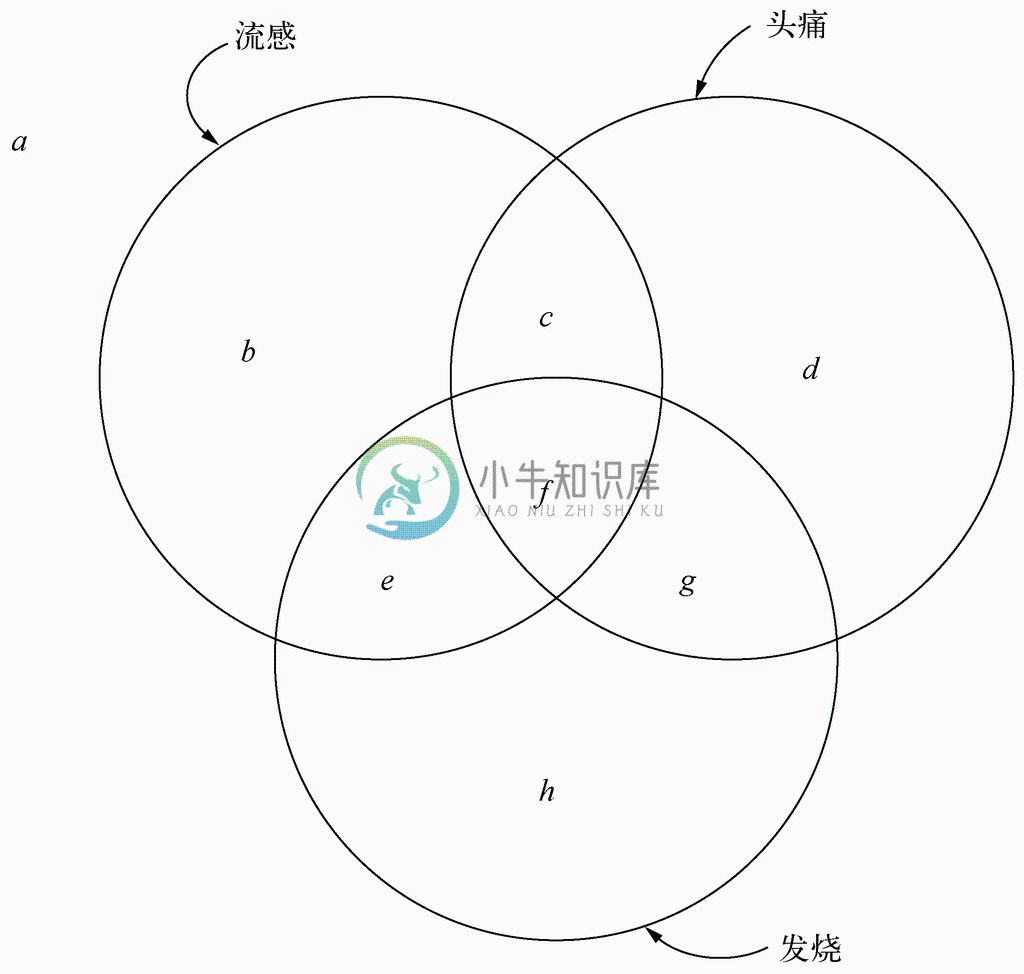
图 4-18　“流感”、“头痛”和“发烧”事件

给定的这些概率信息对图4-18中事件的大小提出了一些限制。若不仅用a 到h 表示图4-18中的那些区域，还用这些字母表示对应事件的概率。那么条件概率PROB(流感 | 头痛)=0.5就表示区域c+f 的和是“头痛”事件总大小的一半，或者换种形式就是

c+f =d+g　　　　　　(4.13)

同样，PROB(流感 | 发烧)=0.5这一事实表示e+f 是“发烧”事件总大小的3/5，或者说

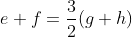$e+f=\frac{3}{2}(g+h)$ 　　　　　　(4.14)

现在来解说“在发烧和头痛同时出现的条件下，患流感的概率是多少”这一问题。实情就是，发烧和头痛同时出现的情况表明要么是在区域f 中，要么是在区域g 中。在区域f 中时流感的诊断是正确的，而在区域g 中时则不是。因此，患流感的概率就是f /(f+g)。

那么f /(f+g)的值是多少呢？答案可能有点惊人。显然没有任何关于“流感”事件概率的信息，它可能是0，也可能是1，还可能是0和1之间的任意数字。下面有两个例子，它们分别表示图4-18所示概率空间中的点有可能出现的实际分布情况。

示例 4.35

假设图4-18中与众事件关联的概率分别是：d=f=0.3，a=h=0.2，而其他4个区域的概率都是0。请注意，这些值都满足(4.13)式和(4.14)式给出的限制。在本例中，f /(f+g)=1，也就是说，同时有头痛和发烧症状的患者肯定得了流感。那么图4-18中的概率空间实际就成了图4-19所示的样子。从该图中可看出，只要患者同时有发烧和头痛的情况，那么他肯定患了流感，而且反过来，只要他得了流感，那么肯定有发烧和头痛的症状。5

5虽然也有b≠0的其他例子，也就是患者患了流感却既不发烧也不头痛，但还是有f /(f+g)=1。

图 4-19　当“发烧”和“头痛”确保“流感”时的空间示例

示例 4.36

另一个例子是给定概率c=g=0.2，a=e=0.3，而其他概率则是0。(4.13)式和(4.14)式还是能得到满足。不过，现在f /(f+g)=0。也就是说，如果患者同时有发烧和头痛的情况，那么他肯定不会得流感。这一表述相当可疑，不过(4.13)式和(4.14)式又不能推倒这一表述。这一情形如图4-20所示。

图 4-20　当“发烧”和“头痛”确保不“流感”时的空间示例

4.11.1　`OR`结合的两个事件的概率

如果没法分辨上述情形中当患者既发烧又头痛时会发生什么，我们可能想知道有没有什么可说的。在更简单的情形下，事件结合时概率的行为其实是有一些限制的。最简单的情况可能就是用析取（disjunction）或者说逻辑OR（逻辑“或”）结合两个事件时的情况了。

示例 4.37

再来看看图4-18。假设已知在任意时间，有2%的人发烧，且有3%的人感到头痛。也就是说，“发烧”事件的大小为0.02，而“头痛”事件的大小为0.03。那么，有发烧或头痛中任一种情况，或是两种情况都有的人所占比例是多大呢？

答案是至少有一种症状的人所占比例在3%到5%之间。要知道为何，用图4-18定义的8个区域来进行一些计算吧。如果“发烧”的概率为0.02，也就是说

e+h+f+g=0.02　　　　　　(4.15)

如果“头痛”的概率是0.03，那么有

c+d+f+g=0.03　　　　　　(4.16)

之前的问题是至少有一种症状的区域为多大，也就是问e+h+f+g+c+d有多大。

如果将(4.15)和(4.16)相加，就得到e+h+2(f+g)+c+d=0.05，或者换种方式表示：

e+h+f+g+c+d=0.05-(f+g)　　　　　　(4.17)

因为“发烧OR头痛”的概率是(4.17)式的左边部分，所以(4.17)式的右边部分0.05-(f+g)也是这一概率。

f+g至少为0，所以“发烧OR头痛”的概率最高是0.05，不可能超过0.05。也就是说，头痛和发烧的症状有可能从不同时出现。那么区域f 和g 都为空，而e+h=0.02，且c+d=0.03。在这种情况下，“发烧OR头痛”的概率是“发烧”的概率与“头痛”的概率之和。

那么f+g 的最大值可能是多少？当然，f+g 既不可能大于整个“发烧”事件，也不可能大于整个“头痛”事件。因为“发烧”更小，所以可知f+g≤0.02。因此，“发烧OR头痛”的最小概率可以是0.05-0.02，也就是0.03。这一结果正好是两个事件中较大的“头痛”事件的概率，这并非巧合。换种方式看，“发烧OR头痛”概率的最小值会在两个事件中较小那个完全被较大那个包含时出现。在本例中，这种情况会在e+h=0，也就是“发烧”完全包含在“头痛”中时出现。在那种情况下，除非有头痛，不然不会发烧，所以“发烧OR头痛”的概率就是“头痛”的概率——0.03。

现在可以将示例4.37中的探索一般化为针对任意两个事件，求和规则如下所示。如果E和F是任意两个事件，而G是E或F有一个发生或两者都发生的事件，那么

max(PROB(E ),PROB(F ))≤PROB(G )≤PROB(E )+PROB(F )　　　　　　(4.18)

也就是说，E-OR-F 的概率是在E 的概率和F 的概率中较大者与二者的和之间。

同样的概念放在任意其他事件H 中也成立。也就是说，(4.18)中的所有概率都可以是某事件H 条件下的条件概率，这样就能给出更具概括性的规则：

示例 4.38

假设在图4-18所示情形中已知得流感的人中有70%会发烧，而且得流感的人中有80%会头痛。那么在(4.19)中，“流感”就是事件H，E 就是“发烧”事件，F 是“头痛”，G 是“头痛OR发烧”。已知PROB(E | H )=PROB(发烧 | 流感)=0.7，而PROB(F | H )=PROB(头痛 | 流感)=0.8。

规则(4.19)表示PROB(G | H )至少是0.7和0.8中的较大者。也就是说，如果患了流感，那么发烧或头痛或两种情况都有的概率至少是0.8。规则(4.19)还表明PROB(G | H )至多是

PROB(E | H )+PROB(F | H )

或者说是0.7+0.8=1.5。不过这一上界是没有意义的，因为事件的概率不可能大于1，所以1才是PROB(G | H )更佳的上界。

4.11.2　`AND`结合的事件的概率

假设已知“发烧”的概率是0.02，而“头痛”的概率是0.03。那么“发烧AND头痛”的概率是多少？也就是说，一个人同时有发烧和头痛症状的概率是多少？就像之前两个事件OR结合的情况那样，没办法给出精确的值，不过有时候可以为两个事件的合取（conjunction）或者说逻辑AND（逻辑“与”）的概率给出一些限制。

在图4-18的情况下，是要问f+g 可以有多大。我们已经得知，如果用OR关系连接事件，那么当两个事件中较小者（在该情况下是“发烧”事件）完全被另一个事件包含时，f+g 会有最大值。那么，“发烧”事件的概率都集中在f+g 中，而且有f+g=0.02，也就是“发烧”事件单独的概率。一般而言，两个事件AND结合的概率不会超过较小者的概率。

那么f+g 可以有多小？显然，没什么情况能阻止“发烧”和“头痛”完全没交集的情况出现，所以f+g 是可以为0的。也就是说，可能没人同时具有发烧和头痛的症状。

不过上述想法并不具有一般性。假设事件“发烧”和“头痛”并不是0.02和0.03这样的微小概率，而是分别有着60%和70%的概率。那么还可能说没人同时具有发烧和头痛的症状吗？如果在这种情况下还有f+g=0，那么就有e+h=0.6，而且c+d=0.7。这样一来e+h+c+d=1.3，也就是说，图4-18中的事件e+h+c+d的概率就大于1了，而这是不可能的。

显然，两个事件的AND连接的大小不能比两事件概率之和减1还小。否则，相同的两个事件的OR连接的概率就会大于1。这一结论是在乘积法则中总结出来的。如果E 和F 是两个事件，而

G 事件是指E 和F 同时发生，那么

PROB(E )+PROB(F )-1≤PROB(G )≤min(PROB(E )，PROB(F ))

与求和规则一样，相同的概念也适用于另一事件H 条件下的情况。也就是有

示例 4.39

再来看看图4-18。假设患流感的人中有70%会发烧，而且有80%会头痛。那么有多少人同时有发烧和头痛症状？根据(4.20)，其中H 为“流感”事件，那么在某人患流感的条件下，同时有发烧和头痛症状的概率至少是0.7+0.8-1=0.5，至多是min(0.7,0.8)=0.7。

涉及若干事件的规则总结
下面的内容对本节介绍的规则和4.10节中有关独立事件的规则进行了总结。假设事件E 和F 的概率分别为p 和q，那么有下列结论。
事件E-or-F（即E 和F 至少有一个发生）的概率至少是max(p,q)，且至多是p+q（或者如果p+q>1，就是1）。
事件E-and-F（即E 和F 同时发生）的概率至多是min(p,q)，且至少是p+q-1（或者如果p+q<1，就是0）。
如果E 和F 是相互独立的事件，那么E-and-F 的概率就是pq。
如果E 和F 是相互独立的事件，那么E-or-F 的概率就是p+q-pq。
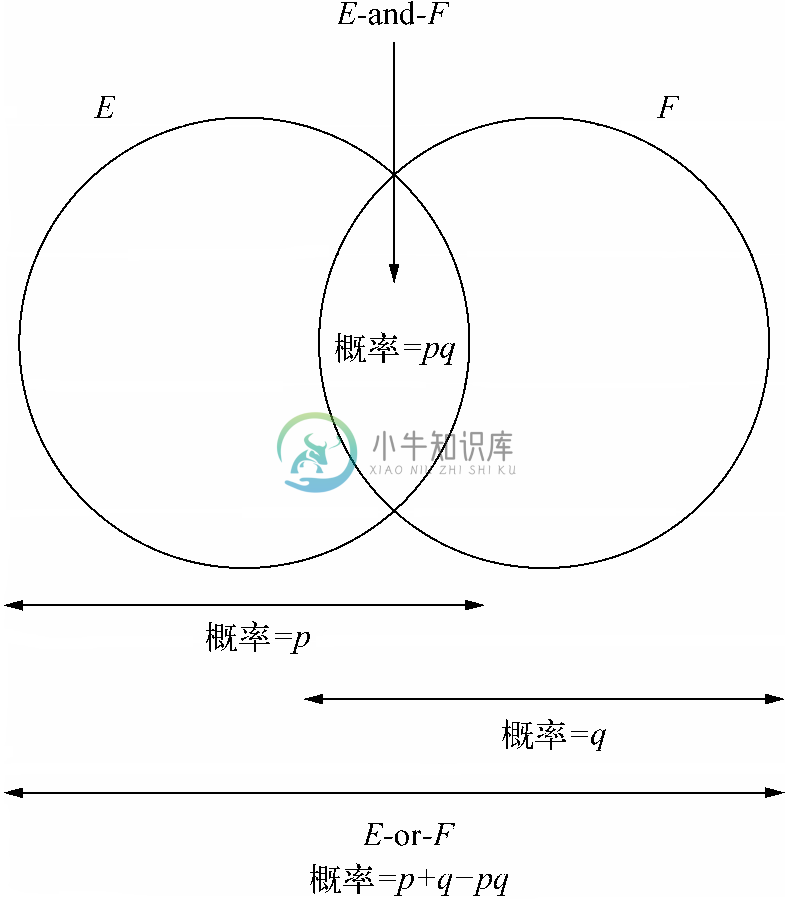
最后一个规则可能要费些思量。E-or-F 的概率是p+q减去事件同时发生的那部分空间，因为在将E 和F 的概率相加时那部分空间被计算了两次。而同在E 和F 中的点正好是事件E-and-F，它的概率就是pq，因此，
PROB(E-or-F )=PROB(E )+PROB(F )-PROB(E-and-F )=p+q-pq
下图展示了这若干事件之间的关系。

4.11.3　处理事件间关系的一些方法

在那些需要计算复合事件（就是若干其他事件的AND或OR结果事件）的概率的应用中，往往不需要知道确切的概率。不过，我们需要确定最可能的情形或者说高概率（即概率接近1）的情形。因此，只要能推断出事件的概率为“高”，复合事件的概率范围就不太可能会带来大问题。

例如，在示例4.35引入的医疗诊断问题中，我们可能永远都没法推断出患者患流感的概率为1。不过只要结合观察到的症状和患者未出现的症状，就能得出他患流感的概率非常高，将患者诊断为流感就应该是很明智的。

然而，我们发现在示例4.35中，基本上说不出同时具有头痛和发烧症状的患者患流感的概率，即便知道每种症状都能强有力地表示患者患了流感，也是如此。真正的推理系统需要更多用来估算概率的信息或规则。作为一个简单的例子，可以明确给出PROB。流感 | 头痛AND发烧。这一概率，这样就可以立刻解决该问题。

不过，如果将E₁、E₂、…、E_n这n个事件结合起来得出另一个事件F，那么就需要明确给出2ⁿ-1个不同的概率，这些概率分别是在E₁、E₂、…、E_n中一个或多个形成的条件下F 的条件概率。

示例 4.40

对n=2的情况，比如示例4.35的情况，就只需要给出3个条件概率。因此，正如之前所做的那样，我们可以断言PROB(流感 | 发烧)=0.6且PROB(流感 | 头痛)=.5。然后，可以加上诸如PROB(流感 | 头痛AND发烧)=0.9这样的信息。

要避免指定指数数量条件概率的情况出现，有很多种限制可帮助我们推断或估计概率。一项简单的限定就是声明某一事件表明另一事件，也就是说，第一个事件是第二个事件的子集。通常，这样的信息能提供一些有用的东西。

示例 4.41

假设我们声明只要患者患流感，他一定会头痛。那么按图4-18来看，可以说区域b和e是空的。同时假设只要患者患流感，他一定会发烧。那么图4-18中的区域c也是空的。图4-21就表示依据这两项假设简化后的图4-18。

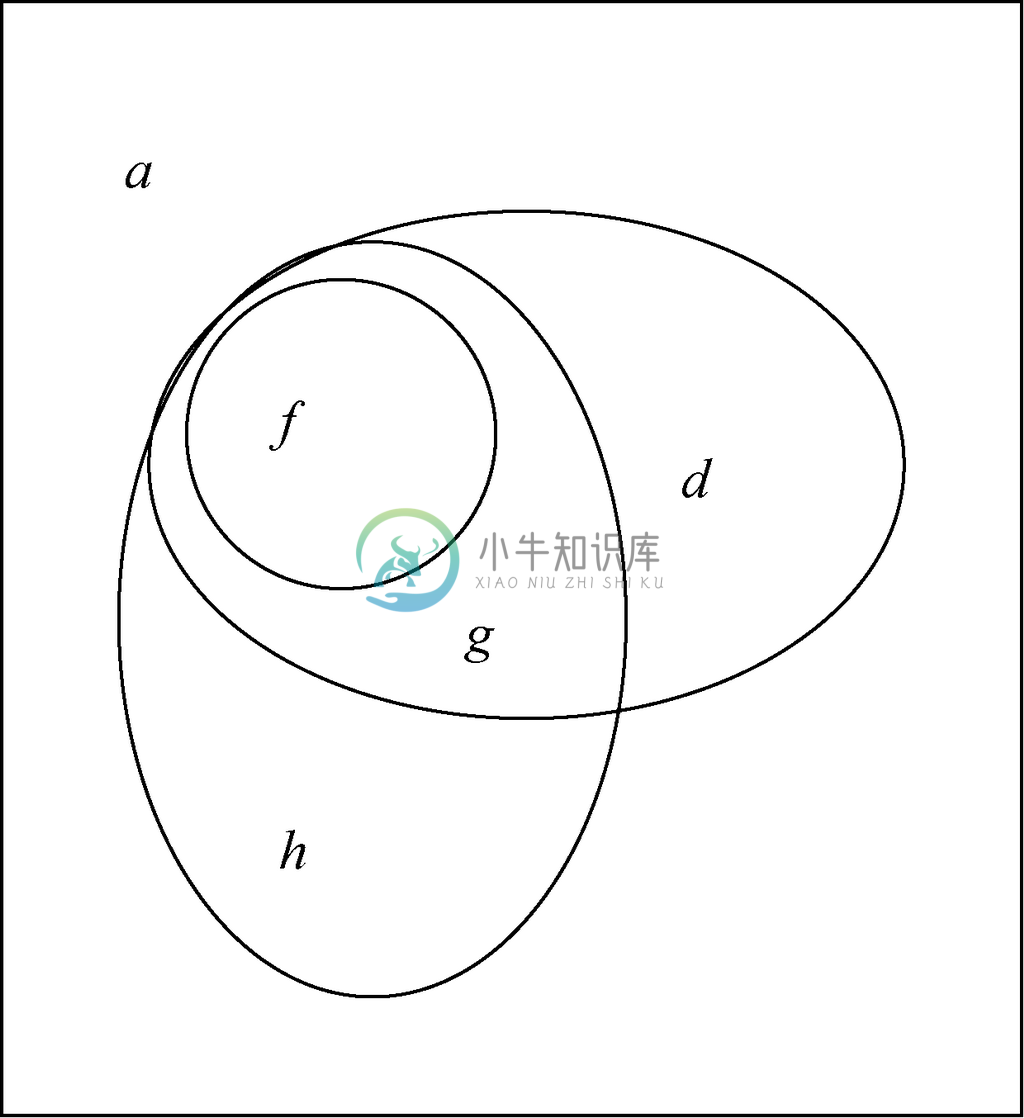
图 4-21　这里，“流感”发生就表示“头痛”和“感冒”都发生

在b、c 和e 都为0的条件下，假设PROB(流感 | 头痛)=0.5且PROB(流感 | 发烧)=0.6，就可以将(4.13)式和(4.14)式改写为

f = d + g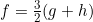
$f=\frac{3}{2}(g+h)$

因为d 和h 都至少为0，所以第一个等式说明f ≥g，而第二式说明f ≥3g/2。

再来看看同时有发烧和头痛症状的条件下患流感的概率，即PROB(流感 | 头痛AND发烧)。该条件概率在图4-18或图4-21中都是f /(f+g)。因为f ≥3g/2，所以可得出f /(f+g)≥0.6的结论。也就是说，同时有头痛和发烧症状的患者患流感的概率至少是0.6。

可以将示例4.41推广到任意3个事件中一个事件意味着另两个事件的情况。假设这些事件分别是E、F 和G，那么

PROB(E |G )=PROB(F |G )=1

也就是说，只要G 发生，E 和F 肯定会发生。进一步假设PROB(E |G )=p，且PROB(G |F )=q，则有

PROB(G |E-and-F )≥max(p,q)　　　　　　(4.21)

如果将图4-21中的“流感”、“发烧”、“头痛”分别解释为G、E、F，就可以看出(4.21)式的推理是成立的。那么有p=f/(f+g+h)且q=f/(f+g+d)。因为d和h至少为0，所以可得知p≤f/(f+g)且q≤f/(f+g)。而f/(f+g)就是PROB(G |E-and-F )。因此，该条件概率大于等于p 和q 二者中的较大者。

4.11.4　习题

1. 将求和规则和乘积法则推广到两个以上的事件上。也就是说，如果E₁、E₂、…、E_n这些事件的概率分别是p₁、p₂、…、p_n，那么回答下列问题。

(a) n个事件中至少有一件发生的概率是多少？

(b) n个事件全部发生的概率是多少？

2. * 如果PROB(F |E )=p，那么以下概率分别是多少?

(a) PROB(F |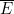 $\overline{E}$ )

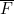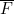(b) PROB( $\overline{F}$ |E )

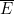回想一下， $\overline{E}$ 是E 的互补事件，而 $\overline{F}$ 是F 的互补事件。

3. 智能建筑控制会试着预测夜晚是否会“冷”，也就是说晚间温度至少比白天温度低20华氏度（约6.7摄氏度）的情况。如果控制系统知道日落前照在它传感器上的阳光指数为高，那么当晚会冷的概率就是60%，因为显然是没有云层，使得热量更容易从地面散逸。而且控制系统还知道，如果日落后一小时内温度的变化至少达到5度（约1.67摄氏度），那么晚上会冷的概率就是70%。将这3个事件分别表示为“冷”、“高”和“降”，并假设PROB(高)=0.4且PROB(降)=0.3。

(a) 给出PROB(高-AND-降)的上限和下限。

(b) 给出PROB(高-OR-降)的上限和下限。

(d) ** 在与(c)小题相同的假设下，给出PROB(冷|高-OR-降)的上限和下限。请注意，本题所需的推理在本节中并未提及。

4. 在很多情况下，比如示例4.35的情况，两个或多个事件会相互强化某一结论。也就是说，我们从直觉上期望不管PROB(流感|头痛)是多少，得知患者有发烧及头痛的症状都能提高流感的概率。假设如果PROB(G|E-AND-F )≥PROB(G |F )就说事件E 强化了结论G 中的事件F。证明：如果事件E 和F 在结论G 中互相强化，那么有(4.21)式成立。也就是说，E-AND-F 条件下G 的概率，不小于E 条件下G 的条件概率与F 条件下G 的条件概率中的较大者。

概率推理的其他应用
本节中我们已经看到了概率推理的一种重要应用：医疗推理。下面还列出了其他一些领域，在这些领域中有一些相似的概念出现在计算机解决方案中。
系统诊断。设备出现故障，表现出一些不正常的行为。例如，计算机屏幕一片空白，但硬盘还在运转。导致这一问题的原因是什么？
统筹性规划。给定经济条件的概率，比如通货膨胀以及某种商品供给的减少等，哪种战略的成功概率最大？
智能家电。多种高端家电可以使用概率推理（常被称为“模糊逻辑”）为用户作出决定。例如，洗衣机可以旋转并称量它盛装的衣物，预测最有可能的面料（比如免烫材料或羊毛），并据此调整洗衣的程序。

4.12　期望值的计算

通常，实验可能出现的结果都有相关联的值。在本节中，我们将利用一些简单的博彩游戏作为示例，在这些游戏中赢钱或输钱取决于实验的结果。而在下一节中，我们还将讨论计算机科学领域更复杂的示例，即计算某些算法预期运行时间的例子。

假设拥有某个概率空间，以及该空间中点上的收益函数f。f 的期望值就是f (x)PROBf (x)上所有点x 的和。用EV(f )表示该值，当所有点都是等可能时，可以通过

1. 将空间中所有x 对应的f (x )相加，然后

2. 将和值除以空间中点的数目，

计算该期望值EV(f )。该期望值有时被称为均值，而且可以被视作“重心”。

示例 4.42

假设该概率空间是表示投一颗公平骰子的结果的6个点，这些点会自然而然地被视为1到6这些整数。设该收益函数为恒等函数f (i )=i,i=1、2、…、6，那么f 的期望值就是

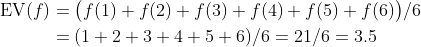
$\begin{align*}\text{EV}(f)&=\bigl(f(1)+f(2)+f(3)+f(4)+f(5)+f(6)\bigr)/6\\&=(1+2+3+4+5+6)/6=21/6=3.5\\\end{align*}$

也就是说，一颗骰子投出点数的期望值是3.5。

再看一个例子，设g 是收益函数g(i )=i ²。那么，对同样的实验——投一颗骰子，期望值g 为

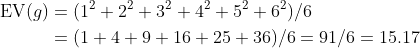
$\begin{align*}\text{EV}(g)&=(1^2+2^2+3^2+4^2+5^2+6^2)/6\\&=(1+4+9+16+25+36)/6=91/6=15.17\end{align*}$

非正式地讲，一颗骰子掷出点数平方的期望值是15.17。

示例 4.43

再来考虑示例4.16首次引入的掷骰子游戏。该游戏的收益规则如下。玩家对某个数字下注1美元。如果该数字出现1次或多次，那么该玩家就会得到该数字出现次数那么多的美元。如果该数字未出现，那么该玩家就会输掉他下注的那些钱。

掷骰子游戏的概率空间是由1到6这几个数字的三元组构成的216个点。这些点表示掷三颗骰子的结果。我们假设玩家下注的数字是1。很明显可知，只要这些骰子都是公平的，该玩家输赢钱数的期望值就与他下注的数字无关。

该游戏的收益函数f 为下列情况。

1. g(i,j,k)=-1，如果i、j 和k 都不为1。也就是说，如果没出现1点，那么玩家将会输掉他下注的那1美元。

2. g(i,j,k)=1，如果i、j 或k 中刚好有一个为1。

3. g(i,j,k)=2，如果i、j 或k 中刚好有两个为1。

4. g(i,j,k)=3，如果i、j 和k 都为1。

接下来的问题就是求g 在这216个点上的平均值。因为枚举所有的点会很乏味，所以最好是先试着分别数出4种不同结果对应的点的数量。

首先，看看3颗骰子都不是1点的情况有多少种。如果没有1，则每个位置有5个数字可供选择，所以这就成了4.2节中的分配问题。因此，没有1的情况共有5³=125种。按照上述的规则(1)，这125个点为收益的和值贡献了-125。

接着，数一下3颗骰子刚好有一颗为1点的情况有多少。1可以出现在3个位置中的任何一个。对每个存放1的位置，剩下两个位置都可以从5个数字中选择。因此，刚好有一个1的点共有3×5×5=75个。根据规则(2)，这些点为收益贡献了+75。

而3颗骰子都为1的情况显然只有一种，所以这一概率为收益作出了+3的贡献。而剩下的216-125-72-1=15个点肯定是有两个1的，所以根据规则(2)，这些点贡献了+30的收益。

最后，将4类点对应的收益值都加起来，并除以概率空间中点的总数目，便能得出该游戏收益的期望值，因此得到

EV(f )=(-125+75+30+3)/216=-17/216=-0.079

也就是说，玩家平均每下注1美元就会输掉约8美分。这一结果可能会让人吃惊，因为游戏表面上看起来是一次机会平等的打赌。这一点将在本节的习题中加以讨论。

正如示例4.43所表示的，有时候根据收益函数的值将概率空间中的点分组也更易于计算。一般而言，假设有某个收益函数为f 的概率空间，而且f 只产生有限数量的不同值。例如，在示例4.43中，f 产生的值只有-1、1、2和3。对每个由f 产生的值v，设E_v 是由满足f (x )=v 的点x 组成的事件。也就是说，E_v 是让f 产生值v 的点的集合，那么

EV(f ) = 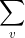$\sum_v$ v PROB(E_v)　　　　　　(4.22)

在这些点概率相同的一般情况下，设n_v 是事件E_v 中点的数目，并设n 是该概率空间中点的总数。那么PROB(E_v)就是n_v /n，这样就可以有

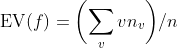
$\text{EV}(f)=\biggl(\sum_vvn_v\biggr)/n$

示例 4.44

在示例4.25中，我们介绍了基诺游戏，并计算了在5个数字里猜中3个的概率。现在来计算一下基诺5点游戏收益的期望值。回想一下，在5点游戏中，玩家要从1到80中竞猜5个数字。在游戏开始后，会从1到80这些数字中选取20个。如果这20个数字中有3个或3个以上与玩家所选的5个数字相同，那么玩家就中奖了。

不过，收益取决于玩家所选的5个数字中猜对了多少个。通常，如果下注1美元，那么玩家所选5个数字中要是猜中3个，就可以得到2美元，也就是有1美元的净收益。如果他所选的5个数字中有4个是对的，就将得到15美元。如果5个数字全对，就能赢得300美元的奖励。如果猜中的数字不足3个，就不会得到奖励，并会输掉他投注的那1美元。

在示例4.25中，我们计算出5个数字中猜对3个的概率是0.08394（保留4位有效数字）。同样，可以计算出5个数字中猜对4个的概率是0.01209，而5个数字全对的概率是0.0006449。那么，猜对的数字不足3个的概率就是1减去这些小数，或者说约为0.90333。少于3个、对3个、对4个和对5个的收益分别为-1、+1、+14和+299。因此，利用(4.22)式就能得出基诺5点游戏的期望收益，就是

0.90333×(-1)+0.08394×1+0.01209×14+0.0006449×299=-0.4573

因此，玩家平均每在该游戏中投注1美元，就大约会损失46美分。

习题

1. 证明：如果掷3颗骰子，出现1点的预期数量是1/2。

2. *只要有1就能中奖，而没有1就不中，那么，为什么习题(1)中的事实并不意味着掷骰子游戏是一场机会平等的游戏（即在1或任一数字上下注的期望收益为0）？

3. 假设在基诺4点游戏中，玩家要竞猜4个数字，而回报如下：猜中两个数字，得1美元（即玩家可以拿回他下注的那1美元）；猜中3个数字，得4美元；4个数字全中，得50美元。那么回报的期望值是多少？

4. 假设在基诺6点游戏中回报如下：猜中3个，得1美元；猜中4个，得4美元；猜中5个，得25美元；全中，得1000美元。那么回报的期望值是多少？

5. 假设要玩6颗骰子的掷骰子游戏。玩家会为某个数字下注1美元，然后掷出骰子。他选择的数字每出现一次，就会得到1美元的奖励。例如，如果出现一次，那么净回报为0；如果出现两次，则净回报为+1，等等。那么这是种公平游戏（即回报的期望值为0）吗？

6. * 根据习题5表示的回报设计，我们可以对标准形式的掷3颗骰子的游戏的回报规则加以改变，让玩家可以下注一定数额。那么玩家下注的数字出现一次他就会得到1美元。为了使游戏成为一场公平游戏，玩家应该下注多少才合适？

4.13　概率在程序设计中的应用

在本节中，我们将考虑概率计算在计算机科学中的两类应用。第一类是对算法期望运行时间的分析。第二类则是一种常被称为“蒙特卡洛”算法的新算法，因为这种算法具有不正确的风险。而正如我们将看到的，通过对参数的调整，是有可能将蒙特卡洛算法正确的概率提高到令人满意的程度的，只不过没法让正确的概率达到1，或者说绝对正确。

4.13.1　概率分析

考虑以下简单问题。假设有一个含n个整数的数组，并询问某整数x 是否为数组A[0..n-1]中的项。图4-22所示的算法就是完成这一工作的。请注意，它会返回BOOLEAN（布尔）类型，在1.6节中已经定义过它是int类型的，而且还定义了常量TRUE和FALSE，它们分别表示1和0。

     BOOLEAN find(int x, int A[], int n)
     {
         int i;

(1)      for(i = 0; i < n; i++)
(2)          if(A[i] == x)
(3)              return TRUE;
(4)      return FALSE;
     }

图 4-22　在大小为n 的数组A 中找出元素x

第(1)到第(3)行会检查数组中的每一项，而且如果在数组中找到x，就立即终止循环并返回TRUE作为答案。而如果未找到x，则会到达第(4)行并返回FALSE。设循环体以及循环的递增与测试所花的时间为c。设第(4)行和循环初始化所花的时间为d。那么如果未找到x，图4-22所示函数的运行时间就是cn+d，也就是O(n)。

不过，假设找到了x，那么图4-22所示函数的运行时间又是多少？显然，越早找到x，所花的时间就越少。如果x 因某种原因一定是在A[0]位置，那么所花的时间就是O(1)，因为循环只会迭代一次。不过如果x 总是在末尾或接近末尾，那么所花的时间就会是O(n)。

当然，最坏的情况就是我们在最后一步才找到x，所以O(n)就是最坏情况下的平滑紧上界。不过，平均情况有没有可能比O(n)好得多呢？要解决这一问题，就需要定义一个概率空间，其中的点都表示x 可能在的位置。最简单的假设就是x 会等可能地被放置在数组A 中的任意一个位置。如果这样的话，该概率空间就有n 个点，每个点分别表示数组A 下标的界限0到n-1这些整数。

接着问题又来了：在该概率空间中，图4-22所示函数运行时间的期望值是多少？考虑该空间中的点i，i 可以是从0到n-1中的任一个。如果x 是在A[i]的位置，循环就会迭代i+1次。因此运行时间的上界就是ci+d。不过这一界限略有常数d 的偏差，因为第(4)行从未执行过。不过，这一差异是无关紧要的，因为在将运行时间转换为大O表达式时，d 就会被消去了。

因此我们必须求出函数f (i )=ci+d 在本概率空间中的期望值。将i 从0到n-1时的ci+d 相加，并除以点的总数量n，就得到

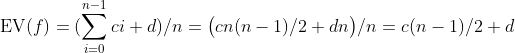
$\text{EV}(f)=(\sum^{n-1}_{i=0}ci+d)/n=\bigl(cn(n-1)/2+dn\bigr)/n=c(n-1)/2+d$

对较大的n，该表达式的值约为cn/2。因此，O(n)就是该期望值的平滑紧上界。也就是说，在大约为2的常数因子内，这个期望值与最坏的情况是相同的。这一结果从直觉上讲是成立的。如果x 等可能地出现在数组中的任意位置，它“通常会”在数组的某一半中，因此大约只需要下x 根本不在数列中或在最后一个元素的位置时一半的工夫即可。

4.13.2　使用概率的算法

图4-22所示的算法是确定的，它总是对同样的数据进行同样的处理。只有对期望运行时间的分析利用到了概率的计算。几乎我们遇到的每种算法都是确定的。不过，有一些问题靠虽不确定但会以某种基本方式从概率空间中进行选择的算法能更好地得到解决。从假想的概率空间中进行这样的选择并不难，方法就是利用4.9节中介绍的随机数生成器。

一类常见的概率算法是蒙特卡洛算法，在每次迭代时会进行随机选择。根据这一选择，它既有可能说“真”，就是保证会得到正确答案的情况，也有可能说“我不知道”，就是正确答案既可能为“真”也可能为“假”的情况。其可能性如图4-23中的概率空间所示。

{%}

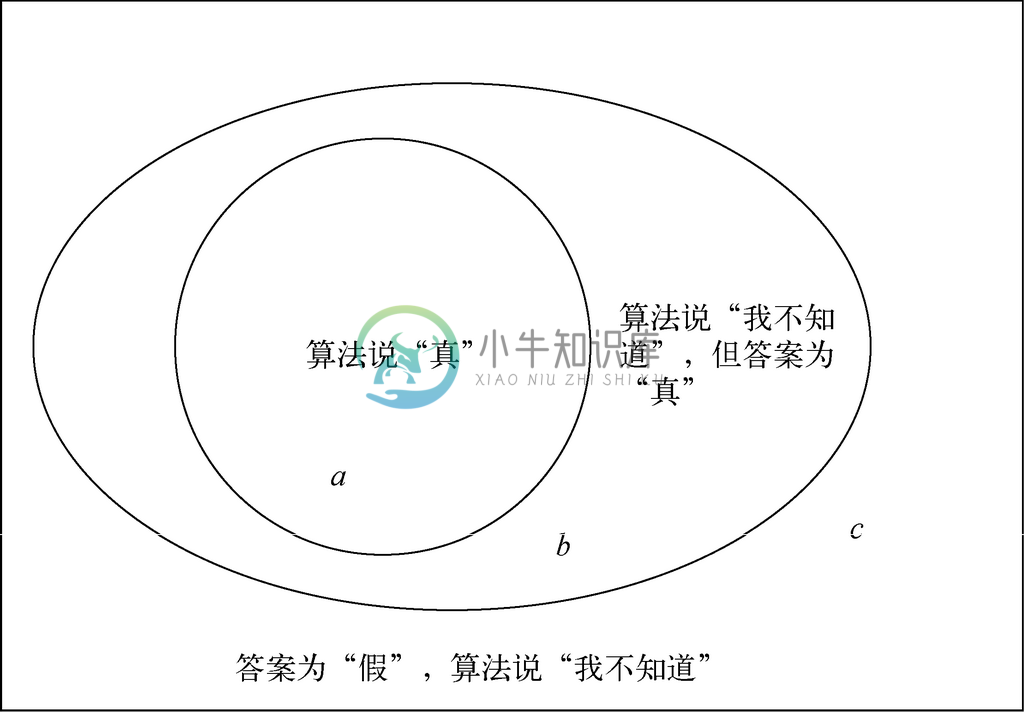
图 4-23　蒙特卡洛算法一次迭代可能的结果

在答案为真的条件下，算法说“真”的概率是a/(a+b)。也就是说，该概率是图4-23中给定a或b的条件下事件a 的条件概率。只要该概率p大于0，就可以随便迭代多少次，并迅速减小失败的概率。通过“失败”，我们表示了正确答案为“真”，但算法中没有哪次迭代可以得出这一结果。

因为每次迭代都是独立实验，如果正确答案是“真”，而且要迭代n 次，那么算法从不说“真”的概率是(1-p)ⁿ。只要1-p是严格小于1，就知道(1-p)ⁿ会随着n的增长迅速减小。例如，如果p=1/2，那么1-p也是1/2。n=10时，(0.5)ⁿ大约是1/1000（见4.2节附注栏内容），n=20时，这个量约是1/1 000 000，等等。n每增加10，这个量就缩小约1000倍。

蒙特卡洛算法会进行n次这样的实验。如果任意实验的答案都为“真”，那么算法的答案也为“真”。如果所有答案都为“假”，那么算法的答案为“假”。因此，

1. 如果正确答案是“假”，该算法一定会回答“假”。

2. 如果正确答案是“真”，该算法有(1-p)ⁿ的概率回答“假”，我们可以假设这一概率非常小，因为选择了足够大的n来使它很小。该算法回答“真”的概率是1-(1-p)ⁿ，这个值很可能是非常接近1的。

因此，当正确答案为“假”时是不会失败的，而当正确答案为“真”时也几乎很难失败。

示例 4.45

本例要讲一个用蒙特卡洛算法解决起来更有效的问题。XYZ计算机公司订购了若干箱芯片，这些芯片应该在出厂前都经过测试以确保都是良品。不过，XYZ公司相信某几箱芯片在出厂前未经过检测，在这种情况下任一芯片不合格的概率是1/10。XYZ公司有种简单的解决方法，就是亲自检测收到的全部芯片，不过这一过程既费钱又费时。如果一箱中有n块芯片，对该箱芯片进行测试所花的时间就是O(n)。

更佳的方式是利用蒙特卡洛算法。从每箱芯片中随机选出k块进行测试。如果某块芯片是坏的，就回答“真”——表示该箱芯片在出厂前未经过测试，不然这块坏芯片当时就被检出了。如果该芯片是合格的，就回答“我不知道”，并继续检测下一块芯片。如果测试的k块芯片全是良品，那么就声明整箱芯片都是良品。

就图4-23而言，区域c 就表示从一箱合格芯片中选出芯片的情况；区域b是某箱芯片未经测试，但芯片凑巧合格的情况；而区域a则是某箱芯片未经测试，而且芯片不合格的情况。之前“如果某箱芯片未经测试则有1/10的芯片不合格”这一假设表示圆形区域a的面积是封闭椭圆区域a和b面积的十分之一。

现在来计算一下失败的概率即k 块芯片全合格，但该箱芯片未经测试。在测试完一块芯片之后说“我不知道”的概率1-1/10=0.9是。因为测试每块芯片的事件都是独立的，所以对k块芯片都说“我不知道”的概率是(0.9)^k。假设选择k=131。那么失败的概率就是(0.9)¹³¹，大约是0.000001，或者说是百万分之一。也就是说，如果某箱芯片是合格的，就永不会在该箱中找出不合格的芯片，所以我们可以笃定该箱芯片是合格的。如果某箱芯片未经测试，那么在测试的131块芯片中发现不合格芯片的概率是0.999999，而且会说该箱芯片需要全面测试。有0.000001的概率是，某箱芯片未经测试但我们还说这是一箱合格芯片，而且不需要测试该箱芯片中的其余芯片。

该算法的运行时间为O(1)。也就是说，测试至多131块芯片的事件是个与箱中所装芯片数n无关的常量。因此，与更直观的测试全部芯片的算法相比，测试每箱芯片的时间开销从O(n)降到了O(1)，代价是每一百万个未测试的箱子中会出错一次。

此外，通过改变在得出某箱芯片合格的结论之前所测试芯片的数量，可以让出错的概率尽可能小到让我们满意。例如，如果让测试的芯片数翻番，达到262块，那么失败的概率就成了之前的平方了，也就是成了万亿分之一，或者说是10^-12。还有，我们能以更高的失败率为代价节省常数倍的时间。例如，如果将测试的芯片数减半，减至每箱测试66块芯片，那么失败率就会达到约1000箱未测试芯片中就有一箱出问题。

4.13.3　习题

1. 377、383和391哪个是质数？

2. 假设使用图4-22所示的函数查找元素x，不过在项i 处找到x的概率与n-i 成正比。也就是说，设想一个具有n(n+1)/2个点的概率空间，其中n个点表示x在A[0]的情况，n-1个点表示x在A[1]的情况，以此类推，直到1个点表示x在A[n-1]的情况。该算法在本概率空间中的期望运行时间是多少？

3. 1993年，美国职业篮球联赛（NBA）设立了由未参加季后赛的11支球队构成的选秀乐透区。战绩最差的球队拿到11张彩票，次差的球队拿到10张，以此类推，直到第11差的球队拿到1张彩票。然后随机选出一张彩票，并将第一位选秀权奖励给该彩票的所有者。那么，被选中的彩票t的所有者排名（从底部算起）的函数f(t)的期望值是多少？

4. ** 继续习题3中描述的乐透机制。中签的球队会失去所有彩票，接着会选出代表第二位选秀权的彩票。而此次中签队伍剩下的彩票都会被收回，接着抽出第三位选秀权的彩票。那么得到第二位和第三位选秀权的队伍排名的期望值是多少？

5. * 假设有大小为n 的数组，它可能是有序的，也可能是随机装满整数。我们希望能构建某个蒙特卡洛算法，若它发现该数组是无序时就说“真”，否则就说“我不知道”。通过重复这种测试k 次，我们很想知道失败的概率不超过2^-k。给出这样的算法。提示：确保测试是相互独立的。这里举个测试不独立的例子，我们可能测试是否有A[0]<A[1]，并测试A[1]<A[2]。这两项测试是相互独立的。然而，如果接着测试A[0]<A[2]，该测试就不再是独立的了，因为知道前两个关系成立的话就能肯定第三个关系是成立的。

6. ** 假设有大小为n，且存放着从1到n这一范围内整数的数组。这些整数可能在选出时就是不同的，也可能是随机独立选出的，因此数组中可能有相等的项。给出运行时间为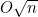 $O\sqrt{n}$ 的蒙特卡洛算法，而且该算法随机装入的数字各不相同的概率最多只有10^-6。

测试整数是否为质数
尽管示例4.45不是个真正的程序，但它仍然展示了一种实用的算法原则，而且其实是衡量产品可靠性的技术的一种真实写照。一些有趣的计算机算法也用到了蒙特卡洛算法的思路。
排在首位的大概是测试某个数字是否为质数的问题。这一问题并非是无聊的数论问题。事实表明，计算机安全的诸多中心思想都涉及知道一个非常大的数为质数。粗略地讲，当使用具有n位数字的质数为信息加密时，如果要在不知道密钥的情况下解密信息，就需要从几乎所有10ⁿ种可能中猜测。如果让n足够大，就可以确保“攻破”代码要么需要超乎寻常的运气，要么需要远超可达水平的计算时间。
因此，我们想要有种方式来测试一个非常大的数是否为质数，并希望在远小于该质数的值的时间内完成测试，理想状态下，希望测试所花的时间与数字的位数成比例，即与数字的对数成比例。检测合数（非质数）的问题似乎并不难。例如，除2之外的所有偶数都是合数，所以看起来已经解决一半问题了。同样地，那些能被3整除的数各位数字之和要能被3整除，所以可以编写一个稍慢于与数字位数存在线性关系的递归算法来测试某数能否被3整除。然而，对很多数字而言，这个问题还是很棘手。例如，377、383和391中有一个是质数，是哪一个呢？
有一种测试合数的蒙特卡洛算法。在每次迭代时，它至少有1/2的概率在被测试的数字为合数时说“真”，而且如果该数字为质数，它绝对不说“真”。下面要描述的并非确切的算法，不过除了一小部分合数外，它对大部分合数都起作用。完整的算法已经超出本书要讲的范围了。
该算法的依据是费马小定理，该定理是说，如果p为质数，且a 是介于1和p-1之间的某个整数，那么当a^p-1除以p 时，余数为1。6此外，除了小部分“坏”合数之外，如果a是在1到p-1之间的整数中随机选出的，那么a^p-1除以p 时余数不是1的概率至少有1/2。例如，假设p=7，那么1⁶、2⁶、…、6⁶分别为1、64、729、4096、15625和46656。它们除以7的余数全是1。不过，如果p=6，是个合数，那么1⁵、2⁵、…、2⁵分别等于1、32、243、1024和3125，它们除以6的余数分别是1、2、3、4、5。只有20%是1。
因此，这种测试某数字p 是否为质数的“算法”要从1到p-1中独立且随机地选出k 个整数。如果对任何选出的a 来说，都有a^p-1/p 的余数不是1，就说p为合数，否则说它是质数。如果没遇到“坏”合数，就可以说失败的概率至多为2^-k，因为对某个给定的a 而言，合数满足测试的概率至少为1/2。如果让k 为40，那么只有万亿分之一的概率将某个合数当成质数。不过，若是要处理那些“坏”合数，就需要更复杂的测试。该测试仍然是p 的位数的多项式，就像上述简单测试那样。

6费马小定理的确切表述为，若p 为质数，且a 和p 互质，则当a^p-1除以p 时，余数恒为1。

4.14　小结

大家应该记住以下与计数相关的公式和范例。

将k个值分配给n个对象的方法共有kⁿ 种。范例问题是粉刷n 所房屋，其中每所房屋可从k种颜色中任选其一。
排列n个不同的项共有n!种不同方式。
从n 项中选出k 项，并为选出的k 项排序，共有n!(n-k)!种不同的方式。范例问题是为有n匹赛马参加的比赛排定冠亚季军（k=3）。
从n个对象中选出m个，不考虑顺序，有 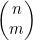$\begin{pmatrix}n\\m\end{pmatrix}$ 或者说n!(/m!(n-m)!)种方式。范例问题是扑克牌型问题，其中n=52，m=5。
如果想排列其中存在相同项的n个项，可以按照如下方式计算排列方法数。首先有n!。然后，如果某个值在这n项中出现k>1次，就除以k!。对每个出现超过1次的值都进行该除法处理。范例问题是计算n个字母组成的单词的构词方式，其中必须在n!的基础上为单词中每个出现次数k>1的字母除以k!。
如果要将n个相同的对象放入m个容器，共有 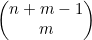$\begin{pmatrix}n+m-1\\m\end{pmatrix}$ 种方式。范例问题是给孩子分苹果。
如果要将n个对象放入m个容器，而其中有一些对象是不同的，那么要依照以下方式计算分装方法数。首先有(n+m-1)!/(m-1)!。然后，如果有一组有k个相同对象，而且k>1，就除以k!。对每个出现次数超过1次的值都执行该除法处理。范例问题是将若干种水果分给孩子们。

除此之外，大家还应该记住有关概率的如下要点。

概率空间由点组成，其中每个点都是某个实验的结果。每个点x 都与一个被称为x 的概率的非负实数相关联。某个概率空间中各点概率之和是1。
事件是概率空间中的点的子集，事件的概率是事件中各点概率之和。任一事件的概率都是在0到1之间的。
如果所有点都是等可能的，那么事件E 条件下事件F 的条件概率就是事件E 中也在事件F 中的点所占的比例。
如果事件F 条件下事件E 的条件概率与事件E 本身的概率相等，就表示事件E 是独立于事件F 的。如果事件E 是独立于事件F 的，那么事件F 也是独立于事件E 的。
求和规则表明，事件E 和F 中有一个发生的概率，至少是两者概率中的较大者，而且不会大于两者概率之和（如果该和大于1，则是不大于1）。
乘积规则表明，某项实验的结果既在事件E 中又在事件F 中的概率不大于E 和F 二者概率中的较小者，并至少是两者概率之和减去1（或者如果说该值为负，则是至少为0）。
最后，要讲一些本章所介绍的原则在计算机科学领域的应用。
对于能处理具有“小于”关系的任意类型数据的排序算法，在为n个项排序时都至少需要与n logn 成正比的时间。
长度为n 的位串共有2ⁿ个。
随机数生成器是生成看似独立实验结果的数字序列的程序，虽然这些数字其实完全是由该程序确定的。
概率推理系统需要一种方式表示由若干事件形成的复合事件的概率。求和规则和乘积法则有时能帮上忙。我们还了解了其他一些为复合事件的概率设定边界的简化假设。
蒙特卡洛算法使用随机的数字生成期望的结果（“真”）或者完全不生成结果。通常重复该算法固定次，如果没有哪次重复过程生成答案“真”，就可以得出答案为“假”的结论，从而解决手头的问题。通过对重复的次数加以选择，可以将错误得出结果为“假”的概率调整到低得令自己满意，但不能将出错的概率降到0。

4.15　参考文献

Liu [1968]是一本传统的组合学精彩之作。Graham, Knuth, and Patashnik [1989]对这一主题进行了更深的探讨，Feller [1968]则是概率论及其应用方面的经典作品。

Rabin [1976]中介绍了测试一个数字是否为质数的蒙特卡洛算法。对该算法的讨论，以及其他一些利用到随机性的有趣的计算机安全和算法问题，可以在Dewdeney [1993]中找到。Papadimitriou [1994]中呈现了一些有关这些主题的更高深的讨论。

Dewdeney, A. K. [1993]. The Turing Omnibus, Computer Science Press, New York.

Feller, W. [1968]. An Introduction to Probability Theory and Its Applications, Third Edition, Wiley, New York.

Graham, R. L., D. E. Knuth, and O. Patashnik [1989]. Concrete Mathematics: A Foundation for Computer Science, Addison-Wesley, Reading, Mass.

Liu, C.-L. [1968]. An Introduction to Combinatorial Mathematics, McGraw-Hill, New York.

Papadimitriou, C. H. [1994]. Computational Complexity, Addison-Wesley, Reading, Mass.

Rabin, M. O. [1976]. “Probabilistic algorithms,”in Algorithms and Complexity: New Directions and Recent Trends (J. F. Traub, ed.), pp. 21–39, Academic Press, New York.

第 4 章 组合与概率

4.1 本章主要内容

4.2 为分配计数

示例 4.1

4.2.1 为分配计数的规则

4.2.2 为位串计数

4.2.3 习题

4.3 为排列计数