第 3 章　程序的运行时间

优质

小牛编辑

132浏览

2023-12-01

在第2章中，我们看到两种截然不同的排序算法：选择排序和归并排序。其实排序算法有很多种，常见的情况是通常每一个可以解决的问题都可以通过多种算法来解决。

那么，应该如何选择解决给定问题的算法呢？一般来说，应该选择易于理解、实现和记录的算法。当性能很重要时（它往往确实很重要），还需要选择能够迅速运行而且能有效使用可用计算资源的算法。因此，我们要考虑一些很微妙的问题，即如何衡量程序或算法的运行时间，以及可以采取哪些措施使程序运行得更快。

3.1　本章主要内容

本章中，我们将介绍以下主题。

程序性能的重要指标。
评估程序性能的方法。
大O表示法。
使用大O表示法估算程序的运行时间。
使用递推关系估算递归程序的运行时间。

3.4节和3.5节介绍的大O表示法，免去了处理那些几乎不可能确定的常量（比如常见的C语言编译器在编译某个给定的源程序时会生成的机器指令数）的麻烦，从而简化了估算程序运行时间的过程。

我们将循序渐进地介绍估算程序运行时间所需的技巧。3.6节和3.7节会展示分析不含函数调用的程序的方法。3.8节将分析具有非递归函数调用的程序。接着3.9节和3.10节会介绍如何处理递归函数。最后，3.11节将讨论递推关系的解决方案，在分析递归函数的运行时间时，对这些函数的归纳定义即称为递推关系。

3.2　算法的选择

如果需要编写的程序只是一次性处理少量数据后就弃之不用的，就应该选择自己所知的最容易实现的算法，编写并调试程序，然后就不用多管了。不过，如果需要编写在很长一段时间里由很多人使用和维护的程序，就会出现其他问题了。其一就是底层算法的可理解性，或者说是简单性。要求算法简单的原因有不少，不过最重要的也许在于，与复杂的算法相比，简单的算法实现起来不容易出错。用简单算法实现的程序，哪怕在使用相当长一段时间后，遇到一些意外输入时曝出奇怪bug的可能性也较小。

应该将程序写得清晰明确，并仔细地记下文档，这样可便于他人维护这些程序。如果算法简单且易于理解，就更易于描述。有了好的文档，原作者之外的程序员就能方便地对原始程序加以修改（原作者经常不会做这些）；或者，如果程序完成得比较早，原作者也会对其加以修改。有很多程序员写出巧妙高效的算法后就从公司拍屁股走人了，结果后续的代码维护者只能放弃他们的算法，转而用更慢但更好理解的算法来代替，这种情况屡见不鲜。

当程序要重复运行时，它的效率以及其底层算法的效率就很重要了。我们通常会将效率与程序运行所花的时间挂钩，虽然有时程序也必须占用一些其他资源，比如：

1. 程序变量占用的存储空间；

2. 程序在计算机网络中产生的流量；

3. 必须出入磁盘的数据量。

不过，对大的问题来说，对给定程序是否堪用起着决定性作用的是运作时间，而本章的主题就是运行时间。我们所要讲的程序的效率，其实就是它耗费的时间，是用程序输入大小的函数来衡量的。

通常，可理解性和效率是相互矛盾的目标。例如，比较过图2-3中的选择排序程序和图2-32中的归并排序程序的读者肯定都会认同，后者不仅更长，而且难理解得多。就算我们总结了2.2节和2.8节中给出的那些解释，在程序中添加了经过深思熟虑的注释，结果依然如此。不过，也正如我们将要了解的，只要待排序的元素个数过百，归并排序的效率就会比选择排序的效率高得多。不巧的是，这种情况太普遍了——对大数据量来说有效率的算法，编写和理解起来往往比那些相对低效的算法更加复杂。

算法的可理解性，或者说是简单性，是有些主观的概念。我们可以在某种程度上克服算法不够简单的问题，即在注释和程序文档中对算法进行到位的解释。编写文档的人始终要考虑阅读这些代码及其注释的人：一般人能明白这是在说什么吗？是否需要进一步的解释、细节、定义和示例？

另一方面，程序的效率是个客观的问题：程序所花的时间就是那么多，没什么争议的余地。不过我们没办法用所有可能的（通常是无数的）输入来运行程序。因此，我们要对程序运行时间加以度量，因为它总结了程序处理所有输入的性能，通常是用一个诸如“n²”这样的简单表达式来度量的。本章下面几节的主题就是如何度量程序的运行时间。

3.3　度量运行时间

一旦我们认同可以通过度量程序的运行时间对程序加以评估，就要面对确定实际运行时间的问题。总结运算时间的两种主要方法是：

1. 基准测试；

2. 分析。

我们将依次介绍这两种方法，不过本章主要讲的还是用于分析程序或算法的技术。

3.3.1　基准测试

在比较用于完成相同任务的两个或多个程序时，制定一小组可用作基准的典型输入是一种惯例。也就是说，我们愿意接受基准输入作为这些任务组合的代表，并假设能顺利处理基准输入的程序能顺利处理所有输入。

例如，评估排序算法的基准可能包含一小组数字（比如圆周率的前20位数字）、一个中等规模的输入组（比如得克萨斯州的邮政编码集合），以及一个大规模输入组（比如布鲁克林区电话目录中的电话号码集合）。我们可能还想知道，在对空集、单元素集以及已排序表排序时，程序是否能有效及正确地工作。有趣的是，有些排序算法在处理已排序表时的性能惨不忍睹。1

1选择排序和归并排序都不在此列，它们在处理有序列表时所花的时间几乎与为相同长度的任一列表排序所花的时间相同。

90-10法则
与基准测试一样，确定要分析的程序在哪里花了时间通常也是很实用的。这种评估程序性能的方法称为剖析（profiling），而且多数程序设计环境都包含有剖析器（profiler）这种工具，会为程序中每条语句关联一个表示执行这条语句所花时间的数字。还有一种相关的实用程序，名叫语句计数器，用于确定对于给定的输入集，源程序中每条语句执行的次数。
很多程序都具有这样的特性，即大部分运行时间都花在一小部分源代码上了。有这么一条非正式的法则：90%的运行时间花在了10%的代码上。尽管准确的百分比是视程序而定的，不过“90-10法则”还是表明了多数程序中运行时间主要花在了哪里。想要加快程序运行速度，最简单的一种方法就是对程序加以剖析，并对程序“热点”（也就是程序中花掉大部分运行时间的部分）的代码加以改进。例如，我们在第2章中提到过，用等价的迭代函数替代递归函数是可能为程序提速的。不过，这种做法只有在递归函数正好是程序中占用大部分运行时间的部分时才奏效。
在极端情况下，即便我们将只占用10%时间的那90%的代码所花的时间变为0，程序总的运行时间也只减少了10%。然而，如果将10%的程序所占用的那90%的时间减半，总运行时间就将减少45%。

3.3.2　对程序的分析

要分析程序，首先要按大小为输入分组。正如在2.9节中与证明递归程序属性一起讨论的那样，用来表示输入大小的度量是因程序而异的。对排序程序来说，待排序元素的数量就是个很不错的度量。对于求解n元线性方程组的程序，拿n作为问题的大小是很平常的。其他的程序可能使用某个特定输入的值作为程序输入的表的长度，或作为输入的数组的大小，或是诸如此类的度量的组合。

3.3.3　运行时间

用函数T(n)来表示程序或算法处理大小为n的任意输入所花的时间是很方便的。我们将T(n)称为程序的运行时间。例如，某个程序的运行时间可能是T(n)=cn，其中c 是某个常数。换个说法就是，该程序的运行时间，与其要处理的输入的大小是线性相关的。这样的程序或算法就是线性时间的，或者直接说成是线性的。

我们可以将运行时间T(n)看作程序执行的C语言语句的数量，或是在某标准计算机上运行程序所花的时长。在多数情况下，我们都不会明确指出T(n)的具体单位。事实上，正如我们在下一节中将要看到的，在谈论程序的运行时间时，可以只用某个（未知的）常数因子乘上T(n)来表示。

很多时候，程序的运行时间取决于某个特定的输入，而不仅仅取决于输入的大小。在这类情况下，我们将T(n)定义为最坏情况运行时间，也就是所有大小为n的输入所能造成的最大运行时间。

另一种常见的性能度量是T_avg(n)，即程序处理所有大小为n 的输入的平均运行时间。平均运行时间有时候是对实际性能更为现实的反映，不过它往往比最坏情况运行时间更难计算。“平均运行时间”中“平均”的概念还意味着，所有大小为n 的输入是等可能性的，而这在某个给定情况下既可能为真，也可能不为真。

示例 3.1

让我们估算一下图3-1中所示的SelectionSort程序段的运行时间。这些语句的编号与图2-2中的编号如出一辙。这段代码的目的是要将数组A从A[i]到A[n-i]这部分中最小元素的下标赋值给small。

(2)        small = i;
(3)        for(j = i+1; j < n; j++)
(4)            if (A[j] < A[small])
(5)                small = j;

图 3-1　选择排序的内层循环

一开始，我们需要对时间单位加以简单定义。后面我们会详细介绍这一问题，不过在这里，以下简单模式是有效的。可以将每次执行赋值语句记作一个时间单位。在第(3)行，要为for循环开头j的初始化记上一个时间单位，为测试是否有j<n记上一个单位，并为减少j记上一个单位，每次循环皆是如此。最后，每执行一次第(4)行的测试，就要记上一个单位。

首先，让我们考虑一下内层循环的循环体：第(4)行和第(5)行。第(4)行的测试总是要执行的，不过第(5)行的赋值只有在测试成功的情况下才执行。因此，该循环体会消耗1到2个时间单位，这取决于数组A中的数据。如果要采纳最坏情况，就可以假设循环体要消耗2个时间单位。我们会进行n-i-1次for循环，而每进行一次循环都要执行一遍循环体（2个时间单位），接着递增j并测试j<n（又是2个时间单位）。因此，进行循环所花的时间单位是4(n-i-1)。除了这个数字之外，我们还要加上第(2)行初始化small的1个时间单位，第(3)行初始化j的1个时间单位，以及在第(3)行第一次测试j<n 的1个时间单位（这与循环的任一次迭代的终止无关）。因此，图3-1中的程序段的总运行时间为4(n-i )-1。

将图3-1所影响数据的“大小”m 指定为m=n-i 是很自然的，因为这是它所影响的数组A[i..n-1]的长度。那么运行时间4(n-i )-1就可以表示为4m-1。因此，图3-1的运行时间T(m)就是4m-1。

3.3.4　不同运行时间的比较

假设对某个问题，可以选择使用运行时间为T_A(n)=100n的线性时间程序A，以及运行时间为T_B(n)=2n²的二次幂时间程序B。假设这两个运行时间是在同一特定计算机上处理大小为n的输入所花的毫秒数。2运行时间图见图3-2。

2这里A和B的关系，与归并排序和选择排序的关系没有太多不同。我们在3.10节中将会看到，归并排序的运行时间是以n logn 的速度增长的。

{%}

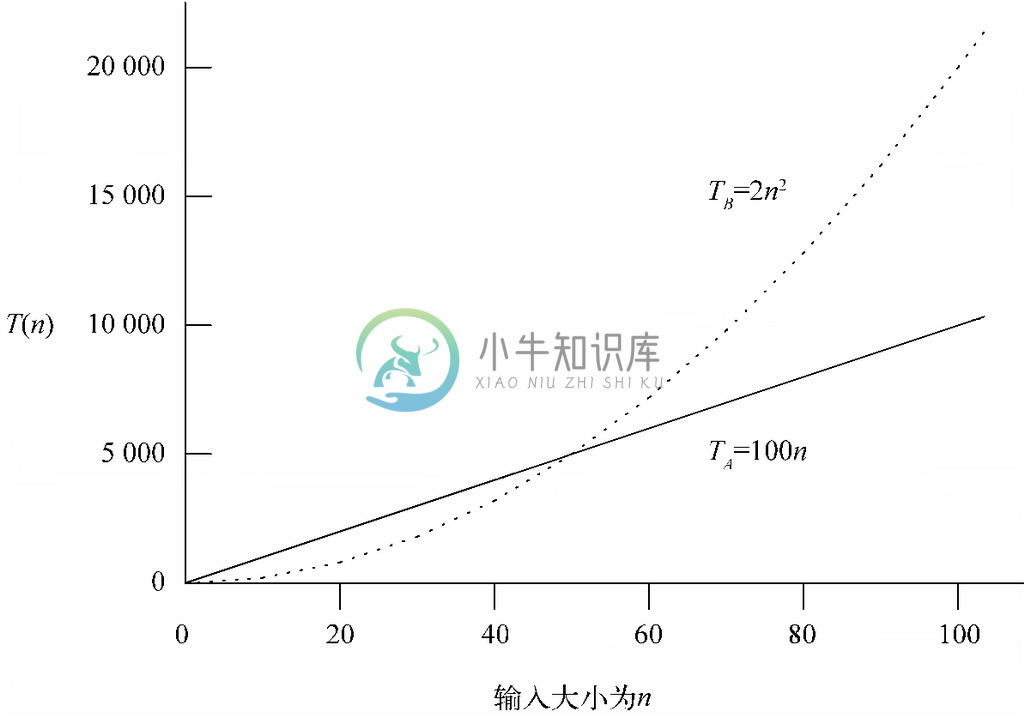
图 3-2　线性程序与二次幂程序的运行时间

从图3-2可知，对大小小于50的输入来说，程序B要比程序A快。当输入的大小大于50时，程序A就要更快了，而且从50这个临界点开始，输入越大，程序A相比程序B而言优势就越大。对大小为100的输入，A要比B快上2倍，而对大小为1000的输入，A要快上20倍。

程序运行时间的函数形式最终确定了我们能用该程序解决多大的问题。随着计算机速度的不断变快，与运行时间增长迅速的程序相比，那些运行时间增长缓慢的程序在可处理问题的规模上能取得更大的提高。

再次假设图3-2所示的程序运行时间是以毫秒计的，图3-3中的表格表示了在同一台计算机上，花同样的时间，使用两种程序分别能解决多大的问题。例如，假设可以接受100秒的计算时间。如果计算机的速度加快10倍，那么在100秒内能处理之前需要花1000秒去处理的问题。对算法A来说，我们现在可以解决10倍大小的问题，而对算法B来说，只可以解决3倍大小的问题。因此，随着计算机速度的持续加快，通过使用低增长率的算法和程序可以获得更为显著的优势。

时间（秒）	使用程序A可解决的最大问题的大小	使用程序A可解决的最小问题的大小
1	10	22
10	100	70
100	1000	223
1000	10000	707

时间（秒）

使用程序A可解决的最大问题的大小

使用程序A可解决的最小问题的大小

100

1000

223

1000

10000

707

图 3-3　在可用时间段函数可解决问题的大小

别在乎算法的效率，再等上几年就行了
大家可能经常听到这样的说法、不需要缩短算法的运行时间或是选择更高效的算法，因为计算机的速度每隔几年就会翻番，而且不需要多久，任何算法，不管有多低效，所花的时间都会少到没有人在意了。这一论调的出现已经有几十年的时间了，但计算资源需求上限尚未出现，因此，我们一般都不接受硬件改善可以让高效算法的研究变成无用功这种观点。
不过，也存在我们不需要过分考虑效率的情况。例如，某所学校在每学期期末都要将存储在某台计算机中的学生电子成绩表打印成纸质成绩单。该操作所花的时间大概与要报告的成绩数量成线性关系，就像假想算法A那样。如果学校更换了一台速度快上10倍的计算机，完成这项工作所花的时间就会变为原来的十分之一。不过，学校因此要扩招10倍，或是要求每个学生增加10倍的课程，这是很不现实的。计算机的提速不会影响到成绩单程序的输入大小，因为这一大小是受其他因素限制的。
另一方面，还会存在另外一些问题，我们凭借新兴的计算资源有了一些解决的头绪，不过它们的“大小”却超出了现有技术的处理能力。这样的问题包括自然语言的理解、计算机视觉（对数字化图像的理解），以及各种对人机“智能”交互的尝试。不管是通过改善算法还是通过提升机器性能，所获得的加速都将提升我们在接下来几年里处理这些问题的能力。此外，当它们变成“简单”的问题后，我们现在很难想象的新一代挑战又会替代它们摆在计算机面前。

3.3.5　习题

1. 考虑一下图2-13中的阶乘程序段，设输入大小为读取的n的值。每次执行赋值、读和写语句记为一个时间单位，每进行一次while循环条件测试记为一个时间单位，计算该程序的运行时间。

2. 为2.5节习题1以及图2-14中的程序段给出恰当的输入大小。运用上一题中的计数规则，确定这两个程序的运行时间。

3. 假设程序A花费2ⁿ/1000个时间单位，程序B花费1000n²个时间单位。对哪些n值来说，程序A花的时间比程序B少？

4. 对上一题中的两个程序，在10⁶个、10⁹个和10¹²个时间单位内能解决的问题各有多大？

5. 假设程序A花费1000n⁴个时间单位，程序B花费n¹⁰个时间单位，重复习题3和习题4中的练习。

3.4　大 O 运行时间和近似运行时间

假设我们编写了一个C语言程序，并选择了想要它处理的特定输入。程序处理这一输入的运行时间仍取决于以下两个因素。

1. 运行该程序的计算机。一些计算机执行指令的速度比其他计算机更快，最快的超级计算机与最慢的个人计算机之间的性能比远大于1000∶1。

2. 生成计算机可执行程序所使用的特定C语言编译器。在同一计算机上，执行不同程序所用的时间是不一样的，即便这些程序有着相同的功效。

这样一来，我们就不能看着C语言程序及其输入，然后判断说：“这个任务要花上3.21秒。”除非知道用的什么计算机和编译器。此外，就算我们知道程序、输入、机器和编译器，要准确预计将要执行的机器指令数通常也是一项过于复杂的任务。

出于这些原因，我们通常用大O表示法来表示程序的运行时间，该方法让我们可以不去考虑如下常数因子。

1. 特定编译器生成机器指令的平均数。

2. 特定计算机每秒执行机器指令的平均数。

例如，就像在示例3.1中那样，我们研究的SelectionSort程序段处理长度为m的数组将耗时4m-1。不过这里我们不这么说，而是说它耗时O(m)，非正式的含义是“某个常数乘以m”。

“某个常数乘以m”这一表述不仅能让我们忽略那些与编译器和计算机相关的未知常数，还让我们可以作出一些起简化作用的假设。例如，在示例3.1中，假设所有的赋值语句会消耗长短相同的一段时间，而在测试for循环的终止、随着循环进行递增j，以及进行变量初始化等工作时，也都会消耗这样长的一段时间。因为这些假设在实际情况中都是不可能的，所以在运行时间方程T(m)=4m-1中，常数4和-1是对事实的最佳逼近。可以更近似地将T(m)描述为“某个常数乘以m，再加上或减去某个常数”，甚至描述为“最多与m成正比”。O(m)表示法使我们可以在不涉及不可知或无意义常数的情况下作出这些陈述。

另一方面，将程序段的运行时间表示为O(m)，也告诉我们一些非常重要的事情。它表明，执行处理逐步变大的数组的程序，所花的时间是线性增长的，就像3.3节末尾的图3-2和图3-3中假想的程序A那样。因此，该程序段表示的算法，优于运行时间增长更快的算法（比如在上文的讨论中与程序A相对比的假想程序B）。

3.4.1　大O的定义

我们现在要给出某个函数是另一个函数的“大O”的正式定义。设有函数T(n)，这通常是某个程序的运行时间，以输入大小为n的函数来度量。要让函数适用于度量程序的运行时间，我们假设有：

1. 参数n 被限定为非负整数；

2. 值T(n)对所有的参数n 来说都非负。

设f (n)是某个定义在非负整数n之上的函数。如果除了对某些较小的n值之外，T(n)至多是某个常数乘以f (n)，我们就可以说

“T(n)是O(f (n))”。

正式地说，如果存在某个整数n₀以及某个大于0的常数c，使得对所有大于n₀的整数n，都有T(n)≤cf (n)，那么我们就说T(n)是O(f (n))。

我们把数对n₀和c 称为“T(n)是O(f (n))”这一事实的证物（witness）。在接下来的证明中，该证物可以为T(n)和f(n)的大O关系“作证”。

3.4.2　证明大O关系

可以应用“大O”的定义证明对特定的函数T和f，T(n)就是O(f(n))。我们会通过选择特定的证物n₀和c，接着证明T(n)≤cf(n)，从而完成这一证明。证明过程必须假设n是非负整数，且不小于我们选择的n₀。通常，证明过程涉及一些代数和不等式的变换。

示例 3.2

假设有某个程序，其运行时间为T(0)=1，T(1)=4，T(2)=9，一般表示为T(n)=(n+1)²。我们就可以说T(n)是O(n²)，或者说T(n)是二次幂的，因为可以选择证物n₀=1和c=4。然后需要证明(n+1)²≤4n²，其中有n≥1。在证明过程中，我们将表达式(n+1)²展开为n²+2n+1。只要n≥1，我们就知道有n≤n²而且有1≤n²。因此

n²+2n+1≤n²+2n²+n²=4n²

此外，也可以选择证物n₀=3和c=2，因为，正如大家可以验证的，对所有的n≥3，都有(n+1)²≤2n²。

不过，不能选择n₀=0，因为若n₀=0，那么对n=0，我们可以证明(0+1)²≤c 0²，也就是有1小于等于c 乘以0。因为不管选择什么c，都有c×0=0，而1≤0是不成立的，所以如果我们选择n₀=0就玩完了。不过没关系，因为要证明(n+1)²是O(n²)，所以只要找出一组可行的证物n₀和c 就行了。

大O证明的模版
请记住：所有的大O证明基本遵循相同的形式，只有代数变换是各异的。要证明T(n)就是O(f(n))，要做的只有下面两件事。
1. 说明证物n₀和c。这些证物必须是特定的常数，比如n₀=47和c=12.5。还有，n₀必须是非负整数，而c 必须是正实数。
2. 通过适当的代数变换，证明对所选择的特定证物n₀和c，如果n≥n₀，则有T(n)≤cf(n)。

这可能看起来有些奇怪，虽然(n+1)²大于n²，但是我们还是说(n+1)²是O(n²)。其实，也可以说(n+1)²是任意分之n²的大O，例如O(n²/100)。要看看原因的话，选择证物n₀=1和c=400。那么如果n≥1，由与示例3.2中一样的推导可知

(n+1)²≤400(n²/100)=4n²

这些现象背后的基本原则如下。

1. 常数因子不产生影响。对于任意正值常数d 和任意函数T(n)，T(n)是O(dT(n))，不论d 是很大的数，还是很小的分数，只要d>0即可。要知道为什么，可以选择证物n₀=0和c=1/d。3那么就有T(n)≤c(dT(n))，因为cd=1。类似地，若已知T(n)是O(f (n))，便也知道对任何的d>0，有T(n)是O(df (n))，即便d 很小。因为我们知道，对某个常数c₁和所有的n≥n₀，有T(n)≤c₁f (n)。如果选择c=c₁/d，那么就可以看到，对n≥n₀，有T(n)≤c(df(n))。

3请注意，虽然要求选择常数而不是函数作为证物，但选择c=1/d 是没有错的，因为d 本身也是个常数。

2. 低阶项不产生影响。假设T(n)是形如

a_kn^k+a_k-1n^k-1+…+a₂n²+a₁n+a₀

的多项式，其中开头的系数a_k为正数。然后我们可以扔掉除第一项（就是具有最高指数k的那项）之外的所有项，并利用规则(1)，忽略常数a_k，直接用1代替它。也就是说，我们可以得出T(n)就是O(n^k)。为了证明这一点，设n₀=1，并设c是各系数a_i中所有正系数的和，其中0≤i≤k。如果系数a_j 是0或负数，那么肯定有a_jn ^j≤0。如果a_j 为正，那么对所有的j< k，只要n≥1，都有a_jn ^j≤a_kn^k。因此T(n)不大于n^k乘以所有正系数之和，或者说是T(n)≤cn^k。

关于大O的谬论
对“大O”的定义是很诡异的，在该定义中，在检查完T(n)和f (n)后，我们要一次性选择证物n₀和c，接着证明对所有的n≥n₀，都有T(n)≤cf (n)。不能为每个n值重新选择c 和（或）n₀。例如，大家可能偶尔会看到如下证明n²为O(n)的谬误“证明”。“选择n₀=0，并为每个n 选择c=n。然后有n²≤cn。”这种论述是无效的，因为我们要求在不知道n 的情况下一次性选定c。

示例 3.3

作为规则(1)（“常数因子不产生影响”）的例子，我们看到2n³是O(0.001n³)。令n₀=0，而且c=2/0.001=2000。那么显然有，对所有的n≥0，2n³≤2000(0.001n³)=2n³。

作为规则(2)（“低阶项不产生影响”）的例子，考虑多项式T(n)=3n⁵+10n⁴-4n³+n+1。最高位的项是n⁵，我们就说T(n)是O(n⁵)。要验证该说法，令n₀=1，c等于所有正系数的和。正系数的项包含指数为5、4、1和0的这些项，其系数分别为3、10、1和1。因此，令c=15。我们可以说，对n≥1，有

3n⁵+10n⁴-4n³+n+1≤3n⁵+10n⁵+n⁵+n⁵=15n⁵　　　　　　(3.1)

我们可以通过对正系数项的匹配来验证不等式(3.1)，也就是，3n⁵≤3n⁵，10n⁴≤10n⁵，n≤n⁵，以及1≤n⁵。而且，因为-4n³≤0（之前假设n为正数），所以可以忽略不等式(3.1)左边的负系数项。因此，不等式(3.1)的左边，也就是T(n)，要小于等于不等式的右边，也就是15n⁵，或者说是cn⁵。由此可以得出T(n)是O(n⁵)的结论。

其实，低阶项可以删除的原则不仅适用于多项式，而且适用于任何表达式之和。也就是说，如果随着n趋近无穷大，h(n)/g(n)的比值趋近于0，则可以说h(n)比g(n)“增长得慢”，或者说h(n)的“增长率低于”g(n)，这样就可以忽略h(n)。也就是说h(n)+g(n)是O(g(n))。

例如，设T(n)=2ⁿ+n³。众所周知，多项式（比如n³）要比指数式（比如2ⁿ）增长得慢。因为随着n的增大，n³/2ⁿ趋近于0，所以我们可以扔掉低阶项，并得出T(n)是O(2ⁿ)的结论。

要正式地证明2ⁿ+n³是O(2ⁿ)，令n₀=10，c=2。必须证明，对n≥10，有

2ⁿ+n³≤2×2ⁿ

如果从两边都减去2ⁿ，就会发现这是要证明对n≥10，有n³≤2ⁿ。

对n=10，我们有2¹⁰=1024。而10³=1000，因此对n=10，有n³≤2ⁿ。n每增加1，2ⁿ就会翻倍，而n³则是会乘以(n+1)³/n³这个量，而当n≥10时，这个量是小于2的。因此，随着n的增大，n³会逐步小于2ⁿ。我们可以得出结论：对n≥10，有n³≤2ⁿ，因此有2ⁿ+n³是O(2ⁿ)。

3.4.3　证明大O关系不成立

如果两个函数之间的大O关系成立，就可以通过找出证物来证明这种关系。然而，如果某个函数T(n)不是另一个函数f(n)的大O呢？答案就是，经常可以证明某个特定的函数T(n)不是O(f(n))。证明方法是，假设证物n₀和c存在，并推理出矛盾。下面要介绍这种证明的一个例子。

示例 3.4

在前文附注栏“关于大O的谬论”中，我们声称n²不是O(n)。我们可以证明该声明，方法如下。假设n²是O(n)，然后就存在证物n₀和c，使得对所有的n≥n₀，都有n²≤cn。不过如果我们选择n₁等于2c 和n₀中较大者，就会有不等式

(n₁)²≤cn₁　　　　　　(3.2)

一定成立（因为n₁≥n₀，而且对所有的n≥n₀，n²≤cn都是成立的）。

如果将不等式(3.2)两边都除以n₁，就有n₁≤c。然而，我们还选择了n₁至少是2c。因为证物c一定为正数，所以n₁不可能既小于c 又大于2c。因此，可以证明“n²是O(n)”的证物n₀和c 不存在，由此可以得出结论：n²不是O(n)。

3.4.4　习题

1. 考虑以下4个函数。

f₁:n²

f₂:n³

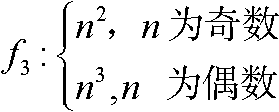
对等于1、2、3、4的i 和j，分别确定f_i (n)是不是O(f_j (n))。要么给出证明大O关系的n₀和c 的值，要么假设存在这样的n₀和c，并推理出矛盾，证明f_i (n)不是O(f_j (n))。提示：请记住，除了2之外，所有的质数都是奇数。还要记住，质数有无数个，而合数也有无数个。

2. 有以下一些大O关系。请为每个大O关系给出可用来证明这种关系的证物n₀和c。选择最小的一组证物，也就是说n₀-1和c不是证物，而如果d< c，那么n₀和d 也不是证物。

(a) n²是O(0.001n³)。

(b) 25n⁴-19n³+13n²-106n+77是O(n⁴)。

(d) n¹⁰是O(3ⁿ)。

(e) * log₂n是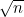 $\sqrt{n}$

3. * 证明：如果对所有的n有f(n)<g(n)，那么f(n)+g(n)是O(g(n))。

4. ** 假设f (n)是O(g(n))，而且g(n)是O(f (n))。那么f (n)和g(n)之间有什么关系？是不是一定有f (n)=g(n)？随着n 趋近无穷大，f (n)/g(n)的极限是否一定存在？

证明大O关系不成立的模板
证明函数T(n)不是O(f (n))的常见证明过程如下。示例3.4就展示了这样的证明过程。
1. 首先假设存在证物n₀和c，使得对所有的n≥n₀，都有f (n)≤cg(n)。这里，n₀和c 是表示未知证物的符号。
2. 定义特定的整数n₁，用与n₀和c 相关的形式表示（例如，在示例3.4中，我们选择的是n₁=max(n₀,2c )）。该n₁是用来证明T(n₁)≤cf (n₁)的n 的值。
3. 证明，对于这个选定的n₁，有n₁≥n₀。这一部分是非常简单的，因为我们在第(2)步中选择的n₁至少是n₀。
4. 声明因为有n₁≥n₀，所以一定有T(n₁)≤cf (n₁)。
5. 通过证明对我们选择的这个n₁有T(n₁)>cf (n₁)，从而推导出矛盾。选择与c 有关的n₁可以让这个部分变得很简单，就像示例3.4中所做的那样。

3.5　简化大 O 表达式

正如我们在3.4节中看到的，通过舍弃一些常数因子和低阶项，可以简化大O表达式。我们将会看到，在分析程序时，作出这样的简化有多重要。一般来说，某个程序的运行时间来源于程序中很多不同的语句或程序段，而一小部分程序占用大量运行时间的情况也很平常（由“90-10”法则可知）。通过舍弃一些低阶项，并将相等或近似相等的项结合起来，通常能大大简化表示运行时间的大O表达式。

3.5.1　大O表达式的传递律

首先，我们要拿出考虑大O表达式时的一个实用规则。诸如≤这样的关系，就被称为传递的，因为它遵循“若A≤B，且B≤C，则A≤C”这样的法则。例如，因为3≤5，5≤10，所以我们可以确定3≤10。

而“是f的大O”这样的关系是另一种具有传递性的关系。也就是说，如果f(n)是O(g(n))，而且g(n)是O(h(n))，就有f(n)是O(h(n))。要知道原因，首先假设f(n)是O(g(n))。那么存在证物n₁和c₁，使得对所有的n≥n₁，都有f(n)≤c₁g(n)。类似地，如果g(n)是O(h(n))，就存在证物n₂和c₂，使得对所有的n≥n₂，都有g(n)≤c₂h(n)。

多项和指数大O表达式
多项式的次数是指多项式所有项中的最高指数。例如，示例3.3和示例3.5中提到的多项式T(n)的次数为5，因为其最高阶项为3n⁵。从我们已经阐明的两个原则（常数因子不产生影响，以及低阶项不产生影响），以及大O表达式的传递律，可知以下几点。
1. 如果p(n)和q(n)都是多项式，且q(n)的次数大于等于p(n)的次数，就有p(n)是O(q(n))。
2. 如果q(n)的次数小于p(n)的次数，那么p(n)不是O(q(n))。
3. 指数式是指形如aⁿ的表达式（其中a>1）。指数式要比多项式增长得更快。也就是说，我们可以为任一多项式p(n)证明，p(n)是O(aⁿ)。例如，n⁵是O((1.01)ⁿ)。
4. 反过来，对a>1，不存在指数式aⁿ为多项式p(n)的O(p(n))。

设n₀是n₁和n₂二者中的较大值，而且令c=c₁c₂。我们声称n₀和c为“f(n)是O(h(n))”这一事实的证物。这里假设n≥n₀。因为n₀=max(n₁,n₁)，所以我们知道n≥n₁且n≥n₂。因此，f(n)≤c₁g(n)，且g(n)≤c₂h(n)。

现在用c₂h(n)替换不等式f(n)≤c₁g(n)中的g(n)，就证明了f(n)≤c₁c₂h(n)。该不等式就证明了f(n)是O(h(n))。

示例 3.5

从示例3.3中可知

T(n)=3n⁵+10n⁴-4n³+n+1

是O(n⁵)，还可以从规则“常数因子不产生影响”中知道n⁵是O(0.01n⁵)。通过大O的传递律，可知T(n)是O(0.01n⁵)。

3.5.2　描述程序的运行时间

我们之前对程序的运行时间T(n)的定义是，程序处理大小为n的任意输入所耗费时间单位的最大值。我们还说过，要确定T(n)的准确公式，就算不是不可能，也将非常困难。通常，可以用大O表达式O(f(n))作为T(n)的上限，从而将问题大大简化。

例如，SelectionSort程序的运行时间T(n)的上限是an²，其中a是某个常数，而且n≥1，我们将在3.6节中展示这一事实。然后可以说SelectionSort的运行时间是O(n²)。从直觉上讲，这一陈述是最为实用的，因为n²是个非常简单的函数，而且有关其他简单函数的更强陈述（比如“T(n)是O(n)”）都为假。

不过，因为大O表示法的本性，还可以说运行时间T(n)是O(0.01n²)，或O(7n²-4n+26)，或者是任何二次多项式的大O。原因在于，n²是任意二次式的大O，而根据传递律，就可以从T(n)是O(n²)这一事实得出T(n)是任意二次式的大O。

更糟的是，n²还是任意三次或更高次多项式，或者是任意指数式的大O。因此，再次利用传递性，T(n)是O(n³)，O(2ⁿ+n⁴)，等等。不过我们将会解释，为什么O(n²)是表示SelectionSort程序的运行时间的首选。

3.5.3　紧凑性

首先，我们一般都想要达到可以证明的“最紧”大O上界。也就是说，如果T(n)是O(n²)，我们就想作出这一表述，而不是作出“T(n)是O(n³)”这种技术上正确但更弱的表述。另一方面，这种方式又存在某种疯狂性，因为如果我们喜欢用O(n²)作为运行时间的表达式，就应该更喜欢O(0.5n²)，因为它更“紧凑”，而对O(0.01n²)的喜爱应该就更甚了。不过，因为在大O表达式中，常数因子是不产生影响的，所以通过缩小常数因子让预估运行时间“更紧凑”的尝试是没有意义的。因此，只要有可能，我们就会试着使用常数因子为1的大O表达式。

图3-4列出了一些比较常见的程序运行时间，以及它们的非正式名称。特别要注意，O(1)是表示“某个常数”的惯用简写形式，而且我们还将反复使用这种用意的O(1)。

大O	非正式名称
O(1)	常数
O(logn)	对数
O(n)	线性
O(n logn)	n logn
O(n²)	二次
O(n³)	三次
O(2ⁿ)	指数

图 3-4　一些常见大O运行时间的非正式名称

更精确地讲，如果同时满足如下两点

1. T(n)是O(f(n))；

2. 如果T(n)是O(g(n))，那么f (n)是O(g(n))也为真（通俗地讲，我们找不出这样一个函数g(n)，它至少与T(n)增长得一样快，却又比f (n)增长得慢）。

那么我们就说f (n)是T(n)的紧大O边界（tight big-oh bound）。

示例 3.6

设T(n)=2n²+3n，而且f (n)=n²。我们说，f (n)是T(n)的紧边界（tightbound）。要知道为什么，先假设T(n)是O(g(n))。然后，存在常数c和n₀，使得对所有的n≥n₀，有T(n)=2n²+3n≤cg(n)。那么对n≥n₀，有g(n)≥(2/c)n²。因为f (n)是n²，所以可得出，对n≥n₀，有f (n)≤(c/2)g(n)。因此，f (n)是O(g(n))。

另一方面，f (n)=n³不是T(n)的紧大O 边界。现在可以选择g(n)=n²。我们已经看到，T(n)是O(g(n))，不过不能证明f (n)是O(g(n))，因为n³不是O(n²)。因此，n³不是T(n)的紧大O 边界。

3.5.4　简单性

在我们选择大O边界时，另一个目标就是函数表达式的简单性。与紧凑性不同，简单性有时候是种偏好问题。不过，一般还是可以按照如下标准认定函数f (n)是简单的：

1. 它只有一项；

2. 这项的系数是1。

           int PowersOfTwo(int n)
           {
               int i;
(1)            i = 0;
(2)            while (n%2 == 0) {
(3)                n = n/2;
(4)                i++;
               }
(5)            return i;
           }

图 3-5　计算一个正整数n 中因数2的数量

示例 3.7

函数n²是简单的，2n²则不是简单的，因为系数不为1；而n²+n也不是简单的，因为它包含了两项。

不过，也存在某些情况，其中大O 紧凑性的上界和简单性的边界是相互冲突的目标。简单性边界并不能说明一切，以下就是一个例子，好在这样的情况在现实中很少出现。

示例 3.8

考虑一下图3-5中的PowersOfTwo函数，它会接受一个正参数n，并计量n 被2整除的次数。也就是说，第(2)行的测试询问n是否为偶数，如果是，就在第(3)行的循环体中删除一个因数2。同样在这次循环中，我们递增i，而参数i的作用是计量我们从n原本的值中删除的因数2的个数。

设输入的大小就是n 本身的值。while循环的循环体由两条语句组成，即第(3)行和第(4)行，因此可以说执行该循环体一次所需的时间为O(1)，也就是某个与n无关的不变时间量。如果该循环要执行m次，那么花在执行循环上的总时间就将是O(m)，或者是某个与m成比例的时间量。为单独执行第(1)行和第(5)行，以及进行第一次while循环条件的测试（从技术上讲不属于任何循环迭代的一部分），还要在这个量上加上O(1)或者某个常数。因此，该程序消耗的时间是O(m)+O(1)。根据低阶项可被忽略的规则，这一时间就是O(m)，除非m=0，此时这个时间就是O(1)。换个说法就是，在输入n上所花的时间与1加上2整除n的次数是成比例的。

在数学表达式中使用大O表示法
严格地讲，大O表达式在数学上正确的使用方式只有出现在“是”字后这一种情况，比如“2n²是O(n³)”。不过，在示例3.8以及本章余下的内容中，我们将直接把大O表达式当作加号以及其他算术运算符的操作数，比如表示为O(n)+O(n²)。应将这样使用的大O表达式解释成“作为大O的某个函数”。例如O(n)+O(n²)就表示“某个线性函数和某个二次函数的和”。此外，O(n)+T(n)应该解释为某个线性函数与某个特定函数T(n)的和。

n 能被2整除多少次？对每个奇数n来说，答案为0。所以对每个奇数n，都有PowersOfTwo函数花的时间为O(1)。不过，当n是2的乘方，也就是说当n对某个k而言是2^k时，2能整除n的次数正好是k。当n=2^k时，可以在等式两边同时取以2为底的对数，得到log₂n=k。也就是说，m至多是n的对数，或者说m=O(logn)。4

4请注意，在大O表达式中说到对数时，是不需要指出底数的。原因在于，如果底数分别为a和b，那么log_an=(log_bn)(log_ab)。因为log_ab是个常数，所以可以看到log_an 和log_bn 只有一个常数因子的差别。因此，函数log_xn 对于任何不同底数x 来说都互为大O，所以根据传递律，可以在大O表达式中用任意的log_bn 来代替log_an，其中b是不同于a 的底数。

因此，可以说PowersOfTwo的运行时间是O(logn)。这一边界满足了我们对简单性的定义。不过，还有更精确的方法来统计PowersOfTwo运行时间的上界，这就是说，它是函数f (n)=m(n)+1的大O，其中m(n)是n 被2整除的次数。如图3-6所示，该函数一点都不简单。它的值在剧烈摆动，但从没有超过1+log₂n。

{%}

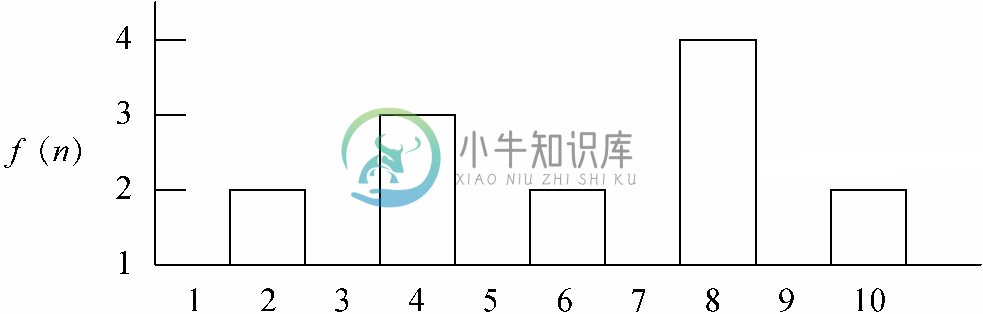
图 3-6　函数f (n)=m(n)+1，其中m(n)是n 被2整除的次数

因为PowersOfTwo的运行时间是O(f (n))，而logn又不是O(f (n))，所以可以说logn不是该程序运行时间的紧边界。另一方面，f (n)是紧边界，但它不简单。

运行时间中的对数
如果要考虑的算法需要处理积分（ $\ln{a}=\int^a_1\frac{1}{x}\text{d}x$ ），大家可能会因为它们出现在算法的分析中而感到惊讶。计算机科学家们通常会把“logn”考虑为log₂n，而不是lnn和lgn。请注意，log₂n 就是将n 除以2直到得到1为止的次数，或者换句话说，是为了得到n，相乘的2的个数。大家可能很容易看出，n=2^k其实和说log₂n=k 是一样的，只要在两边同时取以2为底的对数即可。
PowersOfTwo函数会尽可能多次地用2整除n，而且当n 是2的乘方时，n 能被2整除的次数就是log₂n。对数在对分治算法（就是在每个阶段将输入等分为两个部分，或者分为近似相等的两部分的算法，比如归并排序算法）的分析中会频繁地出现。如果我们一开始有大小为n的输入，那么将输入对半分，直到大小为1的阶段数是log₂n。或者，如果n不是2的乘方，就是比log₂n 大的最小整数。

3.5.5　求和规则

假设某个程序由两部分组成，一部分耗费的时间是O(n²)，而另一部分消耗的时间为O(n³)。可以将这两个大O边界“相加”，从而得出整个程序的运行时间。在很多情况下（包括上述情况），通过应用如下求和规则，可以将大O表达式“相加”。

假设已知T₁(n)是O(f₁(n))，而且T₂(n)是O(f₂(n))。此外，假设f₂的增长率不大于f₁的增长率，也就是说，f₂(n)是O(f₁(n))。那么就可以得出“T₁(n)+T₂(n)是O(f₁(n))ⁿ ”的结论。

要证明这一规则，我们知道存在常数c₁、c₂、c₃、n₁、n₂和n₃，使得

1. 如果n≥n₁，则T₁(n)≤c₁f₁(n)；

2. 如果n≥n₂，则T₂(n)≤c₂f₂(n)；

3. 如果n≥n₃，则f₂(n)≤c₃f₁(n)。

设n₀是n₁、n₂和n₃中最大的那个，则当n≥n₀时，(1)、(2)和(3)都成立。因此，对n≥n₀，有

T₁(n)+T₂(n)≤c₁f₁(n)+c₂f₂(n)

如果使用(3)提供f₂(n)的上边界，那么完全可以消去f₂(n)，并得出

T₁(n)+T₂(n)≤c₁f₁(n)+c₂c₃f₁(n)

因此，如果定义c为c₁+c₂c₃，就证明了对于所有的n≥n₀，有

T₁(n)+T₂(n)≤cf₁(n)

这一命题刚好就是我们需要得出的结论——T₁(n)+T₂(n)是O(f₁(n))。

示例 3.9

考虑一下图3-7中的程序段。该程序会使A成为n 阶单位矩阵。第(2)行至第(4)行在该n×n二维数组的每个单元中都放上0，接着第(5)行和第(6)行会在从A[0][0]到A[n-1][n-1]的对角线线上的位置中放入1。结果就形成了具有对于任意n×n 矩阵M都有如下属性的单位矩阵A。

           A × M = M × A = M
(1)        scanf("%d",&n);
(2)        for (i = 0; i < n; i++)
(3)            for (j = 0; j < n; j++)
(4)                A[i][j] = 0;
(5)        for (i = 0; i < n; i++)
(6)            A[i][i] = 1;

图 3-7　创建单位矩阵A的程序段

第(1)行会读取n，花的时间为O(1)，也就是某个和n值无关的固定时间量。第(6)行中的赋值语句花的时间也是为O(1)，第(5)行和第(6)行的循环要进行n次，在该循环上花的总时间就是O(n)。类似地，第(4)行中的赋值语句花的时间是O(1)。第(3)行和第(4)行的循环要进行n次，花费的总时间为O(n)。第(2)行至第(4)行的外层循环要执行n次，在每次迭代中花费的时间为O(n)，所以总时间就是O(n²)。

因此，图3-7所示程序的运行时间就是O(1)+O(n²)+O(n)，分别表示语句(1)、第(2)行至第(4)行的循环，以及第(5)行和第(6)行的循环。更正式地讲，如果以下几点同时成立：

T₁(n)是第(1)行所花的时间；

T₂(n)是第(2)行至第(4)行所花的时间；

T₃(n)是第(5)行和第(6)行所花的时间。

那么可以得出如下结论。

T₁(n)是O(1)；

T₂(n)是O(n²)；

T₃(n)是O(n)。

因此我们需要T₁(n)+T₂(n)+T₃(n)的上界，从而得出整个程序的运行时间。

因为常数1显然是O(n²)，所以可以应用求和规则得出T₁(n)+T₂(n)是O(n²)。因为n是O(n²)，就可以对(T₁(n)+T₂(n))和T₃(n)应用求和规则，从而得出T₁(n)+T₂(n)+T₃(n)是O(n²)。也就是说，图3-7所示的整个程序段的运行时间是O(n²)。通俗地讲，就是整个程序几乎将所有的运行时间都花在了第(2)行至第(4)行的循环上，正如我们从以下事实中很容易就能想到的：对于很大的n，矩阵的面积n²要比由n个单元组成的对角线大得多。

示例3.9应用了“低阶项不产生影响”这条规则，因为我们舍弃了1和n这两项比n²次数更低的多项式。不过，求和规则不仅仅能让我们舍弃低阶项。如果有任意多个相同的大O常数项，比如有一列10个赋值语句，每个赋值语句所花的时间都是O(1)，那么就可以将这10个O(1)“加起来”，得到O(1)。不那么严格地讲就是，10个常数的和还是个常数。要知道原因，请注意1是O(1)，所以10个O(1)中任何一个都可以“被加到”其他任意一个O(1)上，从而得出O(1)这个结果。我们可以不断合并项，直到只剩下O(1)为止。

不过，必须要小心，不要把某个像O(1)这样的“常数”项，与这些随输入大小变化的项弄混了。例如，我们有可能错误地认为，每进行一次图3-7中第(5)行和第(6)行所示的循环，花的时间为O(1)，而该循环总共循环了n次，所以第(5)行和第(6)行的总运行时间就是O(1)+O(1)+O(1)+…+(n个O(1))，而求和规则告诉我们两个O(1)的和也是O(1)，这样，根据归纳法就可以得出结论：任意多个O(1)的和都是O(1)。但是，在这个程序中，n不是常数，它会因输入大小而异。因此，我们没法通过多次应用求和规则推断出n个O(1)具有任何特殊的值。当然，如果真要考虑这个问题，那么我们知道n个c 的和（其中c 是某个常数）是cn，该函数的大O 形式是O(n)，而这就是第(5)行和第(6)行真正的运行时间。

3.5.6　不相称函数

任意两个函数f (n)和g(n)可由大O相比较。也就是说，要么f (n)是O(g(n))，要么g(n)是O(f (n))。或者二者互为对方的大O，因为我们看到过，2n²和n²+3n这两个函数就是这种互为大O的关系。这种情况是很不错的。不过不巧的是，也有一些不相称的函数对，它们之间不存在任何大O关系。

示例 3.10

考虑如下函数

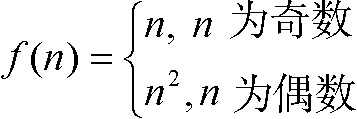
也就是，f(1)=1，f(2)=4，f(3)=3，f(4)=16，f(5)=5，等等。类似地，假设有函数

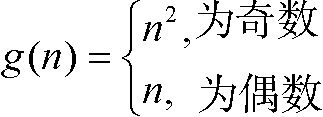
那么f(n)不可能是O(g(n))，因为那些偶数n。因为如我们在3.4节中看到的，n²绝对不是O(n)。类似地，g(n)也不可能是O(f(n))，因为那些奇数n，当n为奇数时，g的值比f 的值增长得更快。

3.5.7　习题

1. 证明如下命题。

(a) 如果a≤b，那么n^a是O(n^b)。

(b) 如果a>b，那么n^a不是O(n^b)。

(d) 如果1< b< a，那么aⁿ不是O(bⁿ)。

(e) 对任意a和任意b>1，n^a是O(bⁿ)。

(f) 对任意b和任意a>1，aⁿ是O(n^b)。

(g) 对任意a和任意b>0，(logn)^a是O(n^b)。

(h) 对任意b和任意a>0，n^a不是O((logn)^b)。

2. 证明：f(n)+g(n)是O(max(f(n),g(n)))。

3. 假设T(n)是O(f(n))，且g(n)是某个值不为负的函数。证明：g(n)T(n)是O(g(n)f(n))。

4. 假设S(n)是O(f(n))，且f(n)是O(g(n))，而且这些函数对任意n都不为负值。证明：S(n)T(n)是O(f(n)g(n))。

5. 假设f(n)是O(g(n))。证明：max(f(n),g(n))是O(g(n))。

6. * 证明：如果f₁(n)和f₂(n)都是某个函数T(n)的紧边界，那么f₁(n)和f₂(n)互为对方的大O。

7. *证明：对于图3-6所示的函数f(n)，log₂n不是O(f(n))。

8. 在图3-7所示的程序中，通过先在矩阵中每个位置放上0，然后在对角线上放上1，我们创建了一个单位矩阵。将第(4)行的测试改为询问是否有i=j，如果是，则在A[i][j]中放上1，如果不是，则放上0，这样修改后似乎能更快地完成这一工作。然后我们还可以删除第(5)行和第(6)行。

(a) 写出这一程序。

(b) * 考虑图3-7中的程序以及自己为问题(a)编写的程序。作出示例3.1中那样的简化假设，计算两个程序分别耗费了多少个时间单位。哪个程序更快？用不同大小的二维数组运行这两个程序，并绘制它们的运行时间曲线。

3.6　分析程序的运行时间

掌握了大O的概念，以及3.4节和3.5节中介绍的那些处理大O表达式的规则之后，我们将要学习如何获得常见程序运行时间的大O上界。只要有可能，我们将只考虑那些不含函数调用（除了诸如printf那样的库函数）的程序，将含有函数调用的问题留待3.8节及以后的内容中介绍。

我们不指望能够分析任意程序，因为有关运行时间的问题可能是非常难的数学问题。另一方面，只要了解一些简单的规则，我们就能够计算出实践中遇到的多数程序的运行时间。

3.6.1　简单语句的运行时间

这里要求读者接受这样一个原则，即某些对数据的简单操作可以在O(1)时间内完成，也就是说，这个时间是和输入大小无关的。C语言中的这些基本操作包括：

1. 算术运算（比如+或%）；

2. 逻辑运算（比如&&）；

3. 比较运算（比如<=）；

4. 结构体存取操作（比如A[i]这样的数组索引，或者跟在指针后的->运算符）；

5. 简单的赋值（比如将某个值复制到某个变量中）；

6. 对库函数（比如scanf、printf）的调用。

对这一原则的验证需要对常见计算机的机器指令（初始步骤）进行详细研究。我们很容易看出，之前描述的每种操作都只需要少量机器指令便可完成，通常只需要1条或2条指令。

因此，在C语言中有好几种语句都能在O(1)时间内执行完，也就是说，可以在与输入无关的某个时间段内执行完。这些简单语句包括：

1. 表达式中不涉及函数调用的赋值语句；

2. 读语句；

3. 不需要调用函数确定参数值的写语句；

4. 跳转语句break、continue、goto和return表达式，其中表达式不含函数调用。

在第(1)到第(3)条中，这些语句都是由有限数量的基本操作构成的，每个操作花的时间都是O(1)。由求和规则可知，整个语句花的时间是O(1)。当然，语句对应的时间常数要比单个操作对应的常数大，不过我们已经知道，无论如何也不能将具体的常数与C语言语句的运行时间关联起来。

示例 3.11

我们在示例3.9中看到，图3-7中第(1)行的读语句，以及第(4)行和第(6)行中的赋值，每一行花费的时间都是O(1)。再看一个例子，即图3-8中展示的选择排序程序段。第(2)、(5)、(6)、(7)和第(8)行，每一行花费的时间都是O(1)。

(1)        for (i = 0; i < n-1; i++) {
(2)            small = i;
(3)            for (j = i+1; j < n; j++)
(4)                if (A[j] < A[small])
(5)                    small = j;
(6)            temp = A[small];
(7)            A[small] = A[i];
(8)            A[i] = temp;
           }

图 3-8　选择排序程序段

我们经常会看到由连续执行的简单语句构成的程序块。如果每条语句的运行时间都是O(1)，那么根据求和规则，整个程序块花费的时间也是O(1)。也就是说，任意固定多个O(1)的和还是O(1)。

示例 3.12

图3-8中的第(6)行到第(8)行形成了一个程序块，因为它们永远是连续执行的。由于每一行花的时间都是O(1)，所以第(6)行到第(8)行的程序块所花的时间也是O(1)。

请注意，不应该把第(5)行算在程序块中，因为它是第(4)行if语句的一部分。也就是说，有时候即便不执行第(5)行，第(6)行至第(8)行也会执行。

3.6.2　简单`for`循环的运行时间

在C语言中，很多for循环的构成包括初始化指标变量为某个值的语句，以及每进行一次循环就将该标量递增1的语句。当该指标达到某个限制后，for循环就终止了。例如，图3-8中第(1)行的for循环使用了指标变量i。每进行一次循环，它就将i递增1，而当i达到n-1时，迭代就停止了。

在C语言中，还有更复杂的for循环，其行为更类似while语句，这些循环迭代的次数是不可预知的。本节后面将会介绍这种循环。不过在这里，还是将注意力集中在形式简单的for循环上，在这种for循环中，最终值和初始值之间的差，除以指标变量每次递增的量，就可以得出循环了多少次。这种计数是精确的，除非还存在一些通过跳转语句退出循环的方式，否则这在任何情况下都是迭代次数的上界。例如，图3-8中for循环的第1行会迭代((n-1)-0)/1=n-1次，因为0是i 的初始值，n-1是i 达到的最高值（即当i 达到n-1时，循环就会终止，i=n-1时不会发生迭代），而且循环每次迭代i都会增加1。

要为for循环的运行时间找出边界，必须先找到循环体进行一次迭代所花时间的上界。请注意，进行一次迭代的时间包括递增循环指标（比如图3-8第(1)行中的递增语句i++）所花的时间O(1)，以及比较循环指标与上限（比如图3-8第(1)行中的测试语句i<n-1）所花的时间O(1)。除了循环体为空的异常情况，其他所有情况下的这些O(1)都可以根据求和规则舍弃掉。

在最简单的情况，也就是循环体每次迭代所花的时间均相同的情况下，可以用循环体的大O上界乘上循环的次数。严格地说，还必须加上初始化循环指标的时间O(1)，以及第一次比较循环指标和上限的时间O(1)。不过，除非有可能不执行循环，否则初始化循环和测试上限的时间都是根据求和规则可被舍弃的低阶项。

示例 3.13

考虑图3-7第(3)行和第(4)行中的for循环，也就是

(3)        for (j = 0; j < n; j++)
(4)            A[i][j] = 0;

我们知道第(4)行花的时间为O(1)。显然，我们要进行n次循环，这可以由第(3)行找到的上限减去下限再加上1来确定。因为循环体，也就是第(4)行，花费的时间为O(1)，所以可以忽略递增j的时间O(1)以及比较j与n的时间O(1)。因此，第(3)行和第(4)行的运行时间为n与O(1)的积，也就是O(n)。

类似地，可以确定由第(2)行至第(4)行构成的外层循环的运行时间边界，外层循环如下。

(2)        for (i = 0; i < n; i++)
(3)            for (j = 0; j < n; j++)
(4)                A[i][j] = 0;

我们已经得到第(3)行和第(4)行的循环所花的时间为O(n)。因此，可以忽略递增i的时间O(1)以及每次迭代时测试是否有i< n所花的时间O(1)，并得出外层循环每次迭代所花的时间为O(n)。外层循环初始化i=0，以及第(n+1)次i< n 的条件测试花的时间都是O(1)，而且都可以忽略。最终，我们看到外层循环要循环n次，而每次迭代的时间都是O(n)，因此总运行时间就是O(n²)。

示例 3.14

现在来考虑图3-8第(3)行到第(5)行中的for循环。在这里，循环体是if语句，是我们接下来将要了解如何进行分析的结构。不难推断出第(4)行花费时间O(1)执行测试，第(5)行如果执行的话也会花费时间O(1)，因为它是不含函数调用的赋值语句。因此，不管第(5)行是否执行，执行for循环循环体所花的时间都为O(1)，循环中的递增和测试增加的时间都是O(1)，所以循环进行一次迭代的总时间也只是O(1)。

现在我们必须计算进行循环的次数。迭代次数是与输入大小n无关的。而公式“最后的值减去初始值除以递增量”告诉我们，(n-(i+1))/1，或者说n-i-1，是循环迭代的次数。严格地说，该公式只有在i<n时才成立。好在我们从图3-8的第(1)行可以看出，除非i≤n-2，否则我们不会进入第(2)至第(8)行的循环体。因此，我们不仅知道了n-i-1是循环迭代的次数，而且知道了这个数值不可能为0。由此可以得出该循环所花的时间为(n-i-1)×O(1)，或者说是O(n-i-1)。5此处不必加上初始化j所花的时间O(1)，因为已知n-i-1不可能为0。如果看不出n-i-1为正的话，就必须将运行时间的上界写为O(max(1,n-i-1))。

5从技术上讲，我们没有讨论过应用到多变量函数上的大O运算符。在这种情况中，可以将O(n-i-1)说成是“最多为某个常数乘以n-i-1”。也就是说，可以将n-i-1视为某个单变量函数的替代物。

3.6.3　选择语句的运行时间

if-else选择语句具有如下形式：

if(<condition>)
　　<if-part>
else
　　<else-part>

其中

1. 条件是待评估的表达式；

2. if部分的语句只有在条件为真（表达式的值不为0）时才执行；

3. else部分的语句只有在条件为假（评估为0）时才执行，else后的<else-part>是可选的。

只要条件中没有函数调用，不管条件多么复杂，都只需要计算机执行一定量的基本操作。因此，条件评估所花的时间为O(1)。

假设在条件中没有函数调用，而且if部分和else部分分别具有大O上界f (n)和g(n)。还假设f (n)和g(n)不会都为0，也就是说，尽管else部分可能不存在，但if部分是不会为空的。我们将确定两部分都为空的时候会发生什么留作本节的习题。

如果f (n)是O(g(n))，那么可以将O(g(n))作为选择语句运行时间的上界。原因包括：

1. 可以忽略条件所花的时间O(1)；

2. 如果else部分执行，就可知g(n)是运行时间的边界；

3. 如果if部分（而不是else部分）执行，那么运行时间将是O(g(n))，因为f (n)是O(g(n))。

类似地，如果g(n)是O(f (n))，就可以通过O(f (n))确定选择语句运行时间的边界。请注意，当else部分不存在时（情况也常常是这样），g(n)为0，就肯定是O(f (n))。

当f 和g之间不存在大O关系时，问题出现了。我们知道if部分或else部分肯定有一种要执行，但不可能都执行，所以运行时间的安全上界就是f (n)和g(n)中的较大者。正如我们在示例3.10中看到的，二者谁比较大可能取决于n。因此，要将选择语句的运行时间表示为O(max(f (n),g(n)))。

示例 3.15

正如我们在示例3.12中看到的，图3-8中第(4)行和第(5)行是选择语句，其中第(5)行是if部分，所花时间为O(1)，而不存在else部分（也就是所花时间为0）。因此，f (n)是1且g(n)是0。由于g(n)是O(f (n))，可以得出O(1)是第(4)行和第(5)行运行时间的上界。请注意，在第(4)行执行测试A[j]<A[small]的时间O(1)可以忽略。

示例 3.16

图3-9所示的代码段是个更为复杂的例子，它执行的（相对无意义的）任务是将矩阵A置为0，或是将矩阵的对角线置为1。一如我们在示例3.13中所了解的，第(2)行至第(4)行的运行时间是O(n²)，而第(5)行和第(6)行的运行时间是O(n)。因此这里的f (n)是n²，g(n)是n。因为n是O(n²)所以可以忽略else部分的时间，并将O(n²)作为图3-9中整个程序段运行时间的边界。也就是说，我们不知道第(1)行的条件是否将为真或者什么时候将为真，不过唯一安全的上界是从最坏的假设中得出的，即条件为真而且if部分执行了。

(1)        if (A[1][1] == 0)
(2)            for (i = 0; i < n; i++)
(3)                for (j = 0; j < n; j++)
(4)                    A[i][j] = 0;
           else
(5)            for (i = 0; i < n; i++)
(6)                A[i][i] = 1;

图 3-9　if-else选择语句的示例

3.6.4　程序块的运行时间

前文已经提到，一系列赋值、读、写操作，每一次操作的时间都是O(1)，总时间也是O(1)。一般的情况是，必须能将一系列语句（其中有一些是复合语句，也就是选择语句或循环）组合起来。这样一系列简单的复合语句就是程序块（block）。要计算程序块的运行时间，需要对程序块中每条（可能是复合的）语句的大O上界求和。好在可以使用求和规则消除和中的一些项。

示例 3.17

在图3-8的选择排序程序段中，可以将外层循环的循环体（也就是第(2)行至第(8)行）视为一个程序块。该程序块由5条语句组成。

1. 第(2)行的赋值语句。

2. 第(3)行、第(4)行和第(5)行的循环。

3. 第(6)行的赋值语句。

4. 第(7)行的赋值语句。

5. 第(8)行的赋值语句。

请注意，第(4)和第(5)行的选择语句以及第(5)行的赋值在程序块这一级是不可见的，它们已经隐藏在更大的语句，也就是第(3)行至第(5)行的循环中了。

我们知道，4条赋值语句每条所花的时间都是O(1)。在示例3.14中，已经了解到该程序块中第2条语句（也就是第(3)行至第(5)行）的运行时间是O(n-i-1)。因此，该程序块的运行时间是：

O(1)+O(n-i-1)+O(1)+O(1)+O(1)

因为1是O(n-i-1)（回想一下，我们还推导出i从不会大于n-2），所以可以通过求和规则消除所有的O(1)项。因此，整个程序块的运行时间就是O(n-i-1)。

再看一个例子，考虑一下图3-7中的程序段。它可被视为由3条语句组成的单一程序块。

1. 第(1)行的读语句。

2. 第(2)行至第(4)行的循环。

3. 第(5)行和第(6)行的循环。

我们知道，第(1)行花的时间为O(1)。从示例3.13可知，第(2)行至第(4)行花的时间是O(n²)，第(5)行和第(6)行花的时间是O(n)。所以整个程序块的运行时间就是：

O(1)+O(n²)+O(n)

根据求和规则，由O(n²)可以消去O(1)和O(n)。因此可以得出图3-7中程序段的运行时间为O(n²)。

3.6.5　复杂循环的运行时间

在C语言中，有一些while循环、do-while循环和for循环并未提供显式的计数变量。对于这些循环，一部分分析工作就是要找到为循环迭代次数提供上界的参数。这些证明过程通常都遵循我们在2.5节中了解的模式。也就是说，通过对循环次数的归纳证明某个命题，而该命题表明在迭代次数达到某个限制后，循环条件一定会变为假。

我们还必须建立执行一次循环迭代所花时间的边界。因此，可以对循环体加以研究，并获得其执行的边界。为了实现这个目标，必须在循环体执行后加上测试条件的时间O(1)，不过除非循环体不存在，否则我们都会忽略该O(1)项。通过用迭代次数的上界乘以一次迭代所花时间的上界，可以得到循环运行时间的边界。从技术上讲，如果该循环是for循环或while循环，而不是do-while循环，就必须将进入循环体之前第一次测试条件所需的时间包含在内。不过，这个O(1)经常是可以忽略掉的。

示例 3.18

考虑如图3-10所示的程序段。该程序会搜索数组A[0..n-1]，找出该数组中的元素x。

(1)        i = 0;
(2)        while(x != A[i])
(3)            i++;

图 3-10　线性查找的程序段

图3-10中第(1)行和第(3)行的两条赋值语句的运行时间均为O(1)。第(2)和第(3)行的while循环可能会执行n次，但不会超过n次，因为我们假设x确实是数组元素之一。因为第(3)行的循环体所需时间为O(1)，所以该while循环的运行时间就是O(n)。根据求和规则，整个程序段的运行时间为O(n)，因为这是第(1)行的赋值语句以及整个while循环所花的最大时间。在第6章中，我们还将看到这种O(n)程序是如何被使用二叉查找的O(logn)程序所代替的。

3.6.6　习题

1. 对开头为for (i = a; i <= b; i++)的for循环，用a 和b 的函数表示其循环次数。对开头为for (i = a; i <= b; i--)的for循环又是怎样表示的呢？对开头为for(i = a; i <= b; i = i+c)的for循环呢？

2. 给出某个普通的选择语句if(C) {} 运行时间的大O上界，其中C 是不涉及任何函数调用的条件。

3. 给出某个普通的while循环while(C ) {}运行时间的大O上界，其中C 是不涉及任何函数调用的条件。

4. * 给出C语言switch语句运行时间的规则。

5. 给出我们能确定哪条分支被执行的选择语句运行时间的规则，比如

if (1==2)
　　something O(f (n));
else
　　something O(g(n));

6. 给出循环开始前条件已知为假的退化while循环（degenerate while-loop）运行时间的规则，比如

while (1 != 1)
　　something O(f (n))

3.7　边界运行时间的递归规则

在3.6节中，我们简略地描述了一些规则，它们用程序结构各部分的运行时间来定义整个程序结构的运行时间。例如，我们说过for循环的运行时间大致等于循环体所花的时间乘以迭代的次数。隐藏在这些规则背后的概念是，程序是使用归纳规则构成的，复合语句（循环、选择和其他由子语句组成的语句）通过这些规则由诸如赋值、读、写和跳转语句这样的简单语句组成。这些归纳规则涵盖循环的形成、选择语句及程序块等一系列复合语句。

我们要将一些构建C语言语句的句法规则表述为递归定义。这些规则符合经常出现在C语言教材中的那些定义C语言的语法规则。我们在第11章中还将看到，语法可以用作简洁递归表示法，来指明编程语言句法（syntax）。

更具防御性的程序设计
如果大家只是因为相信示例3.18中的数组A总会存在元素x，就认为它总会存在，那就太天真了。请注意，如果数组中不存在x，图3-10中的循环将最终会出错，因为它要试着访问一个超过数组上限的数组元素。
好在有一种简单的方法可以避免这一错误，而且不会给循环的每次迭代增加很多时间。我们允许数组末尾有第n+1个单元，而在开始循环前，将x 放在该单元中。那么确实能确定x 会出现在数组中的某个位置。当循环结束后，我们会测试是否有i=n。如果是，那么x 并非真正在数组中，我们会穿过数组到达作为哨兵（sentinel）的x 的副本。如果i<n，那么i 就表示x 出现的位置。带有这种保护功能的程序如下所示。
A[n] = x;
i = 0;
while (x != A[i])
   i++;
if (i == n) /* do something appropriate to the case
                      that x is not in the array */
else /* do something appropriate to the case
                      that x is found at position i */

依据。

C语言中的简单语句如下。

1. 表达式。包括赋值语句以及读和写语句，后者是对printf和scanf等函数的调用；

2. 跳转语句。包含goto、break、continue和return；

3. 空语句。

请注意，在C语言中，简单语句都是以分号结尾的，我们要将分号视为这些语句的一部分。

归纳。

以下规则让我们可以用较小的语句来构建语句。

1. while语句。如果S是语句，而C 是条件（带有算术值的表达式），那么

while (C )S

是语句。只要C 为真（具有非0的值），循环体S 就会执行。

2. do-while语句。如果S 是语句，而C 是条件，那么

do S while(C )

是语句。do-while循环和while循环类似，只不过do-while循环的循环体S至少会执行一次。

3. for语句。如果S 是语句，而E₁、E₂和E₃是表达式，那么

for (E₁; E₂; E₃) S

是语句。第一个表达式E₁会进行一次评估，并指定循环体S 的初始化。第二个表达式E₂是对循环终止的测试，会在每次迭代前进行评估。如果它的值不为0，那么循环体就会执行，否则该for循环就将终止。第三个表达式E₃会在每次迭代后进行评估，并为循环的下一次迭代指定重初始化（递增）。例如，如下常见的for循环

for (i = 0; i < n; i++) S

其中S会迭代n 次，对应i 的值分别为1、2、3、…、n-1。在这里，i = 0是初始化，i < n 是终止测试，i++是重初始化。

4. 选择语句。如果S₁和S₂是语句，而C 是条件，那么

if ( C ) S₁ else S₂

是语句，而且

if ( C ) S₁

也是语句。在第一种情况中，如果C为真（非0），就执行S₁，否则就执行S₂。在第二种情况中，只有当C 为真，才执行S₁。

5. 程序块。如果S₁、S₁、…、S_n都是语句，那么

{S₁ S₂…S_n}

也是语句。

我们在上面没有列出开关语句，它形式复杂，但在分析运行时间时可以被当作嵌套的选择语句。

利用上述对语句的递归定义，就可以通过分辨程序的组成部分来解析程序。也就是说，首先有简单的语句，再进一步将这些简单的语句组成更大的复合语句。

示例 3.19

考虑图3-11所示的选择排序程序段。作为根据，第(2)行、(5)行、(6)行、(7)行和第(8)行的每次赋值都各为一条语句；而第(4)行和第(5)行组成了选择语句；第(3)行至第(5)行又组成了for语句；然后第(2)行至第(8)行组成了一个程序块；最后，整个程序段也是for语句。

(1)        for (i = 0; i < n-1; i++) {
(2)            small = i;
(3)            for (j = i+1; j < n; j++)
(4)                if (A[j] < A[small])
(5)                    small = j;
(6)            temp = A[small];
(7)            A[small] = A[i];
(8)            A[i] = temp;
           }

图 3-11　选择排序程序段

3.7.1　程序结构的树表示

我们可以用如图3-12所示的树表示程序的结构。树叶（那些圆圈）是简单语句，而其他的节点则表示复合语句。6节点会被标记上它们所表示结构的种类，以及构成该节点所表示简单语句或复合语句的代码行。从每个表示复合语句的节点N 都会向下引出到达其“子节点”的连线。节点N 的子节点表示构成N 所表示复合语句的那些子语句。这样的树就称为程序的结构树。

6我们将在第5章中详细讨论树。

{%}

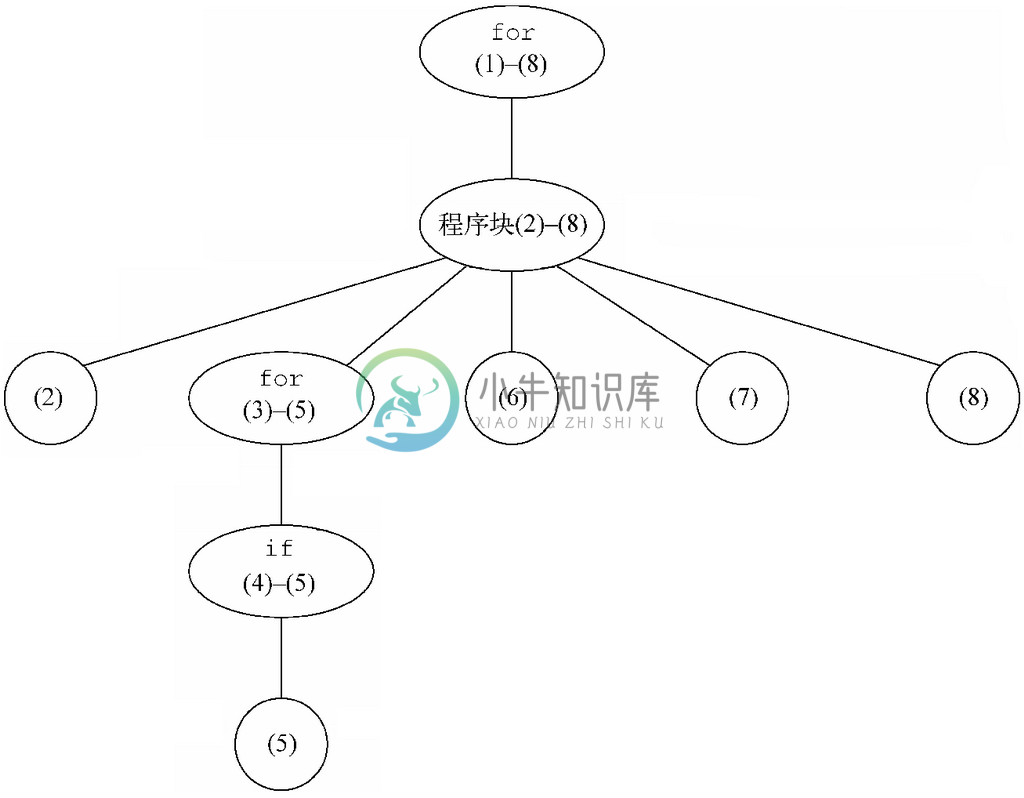
图 3-12　表示语句组合的树

示例 3.20

图3-12是图3-11所示程序的结构树。每个圆圈分别是表示图3-11中5条赋值语句的树叶。我们在图3-12中没有说明这5条语句是赋值语句。

在树的顶端（也就是“根”）是表示第(1)至第(8)行整个程序段的节点。for循环的循环体是由第(2)行至第(8)行组成的程序块。7该程序块是用根节点下方的节点表示的。而这个表示程序块的节点又有5个子节点，分别表示该程序块的5条语句。其中第(2)、(6)、(7)和第(8)行这4条是赋值语句，而第5条是第(3)行至第(5)行的for循环。

7更为详细的结构树还有表示for循环初始化表达式、终止测试表达式和重初始化表达式的子节点。

第(3)行至第(5)行表示for循环的节点又有表示其循环体（就是第(4)行和第(5)行的if语句）的子节点。而表示第(4)行和第(5)行if语句的节点又具有表示其组成语句（第(5)行的赋值语句）的子节点。

3.7.2　攀爬结构树以确定运行时间

正如递归构建的程序结构那样，我们可以使用类似的递归方法来定义程序运行时间的大O上界。就像在3.6节中那样，我们假定在下列几类表达式中都不存在函数调用。(1)构成赋值语句、打印语句、选择语句条件的表达式；(2)构成while循环、for循环和do-while循环条件的表达式；(3)for循环初始化或重初始化的表达式。唯一的例外是对诸如printf这样的读函数或写函数的调用。

依据。简单语句（也就是赋值、读、写或跳转语句）的边界是O(1)。

归纳。对于我们已经讨论过的5种复合结构，计算其运行时间的规则如下。

1. while语句。设O(f(n))是while语句循环体的运行时间上界，f (n)是通过递归地应用这些规则得到的。再假设g(n)是循环次数的上界。那么O(1+(f (n)+1)g(n))就是整个while循环的运行时间上界，其中O(f (n)+1)是循环体加上循环体后测试的运行时间上界。开头那个多出来的1表示循环开始前的第一次测试。在f (n)和g(n)都至少为1（或者如果不定义其值为1，则其值为0，我们就可以定义它们为1）的平常情况下，可以将该while循环的运行时间记为O(f (n)g(n))。这一运行时间的通用公式如图3-13a所示。

2. do-while语句。如果O(f (n))是循环体运行时间的上界，且g(n)是循环次数的上界，那么O((f (n)+1)g(n))就是该do-while循环的运行时间上界。这里“+1”表示的是循环每次迭代之末计算和测试循环条件的时间。请注意，对do-while循环来说，g(n)总是至少为1。在对所有n 都有f (n)≥1的情况中，do-while循环的运行时间为O(f (n)g(n))。图3-13b表示了计算普通情况下的do-while循环运行时间的方法。

3. for语句。如果O(f (n))是循环体运行时间的上界，且g(n)是循环次数的上界，那么for语句运行时间的上界就是O((1+f (n)+1)g(n))。因子f (n)+1表示每进行一次循环所花的时间。开头的“1+”表示第一次初始化，以及第一次测试为负从而导致循环体不执行这种可能。在f (n)和g(n)都至少为1，或者可重新定义为至少是1的一般情况下，for语句的运行时间是O(f (n)g(n))，如图3-13c所示。

图 3-13　计算不含函数调用的循环语句的运行时间

4. 选择语句。如果O(f₁(n))和O(f₂(n))分别是if部分和else部分的运行时间（如果没有else部分，则O(f₂(n))为0），那么选择语句运行时间的上界就是O(1+max(f₁(n),f₂(n)))。“1+”表示条件测试，在f₁(n)和f₂(n)至少有一个为正数的一般情况下，这个“1+”是可以忽略的。此外，如果f₁(n)和f₂(n)中有一个是另一个的大O，那么该表达式如3.5节习题(5)中所述那样可以简化为二者中的较大者。图3-14表示了if语句运行时间的计算。

{%}

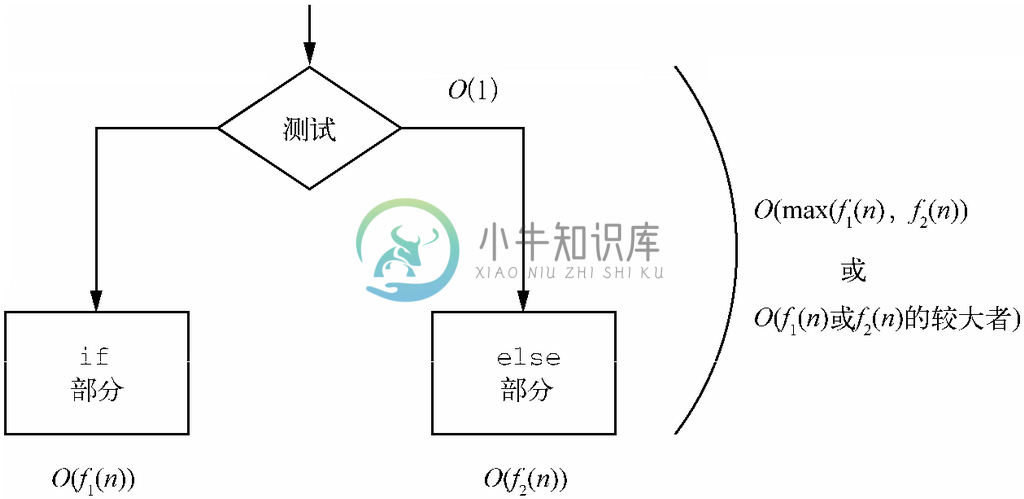
图 3-14　计算不含函数调用的if语句的运行时间

5. 程序块。如果程序块中各语句的运行时间上界分别是O(f₁(n))、O(f₂(n))、…、O(f_k(n))，那么整个程序块运行时间的上界就是O(f₁(n)+f₂(n)+…+f_k(n))。如果可能的话，请使用求和规则简化这个表达式。程序块运行时间的计算规则如图3-15所示。

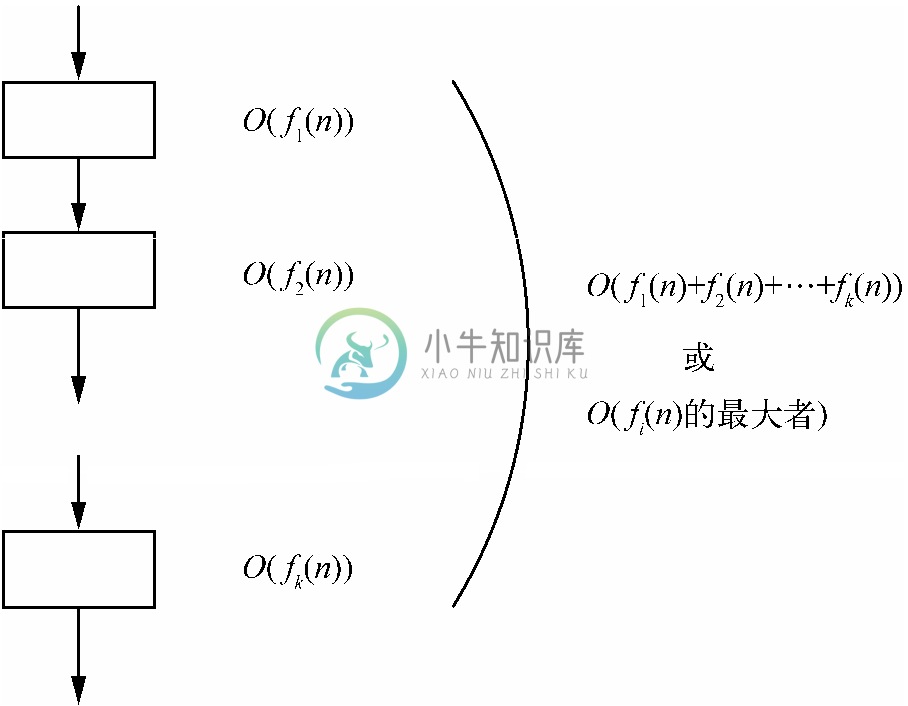
图 3-15　计算不含函数调用的程序块的运行时间

可以应用这些规则，从较小的语句开始向上遍历表示复合语句构造的结构树。或者，可以将这些规则的应用视为从递归依据所涵盖的简单语句开始，逐步变成更大的符合语句，在每一步应用5种归纳规则中任意一种合适的规则。不管我们怎样看待计算运行时间上界的过程，都需要在分析过组成复合语句的所有语句之后，再对复合语句加以分析。

示例 3.21

我们来重新审视一下图3-11中的排序程序，它的结构树如图3-12所示。首先，已知图3-12中树叶位置的每条赋值语句所花的时间为O(1)。继续向树的上方行进，就会遇到第(4)行和第(5)行的if语句。从示例3.15中可以回想起这一复合语句所花的时间为O(1)。

接下来随着向上遍历该树（或者说从较小语句向它们所围绕的较大语句行进），就必须分析第(3)行至第(5)行的for循环。示例3.14就是完成这一工作的，从中可得出运行时间为O(n-i-1)。在这里，我们选择将运行时间表示为具有n和i两个变量的函数。这一选择给我们带来了一些计算上的困难，而正如接下来将要看到的，其实可以选择O(n)这个更松散的上界。要以O(n-i-1)作为边界，就必须从图3-11的第(1)行看出i从不可能有n-1这么大。因此n-i-1是严格大于0的，并主导O(1)。所以，我们不需要在O(n-i-1)之外加上初始化for循环的指标j所花的时间O(1)。

现在到了第(2)行至第(8)行的程序块。正如示例3.17中所描述的，该程序块的运行时间是对应4条赋值语句的4个O(1)的和，加上第(3)至第(5)行复合语句的O(n-i-1)。根据求和规则，以及我们看出的i<n 的结论，可以舍弃这些O(1)，留下O(n-i-1)作为这个程序块的运行时间。

最后，必须考虑从第(1)行到第(8)行的这个for循环。该循环在3.6节中没有得到分析，不过我们可以运用归纳规则(3)。该规则需要循环体（也就是第(2)行至第(8)行）的运行时间上界。我们刚确定了该程序块的边界为O(n-i-1)，这展现了之前从未见过的情形。尽管i在该程序块内是个常量，然而i是外层for循环的循环指标，会随着循环变化。因此，我们不能将边界O(n-i-1)视作该循环全部迭代的运行时间。好在从第(1)行可以看出i不会小于0，所以O(n-1)是O(n-i-1)的上界。此外，根据低阶项不产生影响的规则，可以将O(n-1)简化为O(n)。

接下来需要确定循环进行的次数。因为i是从0到n-2，所以显然要循环n-1次。用n-1乘上O(n)，便得到O(n²-n)。再次舍去低阶项，就得到O(n²)是整个选择排序程序的运行时间上界。也就是说，选择排序的运行时间具有二次的上界。该二次上界是可能存在的最紧上界了，因为可以证明，如果这些元素一开始是倒序排列的，那么选择排序就要进行n(n-1)/2次比较。

一如我们将要看到的，可以为归并排序得出n logn 的运行时间边界。在实践中，除了对那些小的n值之外，归并排序要比选择排序更高效。归并排序有时比选择排序慢的原因就在于，O(n logn)的上界与选择排序的边界O(n²)相比，隐藏了一个更大的常数。真实的情况是一对交叉的曲线，如3.3节中的图3-2所示。

3.7.3　循环运行时间更精确的上界

我们已经说过，要评估循环的运行时间，需要找出适用于循环每一次迭代的统一边界。不过，对循环更为细致的分析要分开处理每次迭代，并为每次迭代的上界求和。从技术上讲，必须将递增循环指标（如果循环是for循环）和测试循环条件的时间包括在内，以防出现操作的时间能引起决定性变化的罕见情况。一般来讲，更加细致的分析并不会改变答案，虽然在一些不寻常的循环中大多数迭代只花费很少时间，而一次或几次迭代却占据大量运行时间（这会使这种循环每次迭代时间之和，要明显小于迭代次数乘上每次迭代可能花的最大时间的积）。

示例 3.22

我们要对选择排序的外层循环进行这种更精确的分析。尽管付出了额外的努力，可还是会得到二次的上界。正如示例3.21所示，当指标变量i的值为i 时，外层循环此次迭代的时间为O(n-i-1)。i的范围是0到n-2，因此所有迭代所花时间的上界就是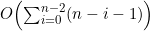 $O\Bigl(\sum^{n-2}_{i=0}(n-i-1)\Bigr)$ 。这个和式中所有项形成了一个算术级数，所以可以利用公式“第一项和最后一项的平均数乘以项数”。该公式告诉我们：

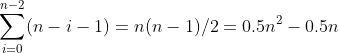
$\sum^{n-2}_{i=0}(n-i-1)=n(n-1)/2=0.5n^2-0.5n$

忽略低阶项和常数因子，可以看到O(0.5n²-0.5n)与O(n²)是相同的。这样就再次得出了结论：选择排序具有二次的运行时间上界。

示例3.21中的简单分析与示例3.22中更细致分析的区别如图3-16所示。在示例3.21中，将任一次迭代可能花费的最大时间当作每次迭代的时间，因此得到了长方形的区域作为图3-11中for循环运行时间的边界。在示例3.22中，通过图中的对角线为每次迭代确定了运行时间边界，因为每次迭代的时间是随着i 线性递减的。因此，可以得出该三角形的面积以作为对运行时间的估计。不过，众所周知，图中三角形的面积是长方形面积的一半。因为常数因子2与其他被大O表示法隐藏的常数因子一样会消失，所以这两个运行时间上界其实是一样的。

{%}

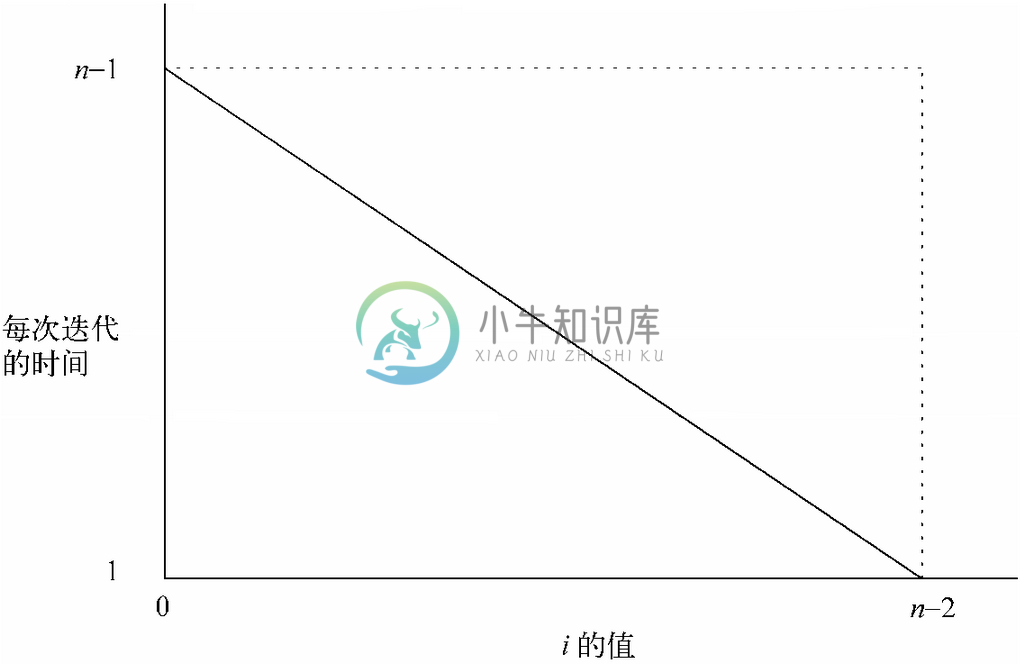
图 3-16　对循环运行时间的简单估算和精确估算

3.7.4　习题

1. 图3-17中的C语言程序会计算数组A[0..n-1]中各元素的平均值，并将最接近该平均值的元素的下标打印出来（若不止有一个这样的元素，则以先出现的为准）。假设n≥1，而且不含对空数组的必要检测。画出结构树，展示这些语句是如何进一步组成更复杂的语句的，并给出该结构树中每一语句运行时间的简单大O上界和紧大O上界。整个程序的运行时间是多少？

      #include <stdio.h>
      #define MAX 100
      int A[MAX];

     main()
      {
          int closest, i, n;
          float avg, sum;

 (1)      for (n = 0; n < MAX && scanf("%d", &A[n]) != EOF; n++)
 (2)          ;
 (3)      sum = 0;
 (4)      for (i = 0; i < n; i++)
 (5)          sum += A[i];
 (6)      avg = sum/n;
 (7)      closest = 0;
 (8)      i = 1;
 (9)      while (i < n) {
              /* 在下面的测试中为元素求平方，就不再
                 需要区分正数和负数的差异了。 */
(10)          if ((A[i]-avg)*(A[i]-avg) <
                (A[closest]-avg)*(A[closest]-avg))
(11)                  closest = i;
(12)          i++;
          }
(13)      printf("%d\n",closest);
      }

图 3-17　习题(1)的程序

2. 图3-18所示的程序段会将n×n的矩阵A变形。画出该程序段的结构树，给出每一复合语句运行时间的大O上界。

(a) 用n 和i 的函数表示两个内层循环运行时间的边界。

(b) 用n 的函数表示所有循环运行时间的边界。

对整个程序，你的答案和(a)、(b)部分之间是否存在大O差异？

(1)  for (i = 0; i < n-1; i++)
(2)      for (j = i+1; j < n; j++)
(3)          for (k = i; k < n; k++)
(4)              A[j][k] = A[j][k] - A[i][k]*A[j][i]/A[i][i];

图 3-18　习题(2)的程序

3. * 图3-19中的程序段对范围从1到n的整数i应用了示例3.8中讨论的“2的乘方”操作。画出该程序段的结构树，给出每一复合语句运行时间的大O上界。

(a) 用i 的函数表示该while循环运行时间的边界。

(b) 用n 的函数表示该while循环运行时间的边界。

对整个程序，你的答案和(a)、(b)部分之间是否存在大O差异？

(1)        for (i = 1; i <= n; i++) {
(2)            m = 0;
(3)            j = i;
(4)            while (j%2 == 0) {
(5)                j = j/2;
(6)                m++;
               }
           }

图 3-19　习题(3)的程序

4. 图3-20中的函数会确定参数n 是否为质数。请注意，如果n 不是质数，它就可以被某个在2和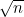 $\sqrt{n}$ 之间的整数i整除。画出该函数的结构树，用n 的函数表示每一复合语句运行时间的大O上界。整个函数的运行时间又是多少？

     int prime(int n)
     {
         int i;

(1)      i = 2;
(2)      while (i*i <= n)
(3)          if (n%i == 0)
(4)              return FALSE;
             else
(5)              i++;
(6)      return TRUE;
     }

图 3-20　习题(4)的程序

3.8　含函数调用的程序的分析

现在要展示的是如何分析包含函数调用的程序或程序段的运行时间。首先，如果所有的函数都是非递归的，可以从那些不调用其他函数的函数开始，每次确定一个组成该程序的函数的运行时间，然后为那些“只调用已确定运行时间的函数”的函数评估运行时间。我们以这种方式继续评估，直到评估完所有函数的运行时间。

不同函数可能有不同的输入大小的自然量度，这一事实带来了一些复杂性。在一般情况下，函数的输入就是该函数的参数列表。如果函数F调用了函数G，就必须将函数G 中参数的大小量度与函数F所使用的大小量度联系起来。这里很难给出实用的通则，不过本节和下一节中的一些示例将有助于我们了解简单情况下为函数确定运行时间边界的过程是怎样的。

假设已经确定，函数F 运行时间的良好上界是O(h(n))，其中n是函数F 参数大小的度量。那么在某条简单语句（比如一条赋值语句）中对F进行调用时，就要将O(h(n))的开销加到那条语句的运行时间中。

当上界为O(h(n))的函数出现在while语句、do-while语句或if语句的条件中，或出现在for语句的初始化、测试或重初始化中时，该函数调用的时间是按如下方法计算的。

1. 如果函数调用是在while循环或do-while循环的条件中，或在for循环的条件或重初始化中，那么就要在每次迭代的时间边界上加上h(n)，然后按照3.7节中获取循环运行时间的方式继续下去。

2. 如果函数调用是在for循环的初始化中，就在循环的时间开销上加上O(h(n))。

3. 如果函数调用是在if语句的条件中，就在该语句的时间开销上加上h(n)。

简述程序分析
大家应该从3.7节和3.8节中了解到的主要观点如下。
一系列语句的运行时间就是每一条语句运行时间的和。通常，如果某一语句的运行时间至少与其他语句一样大，那么它就可以主导其他语句。根据求和规则，主导语句的运行时间就是这一系列语句的大O运行时间。
要计算循环的运行时间，先要将循环体的时间与各控制步骤（比如重初始化for循环的循环指标并将其与上限相比较）的运行时间相加。用这个时间去乘以循环迭代次数的上界。接着，将那些一次性完成的步骤（比如初始化或第一次终止测试）的时间加上，以防循环迭代0次的情况出现。
选择语句（例如if-else语句）的运行时间是决定执行哪个分支所花的时间与各分支运行时间中较大的那个相加而得到的之和。

示例 3.23

让我们分析一下图3-21中的（无意义的）程序。首先，你会注意到这不是一个递归程序。main函数会调用foo函数和bar函数，而且foo函数会调用bar函数，不过这就是全部的调用关系了。图3-22所示的图称为调用图，表示函数调用其他函数的方式。因为图中不含循环，所以程序中没有递归调用，而且可以首先从“第0组”（就是不调用其他函数的函数，在本例中就是bar函数）开始分析这些函数，接着处理“第1组”（就是只调用第0组中函数的函数，在本例中就是foo函数），再处理“第2组”（就是只调用第0组和第1组中函数的函数，在本例中就是main函数）。至此，工作就完成了，因为所有的函数都已经被分组了。在一般情况下，可能要考虑分更多的组，不过只要其中不含循环，最终就能将每个函数都放在一个组别中。

     #include <stdio.h>
     int bar(int x, int n);
     int foo(int x, int n);

     main()
     {
         int a, n;

(1)      scanf("%d", &n);
(2)      a = foo(0,n);
(3)      printf("%d\n", bar(a,n));
     }

     int bar(int x, int n)
     {
         int i;

(4)      for (i = 1; i <= n; i++)
(5)          x += i;
(6)      return x;
     }

     int foo(int x, int n)
     {
         int i;

(7)      for (i = 1; i <= n; i++)
(8)          x += bar(i,n);
(9)      return x;
     }

图 3-21　展示非递归函数调用的程序

{%}

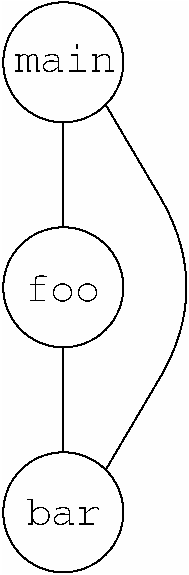
图 3-22　图3-21所示程序的调用图

我们分析函数运行时间的顺序，也就是为了理解该程序的行为而对其进行研究的顺序。因此，首先考虑一下bar函数是做什么的。第(4)行和第(5)行的for循环会将从1到n 的这n 个整数都加到x 上，结果就是bar(x,n)等于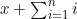 $x+\sum^{n}_{i=1}i$ 。这里的和式 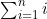$\sum^{n}_{i=1}i$ 又是个为算术级数求和的例子，只要将第一项与最后一项相加，乘以项数，然后再除以2即可。也就是 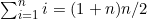$\sum^{n}_{i=1}i=(1+n)n/2$ 。因此，bar(x,n)=x+(1+n)n/2。

现在，考虑一下foo函数，它会给它的参数x加上和式

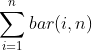
$\sum^{n}_{i=1}bar(i,n)$

根据我们对bar函数的了解可知，bar(i,n)=i+n(n+1)/2。因此，foo函数就是给x加上了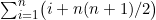 $\sum^{n}_{i=1}\bigl(i+n(n+1)/2\bigr)$ 这个量。这样就要为另一个算术级数求和了，而这个算术级数需要更多的代数变换。不过，读者可以验证一下，foo函数加到x上的这个量就是(n³+2n²+n)/2。

最后看看main函数。我们在第(1)行读入n，在第(2)行将foo应用到0和n上。根据我们对foo函数的理解，第(2)行foo(0,n)的值就是0加上(n³+2n²+n)/2。在第(3)行，要将bar(foo(0,n),n)的值打印出来，根据我们对bar函数的理解，这就是n(n+1)/2与foo(a,n)当前值的和。因此，要打印的值就是(n³+2n²+n)/2。

现在来分析图3-21所示程序的运行时间，从bar函数开始，到foo函数，再到main函数，一如我们在示例3.23中所做的那样。在这种情况下，我们要确定值n是所有三个函数的输入的大小。也就是说，即便我们通常想考虑函数所有参数的“大小”，但在本例中函数的运行时间只取决于n。

要分析bar函数，先要注意到第(5)行所花的时间为O(1)。第(4)行和第(5)行的for循环要迭代n次，所以第(4)行和第(5)行的运行时间是O(n)。第(6)行花的时间也是O(1)，所以第(4)行至第(6)行的程序块的运行时间是O(n)。

接着分析foo函数。第(8)行的赋值语句花的时间是O(1)加上调用bar(i,n)所用的时间。而我们已经知道，该调用花的时间为O(n)，所以第(8)行的运行时间就是O(n)。第(7)行和第(8)行的for循环要迭代n次，所以可以用循环体的运行时间O(n)乘上循环迭代的次数n，得到调用foo函数的运行时间是O(n²)。

最后来分析main函数。第(1)行所花的时间为O(1)，第(2)行对foo函数的调用所花的时间为O(n²)，第(3)行的打印语句所花的时间为O(1)加上调用bar函数所花的时间。而后者所花时间为O(n)，所以整个第(3)行所花的时间为O(1)+O(n)。因此从第(1)行到第(3)行的整个程序块的运行时间为O(1)+O(n²)+O(1)+O(n)。根据求和规则，可以消除第二项之外的所有项，得出该函数的运行时间为O(n²)。也就是说，第(2)行对foo函数的调用决定了整个时间开销。

证明和对程序的理解
读者可能注意到，在对图3-21所示程序的研究中，我们能理解程序在做什么，却不能像在第2章中那样正式地证明点什么。不过，在这表面之下却潜藏着诸多简单的归纳证明。例如，需要对第(4)行和第(5)行循环迭代的次数进行归纳，证明在我们用值为i 的i开始迭代之前，x的值是x的初始值加上 $\sum^{i-1}_{j-1}j$ 。请注意，如果i=1，这个和式不含任何项，则其值会为0。

习题

1. 证明示例3.23中的结论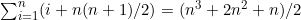： $\sum^{n}_{i=1}(i+n(n+1)/2)=(n^3+2n^2+n)/2$

2. 假设prime(n)是运行时间为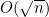 $O(\sqrt{n})$ 的函数调用。考虑一下函数体如下的函数：

if ( prime(n) )
　　A;
else
　　B;

分别假设：

(a) A所花的时间为O(n)，B所花的时间为O(1)；

(b) A和B所花的时间都为O(1)。

用n的函数表示出这两种情况下该函数运行时间的简单大O上界和紧大O上界。

3. 考虑函数体如下的函数：

sum = 0;
for (i = 1; i <= f(n); i++)
    sum += i;

其中f(n)是函数调用。分别假设：

(a) f (n)的运行时间是O(n)，而f (n)的值是n!；

(b) f (n)的运行时间是O(n)，而f (n)的值是n；

(d) f (n)的运行时间是O(1)，而f (n)的值是0。

用n 的函数表示出这4种情况下该函数运行时间的简单大O上界和紧大O上界。

4. 绘出2.8节归并排序程序中函数的调用图。那个程序是否为递归程序？

5. * 假设图3-21中foo函数的第(7)行被替换为

for (i = 1; i <= bar(n,n); i++)

那么main函数的运行时间会是多少？

3.9　递归函数的分析

确定递归调用自身的函数的运行时间，需要比分析那些非递归函数耗费更多的精力。递归函数的分析需要我们将程序中的每个函数F 与某个未知的运行时间T_F (n)关联起来。这一未知的函数将F 的运行时间表示为F 函数参数的大小n 的函数。然后构建一套归纳定义，称为T_F (n)的递推关系，将T_F (n)与同一程序中其他函数G 及其相应的参数大小k 表示的T_G(k)形式关联起来。如果F 是直接递归的，那么G 中至少有一个将与F 是相同的。

T_F (n)的值通常是通过对参数大小n 的归纳取得的。因此，需要选择合适的参数大小，保证随着递归的进行，函数在被调用时所使用的参数在逐渐减小。这一要求与我们在2.9节中试图证明有关递归程序的命题时遇到的要求别无二致。这应该没什么可奇怪的，因为有关程序运行时间的命题正是我们可能试着证明的与程序相关的某种内容。

一旦找到了合适的参数大小，就可以考虑以下两种情况了。

1. 参数大小足够小，使F 不进行递归调用。这种情况对应T_F (n)归纳定义中的依据。

2. 对于较大的参数大小，将至少会发生一次递归调用。请注意，无论F进行怎样的递归调用，不管是对其自身还是对某个其他函数G 进行递归调用，都只可能使用更小的参数。这种情况对应T_F (n)归纳定义中的归纳步骤。

通过对函数F 的代码的研究，并完成如下操作，可以得出T_F (n)递推关系的定义。

(a) 对函数G 的每次调用或表达式中函数G 的每次使用（请注意，G 可能就是F），用T_G (k)表示该次调用的运行时间，其中k 是对该次调用中参数大小的合理度量。

(b) 运用前面几节中介绍的技巧评估函数F 的函数体的运行时间，不过要将T_G (k)这样的项留作未知函数，而不是诸如n²这样的具体函数。一般不能用求和规则这样的简化技巧把这些项与具体函数结合起来。我们必须对F 进行两次分析，一次假设F 的参数大小n 足够小，使得函数未进行递归调用，而另一次假设n 不是那么小。因此，我们得到了两个表示F 函数运行时间的表达式。其一（依据表达式）是T_F (n)递推关系的依据，另一个（归纳表达式）则是T_F (n)递推关系的归纳部分。

(d) 如果输入大小的依据值为a，令T_F (a)是在假设不存在递归调用的情况下，由步骤(c)得出的依据表达式。还有，令T_F (n)是从步骤(c)得到的n 值不为依据值a 的情况下的归纳表达式。

           int fact(int n)
           {
(1)            if (n <= 1)
(2)                return 1; /* 依据*/
               else
(3)                return n*fact(n-1); /* 归纳 */
           }

图 3-23　计算n!的程序

通过求解这个递推关系，就可以确定整个函数的运行时间。在3.11节中，我们将介绍一些一般性的技巧，用来在对普通递归函数的分析中求解这种递推关系。而现在，我们要通过特别手段来求解这些递推关系。

示例 3.24

我们来重新考虑一下2.7节中计算阶乘函数的递归程序。因为只涉及fact这一个函数，所以使用T(n)表示该函数未知的运行时间。我们将使用参数的值n作为参数的大小。显然，当参数为n 时进行的fact函数的递归调用，要使用更小的参数，准确地说是n-1。

我们选择n=1作为T(n)归纳定义的依据，因为当fact函数的参数为1时，它不执行任何递归调用。当n=1时，第(1)行的条件为真，因此对fact的调用会执行第(1)行和第(2)行。每一行花的时间都是O(1)，所以依据情况中fact的运行时间为O(1)。也就是说T(1)是O(1)。

现在考虑当n>1时会发生什么。第(1)行的条件为假，因此只执行第(1)行和第(3)行。第(1)行花的时间是O(1)，而第(3)行会在乘法和赋值上用掉O(1)，并在对fact的递归调用上花费T(n-1)。也就是说，当n>1时，fact的运行时间是O(1)+T(n-1)。因此可以用以下递推关系定义T(n)。

依据。 T(1)=O(1)。

归纳。对n>1，T(n)=O(1)+T(n-1)。

现在要引入一些常数符号来表示隐藏在各大O表达式中的常数，就像之前在规则(c)中表述的那样。在这种情况下，可以用某个常数a代替依据中的O(1)，并用某个常数b替代归纳中的O(1)。这些变化给了我们如下的递推关系。

依据。 T(1)=a。

归纳。对n>1，T(n)=b+T(n-1)。

现在必须求解T(n)的这一递推关系。我们很容易计算出靠前的一些值，由递推依据T(1)=a，

以及归纳规则，我们得到

T(2)=b+T(1)=a+b

继续使用归纳规则，就得到

T(3)=b+T(2)=b+(a+b)=a+2b

然后是

T(4)=b+T(3)=b+(a+2b)=a+3b

至此，不难猜测，对所有的n≥1，有T(n)=a+(n-1)b。其实，计算一些样本值，接着猜测解决方案，并最终通过归纳法证明猜测正确，这就是我们常用来处理递推关系的方法。

不过，在这个例子中，我们可以使用反复代换（repeated substitution）的方法直接得出解决方案。首先，在递归等式中进行如下变量代换，用m替换n，就得到

对m>1，T(m)=b+T(m-1)　　　　　　　　　　　　（3.3）

现在，可以用n、n-1、n-2、…、2替换等式(3.3)中的m，得到一系列的等式

　　(1) T(n)　=b+T(n-1)
　　(2) T(n-1)=b+T(n-2)
　　(3) T(n-2)=b+T(n-3)
　　　　　　　…
　 n-1) T(2)　=b+T(1)

接下来，可以利用上述系列等式中的第(2)行，来替换第(1)行中的T(n-1)，从而得到等式

T(n)=b+(b+T(n-2))=2b+T(n-2)

现在用第(3)行替换上式中的T(n-2)，就得到

T(n)=2b+(b+T(n-3))=3b+T(n-3)

按这种方式继续下去，每一次都将T(n)-i 替换为b+T(n-i-1)，直到向下达到T(1)。至此，就得到了等式

T(n)=(n-1)b+T(1)

接着可以利用依据，用a 替换T(1)，就可以得到T(n)=a+(n-1)b。

如果想让该分析过程更正式，就需要通过归纳法，对我们在反复对T(n-i )进行替换时的直观观察结果加以证明。因此，我们要通过对i 的归纳证明如下命题。

命题 S(i )。如果1≤i≤n，那么T(n)=ib+T(n-i)。

依据。依据为i=1，S(1)是说T(n)=b+T(n-1)。这是对T(n)的定义中的归纳部分，因此已知为真。

归纳。如果i≥n-1，就没什么要证明的，因为命题S(i+1)的开头是“如果1≤i+1≤n”，而当if语句的条件为假时，不管“那么”后面是如何表述的，该命题都为真。在这种情况下，若i≥n-1，则条件i+1<n一定为假。所以S(i+1)一定为真。

难点就在于，当i≤n-2的时候。在这种情况下，S(i )就是T(n)=ib+T(n-i )。因为i≤n-2，所以T(n-i )的参数至少为2。因此可以将该归纳规则应用到T上，也就是用n-i 替换等式(3.3)中的m，从而得出等式T(n-i )=b+T(n-i-1)。当我们用b+T(n-i-1)替换掉等式T(n)=ib+T(n-i )中的T(n-i )时，就得到T(n)=ib+(b+T(n-i-1))，重组这些项就得到

T(n)=(i+1)b+T(n-(i+1))

这个等式就是命题S(i+1)，而且我们现在已经证明了归纳步骤。

现在已经证明了T(n)=a+(n-1)b。不过，a和b都是未知的常数。因此，这样表示解决方案是不行的。不过，可以将T(n)表示为n的多项式，即bn+(a-b)，接着再用大O表达式来替代这些项，就得到了O(n)+O(1)。利用求和规则，还可以消掉O(1)，从而得出T(n)是O(n)。这就有意义了，它表示：要想计算n!，就要利用对fact的n次（实际调用次数刚好为n）调用的顺序，其中每次调用所需时间为O(1)，不计入花在执行对fact的递归调用上的时间。

习题

1. 为2.9节习题2中提到的sum函数（它是作为程序输入的表的长度的函数）的运行时间建立递推关系。请用（未知的）常数替换大O项，并试着求解这种递推关系。sum的运行时间是多少？

2. 对2.9节习题3中提到的find0函数重复习题1中的练习。合适的大小量度是什么？

3. * 对2.7节中图2-22所示的选择排序程序重复习题1中的练习。合适的大小量度是什么？

4. ** 对图3-24中的函数重复习题1中的练习，该函数是计算斐波那契数的（最开始的两个数是1，之后的每个数都是其前两个相邻数字之和。前7个斐波那契数分别是1、1、2、3、5、8、13）。请注意，n 的值是合适的参数大小，而且大家需要使用1和2作为依据情况。

int fibonacci(int n)
{
    if (n <= 2)
        return 1;
    else
        return fibonacci(n-1) + fibonacci(n-2);
}

图 3-24　计算斐波那契数的C语言函数

5. * 编写递归程序计算gcd(i,j)，就是两个整数i和j的最大公约数，如2.7节习题(8)中概述的那样。证明该程序的运行时间是O(logi)。提示：在我们调用gcd(m,n)两次后证明这一点（其中m≤i/2）。

3.10　归并排序的分析

我们现在要分析2.8节中介绍过的归并排序算法。首先要证明，merge函数和split函数在处理长度为n的表时，所花的时间都是O(n)；接着使用这些边界来证明MergeSort函数在处理长度为n的表时所花的时间为O(n logn)。

3.10.1　`merge`函数的分析

首先分析递归函数merge，我们在图3-25中再次展示了它的代码。merge函数参数大小n 的合适概念是表list1和list2的长度之和。因此，设T(n)是当参数表的长度之和为n 时merge函数所花的时间。我们可以拿n=1的情况作为依据情况，因此必须在list1和list2二者中有一个为空而另一个仅含一个元素的假设下对图3-25进行分析。有以下两种情况。

1. 如果第(1)行的测试（也就是list1等于NULL的测试）成功，我们就返回list2，这所花的时间为O(1)。第(2)行至第(7)行就不会执行。因此，整个函数调用所花的时间为测试第(1)行选择的O(1)和执行第(1)行赋值的O(1)，总共是O(1)。

2. 如果第(1)行的测试失败，就说明list1不为空。因为我们假设两个表的长度之和只是1，所以list2一定为空。因此，第(2)行的测试（即list2等于NULL的测试）一定会成功。那么我们就要花O(1)来执行第(1)行的测试，花O(1)执行第(2)行的测试，再花O(1)在第(2)行返回list1。第(3)行至第(7)行不会执行。所花的时间还是O(1)。

这样可以得出在依据情况中merge的运行时间为O(1)。

     LIST merge(LIST list1, LIST list2)
     {
(1)      if (list1 == NULL) return list2;
(2)      else if (list2 == NULL) return list1;
(3)      else if (list1->element <= list2->element) {
(4)          list1->next = merge(list1->next, list2);
(5)          return list1;
         }
         else { /* list2 的第一个元素更小 */
(6)          list2->next = merge(list1, list2->next);
(7)          return list2;
         }
     }

图 3-25　merge函数

现在来考虑归纳情况，也就是表长度之和大于1的情况。当然，即便长度之和为2或者更大，仍然可能有一个表为空。因此，嵌套的选择语句所表示的4种情况都可能发生。图3-25中程序的结构树如图3-26所示。我们可以从结构树的底部开始，向上分析该程序。

{%}

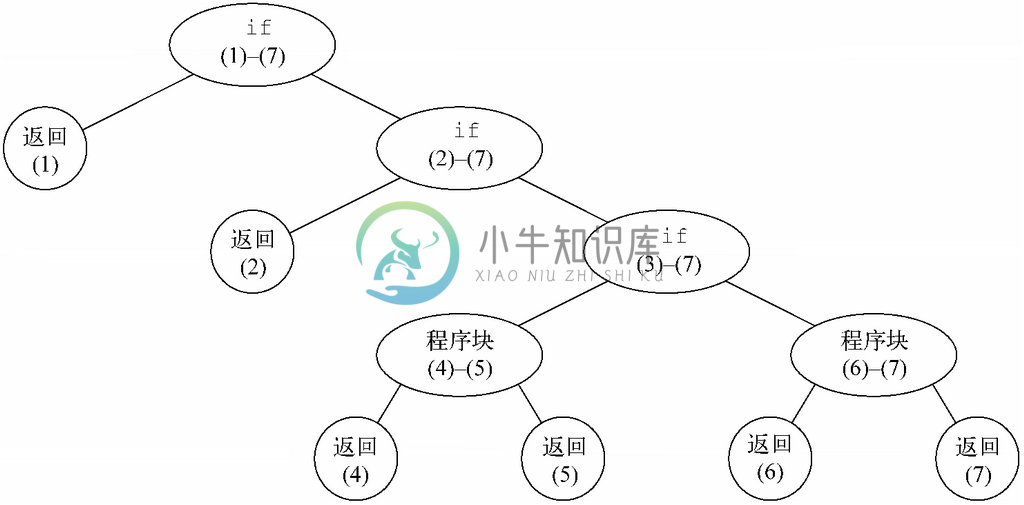
图 3-26　merge的结构

最内层的选择是从第(3)行的“if”开始的，我们在那里会测试哪个表的第一个元素更小，并根据测试的结果选择执行第(4)行和第(5)行，或执行第(6)行和第(7)行。第(3)行的条件需要花O(1)的时间来评估，第(5)行要花上O(1)来评估，而第(4)行所花的时间是O(1)加上递归调用merge所花的时间T(n-1)。请注意，n-1是递归调用的参数大小，因为我们已经从一个表中剔除了一个元素，并保持另一个表不变。因此第(4)行和第(5)行的程序块所花的时间为O(1)+T(n-1)。

对第(6)和第(7)行中else部分的分析是完全一样的：第(7)行所花时间为O(1)，而第(6)行所花时间为O(1)+T(n-1)。因此，在选取if部分和else部分运行时间的最大值时，会发现这两者其实是相同的。测试条件所花的时间O(1)可以忽略，因此可以得出结论：最内层选择的运行时间是O(1)+T(n-1)。

现在继续分析从第(2)行开始的选择。我们要在这一行测试list2是否等于NULL。测试条件的时间为O(1)，而if部分的时间（就是第(2)行的返回）也是O(1)。不过，else部分是第(3)行至第(7)行的选择语句，这部分语句的运行时间我们刚才确定过了，是O(1)+T(n-1)。因此，第(2)行至第(7)行的选择所花的时间为

O(1)+max(O(1),O(1)+T(n-1))

最大值中的第二项主导了第一项，也主导了测试条件所花的时间O(1)。因此，从第(2)行开始的if语句的运行时间也是O(1)+T(n-1)。

最后，要对最外层的if语句进行同样的分析。从根本上讲，对时间起主导作用的还是由第(2)行至第(7)行组成的else部分的时间。

递归的共通形式
很多极简单的递归函数（比如fact和merge）都会执行一些所需时间为O(1)的操作，然后对它们自己执行参数大小减小1的递归调用。假设依据情况花的时间为O(1)，可以看到这样的函数总能形成T(n)=O(1)+T(n-1)这样的递推关系。T(n)的解是O(n)，或者是参数大小的线性关系。在3.11节中我们还将看到对这一原则的一些概括。

也就是说，这些含递归调用的情况（比如第(4)行和第(5)行，或第(6)行和第(7)行）下的时间，主导了不含递归调用情况下的时间，还主导了第(1)、(2)和(3)行中所有3次测试的时间。因此，当n>1时，merge函数的运行时间上界就是O(1)+T(n-1)。因此可以得到用于定义T(n)的如下递推关系。

依据。T(1)=O(1)。

归纳。对n>1，T(n)=O(1)+T(n-1)。这些等式与示例3.24中为fact函数得出的那些等式如出一辙。因此，求解过程是相同的，可以得出T(n)是O(n)的结论。该结果从直观上讲是成立的，因为merge函数的工作原理就是花O(1)的时间从其中一个表里删除一个元素，然后对剩余的表递归地调用自身。这种递归调用遵循着递归调用的次数不大于表长度之和的原则。如果不考虑其递归调用所花时间，那么每次调用均耗时O(1)，如此就可以得出merge的运行时间将会是O(n)。

3.10.2　`split`函数的分析

现在来考虑一下split函数，我们在图3-27中再次展示了该函数。对split函数的分析和对merge函数的分析非常相似。我们令表的长度为参数的大小n，而且这里使用T(n)表示split函数处理长度为n的表所花的时间。

     LIST split(LIST list)
     {
         LIST pSecondCell;

(1)      if (list == NULL) return NULL;
(2)      else if (list->next == NULL) return NULL;
         else { /* 至少有两个单元 */
(3)          pSecondCell = list->next;
(4)          list->next = pSecondCell->next;
(5)          pSecondCell->next = split(pSecondCell->next);
(6)          return pSecondCell;
         }
     }

图 3-27　split函数

我们选取n=0和n=1作为依据。如果n=0，也就是说表为空，那么第(1)行的测试就会成功，而我们将在第(1)行返回NULL。第(2)行至第(6)行就不会执行。因此所花的时间为O(1)。如果n=1，也就是表只含一个元素，那么第(1)行的测试失败，不过第(2)行的测试成功。因此我们会在第(2)行返回NULL，而且不执行第(3)行至第(6)行。同样，这两条测试语句和一条返回语句只需要O(1)的时间。

接着考虑n>1时的归纳部分，这里存在3条选择分支，类似我们在分析merge函数时遇到的4条分支。简单来说，可以看出，第(1)行和第(2)行的测试不论是执行一个还是两者都执行，所花时间都是O(1)，正如我们最终为merge函数得出的结论那样。而且，如果这两个测试中有一个为真，就会致使我们在第(1)行或第(2)行返回的情况中，多花的时间也是O(1)。占主导的时间是两个测试均失败的情况，也就是表长度至少为2的情况。在这种情况下，第(3)行至第(6)行的语句都要执行。除了第(5)行的递归调用外，其他的内容所花的时间为O(1)。而递归调用的时间是T(n-2)，因为该参数表是list原来的值减去它的前两个元素（想知道原因，可以参考2.8节中的内容，特别是图2-28）。因此，归纳情况下的T(n)是O(1)+T(n-2)。

可以建立如下递推关系。

依据。T(0)=O(1)，且T(1)=O(1)。

归纳。对n>1，T(n)=O(1)+T(n-2)。

如示例3.24所述，接下来必须引入某些常数来表示隐藏在O(1)背后的比例常数。可以分别用常数a 和b 表示依据中T(0)和T(1)的O(1)，并用常数c 表示归纳步骤中的O(1)。因此，可以将上述递归定义重写为

依据。T(0)=a，且T(1)=b。

归纳。对n≥2，T(n)=c+T(n-2)。

我们先来求一下T(n)的前几个值。由依据，显然有T(0)=a和T(1)=b。可以使用归纳步骤得出

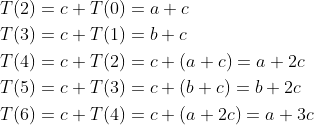
$\begin{align*}&T(2)=c+T(0)=a+c\\&T(3)=c+T(1)=b+c\\&T(4)=c+T(2)=c+(a+c)=a+2c\\&T(5)=c+T(3)=c+(b+c)=b+2c\\&T(6)=c+T(4)=c+(a+2c)=a+3c\end{align*}$

对T(n)的计算其实是两部分单独的计算，一部分是n为奇数的情况，一部分是n为偶数的情况。对偶数n，我们有T(n)=a+cn/2。这是可行的，因为对长度为偶数的表，剔除两个元素所花的时间为c，而且在经过n/2次递归调用后，就会得到不再对其进行递归调用而且所花时间为a 的空表。

对奇数长度的表来说，还是要花时间c 来剔除两个元素的。在经过(n-1)/2次调用后，我们得到了一个长度为1的表，而且需要的时间为b。因此，奇数长度的表所需的时间将是b+c(n-1)/2。

对这些观察结果的归纳证明与示例3.24中的证明过程非常近似，就是要证明如下命题。

命题S(i )。如果1≤i≤n/2，那么T(n)=ic+T(n-2i)。

在该命题的证明过程中，我们使用T(n)定义中的归纳规则，用参数m将其重写为

对　　　　　　　　　　　m≥2， T(m)=c+T(m-2)　　　　　　　　　　　(3.4)

接着就可以按照如下方式用归纳法证明S(i )了。

依据。依据是i=1，也就是用n 替代m 后的等式(3.4)。

归纳。因为S(i )是“如果……那么……”的形式，所以若i≥n/2，则S(i+1)恒为真。因此，若i≥n/2，我们就不需要对归纳步骤（即由S(i )可得到S(i+1)）加以证明。

难点是当1≤i≤n/2时。在这种情况下，假定归纳假设S(i)为真，即T(n)=ic+T(n-2i)。用n-2i替换(3.4)中的m，就得到

T(n-2i)=c+T(n-2i-2)

如果替换S(i )中的T(n-2i )，就得到

T(n)=ic+(c+T(n-2i-2))

如果对等式右边的项加以组合，就有

T(n)=(i+1)c+T(n-2(i+1))

这就是命题S(i+1)。因此我们证明了归纳步骤，而且得出T(n)=ic+T(n-2i)。

现在，若n为偶数，则令i=n/2。则S(n/2)就表示T(n)=cn/2+T(0)，也就是a+cn/2。如果n为奇数，就令i=(n-1)/2。S((n-1)/2)就表示T(n)=c(n-1)/2+T(1)，也就等于b+c(n-1)/2，因为有T(1)=b。

最后，必须将特定于编译器和机器的常数a、b和c改写为大O表示。多项式a+cn/2和b+c(n-1)/2都具有与n成比例的高阶项。因此，该问题中不论n是奇数还是偶数其实是没关系的，两种情况下split的运行时间都是O(n)。这又是个很直观的正确解答，因为对长度为n的表来说，split会进行约n/2次递归调用，每次调用的时间都是O(1)。

3.10.3　`MergeSort`函数

最后要介绍一下MergeSort函数，我们在图3-28中再次展示了该函数。对参数大小的合适量度n还是待排序表的长度。在这里，我们要使用T(n)表示MergeSort处理长度为n的表的运行时间。

我们选取n=1的情况作为依据情况，而n>1（发生递归调用）的情况则作为归纳情况。如果对MergeSort加以研究，就会发现，除非从另一个函数中调用参数为空表的MergeSort，不然是没办法在参数为空表的情况下进行调用的。原因在于，只有当表中至少具有两个元素时也就是分拆后得到的两个表中都至少有一个元素时，才会执行第(4)行。因此可以忽略n=0的情况，并直接从n=1开始进行归纳证明。

     LIST MergeSort(LIST list)
     {
         LIST SecondList;

(1)      if (list == NULL) return NULL;
(2)      else if (list->next == NULL) return list;
         else {
             /* 表中至少有两个元素 */
(3)          SecondList = split(list);
(4)          return merge(MergeSort(list), MergeSort(SecondList));
         }
     }

图 3-28　归并排序算法

依据。如果list由一个元素构成，就会执行第(1)行和第(2)行，而不执行其他代码。因此，在依据情况中，T(1)是O(1)。

归纳。在归纳情况中，第(1)行和第(2)行的测试都是失败的，因此可以执行第(3)行和第(4)行的程序块。为了简化问题，可以假设n是2的乘方。作出这种假设的好处在于，当n为偶数时，刚好会将表分割成长度为n/2的两等分。此外，如果n是2的乘方，那么n/2也是2的乘方，每次递归结束二分出来的都是等分的表，直到每个表中只含一个元素为止。当n>1时，MergeSort所花的时间为下列各项之和。

1. 两次测试所花的O(1)。

2. 第(3)行的赋值和对split的调用所花的O(1)??O(n)。

3. 第(4)行对MergeSort第1次递归调用所花的T(n/2)。

4. 第(4)行对MergeSort第2次递归调用所花的T(n/2)。

5. 第(4)行调用merge所花的O(n)。

6. 第(4)行的返回语句所花的O(1)。

跳过某些值的归纳法
读者不应该为MergeSort函数的分析中涉及的新型归纳法感到担心，尽管在证明过程中我们跳过了除2的乘方之外的所有数值。一般情况下，如果i₁、i₂、…是一列与我们想证明的命题S有关的整数，就可以证明S(i₁)作为依据，并对所有的j证明，S(i₁)可推出S(i_j+1)。这就是一般情况下我们所认为的对j 进行归纳的归纳证明。更精确地说，由S' (j )=S(i_j )定义命题S'。然后通过对j 的归纳证明S' (j )。这样的话，就可以是i₁=1、i₂=2、i₃=4，而一般形式就是i_j=2^j-1。
顺便提一句，请注意，MergeSort的运行时间T(n)不会随着n的增加而减少。因此，证明了对等于2的乘方的n有T(n)是O(n logn)，也就证明了对所有的n都有T(n)是O(n logn)。

如果将这些项加起来，然后依据调用split和merge的O(n)更大而舍弃O(1)，就可以得出在归纳情况中，MergeSort的运行时间边界是2T(n/2)+O(n)。因此得到以下递推关系。

依据。T(1)=O(1)。

归纳。T(n)=2T(n/2)+O(n)，其中n是2的乘方而且大于1。

下一步是要用含具体常数的函数代替大O表达式。我们在依据中用常数a代替O(1)，并在归纳步骤中用bn代替O(n)，因此递推关系就变形为

依据。T(1)=a。

归纳。T(n)=2T(n/2)+bn，其中n是2的乘方而且大于1。

这一递推关系要比我们之前了解的更难，不过我们还是可以利用相同的技巧。首先，可以为一些较小的n值直接写出O(n)的值。依据说明了T(1)=a，而归纳步骤则告诉我们

T(2)　　= 2T(1) + 2b　　　　　　　　　　　　　= 2a + 2b
T(4)　　= 2T(2) + 4b　　= 2(2a + 2b) + 4b　　= 4a + 8b
T(8)　　= 2T(4) + 8b　　= 2(4a + 8b) + 8b　　= 8a + 24b
T(16) 　= 2T(8) + 16b　 = 2(8a + 24b) + 16b　= 16a + 64b

想直接看出接下来的情况可不容易。显然，a 的系数与n 的值是同步的，也就是说T(n)是n 乘上a，再加上某个数量的b。不过b 的系数要比n 增长得更快。b 的系数与n 之间的关系可以归纳为如下：

n 的值	2	4	8	16
b 的系数	2	8	24	64
比率	1	2	3	4

比率是用系数b 除以n 的值得到的。因此，看起来b 的系数是n 乘上n 每次翻倍便会增长1的另一个因子。具体来讲，我们可以看出这个比率是log₂n，因为log₂2=1，log₂4=2，log₂8=3，且log₂16=4。因此推测递推关系的解为T(n)=an+bn log₂n是合理的，至少对表示2的乘方的n来说如此。我们将看到该公式是正确的。

要为该递推关系求解，先遵从前面的示例中使用过的策略。我们将归纳规则写成参数m的函数，形如

对m为2的乘方且m>1，　　　　　　　　T(m)=2T(m/2)+bm　　　　　　　　(3.5)

接着可以从T(n)开始，利用(3.5)，用具有较小参数的表达式来代替T(n)，在这种情况下，要替换的表达式是关于T(n/2)的。也就是，首先有

T(n)=2T(n/2)+bn　　　　　　(3.6)

接下来，利用(3.5)，将m替换为n/2，从而得到替换(3.6)中T(n/2)的表达式。也就是，(3.5)说明有T(n/2)=2T(n/4)+bn/2，而我们可以将(3.6)替换为

T(n)=2(2T(n/4)+bn/2)+bn=4T(n/4)+2bn

然后，可以用n/4代替(3.5)中的m，从而将T(n/4)替换为2T(n/8)+bn/4，从而得到

T(n)=4(2T(n/8)+bn/4)+2bn=8T(n/8)+3bn

我们要通过对i的归纳证明的命题就是

命题S(i )。如果1≤n≤log₂n，那么T(n)=2ⁱT(n/2ⁱ )+ibn。

依据。对i=1，命题S(1)就是说T(n)=2T(n/2)+bn。这个等式是对归并排序运行时间T(n)的定义中的归纳规则，因此可知依据是成立的。

归纳。就像那些归纳假设是“如果……那么……”形式的归纳证明一样，如果i 在假设范围之外，那么归纳步骤必定成立，这里，i≥log₂n 时就是这种简单的情况，这时S(i+1)显然成立。

再来看看困难的情况，假设i<log₂n。还要假定归纳假设S(i )成立，就是T(n)=2ⁱT(n/2ⁱ )+ibn。用n/2ⁱ 替换(3.5)中的m，就得到

T(n/2ⁱ )=2T(n/2ⁱ⁺¹)+bn/2ⁱ　　　　　　(3.7)

用(3.7)的右边替换S(i )中的T(n/2ⁱ )，就得到

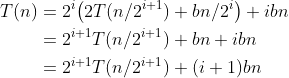
$\begin{align*}T(n)&=2^i\bigl(2T(n/2^{i+1})+bn/2^i\bigr)+ibn\\&=2^{i+1}T(n/2^{i+1})+bn+ibn\\&=2^{i+1}T(n/2^{i+1})+(i+1)bn\end{align*}$

最终的等式就是命题S(i+1)，这样就证明了归纳步骤。

于是可以得出S(i )，也就是T(n)=2ⁱT(n/2ⁱ )+ibn对在1和log₂n之间的任意i 都是成立的。现在要考虑公式S(log₂n)，也就是

T(n)=2^log₂nT(n/2^log₂n)+(log₂n)bn

我们知道2^log₂n=n（请回想一下，log₂n 的定义就是，使2变为n，要对2乘方的次数）。还有n/2^log₂n=1。因此S(log₂n)可以写为

T(n)=nT(1)=bn log₂n

由T 的定义中的依据，还知道T(1)=a。因此，

T(n)=an+bn log₂n

在经过这段分析后，必须将常数a 和b 替换为大O表达式，即T(n)是O(n)+O(n logn)。8因为n 比n logn增长得更慢，所以可以忽略O(n)这项，直接说T(n)是O(n logn)。也就是说，归并排序算法的时间量级是O(n logn)。请记住，我们已经证明了选择排序的运行时间是O(n²)。虽然严格地讲，这里的O(n²)只是个上界，但是它其实是选择排序的最紧简单边界。因此，可以确定，随着n不断变大，归并排序要一直比选择排序运行得更快。从实践上讲，对值大于几十的n来说，归并排序要比选择排序更快。

8请记住，在大O表达式中，我们不必为对数指定底数，因为这里的对数是在常数因子中，所以所有底数的对数都是一样的。

3.10.4　习题

1. 绘出下列函数的结构树。

(a) split

(b) MergeSort

2. * 将k 路归并排序函数定义为把一个表分为k 部分，在为每部分排序后合并各部分得到结果。

(a) 用k 和n 的函数表示的k 路归并的运行时间是怎样的？

(b) **什么样的k 值可以带来最快的算法（用n 的函数表示）？这个问题要求大家对运行时间作出足够精确的估算，从而保证自己可以区分一些常数因子。出于我们在本章开头所讨论过的原因，在实践中不可能那样精确，所以大家需要研究一下由习题(a)中得到的运行时间是怎样随着k 变化的，并据此得出近似的最小值。

3.11　为递推关系求解

求解递推关系的技巧有很多。本节将讨论两种方法。第一，就是我们已经看到的，反复将递归规则代换到它们自身中，直到得出T(n)与T(1)的关系，或者T(n)与依据给出的某个T(i )之间的关系（如果1不是依据的话）。第二种方法是猜测一种解，并将其替换到依据和归纳规则中以验证其正确性。

在3.9和3.10两节中，我们已经为T(n)准确求解了。不过，因为T(n)实际上是确切运行时间的大O上界，所以找出T(n)的紧上界就够了。因此，特别是对于“猜测并验证”的方法，只需要求出的解是递推关系真正解的上界就可以了。

3.11.1　通过反复代换为递推关系求解

示例3.24所示的递推关系可能是我们在实践中遇到的最简单的递推关系了。

依据。T(1)=a。

归纳。对n>1，T(n)=T(n-1)+b。

如果可以在归纳中将常数b换成某个函数g(n)，就可以将这种形式进一步一般化，于是我们可以将这种形式写成下面这样。

依据。T(1)=a。

归纳。对n>1，T(n)=T(n-1)+g(n)。

只要递归函数花了时间g(n)，并接着用比当前函数调用所使用的参数小1的参数调用自身，就出现了这种形式。例子有示例3.24中的阶乘函数、3.10节中的merge函数，以及2.7节中的递归选择排序。在前两个函数中，g(n)是常数，而在第三个函数中，g(n)是n 的线性函数。3.10节中的split函数也基本是这种形式，只不过它递归地调用自身所使用的参数是依次减小2的。我们应该明白，这种差别是不重要的。

接下来通过反复代换来求解该递推关系。正如示例3.24中那样，首先将归纳规则用参数m的函数表示出来，即

T(m)=T(m-1)+g(m)

接着反复替换原归纳规则右边的T。这样做，就可以得到一串表达式：

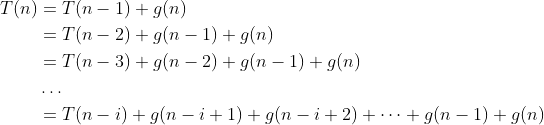
$\begin{align*}T(n)&=T(n-1)+g(n)\\&=T(n-2)+g(n-1)+g(n)\\&=T(n-3)+g(n-2)+g(n-1)+g(n)\\&\dots\\&=T(n-i)+g(n-i+1)+g(n-i+2)+\dots+g(n-1)+g(n)\end{align*}$

运用示例3.24中介绍的技巧，就可以通过对i的归纳，证明对i=1、2、…、n-1，有

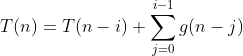
$T(n)=T(n-i)+\sum^{i-1}_{j=0}g(n-j)$

我们希望选择一个i值，让依据情况可以涵盖T(n-i )，因此我们选择i=n-1。因为T(1)=a，所以有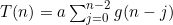 $T(n)=a\sum^{n-2}_{j=0}g(n-j)$ 。换句话说，T(n)就是常数a加上从2到n 的所有g之和，或者说是a+g(2)+g(3)+…+g(n)。除非所有的g(j )都为0，否则在将该表达式转换为大O表达式时，a这项都是无关轻重的，因此一般只需要g(j )的和就行了。

示例 3.25

考虑一下图2-22所示的递归选择排序函数，我们在图3-29中重新展示了该函数的函数体。在需要为含m个元素的数组排序时，也就是当参数i的值为n-m时，如果设SelectionSort函数的运行时间为T(m)，那么就可以得出关于T(m)的如下递推关系。首先，依据是m=1。这时，只有第(1)行执行，花的时间为O(1)。

(1)      if (i < n-1) {
(2)              small = i;
(3)              for (j = i+1; j < n; j++)
(4)                  if (A[j] < A[small])
(5)                      small = j;
(6)              temp = A[small];
(7)              A[small] = A[i];
(8)              A[i] = temp;
(9)              recSS(A, i+1, n);
             }
     }

图 3-29　递归的选择排序

对m>1时的归纳，我们会执行第(1)行的测试以及第(2)、(6)、(7)、(8)行的赋值，这些语句的运行时间是O(1)。而第(3)至第(5)行的for循环的运行时间为O(n-i )，或者O(m)，就像我们在示例3.17中讨论过的迭代选择排序程序那样。要知道原因，请注意第(4)行和第(5)行的循环体所花的时间为O(1)，而我们要进行m-1次循环。所以，该for循环的运行时间主导了第(1)至第(8)行的运行时间，这样就可以将整个函数的运行时间T(m)写为T(m-1)+O(m)。第2项O(m)覆盖了第(1)至第(8)行，而T(m-1)这项则是第(9)行的递归调用的时间。如果将隐藏在大O表达式背后的常数因子替换为某个具体的常数，就可以得到以下递推关系。

依据。T(1)=a。

归纳。对m>1，T(m)=T(m-1)+bm。

该递推关系具有我们研究过的形式，其中g(m)=b(m)。也就是说，该递推关系的解为

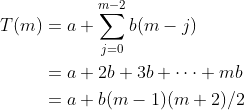
$\begin{align*}T(m)&=a+\sum^{m-2}_{j=0}b(m-j)\\&=a+2b+3b+\dots+mb\\&=a+b(m-1)(m+2)/2\end{align*}$

因此T(m)是O(m²)。我们感兴趣的是SelectionSort函数处理长度为n的整个数组时的运行时间，也就是说，当用i=1调用函数时，我们需要T(n)的表达式，并得出它是O(n²)。因此，递归的选择排序是二次的，就像迭代的选择排序那样。

递推的另一种常见形式是在3.10节中为MergeSort函数得出的递推关系。

依据。T(1)=a。

归纳。T(n)=2T(n/2)+g(n)，其中n是2的乘方而且大于1。

该递推关系表示的是一个递归算法，它通过将大小为n 的问题细分为两个大小为n/2的子问题来解决问题。这里g(n)是创建子问题以及结合解决方案所花的时间。例如，MergeSort将大小为n的问题分为大小为n/2的两个部分。函数g(n)具有bn 的形式，其中b是某个常数，因为MergeSort除了递归调用自身之外，所花的时间是O(n)，主要就是用在split和merge算法上。

要求解该递推关系，需要替换等式右边的T。这里我们假设对某个k 有n=2^k。递推关系可以写为参数为m 的函数：T(m)=2t(m/2)+g(m)。如果用n/2ⁱ 替换m，就得到

T(n/2ⁱ )=2T(n/2ⁱ⁺¹)+g(n/2ⁱ )　　　　　　(3.8)

如果由归纳规则开始，接着用i 值逐渐变大的(3.8)替换T，就会发现

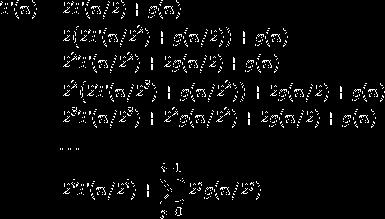
$\begin{align*}T(n)&=2T(n/2)+g(n)\\&=2\bigl(2T(n/2^2)+g(n/2)\bigr)+g(n)\\&=2^2T(n/2^2)+2g(n/2)+g(n)\\&=2^2\bigl(2T(n/2^3)+g(n/2^2)\bigr)+2g(n/2)+g(n)\\&=2^3T(n/2^3)+2^2g(n/2^2)+2g(n/2)+g(n)\\&\quad\dots\\&=2^iT(n/2^i)+\sum^{i-1}_{j=0}2^jg(n/2^j)\\\end{align*}$

如果n=2^k，我们知道T(n/2^k)=T(1)=a。因此，当i=k时，也就是当i=log₂n 时，可以得到递推关系的解为

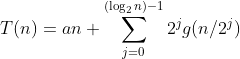$T(n)=an+\sum^{(\log_2n)-1}_{j=0}2^jg(n/2^j)$ 　　　　　　(3.9)

直观地讲，(3.9)的第一项表示依据值a 带来的时间，也就是以大小为1的参数调用该递归函数n 次的时间。而和项则是递归所花的时间，它表示以大小大于1的参数执行的所有调用的总时间。图3-30展示了MergeSort函数执行期间的时间积累情况。它表示为8个元素排序的时间。

第一行表示最外层的调用，涉及全部8个元素；第二行表示对两组4个元素的两次调用；第三行表示对4组两个元素的4次调用。最后，底部那行表示对长度为1的表调用MergeSort共8次。一般来说，如果原始无序表中有n个元素，那么通过引发其他调用的MergeSort调用完成bn 的工作就需要log₂n层调用，因此这些调用累计的时间就是bn log₂n。还将有一层的调用不会引起进一步的调用，这些调用所花的总时间是an。请注意，前log₂n层调用表示的是(3.9)中的和项，而最下面的那层表示an那项。

{%}

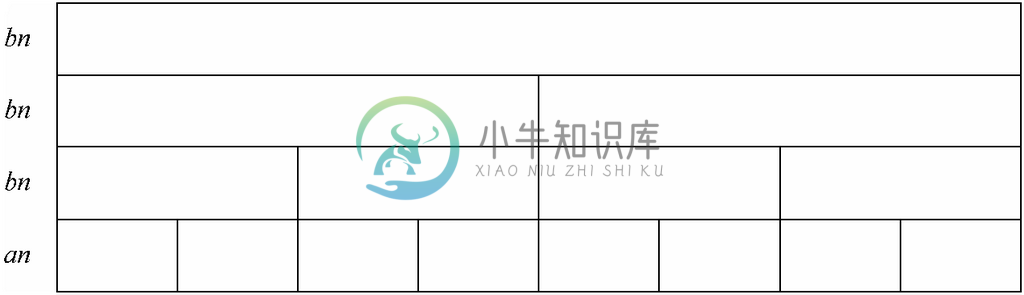
图 3-30　对MergeSort的调用所花的时间

示例 3.26

在MergeSort的情况中，函数g(n)是bn，其中b是某个常数。因此含这些参数的(3.9)的解就是

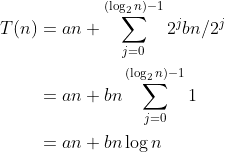
$\begin{align*}T(n)&=an+\sum^{(\log_2n)-1}_{j=0}2^jbn/2^j\\&=an+bn\sum^{(\log_2n)-1}_{j=0}1\\&=an+bn\log{n}\end{align*}$

最后得出的等式是因为和项中有log₂n个项，而这些项都是1。因此，当g(n)是线性函数时，式(3.9)的解就是O(n logn)。

3.11.2　通过猜测解为递推关系求解

求解递推关系的另一种实用方法就是猜测一个解f (n)，接着使用递推关系证明T(n)≤f (n)。这可能不会给出T(n)的精确值，不过如果它给出了紧上界，也是能令人满意的。通常我们只会猜测f (n)这样的函数形式，不去指定一些参数。例如，我们可以猜测对某a和b，f (n)=an^b。这些参数的值都是确定的，因为我们要为所有n证明T(n)≤f (n)。

虽然可能觉得能准确猜测解是件离奇的事，但我们经常能通过观察一些较小n 值所对应的T(n)来推断出高阶项。然后就可以舍弃某些低阶项，并看看它们的系数是否非0。9

9要知道，与递推关系理论很类似的微分方程理论也依赖于一些常见形式的方程的已知解，并据此通过合理的猜测求解其他方程。

示例 3.27

我们再来研究一下3.10节中介绍过的MergeSort递推关系，将其写为

依据。T(1)=a。

归纳。T(n)=2T(n/2)+g(n)，其中n是2的乘方而且大于1。

我们要猜测T(n)的上界是f(n)=cn log₂n+d，其中c 和d 是某些常数。回想一下，这种形式并不完全正确，在之前的示例中，我们得出的解都具有O(n logn)项以及O(n)项，而不带常数项。不过，这个猜测对证明O(n logn)是T(n)的上界来说已经足够好了。

接着要对n进行完全归纳，证明以下命题，其中c 和d 是某些常数。

命题S(n)。如果n是2的乘方而且n≥1，那么T(n)≤f (n)，其中f (n)是函数cn log₂n+d。

依据。当n=1时，T(1)≤f (1)表示a≤d，因为当n=1时，f (n)中cn log₂n这项的值为0，则f (1)=d，而且之前已经给定了T(1)=a。

归纳。对所有的i< n，假设S(i )为真，并证明对某些n>1，S(n)为真。如果n不是2的乘方，就没什么好证明的，因为这时具有“如果……那么……”形式的命题S(n)的如果部分不为真。因此，考虑困难的情况，也就是n是2的乘方的情况。可以假设S(n/2)为真，也就是假设

T(n/2)≤(cn/2)log₂(n/2)+d

因为它是归纳假设的一部分。对归纳步骤来说，需要证明

T(n)≤f(n)=cn log₂n+d

当n≥2时，T(n)定义的归纳部分告诉我们

T(n)≤2T(n/2)+bn

将归纳假设应用到T(n/2)的边界，就有

T(n)≤2[c(n/2)log₂(n/2)+d]+bn

因为log₂(n/2)=log₂n-log₂2=log₂n-1，所以可以将这一表达式简化为

T(n)≤cn log₂n+(b-c)n+2d　　　　　　(3.10)

现在要证明T(n)≤cn log₂n+d，条件是(3.10)右边的式子中，cn log₂n+d之外的部分最多为0，也就是说(b-c)n+d≤0。因为n>1，所以当d≥0且b-c≤-d时该不等式成立。

要让f(n)=cn log₂n+d成为T(n)的上界，需要满足以下3条约束。

1. 约束a≤d 来自依据部分。

2. d>0来自归纳部分，不过因为已知a>0，所以由(1)便可得到该不等式。

3. b-c≤-d，或者说c≥b+d，也是来自归纳部分。

如果令d=a而且c=a+b，那么这些约束显然可得到满足。我们现在就通过对n 的归纳证明了，对所有大于等于1且为2的乘方的n，有

T(n)≤(a+b)n log₂n+a

该参数表明了T(n)是O(n logn)，也就是说T(n)的增长速度不会比n logn 快。不过，我们得到的边界(a+b)n log₂n+a要比示例3.26中得到的确切解答bn log₂n+an 稍大一些，但至少是成功得到了边界。假使我们选择了更简单的猜测f (n)=cn log₂n，可能就失败了，因为不存在可以使f (1)≥a的c值。原因在于，c×1×log₂1=0，这样就有f (1)=0。如果a>0，就显然不能使f (1)≥a。

不等式的处理
示例3.27中的不等式T(n)≤cn log₂n+d，是从另一个不等式T(n)≤cn log₂n+(b-c)n+2d 得出的。方法是找出“多余的量”，并要求它至多为0。一般的原则是，假设有不等式A≤B+E，那么如果要证明A≤B，只需要证明E≤0就够了。在示例.27中，A是T(n)，B是cn log₂n+d，而那个“多余的量”是(b-c)n+d。

示例 3.28

现在考虑的是在本书后续内容中将要遇到的一个递推关系。

依据。G(1)=3。

归纳。对n>1，G(n)=(2^n/2+1)G(n/2)。

该递推关系包含的是实际的数字，而不是像a这样的符号常数。在第13章中，我们将使用这样的递推关系计算电路中门的数量，而且门的数量是可以准确计出的，不需要用大O表示法去隐藏不可知的常数因子。

如果我们考虑一下通过反复代换得到的解，就可能发现，要将G(n)用含G(1)的项表示出来，需要进行log₂(n-1)次代换。随着代换的不断进行，就会得到因子

(2^n/2+1)(2^n/4+1)(2^n/8+1)…(2¹+1)

如果舍去每个因子中的“+1”项，就会近似地得出积2^n/22^n/42^n/8…2¹，也就是

2^{n/2++n/4+n/8+…+1}

或者如果为指数部分的几何级数求和，就是2^n-1，也就是2ⁿ的一半，因此可以猜测，2ⁿ是解G(n)中的项。不过，如果猜测f(n)=c 2ⁿ是G(n)的上界，就可能会求解失败，读者可以自行验证。也就是说，我们得到了两个涉及c的不等式，但它们不是解。

因此我们会猜测下一种最简单的形式，f(n)=c 2ⁿ+d，而这样就能成功求解了。也就是说，可以通过对n的完全归纳证明以下命题，其中c 和d 是某些常数。

命题 S(n)。如果n是2的乘方且n≥1，那么G(n)≤c 2ⁿ+d。

依据。如果n=1，那么必须证明G(1)≤c 2¹+d，也就是3≤2c+d。该不等式变成了对c 和d 的约束。

归纳。像示例3.27那样，唯一的难点出现在当n为2的乘方而且要从S(n/2)证明S(n)时。这种情况下等式就成了

G(n/2)≤c 2^n/2+d

必须证明S(n)，也就是G(n)≤ c 2ⁿ+d。首先从G的归纳定义开始。

G(n)=(2^n/2+1)G(n/2)

然后用得到的上界替换G(n/2)，就将上述表达式转换成了

G(n)≤(2^n/2+1)(c 2^n/2+d)

加以简化，就得到

G(n)≤c 2ⁿ+(c+d)2^n/2+d

这要给出所需的G(n)的上界c 2ⁿ+d，因此就要有右侧多余的部分(c+d)2^n/2不大于0，而这只需有c+d≤0就足够了。

我们需要选择c 和d 来满足两个不等式。

1. 源于依据部分的2c+d≥3。

2. 源于归纳部分的c+d≤0。

例如，如果c=3且d=-3，则两个不等式都能满足。那么我们就知道G(n)≤3(2ⁿ-1)。因此，G(n)是随着n指数增长的。刚好这个函数就是确切的解，也就是说G(n)=3(2ⁿ-1)，读者可以自己通过对n的归纳来证明这一点。

对解的总结
下面的表格中列出了一些最常见的递推关系，其中包括本节未曾介绍的。在每种情况中，假设依据等式为T(1)=a，而且有k>0。
归纳等式
T(n)
T(n)=T(n-1)+bn^k
O(n^k+1)
T(n)=cT(n-1)+bn^k其中c>1
O(cⁿ)
T(n)=cT(n/d)+bn^k其中c>d^k
O(n^log_dc)
T(n)=cT(n/d)+bn^k其中c< d^k
O(n^k)
T(n)=cT(n/d)+bn^k其中c=d^k
O(n^k logn)
若上述等式中的bn^k 被替换为任意的k 次多项式，其结论也都是成立的。

归纳等式	T(n)
T(n)=T(n-1)+bn^k	O(n^k+1)
T(n)=cT(n-1)+bn^k其中c>1	O(cⁿ)
T(n)=cT(n/d)+bn^k其中c>d^k	O(n^log_dc)
T(n)=cT(n/d)+bn^k其中c< d^k	O(n^k)
T(n)=cT(n/d)+bn^k其中c=d^k	O(n^k logn)

3.11.3　习题

1. 设T(n)是由如下递推关系定义的

对n>1，T(n)=T(n-1)+g(n)

通过对i的归纳证明，如果1≤i≤n，那么

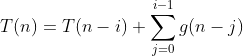
$T(n)=T(n-i)+\sum^{i-1}_{j=0}g(n-j)$

2. 假设有如下形式的递推关系

T(1)=a

对n>1，T(n)=T(n-1)+g(n)

如果g(n)分别是

(a) n²

(b) n²+3n

(d) nlogn

(e) 2ⁿ

给出解的紧大O上界。

3. 假设有如下形式的递推关系

T(1)=a

当n是2的乘方且n>1时，T(n)=T(n/2)+g(n)

如果g(n)分别是

(a) n²

(b) 2n

(d) nlogn

(e) 2ⁿ

给出解的紧大O上界。

4. *将下列各项作为如下递推关系的解进行猜测。

T(1)=a

当n是2的乘方且n>1时，T(n)=2T(n/2)+bn

(a) cn log₂n+dn+e

(b) cn+d

这暗示了未知常数c、d 和e 所具有的哪些约束？对哪些形式而言，存在T(n)的上界？

5. 证明：如果我们为示例3.28中的递推关系猜测G(n)≤c 2ⁿ，那么将没法找到解。

6. * 证明：如果

T(1)=a

对n>1，T(n)=T(n-1)+n^k

那么T(n)是O(n^k)。大家可以假设k≥0。证明这是T(n)的最紧简单大O上界，也就是说，如果m< k+1，T(n)就不是O(n^m)了。提示：用T(n-i)（其中i=1、2、…）展开T(n)，从而得到上界。要得到下界，就要证明对某个特定的c>0而言，T(n)至少是cn^k+1。

7. ** 证明：如果

T(1)=a

对n>1，T(n)=cT(n-1)+P(n)

其中p(n)是n的任意多项式且c>1，那么T(n)是O(cⁿ)。还有，证明这是最紧简单大O上界，也就是说，如果d< c，那么T(n)不是O(d^m)。

8. ** 考虑递推关系

T(1)=a

当n是d的乘方时，T(n)=cT(n/d)+bn^k

用T(n/dⁱ)（其中i=1、2、…）迭代地展开T(n)，证明

(a) 如果c>d^k，那么T(n)是O(n^log_dc)

(b) 如果c=d^k，那么T(n)是O(n^k logn)

9. 求解以下递推关系，其中每个关系都有T(1)=a。

(a) 当n是2的乘方且n>1时，T(n)=3T(n/2)+n²

(b) 当n是3的乘方且n>1时，T(n)=10T(n/3)+n²

可能会用到习题(8)中的解答。

10. 求解递推关系

T(1)=a

当n是2的乘方且n>1时，T(n)=3ⁿT(n/2)

11. 斐波那契递推关系是F(0)=F(1)=1，且

对n>1，F(n)=F(n-1)+F(n-2)

来自该数列的值F(0)、F(1)、F(2)…就是斐波那契数，其中从第3个数起，每个数都是相邻前两个数的和，见3.9节习题(4)。设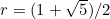 $r=(1+\sqrt{5})/2$ ，该常数r称为黄金比例，而且其值约为1.62。证明：F(n)是O(rⁿ)。提示：对于归纳部分，可以猜测对某个n有F(n)≤arⁿ，并尝试通过对n的归纳证明该不等式。依据必须是由n=0和n=1这两个值组成。在归纳步骤中，可以注意到r满足r²=r+1这一关系。

3.12　小结

以下是本章涵盖的一些重点概念。

许多因素会对程序算法的选择产生影响，不过通常简单、易于实现和高效起主导作用。
大O表达式提供了一种很方便的程序运行时间上界表示法。
在评估C语言复合语句（比如for循环和条件语句）的运行时间时，存在一些递归规则，这些规则是用这些复合语句各组成部分的运行时间表示的。
通过绘制表示语句嵌套结构的结构树，并按照从下至上的顺序评估结构树中各部分的运行时间，可以评估函数的运行时间。
递推关系是为递归程序运行时间建模的一种自然方法。
要为递推关系求解，既可以通过反复代换，也可以通过先猜测解并验证猜测为正确的方式。

分治法是一种重要的算法设计技巧。使用分治法时会将问题分为若干个子问题，这些子问题的解答将会组合成整个问题的解答。可根据一些经验法则来评估由此产生的算法（运行时间为O(1)，且对大小为n-1的子问题调用自身所花时间为O(n)）的运行时间。这种算法的例子包括阶乘函数和merge函数。

更为一般的情况是，函数花的时间为O(n^k)，而且对大小为n-1的子问题调用自身花的时间是O(n^k+1)。
如果函数调用自身两次，而递归行进了log₂n层（就像归并排序那样），那么总运行时间就是O(n logn)乘上每次调用的开销，再加上O(n)乘上依据部分的开销。在归并排序中，包括依据调用在内，每次调用的开销都是O(1)，所以总运行时间就是O(n logn)+O(n)，或者是O(n logn)。
如果函数调用自身两次，而递归行进了n层，就像3.9节习题(4)的斐波那契程序那样，那么运行时间就是指数为n的指数形式。

3.13　参考文献

对程序运行时间及问题计算复杂度的研究始于Hartmanis and Stearns [1964]。Knuth [1968]

这本书使算法运行时间的研究成为了计算机科学的重要部分。自那时起，大量有关问题难度的理论涌现出来。其中很多关键的概念都能在Aho, Hopcroft, and Ullman [1974, 1983]中找到。在本章中，我们将精力都集中在了程序运行时间的上界上。而 Knuth [1976]则描述了类似的下界表示法以及运行时间的精确边界。

要了解更多有关分治法这种算法设计技巧的讨论，请参考Aho, Hopcroft, and Ullman [1974] 或Borodin and Munro [1975]。更多与求解递推关系的技巧有关的信息可以在Graham, Knuth, and Patashnik [1989]中找到。

Aho, A. V., J. E. Hopcroft, and J. D. Ullman [1974]. The Design and Analysis of Computer Algorithms, Addison-Wesley, Reading, Mass.

Aho, A. V., J. E. Hopcroft, and J. D. Ullman [1983]. Data Structures and Algorithms, Addison-Wesley, Reading, Mass.

Borodin, A. B., and I. Munro [1975]. The Computational Complexity of Algebraic and Numeric Problems, American Elsevier, New York.

Graham, R. L., D. E. Knuth, and O. Patashnik [1989]. Concrete Mathematics: a Foundation for Computer Science, Addison-Wesley, Reading, Mass.

Knuth, D. E. [1968]. The Art of Computer Programming Vol. I: Fundamental Algorithms, Addison-Wesley, Reading, Mass.

Knuth, D. E. [1976].“Big omicron, big omega, and big theta,”ACM SIGACT News 8:2, pp. 18–23.

第 3 章 程序的运行时间

3.1 本章主要内容

3.2 算法的选择

3.3 度量运行时间

3.3.1 基准测试

3.3.2 对程序的分析

3.3.3 运行时间

示例 3.1

3.3.4 不同运行时间的比较

3.3.5 习题

3.4 大 O 运行时间和近似运行时间

3.4.1 大O的定义

3.4.2 证明大O关系

示例 3.2

示例 3.3

3.4.3 证明大O关系不成立

示例 3.4

3.4.4 习题

3.5 简化大 O 表达式

3.5.1 大O表达式的传递律

示例 3.5

3.5.2 描述程序的运行时间

3.5.3 紧凑性

示例 3.6

3.5.4 简单性

示例 3.7

示例 3.8

3.5.5 求和规则

示例 3.9

3.5.6 不相称函数

示例 3.10

3.5.7 习题

3.6 分析程序的运行时间

3.6.1 简单语句的运行时间

示例 3.11

示例 3.12

3.6.2 简单for循环的运行时间

示例 3.13

示例 3.14

3.6.3 选择语句的运行时间

示例 3.15

示例 3.16

3.6.4 程序块的运行时间

示例 3.17

3.6.5 复杂循环的运行时间

示例 3.18

3.6.6 习题

3.7 边界运行时间的递归规则

示例 3.19

3.7.1 程序结构的树表示

示例 3.20

3.7.2 攀爬结构树以确定运行时间

示例 3.21

3.7.3 循环运行时间更精确的上界

示例 3.22

3.7.4 习题

3.8 含函数调用的程序的分析

示例 3.23

习题

3.9 递归函数的分析

示例 3.24

习题

3.10 归并排序的分析

3.10.1 merge函数的分析

3.10.2 split函数的分析

3.10.3 MergeSort函数

3.10.4 习题

3.11 为递推关系求解

3.11.1 通过反复代换为递推关系求解

示例 3.25

示例 3.26

3.11.2 通过猜测解为递推关系求解

示例 3.27

示例 3.28

3.11.3 习题

3.12 小结

3.13 参考文献

第 3 章　程序的运行时间

3.1　本章主要内容

3.2　算法的选择

3.3　度量运行时间

3.3.1　基准测试

3.3.2　对程序的分析

3.3.3　运行时间

3.3.4　不同运行时间的比较

3.3.5　习题

3.4　大 O 运行时间和近似运行时间

3.4.1　大O的定义

3.4.2　证明大O关系

3.4.3　证明大O关系不成立

3.4.4　习题

3.5　简化大 O 表达式

3.5.1　大O表达式的传递律

3.5.2　描述程序的运行时间

3.5.3　紧凑性

3.5.4　简单性

3.5.5　求和规则

3.5.6　不相称函数

3.5.7　习题

3.6　分析程序的运行时间

3.6.1　简单语句的运行时间

3.6.2　简单`for`循环的运行时间

3.6.3　选择语句的运行时间

3.6.4　程序块的运行时间

3.6.5　复杂循环的运行时间

3.6.6　习题

3.7　边界运行时间的递归规则

3.7.1　程序结构的树表示

3.7.2　攀爬结构树以确定运行时间

3.7.3　循环运行时间更精确的上界

3.7.4　习题

3.8　含函数调用的程序的分析

3.9　递归函数的分析

3.10　归并排序的分析

3.10.1　`merge`函数的分析

3.10.2　`split`函数的分析

3.10.3　`MergeSort`函数

3.10.4　习题

3.11　为递推关系求解

3.11.1　通过反复代换为递推关系求解

3.11.2　通过猜测解为递推关系求解

3.11.3　习题

3.12　小结

3.13　参考文献