第 8 章 关系数据模型
计算机最为重要的一项应用就是存储和管理信息。信息的组织方式对访问和管理信息的容易程度有着深刻的影响。也许最简单而最万能的信息组织方式就是将其存储在表中。
关系模型就是这一概念的核心:数据被组织成称为“关系”的二维表集合。我们还可以将关系模型视作第7章讨论的集合数据模型的一般化,是将二元关系扩展到任意元的关系。
之所以最初要研发关系数据模型,是因为要用于数据库,即长时间存储在计算机系统中的信息,并用于数据库管理系统,即让人们可以存储、访问和修改这些信息的软件。数据库仍然是我们理解关系数据模型的重要动机。现在它们不仅存在于最初的那些大规模应用中,比如航空订票系统或银行系统,而且可以应用于桌面计算机,处理一些个人活动,诸如维持支出记录、作业成绩,此外还有其他很多用途。
除了数据库系统,其他类型的软件也可以很好地利用信息表,而关系数据模型有助于我们设计这些表,并研究出高效访问这些信息表所需的数据结构。例如,这样的表可被编译器用来存储与程序中变量有关的信息,记录它们的数据类型以及定义它们的函数。
8.1 本章主要内容
本章有3个相互交织的主题,首先要向大家介绍的是使用关系模型的信息结构的设计,我们会看到如下内容。
信息表,称作“关系”,是强大而灵活的信息表示方式(8.2节)。
设计过程中的重要环节是在不引入“冗余”,即某一事实重复若干次的情况下,选择可一起存储在表中的“属性”或所描述对象的属性(8.2节)。
表中的列是用属性命名的。表(或关系)的“键”是其值能唯一确定表中整行值的属性构成的集合。知道表的键有助于设计表示表的数据结构(8.3节)。
索引是有助于我们迅速检索或更改表中信息的数据结构。如果想高效地操作表,明智地选择索引是至关重要的(8.4节、8.5节和8.6节)。
第二个主题是数据结构加速数据访问的方式,在这部分内容中我们会了解到如下内容。
诸如散列表这样的主索引结构将表中各行安排在计算机的内存中,合适的结构可以提高诸多操作的效率(8.4节)。
辅助索引提供了额外的结构,而且有助于高效执行其他操作(8.5节和8.6节)。
第三个主题是一种非常高级的表示“查询”的方式,其中查询是指与表集合中的信息有关的问题,这部分有以下要点。
关系代数是一种强大的表示法,可以在不给出运算执行细节的情况下表示查询(8.7节)。
关系代数的运算符可以用本章讨论的数据结构来实现(8.8节)。
为了迅速得出用关系代数表示的查询的解答,通常有必要对它们加以“优化”,也就是说,使用代数法则将一个表达式转换成有着更快求值策略的等价表达式。我们将在8.9节中了解一些这样的技巧。
8.2 关系
7.7节介绍的“关系”的概念是元组的集合。关系中的每个元组都是一列组分,而每个关系都具有固定的元数,它表示每个元组中所含组分的数量。尽管我们主要研究了二元关系,也就是元数为2的关系,但也说过其他元数的关系不仅存在,而且相当实用。
关系模型中用到的“关系”的概念与关系的集合论定义是紧密相关的,但在某些细节上存在差异。在关系模型中,信息被存储在如图8-1所示的表中。图中的表所表示的数据可能存储在教务老师的计算机中,是与课程、选择这些课程的学生以及他们所取得的成绩有关的信息。
表中的列都被给定了名称,这些名称就叫做属性(attribute)。在图8-1中,属性分别有课程(Course)、学号(StudentID)和成绩(Grade)。
课程 | 学号 | 成绩 |
|---|---|---|
CS101 | 12345 | A |
CS101 | 67890 | B |
EE200 | 12345 | C |
EE200 | 22222 | B+ |
CS101 | 33333 | A- |
PH100 | 67890 | C+ |
图 8-1 信息表
作为集合的关系与作为表的关系
在关系模型中,正如我们在7.7节中对集合论关系的讨论那样,关系也是元组的集合。因此,表中各行排列的次序是不重要的,可以随意重新排列表中各行而不会改变表的值,就像重新排列集合中元素的次序而不改变集合的值那样。
表的每一行中各组分的次序则是关键的,因为不同的列有着不同的名称,而且每个组分所表示的项,必须具有该列标题所指示的类型。不过,在关系模型中,可以将一整列连同标题的名称一起改变次序,这样就能保持该关系不发生变化。数据库关系在这方面与集合论关系不同,不过我们很少会重新排列表中的列,因此可以保留同样的术语。为了避免疑问,本章中的术语“关系”总是具有数据库的含义。
表中各行被称为元组,且表示基本事实。第一行,(CS101,12345,A),表示学号12345的学生在课程CS101中得了A。
表包含两个方面。
1. 列名的集合;
2. 包含信息的行。
术语“关系”指的是后者,也就是行的集合。每一行表示关系的一个元组,而且这些行在表中出现的次序是无关紧要的。相同表中不存在各列的值全部相同的两行。
第(1)项,列名(属性)的集合被称为关系的模式(scheme)。属性在模式中出现的次序无关紧要,不过为了正确地写出元组,需要知道属性与表中的列之间的对应关系。我们通常会使用模式作为关系的名称。因此,图8-1中的表通常称为“课程-学号-成绩”关系。此外,还可以用首字母缩写CSG 来为该关系命名。
8.2.1 关系的表示
就像集合那样,用数据结构表示关系的方式也多种多样。表的各行就应该是结构体,其中各个字段与各列名相对应。例如,图8-1所示关系中的元组可以表示为如下类型的结构体。
struct CSG {
char Course[5];
int StudentId;
char Grade[2];
};
表本身可以从多种方式中任选其一来表示,比如
1. 该类型结构体组成的数组。
2. 该类型结构体组成的链表,其中还要有链接链表各单元的next字段。
此外,也可以将一个或多个属性视为该关系的“定义域”,而将其余属性视作“值域”。例如,图8-1中的关系可以被看作从定义域“课程”到由“学号-成绩”有序对组成的值域的关系。然后可以按照7.9节中讨论过的二元关系的模式,将该关系存储在散列表中。也就是说,我们会散列“课程”的值,而存储在散列表元中的元素是“课程-学号-成绩”三元组。我们将从8.4中起更为详细地讲解表示关系的数据结构的这一问题。
8.2.2 数据库
关系的集合称为数据库。在为某些应用设计数据库时,首先要做的就是决定待存储的数据该如何安排在表中。与所有设计问题一样,数据库的设计也是个业务需求和判断的问题。在接下来的示例中,我们将扩展这里涉及课程的教务数据库应用,而且要揭示优秀数据库设计的一些原则。
数据库最强大的那些操作涉及将若干关系用来表示协调的数据类型。通过建立恰当的数据结构,可以高效地从一个关系跳转到另一个关系,从而从数据库中获取一些无法从单个关系发现的信息。与关系间“导航”相关的数据结构和算法将在8.6节和8.8节中加以介绍。
数据库中各关系的模式组成的集合就是数据库的模式。要注意数据库模式(它告诉我们与数据库中信息组织方式有关的信息)与各关系中元组的集合(数据库中存储的实际信息)之间的区别。
示例 8.1
我们为图8-1中具有模式{课程,学号,成绩}的关系补充4个其他的关系,它们的模式和直观意义如下。
1. {学号,姓名,地址,电话}。学生的学号出现在元组的第一个组分,而姓名、地址和电话号码分别出现在第二、第三和第四个组分中。
2. {课程,前提}。该元组第二个组分表示的课程,是选修第一个组分所表示课程的前提。
3. {课程,日子,时刻}。第一个组分表示的课程,是在由第二个组分指定的日子,第三个组分给出的时刻上课。
4. {课程,教室}。第一个组分表示的课程是在第二个组分表示的教室上课。
这4个模式,加上之前提到的{课程,学号,成绩}模式,就构成了用于本章示例的数据库模式。我们还需要一个表示数据库可能的“当前值”的示例。图8-1给出了“课程-学号-成绩”关系的一个例子,而对应其他4个模式的示例关系如图8-2所示。请记住,这些关系远比我们在现实中遇到的关系简短,在这里只是需要提供一些对应这些模式的样本元组而已。
学号 | 姓名 | 地址 | 电话 |
|---|---|---|---|
12345 | C.Brown | 12 Apple St. | 555-1234 |
67890 | L.Van Pelt | 34 Pear Ave. | 555-5678 |
22222 | P.Patty | 56 Grape Blvd. | 555-9999 |
(a) 学号-姓名-地址-电话
课程 | 前提 |
|---|---|
CS101 | CS100 |
EE200 | EE005 |
EE200 | CS100 |
CS120 | CS101 |
CS121 | CS120 |
CS205 | CS101 |
CS206 | CS121 |
CS206 | CS205 |
(b) 课程-前提
课程 | 日子 | 时刻 |
|---|---|---|
CS101 | M | 9AM |
CS101 | W | 9AM |
CS101 | F | 9AM |
EE200 | Tu | 10AM |
EE200 | W | 1PM |
EE200 | Th | 10AM |
(c)课程-日子-时刻
课程 | 教室 |
|---|---|
CS101 | Turing Aud. |
EE200 | 25 Ohm Hall |
PH100 | Newton Lab |
(d) 课程-教室
图 8-2 样本关系
8.2.3 数据库的查询
我们在第7章中看到过对关系和函数执行的一些特别重要的操作,虽然根据处理的是词典、函数或是二元关系,它们相应的意义会有所区别,但这些操作都名为插入、删除和查找。我们能对数据库关系,特别是对两个或多个关系的结合,执行大量的操作,而且8.7节中还会概述对两个或多个关系的结合执行的操作。不过现在让我们将注意力集中在对单一关系执行的基本操作上。这些操作是对第7章中讨论过的那些操作的自然概括。
1. insert (t,R )。如果元组t 尚未出现在关系R 中,就将它添加到R 中。该操作与词典或二元关系的插入操作有着相同的精神。
2. delete (X,R )。在这里,X 是某些元组的规范。它是由对应R 各属性的组分组成的,每个组分都会是下面两者之一。
(a) 一个值。
(b) 符号*,表示可以接受任意值。
该操作的效果是删除满足规范X 的所有元组。例如,如果要取消课程CS101,就要从课程-日子-时刻关系中删除所有课程属性为“CS101”的元组。我们可以用
Lookup((“CS101”,*,8),课程-日子-时刻)
表示这种情况。该操作会删除图8-2(c)中的前3个元组,因为它们的第一个组分与该规范的第一个组分有着相同的值,而且它们的第二和第三个组分也都像任意值那样能与*匹配。
3. lookup (X,R )。该操作的结果是得到R 中匹配规范X 的元组形成的集合,X 是个象征性的元组,就跟第(2)项中描述的一样。例如,如果我们想要知道哪些课程是以CS101为前提,就可以询问
lookup ((*,"CS101"),课程-前提)
结果是由两个与条件匹配的元组(CS120,CS101)和(CS205,CS101)组成的集合。
示例 8.2
下面有更多对教务数据库进行操作的例子。
(a) lookup (("CS101",12345,*),课程-学号-前提)可以找到学号为12345的学生CS101课程的成绩。正式地讲,得到的结果只有一个匹配的元组,也就是图8-1中的第一个元组。
(b) lookup (("CS205","CS120"),课程-前提)会询问CS120是否为CS205的前提。正式地讲,如果元组("CS205","CS120")在该关系中,产生的回答就是该元组,如果该元组不在该关系中,那么回答就是空集。对图8-2b中的关系而言,得到的回答是空集。
(c) delete (("CS101",*),课程-教室)会剔除图8-2d中的第一个元组。
(d) insert (("CS205","CS120"),课程-前提)会使CS120成为CS205的前提。
(e) insert (("CS205","CS101"),课程-前提)不会对图8-2b的关系造成影响,因为要插入的元组已经在该关系中了。
8.2.4 表示关系的数据结构的设计
在本章接下来的部分中,有大量篇幅用来讨论如何为关系选择数据结构的问题。在7.9节中讨论二元关系的实现时,我们已经见识过有关该问题的一些内容。我们为品种-传粉者关系给定了一个有关品种的散列表作为其数据结构,而且我们看到该结构在回应诸如
lookup(("Wickson",*),品种-传粉者)
这样的查询时会非常实用,因为值“Wickson”让我们找到了有待查找的特定散列表元。不过该结构对回应诸如
lookup((*,"Wickson"),品种-传粉者)
这样的查询是无所帮助的,因为我们必须要在所有的散列表元中查找。
有关品种的散列表是否为合适的数据结构,取决于预期的查询组合。如果我们预期品种总是已指定的,那么散列表就是合适的,而如果预期品种有时候是未指定的,就如先前的查询那样,那么就需要设计一种更强大的数据结构。
数据结构的选择是我们在本章中要面对的基本设计问题之一。在8.3节中,我们要推广7.8节和7.9节中用于函数和二元关系的基本数据结构,从而让一些属性要么在定义域中,要么在值域中。这些结构将被称为“主索引结构”。然后,在8.5节中要介绍“辅助索引结构”,它们是让我们能高效回应更多种类查询的额外的结构。到那时,我们就将看到如何能让上述两个查询以及其他与品种-传粉者关系有关的查询得到高效回应,也就是说,大约在列出所有这些回应所花的这段时间内。
设计I:数据库模式的选择
在使用关系数据模型时,如何选择合适的数据库模式是个重要的问题。例如,为什么我们要把与课程有关的信息分为5个关系,而不是将其放在具有以下模式的一张表中
{课程,学号,成绩,前提,日子,时刻,教室}
直觉上的原因在于下列两点。
- 如果将两个独立类型的信息结合成一个关系模式,就可能被迫多次重复同样的事实。
例如,与课程有关的前提信息,是独立于日子和时刻信息的。如果我们将前提信息与日子-时刻信息结合在一起,就不得不在列出某课程的前提时还要加上每次上课的时间,反之亦然。那么,如果将图8-2b和图8-2c中有关课程EE200的数据放在具有{课程,前提,日子,时刻}模式的单一关系中,就成了
课程
前提
日子
时刻
EE200
EE005
Tu
10AM
EE200
EE005
W
1PM
EE200
EE005
Th
10AM
EE200
CS100
Tu
10AM
EE200
CS100
W
1PM
EE200
CS100
Th
10AM
请注意,要完成之前各含2到3个组分的5个元组就能完成的工作,这里要用到6个元组,而且每个元组有4个组分。
- 反过来,在属性表示相互联系的信息时,不要把它们分开。
例如,我们不能把“课程-日子-时刻”关系替代为分别具有“课程-日子”模式和“课程-时刻”模式的两个关系。因为那样的话,我们只能告知EE200会在星期二、星期三和星期四上课,而且会在上午10点及下午1点上课,但没办法说明这3天分别是在几点上课。
8.2.5 习题
1. 为图8-2a到图8-2d的这些关系中的元组给出合适的结构体声明。
2. * 对以下问题来说,合适的数据库结构是什么?
(a) 电话簿,包含电话簿中所有常见信息,比如区号。
(b) 英语词典,包含词典中所有常见信息,比如词源和词性。
(c) 日历,包含日历中所有常见信息,比如节假日,要含有从公元1年到公元4000年的所有内容。
8.3 键
很多数据库关系可被视作从某些属性的集合到其余属性的函数。例如,我们可将“课程-学号-成绩”关系看作定义域为“课程-学号”有序对,值域为成绩的函数。因为函数的数据结构比一般关系的数据结构多少要简单一些,所以如果我们知道可以作为函数定义域的属性集合,是能派上用场的。这样的属性集合就叫作“键”。
更正式地讲,关系的键是一项或多项属性的集合,它满足这样的条件,就是在任何情况下,以键属性为标题的列中不会出现相同的值。通常,有很多不同的属性集合可以作为关系的键,不过我们一般只选择一个,并称为“键”。
8.3.1 键的确定
因为键可以用作函数的定义域,所以它们在8.4节中讨论主索引结构时扮演了重要角色。一般而言,我们没法证实或证明属性集合可以形成键,而是需要小心地检查与要建模的应用有关的假设,以及这些假设如何反映在我们设计的数据库模式中。只有这样才能知道给定的属性集合是否适合作为键。接下来有一系列的示例用来说明一些问题。
示例 8.3
考虑图8-2a中的“学号-姓名-地址-电话”关系。显然,每个元组都是用来表示不同学生的信息的。我们不希望找到两个具有相同学号的元组,因为这一编号存在的意义就是要为每个学生指定一个唯一的标识符。如果让同一个关系中有了两个学号相同的元组,那么其中有一个就是出错了。
1. 如果两个元组所有的组分都相同,那么就违背了关系是集合的假设,因为集合中每个元素最多只能出现一次。
2. 如果两个元组有着相同的学号,但在姓名、地址或电话这3列中至少有一个不同,就说明数据存在错误。要么是我们给了不同的学生同一个学号(如果元组中的“姓名”有区别),或是错给同一个学生记录了两个不同的地址和(或)电话号码。
因此,将“学号”属性作为“学号-姓名-地址-电话”关系的键是合理的。
不过,要将“学号”声明为键,就要作出一项关键的假设,就是在之前的第(2)项中阐明的,决不会为同一个学生存储两个姓名、地址或电话号码。不过我们还可能作出其他的决定,例如为每个学生存储家庭地址和校园地址。如果这样的话,就最好将该关系设计成具有5项属性,将“地址”属性替换为家庭地址(HomeAddress)和本地地址(LocalAddress)这两个属性,而不是为每个学生使用两个只有地址组分不同的元组,因为那样的话学号就不再能作为键了,而{学号,地址}就能作为键。
示例 8.4
审视图8-1中的“课程-学号-成绩”关系,我们可能想将“成绩”作为键,因为表中没有两个元组的成绩是相同的。不过,这种推理是不合理的。在这个只有6个元组的示例中,确实没有两个元组具有相同的成绩,不过在常见的“课程-学号-成绩”关系中,可能有着成千上万个元组,肯定有很多成绩会出现多次。
最有可能的是,数据库设计人员的想法是用“课程”和“学号”这两个属性一起形成键。也就是说,假设学生不可能选修同一课程两次,因此,不可能出现课程与学号都相同的两个不同元组。因为我们预见可以找出多个具有相同“课程”组分的元组,以及很多有着同样“学号”组分的元组,所以“课程”和“学号”都不能单独作为键。
不过,学生在任意课程中只可以获得一个成绩的假设也是有待推敲的,这取决于学校的具体政策。也许在课程内容发生重大改变时,学生可以重新注册该课程。如果有这种情况,就不能将{课程,学号}声明为“课程-学号-成绩”关系的键,只有全部3个属性的集合才可以作为键。请注意,具有关系中所有属性的集合总能作为键,因为关系中不可能出现两个相同的元组。事实上,最好是添加第四项属性,日期来表示课程被选择的时间,这样一来就可以处理学生选了同样课程两次并且两次都获得相同成绩的情况了。
示例 8.5
在图8-2b的“课程-前提”关系中,两项属性都不能单独作为键,不过两项属性一起就能形成键。
示例 8.6
在图8-2c所示的“课程-日子-时刻”关系中,全部3项属性一起形成了唯一合理的键。可能只要课程和日子加在一起就能声明为键,不过这样就没法存储同一天中要出现两次的课程了(比如演讲和实验)。
设计II:键的选择
为关系确定键是数据库设计中的一个重要方面,当我们在8.4节中选择主索引结构时就会用到。
- 不能只靠观察关系的几个示例值就确定键。
也就是说,外表可能有欺骗性,就像我们在示例8.4中讨论过的,图8-1所示“课程-学号-成绩”关系中的“成绩”属性那样。
- 不存在所谓的“正确的”键选择,选择什么属性作为键,取决于对关系所含数据的类型作出的假设。
示例 8.7
最后,考虑一下图8-2d中的“课程-教室”关系。我们认为“课程”可以作为键,也就是说,不会有课程会在两个或多个不同的教室中进行。如果情况不这样,就应该将“课程-教室”关系与“课程-日子-时刻”关系结合起来,这样就可以区分一门课程是在哪间教室里上课了。
8.3.2 习题
1. * 假设我们想为“学号-姓名-地址-电话”关系中的学生分别存储家庭地址及本地地址,以及家庭电话及本地电话。
(a) 这样一来,该关系最为合适的键是什么?
(b) 这一改变会带来冗余,例如,如果某学生的两个地址和两个电话号码以所有可能的方式结合后出现在不同元组中,那么该学生的姓名就会重复4次。我们在示例8.3中提供过一种解决方案,就是使用不同的属性来表示不同的地址和不同的电话。那么这样一来关系模式会是怎样的?而这一关系最合适的键是什么?
(c)8.2节中介绍过另一种处理冗余的方式,就是将该关系分解成两个具有不同模式的关系,一起存放原关系的所有信息。如果要为同一学生存储多个地址和电话,应该将“学号-姓名-地址-电话”关系分解为哪几个关系?提示:关键问题在于地址和电话是否为独立的。也就是说,是否期望一个电话号码会在某学生的所有地址都能接通(在地址和电话相互独立的情况下),还是说电话号码是与单个地址相关联的。
2. * 车管所维护着含有如下若干类信息的数据库。
驾驶员的姓名(Name)。
驾驶员的地址(Addr)。
驾驶员的驾驶证编号(LicenseNo)。
车辆的序列号(SerialNo)。
车辆的生产商(Manf)。
车辆的型号名称(Model)。
车辆的注册(车牌)号(RegNo)。
车管所希望将每个驾驶员关联到相关信息:地址、驾驶证和所拥有的车辆。还希望将每辆车关联到相关信息:所有者、序列号、生产商、型号和注册号。我们假设熟悉车管所运作的基本要求,例如,不可能将同样的车牌发给两辆汽车。大家可能不知道(但这确实是事实),即便是来自不同生产商的两辆汽车,也不可能具有同样的序列号。
(a) 选择数据库模式,也就是关系模式的集合,其中每个关系模式都由上面列出的从1到7这几种属性的集合组成。大家必须让所需的联系都可以通过存储在这些关系中的数据体现出来,而且必须避免冗余,也就是说,大家设计的模式不应该重复存储相同的事实。
(b) 说明哪些属性可以作为(a)小题中设计的关系的键。
8.4 关系的主要存储结构
在7.8节和7.9节中,我们看到如何通过根据有序对的定义域值存储有序对,以使对函数和二元关系的某些操作提速。在提到我们在8.2节中定义的一般的插入、删除和查找操作时,能有所帮助的是那些指定了定义域值的操作。再次回想一下7.9节中的“品种-传粉者”关系,如果将品种作为关系的定义域,就有利于那些指定了品种而不关心是否指定了传粉者的操作。
这里有一些可用于表示关系的结构。
1. 二叉查找树,在定义域值上有“小于”关系以安排元组的位置,可以用来促进指定了定义域值的操作。
2. 以定义域值作为数组索引,用作特征向量的数组有时是有用的。
3. 散列定义域值以找到散列表元的散列表是有用的。
4. 原则上讲,元组组成的链表是一种候选结构。我们将忽略这种可能,因为它对任何类型的操作都没有促进作用。
当关系不是二元关系时,同样的结构也是可以使用的。定义域不是只有单个属性,而是可能结合k个属性,我们将其称为定义域属性,或是在明确所指的是属性集合时,将其直接称为“定义域”。这样一来,定义域的值就是k元组,各组分对应定义域的各属性。而值域属性是那些定义域属性之外的属性。值域值也可以有多个组分,每一个都对应着一个值域的属性。
一般来说,我们必须选出想要作为定义域的那些属性。最简单的情况是一个属性或少量属性作为关系的键的情况。这样的话就可以选择键属性作为定义域,而将其余属性作为值域。在没有键的情况下(所有属性的集合这种不实用的键除外),我们可以选择任意属性集合作为定义域。例如,可以考虑期望对该关系执行的那些常用操作,并选择预期经常要指定的属性作为定义域。我们很快就将看到一些具体的例子。
一旦选择了定义域,就可以从刚提到的4种数据结构中任选其一表示该关系,或者其实也可以选择另一种结构。不过,通常会选择以定义域值作为索引的散列表,而且我们在这里一般都会这么做。
所选的结构就称为该关系的主索引结构。形容词“主”表示元组的位置是由该结构确定的。索引则是在给定所需要的元组的一个或多个组分的情况下协助找到元组的数据结构。在8.5节中,我们将讨论“辅助”索引,它有助于回应查询,但不影响数据的位置。
typedef struct TUPLE *TUPLELIST;
struct TUPLE {
int StudentId;
char Name[30];
char Address[50];
char Phone[8];
TUPLELIST next;
};
typedef TUPLELIST HASHTABLE[1009];
图 8-3 作为主索引结构的散列表的类型
示例 8.8
我们来考虑一下以“学号”属性作为键的“学号-姓名-地址-电话”关系。学号属性就将作为定义域,而其他3个属性则会形成值域,因此可以将该关系视为从学号到“姓名-地址-电话”三元组的函数。
就和所有的函数那样,我们选择接受定义域值作为参数并生成散列表元号作为结果的散列函数。在这种情况下,散列函数会接受学生的学号(整数)作为参数。我们将选择10091作为散列表元的数量B,这样散列函数就是
11009是1000左右的质数。如果数据库要记录数千学生的信息,就可以使用1000个左右的散列表元,这样一来每个散列表元中的平均元组数就会很小。
h (x )=x %1009
散列函数将学号映射到从0到1008这个范围的整数。
含1009个散列表元头部的数组给我们带来了一列列的结构体。i号散列表元对应的链表中的结构体表示的是学号组分除以1009余数为i 的那些元组。对“学号-姓名-地址-电话”关系来说,图8-3中的声明对散列表元链表中的结构体和散列表元头部数组来说都是合适的。图8-4展示了散列表看起来的样子。
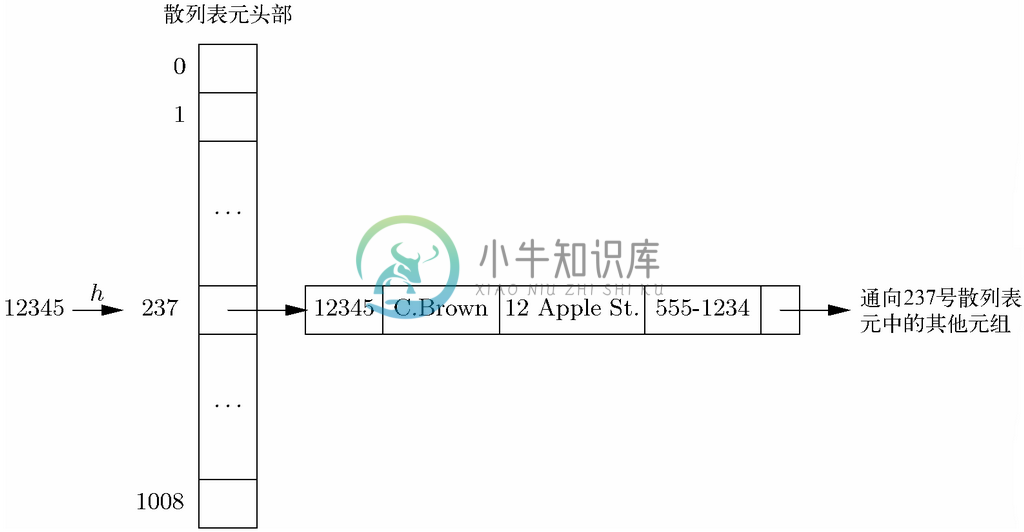
图 8-4 表示“学号-姓名-地址-电话”关系的散列表
示例 8.9
再看一个更复杂的例子,考虑一下“课程-学号-成绩”关系。我们可以用散列表作为主结构,该散列表的散列函数接受课程和学号(即构成该关系的键的两项属性)作为参数。这样的散列函数要接受表示课程名称的字符,再加上表示学生学号的整数,然后再除以1009取余数。
如果我们要进行的操作都是在给定课程与学号的情况下查找成绩,这一数据结构就很实用。也就是说,它适用于执行如下操作:
lookup ((“CS101”,12345,*),课程-学号-成绩)
不过它对诸如下面这样的操作来说就不实用。
1. 找出所有选修CS101课程的学生;
2. 找出学号12345的学生选修的所有课程。
在这两种情况下,我们都没法计算散列值。例如,只给定课程,就没有学号可加到课程名字符对应整数的和上,因此就没有值除以1009以得出散列表元号。
不过,假设经常要进行“谁选修了CS101”这样的查询,也就是
lookup ((“CS101”,*,*),课程-学号-成绩)
那么使用只基于“课程”组分的值的主结构会更有效。也就是说,可以将该关系视作集合论中的二元关系,其中定义域是课程,而值域则是学号-成绩有序对。
例如,假设我们将课程名称的字符转换成整数,并求出它们的和,除以197,然后取余数。那么“课程-学号-成绩”关系的元组就会被该散列函数分装到标号为0至196的197个散列表元中。不过,如果有100个学生选修了CS101课程,那么不管我们为散列表安排了多少个散列表元,对应课程CS101的散列表元中都至少有100个结构体,这就是使用不是键的属性作为主索引结构的定义域的缺点。如果其他课程也被散列到对应CS101的散列表元,那么该散列表元中甚至会有100个以上的结构体。
另一方面,当想要在给定的课程中找到学生时,仍然能从中受益。如果课程的数量明显大于197,那么平均下来,只需要查找整个“课程-学号-成绩”关系的1/197,这是一笔巨大的节省。此外,当我们执行在特定课程中查找特定学生的成绩,或是插入或删除“课程-学号-成绩”元组这样的操作时,也会受益于该结构。在每种情况下,都可以使用“课程”值将查找范围限定在散列表197个散列表元中的某一个上。唯一帮不上忙的情况就是处理没有指定课程的操作。例如,要找到学生12345选修的课程,就必须查找所有的散列表元。这样的查询只有在使用辅助索引结构时才可以更有效率地进行,这一点会在8.5节中讨论。
设计III:主索引的选择
- 将关系模式的键作为函数的定义域,并将其余属性作为值域通常是很实用的。
然后就可以像实现函数那样,使用诸如带有基于键属性的散列函数的散列表这样的主索引来实现关系。
- 不过,如果最常见的查询所指定的是不构成键的属性的值,就可能要选用该属性集合作为定义域,而将其余属性作为值域。
接着就可以像实现二元关系那样来实现该关系了。比如,利用散列表。唯一的问题就在于,元组在散列表元中的分布可能不像以键作为定义域时那么平均。
- 主索引结构定义域的选择可能对执行“常规”查询的速度有着最大的影响。
8.4.1 插入、删除和查找操作
鉴于第7章中对二元关系的同样主题的探讨,这里用主索引结构执行插入、删除和查找操作的方式应该很明了。要回顾这些概念,就要将注意力放在作为主索引结构的散列表上。如果操作指定了定义域的值,那么就要散列该值以找到散列表元。
1. 要插入元组t,就要检查相应的散列表元,看看t是否已经位列其中,如果没有就在该散列表元对应的链表中创建新单元来容纳t。
2. 要删除匹配规范X 的元组,就要根据X 找出定义域值,进行散列以得出相应的散列表元,然后沿着该散列表元对应的链表向下查找,将匹配规范X 的各元组都删除掉。
3. 要根据规范X 查找元组,还是要从X 找到定义域值,进行散列以得出相应的散列表元。沿着对应该散列表元的链表向下查找,将链表中匹配规范X 的各元组分别作为回应生成。
如果操作没有指定定义域值,就不会这么走运了。插入操作就总是要完整地指定被插入的元组,而删除或查找操作可能不能这样。在那样的情况下,我们必须对所有的散列表元列表进
行查找,找到匹配的元组,并分别删除或列出它们。
8.4.2 习题
1. 8.3节中习题2的车管所数据库应该设计成能处理如下类型的查询,而且要假设这些查询发生的频率都相当高。
(a) 给定驾驶员的地址是什么?
(b) 给定驾驶员的驾驶证编号是多少?
(c) 给定驾驶证编号对应驾驶员的姓名是什么?
(d) 拥有给定车辆(以其注册号作为标识)的驾驶员的姓名是什么?
(e) 具有给定注册号的车辆的序列号、生产商和型号各是什么?
(f) 拥有给定注册号所对应车辆的是谁?
为自己在8.3节习题2中设计的那些关系给出合适的主索引结构,每种情况下都使用散列表。陈述有关驾驶员数与车辆数的假设。说出要使用多少散列表元,以及要使用什么属性作为定义域。这几类查询中有多少可以得到高效的回应,也就是说,平均只花费O(1)的时间而不用考虑关系的大小。
2. 图8-2c中“课程-日子-时刻”关系的主结构可能取决于我们打算执行的常见操作。如果常需要执行的操作分别为下面列出的这几类,给出合适的散列表,要说清定义域中的属性以及散列表元的数量。大家可以对课程的数量以及不同的上课时段作出合理假设。在每种情况下,像“CS101”这样的指定值是用来表示“常见”值的,这样的话,我们的意思是“课程”被指定为某一特定的课程。
(a) lookup (("CS101","M",*),课程-日子-时刻)。
(b) lookup ((*,"M",*,"9AM"),课程-日子-时刻)。
(c) lookup (("CS101",*,*),课程-日子-时刻)。
(d) (a)类和(b)类各占一半。
(e) (a)类和(c)类各占一半。
(f) (b)类和(c)类各占一半。
8.5 辅助索引结构
假设把“学号-姓名-地址-电话”关系存储到如图8-4所示、散列函数是基于“学号”键的散列表中。该主索引结构有助于回应那些指定了学生学号的查询。不过,我们可能希望以学生的姓名提问,而不是用客观而且可能未知的学号提问。例如,我们可能会问,“名叫C.Brown的学生的电话号码是多少?”这样一来主索引结构就帮不上忙了。我们必须行经每个散列表元,并检查一列列的记录,直到找到“姓名”字段的值为“C.Brown”的记录为止。
要迅速回应这样的查询,就需要额外的数据结构让我们可以用姓名找到“姓名”组分中含有该姓名的元组2。可以在给定某一属性或某些属性的值的情况下帮我们找到元组,但不能用来在整个结构中放置元组的数据结构,就是辅助索引。
2要记住,“姓名”并不是“学号-姓名-地址-电话”关系的键,尽管在图8-2a所示的样本关系中,各元组的姓名组分的值都是不同的。例如,如果Linus和Lucy上了同一所大学,那么就有两个元组的姓名组分等于“L. Van Pelt”,但这两个元组的学号组分是不同的。
这里我们需要的辅助索引是具备以下两个条件的二元关系。
1. 定义域是“姓名”。
2. 值域是指向“学号-姓名-地址-电话”关系的元组的指针。
一般而言,关系R 属性A 上的辅助索引是满足以下条件的有序对(v,p)的集合。
(a) v 是属性A 的值。
(b) p 是指向关系R 主索引结构中某个元组的指针,该元组的“A ”组分的值为v。对属性A 的值为v 的各元组来说,辅助索引都有对应的有序对。
我们可以使用表示二元关系的任意数据结构来存储辅助索引。通常会期望使用基于属性A 的值的散列表。只要散列表元的数量不大于属性A 不同值的数量,在给定所需的v 值的情况下,在散列表中查找有序对(v,p)通常都可以预期不错的性能——也就是平均O(n/B )的时间。这里的n 是有序对的数量,而B 是散列表元的数量。为了表明其他的结构也可以用于辅助索引(或主索引),我们在下一个示例中要使用二叉查找树作为辅助索引。
示例 8.10
我们来为图8-2a所示的“学号-姓名-地址-电话”关系设计数据结构,其中使用基于学号的散列表作为主索引,而使用二叉查找树作为对应姓名属性的辅助索引。为了简化表达,这里要使用只含两个散列表元的散列表作为主结构,而要使用的散列函数是用学号除以2的余数。也就是说,偶数学号会放进0号散列表元,而奇数学号会放进1号散列表元。
typedef struct TUPLE *TUPLELIST;
struct TUPLE {
int StudentId;
char Name[30];
char Address[50];
char Phone[8];
TUPLELIST next;
};
typedef TUPLELIST HASHTABLE[2];
typedef struct NODE *TREE;
struct NODE {
char Name[30];
TUPLELIST toTuple; /* 其实是指向元组的指针 */
TREE lc;
TREE rc;
};
图 8-5 对应主索引和辅助索引的类型
这里将使用二叉查找树作为辅助索引,该二叉查找树的节点中存储着由学生姓名与指向元组的指针组成的有序对。元组本身被存储为记录,这些记录链接成链表,构成了散列表的散列表元,所以指向元组的指针实际上就是指向记录的指针。因此,我们需要如图8-5所示的结构体。TUPLE和HASHTABLE类型与图8-3中的定义是一致的,只不过现在使用的是两个散列表元而不是1009个。
NODE类型是二叉树的节点,它具有Name和toTuple这两个字段,分别表示该节点处的元素(即某一学生的姓名),以及指向该学生对应的元组所在记录的指针。而其余的两个字段,lc和rc,分别是指向该节点左子节点与右子节点的指针。我们会用学生的姓的字母表次序作为比较树中接点处各元素所使用的“小于”次序。而辅助索引本身是TREE类型的变量,也就是指向节点的指针,它会将我们带到该二叉查找树的根。
图8-6展示了整个结构体的一个示例。为了节省空间,元组的地址和电话组分并没有表示出来。而图中的L 1和L 2等字样表示主索引结构中的记录在内存中的存储位置。
现在,如果想要回应诸如“P.Patty的电话号码是多少”这样的查询,就要从辅助索引的根开始,查找Name字段为“P.Patty”的节点,并跟着该指针到达toTuple字段,如图8-6中的L 2所示。这样就可以找到P.Patty的记录,并从该记录查阅Phone字段并生成该查询的回应。
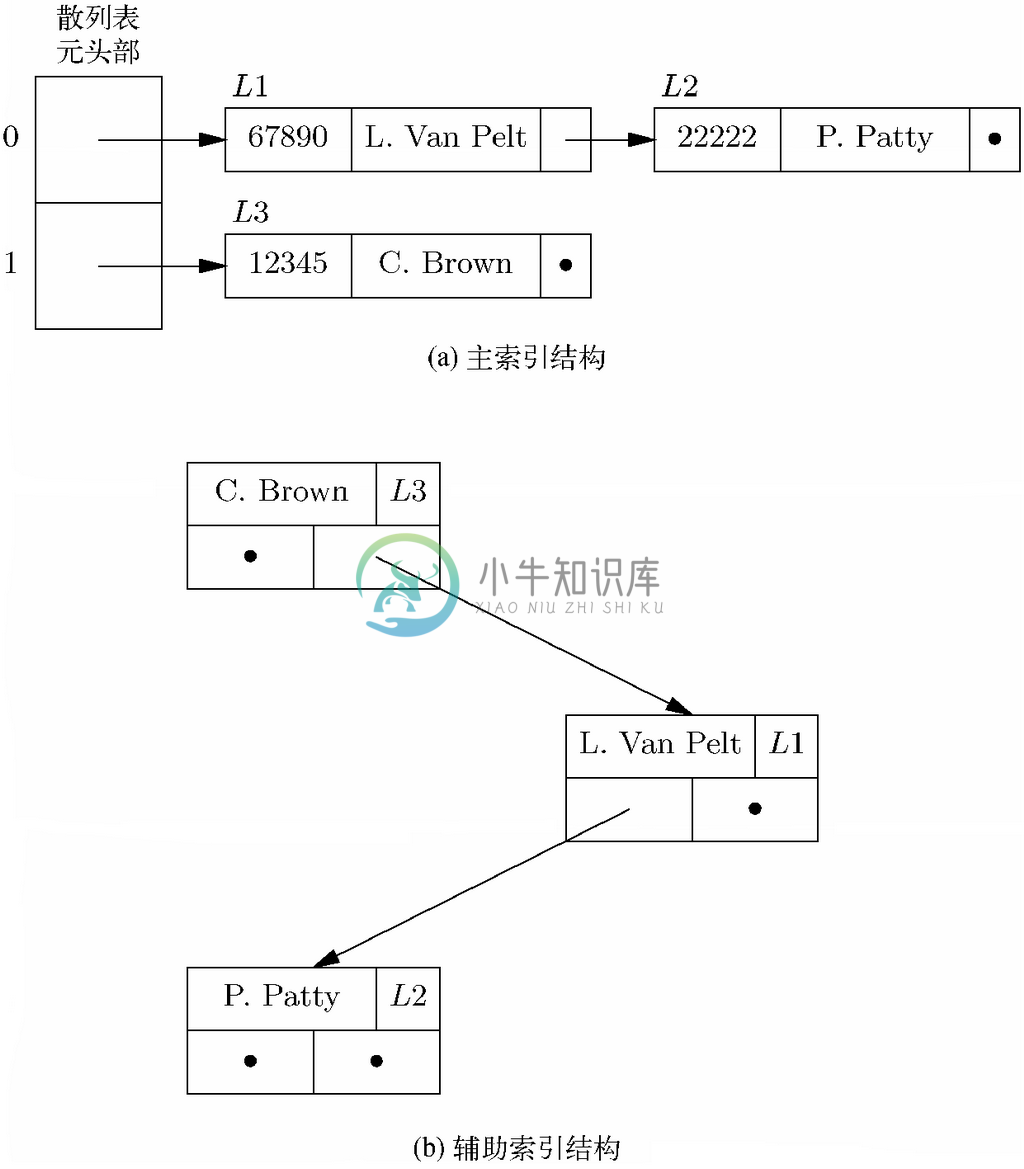
图 8-6 主索引结构与辅助索引结构的示例
8.5.1 非键字段上的辅助索引
看起来在示例8.10中构建辅助索引所依据的“姓名”属性是键,因为没有重复出现的姓名。不过,正如我们所知,存在两个学生同名的可能,所以“姓名”其实不是键。正如在7.9节讨论过的,虽然非键属性可能让元组在散列表元中的分布不如预期的那样平均,但它并不会影响到散列表的数据结构。
二叉查找树是另一个问题,因为这种数据结构不能处理不存在“小于”关系的两个元素,如果两个有序对有着相同的姓名和不同的指针,就会出现这种情况。对图8-5所示结构进行一个小的修正,用字段toTuple作为指向元组的指针组成的链表的表头,具有Name字段中给定值的各元组都与一个指针对应。例如,如果有很多个P.Patty,那么图8-6b中底部的节点就会在L 2的位置具有链表的表头。而该链表中的元素就是指向“姓名”属性等于“P.Patty”的各元组的指针。
设计VI:何时应该创建辅助索引?
如果元组的一个或多个组分的值已经给定,辅助索引的存在通常会让查找元组的工作变得更容易。不过还要考虑如下两点。
所创建的每个辅助索引都会让我们在关系中插入或删除信息时花费额外的时间。
因此,只为那些可能需要查找数据的属性构建辅助索引是说得通的。
例如,如果从不打算在只给定电话号码的情况下找到学生,就没必要在“学号-姓名-地址-电话”关系中的“电话”属性上创建辅助索引。
8.5.2 辅助索引结构的更新
当某个关系存在辅助索引时,元组的插入和删除操作就会变得更困难。除了要像8.4节概述的那样更新主索引结构,还可能需要更新各辅助索引结构。以下方法可用来在涉及属性A 的元组被插入或删除时更新基于A 的辅助索引结构。
1. 插入。如果要插入一个新元组,其对应属性A 的组分的值为v,就必须创建有序对(v,p),其中p 是指向主结构中新记录的指针。然后,再把有序对(v,p)插入到辅助索引中。
2. 删除。要删除对应A 的组分的值为v 的元组时,首先一定要记得已经删除了指向该元组的指针,比方说是p。然后,要深入辅助索引结构,并检查所有第一个组分为v 的有序对,直到从其中找出第二个组分为p 的有序对为止。然后将该有序对从辅助索引结构中删除。
8.5.3 习题
1. 给出如何修改图8-5中的二叉查找树结构,以使“学号-姓名-地址-电话”关系可以存在学生姓名相同的多个元组。编写C语言函数,接受姓名作为参数,并列出关系中“姓名”属性为该姓名的所有元组。
2. ** 假设已决定用“学号”属性上的主索引来存储“学号-姓名-地址-电话”关系,还决定创建一些辅助索引。假设所有的查找都只会指定姓名、地址或电话属性中的某一个。并假设所有的查找操作中有75%是指定了姓名的,有20%是指定地址的,还有5%是指定电话的。还假设每次插入或删除操作的开销都是1个时间单位,再加上我们构建的每个辅助索引会用掉1/2个时间单位。比方说,如果我们要构建所有3个辅助索引的话,总的时间开销就是2.5个时间单位。设如果指定了具有辅助索引的属性,那么一次查找的开销是1个时间单位,而如果指定的属性没有辅助索引则会花费10个时间单位。设a是对指定了全部3项属性的元组进行的插入和删除操作所占的比例。其余的1-a 是指定了某一项属性的操作所占比例,并且符合我们之前对这类查找操作出现概率的假设。比如,所有操作中有0.75(1-a)的比例是给定了“姓名”值的查找。如果目标是让一次操作的平均时间最小化,那么当参数a 的值分别为(a)0.01;(b)0.1;(c)0.5;(d)0.9;(e)0.99时,分别应该创建哪些辅助索引?
3. 假设车管所希望能高效回应如下类型的查询,也就是说,要比查找整个关系快得多。
(i) 给定驾驶员的姓名,找到发放给具有该姓名的人们的驾驶证。
(ii) 给定驾驶证编号,找到驾驶员的姓名。
(iii) 给定驾驶证编号,找到该驾驶员拥有的车辆的注册号。
(vi) 给定地址,找到所有登记为该地址的驾驶员的姓名。
(v) 给定注册号(即车牌号),找到该车辆所有者的驾驶证。
为8.3节习题2中建立的关系给出合适的数据结构,从而使得这些查询能得到高效回应。假设每个索引都是从散列表构建的,并说出各关系的主索引结构和辅助索引结构,这样就足够了。解释一下这样一来要如何回应各类型的查询。
4. * 假设需要高效地从给定的辅助索引中找到指向主索引结构中特定元组t的指针。给出数据结构,让我们能在与找到的指针数成正比的时间内找到这些指针。哪些操作会因为这一额外的数据结构而变得更加费时?
8.6 关系间的导航
直到现在,我们只考虑了涉及单一关系的操作,比如在给定元组的一个或多个组分的值的情况下找到该元组。关系模型的威力要得到最好的体现,就需要考虑那些要求我们“导航”,或者说从一个关系跳转到另一个关系的操作。例如,我们在回应“学号为12345的学生CS101课程的成绩是多少”这样的查询时,所有的处理都是在“课程-学号-成绩”关系之内展开的。不过,如果查询是更为自然的“C.Brown在CS101课程中取得了怎样的成绩”呢?该查询只在“课程-学号-成绩”关系之内就不能得到回应了,因为该关系使用的是学号,而非姓名。
要回应这一查询,首先必须查阅“学号-姓名-地址-电话”关系,并将姓名C.Brown转换成一个学号,或若干学号,因为有可能存在两个或多个学生姓名相同而学号不同的情况。然后,对每个这样的学号,都要在“课程-学号-成绩”关系中查找对应该学号而且课程组分为CS101的元组。可以从每个这样的元组中读取出名为C.Brown的学生CS101课程的成绩。图8-7表示了该查询是如何将给定值与这些关系以及所需的回应联系在一起的。
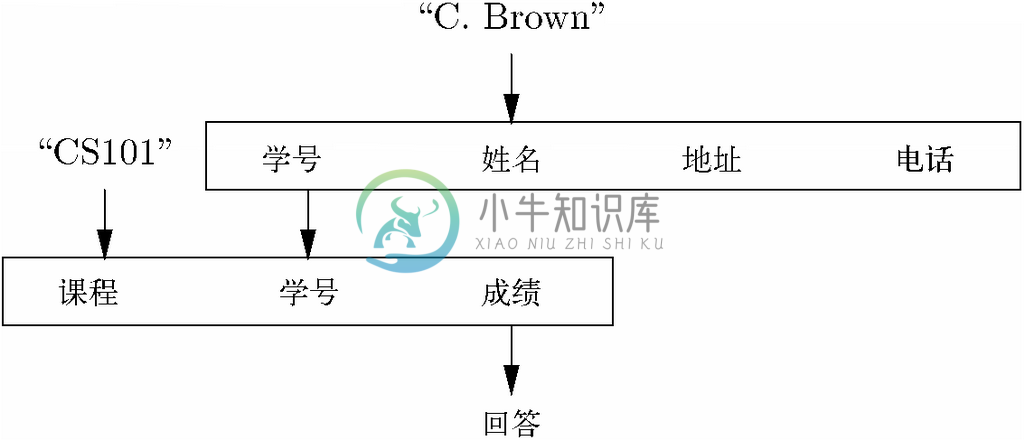
图 8-7 表示查询“C.Brown在CS101课程中取得了怎样的成绩”的图
如果没有索引可用,回应该查询就可能会相当费时。假设在“学号-姓名-地址-电话”关系中有n 个元组,而且在“课程-学号-成绩”关系中有m 个元组。再假设名叫C.Brown的学生共有k 个。在假设没有索引可用的情况下,找出这一(或这些)学生在CS101课程拿到的成绩的算法提纲就如图8-8所示。
接着来确定图8-8所示程序的运行时间。从里层开始向外分析,第(6)行的打印语句要花O(1)的时间。而第(5)和第(6)行的条件语句也要花O(1)的时间,因为第(5)行的测试是O(1)时间的测试。由于我们假设在“课程-学号-成绩”关系中有m 个元组,这样一来,第(4)到第(6)行的循环要迭代m 次,因此总共要花O(m )的时间。因为第(3)行花费的是O(1)时间,所以第(3)到第(6)行的程序块花的时间就是O(m )。
现在考虑一下第(2)到第(6)行的if语句。因为第(2)行的测试花费O(1)的时间,所以如果条件为假则整个if语句花费O(1)时间,如果为真则花费O(m )的时间。不过,我们已经假设了该条件对k 个元组为真而对其余元组为假,也就是说,有k 个元组t 的姓名组分是C.Brown。因为当条件为真与条件为假时所花的时间存在很大的区别,所以应该对分析第(1)到第(6)行的for循环的方式格外谨慎小心。也就是说,我们不能记下循环迭代的次数并将其乘上循环体可能花费的最大时间,而是要分开考虑第(2)行测试的两种结果。

图 8-8 找到C.Brown在CS101课程取得的成绩
首先,要进行n 次循环,因为这是不同t 值的数量。对令第(2)行的测试为真的k 个元组t 来说,我们在每个元组上所花时间为O(m ),或者说总共要花上O(km )的时间。对其余n-k 个令该测试为假的元组来说,每个元组要花O(1)的时间,或者说总共要花O(n-k )的时间。因为估计k 是大大小于n 的,所以我们选择O(n )而非O(n-k )作为更简单的紧上界。因此整个程序的时间开销就是O(n+km )。在很可能出现的k=1的情况中,当只有一个学生姓名为C.Brown时,所需的时间就是O(n+m ),它是与所涉及两个关系的大小之和成正比的。如果k 大于1,这个时间就会更大。
8.6.1 利用索引为导航提速
有了合适的索引,我们在回应同样的查询时平均只需要O(k)的时间,也就是说,如果名字叫C.Brown的学生数k 为1,就只需要O(1)的时间。这样是说得通的,因为我们肯定会检查2k 个元组,就是两个关系各要检查k 个。如果散列表使用了数量恰当的散列表元,这些索引让我们能以平均每个元组O(1)时间的开销找到所需的元组。如果拥有对应“学号-姓名-地址-电话”关系的“姓名”索引,以及对应“课程-学号-成绩”关系的“课程-学号”有序对上的索引,那么找出C.Brown在CS101课程中取得的成绩的算法可以大致描述为图8-9所示的样子。

图 8-9 使用索引找到C.Brown在CS101课程中取得的成绩
我们假设“姓名”索引是具有约n 个散列表元的散列表,是用作辅助索引的。因为n 是“学号-姓名-地址-成绩”关系中的元组数量,所以每个散列表元中平均有O(1)个元组。如果具有该姓名的元组有k 个,在散列表元中找到这些元组就要花费O(k)的时间,而且跳过该散列表元中可能存在的其他元组要花O(1)的时间。因此,图8-9的第(1)行平均要花O(k)的时间。
第(2)到第(5)行的循环要执行k 次。假设把在第(1)行找到的k 个元组t 存储在一个链表中,那么不管是找到下一个元组t,还是发现没有更多的元组,进行循环所花的时间都为O(1),而且第(3)到第(5)行的开销也是一样的。我们声明第(4)行也能在O(1)时间内执行,因此第(2)到第(5)行的运行时间也是O(k)。
下面来分析一下第(4)行。第(4)行要求在给定某一元组的键值的情况下对其进行查找。假设“课程-学号-成绩”关系具有其键{课程,学号}上的主索引,而且该索引是约有m 个散列表元的散列表。那么,每个散列表元中所含元组的平均数就是O(1),因此图8-9的第(4)行所花的时间就是O(1)。这样我们就能得出第(2)到第(5)行的循环体平均会花费O(1)的时间,因此图8-9所示的整个程序就平均会花费O(k)的时间。也就是说,这一时间开销是与具有我们要查询的姓名的学生的数量成比例的,而不用考虑涉及的关系的大小。
8.6.2 多关系上的导航
有些导航技巧让我们可以高效地从一个关系跳转到另一个关系,这些技巧也可以用于涉及多个关系的导航。例如,假设想知道“C.Brown星期一上午9点在哪里?”假设他在上课,我们就可以通过如下方式回应该查询,找到C.Brown选修的课程,看看其中是否有课是在星期一上午9点上,如果有的话,找到该课程上课的教室就行了。图8-10展示了从给定值C.Brown到得出的回应期间在各关系间的导航。
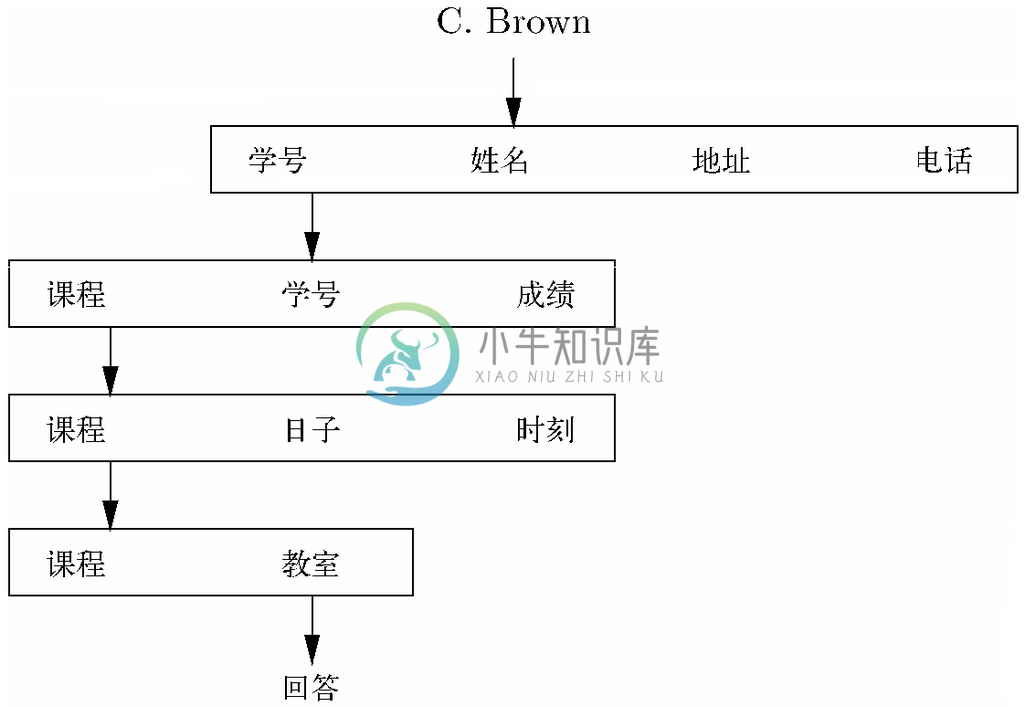
图 8-10 表示“C.Brown星期一上午9点在哪里”这一查询的图
以下方案假设只有一个名为C.Brown的学生,如果有多个名叫C.Brown的学生,就可以得到星期一早上9点他们中的一个或多个人所在的教室。这里还假设这名学生没有选修相互冲突的课程,也就是说,他在星期一早上9点最多只上一门课。
(1) 利用对应C.Brown的“学号-姓名-地址-电话”关系,找到C.Brown的学号,设他的学号为i。
(2) 在“课程-学号-成绩”关系中查找所有学号组分为i的元组,设{c1,…,ck }是这些元组中“课程”值的集合。
(3) 在“课程-日子-时刻”关系中,查找“课程”组分为ci(即第(2)步中找到的课程之一)的元组。应该最多只有一个元组的“日子”组分为“M”而且“时刻”组分为“9AM”。
(4) 如果第(3)步中找到的是课程c,那么在“课程-教室”关系中查找c上课的教室。假设C.Brown没打算旷课,这就是他星期一上午9点所在的位置。
如果没有索引,那么我们可以期待的最佳情况就是,在与涉及的4个关系的大小之和成比例的时间内完成这一方案。不过,有若干个索引可供我们利用。
(a) 在第(1)步中,可以使用“学号-姓名-地址-电话”关系中的“姓名”组分作为索引,从而在平均为O(1)的时间内得到C.Brown的学号。
(b) 在第(2)步中,假设C.Brown选修了k门课程,可以利用“课程-学号-成绩”关系中的“学号”组分上的索引,在O(k)的时间内得到C.Brown选修的所有课程。
(c) 在第(3)步中,可以利用“课程-日子-时刻”关系中“课程”组分上的索引,这样一来,就可以在与第(2)步得到的k门课程每周上课次数之和成比例的时间内,找出这些课程全部的上课时间。如果假设每门课程每周上课次数不超过5次,那么最多只有5k个元组,因此可以在O(k)的平均时间内找到它们。如果没有该关系“课程”属性上的索引,而是有“日子”和(或)“时刻”属性上的索引,虽然可能要查看远多于O(k)数量的元组(取决于星期一要上多少课,或是某一天的9点要上多少课),但还是能从这种索引中受益。
(d) 在第(4)步中,可以利用“课程-教室”关系中“课程”属性上的索引。在这种情况下,可以在平均为O(1)的时间内检索到所要找的教室。
这样就可以得出这样的结论,有了所有这些合适的索引,可以在O(k)的平均时间内回复这些非常复杂的查询。因为可以假设C.Brown所选课程的数量k 很小,比方说5门左右,那么这一时间通常会特别少,而且特别要指出的是,该时间与所涉及关系的大小都无关。
总结:关系的快速访问
回顾一下我们从渐趋复杂的关系中获得答案的方式是很实用的。首先是在7.8节使用散列表或诸如二叉查找树或(概括化的)特征向量这样的结构实现函数,按照本章中的内容来看就是定义域为键的二元关系。然后,在7.9节中看到,只要关系是二元的,这些概念也适用于定义域不为键的情况。
在8.4节中看到,并不需要要求关系是二元的,可以将属于键的一部分的全部属性作为一个“定义域”集合,而将所有其他属性作为一个“值域”集合。此外,我们在8.4节中还看到定义域不一定要是键。
在8.5节中我们了解到,可以使用某关系上的多个索引结构,提供基于不属于定义域的属性的快速访问。而且在8.6节中我们看到,可以结合多个关系上的索引,在与实际查阅的元组数成比例的时间内执行复杂的信息检索。
8.6.3 习题
1. 假设图8-9中的“课程-学号-成绩”关系不具备“课程-学号”对上的索引,而是只有课程这一个属性上的索引。这会对图8-9所示程序的运行时间造成怎样的影响?如果索引只建立在“学号”属性上呢?
2. 讨论一下如何高效地回应下列查询。在每种情况下都要陈述对中间集合的元素数量(比如,C.Brown所选课程的数量)作出的假设,还要讲出都假设有哪些索引存在。
(a) 找到C.Brown所选课程的所有前提。
(b) 找到会在Turing Aud.上课的所有学生的电话号码。
(c) 找到CS206课程的前提课程的前提。
3. 假设没有索引,那么习题3中的各查询要花多少时间,将其表示为所涉及关系的大小的函数,其中要对所有元组进行迭代,就像本节的那些示例中一样。
8.7 关系代数
我们在8.6节中看到,涉及多个关系的查询可能是相当复杂的。用一种比C语言“高级得多”的语言来表示这样的查询是很实用的,和C语言不同的是,这种语言中的查询在表示我们想要的内容时,比如,“课程”组分等于CS101的所有元组,可以不需要处理诸如在索引中进行查找操作这样的问题。出于这种目的,一种名为关系代数的语言应运而生。
就像任何代数那样,关系代数让我们可以应用代数法则改写查询。因为复杂的查询通常有很多不同的步骤序列,我们要借助这些步骤从存储的数据中得到查询的回应,而且因为不同的步骤序列是由不同的代数表达式表示的,所以关系代数提供了一个将代数作为设计理论的绝佳
例子。其实,这种借助关系代数表达式的变形实现的效率提升,可视作代数的力量在计算机科
学中得到体现的最突出示例。代数变形带来的“优化”查询的能力是8.9节的主题。
8.7.1 关系代数的操作数
在关系代数中,操作数都是关系。与其他代数一样,这里的操作数既可以是常量——在这种情况下就是指定的关系,也可以是表示未知关系的变量。不过,不管是变量还是常量,每个操作数都有特定的模式(为关系中的列命名的属性的集合)。因此,常量参数可能是像下面这样
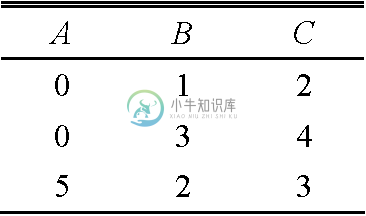
该关系的模式是{A,B,C },它含有3个元组,(0,1,2)、(0,3,4)和(5,2,3)。
变量参数可以用R(A,BC )表示,它表示被称为R 的关系,该关系的各列分别名为A、B 和C,但其组分集合是未知的。如果关系R 的模式{A,B,C }是可以理解或是无关紧要的,就可以将R 当作 操作数。
8.7.2 关系代数的集合运算符
首先要使用的3种运算符是常见的集合元算:并、交、差,我们在7.3节中讨论过这些运算。这里要对这些运算符的操作数提出一个要求:两个操作数的模式一定要相同。这样一来,结果的模式就自然是这两个参数的模式。
示例 8.11
设R 和S 分别是图8-11a和图8-11b中的关系。请注意,这两个关系的模式都是{A,B}。并集运算符会生成这样一个关系,其中各元组要么在R 中,要么在S 中,或者是在两者之中。请注意,因为关系是集合,所以即便某元组可能同时出现在R 和S 中,该元组在得到的关系中也最多只能出现一次,就像本例中的元组(0,1)这样。关系U∪S 如图8-11c所示。
交集运算符会生成由同时出现在两个操作数中的元组构成的关系。因此,关系R ∩S 只含有元组(0,1),如图8-11d所示。差集运算生成的关系包含那些在第一个关系中而不在第二个关系中的元组。关系R-S 如图8-11e所示,具有R 中的元组(2,3),因为该元组不在S 中,而它不含R 中的元组(0,1),因为这一元组也在S 中。
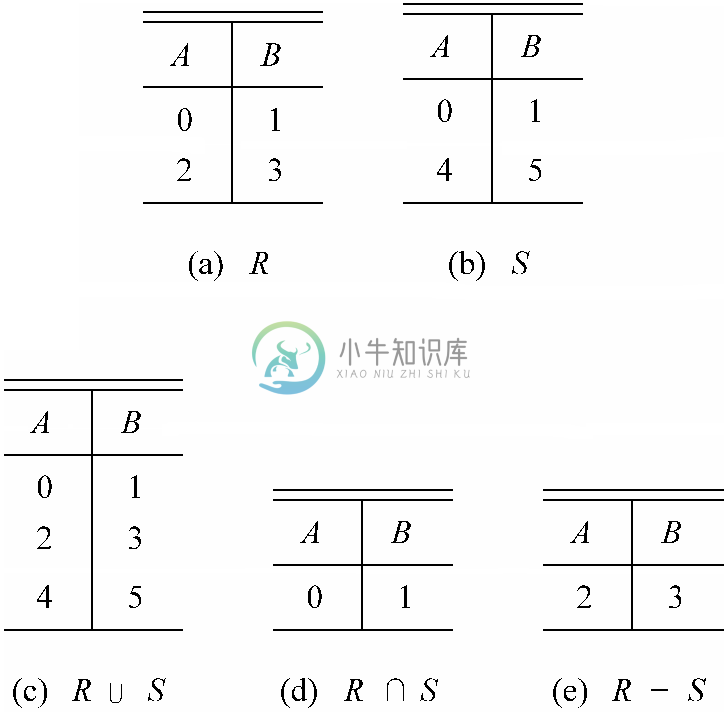
图 8-11 关系代数运算的示例
8.7.3 选择运算符
关系代数中的其他运算符是用来执行本章中研究的这些操作的。例如,我们经常想从关系中提取出满足某些条件的元组,比如从“课程-学号-成绩”关系中提取出“课程”组分为CS101的所有元组。为达成这一目的,要使用选择运算符。该运算符接受一个关系作为操作数,但还要接受一个条件表达式作为“参数”。我们把选择运算符写为σC (R ),其中σ(小写的希腊字母西格玛)是表示选择的符号,C 是条件,而R 是关系操作数。条件C 可以用关系R的模式中的属性以及常数作为操作数。条件C 可以使用的运算符就是常用于C语言条件表达式中的那些,也就是算术比较符和逻辑连接符。
这一运算的结果是模式与R 的模式相同的关系。我们要把在将条件C 中的属性A 替换为元组t 对应列A 的组分时使得条件C 为真的每个元组t 都放入该关系中。
示例 8.12
设CSG 表示图8-1中的“课程-学号-成绩”关系。如果想要那些课程组分为“CS101”的元组,就可以写出如下表达式
σ课程=“CS101”(CSG )
这一表达式的结果是模式与CSG 相同,也就是具有{课程,学号,成绩}模式的关系,而且元组的集合就如图8-12所示。也就是说,只有这些“课程”组分为CS101的元组才能使条件为真。这样一来,当我们用CS101替换了“课程”,条件就成了CS101=CS101。如果该元组的“课程”组分有其他的值,比如EE200,就得到EE200=CS101这样的不成立的表达式。
课程 | 学号 | 成绩 |
|---|---|---|
CS101 | 12345 | A |
CS101 | 67890 | B |
CS101 | 33333 | A- |
图 8-12 表达式σ课程=“CS101”(CSG )的结果
8.7.4 投影运算符
选择运算符会生成某关系删除若干行之后的副本,而我们经常想要生成关系删除若干列之后的副本。为达到这一目的,我们还有用符号π 表示的投影运算符。和选择一样,投影运算符也是接受一个关系作为参数,它还要接受另一个参数,就是从作为参数的关系的模式中选取的属性列表。
如果R 是具有属性集合{A1,…,Ak }的关系,而(B1,…,Bn)是某些A 组成的列表,那么πB1,…,Bn(R),关系R 到属性B1,…,Bn上的投影,是按照以下方式形成的元组集合。取R 中的元组t,提取其属性B1,…,Bn中的组分,假设这些组分分别是b1,…,bn,然后将元组(b1,…,bn)添加到关系πB1,…,Bn(R )中。请注意,R 中可能有不止一个元组在B1,…,Bn中的组分都相同。如果这样的话,这些元组的投影只有一个副本会进入πB1,…,Bn(R ),因为该关系和所有关系一样,不可能含有某一元组的多个副本。
示例 8.13
假设只想看到选修CS101课程的学生的学号。可以应用与示例8.12相同的选择运算,这样就给出了CSG关系中所有对应CS101的元组,不过之后还必须将课程和成绩投影掉,也就是只投影到“学号”上。执行这两项运算的表达式为
π学号(σ课程="CS 101"(CSG))
该表达式的结果是图8-12的关系投影到其“学号”组分上,也就是如图8-13所示的一元关系。
学号 |
|---|
12345 |
图 8-13 选修CS101的学生
8.7.5 关系的联接
最后,我们需要一种方式,用来表示两个关系被关联起来从而可以从一个关系向另一个关系导航的概念。为了达成这一目的,要使用表示为⋈的联接运算符。3假设有两个关系R 和S,其属性集合(模式)分别为{A1,…,An }和{B1,…,Bm }。我们从两个集合中各选出一个属性,比方说是Ai 和Bj,而这些属性将成为以R 和S 为参数的联接运算的参数。
3我们这里描述的“联接”不如关系代数中常见的联接运算更一般化,但它可以用来让我们从这一运算符受益,而不用深入到该主题的所有复杂性中。
要形成R 和S 的写作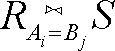 的这种联接,就要从R 中取出各元组r,并从S 中取出各元组s 加以比较。如果元组r 对应Ai 的组分等于元组s对应Bj 的组分,就从r 和s 形成一个元组,否则,就不会从r 和s 的配对中创建元组。要从r 和s 形成元组,就要取r中的组分,后面加上s 中的所有组分,但要去掉对应Bj 的组分,因为它和r 中对应Ai 的组分是相同的。
的这种联接,就要从R 中取出各元组r,并从S 中取出各元组s 加以比较。如果元组r 对应Ai 的组分等于元组s对应Bj 的组分,就从r 和s 形成一个元组,否则,就不会从r 和s 的配对中创建元组。要从r 和s 形成元组,就要取r中的组分,后面加上s 中的所有组分,但要去掉对应Bj 的组分,因为它和r 中对应Ai 的组分是相同的。
关系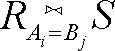 就是上述方式所形成的元组构成的集合。请注意,若R 的Ai 列和S 的Bj 列都没有值出现,则这一关系也可能不含任何元组。在另一种极端情况下,R 中每个元组Ai 组分的值都相同,而该值也出现在S 中每个元组的Bj 组分里。那么,联接得到的关系中元组的数量就等于R 中元组数量乘以S 中元组数量的积,因为元组的每个有序对都能匹配。一般而言,真相就藏在这些极端情况之间的某个地方,R 中的各元组与S 中的一些(而非全部)元组配对。
就是上述方式所形成的元组构成的集合。请注意,若R 的Ai 列和S 的Bj 列都没有值出现,则这一关系也可能不含任何元组。在另一种极端情况下,R 中每个元组Ai 组分的值都相同,而该值也出现在S 中每个元组的Bj 组分里。那么,联接得到的关系中元组的数量就等于R 中元组数量乘以S 中元组数量的积,因为元组的每个有序对都能匹配。一般而言,真相就藏在这些极端情况之间的某个地方,R 中的各元组与S 中的一些(而非全部)元组配对。
联接得到的关系的模式是{A1,…,An ,B1,…,Bj-1,Bj+1,…,Bm },也就是R 和S 中除Bj 之外的全部属性构成的集合。不过,还是可能有属性重名的情况出现,如果说是A 中的某一属性与B 中(除Bj 之外,不是要联接的属性)的某一属性相同。如果出现这种情况,这一对相同的属性中就必须有一个要重命名。
示例 8.14
假设我们要对“课程-日子-时刻”关系(简称CDH)和“课程-教室”关系(简称CR)进行连接。例如,我们可能想知道每间教室都有哪些时间是在上课的。要回应这一查询,就必须将来自CR 的各元组与来CDH 的各元组配对,要求配对的两个元组的课程组分是相同的,也就是说,这两个元组说的是相同的课程。因此,如果在要求二者的“课程”属性相等的情况下联接CR 和CDH,就会得到具有{课程,教室,日子,时刻}模式的关系,它所含的元组(c,r,d,h )满足(c,r )是CR 的元组且(c,d,h )是CDH 的元组这两个条件。定义该关系的表达式为
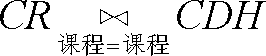
假设CR 和CDH 关系含有图8-2中的那些元组,那么该表达式产生的关系的值就如图8-14所示。
课程 | 教室 | 日子 | 时刻 |
|---|---|---|---|
CS101 | Turing Aud. | M | 9AM |
CS101 | Turing Aud. | W | 9AM |
CS101 | Turing Aud. | F | 9AM |
EE200 | 25 Ohm Hall | Tu | 10AM |
EE200 | 25 Ohm Hall | W | 1PM |
EE200 | 25 Ohm Hall | Th | 10AM |
图 8-14 课程=课程上CR 和CDH 的联接
要知道图8-14中的关系是如何构建的,就要考虑一下CR 的第一个元组,(CS101,Turing Aud.)。我们要检查CDH 中那些“课程”值也是CS101的元组。在图8-2c中,可以看到前3个元组都是能匹配的,而且我们可以由这些元组构建图8-14的前3个元组。例如,CDH 的第一个元组(CS101,M,9AM)与元组(CS101,Turing Aud.)联接,就得到了图8-14的第一个元组。要注意该元组是如何与构成它的两个元组各自对应的。
同样,CR 的第二个元组(EE200,25 Ohm Hall)与CDH 的后3个元组有着相同的“课程”组分。这3个配对就构成了图8-14中的后3个元组。而CR 的最后一个元组(PH100,Newton Lab.)的“课程”组分与CDH 任一元组的“课程”组分都不同。因此,该元组没有对这一联接作出任何贡献。
8.7.6 自然联接
当我们联接两个关系R 和S 时,常会遇到要等同的属性同名的情况。如果此外还有R 和S 没有其他属性同名,那么就可以将联接的参数省略,将其简写为R⋈S。这样的联接就叫作自然联接。
例如,示例8.14中的联接就是自然联接。要等同的属性都叫“课程”,而CR 和CDH 中其他属性的名称都是不同的。因此我们可以将该联接简写为CR⋈CDH。
8.7.7 关系代数表达式的表达式树
就像为算术表达式绘制表达式树那样,可以将关系代数表达式表示为树。叶子都是用操作数标记,也就是用特定的关系或是表示关系的变量来标记。每个内部节点都是由运算符标记的,如果是选择、投影或联接(除了不需要参数的自然联接)运算符,还要包括运算符的参数。各内部节点N 的子节点都是表示应用了节点N 处的运算符的操作数。
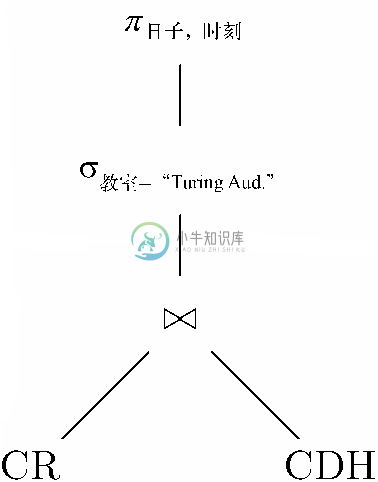
图 8-15 关系代数中的表达式树
示例 8.15
接着示例8.14的情况,假设我们想知道的不是整个CR⋈CDH 关系,而只是想知道在Turing Aud.有课的“日子-时刻”对。然后我们需要取图8-14中的关系,并进行下列操作。
1. 选择那些“教室”组分为“Turing Aud.”的元组;
2. 将这些元组映射到日子和时刻属性上。
按上述次序执行这一系列联接、选择和投影的表达式为
π日子,时刻(σ教室=“Turing Aud”(CR⋈CDH ))
我们可以将这一表达式表示成如图8-15所示的树。在表示联接的节点处计算出的关系就是图8-14所示的关系。而选择节点处的关系是图8-14中的前3个元组,因为它们的“教室”组分中都有Turing Aud.。该表达式树根节点对应的关系如图8-16所示,也就是这3个元组的日子和时刻组分。
日子 | 时刻 |
|---|---|
M | 9AM |
W | 9AM |
F | 9AM |
图 8-16 图8-15中表达式的结果
SQL,基于关系代数的语言
很多现代数据库系统都使用一种名为SQL(Structured Query Language,结构化查询语言)的语言表示查询。尽管对该语言的详细介绍超出了本书范围,不过我们在这里可以用几个例子来给读者一点关于SQL的印象。
SELECT StudentId FROM CSG WHERE Course = "CS101"就是用SQL的方式表示示例8.13的查询,也就是
π学号(σ教室=“CS101”(CSG))
其中
FROM子句表示该查询的对象关系,而WHERE子句给出了选择的条件,SELECT子句则给出了答案投影到的那些属性。很不幸的是,SQL中的关键词SELECT并非对应关系代数中的选择运算符,而是对应投影运算符。举个更复杂的例子,可以将示例8.15中查询π日子,时刻(σ教室=“Turing Aud”(CR⋈CDH ))表示为如下SQL程序。
SELECT Day, Hour FROM CR, CDH WHERE CR.Course = CDH.Course AND Room = "Turing Aud."这里的
FROM子句告诉我们要联接CR 和CDH 这两个关系。WHERE子句的第一部分是联接的条件,它表示CR 的课程属性必须和CDH 的课程属性相等;WHERE子句的第二部分则是选择的条件;而SELECT子句则告诉我们映射中的那些属性。
8.7.8 习题
1. 用关系代数表示8.4节习题2中(a)(b)(c)小题的查询,假设我们想要的答案是完整的元组。
2. 重复习题1的练习,假设想要的只有那些规范中带*的组分。
3. 用关系代数表示8.6节习题2中(a)(b)(c)小题的查询。请注意(c)小题,在将关系与其自身联接时必须要重命名一些属性。
4. 用关系代数表示“C.Brown星期一上午9点在哪里”这一查询。8.6节最后的讨论应该能指示出回应该查询所必需的联接。
5. 画出习题(2)中(a)至(c)的情况、习题3中(a)至(c)的情况以及习题(4)中的查询所对应的表达式树。
8.8 关系代数运算的实现
为关系代数运算使用得当的数据结构和算法可以加快数据库查询的速度。在本节中,我们 将考虑一些相对简单常见的关系代数运算的实现策略。
8.8.1 并交差的实现
这3种基本集合运算的实现方式与在关系和集合中的实现方式相同。可以按照7.4节讨论过的,通过为两个集合排序与合并取两个集合或关系的并集。而交集和差集则可利用相似的技巧求得。如果参加运算的两个关系各含n 个元组,就要花O(n logn)的时间为其排序并用O(n)的时间合并,或者说总共需要O(n logn)的时间。
不过,为关系R 和S 求并集的方式还有很多,而且有些方式还更高效。首先,我们可能不去考虑为同时出现在R 和S 中的元组消除重复副本的事。就是生成R 的副本,比如说,放进链表中,然后将S 的所有元组也添加进该链表,而不去检查S 中的元组是否也出现在R 中。这一操作可以在与R 和S 的大小之和成比例的时间内完成。而这样做的缺点在于,严格地讲,得到的结果并不是R 和S 的并集,因为其中可能存在重复的元组。不过,也许这些重复的存在并无大碍,因为可预期它们很少出现。或者,我们可能发现在后续的阶段中消除这些重复会更方便,比如在取更多关系的并集后进行排序,然后再消除重复。
另一种选择是使用索引。例如,假设R具有属性A上的索引,而该属性是S的键。那么如果要取二者的并集R∪S,首先从S 的元组开始,并依次检查R 的每个元组t。我们会在组分A 中找到t 的值——比方说是a,并使用该索引查找S 中A 组分的值也为a 的元组。如果S 中的这一元组与t 相同,就不要再将t 第二次放入并集中,而如果S 中不存在键的值为a 的元组,或者键值为a 的元组与t 不同,就要将t 加入并集中。
如果索引提供了在给定元组键值的情况下每个元组平均为O(1)的元组查询时间,那么这种方法求并集的平均时间就与R 和S 的大小之和成比例。此外,只要R 和S 都没有重复,那么得到的关系也是没有重复的。
8.8.2 投影的实现
原则上讲,在执行投影运算时,只能检验完每个元组,并略去那些与未出现在投影列表中的属性对应的组分。索引是一点忙都帮不上的。此外,在计算了各元组的投影后,我们可能发现会留下很多重复。
例如,假设有模式为{A,B,C }的关系R,而且要计算πA,B(R )。尽管R 中的元组不可能A、B、C 属性全都相同,但还是可能有很多元组的属性A 和B 会相同而只是对应属性C 的值不同。这样一来,这些元组在投影中全都会得到相同的元组。
因此,在为某关系R 和一列属性L计算了S=πL(R )这样的投影后,必须消除重复。例如,可以为S 排序,然后以排序的次序检查所有元组。那些在次序上与前一个元组相同的元组都要被删除。另一种消除重复的方式是将关系S 看作普通集合。每当我们通过把R 的元组投影到表L中的属性上生成一个元组,就将其插入该集合中。就像所有向集合插入元素的操作那样,如果待插入的元素已经在集合中,就不用做任何事情。散列表这样的结构就很适合表示由投影生成的元组构成的集合S。
如果关系R 中有n 个元组,那么要在消除重复前为关系S 排序所需的时间为O(n logn)。而如果改为在生成S 的元组时对其执行散列操作,而且使用数量与n 成比例的散列表元,那么整个投影运算平均要花O(n)的时间。因此,散列通常要略优于排序。
8.8.3 选择的实现
在执行选择运算S=σC (R )而且没有R 上的索引时,就只能检查R 中的所有元组以应用条件C。不管如何执行选择,只要R 中没有重复,得到的S 中就不会有重复。
不过,如果R 上存在若干索引,就可以利用其中某一索引直接找到满足条件C 的元组,因此就可以避免查看大多数或是所有不满足条件C 的元组。条件C 形如A=b 时的情况最简单,其中A 是R 的某一属性,而b 是某常量。如果R 具有A 上的索引,就可以通过在索引中查找b 来检索满足该条件的所有元组。
如果条件C 是若干条件的逻辑AND,那么可以利用其中某一条件查找使用了索引的元组,然后检查检索到的这些元组,看看有哪些满足其余的条件。例如,假设条件C是
(A=a)AND(B=b)
如果这A 上的索引或是B 上的索引中有某一个或全都存在,就可以选择使用某一个索引。假设有B 上的索引,而且要么A 上没有索引,要么是我们主动选择使用B 上的索引。这样一来,我们就会得到关系R 中B 组分的值为b 的所有元组。这些元组中A 组分为a 的都属于选择运算的结果——关系S,而检索到的其他元组则不属于S。这一选择运算所花的时间是与B 组分的值为b 的元组数量(通常在R 中的元组数和S 中的元组数之间)成比例的。
8.8.4 联接的实现
假设我们想要对模式为{A,B }的关系R 和模式为{B,C }的关系S 进行自然联接。还假设该联接是两个关系的B 属性之间存在相等关系的自然联接。4如何执行这一联接取决于我们能找到属性B 上的何种索引。该问题类似于我们在8.6节中讨论过的那些,当时我们是考虑如何在关系间导航,而导航的本质就是联接。
4这里展示的两个关系分别只有一个属性(分别为A 和C)没有涉及联接,不过这里提到的想法显然可以推广到具有很多属性的关系。
有一种直观而缓慢的联接计算方式,叫作嵌套循环联接。我们会按照如下方式对一个关系中的每个元组与另一关系中的每个元组加以比较。
for R 中的各元素r do
for S 中的个元组s do
if r 和s 的B 属性相同 then
打印结合了r 和s 的
属性A、B、C 的元组
然而,还有很多更高效的联接方式。索引联接就是其中之一。假设S 有属性B 上的索引。那么可以访问R 的各元组t,并找到其B 组分,比方说是b。在S的索引中查找b,这样就能得到B 的值能与t 匹配的所有元组。
同样,如果R 有属性B 上索引,就可以浏览S 的所有元组。对S 中的各元组,我们会使用R 的B 索引查找与之对应的R 的元组。如果R 和S 都有属性B 上的索引,就要任选其一来用。正如我们即将看到的,这会给联接运算所花的时间带来变化。
如果没有属性B 上的索引,利用排序联接还是能比嵌套循环联接做得更好。首先要将R 和S 中的元组合并在一起,不过要重新组织这些元组,使得B 组分成为所有元组的第一个组分,而且要为它们加上一个额外的组分,如果该元组来自关系R,就加上R,而如果该元组来自关系S,就加上S。也就是说,来自关系R 的元组(a,b)就成了(b,a,R ),而来自关系S 的元组(b,c )则成了(b,c,S )。
我们根据第一个组分(也就是b)来为合并后的元组表排序。虽然因为B 值相同而联接的两个关系中元组可能混合在一起了,但是这些元组现在已经是按着次序连续排列了。5我们会沿着已排序表向下,依次访问具有各给定B 值的元组。当到达B 值为b 的元组时,就可以将R 中所有这样的元组与S 中这样的元组配对。因为这些元组都有着相同的B 值,所以它们都要联接,而且生成联接后关系中元组所花的时间是与生成的元组数成比例的,除非是出现R 中没有元组或S 中没有元组的情况。即便是在R中没有元组或S中没有元组的情况下,所花时间仍然与B 值为b 的元组的数量成比例,为的是检查这些元组并在已排序表中跳过这些元组。
5我们可以在排序的同时考虑对最后一个元组(也就是关系名)加以安排,使得来自关系R的具有给定B 值的元组一定会位于来自S 有着相同B 值的元组之前。这样一来,对那些B 值相同的元组而言,来自R 的会先出现,然后是来自S 的那些。
示例 8.16
假设要联接图8-2c所示的CDH 关系与图8-2d所示的CR 关系。在这里,课程属性就扮演着属性B 的角色,日子和时刻属性则一起扮演属性A 的角色,而教室属性就是属性C。CDH 的6个元组和CR 的3个元组首先会各自加上其关系名称。这里不需要重新排列组分,因为两个关系中课程属性都是排在第一位的。当我们对元组加以比较时,首先要比较课程组分,利用词典次序确定哪个课程名称的次序靠前。如果不分先后,也就是说,如果课程名称相同,就要比较最后一个组分,其中CDH 要先于CR。如果还是不分先后,就可以让其中任意一个元组先于另一个元组。
已排好序的元组如图8-17所示。请注意,该表并非关系,因为它所含元组的长度不尽相同。不过,它将对应CS101的元组和对应EE200的元组组织在一起,这样一来就可以很容易地联接这些元组分组了。
| CS101 | M | 9AM | CDH |
| CS101 | W | 9AM | CDH |
| CS101 | F | 9AM | CDH |
| CS101 | Turing Aud. | CR | |
| EE200 | Tu | 10AM | CDH |
| EE200 | W | 1PM | CDH |
| EE200 | F | 10AM | CDH |
| EE200 | 25 Ohm Hall | CR | |
| PH100 | Newton Lab. | CR |
图 8-17 CDH 和CR 中所有元组构成的已排序表
8.8.5 联接方法的比较
假设要联接模式为{A,B }的关系R 和模式为{B,C }的关系S,并设R 和S 分别有r 个元组和s 个元组。还有,设联接中的元组数为m。要记住,如果R 的每个元组都与S 中的每个元组(因为它们都有相同的B 值)联接,那么m 可以有rs 那么大,而如果R 中没有元组的B 值与S中元组的B 值相等,那么m 还可以小到0这么小。最后,假设可以在平均O(1)的时间内查找任意索引中的任意值,就像索引是有着相当大量的散列表元的散列表时能做到的那样。
每种联接方法生产输出都至少要花O(m)的时间。不过,有些方法所花的时间要更多一些。如果使用嵌套循环联接,就要花rs 的时间执行比较。因为m≤rs,所以可以忽略生成输出所花的时间,并说配对所有元组的时间开销为O(rs)。
另一方面,我们可以为这些关系排序。如果使用类似归并排序的算法为含r+s 个元组的表排序,所需的时间就是
O((r+s)log(r+s))
要从已排序表中毗连的元组构建输出元组,就要花O(r+s)的时间检查该表,还要花O(m)的时间生成输出。排序所需的时间主导了O(r+s)项,不过生成输出所花的O(m)既可能大于也可能小于排序的时间。因此通过排序进行联接的算法的运行时间必须包含这两项,这一运行时间就是
O(m+(r+s)log(r+s))
因为m 从不会大于rs,而且(r+s)log(r+s)只有在一些少见的情况下才大于rs(比如,r 或s 为0时),所以可以说排序联接一般而言要比嵌套循环联接更快。
现在假设有关系S 中属性B 上的索引。要花O(r )的时间查看R 的各元组并在索引中查找这些元组的B 组分的值。这时我们必须加上检索对应各B 值的匹配元组以及生成输出元组的时间开销O(m)。因为m既可以大于r 也可以小于r,所以表示该索引联接时间开销的表达式就是O(m+r )。同样,如果有关系R 中属性B 上的索引,就可以在O(m+s )的时间内执行该索引联接。因为除了某些罕见的情形(比如r+s≤1)之外,r 和s 都小于(r+s )log(r+s ),所以索引联接的运行时间要小于排序联接的时间。当然,如果想要进行索引联接,就需要联接中所涉及的某一属性上的 索引,而排序联接则可以对任意关系进行。
8.8.6 习题
1. 假设图8-2a所示的“学号-姓名-地址-电话”关系(SNAP)具有学号属性(键)上的主索引,而且有电话属性上的辅助索引。如果条件C分别为以下3种,那么我们该如何最高效地为查询σC (SNAP )计算回应?
(a) 学号=12345 AND 地址≠“45KumquatBlvd”
(b) 姓名= “C.Brown”AND电话=555-1357
(c) 姓名= “C.Brown”OR电话=555-1357
2. 说明如何通过为示例8.16中合并的元组表排序,来为图8-1中的CSG关系与图8-2a中的SNAP关系进行排序联接。假设是想进行自然联接,或者说是想要“学号”组分上的相等关系。给出排序的结果,就像图8-17那样,并给出联接运算得到的关系中的元组。
3. * 假设要联接关系R 和S,它们各含n 各元组,而且结果中有O(n3/2)个元组。分别写出利用以下各项技术进行联接时大O运行时间的公式,将其表示为n 的函数。
(a) 嵌套循环联接。
(b) 排序联接。
(c) 索引联接,使用R的联接属性上的索引。
(d) 索引联接,使用S的联接属性上的索引。
4. * 我们提出过利用作为某关系的键的属性A 上的索引为两个关系取并集。如果具有索引的属性A不是键,这是否仍为合理的取并集方式?
5. * 假设想使用R 和S 二者之一的某属性A 上的索引计算(a)R∩S;(b)R-S。能否取得与两个关系大小之和接近的运行时间?
6. 如果要将关系R 投影到含有R 的键的属性集合上,是否需要消除重复?为什么?
8.9 关系的代数法则
就像其他代数那样,通过对表达式进行变形,通常能“优化”表达式。也就是说,我们可以接受一个求值开销很大的表达式,并将其转换成求值开销较小的等价表达式。对算术或逻辑表达式的变形有时能节省一些运算,而对关系代数表达式进行合适的变形,可以节省几个数量级的求值时间。因为优化过的和未优化的关系代数表达式在运行时间上有着巨大的差异,所以如果程序员要用非常高级的语言(比如我们在8.7节中提过的SQL语言)编程,优化这种表达式的能力就是很关键的。
8.9.1 涉及并交差的法则
7.3节涵盖了用于集合并交差运算的主要代数法则。这些法则也能应用到集合的特例,关系上,不过读者应该记住关系模型的要求,就是运算所涉及关系的模式必须相同。
8.9.2 涉及联接的法则
从某种意义上讲,联接运算符是可交换的,而从另一种意义上讲,它又不是可交换的。假设要计算自然联接R⋈S,其中R 具有属性A 和B,而S 具有属性B 和C。那么R⋈S 的模式中的各列按次序排列就是A、B、C。如果是求S⋈R,可以得到本质上相同的元组,不过各列的次序是B、C、A。因此,如果我们坚信各列的次序并非无关紧要,那么联接就不具交换性。不过,如果我们认可连带列名一起整列交换的关系其实是相同的关系,就可以认为联接是可交换的,在这里我们要采纳这一观点。
联接运算符并不总是符合结合律。例如,假设有模式分别为{A,B }、{B,C }和{A,D }的3个关系R、S 和T。假设要取自然联接(R⋈S )⋈T,其中首先要让R 和S 的B 组分相等,接着让结果的A 组分与关系T 的A 组分相等。如果是从右边关联,就得到R⋈(S⋈T )。关系S 和T 的模式分别为{B,C }和{A,D }。没有办法选择令其相等以达到自然联接效果的属性对。
不过,在某些条件下结合律对联接运算来说是成立的。我们将如下公式的证明留给读者作为练习
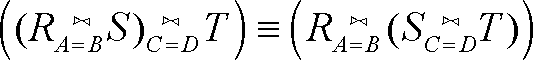
只要A 是R 的属性,B 和C 是S 的两个不同属性,而D 是T 的属性就行。
8.9.3 涉及选择的法则
关系代数最实用的法则涉及选择运算符。如果选择的条件就像实践中常见的那样是要求指定的组分有特定的值,则选择运算的结果关系中的元组数要比原关系的元组数少很多。因为一般而言当运算应用到较小的关系上时所花的时间较少,所以尽可能早地应用选择运算是极为有利的。就代数学而言,如果想早点应用选择运算,就要动用代数法则让选择运算符沿着表达式树向下传递,达到其他运算符下方。
这种法则的一个例子就是
(σC (R⋈S ))≡(σC(R )⋈S )
只要条件C 中提到的属性都是关系R 的属性,它就成立。同样,如果条件C 提及的所有属性都是S 的属性,就可以使用如下法则将选择运算符下压到S
(σC(R⋈S))≡(R⋈σC(S))
这两条法则都称为选择的下压(selection pushing)。
当选择中的条件很复杂时,可能要用一种方式下压一部分,而用另一种方式下压另一部分。为了将选择分割为两个或多个部分,就需要法则
σC AND D(R )≡σC(σD(R ))
请注意,如果这些分割出的部分用AND相连,就只能将条件分为两个部分——这里是C 和D。直觉上讲,当我们为C 和D 这两个条件的AND进行选择时,要么是检查关系R 中的所有元组,看看这些元组是否同时满足C 和D,要么是检查R 的所有选择,选出那些满足条件D 的,然后再检查满足条件D 的元组,看看其中有哪些满足条件C。我们将该法则称为选择的分割(selection splitting)。
另一种必要的法则是选择的交换律。如果要对某关系应用两次选择,那么应用这些选择的次序是无关紧要的,选出的元组都会是相同的。我们可以正式地将其写为,对任何条件C 和D,有
σC(σD(R ))≡σD(σC(R ))
示例 8.17
我们再来看看8.6节中考虑过的复杂查询:“C.Brown星期一上午9点在哪里?”这一查询涉及4个关系上的导航:
1. CSG(课程-学号-成绩);
2. SNAP(学号-姓名-地址-电话);
3. CDH(课程-日子-时刻);
4. CR(课程-教室)。
为了得出表示该查询的代数表达式,首先可以求这4个关系的自然联接。也就是通过让学号组分相等连接CSG 和SNAP。可以把该运算视为对“课程-学号-成绩”元组进行扩展,为该元组加上所提及学生的姓名、地址和电话号码。当然,我们不会希望用这种方式存储数据,因为这会迫使我们为某学生选修的每门课程将该学生的这些信息重复一遍。不过,我们并不是要存储这些数据,而只是要设计表达式计算它。
通过让课程组分相等,我们要将CSG⋈SNAP 的结果与CDH 联接。这次联接会取各CSG 元组(已经扩展了学生信息),为每个上课时段制作一个副本,并将各元组扩展为具有一对可能“日子-时刻”值。最后要将(CSG⋈SNAP )⋈CDH 的结果与CR 联接,还是让课程组分相等,结果就是通过添加带有某一上课时段所在教室的组分扩展了各元组。得到的关系模式为:
{课程,学号,成绩,姓名,地址,电话,日子,时刻,教室}
而元组(c,s,g,n,a,p,d,h,r )的含义就是:
1. 学生s 选修了课程c 并拿到了g 的成绩;
2. 学号为s 的学生的姓名是n,他(她)的地址是a 而且电话号码为p;
3. 课程c 是在教室r 上课,而且该课程某一次上课时间是d 日的h 时。
对该元组集合,必须应用将考量限制到相关元组的选择,也就是姓名组分为“C.Brown”,日子组分为“M”,而且“时刻”组分为“9AM”的元组。假设C.Brown最多选修了一门在星期一上午9点上课的课程,这样的元组就最多只有一个。因为我们想要的回应是该元组的“教室”组分,所以要通过投影到“教室”属性上来完成表达式。表示这一查询的表达式树如图8-18所示。它由4路联接组成,接着是选择,然后是投影。
如果按照图8-18这样的写法为该表达式求值,就要通过联接CSG、SNAP、CDH 和CR 构建一个巨大的关系,然后将其限制到一个元组,再将该元组投影到一个组分上。请记住,由8.6节我们可知并不一定要构建如此庞大的关系,而是可以“将选择沿着树向下压”,从而限制联接运算中涉及的关系,因此就大大限制了我们要构建的关系的大小。
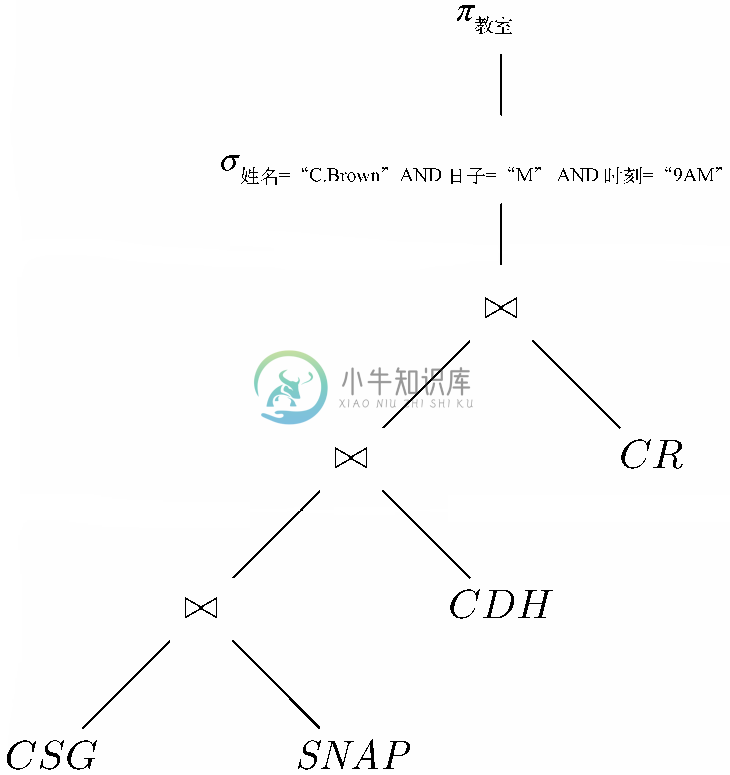
图 8-18 确定C.Brown星期一上午在哪里的初始表达式
第一步如图8-19a所示。请注意,选择只涉及姓名、日子和时刻属性。它们中没有一个来自图8-18顶层联接的右操作数,而都来自左侧,也就是CSG、SNAP 和CDH 的联接。因此可以将选择压到顶层联接之下,并只将其应用到该运算的左操作数,一如我们在图8-19a中所见。
现在就没法继续下压选择运算符了,因为所涉及的姓名属性来自图8-19a中层联接的左操作数,而其他两个属性,日子和时刻,则来自其右操作数,CDH 关系。因此必须分割选择中的条件,它是3项条件的AND,可以分割成3个选择,不过在本例中只要把姓名=C.Brown这一条件与其他两个分开即可,分割的结果如图8-19b所示。
现在,涉及日子和时刻的选择可以下压到中层联接的右操作数,因为右操作数是同时具有日子和时刻属性的CDH 关系。然后另一个涉及姓名的选择就可以下压到中层联接的左操作数,因为该操作数是CSG⋈SNAP,含有姓名属性。这两项改变会带来如图8-19c所示的表达式树。
最后,姓名上的选择涉及SNAP 的属性,因此可以将该选择下压到底层联接的右操作数。这一改变如图8-19d所示。
现在该表达式给我们的计划与8.6节中为该查询设计的计划几乎是相同的。首先从图8-19d总的表达式底层开始,找到名为C.Brown的学生的学号。把姓名=C.Brown的SNAP 元组与CSG 关系联接,得到C.Brown选修的课程。当我们把第二次选择应用到CDH 关系时,就得到星期一上午9点上课的课程。因此图8-19d所示的中层联接给了我们C.Brown选修了而且在星期一上午9点上课的课程。而顶层联接则得到这一时间这门课程上课的教室,而这里的投影就给出了这些教室作为回应。
这一计划与8.6节中的计划主要的差别在于,后者是先将元组中无用的组分投射走,而这里的计划则是要带着这些组分直到最后。因此要完成对关系代数表达式的优化,就需要可以将投影沿着树向下压的法则。正如我们将在8.9.4节中看到的,这些法则与用于选择的法则不尽相同。
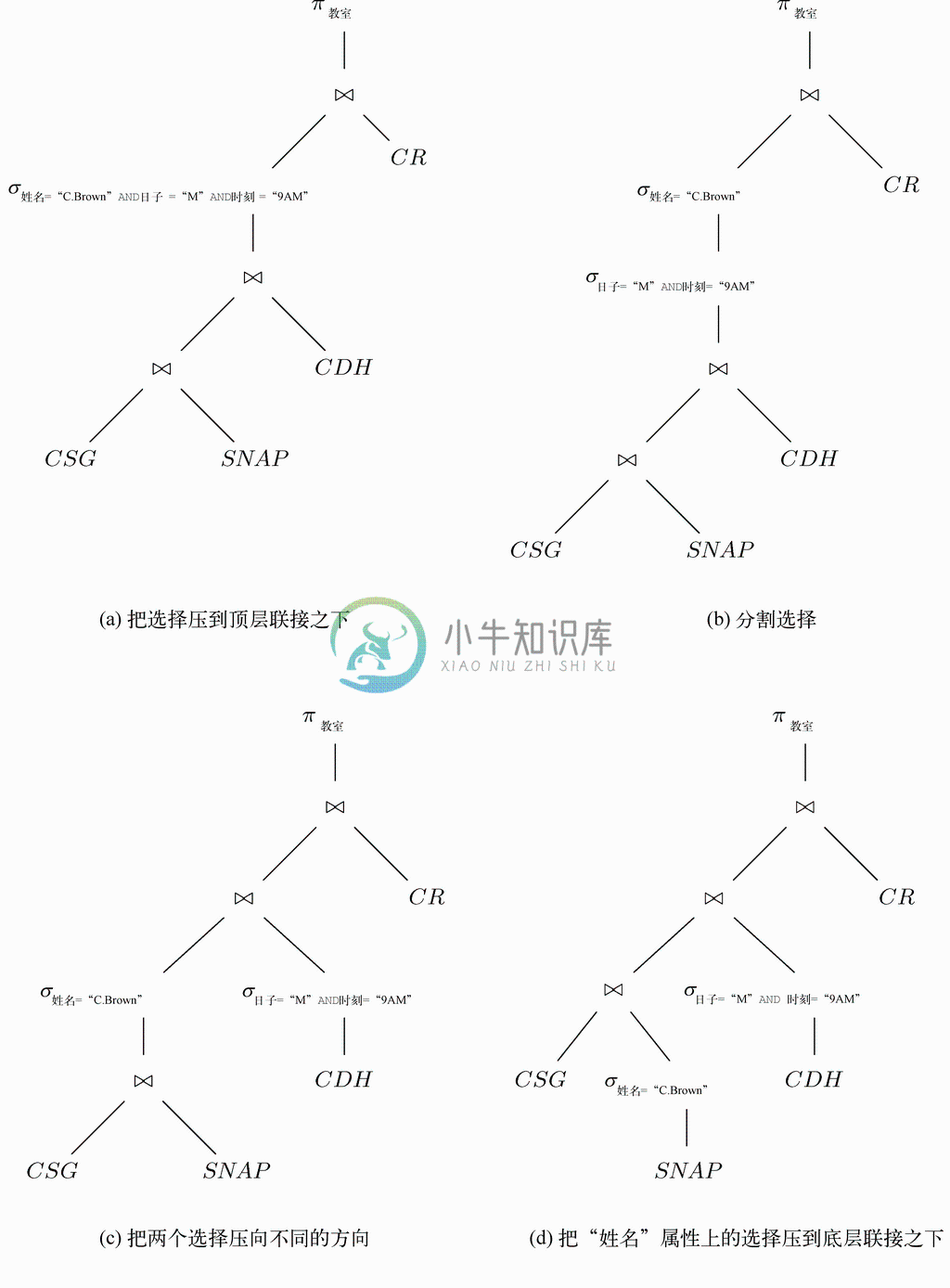
图 8-19 将选择运算下压
8.9.4 涉及投影的法则
首先,与选择可以被压到并集、交集或差集之下(只要我们将选择同时压向两个操作数)不同的是,投影只能压到并集之下。也就是,法则
(πL(R∪S ))≡(πL(R )∪πL(S ))
成立。不过,πL(R∩S )不一定等同于。例如,假设R 和S 都是模式为{A,B }的关系,R 只包含元组(a,b),而S 只包含元组(a,c)。那么πA(R )∩πA(S )只含(单组分)元组(a),而πA(R∩S )则不含元组(因为R ∩S 为空)。因此就有了的情况。
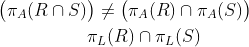
将投影压到联接以下是有可能的。一般而言,我们需要为联接运算的每个操作数都加上投影运算符。如果有表达式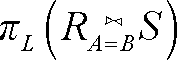 ,那么所需的R 的属性是那些出现在属性表L 中的属性,以 及联接运算所依据的来自关系R 的属性A。同样,我们需要S 中那些在属性表L 上的属性,以及联接依据的属性B,不管B 是否在L 中。正式地讲,将投影压到联接之下的法则是
,那么所需的R 的属性是那些出现在属性表L 中的属性,以 及联接运算所依据的来自关系R 的属性A。同样,我们需要S 中那些在属性表L 上的属性,以及联接依据的属性B,不管B 是否在L 中。正式地讲,将投影压到联接之下的法则是
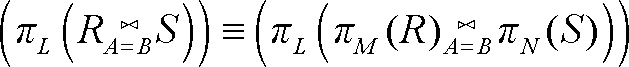
其中
1. 表M 是由L 中那些在R 模式中的属性构成,如果属性A 不在L 中,就还要加上A;
2. 表N 是由L 中那些在S 模式中的属性构成,如果属性B 不在L 中,就还要加上B。
要注意到,应用这一投影下压法则的实用方式是从左向右应用,即便我们因此引入了两项额外的投影而且没有减少任何运算。原因在于,尽早地投影出那些可以投影的属性(也就是将投影尽可能压到表达式树靠下的位置)通常是有利的。如果联接属性A 不在表L 中,我们在联接运算后可能仍然要执行到表L 上的投影运算。回想一下另一个联接属性,来自S 的B 属性,无论如何都不会出现在联接中。
有时候,表M 和(或)表N 分别使用R 或S 的所有属性组成的。如果这样,就没理由执行这一的投影了,因为它是没有效果的,除非关系的各列可能是种毫无头绪的排列。因此我们要使用如下法则。
πL(R )≡R
表明了表L 是由R 的模式中的所有属性组成的。请注意这一法则是认可“整列交换不会改变关系”这一观点的。
还有一种我们不想进行投影的情况。假设子表达式πL(R )是某更大表达式的一部分,并设R 是单一关系而不是涉及运算符的表达式。还假设在表达式树中该子表达式之上的位置还有另一个投影。现在,要执行R 上的投影就要求我们检查整个关系,而不管有没有索引的存在。如果我们带着R 中未在表L 上的属性继续向下,直到下一次有机会将这些属性投影掉,就经常能节省大量时间。
例如,在接下来的示例中我们将讨论子表达式
π课程,学号(CSG)
它的作用是去掉成绩。因为整个(表示示例8.17中的查询的)表达式最终要将焦点集中在CSG 关系的少量元组上,所以最好是迟一些再将成绩投影走,这样做就避免了检查整个CSG 关系。
示例 8.18
我们将图8-19d变成下压投影运算。根节点处的投影会首先被压到顶层联接之下。投影表只有
“教室”组成,而联接运算两侧的联接属性都是“课程”。因此,在左边我们只投影到“课程”上,因为“教室”不是左侧表达式中的属性。而该联接的右操作数则要投影到“课程”和“教室”属性上。因为这两个属性都是操作数CR中的,所以可以略去这一投影。得到的表达式如图8-20a所示。
现在,可以将到“课程”属性上的投影压到中层联接之下。因为“课程”还是联接运算两边的联接属性,所以我们在中层联接下引入了两个π课程运算符。由于中层联接的结果只有“课程”属性,因此我们不再需要该联接之上的投影了,新表达式就如图8-20b所示。请注意,涉及的两个关系的元组都只有一个组分“课程”的这次联接,其实是集合的交集。这是说得通的,它是C.Brown所选的课程的集合与星期一上午9点上课的课程的集合的交集。
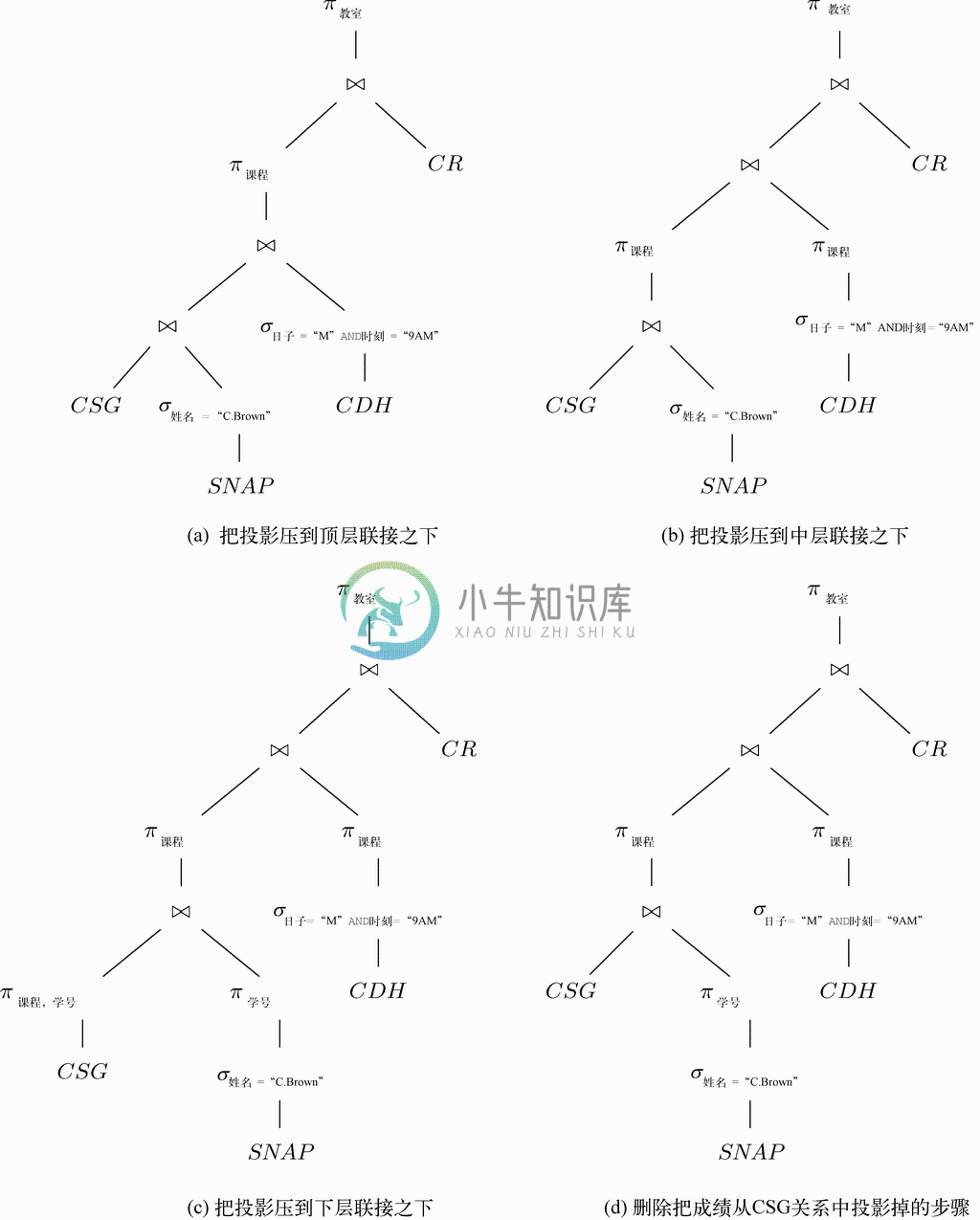
图 8-20 将投影向下压
至此,我们需要将π课程压到底层联接之下。两侧的联接属性都是学号,因此左侧的投影属性表就是(课程,学号),而右侧的则就是学号,因为课程不是右侧表达式中的属性。得到的表达式如图8-20c所示。
最后,正如我们在示例之前的内容中提过的,不立即将CSG 关系中的成绩属性投影掉是有利的。在该投影之上我们会遇到运算符π课程,不管怎样它都会把成绩从中去掉。如果使用图8-20d所示的表达式,从本质上讲就有了8.6节中为这一查询设计的计划。也就是说,表达式π学号(σ姓名="C.Brown"(SNAP ))给了我们名为C.Brown的学生的学号,而后面跟着投影π课程的第一次联接就给了我们那些学生选修的课程。如果关系SNAP 关系有姓名属性上的索引,且CSG 关系有学号属性上的索引,那么这些运算就能很快执行完。
子表达式π课程(σ日子="M" AND 时刻="9AM"(CDH ))的值就是在星期一上午9点上课的课程,而中层联接会将这些结合求交集,以给出姓名为C.Brown的学生选修了的在星期一上午9点上课的课程。最后,后面带着投影的顶层联接会在CR 关系中查找这些课程(如果有课程属性上的索引将会是很快的操作),并生成与之关联的教室作为回应。
8.9.5 习题
1. * 证明:只要A 是R 的属性,B 和C 是S 不同的属性,而且D 是T 的属性,就有
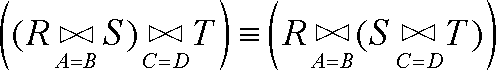
为什么B≠C 这一条件很重要?提示:请记住,这样的属性在联接执行时会消失掉。
2. * 证明:只要A 是R 的属性,B 是S 的属性,C 是T 的属性,就有
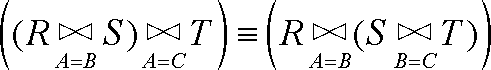
3. 取8.7节习题3中的各关系代数查询,并将选择和投影运算下压到尽可能远的位置。
4. 我们来对关系代数运算得到的关系中元组的数量进行如下全面简化。
(i) 每个操作数关系含有1000个元组。
(ii) 在联接分别具有n 个和m 个元组的关系时,得到的关系中含有mn/100个元组。
(iii) 在执行条件为k 个条件(每个条件都会让一种属性等于一个常数值)的AND的选择时,我们将关系的大小除以10k。
(iv )在执行投影时,关系的大小不变。
此外,让我们来估计一下用为每个内部节点计算出的关系大小之和给表达式求值的开销。给出图8-18、图8-19a到图8-10d和图8-20a到图8-20d中各表达式的开销。
5. * 证明选择的下压法则
(σC(R⋈S ))≡(σC(R )⋈S )
提示:要证明两个集合相等,通常最简单的方式就是如7.3节中描述的那样,证明两个集合互为对方的子集。
6. * 证明以下法则。
(a) (σC(R∩S ))≡(σC(R )∩σC(S ))
(b) (σC(R∪S ))≡(σC(R )∪σC(S ))
(c) (σC(R-S ))≡(σC(R )-σC(S ))
7. * 给出反例,证明下式不成立。
(πL(R-S )≡(πL(R )-πL(S ))
8. ** 有些时候,可以利用“等价关系”
σC(R⋈S )≡(σC(R )⋈σC(S )) (8.1)
将选择同时沿着联接的两个方向下压。
(a) 在什么情形下(8.1)式真正是等价的?
(b) 如果(8.1)式是有效的,不是将选择只压向R 或只压向S,那么何时使用该法则会更合适?
8.10 小结
大家在学习过本章后应该记住以下要点。
被称为“关系”的二维表是一种多功能的信息存储方式。
关系中的行称为“元组”,而列称为“属性”。
“主索引”将关系的元组表示为数据结构,而且会分配这些元组,使得利用某些属性(表示索引的“定义域”)的值的运算会因为这种分配变得容易。
关系的“键”是能唯一确定该关系其他属性的值的属性构成的集合。通常主索引会使用键作为其定义域。
“辅助索引”这种数据结构可以简化指定了某一特定属性(通常不是主索引对应的定义域中的属性)的运算。
关系代数是一种高级表示法,用来表示与一个或多个关系有关的查询。其基本运算包括并、交、差、选择、投影和联接。
有很多实现联接的方式要比直观的“嵌套循环联接”(它会将一个关系中的各个元组与另一个关系中的各元组一一配对)更高效。索引联接和排序联接的运行时间接近于查看所涉及的两个关系并生成联接结果所需的时间。
关系代数表达式的优化可以大大缩短表达式求值的运行时间,因此如果实践中用于表示 查询的语言是基于关系代数的,这种优化是很关键的。
改善给定表达式运行时间的方式有很多种,将选择往下压通常是其中收益最大的。
8.11 参考文献
对数据库,特别是那些基于关系模型的数据库的进一步研究可以在Ullman [1988]中找到。
尽管不少更早的文献中也包含了一些这样的概念,但是Codd [1970]的论文通常被视为关系数据模型的起源。最早使用这一模型实现的系统是伯克利的INGRES(Stonebrake et al. [1976]) 和IBM的System R(Astrahan et al. [1976])。后者是8.7节中简述过的SQL语言的起源,而且至今仍出现在很多数据库管理系统中,见Chamberlin et al. [1976]。还可以在UNIX的awk命令中找到关系模型(Aho, Kernighan, and Weinberger [1988])。
Aho, A. V., B.W. Kernighan, and P. J.Weinberger [1988]. The AWK programming Language, Addison-Wesley, Reading, Mass.
Astrahan, M. M. et al. [1976].“System R: a relational approach to data management,”ACM Trans. on Database Systems 1:2, pp. 97–137.
Chamberlin, D. D. et al. [1976]. “SEQUEL 2: a unified approach to data definition, manipulation, and control,” IBM J. Research and Development 20:6, pp. 560–575.
Codd, E. F. [1970]. “A relational model for large shared data banks,” Comm. ACM 13:6, pp. 377–387.
Stonebraker, M., E. Wong, P. Kreps, and G. Held [1976]. “The design and implementation of INGRES,” ACM Trans. on Database Systems 1:3, pp. 189–222.
Ullman, J. D. [1988]. Principles of Database and Knowledge-Base Systems (two volumes) Computer Science Press, New York.

