第 10 章　模式、自动机和正则表达式

优质

小牛编辑

131浏览

2023-12-01

模式是具有某个可识别属性的对象组成的集合。字符串集合就是一类模式，比如C语言合法标识符的集合，其中每个标识符都是个字符串，由字母、数字和下划线组成，开头为字母或下划线。另一个例子是由只含0和1的给定大小数组构成的集合，读字符的函数可以将其解释为表示相同符号。图10-1就展示了全都可以解释为字母A的3个7×7数组。所有这样的数组就可以构成模式“A”。

0001000　　　0000000　　　0001000
0011100　　　0010000　　　0010100
0010100　　　0011000　　　0110100
0110110　　　0101000　　　0111110
0111110　　　0111000　　　1100011
1100011　　　1001100　　　1000001
1000001　　　1000100　　　0000000

图 10-1　模式“A”的3个实例

与模式相关的两个基本问题是它们的定义与它们的识别，这是本章以及第11章的主题。模式的识别是诸如图10-1所示的光学字符识别（Optical Character Recognition，OCR）这样的任务中不可或缺的一部分。在某些应用中，程序中模式的识别是编译过程，也就是将程序从一种语言（比方说C语言）翻译成另一种语言（比如机器语言）的过程的一个重要部分。

模式应用在计算机科学中还有其他很多例子。模式在设计用于组成计算机和其他数字设备的电子电路的过程中扮演着关键的角色。它们也可以用在文本编辑器中，让我们可以查找特定单词或特定字符串集合的实例，比如“字母if之后跟着任意由then开头的字符序列”。大多数操作系统允许用户在命令中使用模式，例如，UNIX命令“ls *tex”就会列出所有以3字符序列“tex”结尾的名称。

人们围绕着模式的定义和识别建立起了一套庞大的知识体系。这一理论被称为“自动机理论”或“语言理论”，而其基本定义和技术都是计算机科学的核心部分。

10.1　本章主要内容

本章处理的是由字符串集合组成的模式，我们在本章中将会学习以下内容。

“有限自动机”是一种基于图的模式指定方式。有限自动机又分为两种：确定自动机（10.2节）和非确定自动机（10.3节）。
可以用简单的方法把确定自动机转换成识别其模式的程序（10.2节）。
可以利用10.4节介绍的“子集构造”，把非确定自动机转换成识别相同模式的确定自动机。
正则表达式是种代数，用来描述可由自动机描述的同类模式（10.5节到10.7节）。
正则表达式可转换为自动机（10.8节），反之亦然（10.9节）。

我们还要在第11章中讨论串模式，其中会引入一种名为“上下文无关文法”的递归表示法来定义模式。我们将看到这种表示法可以描述没法用自动机或正则表达式表示的模式。不过，在很多情况下，文法都不如自动机或正则表达式那样容易转换为程序。

10.2　状态机和自动机

用来查找模式的程序通常有着特殊的结构。我们可以在代码中确定某些位置，在这些位置可以得知与程序寻找模式实例的过程有关的特殊信息。我们将这些位置称为状态。而程序的整体行为可以视作程序随着读入输入从一种状态转移到另一种状态。

要让这些概念变得更具体，可以考虑一个具体的模式匹配问题：“哪些英语单词按次序含有5个元音字母？”要回答这一问题，可以使用很多操作系统中都能找到的单词表。例如，在UNIX系统中可以在文件/usr/dict/words中找到这样的表，表中每一行都含有一个常用单词。在该文件中，一些含多个元音字母的单词是按以下次序排列的：

abstemious
facetious
sacrilegious

我们来编写一个简单的C语言程序，检查某个字符串并确定5个元音字母是否按次序出现在该字符串中。从字符串的开头开始，该程序首先会查找到a。我们会说该程序处于“状态0”，直到它发现一个a，然后它就进入“状态1”。在状态1中，它会查找字母e，而且当它找到一个之后，就会进入“状态2”。该程序会继续按照这种方式运行，直至到达查找字母u的“状态4”。如果它找到u，那么该单词就是按次序含有5个元音字母，这个程序就能进入一个用于接受的“状态5“。不需要再扫描单词的其余部分，因为已经可知，不管u后面有哪些字母，该单词都是满足条件的。

可以这样解释状态i，就是对i=0、1、…、5，程序已经按次序遇到了前i个元音字母。这6个状态总结了程序在从左到右扫描其输入的过程中需要记住的所有内容。例如，在状态0中，尽管该程序在查找a，但它不需要记住是否已经看到了e。原因在于这样的e不可能先于任何a，因此不能作为序列aeiou中的e。

这种模式识别算法的核心是图10-2中的findChar(pp,c)函数。该函数的参数是pp——指向字符串的指针的地址，以及所需的字符c。也就是说，pp是“指向指向字符的指针的指针”。函数findChar会查找字符c，并且顺便会移动已给定地址的指针，直到该指针指向超过字符c或该串结尾的位置。它返回BOOLEAN类型的值，就是我们定义的与int相同的类型。正如在1.6节中讨论过的，我们预期BOOLEAN类型的值只有TRUE和FALSE，它们分别被定义为1和0。

在第(1)行，findChar会检查当前由pp指示的字符。如果它既不是所需的字符c，也不是C语言中标记字符串末端的字符“\0”，那么在第(2)行我们会移动pp指向的该指针。第(3)行的测试会确定我们是否因为遍历完该串而停止。如果是，就返回FALSE，否则前移该指针并返回TRUE。

      #include <stdio.h>

      #define TRUE 1
      #define FALSE 0
      typedef int BOOLEAN;

      BOOLEAN findChar(char **pp, char c)
      {
 (1)      while (**pp != c && **pp != '\0')
 (2)          (*pp)++;
 (3)      if (**pp == ’\0’)
 (4)          return FALSE;
          else {
 (5)          (*pp)++;
 (6)          return TRUE;
          }
      }

      BOOLEAN testWord(char *p)
      {
          /* 状态 0 */
 (7)      if (findChar(&p, 'a'))
              /* 状态 1 */
 (8)          if (findChar(&p, 'e'))
                  /* 状态 2 */
 (9)              if (findChar(&p, 'i'))
                      /* 状态 3 */
(10)                  if (findChar(&p, 'o'))
                          /* 状态 4 */
(11)                      if (findChar(&p, 'u'))
                              /* 状态 5 */
(12)                          return TRUE;
(13)      return FALSE;
      }

      main()
      {
(14)      printf("%d\n", testWord("abstemious"));
      }

图 10-2　找到带有子序列aeiou的单词

在图10-2中，接下来是testWord(p)函数，它可以区分由p指向的字符串是否按次序含有所有元音字母。该函数在第(7)行前从状态0开始。在该状态中它在第(7)行调用findChar，其中第二个参数是a，用来查找字母a。如果它找到了a，findChar就会返回TRUE。因此在第(7)行如果findChar返回了TRUE，程序就会转移到状态1，其中在第(8)行会对e进行相似的测试，从第一个a之后开始扫描该字符串。因此它会继续查找元音字母，直到第(12)行，如果它找到了字母u，就会返回TRUE。如果有任何一个元音字母未被找到，控制权就会转移到第(13)行，在该行中testWord会返回FALSE。

第(14)行的主程序会测试特定的字符串“abstemious”。在实践中，我们可能会对文件中的所有单词反复使用testWord，以找出那些按次序含有5个元音字母的单词。

10.2.1　状态机的图表示

我们可以把图10-2中这种程序的行为用图表示出来，其中图的节点表示该程序的各个状态。更重要的可能在于，可以通过设计图从而设计出程序，并机械化地将图转化成程序，要么自己动手做，要么利用某种为这个目的编写的程序设计工具。

表示程序状态的图都是有向图，它们的弧都是用字符集标记的。如果当我们在状态s 时，刚好只有当看到集合C 中的一个字符时才能行进到状态t，就存在从状态s 到状态t 的标号为字符集C 的弧。这些弧叫作转换（transition）。如果x 是字符集C 中的某个字符，它标记了从状态s 到状态t 的转换，就说“进行了针对x 的到状态t 的转换”。在集合C 为单元素集{x }这种常见的情况下，我们会使用x 作为该弧的标号，而不用{x }。

我们还会给某些节点标记接受状态（accepting state）。当到达这些状态之一时，就找到了模式并要“接受”它。按照惯例，接受状态是用双层圆圈表示的。最后，这些节点之一会被指定为起始状态，也就是开始模式识别过程所在的状态。我们用一条不知道来自何方的进入箭头表示起始状态。这样的图就被称为有限自动机，或就叫自动机。在图10-3中可以看到自动机的一个例子。

{%}

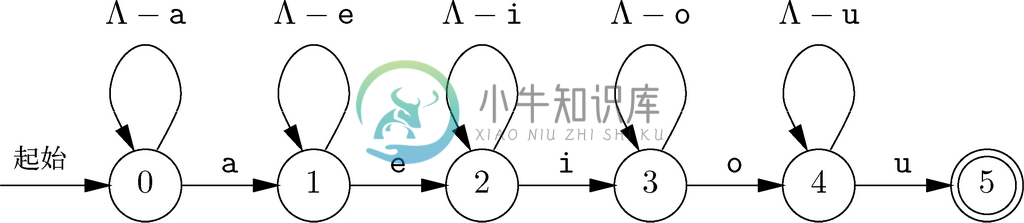
图 10-3　识别含子序列aeiou的字符序列的自动机

从概念上讲，自动机的行为其实很简单。可以想象，自动机接收一列已知字符作为输入序列。它从起始状态开始读输入序列的第一个字符。根据第一个字符的不同，它进行的转换可能是转换到同一状态，也可能是转换到另一状态。这种转换可用自动机的图来表示。然后自动机会读第二个字符，并作出合适的转换，等等。

示例 10.1

对应图10-2中testWord函数的自动机如图10-3所示。在该图中，我们使用了下面都要遵守的一个约定，用希腊字母Λ（拉姆达）代表所有大写字母和小写字母组成的集合。还要用Λ-a这样的简写形式表示除a之外所有大小写字母组成的集合。

节点0是起始状态。针对除了a之外的任意字母，我们都会保持状态0，不过遇到a就要进入状态1。同样，一旦到达状态1，就会停留在状态1，除非看到e，在看到e的情况下就要进入状态2。接下来，当看到i然后看到o时就分别到达状态3和状态4。除非看到u并进入唯一的接受状态——状态5，否则我们会停留在状态4中。再没有任何从状态5出发的转换了，因为我们不再检测待测单词的其余字符，而是要返回TRUE，声明我们已成功完成测试。

在状态0到状态4中遇到空白（或其他非字母字符）也是没有价值的，我们不会进行任何转换。在这种情况下，处理会停止，而且，因为我们现在未到达接受状态，所以会拒绝该输入。

示例 10.2

接下来的例子来源于信号处理。这里不再把所有字符作为自动机可能接收到的输入，而是只允许输入0和1。我们要设计的这种特殊自动机有时也称为反弹过滤器（bounce filter），它接受0和1组成的序列作为输入。该自动机的目的就是“平滑”该序列，方法是将由1包围的一个0当作“噪音”，并把这个0替换为1。同样，由0包围的一个1也会被当作噪声并被0替代。

这里举一个反弹过滤器使用方式的例子，我们可以逐行扫描某数字化的黑白图像。该图像的每一行其实都是0和1组成的序列。因为图片有时候会因胶片瑕疵或拍摄问题造成有一些小点颜色错误，所以，为了减少图像中不同区域的数量，并让我们将精力放在“真实”的特色而非那些虚假的特征上，消除这样的点是很实用的。

图10-4表示的就是对应该反弹过滤器的自动机。其中的4种状态解释如下：

(a) 我们已经看到至少在一行中含两个0的一列0；

(b) 我们已经看到一列0后面跟着一个1；

(d) 我们已经看到一列1后面跟着一个0。

状态a 被指定为起始状态，表示我们的自动机进行处理时就好像在输入之前有一个看不见的前缀0序列那样。

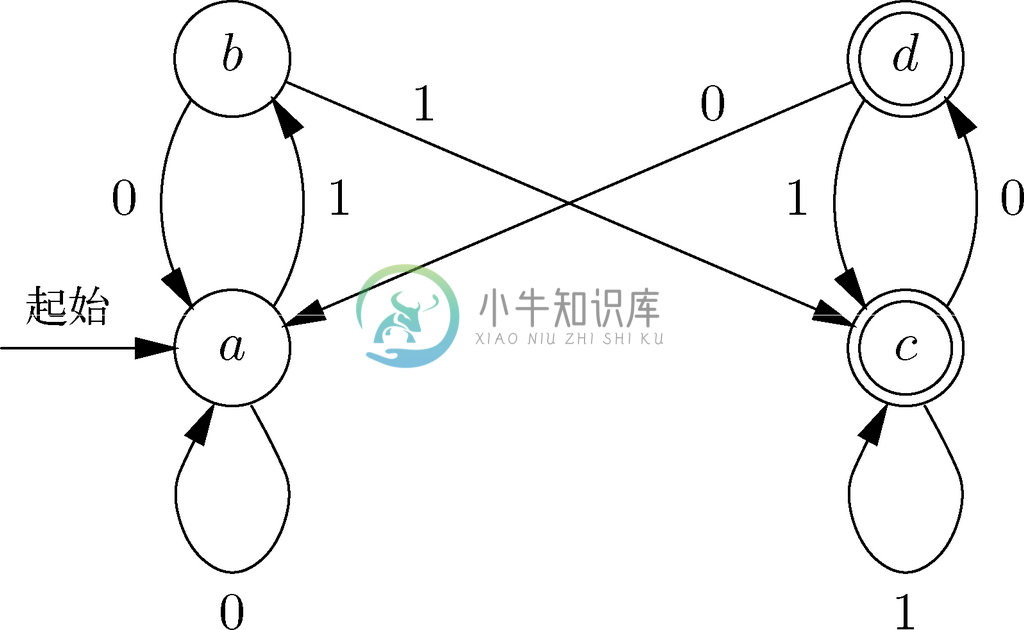
图 10-4　消除虚假的0和1的自动机

接受状态是c 和d。对该自动机而言，其接受过程与图10-3所示的自动机有着一些不同的含义。对图10-3所示的自动机而言，在到达接受状态时，就可以说整个输入都被接受了，包括自动机还没有读到的那些字符。1而在这里，我们想要接受状态表述“输出一个1”，还要一个表述“输出一个0”的非接受状态。在这种解释下，我们会将输入中的每一位都转化成输出中的每一位。通常输出是和输入相同的，不过有时候也会不同。例如，图10-5展示了输入为0101101时的输入、各个状态和它们的输出。

1不过，通过为状态5加一个所有字母上的转换，我们可以修改该自动机，使其能继续读u之后的所有字母。

{%}

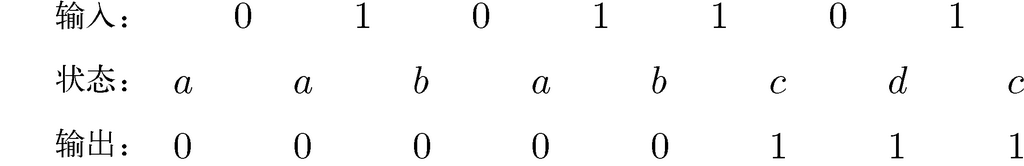
图 10-5　图10-4中的自动机处理输入0101101时的情况模拟

我们从状态a 开始，因为a 是非接受状态，所以输出0。请注意，这一初始输出并不是对任意输入的回应，而是表示在初次开启设备时自动机的条件。

图10-4中从状态a 出发标记了输入0的转换是到达状态a 自身的。因此第二个输出还是0。第二个输入是1，而且从状态a 可以进行针对1的到状态b 的转换。该状态“记住了”我们已经看到过一个1，不过因为b 是非接受状态，所以输出仍然是0。针对第三个输入，也就是另一个0，我们又从状态b 回到了状态a，而且继续发出输出0。

接下来的两个输入都是1，可以先将自动机带到状态b，然后带到状态c。对这两个1中的第一个1，我们发现自己是在状态b 中，这会带来输出0。这个输出是错的，因为我们其实已经开始处理1了，但是在读完第四个输入后还不知道这一点。这种简单设计的影响在于，不管是0还是1组成的，所有的串都被右移了一位，因为在自动机意识到它已经开始处理新的串而不是“噪声”位之前，一行中已经接受了2位。在接收第5个输入时，我们就会遵循从状态b 到状态c 针对输入1的转换。在这一情况下，会得到第一个1输出，因为c 是接受状态。

最后两个输入是0和1。0把我们从状态c 带到状态d，这样我们可以记得自己已经看到了一个0。从状态d 的输出依然是1，因为该状态是接受状态。最后的1将我们带回状态c 并生成输出1。

自动机与其程序之间的区别
自动机是种抽象。从10.3节起将会变得明确，通过确定从起始状态到某个用相应序列标记的接受状态之间是否存在路径，自动机呈现了一种对任意输入字符序列的接受/拒绝决定。举例来说，图10-5表示的反弹过滤器自动机的行为告诉我们，该自动机拒绝ε、0、01、010和0101这些前缀，但它接受01011、010110和0101101这几个前缀，如图10-4所示。图10-3的自动机接受abstemiou这样的字符串，但拒绝abstemious，因为从状态5没办法到达最后的s。
另一方面，由自动机创建的程序能以多种方式使用这种接受/拒绝决定。例如，图10-2中的程序使用了图10-3所示的自动机，但它不是认可标记通向接受状态的路径的字符串，而是认可整行输入，也就是，接受abstemious而非abstemiou。这是绝对合理的，而且反映了我们编写程序测试按次序的5个元音字母的方式，而不管是使用了自动机或是其他的方法。据推测，只要我们到达字母u，该程序就会打印出整个单词而不再继续检查其余字母。
图10-4所示自动机的使用方式就更简单。我们将会看到，图10-7中对应这一反弹过滤器的程序会直接把每个接受状态转化成打印一个1的行动，而将每个拒绝状态转化成打印一个0的行动。

10.2.2　习题

1. 设计自动机，读由0和1组成的串，并能进行下述操作。

(a) 确定目前位置读到的序列是否有偶校验（即存在偶数个1）。特别要指出的是，如果目前为止该串有偶校验，则该自动机会接受它，而如果它具有奇校验，自动机就会拒绝它。

(b) 检验输入串没有两个以上连续的1。也就是说，除非111是当前为止读过的输入串的子串，否则接受。

每种状态的直觉含义各是什么？

2. 在给定输入101001101110时，指出习题(1)中自动机的状态序列和输出。

3. * 设计自动机，读的是单词（字符串），并分辨单词中的字母是否是已排好序的。例如，adept和chilly这样的单词中的字母就是已排好序的，而baby就不是，因为在第一个b后面有个a。单词一定是以空白终止的，这样自动机才会在读完所有字符后知道这一点。与示例10.1不同，这里我们必须在读完所有字符后才能接受，也就是说，必须在到达单词末端的空白之后才能接受。该自动机需要多少种状态？每种状态的直觉含义是什么？从每种状态出发的转换又有多少？总共有多少种接受状态？

4. 设计自动机，使其能分辨字符串是否为合法的C语言标识符（字母后跟上字母、数字或下划线）后跟上空白。

5. 编写C语言程序，实现习题1到习题4的各种自动机。

6. 设计自动机，使其能分辨给定的字符串是否为第三人称单数代词（he、his、him、she、her或hers）后跟上空白。

7. * 将习题(6)设计的自动机转换成C语言函数，并在程序中使用该函数找到某给定字符串中所有出现第三人称单数代词子串的位置。

10.3　确定自动机和非确定自动机

使用自动机进行的最基本的操作之一是接受一系列的符号a₁a₂…a_k，并从起始状态起循着一条由标号依次为这些符号的弧组成的路径行进。也就是说，对i=1、2、…、k 来说，a_i 都是集合S_i 中作为路径上第i 条弧标号的成员。构建这一路径及其状态序列的过程就是自动机对输入序列a₁a₂…a_k 的模拟（simulating）。可以说这一路径标号为a₁a₂…a_k，当然，它也可能有其他标号，因为给路径上的弧提供标号的各集合S_i 可能各自含有很多字符。

示例 10.3

我们在图10-5中进行过一次这样的模拟，其中模仿了图10-4中的自动机对序列0101101的处理。另外，以图10-3中用来识别单词中是否含有序列aeiou的自动机为例，考虑对字符串adept的处理。

我们从状态0中开始。从状态0出发的转换有两次，一次是针对字符集Λ-a的转换，另一次是针对单独一个字母a的。因为adept的第一个字符就是a，所以要遵循后一个转换，这把我们带到了状态1。从状态1出发，又有针对Λ-e和e的转换。因为第二个字符是d，所以必须遵循前一种转换，因为Λ-e包含除了e之外的所有字母。这把我们再次留在状态1中。因为第三个字母是e，所以要循着从状态1出发的第二种转换，将我们带到状态2。adept的最后两个字母都在集合Λ-i中，所以下两次转换都是从状态2到状态2。因此在状态2中就完成了对adept的处理。相应的状态转换序列如图10-6所示。因为状态2不是接受状态，所以我们没有接受输入adept。

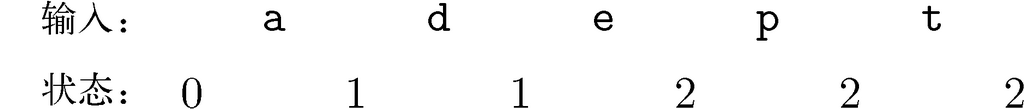
图 10-6　对10-3中的自动机针对输入adept的模拟

有关自动机输入的术语
在这里将要讨论的例子中，自动机的输入是字符，比如字母和数字，而且将输入当作字符并将输入序列当作字符串是很方便的。我们在这里一般会使用这一术语，不过偶尔会将“字符串”简称为“串”。不过，在有些应用中，自动机要转换的输入是从比ASCII字符集更广泛的集合中选出的。例如，编译器可能会把while这样的关键词看作单个输入符号，我们将这种情况用加粗的字符串while表示。因此有时候我们会把这种单独的输入称作“符号”而非“字符”。

10.3.1　确定自动机

在10.2节中讨论过的自动机有个重要的属性。对任意状态s 和任意输入字符x 来说，至多只有一种从状态s 出发的转换的标号中含有x。这样的自动机就称为确定自动机。

为给定输入序列模拟确定自动机是很简单的。在任意状态s 中，给定下一个输入字符x，考虑从s 出发的每种转换的标号。如果我们找到标号含x 的转换，那么该转换就指向适当的下一个状态。如果没有含x 的转换，那么该自动机就“死机”了，而且不能再继续处理输入，就像图10-3中的自动机在到达状态5后就会停机那样，因为它知道自己已经找到了子序列aeiou。

将确定自动机转变为程序是很容易的。我们为每个状态编写一段代码。对应状态s 的代码会检查它的输入，并决定应该遵循从s 出发的哪种转换（如果存在这样的转换）。如果选定了从状态s 到状态t 的转换，那么必须安排表示状态t 的代码接着表示状态s 的代码执行，可能是通过goto语句来实现。

示例 10.4

这里我们编写了一个对应图10-4所示反弹过滤器自动机的函数bounce()。变量x是用来从输入中读字符的。状态a、b、c 和d 将分别用标号a、b、c和d来表示，而且要使用标号finis表示程序的结尾，也就是在输入中遇到0和1之外的字符时会到达的地方。

代码如图10-7所示。例如，在状态a 中我们会打印字符0，因为a 是非接受状态。如果输入字符是0，就停留在状态a，而且如果输入字符是1，就进入状态b。

void bounce()
{
         char x;

         /* 状态 a */
a:       putchar('0');
         x = getchar();
         if (x == '0') goto a; /* transition to state a */
         if (x == '1') goto b; /* transition to state b */
         goto finis;

         /* 状态 b */
b:       putchar('0');
         x = getchar();
         if (x == '0') goto a; /* transition to state a */
         if (x == '1') goto c; /* transition to state c */
         goto finis;

         /* 状态 c */
c:       putchar('1');
         x = getchar();
         if (x == '0') goto d; /* transition to state d */
         if (x == '1') goto c; /* transition to state c */
         goto finis;

         /* 状态 d */
d:       putchar('1');
         x = getchar();
         if (x == '0') goto a; /* transition to state a */
         if (x == '1') goto c; /* transition to state c */
         goto finis;

finis:   ;

}

图 10-7　实现图10-4中确定自动机的函数

在“自动机”的定义中没有要求从某给定状态出发的转换的标号必须是不相交的，如果集合没有相同的成员则说它们是不相交的，即它们的交集为空。如果有图10-8所示的这种图，其中针对输入x 有从状态s 到状态t 和状态u 的转换，这样一来该自动机要如何用程序来实现就不是很清楚了。也就是说，在执行对应状态s 的代码时，如果发现x 是下一个输入字符，就得知接下来一定要进入表示状态t 的代码的开头，而且还要进入表示状态u 的代码的开头。因为程序一次不能到达两个位置，所以要如何模拟从状态出发的转换具有相同标号的自动机是很不明朗的。

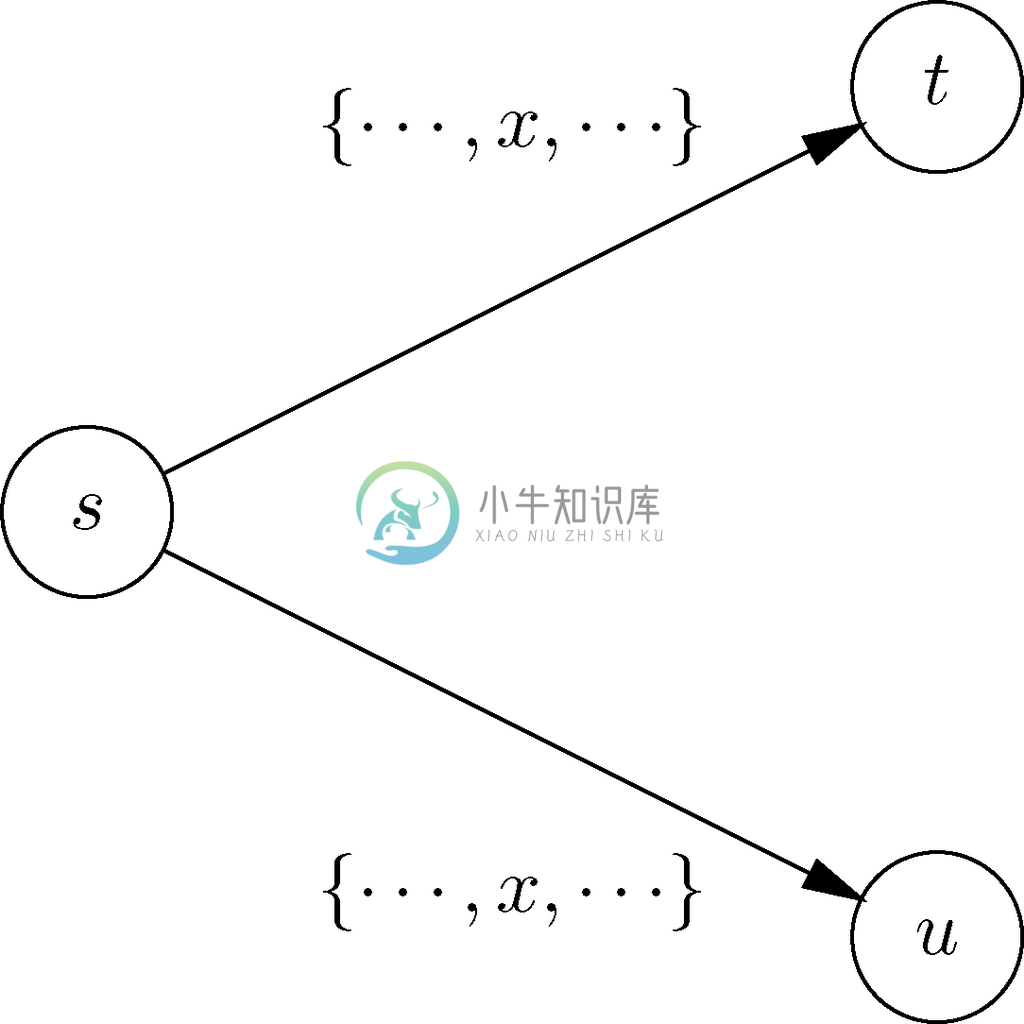
图 10-8　从状态s 出发的针对输入x 的非确定转换

10.3.2　非确定自动机

非确定自动机可以具有从某一状态出发的包含相同符号的两个或多个转换，但这不是必须的。请注意，严格地讲，确定自动机也是一种非确定自动机，它只是刚好没有针对同一符号的多种转换。一般来说“自动机”都是不确定的，不过我们在强调自动机不是确定自动机时还是会使用“非确定自动机”的说法。

正如上文提过的，非确定自动机不能直接用程序实现，不过它们对这里将要讨论的若干应用来说是很实用的概念工具。此外，通过利用10.4节中将要介绍的“子集构造”，可以将任意非确定自动机转换成接受相同字符串集合的确定自动机。

10.3.3　非确定自动机的接受

在我们试图模拟针对输入字符串a₁a₂…a_k的非确定自动机时，可能发现同一个字符是多条路径的标号。习惯上讲，如果至少有一条由某输入编辑的路径可以通向接受状态，就可以说非确定自动机接受这一输入字符串。以接受状态结尾的那一条路径，要比任意数量以非接受状态结尾的路径更重要。

不确定性和猜测
认为不确定性让自动机可以“猜测”是种看待不确定性的实用方式。如果我们不知道在某给定状态中要对某给定的输入字符做什么，就可以对下一个状态做出若干选择。因为由带向接受状态的字符串标记的任意路径会被解释为接受，所以非确定自动机其实被赋予了进行一次正确猜测的信用，而不管它还会造成多少次错误猜测。

示例 10.5

反性别歧视言论联盟（League Against Sexist Speech，LASS）希望找到含单词man的性别歧视文字。他们不止想捕获ombudsman（特派员）这样的构词，还希望捕获诸如maniac（狂人）或emancipate（解放）这样形式更为微妙的歧视。LASS计划设计一个使用自动机的程序，该程序会扫描字符串，并会在它从输入中任意位置找到字符串man时“接受”该输入。

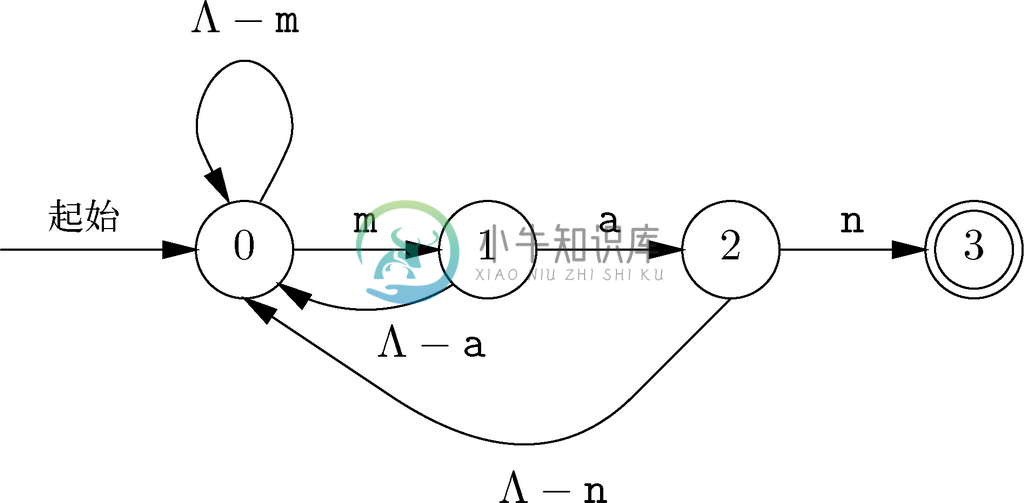
图 10-9　可识别大多数（而非全部）以man结尾的字符串的确定自动机

大家可能首先会尝试如图10-9所示的确定自动机。在该自动机中，状态0，也就是起始状态，表示的是我们还没看到man这几个字母时的情况。状态1是用来表示我们已经看到m的情形，在状态2中我们已经识别了ma，而在状态3中我们已经看到了man。在状态0、状态1和状态2中，如果我们没有看到想找的字母，就回到状态0并再次尝试。

不过，图10-9并不能很正常地完成处理。在处理command这样的输入时，当它读c和o时会停留在状态0中。在读第一个m时它会进入状态1，不过第二个m又会把它带回状态0，随后它就无法离开状态0了。

可以正确识别内嵌了man的字符串的非确定自动机如图10-10所示。关键的革新在于，我们在状态0中会猜测m是否标志着man的开始。因为该自动机是非确定自动机，它允许同时猜测“是”（由从状态0到状态1的转换表示）和“否”（由可以对包括m在内的所有字母执行从状态0到状态0的转换这一事实表示）。因为非确定自动机的接受需要的不过是一条通向接受状态的路径，所以我们可以受益于这两种猜测。

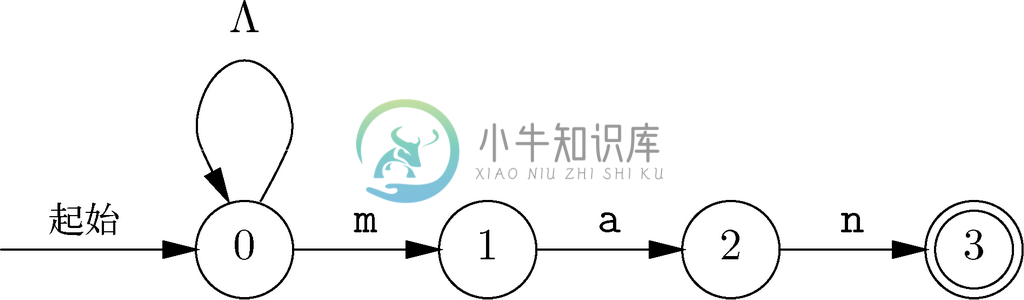
图 10-10　可识别所有以man结尾的字符串的非确定自动机

图10-11展示了图10-10中的非确定自动机在处理输入字符串command时的行动。在回应c和o时，该自动机只能停留在状态0中。在输入第一个m时，自动机可以选择进入状态0或状态1，因此它同时进入了这两个状态。在处理第二个m时，从状态1是没办法继续行进的，所以该分支就成了一条“死路”。不过，从状态0可以再次进入状态0或状态1，这里又同时进入这两种状态。当输入a时，可以从状态0到达状态0，并从状态1到达状态2。同样，在输入n时，可以从状态0到达状态0，并且从状态2到达状态3。

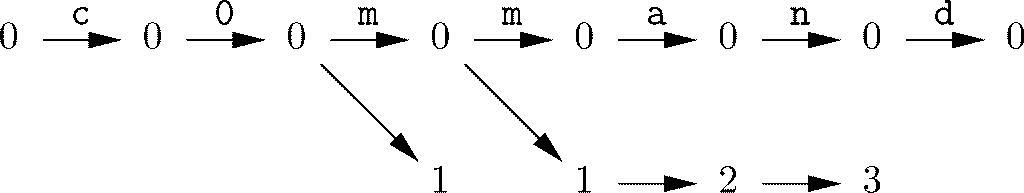
图 10-11　模拟图10-10中的非确定自动机处理输入串command的情况

因为状态3是接受状态，所以在该点处我们可以接受这一输入。2对接受状态而言，在看到comman后也处在状态0中这一事实是无关紧要的。最后的转化是针对输入d的，从状态0到状态0。请注意状态3不会针对任意输入行进到任何位置，所以该分支也完结了。

2请注意，图10-10中的自动机就像图10-3中的自动机那样，在看到它查找的模式时就会接受，而不是在单词的结尾接受。当我们最终把图10-10转换成确定自动机时，就可以根据它设计能打印整个单词的程序了，就像图10-2中的程序那样。

还要注意，图10-9中展示的用来处理未接收到单词man后一个字符这种情况的回到状态0的转换，在图10-10中是不必要的，因为在图10-10中我们看到输入man时不一定要沿着序列从状态0到状态1再到状态2最后到状态3。因此，虽然状态3看起来“已死”，而且在看到man时已终止计算，但是我们在看到man时也停留在状态0中。该状态允许我们在处理manoman这样的输入时，于读第一个man期间停留在状态1中，并在读第二个man时行经状态1、状态2和状态3，以此来接受manoman这样的输入。

当然，图10-10的设计尽管很动人，但不能直接转换为程序。我们将在10.4节中看到如何把图10-10转换成只含4个状态的确定自动机。与图10-9不同的是，该确定自动机可以正确地识别所有出现man的单词。

尽管可以把任意非确定自动机转换成确定自动机，但并非总是像图10-10所示的情况这般幸运。在图10-10中的情况下，可以看到对应的确定自动机的状态不会多于原非确定自动机的状态，也就是各有4个状态。但事实上，还存在另外一些非确定自动机，与它们对应的确定自动机会含有更多状态。一个含n种状态的非确定自动机有可能只能转换成含2ⁿ个状态的确定自动机。下一个示例正好就是确定自动机的状态要比非确定自动机的状态多得多的情况。因此，对同一个问题而言，设计非确定自动机可能比设计确定自动机简单得多。

示例 10.6

当本书作者之一Jeffrey D.Ullman之子Peter Ullman上四年级时，他的一位老师试图通过为学生们布置一些“部分换位构词”问题来增加他们的词汇量。该老师每周会给学生们布置一个单词，并要求他们找出使用该单词的一个或多个字母可以构成的所有单词。

有那么一周，该老师布置的单词是Washington，本书的两位作者聚在一起，决定进行一次穷举查找，看看到底可能形成多少个单词。利用/usr/dict/words文件与含3个步骤的过程，我们找到了269个单词，其中有以下5个含7个字母的单词：

agonist
goatish
showing
washing
wasting

因为字母的大小写对本问题来说不重要，所以第一步就是要把词典中所有的大写字母全部转化为小写字母。执行这一任务的程序是很简单的。

第二步是选取只含来自集合S={a，g，h，i，n，o，s，t，w}中的字母（washington中的字母）的单词。图10-12中的确定自动机就能完成该任务。newline字符是/usr/dict/words中标记行尾的字符。如果我们遇到newline之外的其他任意字符，就不用进行转换，而且自动机决不会到达接受状态1。如果在只读到washington中的字母后遇到newline，就进行从状态0到状态1的转换并接受该输入。

图 10-12　检测由washington中出现的字母所构成单词的自动机

图10-12中的自动机接受hash这样的单词，也就是相应字母出现的次数多于washington本身中字母出现次数的单词。因此，我们的第三步也是最后一步就是，排除那些包含3个或更多n，或是包含两个或更多S中其他字符的单词。这一任务也可以由自动机来完成。例如，图10-13中的自动机接受的是至少有两个a的单词。我们会停留在状态0中，直至看到a，在这种情况下就进入状态1。接着会保持状态1，直到看到第二个a，才进入状态2并接受该输入。该自动机接受那些因为有太多a而不能用washington部分换位构词得到的单词。在这种情况下，我们想要的刚好是那些在处理过程中从不会让自动机进入接受状态2的单词。

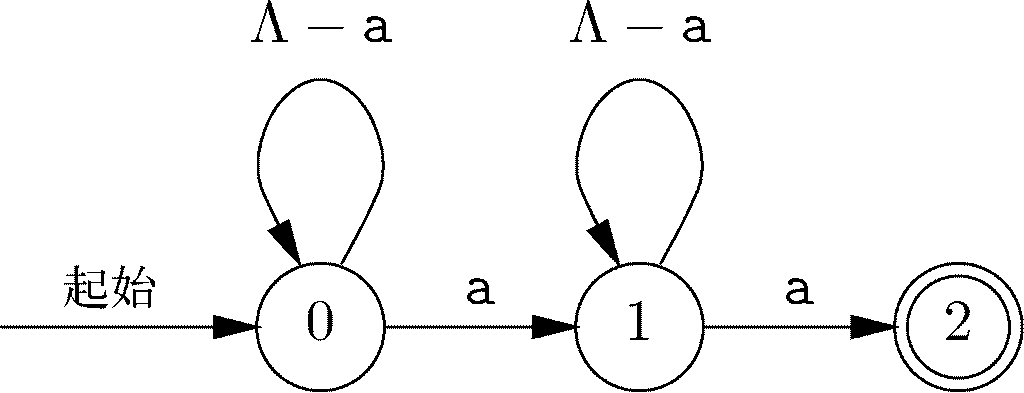
图 10-13　如果输入存在两个a就接受该输入的自动机

图10-13所示的自动机是确定自动机。不过，它只表示了某单词可被图10-12中的自动机接受却仍不是washington经部分换位构词得到的单词的9种原因之一。要接受具有washington中某个字母太多实例的全部单词，我们可以使用图10-14中的非确定自动机。

图10-14从状态0中开始，而且它针对任意字母的一种选择就是留在状态0中。如果输入字符是washington中的任意一个字母，就有另一种选择；该自动机还会猜测它应该转换到这样一个状态，该状态的功能是记住该字母已经出现过一次。例如，针对字母i，我们有进入状态7的选择。然后我们就会留在状态7中，直到看到另一个i，从而进入作为接受状态之一的状态8。回想一下，在该自动机中，接受就意味着输入字符串不是由washington经过部分换位构词得到的单词，在这里描述的情况中就是因为该单词含有两个i。

因为在washington中有两个n，所以对n的处理有些不同。自动机在看到一个n后会进入状态9，而在看到第二个n后会进入状态10，接着在看到第三个n时才进入接受状态11。

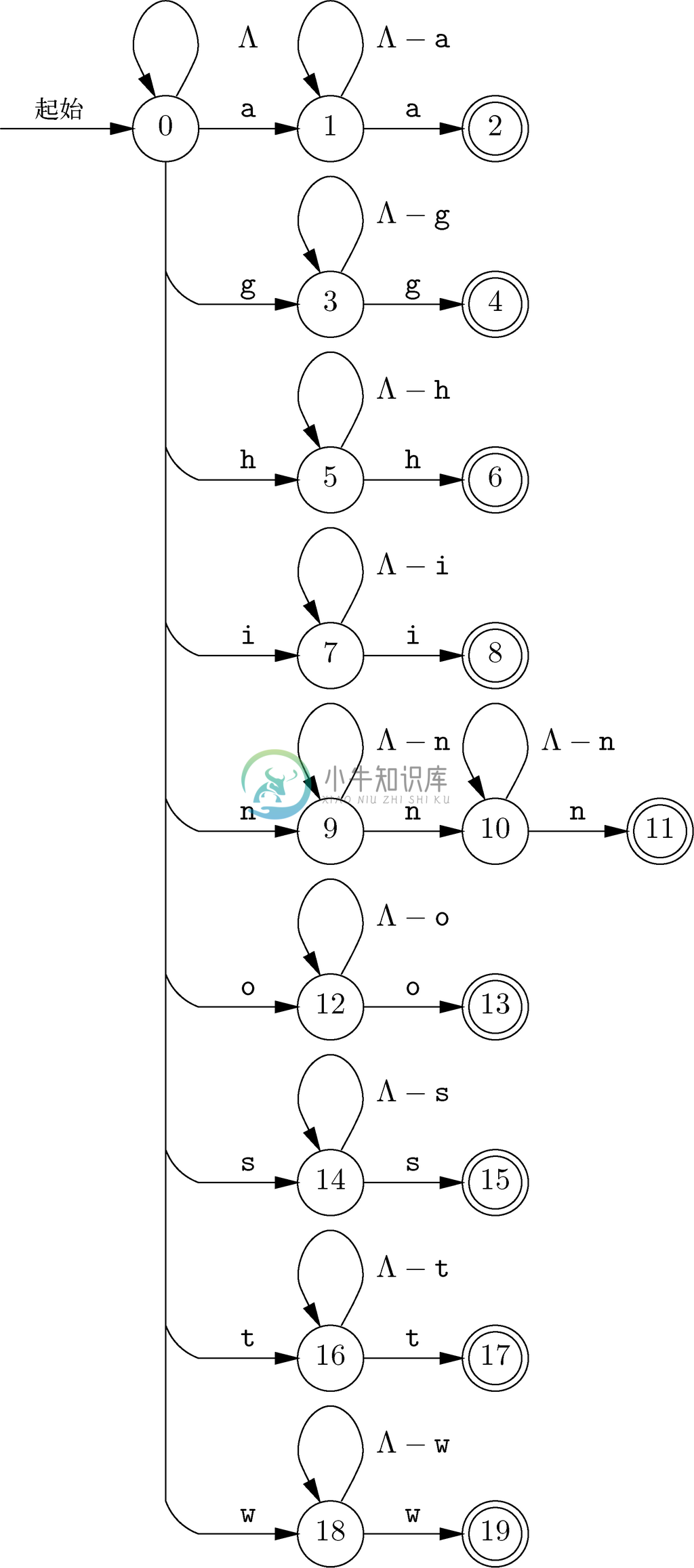
图 10-14　检测含有一个以上的a、g、h、i、o、s、t或w，或者两个以上n的单词的非确定自动机

例如，图10-15展示了读输入字符串shining之后的所有状态。因为我们在读第二个i后会进入接受状态8，所以shining不是由washington经过部分换位构词得到的单词，即便它因为只含有washington中可以找到的字母而能被图10-12中的自动机接受。

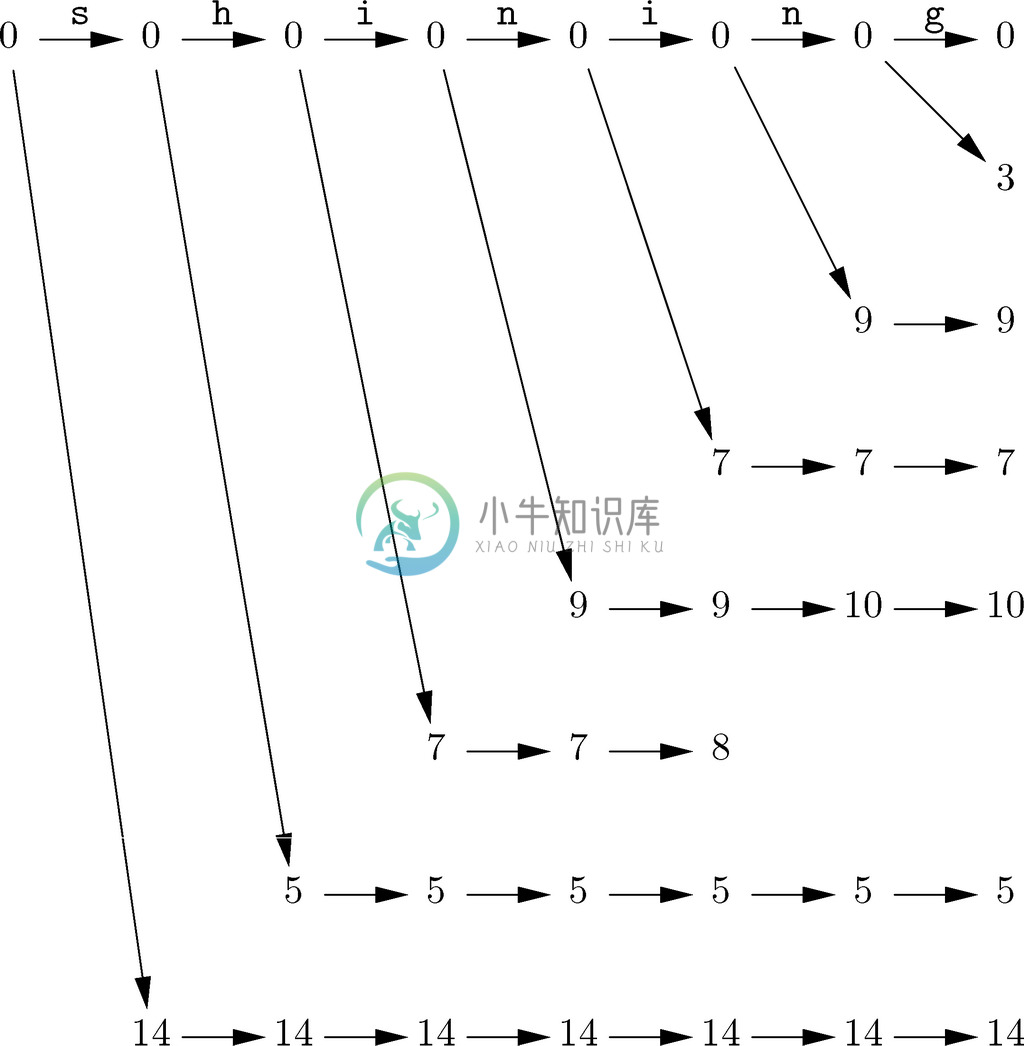
图 10-15　图10-14中的非确定自动机处理输入字符串shining时进入的状态

总结下来，我们的算法由以下3步组成。

(1) 首先将词典中的所有大写字母转换成小写字母。

(2) 找到10-12中的自动机接受的所有单词，这些单词只由washington中的字母组成。

(3) 从步骤(2)得到的单词中删除图10-14中非确定自动机接受的所有单词。

该算法是在/usr/dict/words文件中找到可由Washington经过部分换位构词得到的单词的简单方法。当然，必须找到某种合理的方式来模拟图10-14中的非确定自动机，我们将在10.4 中讨论如何完成这一任务。

10.3.4　习题

1. 编写C语言程序，实现图10-9中确定自动机的算法。

2. 设计确定自动机，使其能正确地找出字符串中出现的所有子字符串man。并将该自动机实现为程序。

3. LASS希望检测出所有含字符串man、son和father的单词。设计非确定自动机，使其只要找到这3个字符串中任意一个就接受相应的输入字符串。

4. * 设计确定自动机，使其可以解决习题(3)中的问题。

5. 模拟图10-9和图10-10中的自动机处理字符串summand时的情况。

6. 模拟图10-14的自动机处理以下字符串的情况。

(a) saint

(b) antagonist

其中哪些字符串会被接受？

7. 可以用具有状态、输入和接下来这些属性的关系来表示自动机。这样做的目的是，如果(s，x，t )是个元组，那么输入符号x 就是从状态s 到状态t 的转换的标号。如果该自动机是确定自动机，那么该关系合适的键是什么？如果该自动机是非确定自动机呢？

8. 如果只是想在给定某状态和某输入符号的情况下找出接下来的（一个或一些）状态，大家会建议用什么数据结构来表示习题(7)中的关系？

9. 将如下图所示的自动机表示为关系。

(a) 图10-10

(b) 图10-9

可以使用椭圆来表示Λ-m 这样针对含大量字母的集合的转换。

不编程找到部分换位构词形成的单词
顺便提一句，我们可以使用UNIX系统的命令，几乎不进行编程就实现示例10.6中的3步算法。对步骤(1)，可以使用UNIX命令
tr A-Z a-z </usr/dict/words　　　　　　(10.1)
把大写字母转化成小写字母。对步骤(2)，可以使用命令
egrep '^[aghinostw]*$'　　　　　　(10.2)
粗略地讲，就是定义了图10-12中那样的自动机。对步骤(3)，可以使用命令
egrep -v 'a.*a|g.*g|h.*h|i.*i|n.*n.*n|o.*o|s.*s|t.*t|w.*w'　　　　　　(10.3)
该命令指定了类似图10-14中自动机的事物。整个任务可以使用以下三元素管道来完成：
(10.1) | (10.2) | (10.3)
也就是说，整个命令是通过用表示各行的文本替换各行形成的。竖线，或者说“管道”符号，使得左侧命令的输出可以成为右侧命令的输入。我们将在10.6节中讨论egrep命令。

10.4　从不确定到确定

在本节中我们将会看到，每一个非确定自动机都可以被确定自动机替代。正如我们已经看到的，在执行某些任务时，考虑非确定自动机有时要更简单些。不过，因为根据不确定自动机编写程序不如根据确定自动机编程那样容易，所以找到一种将不确定自动机变形为等价的确定自动机的算法是很重要的。

10.4.1　自动机的等价性

在10.3节中，我们已经看到两种接受观。在某些示例中，比如在示例10.1（含有子序列aeiou的单词）中，接受就意味着整个单词被接受，即便我们可能没有扫描完整个单词。而在另一些例子中，比方说示例10.2的反弹过滤器中，或是图10-12所示的自动机（字母全在washington中的单词）中，只有在我们想对从启动自动机以来已经看到的确切输入表示认可时才接受该输入。因此，在示例10.2中，我们接受所有能带来输出1的输入序列。在图10-12中，只有在已经看到newline字符，知道已经看到整个单词时才接受该输入。

当谈论正式的自动机行为时，我们只需要第二种解释（当前的输入被接受）。严格地讲，假设A 和B 是两个自动机（确定或不确定）。如果A 和B 接受相同的输入字符串集合，就说它们是等价的。换句话说，如果a₁a₂…a_k 是任意符号串，那么以下两个条件是成立的。

1. 如果从A 的起始状态到A 的某个接受状态存在以a₁a₂…a_k 标记的路径，那么从B 的起始状态到B 的某个接受状态也存在以a₁a₂…a_k 标记的路径。

2. 如果从B 的起始状态到B 的某个接受状态存在以a₁a₂…a_k 标记的路径，那么从A 的起始状态到A 的某个接受状态也存在以a₁a₂…a_k 标记的路径。

示例 10.7

考虑图10-9和图10-10中的自动机。正如我们在图10-11中注意到的，图10-10中的自动机接

受输入字符串comman，因为该字符序列在图10-10中标记了路径0→0→0→0→1→2→3，而且这一路径是从起始状态出发，到达了一个接受状态。不过，在图10-9所示的确定自动机中，可以验证由comman标记的路径只有0→0→0→1→0→0→0。因此如果图10-9是自动机A，而图10-10是自动机B，就违背了上述第(2)点，这样就表明这两个自动机不是等价的。

10.4.2　子集构造

我们现在将会看到，如何通过构造等价的确定自动机来“消除自动机的不确定性”。这一技巧叫作子集构造，而且它的本质就如图10-11和图10-15所示，在这两幅图中我们模拟了处理特殊输入的非确定自动机。从这两幅图中我们注意到，在任何给定的时间，非确定自动机都在某一状态集合中，而且这些状态都出现在模拟图的同一列中。也就是说，在读了某输入列a₁a₂…a_k 之后，非确定自动机就“在”那些从起始状态出发沿着标记有a₁a₂…a_k 的路径可以到达的状态中。

示例 10.8

在读完输入字符串shin之后，图10-15所示的自动机处在状态集合{0，5，7，9，14}中。这些状态都出现在第一个n后的一列中。在读下一个i后，它处在状态集合{0，5，7，8，9，14}中，而在读了接下来的n后，在状态集合{0，5，7，9，10，14}中。

现在就有了如何把非确定自动机N 转换为确定自动机D 的线索。D 的状态各自是N 的状态的集合，而且D 中状态间的转换是由N 的转换确定的。要看到如何构建D 的转换，设S 是D 的某个状态，而且x 是某输入符号。因为S 是D 的状态，所以它是由N 的状态组成的。定义集合T 是自动机N 中那些状态t，这些状态满足存在S 中的状态s，以及自动机N 针对包含输入符号x 的集合的从s 到t 的转换。那么在自动机D 中我们就放置一个在针对符号x 的从S 到T 的转换。

示例10.8展示了多个针对输入符号的从一个确定状态到另一个确定状态的转换。在当前的确定状态是{0，5，7，9，14}，而且输入符号是字母i时，我们在该示例中看到，根据图10-14中的非确定自动机，接下来的不确定状态集是T={0，5，7，8，9，14}。由针对输入符号n 的这一确定状态可知，接下来的不确定状态集是U={0，5，7，9，10，14}。这两个确定转换如图10-16所描述的那样。

图 10-16　确定状态S、T 和U 之间的转换

现在我们知道该如何在确定自动机D 的两个状态之间构建转换了，不过需要确定自动机D 确切的状态集、D 的起始状态，以及D 的接受状态。我们要用归纳法来构建D 的状态。

依据。如果非确定自动机N 的起始状态是s₀，那么确定自动机D 的起始状态是{s₀}，也就是只含s₀这一个元素的集合。

归纳。假设已经确定了N 的状态集S 是D 的一个状态。依次考虑每个可能的输入字符x。对某个给定的x，设T 是N 的状态t 构成的集合，其中状态t 满足对S 中的某个状态s 而言，存在标号含x 的从s 到t 的转换。那么集合T 就是D 的一个状态，而且存在针对输入x 的从S 到T 的转换。

D 的接受状态是N 的状态集中至少包含N 的一个接受状态的。这从直觉上讲是说得通的。如果S 是D 的状态而且是N 的状态集，那么能把D 从其起始状态带到状态S 的输入a₁a₂…a_k 也能把N 从其起始状态带到S 中的所有状态。如果S 含有某个接受状态，那么a₁a₂…a_k 会被N 接受，而且D 也一定会接受该输入。因为D 在接收输入a₁a₂…a_k 时只会进入状态S，所以S 肯定是D 的接受状态。

{%}

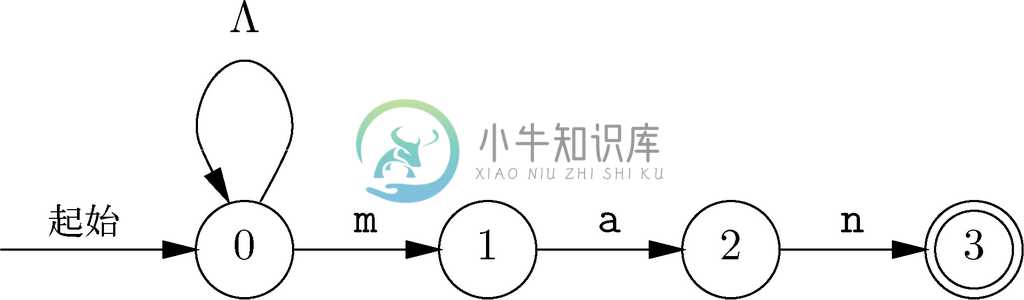
图 10-17　识别以man结尾字符串的非确定自动机

示例 10.9

图10-17重现了图10-10所示的非确定自动机，我们来把它转换成确定自动机D。先从D的起始状态{0}开始。

这一构建过程的归纳部分要求我们查看D 的每个状态，并确定它的转换。对{0}而言，只需要询问状态0通向哪里。分析图10-17得到的答案是，对除了m之外的任意字母，状态0只能进入状态0，而对输入m，它同时通向状态0和状态1。因此自动机D 需要已经具备的状态{0}和我们必须添加的状态{0，1}。目前为止已经为D 构建的转换和状态如图10-18所示。

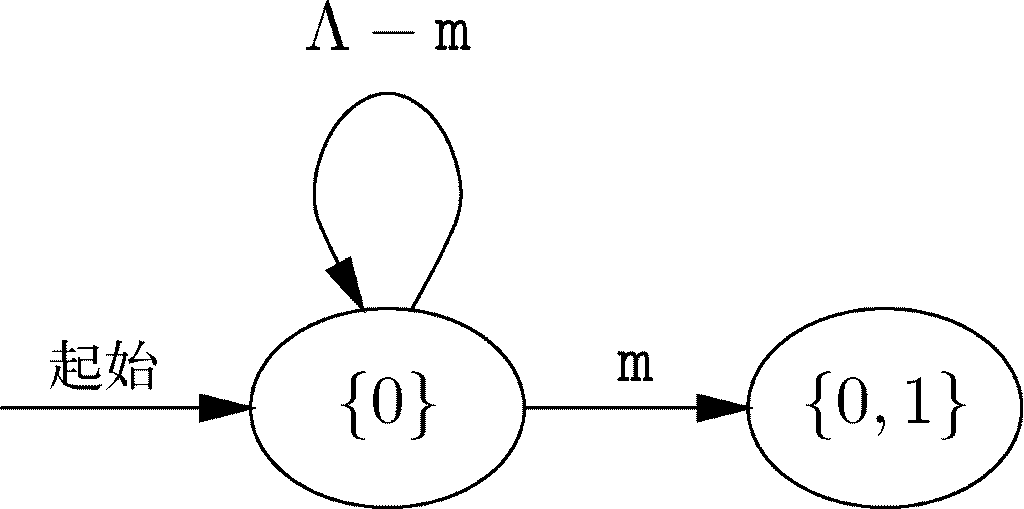
图 10-18　状态{0}及其转换

接下来，必须考虑从状态{0，1}出发的转换。再次研究图10-17，我们看到，对除了m和a之外的所有输入，状态0只通向状态0，而状态1则不能通向任何地方。因此，存在从状态{0，1}到状态{0}的转换，标记为除了m和a之外的所有字母。对输入m，状态1还是不能通向任何地方，不过状态0会同时通向状态0和状态1。因此，存在从状态{0，1}到其本身的转换，标记为m。最后，对输入a，状态0只会通向它自己，不过状态1是通向状态2的。因此存在标记为a的从状态{0，1}到状态{0，2}的转换。目前为止D 已经构建起的部分如图10-19所示。

图 10-19　状态{0}和{0，1}，以及它们的转换

现在需要构建从状态{0，2}出发的转换。对除m和n之外的所有输入，状态0只能通向状态0，而状态2则哪里都去不了，因此存在从{0，2}到{0}的转换，标记为除了m和n之外的所有字母。对输入m，状态2不通向任何状态，而状态0则同时通向状态0和状态1，因此标记为m的从状态{0，2}到状态{0，1}的转换。对输入n，状态0只通向它本身，而状态2会通向状态3。因此存在标记为n的从状态{0，2}到状态{0，3}的转换。D的该状态是接受状态，因为它包含了图10-17中的接受状态——状态3。

最后，必须给出从状态{0，3}出发的转换。因为对任何输入，状态3都不通向任何状态，从状态{0，3}出发的转换只反映从状态0出发的转换，因此会与{0}通向相同的状态。因为从状态{0，3}出发的转换不会将我们带到尚未见过的D的状态，所以对D的构造就完成了。完整的确定自动机如图10-20所示。

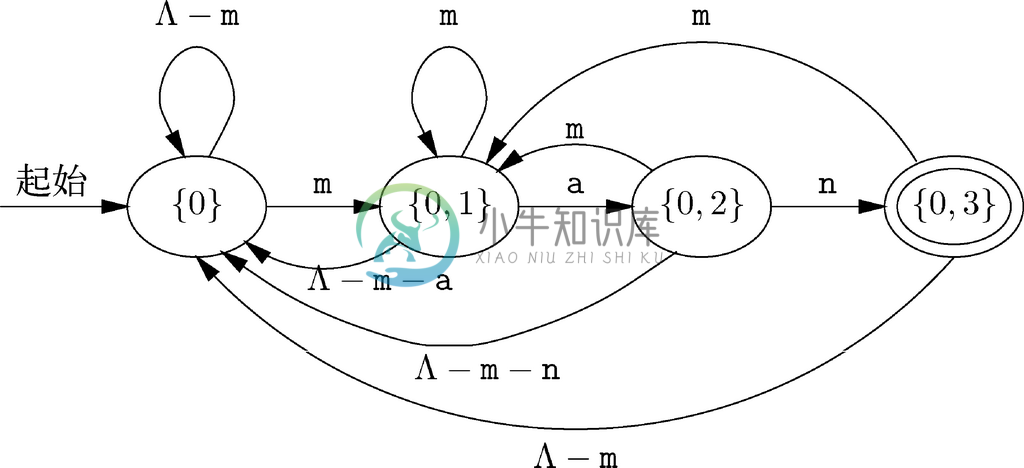
图 10-20　确定自动机D

请注意，这一确定自动机可以正确地接受所有以man结尾的字母串，而且只接受以man结尾的字母串。直觉上讲，只要字符串目前为止不是以m、ma、man结尾，该自动机就会处在状态{0}中。状态{0，1}意味着目前为止看到的字符串是以m结尾的，状态{0，2}表示当前的字符串是以ma结尾，而状态{0，3}则说明当前字符串的结尾为man。

示例 10.10

图10-17中的非确定自动机有4个状态，而图10-20中与它等价的确定自动机也有4个状态。如果所有的非确定自动机都能转换成小型确定自动机就好了，例如，在编译编程语言中常用到的某些自动机其实可以转换成相当小的确定自动机。不过，不能保证确定自动机一定很小，具有k个状态的非确定自动机有可能最终被转换成状态多达2^k 个的确定自动机。也就是说，对非确定自动机状态集的幂集中的每个成员，确定自动机都有相应的状态。

举个会得到很多状态的例子，考虑一下10.3节图10-14中的自动机。因为该非确定自动机有20种状态，可以想象一下，通过子集构造构建的确定自动机可能有约2²⁰个，或者说是超过100万个状态，这些状态全都是{0,1,…,19}的幂集的成员。实际结果并没有这么糟，但也存在相当多的状态。

我们不会尝试画出与图10-14中非确定自动机等价的确定自动机。不过，可以考虑一下实际上需要哪些状态集。首先，因为对每个字母都有从状态0到其自身的转换，所以实际看到的所有状态集都包含0。如果字母a尚未输入，就不能到达状态1。不过，如果刚好已经看到一个a，不管还看到些什么，我们都将在状态1中。我们还可以为washington中其他任何字母得出相似的论断。

如果在状态0中开始图10-14，并为其提供属于washington中所出现字母的子集的一列字母，然后除了在状态0中之外，还可以在状态1、3、5、7、9、12、14、16和18的某个子集中。通过恰当地选择输入字母，我们可以安排在这些状态集的任意一个中。因为有2⁹=512个这样的集合，所以在与图10-14等价的确定自动机中至少有这么多个状态。

不过，其中的状态要更多，因为字母n在图10-14中得到了特殊处理。如果在状态9中，我们还可以在状态10中，而且如果已经看到两个n，其实就将同处状态9和状态10中。因此，尽管对其他8个字母来说都只有两个选择（比如，对字母a，要包含状态1，要么不含状态1），而对字母n来说，共有3种选择（既不含状态9也不含状态10、只包含状态9，或者同时包含状态9和状态10）。因为至少存在3×2⁸=768种状态。

不过这并非全部。如果到目前为止的输入以washington中的字母之一结束，而且我们之前已经看到足够多的该字母，那么我们也应该在对应该字母的接受状态中，比方说，对a来说就是状态2。然而，我们在处理相同输入后不可能在两个接受状态中。为增加的状态集计数变得更麻烦了。

假设接受状态2是该集合的成员。那么可知1也是该集合的成员，0当然也是，不过我们仍然对与除a之外的字母对应的状态拥有所有选择，这类集合的数量是3×2⁷，或者说是384。如果我们的集合包含接受状态4、6、8、13、15、17或19，这样的道理也同样实用，在每种情况中都有384个集合包含相应的接受状态。唯一的例外就是含接受状态11（就是状态9和状态10也出现）的情况。在该情况下，只有2⁸＝256种选择。因此，该等价确定自动机的状态总数为：

768+8×384+256＝4864

第一项768表示那些不含接受状态的集合的数量。接下来的一项，表示的是分别包含与除n之外其他8个字母对应的接受状态的8类集合的数量，第三项256则表示含状态11的集合的数量。

关于子集构造的想法
子集构造是相当不好理解的。特别是确定自动机的状态可以是非确定自动机的状态集这一思路可能需要大家耐心思考才能想通。不过，这种把结构化对象（状态集）与原子对象（确定自动机的各个状态）融合成同一对象的概念，是计算机科学中的一种重要概念。我们已经在程序中看到过这一概念，而且经常必须用到它。例如，函数的参数，比方说L，表面上看是原子的，而对其进行更仔细的检查可能发现它是有着复杂结构的对象，比如，具有连接到其他记录的字段从而能形成表的记录。同样，图10-20中确定自动机D 的状态{0，2}也可以用简单的名称“5”或“a”来代替。

10.4.3　子集构造起效的原因

很明显，如果D 是利用子集构造从非确定自动机N 构建的，那么D 就是确定自动机。原因在于，对每个输入符号x 和D 的每个状态S 而言，我们定义了D 的某特定状态T，它满足从S 到T 的转换的标号中包含x。不过如何得知自动机N 和D 是等价的呢？也就是说，我们需要知道，对任意输入序列a₁a₂…a_k，当且仅当N 接受a₁a₂…a_k 时，在下列情况下，自动机D 到达的状态S 是种接受状态。

1. 从起始状态开始；

2. 并且沿着标记为a₁a₂…a_k 的路径行进。

请记住，当且仅当从N 的起始状态有一条标记为a₁a₂…a_k 的路径能到达N 的某个接受状态时，N 才会接受a₁a₂…a_k。

D 所做的事情与N 所做的事情之间的联系就更紧密了。如果D 具有从它的起始状态到标记为a₁a₂…a_k 的状态的路径，那么被视为自动机N 的某个状态集的集合S，就刚好是从N 的起始状态开始沿着某标记为a₁a₂…a_k 的路径所能到达的状态组成的集合。这种关系如图10-21所示。因为我们已经定义了，只有在S中的某一成员是N 的接受状态时，S才是D的接受状态，所以要得出D和N都接受a₁a₂…a_k 或都不接受a₁a₂…a_k，也就是要得出D 和N 是等价的，就只需要图10-21所示的关系。

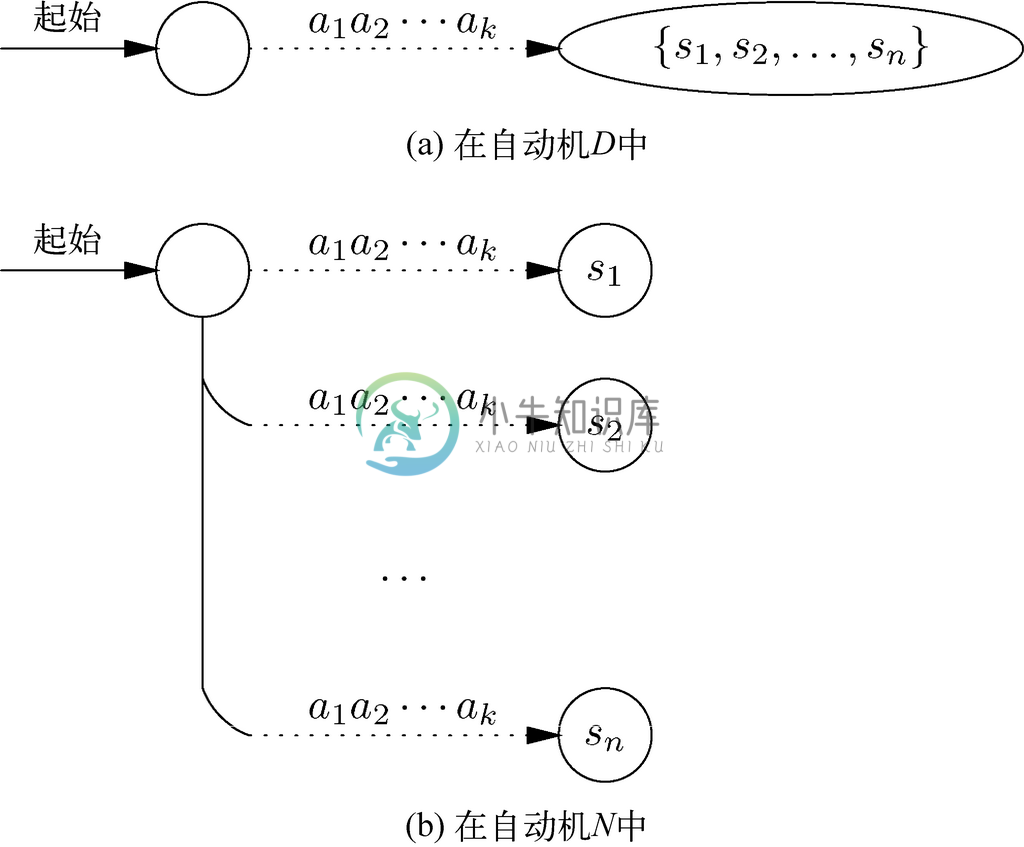
图 10-21　非确定自动机N 的操作与对应的确定自动机D 的操作间存在的关系

我们需要证明图10-21所示的关系，该证明要对输入字符串长度k 进行归纳。需要通过对k 的归纳来证明的正式命题是，从D 的起始状态开始沿着标记为a₁a₂…a_k 的路径到达的状态{s₁，s₂，…，s_n}，刚好是从N 的起始状态开始沿着标记为a₁a₂…a_k 的路径到达的状态构成的集合。

依据。设k=0。长度为0的路径将我们留在出发的位置，也就是，在自动机D 和N 的起始状态中。回想一下，如果s₀是N 的起始状态，D 的起始状态就是{s₀}。因此该归纳命题对k=0来说成立。

归纳。假设该命题对k成立，并考虑输入字符串a₁a₂…a_ka_k+1。那么标记为a₁a₂…a_ka_k+1的从D的起始状态到状态T的路径就如图10-22所示，也就是说，在它针对输入a_k+1进行到T的转换（最后一次转换）之前，会经过某个状态S。

{%}

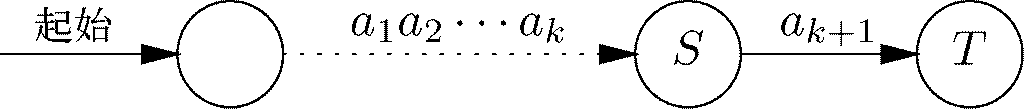
图 10-22　S 是D 在到达状态T 之前到达的状态

通过归纳假设，可以假设S 正好是自动机N 从其起始状态沿着标记为a₁a₂…a_k 的路径所能到达的状态组成的集合，并必须证明T 刚好是从N 的起始状态出发沿着标记为a₁a₂…a_ka_k+1的路径所能到达的状态组成的集合。该归纳步骤的证明包含下列两个部分。

(1) 必须证明，T不含过多的状态，也就是说，如果t是在T中的N的状态，那么t是从N的起始状态沿着标记为a₁a₂…a_ka_k+1的路径可以到达的。

(2) 必须证明，T包含足够的状态，也就是说，如果t是从N的起始状态沿着标记为a₁a₂…a_ka_k+1的路径可以到达的状态，那么t就在T中。

对(1)来说，设t 在T 中。那么，如图10-23所示，在S 中一定存在一个状态s，可以证实t 在T 中。也就是说，在N 中存在从s 到t 的转换，而且它的标号包含a_k+1。根据归纳假设，因为s 在S 中，所以肯定存在从N 的起始状态到s 的标记为a₁a₂…a_k 的路径。因此，存在从N 的起始状态到t，标记为a₁a₂…a_ka_k+1的路径。

图 10-23　S 中的状态s 解释了为何将状态t 放进T 中

现在必须证实(2)，也就是如果存在从N 的起始状态到t 的，标记为a₁a₂…a_ka_k+1的路径，那么t 就在T 中。就在这条路径针对输入a_k+1进行到t 的转换之前，肯定会经过某个状态s。因此，存在从N 的起始状态开始到s，标记为a₁a₂…a_k 的路径。根据归纳假设，s 在状态集S 中。因为N 具有从s 到t 而且标号含有a_k+1的转换，所以应用到状态集S 和输入符号a_k+1上的子集构造需要t 被放置到T 中。因此t 在T 中。

在给定归纳假设的情况下，现在就证明了，T 刚好是由N 中从N 的起始状态开始沿着标记为a₁a₂…a_ka_k+1的路径可达的状态组成的。这就是归纳步骤，因此可以得出，沿着标记为a₁a₂…a_k 的路径到达的确定状态机D 的状态，永远都是N 沿着标号相同的路径可达的状态组成的集合。因为D 的接受状态是那些包含N 的某个接受状态的状态集，所以可以得到D 和N 接受相同字符串的结论，也就是说D 和N 是等价的，所以子集构造是“行得通的”。

10.4.4　习题

1. 利用子集构造，把10.3节习题3中的非确定自动机转换成确定自动机。

2. 图10-24a到图10-24d中的非确定自动机可以识别什么模式？

3. 把图10-24a到图10-24d中的非确定自动机转换成确定有限自动机。

自动机的最小化
与自动机相关，特别是在利用自动机设计电路时会遇到的一个问题就是，执行某给定任务需要多少状态。也就是说，我们可能要问，给定某自动机，是否存在状态更少的等价自动机?如果这样的话，那么这样的等价自动机中最小的状态数量是多少？
事实证明，如果将问题限制在确定自动机的范畴，那么与任意给定自动机等价的最小状态确定自动机是唯一的，而且很容易找到它。关键就在于定义确定状态机两个状态s 和t 什么时候是等价的，也就是说，对任意的输入序列，分别从s 和t 出发而且由该序列标记的路径，要么都能到达接受状态，要么都不能到达。如果状态s 和t 是等价的，就没法通过为自动机提供输入来区分这两者，因此就可以把s 和t 合并为一个状态。事实上，按照如下方式定义不等价的状态要更容易。
依据。如果s 是接受状态而t 是不接受，那么s 和t 是不等价的，反之亦然。
归纳。如果存在某输入符号x，使得针对输入x 存在从状态s 和t 分别到两个已知状态的转换不等价，那么s 和t 就是不等价的。
要让这个测试起效，还需要补充一些细节。特别要提的是，我们可能必须添加一个“停滞状态”，它不接受任何输入，而且针对所有输入都存在到它自身的转换。由于确定自动机可能针对某个给定符号不存在从某给定状态出发的转换，因此在执行这一最小化程序之前，需要针对所有不存在其他转换的输入，添加从任意状态到该停滞状态的转换。可以注意到，不存在类似的用于最小化非确定自动机的理论。

4. * 某些自动机具有一些根本不存在转换的“状态-输入”组合。如果状态s 不存在针对符号x 的转换，我们就可以添加一种针对符号x 的、从s 到某个特殊的“停滞状态”的转换。停滞状态是不接受状态，而且针对任意输入符号都有到其自身的转换。证明，添加了“停滞状态”的自动机与原有的自动机是等价的。

5. 证明，如果为确定自动机添加了停滞状态，就可以得到具有从起始状态出发而且标记为每个可能字符串的路径的等价自动机。

6. * 证明，如果对确定自动机进行子集构造，那么要么得到相同的自动机，其中每个状态s 都重命名为{s }，要么添加了停滞状态（对应空状态集）。

7. ** 假设有某确定自动机，并要把每个接受状态变成不接受状态，还要把每个不接受状态变成接受状态。

(a) 如何用旧自动机的语言来描述新自动机接受的语言？

(b) 如果先为原自动机加上停滞状态，重复(a)小题。

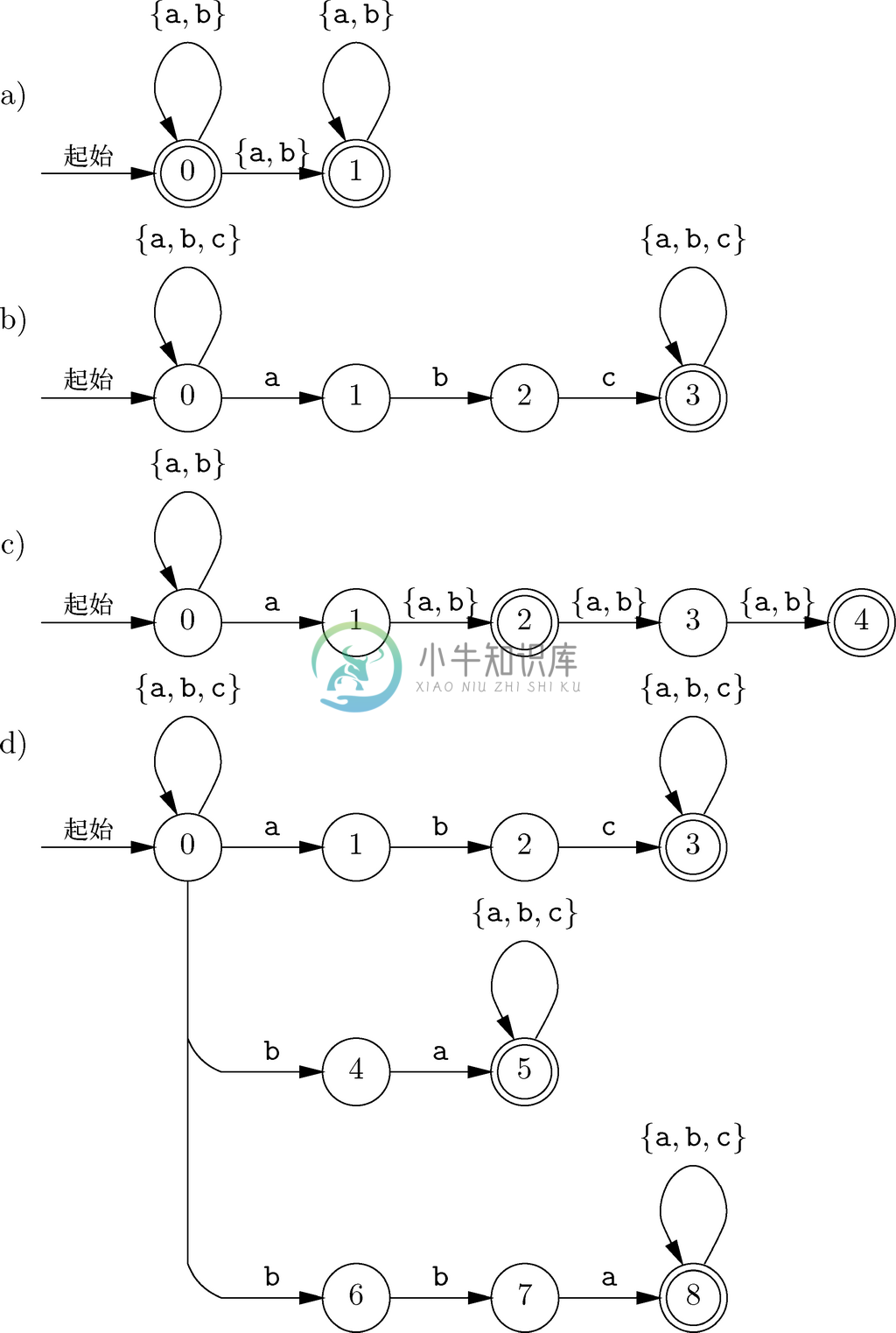
图 10-24　非确定自动机

10.5　正则表达式

自动机定义了模式，即表示自动机的图中，作为从起始状态到某个接受状态的路径标号的字符串组成的集合。在本节中，我们遇到了正则表达式这种用来定义模式的代数方法。正则表达式与我们熟悉的算术表达式代数，以及第8章中遇到的关系代数都是相似的。有趣的是，可以用正则表达式代数表示的模式组成的集合，刚好与可以用自动机描述的模式组成的集合相同。

表示方式的约定
我们还将继续使用等宽字体来表示出现在字符串中的字符。与某给定字符对应的正则表达式原子操作数则会用加粗的该字符来表示。例如，a是对应字符a的正则表达式。在我们需要使用变量时，会把它写为斜体。变量在这里用来代表复杂的表达式。例如，使用变量letter 表示“任意字母”这个我们很快就要看到其正则表达式的集合。

10.5.1　正则表达式的操作数

与所有的代数一样，正则表达式也具有某几类原子操作数。在算术代数中，原子操作数是常数（比如整数或实数），或可能的值是常数的变量；而对关系代数而言，原子操作数要么是固定的关系，要么是可能的值为关系的变量。在正则表达式代数中，原子操作数是如下几种中的一种。

1. 字符；

2. ε 符号；

3. ∅符号；

4. 值可能为由正则表达式定义的任意模式的变量。

10.5.2　正则表达式的值

任意代数中的表达式都具有某一类型的值。对算术表达式来说，值可以是整数、实数，或是我们可以处理的任意类型的数字。对关系代数而言，表达式的值就是个关系。

对正则表达式来说，每个表达式的值都是由通常被称为语言的字符串集合组成的模式。由正则表达式E 表示的语言就被称为L(E )，或者是“E 的语言”。原子操作数的语言有如下定义。

1. 如果x是任意字符，那么正则表达式x表示语言{x}；也就是说，L(x)={x}。请注意，该语言是包含一个字符串的集合，该字符串的长度为1，而且字符串中唯一的位置被字符x占据。

2. L(ε )={ε }。作为正则表达式的特殊字符ε 表示只含一个空字符串（或者说长度为0的字符串）的字符串集合。

3. L(∅)={∅}。作为正则表达式的特殊字符∅表示字符串集合为空。

请注意，我们没有定义原子操作数为变量时的值。只有在将变量替换为具体的表达式时，才可以为这样的操作数取值，而且它的值就是相应的表达式的值。

10.5.3　正则表达式的运算

正则表达式中运算符共有3种。这些运算符都可以用括号分组，就像我们所熟悉的代数中那样。和代数表达式中所做的一样，存在一些让我们可以忽略某些括号对的优先次序和结合律。在探讨完这些运算后，我们将会描述关于括号的规则。

1. 并

第一种，也是我们最熟悉的一种运算符就是并运算符，我们要将其表示为 | 。3为正则表达式取并的规则是，如果R 和S 为两个正则表达式，那么R |S表示R 和S 所表示的语言取并。也就是说，L(R |S )=L(R )∪L(S )。回想一下，L(R )和L(R )都是字符串的集合，所以为它们取并的概念是说得通的。

3在正则表达式中，加号+也常用作并运算符，不过在这里并不这样表示。

示例 10.11

我们知道a是表示{a}的正则表达式，而b是表示{b}的正则表达式。因此a|b就是表示{a，b}的正则表达式。这是一个包含a和b这两个长度为1的字符串的集合，同样，可以写出诸如(a|b)|c这样的表达式，来表示集合{a，b，c}。因为取并是一种有结合性的运算符，也就是说，在为3个集合求并集时，以任意次序组合这些操作数都是没关系的，可以忽略括号，并直接将表达式写为a|b|c。

2. 串接

正则表达式代数的第二个运算符叫作串接（concatenation）。它是用没有任何运算符符号来表示的，就像在写乘法表达式时有时会省略运算符那样，例如，算术表达式ab 就表示a 和b 的积。和取并运算一样，串接运算也是二元的中缀运算符。如果R 和S 是正则表达式，那么RS 就是R 和S 的串接。4

4严格地讲，应该把RS 写为(R )(S )，以强调R 和S 是分开的表达式，因为优先级规则，它们各自的组成部分一定不能混合在一起。这种情况与我们将表达式w+x 与y+z 相乘时类似，一定要将积写为(w+x)(y+z)。请注意，因为乘法要先于加法计算，所以如果把括号去掉，得到的表达式w+xy+z 就不能解释为w+x 与y+z 的积了。正如我们将要看到的，串接与取并具有的优先关系使得它们分别类似与乘法和加法。

RS 表示的语言L(RS )是由语言L(R )和L(S )按照以下方式形成的。对L(R )中的各字符串r 以及L(S )中的各字符串s 来说，字符串r 和s 的串接rs 是在L(RS )中的。回想一下两个表（比如字符串）的串接，是通过按次序取第一个表中的元素，并在它们之后按次序接上第二个表的元素而形成的。

类型之间的一些微妙区别
读者不应该弄混看似相似，实则差别巨大的多种对象。例如，空字符串ε就和空集∅不同，而这两者又都与只包含空字符串的集合{ε }不同。空字符串的类型是“字符串”或“字符表”，而空集和只含空字符串的集合都是“字符串集合”类型的。
我们还应该记得类型为“字符”的字符a，类型为“字符串”的长度为1的字符串a，以及类型为“字符串集合”的正则表达式a的值{a}之间的区别。还要注意到在其他的上下文中，{a}可能表示包含字符a的集合，而且我们没有表示方式上的约定用来区分{a}的这两种含义。不过，在本章的内容中，{a}通常都具有前一种解释，也就是“字符串集合”而非“字符集合”。

示例 10.12

设R是正则表达式a，因此L(R)就是集合{a}。再设S是正则表达式b，所以L(S)＝{b}。那么RS就是表达式ab。要形成L(RS)，需要取L(R)中的每个字符串，将其与L(S)中的每个字符串串接。在这种简单的情况中，L(R)和L(S)都是单元素集，所以对其二者来说都各自只有一种选择。我们从L(R)中选择a，并从L(S)中选择b，然后将这两个长度为1的表串接起来，就得到了字符串ab。因此L(RS)就是{ab}。

可以对示例10.12进行概括，得出任意用粗体表示的字符串，都是表示由一个字符串（相应字符组成的表）构成的语言的正则表达式。比如，then就是语言为{then}的正则表达式。我们将看到，串接是一种具有结合性的运算符，所以不管正则表达式中的字符如何分组都是没关系的，而且不需要使用括号。

示例 10.13

现在来看看两个语言不是单元素集的正则表达式的串接。设R是正则表达式a|(ab)。5语言L(R )就是L(a)和L(ab)的并集，即{a，ab}。设S是正则表达式c|(cb)。同样，L(S )={c，cb}。正则表达式RS 就是(a|(ab))(c|(cb))。请注意，出于运算优先级的原因，R 和S 上的括号是必要的。

5正如接下来将要看到的，串接要优先于取并，所以这里的括号是多余的。

	`c`	`bc`
`a`	`ac`	`abc`
`ab`	`abc`	`abbc`

图 10-25　形成{a，ab}和{c，cb}的串接

要找出L(RS )中的字符串，就要将L(R )中的两个字符串与L(S )中的两个字符串一一配对。这一配对方式如图10-25所示。从L(R )中的a和L(S )中的c，可以得到字符串ac。而字符串abc可以用两种不同方式得到，要么是(a)(bc)，要么是(ab)(c)。最后，L(R )中的ab与L(S )中的bc串接就得到字符串abbc。因此L(RS )就是{ac，abc，abbc}。

请注意，语言L(RS )中的字符串数量不可能大于L(R )中字符串数量和L(S )中字符串数量的积。事实上，L(RS )中字符串的数量刚好就是这个积，除非存在一些“巧合”，也就是同一字符串可以通过两种或多种不同方式形成的情况。示例10.13就是这样一个例子，其中字符串abc就可以用两种方式生成，因此L(RS )中就只有3个字符串，要比R 和S 的语言中字符串数量之积少1。同样，语言L(R | S )中字符串的数量也不大于语言L(R )和L(S )中字符串数量的和，而且在L(R )和L(S)中有相同字符串时只可能比该和小。在讨论这些运算符的代数法则时我们还将看到，正则表达式的取并和串接，与算术运算符+和×之间，存在一种相近但不精确的类比。

3. 闭包

第三个运算符是克林闭包（Kleene closure）或直接称为闭包。6它是个一元的后缀运算符，也就是说，它接受一个操作数并且出现在该操作数之后。闭包是用星号表示的，所以R *是正则表达式R 的闭包。因为闭包运算符有着最高的优先级，所以通常需要在R 两侧放上括号，将其写为(R )*。

6StevenC.Kleene最早撰写了描述正则表达式代数的论文。

闭包运算符的作用是表示“R 中的字符串没有出现或多次出现”。也就是说，L(R *)由下列内容组成。

1. 空字符串ε，可以将其视作R 中的字符串没有出现。

2. 在L(R )中的所有字符串，表示L(R )中的字符串出现一次。

3. 在L(RR )中的所有字符串，也就是L(R )与自身的串接，表示L(R )中的字符串出现两次。

4. 在L(RRR )、L(RRRR )等中的所有字符串，表示L(R )中的字符串出现3次、4次和更多次。可以有如下非正式的表示

R *＝ε | R |RR |RRR |…

不过，一定要理解，等号右侧的表达式并不是正则表达式，因为它包含无数个取并运算符。而所有正则表达式都是用有限数量的这3种运算符构建的。

示例 10.14

设R=a。那么L(R *)是什么？当然，ε 肯定在该语言中，因为它一定在任意闭包中。而L(R )中唯一的字符串a也在该语言中，还有L(RR )中的aa，L(RRR )中的aaa，等等。也就是说，L(a*)是由含0个或多个a的字符串组成的集合，也就是{ε，a，aa，aaa，…}。

示例 10.15

现在设R是正则表达式a|b，那么L(R )={a，b}，并考虑L(R *)是什么。该语言还是含有ε，表示L(R )中字符串没有出现。R中的字符串出现一次就为L(R *)带来了{a，b}。出现两次就给我们4个字符串{aa，ab，ba，bb}，3次出现就给了我们由a和（或）b组成长度为3的8个字符串，以此类推。因此L(R *)是所有由a和（或）b组成的任意有限长度的字符串。

10.5.4　正则表达式运算符的优先级

正如我们在前面的内容中非正式提到的，正则表达式的3个运算符并、串接和闭包之间存在约定的优先级次序。这一次序如下。

1. 闭包（最高）；

2. 然后是串接；

3. 然后是并（最低）。

因此，在解释任何正则表达式时，首先要为闭包运算符分组，也就是找出具有表达式形式（即如果存在括号的话，则它们是配对的）的紧邻某给定*左侧的最短表达式。可以给该表达式和相应的*加上一对括号。

接下来，要从左边起考虑串接运算符。对每个串接运算符，要找到紧邻其左侧的最小表达式并找到紧邻其右侧的最小表达式，再给这一对表达式加上括号。最后，要从左侧起考虑取并运算符。找到紧邻每个取并运算符左右的表达式，并这这一对中间有着取并符号的表达式周围加上括号。

示例 10.16

考虑表达式a|bc*d。首先分析*。该表达式中只有一个*，而且在其左侧的最小表达式为c。因此可以把该*与他的操作数分到一组，就成了a|b(c*)d。

接下来，要考虑上述表达式中的串接。共有两次串接，一次是b和左括号之间的，另一次是在右括号和d之间的。首先分析第一次串接，我们看到b就是紧邻左侧的，而到右侧就必须到将右括号包括在内为止，因为表达式的括号必须是平衡的。因此，第一次串接的操作数分别是b和(c*)。给它们周围加上括号就得到表达式

a|(b(c*))d

对第二次串接来说，紧邻其左的最短表达式现在是(b(c*))，而紧邻其右的最短表达式是d。在给这次串接的操作数分组加上括号后，表达式就成了

a|((b(c*))d)

最后，必须考虑取并运算。该表达式中总共有一次取并运算，它的左操作数为a，而其右操作数就是上述表达式其余的部分。严格来说，必须为整个表达式再加上一层括号，得到

(a|(b(c*)d))

不过最外层的括号是多余的。

10.5.5　正则表达式的其他一些示例

在本节最后，我们要给出一些更复杂的正则表达式。

示例 10.17

可以将示例10.15中的思路扩展到“由符号a₁、a₂、…、a_n 组成的任意长度的字符串”以及如下正则表达式：

(a1|a2|…|an)*

例如，可以按照以下方式描述C语言标识符。首先，定义正则表达式：

letter=A|B|…|Z|a|b|…|z|_

这就是说，C语言中的“字母”包括大小写英文字母和下划线。同样，我们还定义了正则表达式：

digit = 0|1|… | 9

那么正则表达式

letter(letter|digit)*

就表示由字母、数字和下划线组成的所有不以数字开头的字符串。

示例 10.18

现在来考虑一个更难写出的正则表达式：在示例10.2中讨论过的反弹过滤器问题。回想一下，我们描述了这样一种自动机，粗略地讲，就是只要输入的结尾是一列1，就会输出1。也就是说，只要在一行中看到两个1，就认为我们已经在一列1中，不过在确定看到的是一列1后，一个0的出现并不会让我们推翻这一结论。因此，每当输入的结尾有由两个1组成的序列时，只要它后面跟上的内容中每个0之后要么立即跟上一个1，要么是当前为止看到的最后一个输入字符，示例10.2中自动机的输出就是1。可以用如下正则表达式表示这种情况。

(0|1)*11(1|01)*(ε|0)

要理解该正则表达式，首先要注意到(0|1)*表示由0和1组成的任意字符串。这些字符串后面一定要跟上两个1，就如表达式11所表示的。因此(0|1)*11就是所有由0和1组成且结尾（至少）有两个1的字符串。

接下来(0|01)*表示所有由0和1组成，而且其中所有0后面都跟着1的字符串。也就是，该表达式语言中的字符串是以任意次序串接任意数量的字符串1和01构成的。尽管1让我们在任意时刻都可以向正在形成的字符串添加一个1，不过01强迫我们在任何0之后都加上一个1。因此表达式(0|1)*11(1|01)*表示所有由0和1组成的，以两个1后面加上其中的0都要立即加上一个1的任意序列结尾的字符串。而最后的因子(ε|0)表示“可选的0”，也就是说，刚刚描述的字符串后面可能还有一个0，也可能没有，要看我们的选择。

10.5.6　习题

1. 在示例10.13中，我们描述了正则表达式(a|ab)(c|cb)，并看到它的语言是由ac、abc和abbc这3个字符串组成的，也就是说，一个a和一个c，中间被0到2个b分隔开。再写两个定义该语言的正则表达式。

2. 写出定义下列语言的正则表达式。

(a) 对应6个C语言比较运算符=、<=、<、>=、>和!=的字符串。

(b) 所有由0和1组成且结尾为0的字符串。

(d) 所有由0和1组成且至多有一个1的字符串。

(e) 所有由0和1组成且至右起第三位是1的字符串。

(f) 所有由小写字母按已排序次序组成的字符串。

3. * 写出定义下列语言的正则表达式。

(a) 所有由a和b组成，满足其中由a组成的子序列长度都是偶数的字符串。也就是说，诸如bbbaabaaaa、aaaabb和ε这样的字符串，而abbabaa和aaa就不是。

(b) 由C语言中float类型的数字表示的字符串。

4. ** 写出定义下列语言的正则表达式。

(a) 不是关键字的C语言标识符组成的集合。如果忘记了某些关键字也是没关系的，本题的重点在于表示那些不在某个相当大的字符串集合中的字符串。

(b) 所有由a、b和c组成，而且满足任何两个连续位置上的字母都不相同的字符串。

(c) 由两个不同的小写字母形成的所有字符串构成的集合。提示：大家可以用“蛮力”来解决问题，不过用两个不同的字母构成的字母对有650个。更好的思路是进行一些分组。例如，相对较短的表达式(a|b|…|m)(n|o|…|z)就能覆盖这650个字母对中的169个。

(d) 所有由二进制数字0和1组成的，表示为3的倍数的整数的字符串。

5. 根据取并、串接和闭包运算符的优先级，为以下正则表达式加上括号，以表示操作数的恰当分组。

(a) a|bc|de

(b) a|b*|(a|b)*a

6. 从下列正则表达式中删除多余的括号，也就是说，删除那些分组可以由运算符的优先级以及取并

和串接的结合性（因此为邻接的取并或邻接的串接分组是无关紧要的）暗示出的括号。

(a) (ab)(cd)

(b) (a|(b(c)*))

7. * 描述由以下正则表达式定义的语言。

(a) ∅|ε

(b) εa

(d) (a*b*)*

(e) (a*ba*b)*a*

(f) ε *

(g) R **，其中R 是任意正则表达式。

10.6　UNIX 对正则表达式的扩展

UNIX操作系统中有不少命令利用了类似正则表达式的表示法来描述模式。即便对UNIX操作系统与其中的大部分命令并不熟悉，了解这些表示法也还是很实用的。我们发现正则表达式至少用在如下3类命令中。

1. 编辑器。UNIX编辑器ed和vi，以及大多数现代文本编辑器，让用户可以在找到某给定模式实例的位置扫描文本。这一模式是由正则表达式指定的，虽然没有一般的取并运算符，只有下面将要讨论的“字符类”。

2. 模式匹配程序grep及类似程序。UNIX命令grep会对文件进行扫描，检查文件的每一行。如果该行包含某个能与由正则表达式指定的模式匹配的子串，就将该行打印出来（grep代表globally search for regular expression and print，即全局查找正则表达式并打印）。grep命令本身只接受正则表达式的子集，而扩展的命令egrep则可以接受完整的正则表达式表示，而且包含了一些其他的扩展。命令awk允许我们进行全面的正则表达式搜索，并且把文本行当作关系的元组来处理，从而使我们可以对文件执行选择和投影这样的关系代数运算。

3. 词法分析。UNIX命令lex对编写编译器代码及类似任务而言是很使用的。编译器第一件必须完成的事就是将程序分割为一个个标记（token），它们是逻辑上结合在一起的子字符串。标记的例子包括标识符、常量、then这样的关键字，以及+或<=这样的运算符。每种标记类型都可以由一个正则表达式来指定，比方说，示例10.17就展示了如何指定“标识符”标记类。lex命令让用户可以用正则表达式指定标记类。这样就形成了可以用作词法分析器的程序，也就是可以把输入分解为标记的程序。

10.6.1　字符类

我们经常需要写出表示字符集合，或者严格地讲，是表示长度为1的字符串（每个字符串都是由集合中不同的字符构成）组成的集合的正则表达式。因此，在示例10.17中，我们定义了表达式letter 表示任何由一个大写字母或小写字母组成的字符串，并定义了表达式digit 表示任何由一个数字构成的字符串。这些表达式都是相当长的，而UNIX提供了一些重要的简写。

首先，可以用方括号把任意字符表括起来，用来代表对这些字母取并的正则表达式。这样的表达式就叫作字符类。例如，表达式[aghinostw]表示出现在单词washington中的字母组成的集合，而[aghinostw]*则表示只由这些字母形成的字符串所构成的集合。

其次，我们并非总是需要明确地列出所有的字符。回想一下，字母几乎一直都是用ASCII编码的。这种编码会为各种字符指定相应的位串（很自然地就可以解释为整数），而且它是以一种合理的方式来完成这一工作的。例如，ASCII编码为大写字母分配了连续的整数。同样，它也为小写字母以及数字分配了连续的整数。

如果在两个字符间加上破折号，就不仅表示这些字符，而且表示了编码在这两个字符编码之间的所有字符。

示例 10.19

我们可以通过[A-Za-z]定义大写字母与小写字母。前3个字符A-Z表示编码处于A和Z之间的所有字符，也就是所有的大写字母。而接下来的3个字符a-z则表示所有的小写字母。

顺便提一句，因为破折号有这样一种特殊含义，所以如果想要定义包含-的字符类，就一定要谨慎行事。必须把破折号放在这列字符的第一个位置或最后一个位置。例如，可以通过[-+*/]来指定4四种算术运算符组成的集合，但如果写成[+-*/]的形式就是错误的，因为+-*这样的范围会表示编码在+和*的编码之间的所有字符。

10.6.2　行的开头和结尾

因为UNIX命令经常要处理单行文本，所以UNIX正则表达式表示法中包含了用于表示行的开头和结尾的特殊符号。符号^表示行的开头，而$表示行的结尾。

示例 10.20

10.3节图10-12中的自动机是从一行的开头处启动的，它接受的文本行刚好是那些只由单词washington中的字母组成的文本行。可以将这种模式表示为UNIX正则表达式：^[aghinostw]*$。口头上讲，该模式就是“行的开头，后面跟上由单词washington中的字母组成的任意序列，再加上行的结尾”。

举个这种正则表达式使用方式的例子，UNIX命令行：

grep'^[aghinostw]*$ /usr/dict/words

将打印出词典中所有只由来自washington的字符组成的单词。在这种情况下，UNIX要求该正则表达式被写为引用的字符串。这一命令的效果就是指定的文件/usr/dict/words中每一行都会被检查。如果它含有任何处在由该正则表达式表示的字符串集合中的子字符串，那么这一行就要被打印出来，否则这一行就不会被打印。请注意，这一行的开头符号与结尾符号已然存在了。假设它们不存在。因为空字符串是在由正则表达式[aghinostw]*表示的语言中的，所以我们会发现每一行都有一个子字符串（即ε）位于该正则表达式的语言中，因此每一行都会被打印出来。

为字符赋予字面意义
顺便说一下，因为字符^和$在正则表达式中被赋予了特殊意义，所以看起来没办法在UNIX正则表达式中指定这些字符本身了。不过，UNIX用到了反斜杠\，作为转义字符。如果我们在字符^或$之前加上反斜杠，那么这两个字符形成的组合就会被解释为第二个字符的字面意义，而不是其特殊含义。例如\$表示UNIX正则表达式中的$字符。同样，两道反斜杠就被解释为一个反斜杠，而不含有其转义字符的特殊意义。而UNIX正则表达式中的字符串\\$表示的是反斜杠字符后面跟上行的结尾。
还有不少其他的字符也被UNIX在某些情形下赋予了特殊意义，而这些字符也总是能表示它们的字面意义，也就是，通过在它们之前使用反斜杠来“除掉”它们的特殊意义。例如，只有这样处理方括号，方括号在UNIX正则表达式中才不会被解释为字符类分隔符。

10.6.3　通配符

符号.在UNIX正则表达式中代表“除换行符之外的任意字符”。

示例 10.21

正则表达式

.*a*e.*o.*u.

表示按次序包含5个元音字母的所有字符串。我们可以利用grep与该正则表达式来扫描词典，查找单词中5个元音字母按递增次序出现的所有单词。不过，如果忽略掉开头和结尾位置的.*，处理将更具效率，因为grep是按子字符串搜索指定的模式，而不是整行搜索，除非我们显式地包含了表示行开头和行结尾的符号。因此命令

grep'a.*e.*i.*u' /use/dict/words

将会找到含有子序列aeiou的所有单词并将其打印出来。

这些点号会匹配除字母之外的字符，这一实情并不重要，因为在/usr/dict/words文件中除了字符和换行符之外没有其他字符。不过，如果点号可以匹配换行符，那么这一正则表达式就会允许grep一次使用多行来找出依次出现的5个元音字母。不过像本例这样的例子都是点号被定义为不匹配换行符的例子。

10.6.4　额外的运算符

UNIX命令awk和egrep中的正则表达式还含有一些额外的运算符，具体如下。

1. 与grep不同的是，awk和egrep命令还允许取并运算符|出现在它们的正则表达式中。

2. 一元后缀运算符?和+没有允许我们定义额外的语言，但它们通常会让表示语言的工作变得更简单。如果R 是正则表达式，则R?代表ε |R，也就是可选的R。所以L(R?)是L(R )∪{ε }。R+代表RR *，或者等价地讲就是“R 中的单词出现一次或多次”。因此，L(R+)＝L(R )∪L(RR )∪L(RRR )…。特别要说的是，如果ε 在L(R )中，那么L(R+)和L(R *)表示相同的语言。而如果ε 不在L(R )中，那么L(R+)就表示L(R *)-{ε }。运算符 ? 和+与 * 有着相同的结合性与优先级。

示例 10.22

假设我们想通过正则表达式来指定由非空数字串与一个小数点组成的实数。将该表达式写为[0-9]*.[0-9]*是不正确的，因为这样一来，只由一个点号组成的字符串也会被视作实数。该表达式利用egrep的一种写法是

[0-9]+ \.[0-9]*\.[0-9]+

在这里，取并的第一项涵盖了那些小数点左侧至少有一个数字的实数，而第二项则涵盖了以小数点开头，因此在小数点后必须至少有一位数字的那些实数。请注意，放在点号之前的反斜杠是为了表明这里的点号不具有约定的“通配符”含义。

示例 10.23

利用如下egrep命令可以扫描输入中那些字母严格按照字母表增序排列的行。

egrep '^a?b?c?d?e?f?g?h?i?j?k?l?m?n?o?p?q?r?s?t?u?v?w?x?y?z?$'

也就是说，我们会扫描每一行，看看在行的开头和结尾之间是否有可选的a、可选的b，等等。例如，含有单词adept的一行就能匹该表达式，因为a、d、e、p和t之后的?可以解释为“出现一次”，而其他的?可以解释为“没有出现”，也就是ε。

10.6.5　习题

1. 为以下字符类写出表达式。

(a) 所有属于C语言运算符和标点符的字符，例如+和圆括号。

(b) 所有小写元音字母。

2. * 如果可以使用UNIX，编写egrep程序检查/usr/dict/words文件，并找到下列单词：

(a) 所有以dous结尾的单词；

(b) 所有只含一个元音字母的单词；

(d) 所有含四个或更多个连续辅音字母的单词。

10.7　正则表达式的代数法则

两个正则表达式是可以表示同一语言的，就像两个算术表达式可以表示其操作数的相同函数那样。举例来说，x+y 和y+x 这两个表达式就表示x 和y 的相同函数。同样，不管用什么正则表达式来替换R 和S，正则表达式R |S和S |R都表示同一语言，证据就是取并运算也是具有交换性的。

简化正则表达式往往是很实用的。我们很快就会看到，在根据自动机构造正则表达式时，经常会构造出过于复杂的正则表达式。代数等价可以让我们“简化”表达式，也就是说，把一个正则表达式替换为另一个操作数和（或）运算符更少却又表示相同语言的正则表达式。这一过程类似于在处理算术表达式时对繁冗的表达式进行的那些简化。例如，可以将两个很大的多项式相乘，然后通过分组相似项来简化结果。再比如，我们在8.9节中简化了关系代数表达式从而获得更快的求值速度。

如果L(R )=L(S )，就说两个正则表达式R 和S 是等价的，记作R ≡S。如果这样的话，可以说R ≡S是一种等价。在接下来的内容中，我们将假设R、S 和T 是任意的正则表达式，并以这些操作数来陈述要讨论的等价关系。

等价的证明
在本节中，我们要证明若干涉及正则表达式的等价关系。回想一下，两个正则表达式的等价是说，不管为其变量替换怎样的语言，这两个表达式的语言都是相等的。因此我们可以通过证明两种语言，也就是两个字符串集合的相等性，来证明正则表达式的等价。一般而言，要通过证明两个方向上的包含关系来证明集合S₁和集合S₂是等价的。也就是说，证明S₁⊆S₂，还要证明S₂⊆S₁。两个方向对证明集合相等都是必要的。

10.7.1　取并和串接与加法和乘法的类比

在本节中，我们要列举与正则表达式的取并、串接和闭包运算符有关的最重要的那些等价关系。首先要从取并和串接运算与加法和乘法运算的类比开始。正如我们将要看到，这种类比并不是很精确，主要因为串接是不具备交换性的，而乘法当然是具备交换性的。不过，这两对运算之间还是存在诸多相似性。

首先，取并和串接都具有单位元。取并运算的单位元是∅，而串接运算的单位元是ε。

(1) 取并的单位元。(∅|R )≡(R |∅)≡R。

(2) 串接的单位元。εR ≡Rε ≡R。

从空集和取并的定义中应该不难看出(1)成立的原因。要知道(2)成立的原因，如果字符串x 在L(εR )中，那么x 就是L(ε )中某个字符串与L(R )中某个字符串r 的串接。不过L(ε )中唯一的字符串就是ε 本身，因此可知x=εr。不过，空字符串与任意字符串r 串接的结果都是r 本身，所以x=r。也就是说x 在L(R )中。同样可以看到，如果x 在L(Rε )中，那么x 也在L(R )中。

要证明等价对(2)，不仅要证明L(εR )和L(Rε )中的每个字符串都在L(R )中，而且要证明反向的命题，也就是L(R )中的每个字符串都在L(εR )和L(Rε )中。如果r 在L(R )中，那么εr 就在L(εR )中。不过εr=r，所以r 在L(εR )中。同样的推理告诉我们r 也在L(Rε )中。因此就证明了L(R )和L(εR )是相同的语言，而且L(R )和L(Rε )是相同的语言，这就是(2)中的等价关系。

因此∅与算术中的0是类似的，而ε 则与1是类似的。还存在另一种类比，∅是串接的零元（annihilator），也就是

(3) 串接的零元。∅R≡R∅≡∅。换句话说，当将空集与任何内容串接时，得到的都是空集。类似地，0是乘法运算的零元，因为0×x=x×0＝0。

可以通过以下方式验证(3)的真实性。为了让某个字符串x出现在L(∅R )中，就要用L(∅)中的字符串串接L(R )中的字符串。因为L(∅)中是不含字符串的，所以我们没办法形成x。类似的论证也可以证明L(R∅)也必定为空。

接下来的等价关系是我们在第7章中讨论过的并集运算的交换律和结合律。

(4) 取并的交换律。(R | S )≡(S | R )。

(5) 取并的结合律。((R | S ) | T )≡(R | (S | T ))。

正如我们提过的，串接也是有结合性的。也就是

(6) 串接的结合律。(((RS )T)≡(R (ST ))。

要知道(6)为何成立，先假设字符串x 在L((RS )T )中，那么x 就是由L(RS )中的某字符串y 和L(T )中某字符串t 串接而成。还有，y 一定是由L(R )中的某字符串r 和L(S )中的某字符串s 串接而成，因此有x=yt=rst。现在考虑L(R (ST ))。字符串st 一定在L(ST )中，因此rst，也就是x，是在L(R (ST ))中的。因此L((RS )T )中的每个字符串x 都一定也在L(R (ST ))中。相似的论证告诉我们L(R (ST ))中的每个字符串也一定在L((RS )T )中。因此这两种语言是相同的，所以等价关系(6)成立。

(7) 串接对取并的左分配律。(R (S |T ))≡(RS |RT )。

(8) 串接对取并的右分配律。((S |T )R )≡(SR |TR )。

我们看看(7)为什么成立，(8)成立的原因也是相似的，就留作习题吧。如果x 在L(R (S |T ))中，那么x=ry，其中r 在L(R )中，而且y 要么在L(S )中，要么在L(T )中，或者同在这两者中。如果y 在L(S )中，那么x 在L(RS )中，而如果y 在L(R )中，那么x 在L(RT )中。不管是哪种情况，x 都是在L(RS |RT )中。因此L(R (S |T ))中的每个字符串都在L(RS |RT )中。

10.7.2　取并和串接与加法和乘法的区别

取并运算与加法不尽相同的原因之一就是幂等律。也就是说，取并运算是幂等的，但加法不是。

(9) 取并的幂等律。(R |R )≡R。

串接也与乘法有重大差异，因为串接不具交换性，而实数或整数的乘法是满足交换律的。要知道RS 一般来说与SR 不等价的原因，可以举个简单例子，设R=a而且S=b，则有L(RS )={ab}，且L(RS )={ba}，而这两个集合是不同的。

10.7.3　涉及闭包的等价

还有其他一些与闭包运算符有关的实用等价关系。

(10) ∅*≡ε。大家可以验证该式的两边都表示语言{ε }。

(11) RR *≡R *R。请注意，该式两边都与10.6节扩展表示法中的R+是等价的。

(12) (RR *|ε )≡R *。也就是说，R+和空字符串取并是与R *等价的。

10.7.4　习题

1. 证明等价关系(8)，即串接对取并的右分配律是成立的。

2. 通过变量替换，可以从已经陈述的等价关系得出等价关系∅∅≡∅和εε ≡ε，其中要利用到哪些等价关系？

3. 证明等价关系(10)到(12)。

4. 证明：

(a) (R |R *)≡R *；

(b) (ε |R *)≡R *。

5. * 是否存在特定的正则表达式R 和S 满足“交换律”，也就是说，对这些特殊的表达式来说，满足RS=SR？如果不存在，请给出证明，如果存在，请给出示例。

6. * 正则表达式中不需要操作数∅，除非没有∅就找不到语言为空集的正则表达式。如果正则表达式中未出现∅，就说它是无∅的。通过对无∅正则表达式R 中出现的运算符个数进行归纳，证明L(R )不是空集。提示：10.8节中将会展示对正则表达式中出现的运算符的数量进行归纳证明的示例。

7. ** 通过对正则表达式R 中出现的运算符的数量进行归纳证明：R 要么与正则表达式∅等价，要么与某个无∅正则表达式等价。

10.8　从正则表达式到自动机

记得我们在10.2节中对自动机的初步讨论，其中看到了在确定自动机与利用了“状态”概念（用以区分程序中不同部分扮演的角色）的程序之间存在的紧密关系。然后我们说过，设计确定自动机往往是设计这类程序的一种好方法。不过我们还看到，确定自动机可能难于设计。在10.3节中看到，有时候设计非确定自动机要更简单，而且子集构造让我们可以把任意非确定自动机转换成等价的确定自动机。现在我们又知道了正则表达式，接下来会看到，写出正则表达式甚至比设计非确定自动机更简单。

而且很好的是，存在某种方式可以把任意正则表达式转换成非确定自动机，接着就可以使用子集构造将得到的非确定自动机转换成确定自动机。事实上，我们在10.9节中还会看到，也能把任意自动机转换成相应的正则表达式，其中正则表达式的语言刚好是自动机接受的字符串集合。因此自动机和正则表达式有着一模一样的语言描述能力。

并非所有语言都能用自动机描述
尽管我们看到很多语言可以用自动机或正则表达式描述，但还是存在不能这样描述的语言。直觉就是“自动机不会数数”。也就是说，如果为具有n个状态的自动机提供一列n个相同符号，它肯定会进入同一状态两次，这样它就不能确切记住已经看到了多少符号。因此，比方说自动机不可能识别所有只由平衡圆括号组成的字符串。因为正则表达式和自动机定义了相同的语言，所以同样不会有语言刚好全是平衡圆括号字符串的正则表达式。我们将在10.9节中讨论哪些语言是不可以用自动机定义的。

在本节中，我们要完成以下任务，说明如何把正则表达式转换成自动机。

1. 引入具有ε 转换的自动机，也就是，具有标号为ε 的弧的自动机。这些弧用在路径中，但不会对路径的标号产生任何影响。这种形式的自动机是正则表达式与本章先前讨论过的自动机之间的中间体。

2. 展示如何把任意正则表达式转换成定义同一语言的具有ε 转换的自动机。

3. 展示如何把任意具有ε 转换的自动机转换成接受同一语言的不含ε 转换的自动机。

10.8.1　具有 ε 转换的自动机

首先要将自动机的概念扩展到允许为弧标记ε。这样的自动机仍然是当且仅当从起始状态到接受状态存在标记为s 的路径时才接受字符串s。不过请注意，空字符串ε 在字符串中是“不可见的”，因此在为路径构建标号时，我们其实删除了所有的ε，并且只使用“真实”的字符。

示例 10.24

考虑如图10-26所示的具有ε 转换的自动机。在这里，状态0是起始状态，而状态3是唯一的接受状态。从状态0到状态3的一条路径为

0，4，5，6，7，8，7，8，9，3

这些弧的标号就构成了序列

ε b ε ε c ε c ε ε

只要记得ε 与任意其他字符串串接得到的都是那个其他字符串，就可以“丢掉”这些ε得到字符串bcc，这就是正在考虑的路径的标号。

{%}

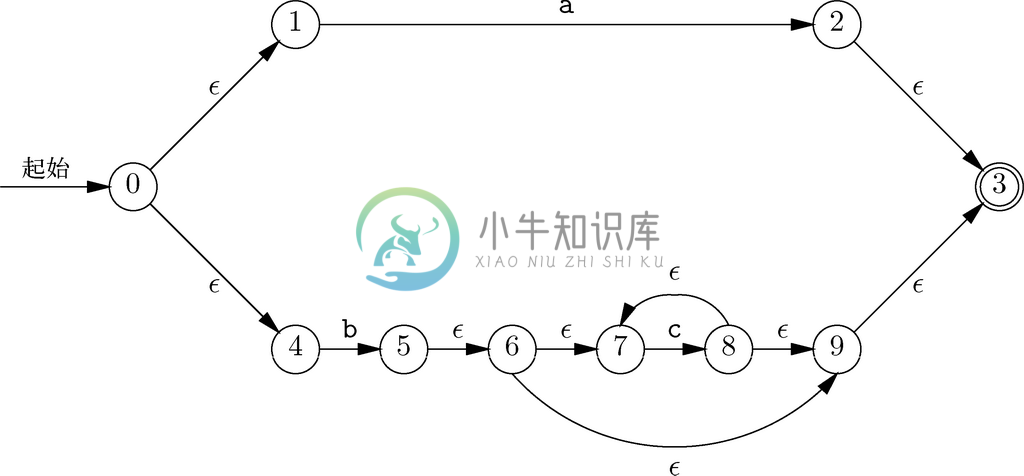
图 10-26　表示a|bc*的具有ε转换的自动机

大家可能会发现，从状态0到状态3的路径的标记只会是a、b、bc、bcc、bccc，等等。表示该集合的正则表达式是a | bc*，而且我们会看到图10-26中的自动机可以自然地由这一正则表达式构建而来。

10.8.2　从正则表达式到具有ε 转换的自动机

我们可以利用根据对正则表达式中运算符数量进行完全归纳得出的算法，把正则表达式转换成自动机。这一思路类似于我们在5.5节中介绍过的对树的结构归纳，而且如果用正则表达式的表达式树（其中原子操作数是树叶，而运算符在中间节点位置）来表示它们，这种对应就会变得更加明朗。要证明的命题如下。

命题S(n)。如果R 是含n 个运算符，而且不含变量作为原子操作数的正则表达式，那么存在具有ε 转换的自动机A，只接受L(R )中的字符串。此外，A 满足如下所有条件：

1. 只有一个接受状态；

2. 没有弧通向它的起始状态；

3. 没有弧从它的接受状态出发。

依据。如果n=0，那么R 一定是一个原子操作数，它可能是∅、ε，或是对应某个符号x的x。在这3种情况下，可以设计满足命题S(0)要求的双状态的自动机，这些自动机如图10-27所示。

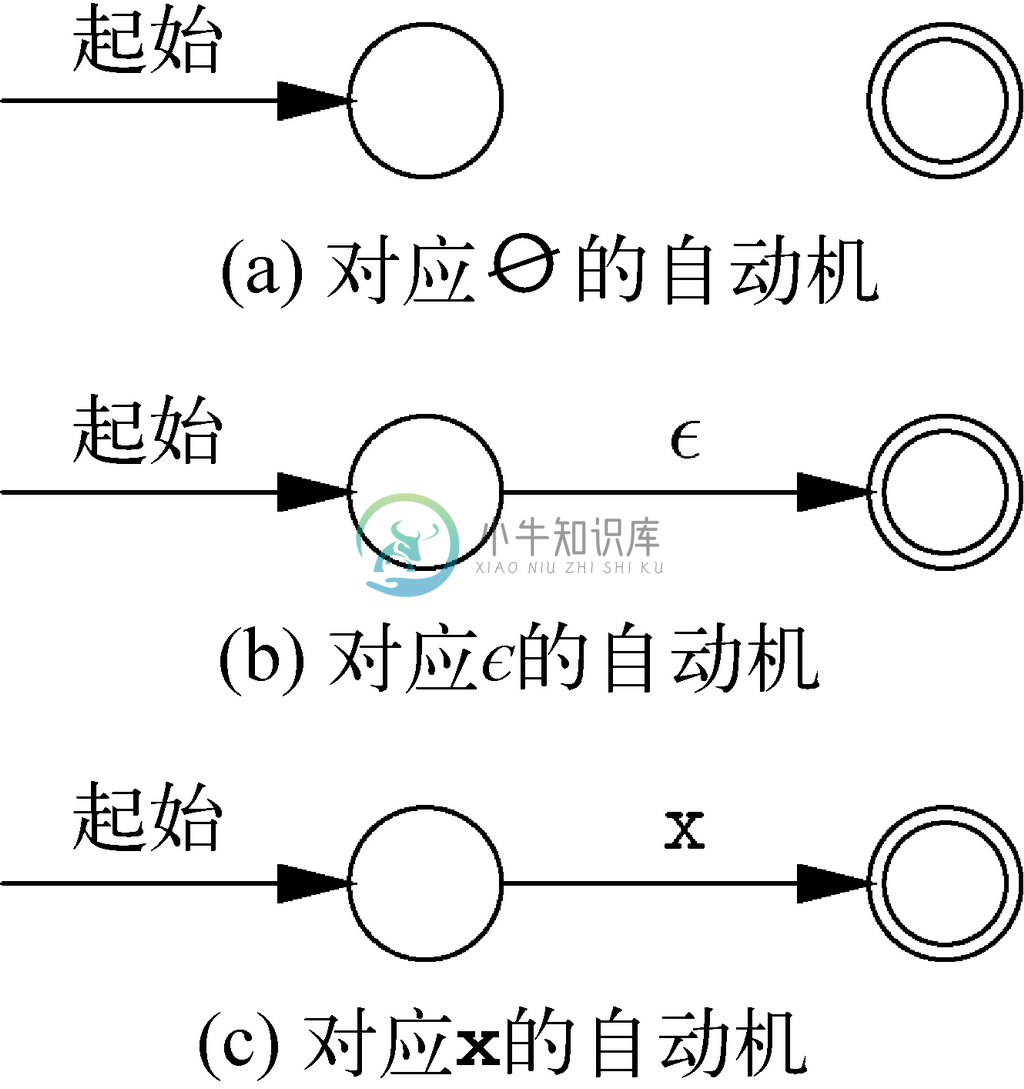
图 10-27　依据情况中的自动机

请务必理解，这里为正则表达式中出现的每个操作数创建了新的自动机，而且所具有的状态与其他任何自动机的状态都不一样。例如，如果在表达式中出现3个a，我们就会创建3个不同的自动机，总共有6个状态，每个自动机都与图10-27c所示的自动机类似，只不过用a替代了其中的x。

图10-27a中的自动机显然不接受任何字符串，因为我们没办法从起始状态到达接受状态，因此它的语言为∅。图10-27b是对应ε 的，因为它只接受空字符串。图10-27c是只接受字符串x的自动机。我们可以用为符号x选择的不同值创建新的自动机。请注意，这些自动机都能满足上述3个要求，只有一个接受状态，没有进入起始状态的弧，也没有从接受状态出发的弧。

归纳。现在假设S(i )对所有的i≤n 都成立，也就是说，对任意最多具有n 个运算符的正则表达式R 来说，存在自动机满足归纳假设的条件，并且只接受L(R )中的所有字符串。现在，设R 是具有n+1个运算符的正则表达式。我们可以将注意力放在R“最外侧”的运算符上，也就是说，R 只可能是R₁|R₂、R₁R₂或R₁*这样的形式，具体取决于形成R 时最后用到的那个运算符是区别、串接还是闭包。

在这3种情况的任意一种中，R₁和R₂都不可能具有n 个以上运算符，因为R中有一个运算符不属于R₁和R₂中的任何一个。7因此，归纳假设在所有这3种情况下都是适用于R₁和R₂的。我们可以通过依次考虑这几种情况来证明S(n+1)。

7不要忘了，即便串接是通过并置操作数来表示的，并没有可见的运算符符号，但在确定R 中出现了多少个运算符时，仍然要将串接的使用记入运算符出现的次数中。

情况1。如果R=R₁|R₂，那么可构建图10-28a中的自动机。取R₁和R₂，并添加两个新状态（一个起始状态和一个接受状态），从而构造了该自动机。与R对应的自动机的起始状态具有到与R₁和R₂对应的自动机起始状态的ε 转换。这两个自动机的接受状态分别有到对应的自动机接受状态的ε 转换。不过，与R₁和R₂对应的自动机的起始状态与接受状态不是构造出的自动机的起始状态和接受状态。

这种构造之所以行得通，是因为从对应R 的自动机的起始状态到接受状态的唯一方式，是沿着一条标记为ε 的弧到与R₁对应或与R₂对应的自动机的起始状态。然后必须沿着所选自动机中的路径到达其接受状态，之后经过ε 转换到达与R 对应的自动机的接受状态。这一路径是由我们行经的自动机所接收的某个字符串s 标记的，因为我们从该自动机的起始状态行至了接受状态。因此，s 要么在L(R₁)中，要么在L(R₂)中，这取决于我们行经的自动机到底是哪个。因为我们只为路径的标号增加了ε，所以图10-28a中的自动机也接受s。因此被接受的字符串都在L(R₁)∪L(R₂)中，也就是在L(R₁|R₂)，或者说L(R )中。

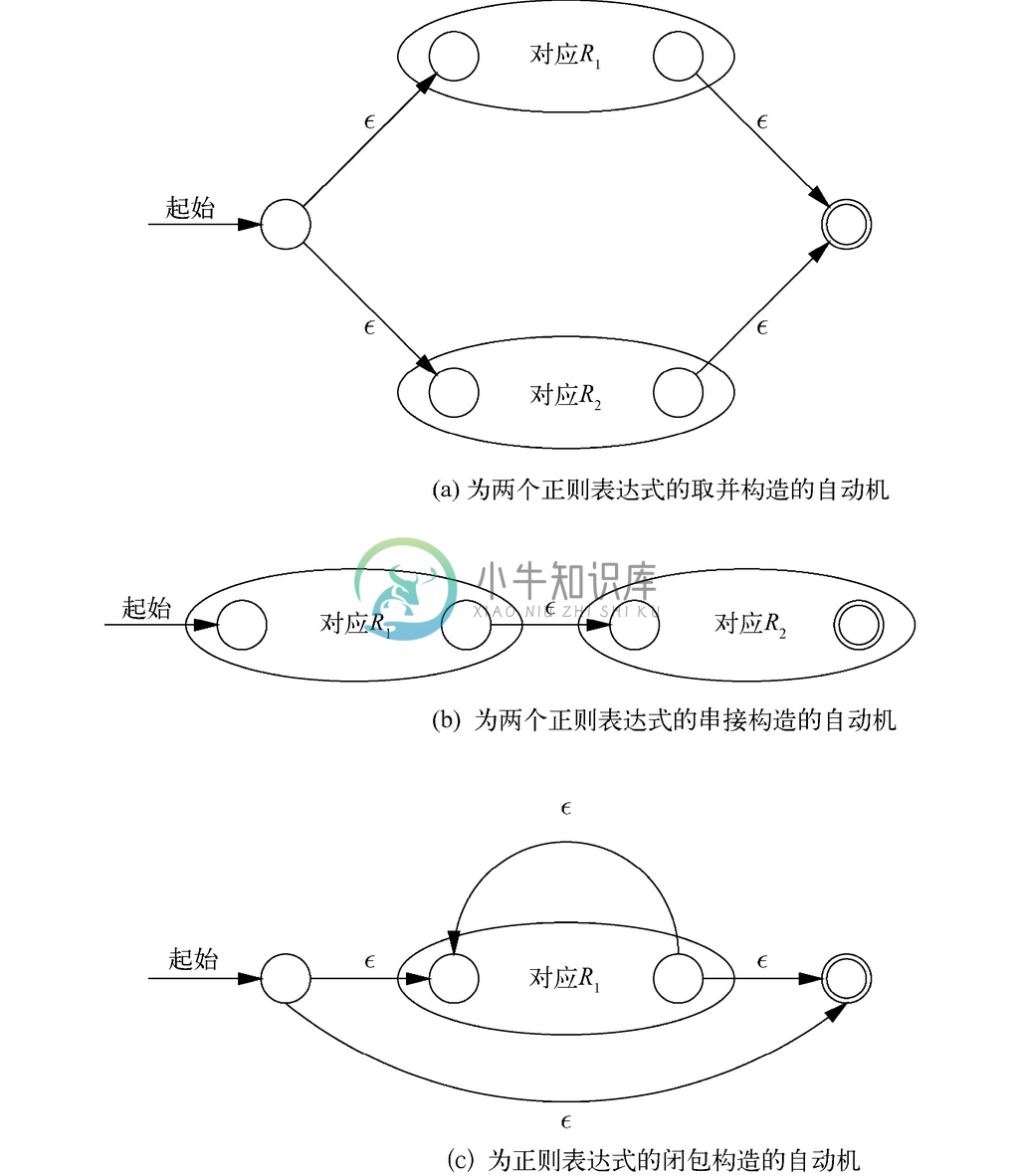
图 10-28　根据正则表达式构造自动机的归纳部分

情况2。如果R=R₁R₂，那么可以构造如图10-28b所示的自动机。该自动机的起始状态是与R₁对应的自动机的起始状态。而它的接受状态是与R₂对应的自动机的接受状态。我们添加了从与R₁对应的自动机的接受状态到与R₂对应的自动机的起始状态的ε 转换。第一个自动机的接受状态不再是接受状态，而第二个自动机的起始状态在构造的自动机中也不再是起始状态。

在图10-28b所示的自动机中，从起始状态到接受状态的唯一方式如下：

1. 顺着由L(R₁)中某字符串s 标记的路径，从起始状态到达与R₁对应的自动机的接受状态；

2. 接着沿着标记为ε 的路径到达与R₂对应的自动机的起始状态；

3. 然后顺着由L(R₂)中某字符串t 标记的路径，到达其接受状态。

这条路径的标号是st。因此图10-28b中的自动机接受的刚好是L(R₁R₁)，也就是L(R )中的字符串。

情况3。如果R＝R₁*，则可以构造如图10-28c所示的自动机。我们为与R₁对应的自动机添加了新的起始状态和接受状态。这个新的起始状态具有到新接受状态的ε 转换（所以字符串ε 会被接受），而且有到与R₁对应的自动机的起始状态的ε 转换。与R₁对应的自动机的接受状态被赋予了回到其起始状态的ε 转换，以及到与R 对应的自动机的接受状态的ε 转换。与R₁对应的自动机的起始状态与接受状态不再是构造出的自动机的起始状态与接受状态。

图10-28c中从起始状态到接受状态的路径要么标记为ε（如果是直接到达），要么是由L(R₁)中一个或多个字符串的串接来标记，一如我们行经与R₁对应的自动机，并且按自己喜好反复回到其起始状态一样。请注意，我们每次在行经与R₁对应的自动机时，并不一定都要沿着相同的路径。因此，经过图10-28c的路径的标号刚好是L(R₁*)，也就是L(R )中的字符串。

示例 10.25

下面我们来为正则表达式a | bc*构造自动机。对应该正则表达式的表达式树如图10-29所示，它类似于我们在5.2节中讨论过的表达式树，并有助于我们了解运算符应用到操作数上的次序。

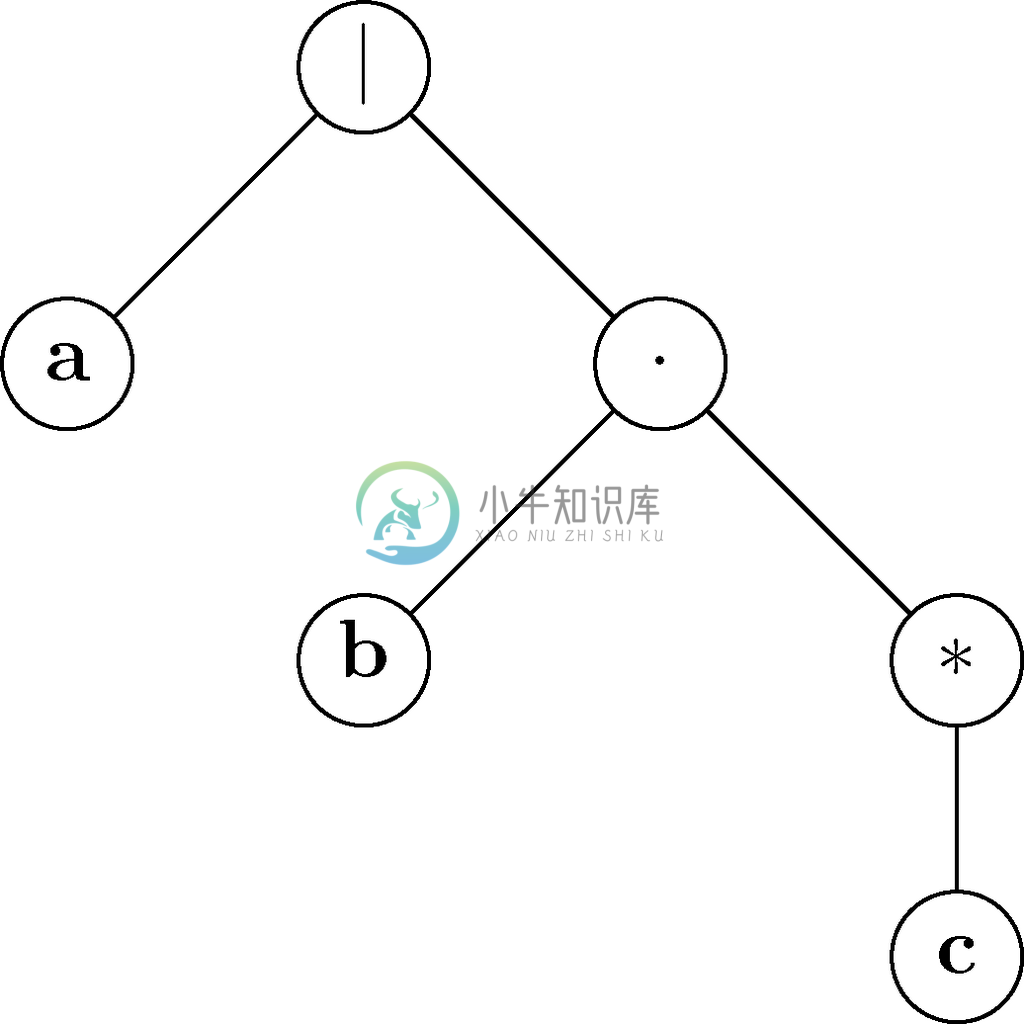
图 10-29　与正则表达式a|bc*对应的表达式树

总共有3个叶子节点，而且我们为每个叶子节点都构造了类似图10-27c所示的自动机实例。这些自动机如图10-30所示，而且使用了与图10-26所示的自动机（正如我们提到过的，这是我们最终要为该正则表达式构造的自动机）一致的状态。不过，大家应该明白，对应多次出现的操作数的自动机有着不同的状态。在这个例子中，因为每个操作数都是不同的，我们能想到要为每个操作数使用不同状态，不过，打个比方说，如果表达式中出现了多个a，就要为每个a创建不同的自动机。

现在必须应用运算符并构建随着进程更大的自动机，逐步建立起图10-29中的树。最先应用的运算符是闭包运算符，它是应用到操作数c上的。我们利用了图10-28c中对应闭包运算的构造方法。引入的新状态分别称为状态6和状态9，还是与图10-26保持一致。图10-31展示了与正则表达式c\*对应的自动机。

图 10-30　对应a、b和c的自动机

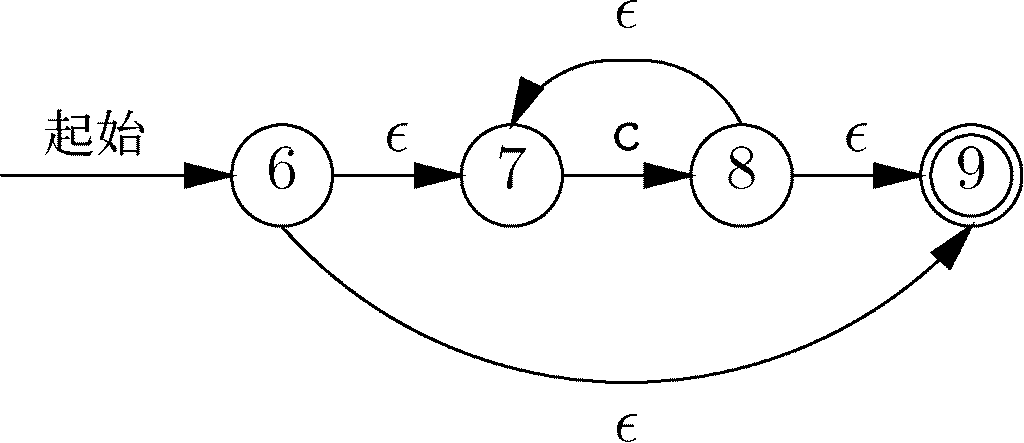
图 10-31　对应c*的自动机

接下来对b和c*应用了串接运算符。利用的是图10-28b的构造方法，得到的自动机如图10-32所示。

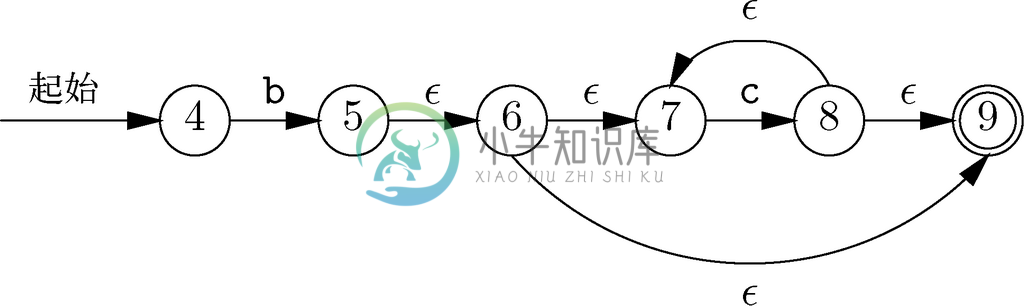
图 10-32　对应bc*的自动机

最后，我们对a和bc*应用取并运算符。这里用到了图10-28a所示的构造方法，而且将引入的新状态称为状态0和状态3，得到的自动机就如图10-26所示。

10.8.3　消除ε 转换

如果我们在具有ε 转换的某自动机的任意状态s 中，其实也是在从状态s 沿着由标记为ε 的弧形成的路径可以到达的任意状态。原因在于，不管是什么字符串标记了到达状态s 所经过的路径，同样的字符串都是用ε 转换扩展过的该路径的标号。

示例 10.26

在图10-26中，可以沿着标记了b的路径到达状态5。从状态5起，可以沿着由标记了ε 的弧形成的路径到达状态6、状态7、状态9和状态3。因此，如果我们在状态5中，其实也就在其他4个状态中。例如，因为状态3是接受状态，所以也可以把状态5视作接受状态，因为能把我们带到状态5的每个输入字符串，也能把我们带到状态3，因此是可以被接受的。

因此，要问的第一个问题是，从各状态开始，只沿着ε转换可以到达哪些其他状态？在9.7节中，我们在了解深度优先搜索的一种应用（可达性问题）时，给出了回答这一问题的算法。对这里的问题来说，要对表示有限自动机的图进行的修改，只是要把图中所有除ε转换之外的转换删除。也就是说，对每个实际的符号x，要删除所有标记为x的弧。然后从剩下的图中各个节点开始进行深度优先搜索。在从节点v 开始的深度优先搜索期间访问过的节点，刚好就是从v 开始只使用ε 转换便可到达的节点组成的集合。

回想一下，深度优先搜索要花费O(m)的时间，其中m 是图中节点数和弧数的较大者。在这种情况下，如果图中有n 个节点，要进行n 次深度优先搜索，总共要花O(mn)的时间。不过，在通过在本节前面的内容中描述的算法从正则表达式构造的自动机中，任意节点出发的弧最多只有两条。因此m≤2n，而且O(mn)就是O(n²)的时间。

示例 10.27

在图10-33中，可以看到从图10-26中删除标记了由实际符号a、b、c标记的3条弧后剩下的弧。图10-34中的表给出了图10-33的可达性信息，也就是说第i 行和第 j 列的1就表示存在从节点i 到节点 j 的长度为0或以上的路径

{%}

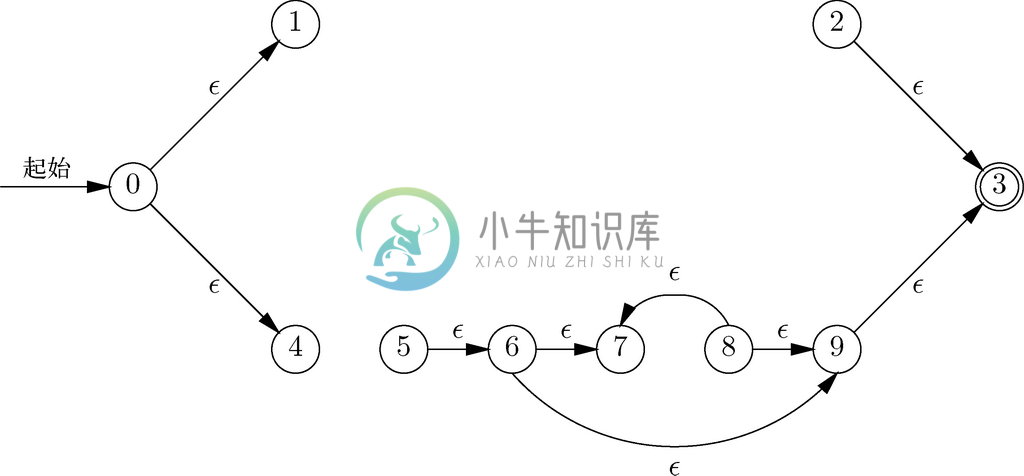
图 10-33　图10-26中的ε 转换

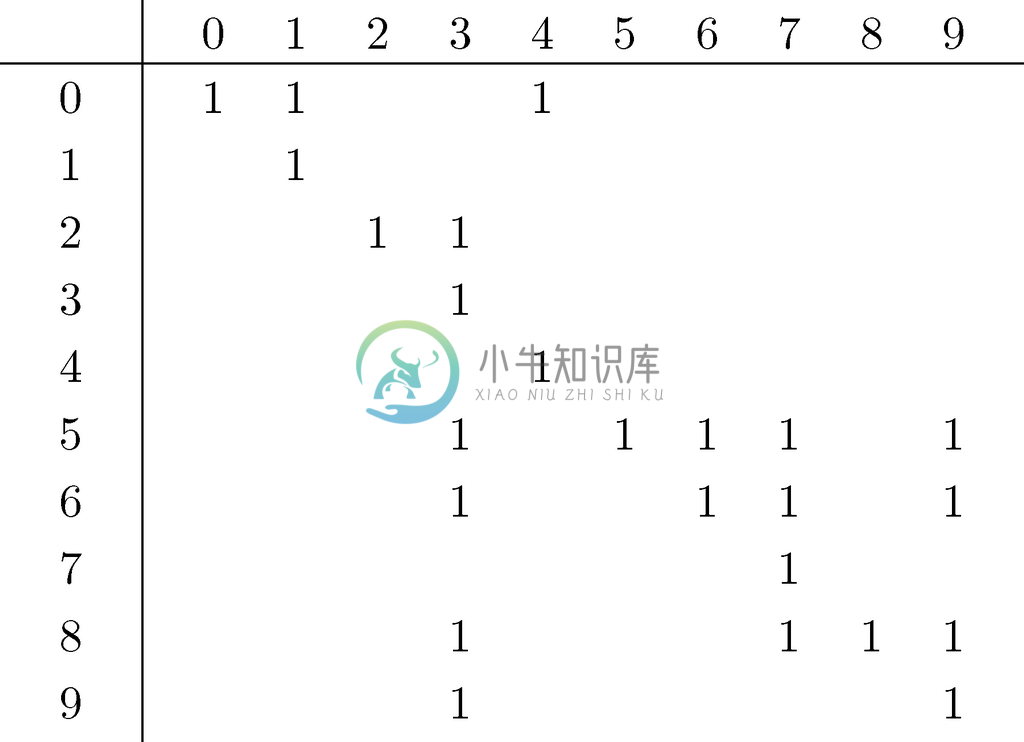
图 10-34　图10-33对应的可达性表

有了可达性信息之后，就可以构造不含ε 转换的等价自动机。思路就是把旧自动机中具有0次或多次ε 转换一条路径以及后面标记为实际符号的一次转换，捆绑成新自动机中的一次转换。每一次这样的转换，都会将我们带到图10-27c的依据规则（操作数为实际符号时的规则）引入的自动机中第二个状态。原因在于，这些状态只有以真实符号为标号的弧才进入。因此，我们的新自动机只需要这些状态，以及对应其自身状态集的起始状态。可以把这些状态叫作重要状态。

在构造的新自动机中，如果存在某个状态k 满足以下条件，就有从重要状态i 到重要状态 j 的，标号中含有符号x的转换。

1. 从状态i 沿着具有0次或多次ε 转换的路径可达状态k。请注意，k=i 一直是可以的。

2. 在旧自动机中，存在从状态k 到状态 j，标记为x的转换。

我们还必须决定新自动机中哪些状态是接受状态。正如上文提到过的，当我们在某个状态中时，其实就是在由该状态沿着标记为ε 的弧所能到达的任意状态中。因此如果在旧自动机中从状态i 到其接受状态之间存在由标记为ε 的弧形成的路径，就将状态i 作为新自动机的接受状态。请注意，状态i 本身可能就是旧自动机的接受状态，并因此在新自动机中仍然是接受状态。

示例 10.28

我们来将图10-26所示的自动机转变为接受相同语言但不带ε 转换的自动机。首先，重要状态包括作为初始状态的状态0，以及由标记了实际符号的弧进入的状态2、状态5和状态8。

首先从找到状态0对应的转换开始。根据图10-34，从状态0可以沿着由标记了 ε 的弧构成的路径到达状态0、状态1和状态4。我们发现有针对a的从状态1到状态2的转换，而且有针对b的从状态4到状态5的转换。因此，在新自动机中，存在从状态0到状态2的标记为a的转换，并存在从状态0到状态5的标记为b的转换。请注意，我们已经把图10-26中的路径0→1→2和0→4→5压缩成标记了这些路径上非 ε 转换的标号的转换。因为状态0，以及从它出发沿着以 ε 标记的路径可达的状态1和状态4都不是接受状态，所以在新自动机中，状态0不是接受状态。

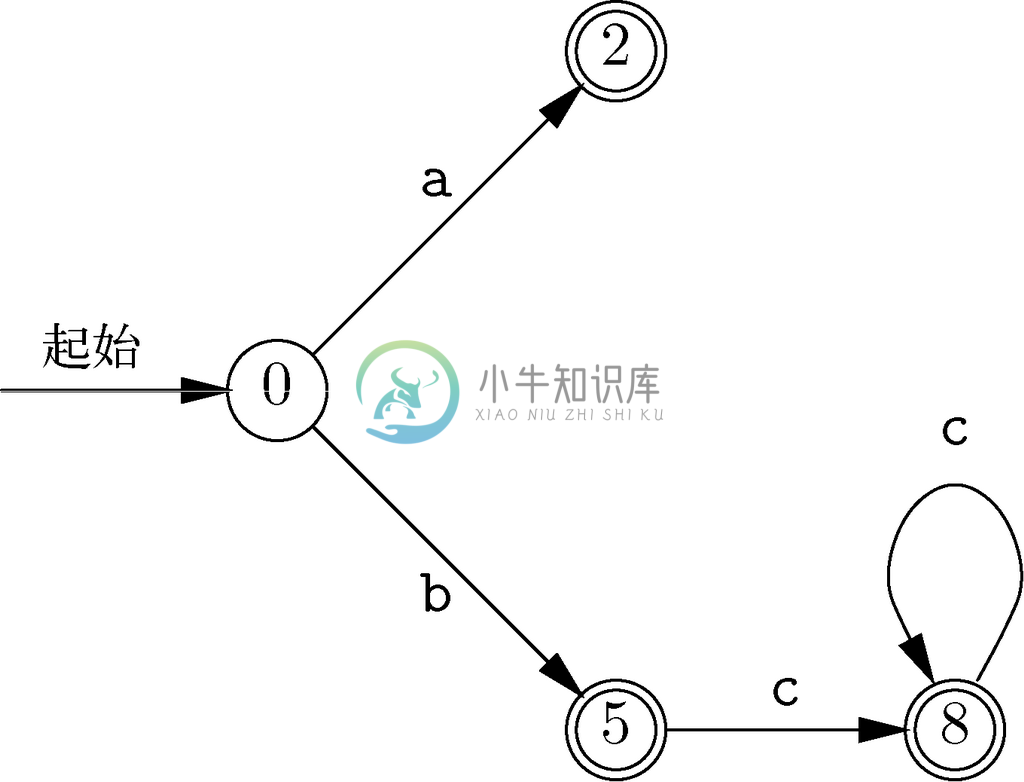
图 10-35　通过消除ε 转换，根据图10-26构造的自动机。请注意，该自动机只接受L(a|bc*)中的所有字符串

接下来，考虑从状态2出发的转换。图10-34告诉我们，从状态2出发，通过ε 转换只能到达它本身和状态3，因此我们必须寻找从状态2或状态3出发针对实际符号的转换。因为没找到，所以可知在新自动机中没有从状态2出发的转换。不过，状态3是接受状态，而且从状态2经过ε 转换可以到达状态3，所以状态2就是新自动机的接受状态。

在考虑状态5时，图10-34表明要查看状态3、状态5、状态6、状态7和状态9。在这些状态中，只有状态7具有从自身出发的非ε 转换，它被标记为c，而且通向状态8。因此，在新自动机中，从状态5出发的唯一转换就是针对c的到状态8的转换。因为从状态5沿着标记了ε 的弧可以到达接受状态3，所以我们把状态5也作为新自动机的接受状态。

最后，一定要查看从状态8出发的转换。经过类似对状态5进行的推理可以得出，在新自动机中，从状态8出发的唯一转换是到它自身的，而且被标记为c。因此，状态8也是新自动机的接受状态。

图10-35展示了该新自动机。请注意，它接受的字符串集正好是L(a|bc*)中的那些字符串，也就是将我们带到状态2的字符串a，将我们带到状态5的字符串b，以及bc、bcc、bccc这些将我们带到状态8的一系列字符串。图10-35中的自动机刚好是确定自动机。如果它不是，假设想设计可以识别原正则表达式的字符串的程序，就可以利用子集构造将其转化为确定自动机。

顺便提一下，存在与图10-35接受同一语言的更加简化的确定自动机，该自动机如图10-36所示。事实上，只要意识到状态5和状态8是等价并可以被合并的，就可以得到这一改进过的自动机。得到的状态就是图10-36中的状态5。

图 10-36　对应语言L(a|bc*)的更简单的自动机

10.8.4　习题

1. 为以下正则表达式构造具有ε转换的自动机。

(a) aaa。提示：请记住，要为出现的每个a创建新自动机。

(b) (ab|ac)*。

2. 为习题1中构造的各个自动机找到由标记为ε 的弧构成的图中节点的可达集。请注意，在大家构造不含ε 转换的自动机时，只需要为初始状态和那些有非ε 转换进入的状态构造可达状态。

3. 为习题1中构造的各个自动机构造不含ε 转换的等价自动机。

4. 习题3得出的自动机中哪些是确定自动机？为其中那些非确定自动机构造等价的确定自动机。

5. * 对由习题3和习题4构造的确定自动机而言，是否存在状态更少的等价确定自动机？如果有，找出状态最少的那个。

6. * 我们可以扩展从正则表达式构造含ε 转换的自动机的过程，将正则表达式的范围扩大到包含那些使用了10.7节中扩展过的运算符的表达式。这一命题从原则上讲是成立的，因为那些扩展都是“原始”正则表达式的简略形式，我们只是用扩展的运算符替代了原有的表达式而已。不过，还可以直接把扩展过的运算符融入到我们的构造过程中。说明如何修改构造过程以涵盖下列运算符：

(a) ? 运算符（不出现或出现1次）；

(b) + 运算符（出现1次或更多次）；

7. 我们可以修改把正则表达式转化为自动机的算法中对应串接的情况。在图10-28b中，引入了从与R₁对应自动机的接受状态到与R₂对应自动机的初始状态的ε 转换。另一种方式就是按照图10-37所示的方式合并R₁的接受状态到R₂的初始状态。使用旧算法与修改过的算法为正则表达式ab*c构造自动机。

图 10-37　另一种与两个正则表达式的串接对应的自动机

10.9　从自动机到正则表达式

本节中还要展示自动机与正则表达式等价性的另一半，证实对每个自动机A，都存在语言刚好是A所接受的字符串集合的正则表达式。尽管我们一般会使用10.8节中的构造过程，其中要把正则表达式形式的“设计”转化为确定自动机形式的程序，不过把自动机转化为正则表达式的构造过程也是很有趣很有益的,它完成了这两种截然不同的模式表示法的表现力之间的等价性的证明。

我们的构造过程涉及从自动机中一个一个地删除状态。随着构造过程的进行，会把弧上的标号由最初的字符串集合替换为更复杂的正则表达式。一开始，如果弧上的标号是{x₁，x₂，…，x_n}，就可以把这些标号替换为正则表达式x₁ | x₂ | … | x_n，该正则表达式从本质上讲表示的是相同的符号集合，虽然严格地讲正则表达式表示的是长度为1的字符串。

一般而言，可以将路径的标号视为路径沿线上正则表达式的串接，或是看作这些表达式的串接定义的语言。这一观点与我们用字符串标记路径的概念是一致的。也就是说，如果路径的弧是用正则表达式R₁、R₂、…、R_n 按此次序标记的，则当且仅当字符串w在语言L(R₁R₂…R_n)中时有该路径被标记为w。

示例 10.29

考虑图10-38中的路径0→1→2。正则表达式a|b和a|b|c依次标记了这两条弧，因此标记该路径的字符串集合是由正则表达式(a | b)(a | b | c)定义的语言中的字符串构成的，也就是{aa，ab，ac，ba，bb，bc}。

{%}

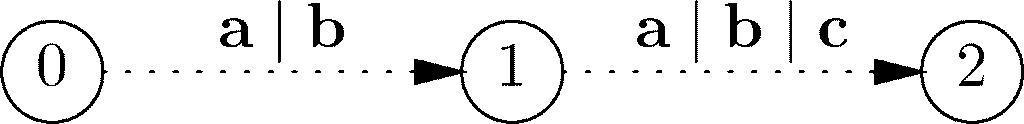
图 10-38　以正则表达式作为标号的路径，路径的标号是由正则表达式的串接定义的语言

10.9.1　状态消除的构造

在从自动机到正则表达式的转化中，关键的步骤就是状态的消除，如图10-39所示。我们希望消除状态u，不过必须保留弧的正则表达式标号，从而使剩余状态中两两之间路径的标号集合不发生改变。在图10-39中，状态u 的前导分别是s₁、s₂、…、s_n，而u 的后继则分别是t₁、t₂、…、t_m 。虽然已经证明了这些s 和t 是不相交的状态集，但其实两组中还是可能存在一些相同的状态。

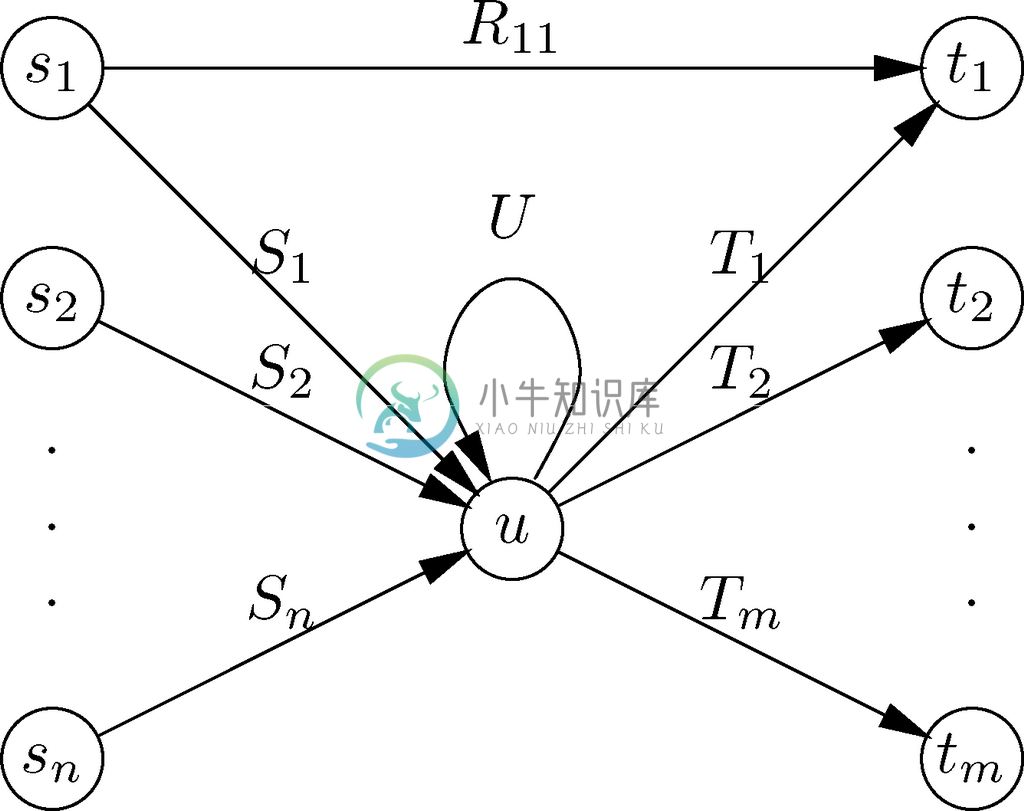
图 10-39　我们想消除状态u

不过，如果u是它本身的后继，我们就要用标记为U 的弧明确表示这一事实。假设在状态u 处没有这样的自环，那么可以引入一个这样的自环，并赋予其标号∅。标号为∅的弧是“不存在的”，因为任意用到这条弧的路径标号都会是含有∅的正则表达式的串接。因为∅是串接的零元，所以这样的串接定义的都是空语言。

我们还要明确给出从s₁到t₁的弧R₁₁。一般而言，假设对每个i=1、2、…、n，以及对每个 j =1、2、…、m，都存在从s_i 到t_j 的弧，由某个正则表达式R_ij 标记。如果弧s_i →t_j 实际上不存在，就引入它并为其赋予标号∅。

最后，在图10-39中存在从各状态s_i 到u 的，由正则表达式s_i 标记的弧，而且存在从u 到各状态t_j 的，由正则表达式T_j 标记的弧。如果消除节点u，那么这些弧与图10-39中标记为U 的弧都将不复存在。要让标记路径的字符串集合保持不变，就必须考虑每对s_i 和t_j，并为弧s_i →t_j 的标号添加一个能表示所失去内容的正则表达式。

在消除u之前，标记了从s_i 到u（包括多次行经的那些u →u 自环）然后从u 到t_j 的路径的那些字符串集合是由正则表达式S_i U *T_j 描述的。也就是说，L(S_i )中的字符串可以把我们从状态s_i 带到到状态u，L(U *)中的字符串可以把我们从状态u 带到状态u，沿着该自环0次、1次或更多次。最后，L(T_j )中的字符串把我们从状态u 带到状态t_j 。

因此，在消除状态u 和所有进出u 的弧之后，必须把弧s_i →t_J 的标号由R_ij 替换为R_ij |S_iU *T_j。

存在不少实用的特例。首先，若U＝∅，即u上的自环并非真正存在，那么U *=∅*=ε。因为ε 是串接的单位元，所以(S_i ε )T_j =S_iT_j，也就是说，U 其实在它应该出现的位置消失了。同样，如果R_ij=∅，意味着之前没有从s_i 到t_j 的弧，我们就引入这条弧，并给予其标号S_iU *T_j，或者如果U=∅，就是S_iT_j。这样做的原因在于，∅是取并运算的单位元，因此∅|S_iU *T_j=S_iU *T_j 。

示例 10.30

我们来考虑一下图10-4所示的反弹过滤器自动机，这里的图10-40重现了该自动机。假设要消除状态b，它们就扮演了图10-39中u 的角色。状态b 有一个前导a，以及两个后继a 和c。b 上不存在自环，所以要引入一个标号为∅的自环。存在从a 到其本身，标记为0的弧。因为a 既是b 的前导又是b 的后继，所以该弧在这一变形中是必须的。唯一一对另外的前导-后继对是a 和c。因为不存在弧a →c，所以可以添加一条标号为∅的弧a →c。相关状态和弧组成的图如图10-41所示。

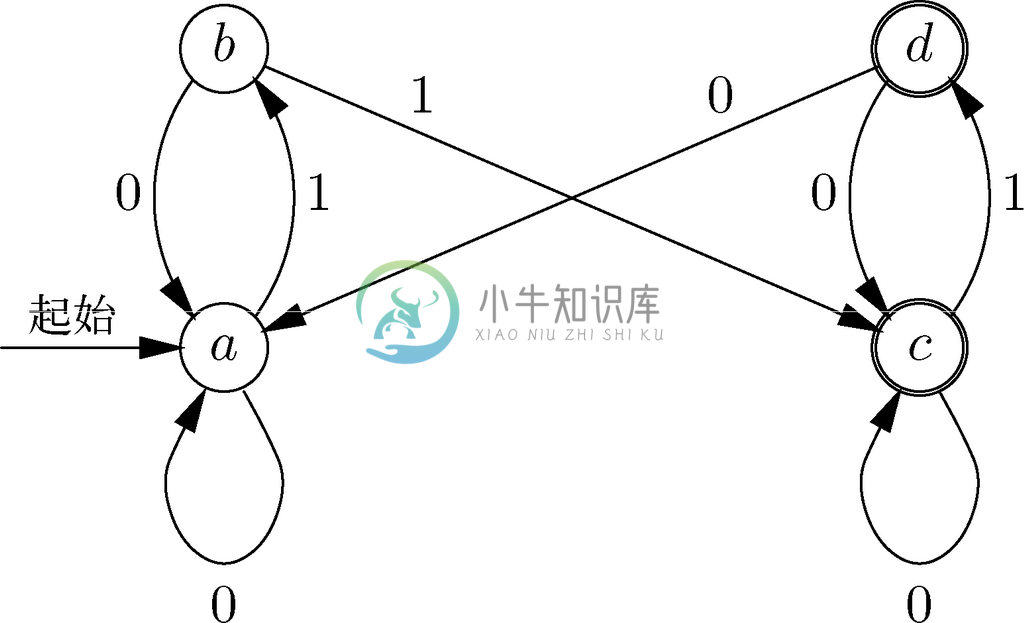
图 10-40　与反弹过滤器对应的有限自动机

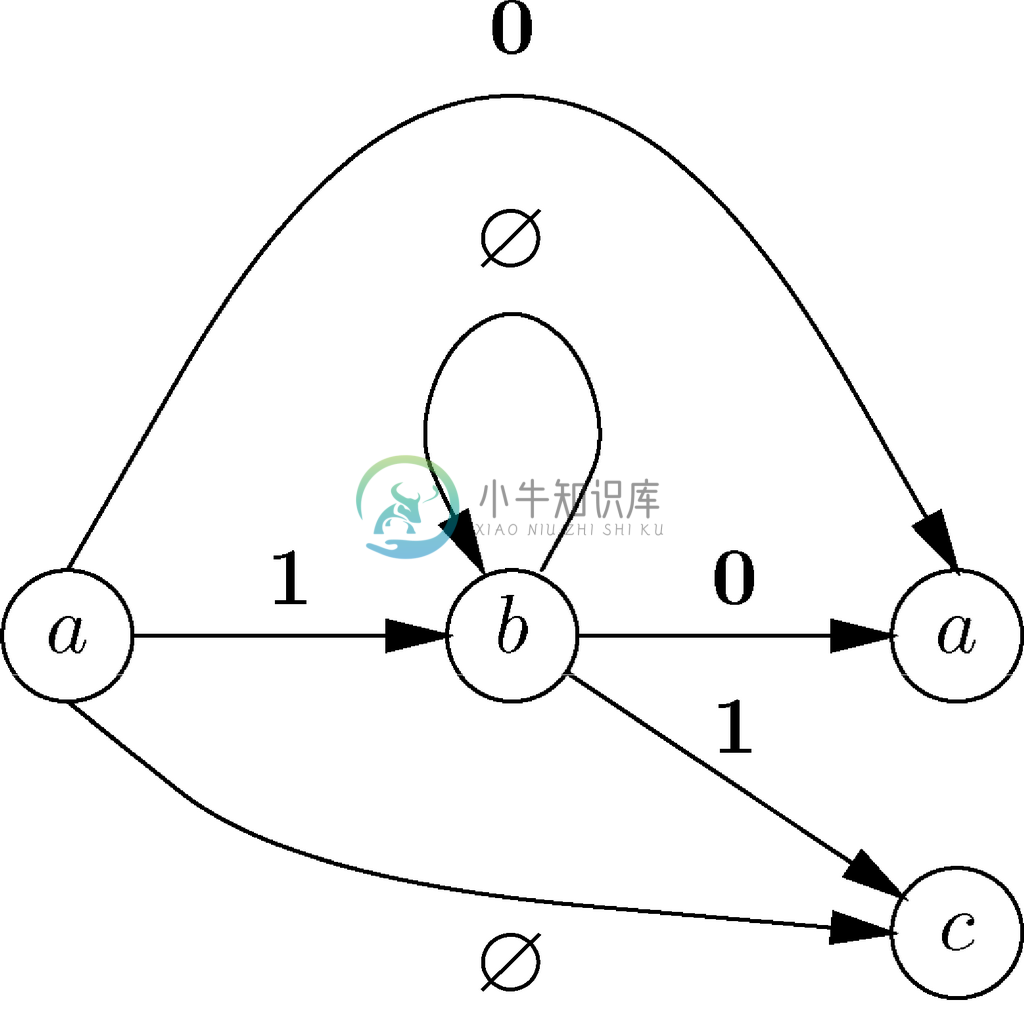
图 10-41　状态b，以及它的前导和后继

对状态对a-a 而言，我们把弧a→a 的标号替换为0|1∅*0。0这项表示该弧的原始标号，而1这项是a →b 的标号，∅是自环b →b 的标号，而第二个0项则是弧b →a 的标号。我们可以按照之前的描述进行简化，消除∅*，留下表达式0|10，这是说得通的。在图10-40中，从a 到a 的路径，行经b 状态0次或多次，而不经过其他状态，其标号集合为{0，10}。

处理状态对a-c 的过程是类似的。我们要用可以简化为11的∅|1∅*1替代弧a→c 的标号∅。这还是说得通的，因为在图10-40中，从a 到c 的唯一路径，经过b 而且标号为11。在消除节点b并改变弧标号后，图10-40就成了图10-42。请注意，在该自动机中，某些弧标号中的正则表达式具有长度大于1的字符串。不过，状态a、c 和d 之间的路径对应的路径标号集合与图10-40相比没有发生改变。

图 10-42　消除了状态b 之后的反弹过滤器自动机

10.9.2　自动机的完全简化

要得到只表示所有由自动机A 接受的字符串的正则表达式，就要依次考虑A 的各接受状态t。每个被A 接受的字符串之所以会被接受，是因为它标记了从起始状态s 到某个接受状态t 的路径。可以按照以下方式，为那些把我们从s 带到某个特定接受状态t 的字符串构造相应的正则表达式。

反复消除自动机A 的状态，直到只剩s 和t 两个状态，这样一来，该自动机就如图10-43这样了。我们已经展示了所有4条可能的弧，每一条都以一个正则表达式作为其标号。如果一条或多条可能的弧不存在，可以引入该弧并为其标记上∅。

图 10-43　减少到两个状态的自动机

需要找出有哪些正则表达式描述了始于s 并终于t 的路径的标号集合。表示该字符串集合的一种方式是认识到每一条这样的路径会先到达t，然后从t 行至其自身0次或多次，还可能在行进的过程中经过s。一开始把我们带到状态t 的字符串集合是L(S *U )。也就是说，要用到L(S )中的字符串0次或多次，这样做就会先留在状态s 中，然后沿着L(U )中的字符串行进。我们既可以跟随L(T )中的字符串停留在状态t 中，这会将我们从t 带到t，也可以沿着VS *U 中的字符串到达s，在s 停顿一会儿，然后又回到t。我们可以沿着这两组中以任意次序排列的0个或多个字符串行进，并将其表示为(T |VS *U )*。因此从状态s 到状态t 的字符串集合对应的正则表达式就是

S *U (T |VS *U )*　　　　　　(10.4)

存在一种特例，就是起始状态s 本身也是接受状态的情况。这样的话，有些字符串被接受的原因是因为它们将自动机A 从状态s 带到了状态s。我们消除了除s 之外的所有状态，留下如图10-44所示的自动机。将A 从状态s 带到状态s 的字符串集合是L(S *)。因此可以用S *作为取代接受状态s 的贡献的正则表达式。

图 10-44　只有起始状态的自动机

将起始状态为s 的自动机A 转化成等价正则表达式的完整算法如下所述。对每个接受状态t 而言，从自动机A 开始，并消除各种状态，直到只剩下状态s 和t。当然，对每个接受状态t 来说，都要从全新的原自动机A 开始进行处理。

如果s ≠t，就使用(10.4)式得出其语言是把A 从状态s 带到状态t 的字符串集合的正则表达式。如果s =t，就利用S *，其中S 是弧s →s的标号。然后，为对应每个接受状态t 的正则表达式取并。该表达式的语言就刚好是被A 接受的字符串的集合。

示例 10.31

下面来为图10-40所示的反弹过滤器自动机得出相应的正则表达式。因为c 和d 是接受状态，

所以需要进行下列操作：

(1) 从图10-40中消除状态b 和d，得到只涉及a 和c 的自动机；

(2) 从图10-40中消除状态b 和c，得到只涉及a 和d 的自动机。

因为在这两种情况下都必须消除状态b，所以图10-42就让我们的最终目标实现了一半。对情况(1)，要在图10-42的基础上消除状态d。存在从c 经过d 到a 的标号为00的路径，所以需要引入一条从c 到a 标记为00的弧。存在从c 经过d 回到其自身的标号为01的路径，因此需要为c 处的自环添加标号01，这样该标号就成了1|01。得到的自动机如图10-45所示。

图 10-45　把图10-40所示的自动机减少到只剩状态a 和状态c

对目标(2)，要再次从图10-42开始，而这次要消除状态c。在图10-42中，我们可以从a 经过c 到达d，而描述可能字符串的正则表达式为111*0。8也就是说，11将我们从a 带到c，1*让我们在c 处循环0次或多次，而最后0把我们从c带到d。因此，我们引入了从a 到d 的标号为111*0的弧。同样，在图10-42中，可以沿着11*0中的字符串，从d 通过c 行至其自身。因此，这一表达式成了d 处自环的标号。简化过的自动机如图10-46所示。

8请记住，因为*的优先级高于串接，111*0会被解释为11(1*)0，并表示由两个或更多1后面加以一个0构成的字符串。

图 10-46　把图10-40中的自动机减少到只剩状态a 和状态d

现在可以把(10.4)中得出的公式应用到图10-45和图10-46所示的自动机上。对图10-45，有S=0|10，U=11，V=00，而且T=1|01。因此表示将图10-40所示的自动机从起始状态a带到接受状态c的字符串集合的正则表达式为

(0|10)*11((1|01)|00(0|10)*11)*　　　　　　(10.5)

而表示把该自动机从起始状态a 带到接受状态d 的字符串的正则表达式为

(0|10)*111*0(11*0|0(0|10)*111*0)*　　　　　　(10.6)

表示由反弹过滤器自动机接受的字符串的正则表达式就是对(10.5)和(10.6)取并，或者说是((0 | 10)*11((1 | 01) | 00(0 | 10)*11)*) | ((0 | 10)*111*0(11*0 | 0(0 | 10)*111*0)*)没有办法对该表达式进行多少简化，因为相同的因式只有(0 | 10)*11，其他就基本没有什么相同的了。我们可以删除(10.5)中因式(1 | 01)周围的括号，因为取并运算是具有结合性的，这样得到的表达式就是

(0 | 10)*11((1 | 01 | 00(0 | 10)*11)*) | 1*0(11*0 | 0(0 | 10)*111*0)*)

大家可以回想一下，我们为同样的语言提出过一个简单得多的正则表达式

(0 | 1)*11(1 | 01)*(ε | 0)

这一区别应该提醒我们，对同一语言来说，可能存在不止一个与之对应的正则表达式，而通过转化自动机得到的正则表达式也不一定是对应该语言的最简表达式。

10.9.3　习题

1. 分别找出下列各图所示自动机对应的正则表达式。

(a) 图10-3

(b) 图10-9

(d) 图10-12

(e) 图10-13

(f) 图10-17

(g) 图10-20

大家可能会希望利用10.6节中的简略形式。

2. 把10.4节习题1中的自动机转化成正则表达式。

3. * 证明，把我们从图10-43中的状态s带到状态t的字符串集合对应的另一个正则表达式是(S |UT *V )*UT *。

4. 如何修改本节中的构造过程，使得正则表达式可以由具有ε 转换的自动机生成？

10.10　小结

10.4节的子集构造，以及10.8节和10.9节中的转化，告诉我们3种表示语言的方式有着相同的表现效用。也就是说，针对某语言L 的以下3个命题要么都为真，要么都为假。

(1) 存在某确定自动机只接受L 中的所有字符串。

(2) 存在某（可能为非确定的）自动机只接受L 中的所有字符串。

(3) L 对某正则表达式R 来说是L(R )。

子集构造说明了(2)可以得到(1)。显然有(1)就有(2)，因为确定自动机就是一种特殊形式的非确定自动机。我们在10.8节中证明了由(3)可以得到(2)，而在10.9节中证实了有(2)就有(3)。因此，(1)、(2)和(3)是等价的。

除了这些等价关系外，我们还应该从第10章获得一些重要思路。

确定自动机可作为识别字符串多种不同模式的程序的核心。
正则表达式通常是一种用于描述模式的便利表示方法。
正则表达式的代数法则使得取并和串接与加法和乘法有着类似的性质，不过还是存在一些区别。

10.11　参考文献

读者在Hopcroft and Ullman [1979]中可以了解更多与自动机和语言理论有关的内容。

虽然有很多类似的模型更早或是同时被提出，但处理字符串的自动机模型最早是由 Huffman [1954]中描述的形式粗略表示的，这段历史可以在Hopcroft and Ullman [1979]中找到。正则表达式以及它们与自动机的等价性源自Kleene [1956]。非确定自动机以及子集构造来自 Rabin and Scott [1959]。10.8节利用的从正则表达式构造非确定自动机的过程源自McNaughton and Yamada[1960]，而10.9节中相反方向的构造过程则来自Kleene的论文。

用正则表达式描述字符串中的模式最早见于Ken Thompson的QED系统（Thompson [1968]），同样的思路随后影响到他开发的UNIX系统中的很多命令。正则表达式在系统软件中还有很多其他的应用，Aho, Sethi and Ullman [1986]描述了其中大量应用。

Aho, A. V., R. Sethi , and J. D. Ullman [1986]. Compiler Design: Principles, Techniques, and Tools, Addison-Wesley, Reading, Mass.

Hopcroft, J.E. and J. D. Ullman [1979]. Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, Reading, Mass.

Huffman, D. A. [1954]. “The synthesis of sequential switching machines,” Journal of the Franklin Institute 257:3-4, pp. 161–190 and 275–303.

Kleene, S. C. [1956]. “Representation of events in nerve nets and finite automata,” in Automata Studies (C. E. Shannon and J. McCarthy ,eds), Princeton University Press.

McNaughton, R. and H. Yamada [1960]. “Regular expressions and state graphs for automata,”IEEE Trans. on Computers 9:1, pp. 39–47.

Rabin, M. O. and D. Scott [1959]. “Finite automata and their decision problems,” IBM J. Research and Development 3:2, pp. 115-125.

Thompson, K. [1968]. “Regular expression search algorithm,” Comm. ACM 11:6, pp. 419–422.

第 10 章 模式、自动机和正则表达式

10.1 本章主要内容

10.2 状态机和自动机

10.2.1 状态机的图表示

示例 10.1

示例 10.2

10.2.2 习题

10.3 确定自动机和非确定自动机

示例 10.3

10.3.1 确定自动机

示例 10.4

10.3.2 非确定自动机

10.3.3 非确定自动机的接受

示例 10.5

示例 10.6

10.3.4 习题

10.4 从不确定到确定

10.4.1 自动机的等价性

示例 10.7

10.4.2 子集构造

示例 10.8

示例 10.9

示例 10.10

10.4.3 子集构造起效的原因

10.4.4 习题

10.5 正则表达式

10.5.1 正则表达式的操作数

10.5.2 正则表达式的值

10.5.3 正则表达式的运算