第 11 章 模式的递归描述
在第10章中,我们看到过两种等价的模式描述方式。一种是图论方式,利用了一种名为“自动机”的图中路径的标号。另一种是代数方式,利用了正则表达式。在本章中,我们将看到第三种描述模式的方式,利用到了一种名为“上下文无关文法”(以下简称“文法”)的递归定义。
文法的重要应用之一就是作为编程语言的规范。文法是用来描述常见编程语言句法的一种简洁表示方式,我们会在本章中看到很多示例。此外,有一种机械的方式可以把常见编程语言的文法转换成“分析器”(parser)——该语言编译器的一个关键部分。分析程序揭示了源程序的结构,通常是将程序中的每条语句表示为表达式树的形式。
11.1 本章主要内容
本章主要讨论如下主题。
文法以及文法是如何用来定义语言的(11.2节和11.3节)。
分析树,根据给定文法显示字符串结构的树表示(11.4节)。
歧义,当某一字符串有两棵或更多分析树,并因此根据给定文法不具有唯一“结构”时出现的问题(11.5节)。
把文法转换成“分析器”的一种方法,“分析器”是可以分辨给定字符串是否在某一语言中的算法(11.6节和11.7节)。
证明文法在描述语言方面要比正则表达式更强大(11.8节)。首先,我们通过证明如何用文法模拟正则表达式,来证明文法的描述性至少与正则表达式一样强。接着我们将描述一种只能用文法来指定而不能用正则表达式指定的特殊语言。
11.2 上下文无关文法
算术表达式可以由递归定义自然而然地定义出来。下面的示例说明了这一定义是如何起效的。我们来考虑涉及如下内容的算术表达式。
1. 4种二元运算符+、-、*和/;
2. 用于分组的圆括号;
3. 作为操作数的数字。
这种表达式的一般定义是具有如下形式的归纳。
依据。一个数字是一个表达式。
归纳。如果E 是表达式,那么以下各种也都是表达式。
(a) (E )。也就是说,我们可以在表达式周围放上圆括号以得到新表达式。
(b) E+E。也就是说,用加号连接的两个表达式是一个新表达式。
(c) E-E。这一条以及接下来的两条规则都与(b)类似,不过使用了其他的运算符。
(d) E *E。
(e) E /E。
这一归纳定义了一种语言,也就是一个字符串集合。依据陈述了任意数字都在该语言中。
规则(a)表示,如果s 是该语言中的字符串,那么加过括号的字符串(s )也在该语言中,这一字符串是s 前面加上左括号并且后面跟上右括号得到的。规则(b)到规则(e)是说,如果s 和t 是该语言中的两个字符串,那么s+t、s-t、s *t 和s/t 也都是该语言中的字符串。
文法让我们可以写出这些简明而且含义精确的规则。举例来说,可以用图11-1所示的文法写出我们对算术表达式的定义。
(1) <表达式> → 数字
(2) <表达式> → (<表达式>)
(3) <表达式> → <表达式>+<表达式>
(4) <表达式> → <表达式>-<表达式>
(5) <表达式> → <表达式>*<表达式>
(6) <表达式> → <表达式>/<表达式>
图 11-1 对应简单算术表达式的文法
这里要对图11-1中用到的符号作出一些解释,符号
<表达式>
称为语法分类(syntactic category),它代表这一算术表达式语言中的任意字符串。符号→的含义是“可由……组成”。例如,图11-1中的规则(2)就表示,表达式可由左括号后跟上属于表达式的任意字符串再跟上右括号组成。规则(3)表明,表达式可由属于表达式的任意字符串、字符+,以及属于表达式的任意其他字符串组成。规则(4)到规则(6)与规则(3)是相似的。
规则(1)则不同,因为箭头右侧的符号数字从字面上看本不是字符串,它只是与可以解释为数字的字符串相对应的占位符。我们在后面的内容中会介绍如何用文法定义数字,但现在先只把数字当作一个抽象符号,而表达式用该符号来表示任意原子操作数。
11.2.1 与文法相关的术语
文法中会出现3种符号。第一种是“元符号”,是那些扮演特殊角色而并不代表它们自身的符号。我们目前为止已经见过的元符号只有→,它的用途是把要定义的语法分类与该语法分类中字符串可能的组成方式分隔开。第二种符号是语法分类,我们说过,这种符号表示的是要定义的字符串集合。第三类符号称为终结符(terminal)。终结符可以是+或(这样的字符,也可以是数字这样的抽象符号,它代表我们希望在随后定义的字符串。
文法是由产生式(production)组成的。图11-1中的每一行都是一个产生式。一般而言,产生式具有以下3个部分。
1. 左部(head),就是箭头符号左侧的语法分类。
2. 元符号→。
3. 右部(body),由箭头右侧0个或以上的语法分类和(或)终结符组成。
例如,在图11-1的规则(2)中,左部是<表达式>,而右部则由终结符(、语法分类<表达式>和终结符)组成。
示例 11.1
我们可以通过为数字提供定义来扩展本节开始时对表达式的定义。这里要假设数字是由数
码(digit)组成的字符串。借用10.6节中扩展过的正则表达式表示法,可以说
digit =[0-9]
number =digit +
不过也可以用文法表示法来表示同样的概念,我们可以写出以下产生式
<数码>→0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<数字>→<数码>
<数字>→<数字><数码>
请注意,根据我们对元符号 | 的约定,第一行其实是以下10个产生式的简化形式。
<数码>→0
<数码>→1
…
<数码>→9
可以用同样的方法把对应<数字>的两个产生式合并成一行。请注意,对应<数字>的第一个产生式表示单个数码是个数字,而第二个产生式的意思是,任何数字后跟上另一个数码也是数字。这两个表达式一起就表示任何由数码组成的串都是数字。
图11-2是扩展过的表示表达式的文法,其中抽象的终结符数字被替换为定义了该概念的产生式。请注意,该文法含有3个语法分类<表达式>、<数字>和<数码>。我们会把语法分类<表达式>当作起始符号(start symbol),它生成了要用该文法定义的串,在这种情况中,就是格式标准的算术表达式。其他两个语法分类<数字>和<数码>代表的补充概念是很关键的,但不是写出该文法所需的主要概念。
表示方式的约定
在表示语法分类时,我们是在其斜体名称(中文为楷体)的两侧加上尖括号表示的,例如,<表达式>。产生式中的终结符或者用代表字符串
x的粗体x来表示(类似正则表达式的约定),或者在终结符为抽象符号的情况下(比如之前例子中的数字),用不带尖括号斜体字符串(中文为楷体)表示。元符号ε 表示空右部。因此产生式<S>→ε 意味着语法分类<S>的语言中包含了空字符串。我们有时会将某一语法分类的右部合并到一个产生式中,分别用可以称作“或”的元符号 | 隔开。例如,如果有以下产生式
<S>→B1,<S>→B2,…,<S>→Bn
其中这些B分别是对应语法分类<S>的各产生式的右部,那么可以将这些产生式写为
<S>→B1 | B2 | … | Bn
(1) <数码> → 0|1|2|3|4|5|6|7|8|9
(2) <数字> → <数码>
(3) <数字> → <数字> → <数码>
(4) <表达式> → <数字>
(5) <表达式> → (<表达式>)
(6) <表达式> → <表达式>+<表达式>
(7) <表达式> → <表达式>-<表达式>
(8) <表达式> → <表达式>*<表达式>
(9) <表达式> → <表达式>/<表达式>
图 11-2 与由用文法定义的数字组成的表达式对应的文法
示例 11.2
2.6节中曾讨论过平衡圆括号串的概念。当时我们是用非正式的方式给出了组成这种串的归纳定义,而正式形式的书写文法正是本节要介绍的。我们定义了“平衡圆括号串”的语法分类,这里称其为<平衡的>。依据规则陈述了空串是平衡的。可以将该规则写为如下产生式
<平衡的>→ε
然后就是归纳步骤,说的是如果x 和y 都是平衡圆括号串,那么(x )y 也是。可以把这一规则写为产生式
<平衡的>→(<平衡的>)<平衡的>
因此,图11-3中的文法可以说是定义了平衡圆括号串。
<平衡的>→ε
<平衡的>→(<平衡的>)<平衡的>
图 11-3 对应平衡圆括号串的文法
还有另一种定义平衡括号串的方式。回想一下2.6节,我们描述这种串的原始动机就是,它们是删除了表达式中除括号外所有内容后留下的括号的子序列。图11-1给出了对应表达式的文法。考虑一下,如果删除掉除括号之外的所有终结符,会发生什么。此时产生式(1)就成了
<表达式>→ε
产生式(2)变成了
<表达式>→(<表达式>)
而产生式(3)到产生式(6)都成了
<表达式>→<表达式><表达式>
如果用更为合适的名称<平衡表达式>来代替<表达式>,就得到另一种表示平衡圆括号串的文法,如图11-4所示。这些产生式都是相当自然的。它们表明了如下3点。
1. 空串是平衡的;
2. 如果为平衡的串加上圆括号,得到的串也是平衡的;
3. 而且平衡串的串接是平衡的。
<平衡表达式> → ε
<平衡表达式> → (<平衡表达式>)
<平衡表达式> → (<平衡表达式>)<平衡表达式>
图 11-4 由算术表达式文法发展来的表示平衡圆括号串的文法
图11-3和图11-4中的文法看起来相当不同,不过它们定义了相同的字符串集合。证明它们确实定义了同一字符串集合最简单的方式也许就是证明由图11-4中<平衡表达式>定义的圆括号串刚好就是2.6节中定义的“量变平衡”圆括号串。好了,现在证明了与图11-3中<平衡的>定义的圆括号串有关的相同断言。
共用文法模式
示例11.1用了两个对应<数字>的产生式来说明“数字是由数码组成的串”。这种模式就是共用的。一般而言,如果有语法分类<X >,而且Y是终结符或是另一个语法分类,产生式
<X>→<X>Y |Y
说明任意由Y组成的串都是<X>。如果用正则表达式来表示,就是<X>=Y +。同样,产生式
<X>→<X>Y |ε
就表示每个由0个或更多的Y 组成的串都是<X>,或者说<X>=Y *。由
<X>→<X>ZY |Y
这样一对产生式表示的也是种共用模式,表示每个开头和结尾都是Y 而且由Y 和Z 交替组成的串都是<X>。也就是说,<X>=Y (ZY )*。
此外,我们可以反转上述3个例子任意一个中递归产生式右部中符号的次序,例如
<X>→Y<X>|Y
也定义了<X>=Y +。
示例 11.3
还可以用文法的方式来描述C语言这样的编程语言中控制流的结构。举个简单的例子,想象条件和简单语句这两个抽象终结符。前者代表条件表达式。我们可以把这一终结符替换为语法分类,假如说是<条件>。<条件>的产生式可以用之前所述的表达式文法来构建,但是用到的运算符包含了&&这样的逻辑运算符、<这样的比较运算符,以及算术运算符。
终结符简单语句代表不含嵌套控制结构的语句,比如赋值、函数调用、读、写或跳转语句。我们再次用语法分类和扩展它的产生式代替了这一终结符。
这里要用<语句>表示C语言语句的语法分类。形成语句的方式之一是通过while结构。也就是说,如果有一条可作为循环体的语句,就可以在它之前加上关键词while和带括号的条件,从而形成另一条语句。对应这一语句形成规则的产生式为
<语句>→while(条件)<语句>
另一种构建语句的方式是通过选择语句。这些语句具有两种形式,取决于是否有else部分,它们可以用以下两个产生式表示
<语句>→if(条件)<语句>
<语句>→if(条件)<语句>else<语句>
还有其他的语句形成方式,比如for语句、repeat语句和case语句。这里将表示它们的产生式留作本节习题,它们从实质上讲与我们已经看到的产生式是类似的。
不过,还有另一种重要的形成规则——程序块,它与我们已经看到的那些多少有些区别。程序块是由花括号{和}包围0条或更多语句构成的。要描述程序块,就需要一个补充语法分类,这里将其称为<语句列>,它代表一列语句。对应<语句列>的产生式很简单,就是
<语句列>→ε
<语句列>→<语句列><语句>
也就是说,第一个产生式说明语句列可以为空。而第二个产生式则表示如果在一列语句后再加上另一条语句,还是会得到一列语句。
现在就可以定义由语句列围上{和}构成的程序块语句了,也就是
<语句>→(<语句列>)
我们已经给出的这些产生式,加上陈述了语句可以是简单语句(赋值、调用、输入/输出或跳转)跟上分号的依据产生式,就如图11-5所示。
<语句> → while(条件)<语句>
<语句> → if(语句)<语句>
<语句> → if(语句)<语句>else<语句>
<语句> → {<语句列>}
<语句> → 简单语句;
<语句列> → ε
<语句列> → <语句列><语句>
图 11-5 定义了C语言中某些语句形成方式的产生式
11.2.2 习题
1. 为所有属于C语言标识符的字符串给出定义了语法分类<标识符>的文法。大家会看到,定义一些像<数码>这样的辅助语法分类是很实用的。
2. C语言中的算术表达式可以接受标识符和数字作为操作数。修改图11-2中的文法,使得操作数也可以是标识符。使用习题(1)中得到的文法来定义标识符。
3. 数字可以是实数,有着小数点和10的任意乘方,也可以是整数。修改图11-2中表示表达式的文法,或修改习题(2)中写出的文法,允许实数作为操作数。
4. * C语言算术表达式的操作数还可以是涉及指针(*和&运算符)的表达式,记录结构体的字段(.和->运算符)或数组索引。数组的索引可以是任意表达式。
(a) 为用来定义由一对方括号包围表达式构成的字符串的语法分类<数组引用>写出相应文法。可以利用语法分类<表达式>作为辅助。
(b) 为用来定义作为操作数的字符串的语法分类<名字>写出相应文法。就像1.4节中介绍过的那样,(*a).b[c][d]就是个名字。可以利用语法分类<数组引用>作为辅助。
(c) 为允许使用名字作为操作数的算术表达式写出相应文法。可以使用语法分类<名字>作为辅助。在将(a)、(b)、(c)这3个小题得到的产生式结合在一起后,能否得到允许a[b.c][*d]+e这种表达式存在的文法?
5. * 证明图11-4的文法可以生成2.6节中定义的量变平衡括号串。提示:与2.6节中的证明过程类似,要两次用到对括号串长度的归纳。
6. * 有时候表达式可以有两种或更多种平衡括号。例如,C语言表达式可以同时具有圆括号和方括号,而且两种括号肯定都是平衡的,也就是说,每个(都必须匹配一个),而每个[都必须匹配一个]。为具有这两种类型括号的平衡括号串写出相应文法。也就是说,该文法生成的平衡括号串只能是格式标准的C语言表达式中可能出现的那些。
7. 为图11-5中的文法添加定义for语句、do-while语句和switch语句的产生式。可以恰当地使用抽象终结符和辅助语法分类。
8. * 扩展示例11.3中的抽象终结符条件,以体现逻辑运算符的使用。也就是说,定义语法分类<条件>取代抽象终结符条件。可以使用抽象终结符比较表示x+1<y+z这样的比较表达式,然后以利用<这样的比较运算符表示的语法分类<比较>和语法分类<表达式>替代抽象终结符比较。语法分类<表达式>可以像11.2节开头那样粗略定义,不过还要加上C语言中的其他运算符,比如一元减号和%。
9. **写出可以定义语法分类<简单语句>的产生式,替换图11-5中的抽象终结符简单语句。可以假设语法分类<表达式>代表了C语言算术表达式。回想一下,简单语句可以是赋值、函数调用或跳转语句,而且严格来说,空串也是简单语句。
11.3 源自文法的语言
文法从本质上讲是涉及字符串集合的归纳定义。2.6节中那些归纳定义的示例与11.2节中很多例子的主要区别在于,对文法而言,一种文法定义若干语法分类的情况很常见。而2.6节中各个例子都定义了单独的概念。虽然存在这种区别,但2.6节中用来构建已定义对象集合的方法也适用于文法。对某文法的各语法分类<S>而言,可以按照如下方式定义语言L(<S>)。
依据。首先假设对文法中的各语法分类<S>而言,语言L(<S>)为空。
归纳。假设该文法具有产生式<S>→X1X2…Xn,其中对i=1、2、…、n,各个Xi 要么是语法分类,要么是终结符。并且对i=1、2、…、n,按照如下方式为各个Xi 选择一个字符串si 。
1. 如果Xi 是终结符,就可以只使用Xi 作为字符串si。
2. 如果Xi 是语法分类,就可以选择任何一个已知在L(Xi )中的字符串作为si 。如果若干个Xi 是相同的语法分类,就可以从各次出现的L(Xi )中分别选不同的字符串作为si 。
那么所选的这些字符串的串接s1s2…sn就是语言L(<S>)中的字符串。请注意,如果n=0,就把ε放到该语言中。
实现这一定义的一种系统化方法是经过该文法各产生式若干轮。在每轮中,我们要以所有可能的方式利用归纳规则更新各语法分类的语言。也就是说,对各个属于语法分类的Xi,要以所有可能的方式从L(Xi )中选出字符串。
示例 11.4
考虑一种由示例11.3介绍的与某几种C语言语句对应的文法中的一些产生式组成的文法。简单起见,我们只会用到对应while语句、程序块和简单语句的产生式,以及对应语句列的两个产生式。此外,还要使用简略表示法来合理压缩这些字符串的长度。简略表示用到了终结符w(while)、c(带括号的条件)和s(简单语句)。该文法使用语法分类<S>表示语句,并使用语法分类<L>表示语句列。该文法的产生式如图11-6所示。
(1) <S> → w c<S>
(2) <S> → { <L> }
(3) <S> → s;
(4) <L> → <L><S>
(5) <L> → ε
图 11-6 简化过的表示语句的文法
设L 是语法分类<L>中字符串的语言,并设S 是语法分类<S>中字符串的语言。一开始,根据依据规则,L 和S 都为空。在第一轮中,只有产生式(3)和产生式(5)是有用的,因为其他产生式的右部都含有语法分类,而此时对应这些语法分类的语言中还没有任何字符串。产生式(3)表明了s;是语言S 中的字符串,而产生式(5)则告诉我们ε 在语言L 中。
第二轮开始时,有L={ε }和S={s;}。产生式(1)现在让我们可以把wcs;添加到S 中,因为s;已经在S 中了。也就是说,在产生式(1)的右部中,终结符w和c只能代表它们本身,语法分类<S>则可以被替换为语言S 中的任意字符串。因为目前s;是S 中唯一的字符串,所以我们只能作出这一个选择,而这一选择的结果就是wcs;。
产生式(2)添加了字符串{},因为终结符{和}只能代表它们自身,不过语法分类<L>可以代表语言L 中的任意字符串,而此刻L 中只含有ε。
因为产生式(3)的右部只由终结符构成,所以它决不会产生除s;之外的字符串,因此从现在开始就可以忘掉该产生式了。同样,产生式(5)也不会产生除ε 之外的字符串,所以在本轮及以后的轮次中也可以忽略它。
最后,当我们用ε 代替<L>并用s;代替<S>之后,产生式(4)就为L 产生了字符串s;。在第二轮结束的时候,语言S={**s;wcs;,{}**},而语言L={ε;s;}。
在下一轮中,可以使用产生式(1)、(2)和(4)产生新的字符串。产生式(1)中替换<S>的选择有3种,分别是s;、wcs;和{}。用s;替换后得到的字符串是语言S 中已经具有的,不过替换了另两个字符串后得到的是新字符串wcwcs;和wc{}。
对产生式(2)而言,可以用ε 或s;替换<L>,为语言S 得出旧字符串{}和新字符串{s;}。在产生式(4)中,可以用ε 或s;替换<L>,并用s;、wcs;或{}替换<S>,这给语言L带来了一个旧字符串s;,以及5个新字符串wcs;、{}、s;s;、s;wcs;和s;{}。1
1我们非常关心用字符串替换语法分类的方式。假设经过每一轮替换,语言L和S都和它们在上一轮结束时的定义保持不变。每个产生式的右部都要进行替换。这些右部可以为左部的语法分类产生新的字符串,不过在同一轮替换中,我们不会在一个产生式的右部使用由另一个产生式新构建的字符串。但这也没关系,所有要生成的字符串最终都会在某一轮中生成,不管我们是立即在右部中循环使用新字符串,还是等待在下一轮中再使用新字符串。
这样语言就成了S={s;,wcs;,{},wcwcs;,wc{},{s;}}和L={ε ,s;,wcs;,{},s;s;,s;wcs;,s;{}}。我们可以按照自己的意愿继续这一过程。图11-7总结了前3轮的情况。
| S | L |
|---|---|---|
Round 1: |
| ε |
Round 2: |
|
|
Round 3: |
|
|
图 11-7 前3轮每轮产生的新字符串
正如示例11.4中那样,由文法定义的语言可能是无限的。如果语言是无限的,我们就不能一一列出所有字符串。能做到的最佳做法就是按轮次枚举这些字符串,就像示例11.4中一开始所做的那样。该语言中的任何字符串都将在某轮出现,不过在任何一轮都不可能产生出所有的字符串。可以被放进语法分类<S>的语言中的那些字符串组成的集合,就形成了(无限)语言L(<S>)。
习题
1. 在示例11.4中,第四轮添加的新字符串都有哪些?
2. * 在示例11.4的第i 轮替换中,为各语法分类产生的新字符串中最短的字符串各是什么?为下列语法分类产生的最长新字符串又分别是什么?
(a) <S>
(b) <L>?
3. 分别使用下列图中的文法按轮次生成平衡括号串。
(a) 图11-3
(b) 图11-4
这两种文法在相同轮次中是否会生成相同的平衡括号串?
4. 假设每个以某语法分类<S>为其左部的产生式在其右部中也含有<S>,那么为什么L(<S>)为空?
5. *在如本节所描述的方式按轮次生成字符串时,为语法分类<S>生成的新字符串只可能是通过替换某有关<S>的产生式中右部的语法分类得到,满足至少有一个被替换的字符串是在上一轮中新发现的。解释一下为什么楷体标记的条件是正确的。
6. ** 假设我们想分辨某个特定的字符串s 是否在某语法分类<S>的语言中。
(a) 解释一下,为什么如果在某轮中所有为任意语法分类生成的新字符串都比s 长,而且s尚未为L(<S>)生成,s 就不可能被放入L(<S>)中。提示:利用习题(5)。
(b) 解释一下,为什么在有限轮次的替换后,一定没法继续生成不长于s 的新字符串。
(c) 使用(a)和(b)的结论设计一种算法,接受某文法、该文法的一种语法分类<S>,以及某个终结符串s,并分辨出s是否在L(<S>)中。
11.4 分析树
正如我们已经看到的,通过反复应用产生式,可以为某语法分类<S>得出字符串s属于语言L(<S>)的结论。从由右部中不含语法分类的依据产生式得到的字符串开始。然后,对已经从各语法分类得到的字符串“应用”产生式。每次应用都要用字符串替换产生式右部中出现的各语法分类,并构造出属于产生式左部中语法分类的字符串。最终,我们将通过应用左部为<S>的产生式来构造字符串s。
把s在L(<S>)中的“证明”画成一棵称作分析树(parsetree)的树往往是很实用的。分析树的节点都是带标号的,要么是终结符,要么是语法分类,要么是符号ε。叶子节点只会被标记为终结符或符号ε,而内部节点只可能用语法分类作为标号。
每个内部节点v 都表示产生式的应用。也就是说,一定存在某个产生式同时满足下列条件:
1. 标号v 的语法分类是该产生式的左部;
2. v 的子节点的标号从左往右构成了该产生式的右部。
示例 11.5
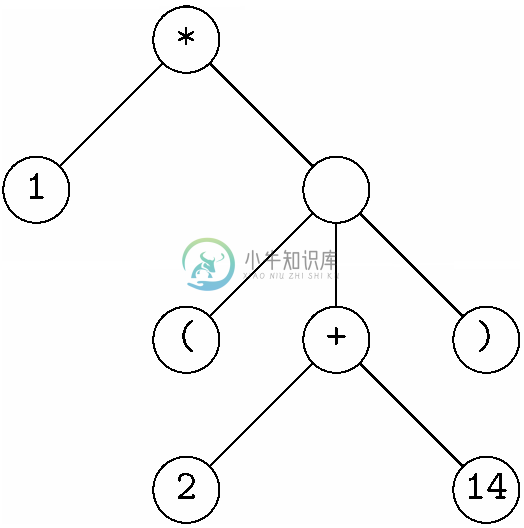
图11-8展示了一棵基于图11-2所示文法的分析树。不过,在这里我们把语法分类<表达式>、<数字>和<数码>分别简称为<E >、<N >和<D >。该分析树表示的字符串是3* (2+14)。
例如,这棵分析树的根节点及其子节点就表示产生式
<E >→<E >*<E >
就是图11-2中的产生式(6)。根节点的最右子节点及其子节点形成了产生式<E >→(<E >),或者说是图11-2中的产生式(5)。
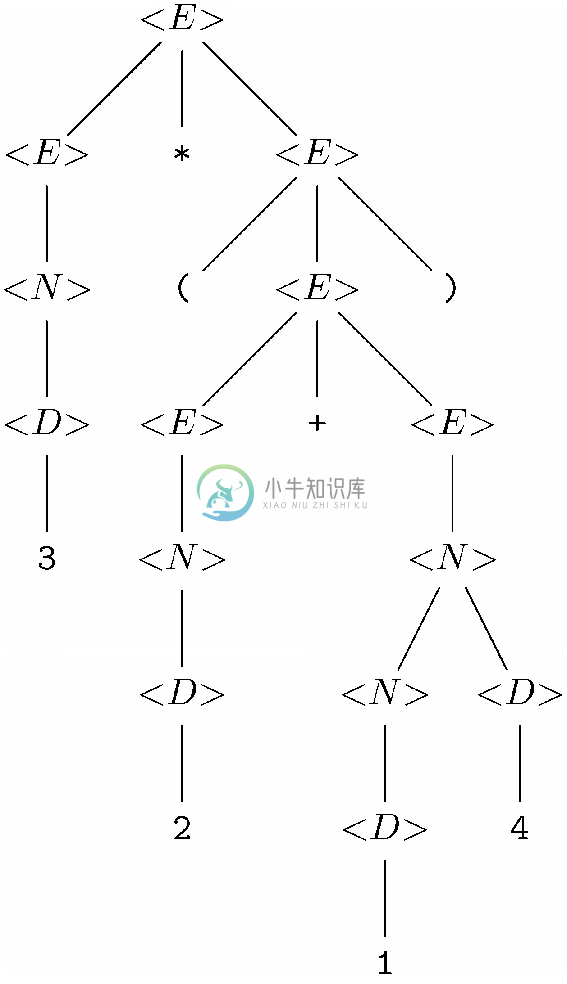
图 11-8 使用图11-2所示文法的字符串3*(2+14)对应的分析树
11.4.1 分析树的构建
每棵分析树都表示某一终结符串s,我们可将该串称为这棵树的产出(yield)。串s 由相应分析树所有叶子节点的标号按照从左到右的次序排列而成。此外,通过对分析树进行前序遍历并只依次列出那些属于终结符的标号,我们也可以得到这一产出。例如,图11-8所示分析树的产出就是3*(2+14)。
如果树只有一个节点,那么该节点的标号就只能是某个终结符或者ε,因为它是个叶子节点。如果该树不止有一个节点,那么根节点的标号就是语法分类,因为在一棵有两个或更多个节点的树中,根节点总是个内部节点。而且该语法分类的字符串中总是会包含该树的产出。与某给定文法对应的分析树的归纳定义如下所述。
依据。对文法中的每个终结符x来说,存在一棵只含一个标号为x的节点的树。当然,该树的产出就是x。
归纳。假设我们有产生式<S>→X1X2…Xn,其中各个Xi 要么是终结符,要么是语法分类。如果n=0,也就是说,该产生式实为<S >→ε,那么就有一棵像图11-9这样的树。其产出为ε,而且根节点为<S >,因为有该产生式,所以空串ε 显然是在L(<S >)中的。
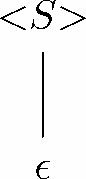
图 11-9 由产生式<S >→ε 得到的分析树
现在假设<S>→X1X2…Xn 而且n≥1。我们可以按照如下方式,对每个i=1、2、…、n 而言,为各个Xi 选择树Ti 。
1. 如果Xi 是终结符,就必须选择标号为Xi 的单节点树。如果有两个或多个X是同一终结符,就必须为该终结符的每次出现选择具有相同标号的不同单节点树。
2. 如果Xi 是语法分类,我们可以选择任何已经构建好的以Xi 作为根节点标号的分析树,然后构建一棵像图11-10这样的树。也就是说,我们创建的根节点标号是该产生式左部的语法分类<S>,而这棵树根节点的子节点从左到右依次是为X1、X2、…、Xn 选择的树的根节点。如果有两个或多个X 是相同的语法分类,我们也许要为各语法分类选择相同的树,但是必须在该树每次被选中时为其生成不同的副本。我们还可以为同一语法分类的不同出现选择不同的树。
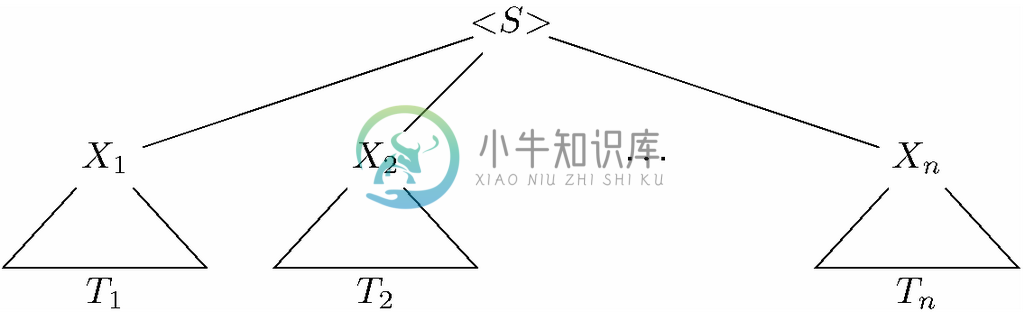
图 11-10 利用产生式和其他分析树构建分析树
示例 11.6
我们来研究一下图11-8中分析树的构造,看看它的结构是如何模仿证明字符串3*(2+14)在L(<E>)中的过程的。首先,可以为该树中的各个终结符构造一棵单节点树。然后图11-2中第(1)行的产生式组说明了10个数码都是属于L(<D>)的长度为1的字符串。我们用到其中的4个产生式创建图11-11所示的4棵树。例如,我们利用产生式<D>→1按照如下方式创建了图11-11a中的分析树,为右部中的符号1创建一棵只有一个标号为1的节点的树,然后,创建一个标号为<D>的节点作为根节点,并以我们为1选择的树的根节点(也是唯一的节点)作为其子节点。

图 11-11 使用产生式<D>→1以及相似的产生式构建的分析树
下一步是要利用图11-2中的产生式(2),或者说是<N>→<D>,来揭示数码就是数字这一事实。例如,可以选择图11-11a所示的树替换产生式(2)右部中的<D>,得出图11-12a所示的树。图11-12中的另两棵树也是用相似的方式产生的。
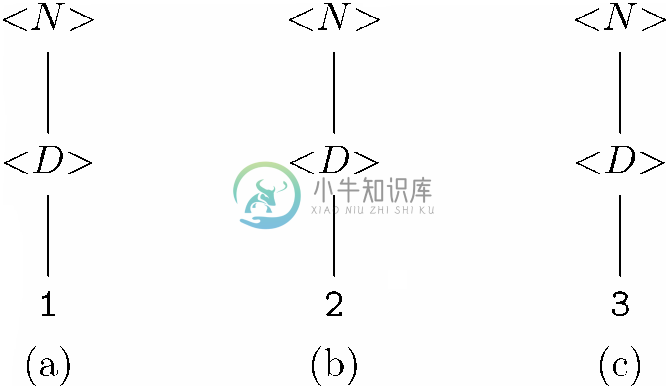
图 11-12 使用产生式<N>→<D>构建的分析树
现在可以利用产生式(3),也就是<N>→<N><D>了。我们将会为右部中的<N>选择图11-12a所示的树,并为<D>选择图11-11d所示的树。还要为左部创建一个标号为<N>的新节点,并为该节点指定两个子节点,也就是选中的两棵树的根节点。得到的树如图11-13所示。该树的产出是数字14。

图 11-13 用产生式<N>→<N><D>构建的分析树
下一个任务就是为和2+14创建分析树。首先,我们要用到产生式(4),即<E>→<N>,以建立图11-14所示的分析树。这些树表明了3、2和14都是表达式。这些树中的第一棵源自图11-12c中为右部中的<N>选择的树,第二棵是通过图11-12b中为<N>选择的树得到的,而第三棵则是选择图11-13中的树得到的。
然后可以使用产生式(6),也就是<E>→<E>+<E>。对右部中的第一个<E>,我们使用了图11-14b中的树,而对右部中的第二个<E>,则是使用了图11-14c所示的树。为右部中的+使用的是一棵标号为+的单节点树。得到的树如图11-15所示,其产出为2+14。
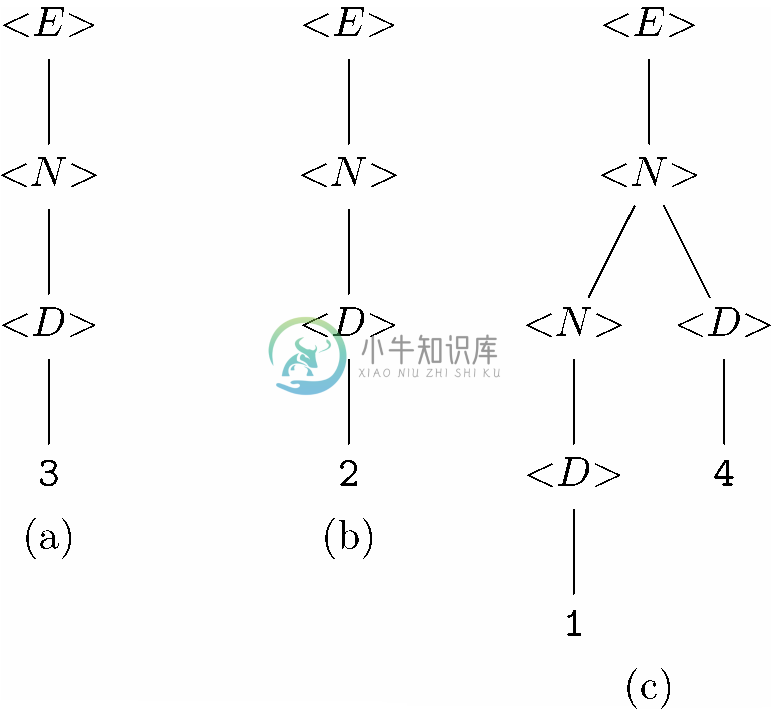
图 11-14 使用产生式<E>→<N>构建的分析树
接下来要用到产生式(5),或者说是<E>→(<E>),构建图11-16所示的分析树。我们只要为右部中的<E>选择图11-15中的树,并为终结符括号选择单节点树即可。
最后,利用产生式(8),也就是<E>→<E>*<E>,构建了我们最初在图11-8中展示的分析树。我们为右部中的第一个<E>选择了图11-14a所示的树,并为第二个<E>选择了图11-16中的树。
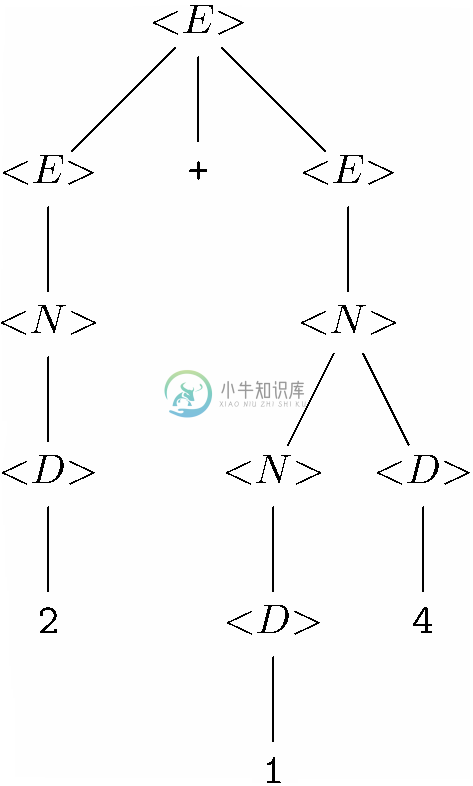
图 11-15 使用产生式<E>→<E>+<E>构建的分析树
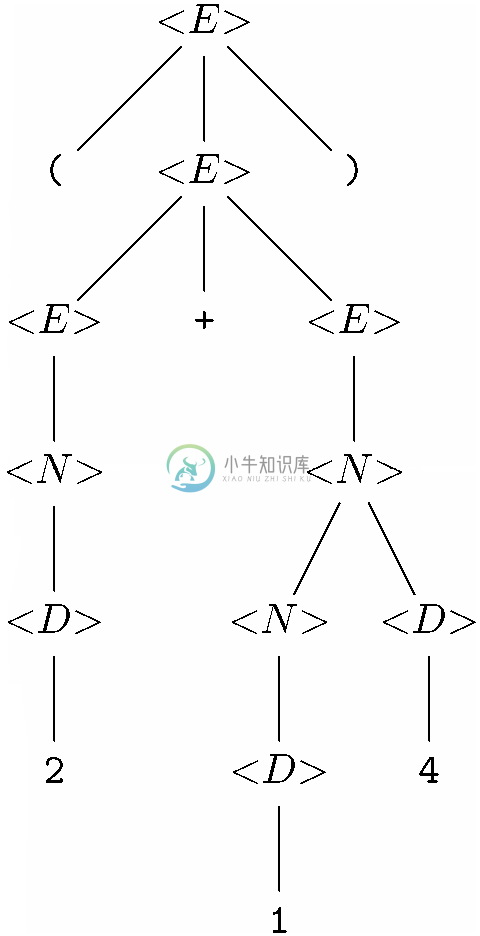
图 11-16 使用产生式<E>→(<E>)构建的分析树
11.4.2 分析树为何“行得通”
分析树的构建与字符串属于某语法分类的归纳定义非常相似。我们可以通过两次简单的归纳来证明,对任意语法分类<S>来说,以<S>为根节点的分析树的产出刚好是L(<S>)中的字符串。也就是如下两点。
(1) 如果T 是根节点标号为<S>而且产出为s的分析树,那么字符串s 在语言L(<S>)中。
(2) 如果字符串s 在语言L(<S>)中,那么存在产出为s 且根节点标号为<S>的分析树。
这一等价关系应该是相当直观的。粗略地讲,分析树是由更小的分析树,按照由较短的字符串构成长字符串的方式,对产生式右部中的语法分类进行替换构成的。我们首先利用对树T 高度的完全归纳证明第(1)部分。
依据。假设分析树的高度是1。那么这棵树就像图11-17所示的这样,或者,在n=0的特例中,就像图11-9所示的树那样。构建这种树的唯一方法是,若存在产生式<S>→x1x2…xn,其中各x都是终结符(如果n=0,该产生式就是<S>→ε)。因此x1x2…xn是L(<S>)中的字符串。
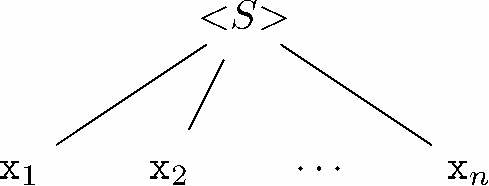
图 11-17 高度为1的分析树
归纳。假设命题(1)对所有高度不超过k 的树都成立。现在考虑像图11-10那样高度为k+1的树。那么,对i=1、2、…、n,各子树Ti 的高度至多为k。如果这些子树中有任何一棵的高度达到或超过k+1,那么整棵树的高度就至少是k+2。因此,归纳假设适用于各棵树Ti 。
根据归纳假设,如果子树Ti 的根节点Xi 是语法分类,那么Ti 产出si 就在语言L(Xi )中。如果Xi 是终结符,就定义字符串si 是Xi,那么整棵树的产出就是s1s2…sn。
根据分析树的定义,可知<S>→X 1X 2…X n是产生式。假设只要Xi 是语法分类就用si 替换Xi 。根据定义,如果Xi 是终结符,Xi 就是si 。这样一来,替换后的右部就成了s1s2…sn,与该树的产出是相同的。根据<S>的语言的归纳规则,我们知道s1s2…sn 是在L(<S>)中的。
现在必须证明命题(2),语法分类L<S>中的每个字符串s都具有以<S>为根节点且以s为产出的分析树。首先要注意到,对每个终结符x,存在根节点和产出都是x的分析树。现在我们要对得出s 在L(<S>)中时的归纳步骤(如11.3节所述,下面的证明中加引号的“归纳步骤”就是表示该归纳步骤)的应用次数进行完全归纳。
依据。假设证明s 在L(<S>)中需要应用“归纳步骤”一次。则一定存在产生式<S>→x1x2…xn,其中所有的x都是终结符,而且<S>=x1x2…xn。我们知道对i=1、2、…、n,都有标号为Xi 的单节点分析树。因此,存在产出为s且根节点标号为<S>的分析树,该树的样子类似图11-17所示。在n=0的特例中,我们知道s=ε,此时就要使用图11-9所示的树。
归纳。假设应用“归纳步骤”不超过k次所发现的任意语法分类<T>的语言中,任何字符串t 都具有以t 为产出而且以<T>为根节点的分析树。考虑通过k+1次应用“归纳步骤”找到的在语法分类<S>的语言中的字符串s 。那么,存在产生式<S>→X1X2…Xn,且s=s1s2…sn,其中每个子串si 都会是如下两种可能之一。
1. 为Xi(如果Xi 是终结符)。
2. 某个至多应用k 次“归纳步骤”就可知在L(Xi )中的字符串(如果Xi 是语法分类)。
因此,对每个i,都可以找到一棵具有产出si 而且根节点标号为Xi 的树Ti 。如果Xi 是语法分类,那么就利用归纳假设声明Ti 存在,而如果Xi 是终结符,则不需要归纳假设就可以声明存在标号为Xi 的单节点树。因此,如图11-10中那样构建的树具有产出s 而且根节点标号为<S>,这样就证明了该归纳步骤。
11.4.3 习题
1. 根据图11-2所示的文法,为以下字符串给出相应的分析树。在各情况中根节点位置的语法分类都应该是<E>。
(a) 35+21
(b) 123-(4*5)
(c) 1*2*(3-4)
2. 使用图11-6中的语句文法,给出以下字符串的分析树。其中每种情况下根节点的语法分类都应该是<S>。
(a) wcwcs;
(b) {s;}
(c) {s;wcs;}
3. 利用图11-3中的平衡括号串文法,给出以下括号串的分析树。
(a) (()())
(b) ((()))
(c) ((())())
4. 利用图11-4中的文法为习题3中的各括号串给出分析树。
语法树和表达式树
通常,像分析树这样的树是用来表示表达式的。例如,我们在第5章中通篇都以表达式树为例。语法树是“表达式树”的另一个名字。当我们拥有如图11-2所示的对应表达式的文法时,就可以通过以下3项变形把分析树转换成表达式树。
1. 原子操作数被压缩为以该操作数为标号的单个节点。
2. 运算符从叶子节点移动到它们的父节点。也就是说,像+这样的运算符符号成为了原本在它上方,以语法分类“表达式”为标号的节点的标号。
3. 仍然以“表达式”为标号的内部节点要删除其标号。
例如,图11-8中的分析树就可以转化成如下表达式树或者说语法树。
11.5 二义性和文法设计
我们来考虑如图11-4所示的表示平衡括号串的文法,这里用语法分类<B>作为图11-4中语法分类<平衡>的缩写。
<B>→(<B>)|<B><B>|ε (11.1)
假设想要一棵表示括号串()()()的分析树。图11-18展示了两棵这样的分析树,第一棵是把前两对括号先分在一组,而另一棵则先把后两对括号分成一组。

图 11-18 有着同样的产出和根节点的两棵分析树
出现这样两棵分析树应该不会让人感到惊讶。一旦确定()和()()都是平衡括号串,使用产生式<B>→<B><B>就可以用()替换右部中的第一个<B>并用()()替换第二个<B>,反之亦然。两种情况下,都能得出括号串()()()在语法分类<B>中。
如果文法中有两棵或多棵分析树具有相同产出,且其根节点标号是相同的语法分类,就说该文法是二义的(ambiguous)。请注意,不一定要每个字符串都是若干分析树的产出,只要有一个这样的字符串就足够让文法具有二义性了。例如,括号串()()()就足以说明文法(11.1)是二义的。不具二义性的文法叫作无二义(unambiguous)文法。在无二义文法中,对每个字符串s和语法分类<S>而言,至多存在一棵产出为s且根节点标号为<B>的分析树。
图11-3所示的文法就是个无二义文法的例子,这里还是用<S>来代替<平衡的>。
<B>→(<B>)<B>|ε (11.2)
证明文法无二义是相当困难的。在图11-19中是对应括号串()()()的唯一一棵分析树,当然,这一字符串有着唯一分析树的事实并不能证明文法(11.2)就是无二义的。我们证明无二义性的唯一方法就是证明语言中的每个字符串都具有唯一的分析树。
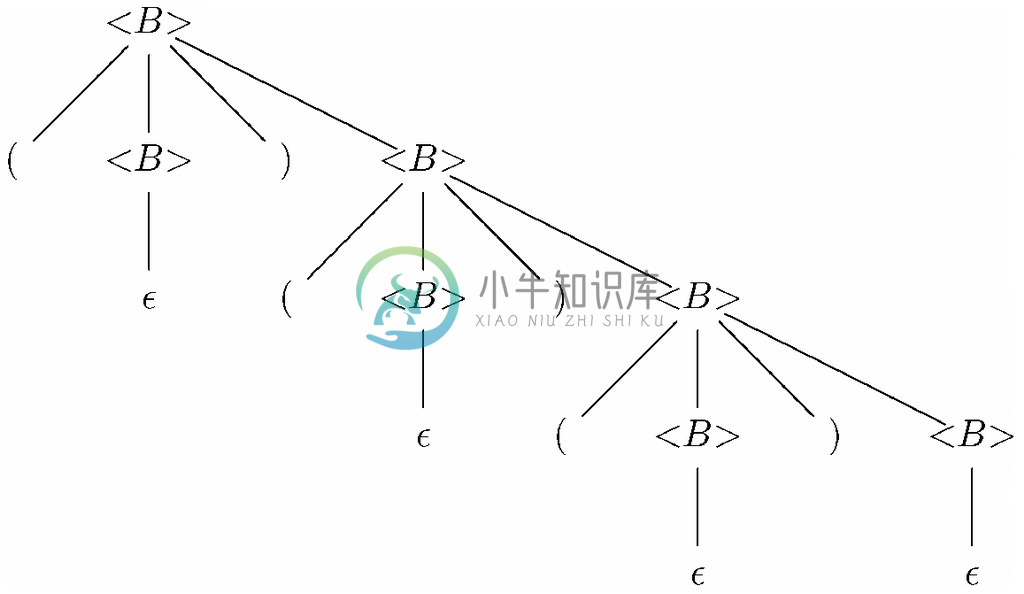
图 11-19 使用文法(11.2)表示字符串()()()的唯一分析树
11.5.1 表达式中的二义性
尽管图11-4中的文法是二义的,但它的二义性并没有太大坏处,因为我们从左起还是从右起分组括号影响不大。在考虑表示表达式的文法(比如11.2节中图11-2所示的文法)时,会发生一些更为严重的问题。具体地讲,尽管一些分析树可以给出正确的表达式值,但另一些分析树表示的是错误的值。
无二义性为何很重要
为程序构建分析树的分析器是编译器的关键部分。如果描述编程语言的文法是二义的,而且如果其二义性未被消除,那么就至少有某些程序具有多棵分析树。而同一程序不同的分析树就为该程序赋予了不同的含义,其中这种情况下“含义”是指由原始程序翻译成的机器语言程序执行的操作。因此,如果与程序对应的文法是二义的,编译器就不能正确地决定该为某些程序使用哪棵分析树,所以就不能决定机器语言程序应该做些什么。出于这种原因,编译器必须使用无二义性的规范。
示例 11.7
这里用简略表示法来表示示例11.5中给出的表达式文法,并考虑表达式1-2+3。它具有两棵分析树,取决于是从左还从右组合运算符。这两棵分析树如图11-20a和图11-20b所示。
图11-20a中的树是从左起结合的,因此操作数是从左起分组的。这种分组是正确的,因为我们一般会从左起分组优先级相同的运算符,1-2+3习惯被解释为(1-2)+3,其值为2。如果我们为构建起图11-20a所示树的子树表示的表达式求值,就要首先在根节点的最左子节点处计算1-2=-1,然后在根节点计算-1+3=2。
另一方面,对从右侧起关联的图11-20b,会把该表达式分组为1-(2+3),其值为-4。不过,对该表达式的这种解释是不合规定的。值-4是在构建图11-20b的树时得到的,因为我们先在根节点的最右子节点处计算了2+3=5,然后在根节点处计算了1-5=-4。
从错误的方向结合优先级相等的运算符可能导致问题。而优先级不同的运算符也可能带来问题,正如我们在接下来的示例中要看到的,有可能在结合更高优先级的运算符之前先结合了低优先级的运算符。

图 11-20 对应表达式1-2+3的两棵分析树
示例 11.8
考虑表达式1+2*3。在图11-21a中,我们看到表达式是从左起分组的,这是不对的,而图11-21b所示的则是正确的从右边起的分组,这样乘法的操作数才在加法之前分组。前一种分组会得出不正确的值9,而后面的分组则会产生合乎规则的值7。
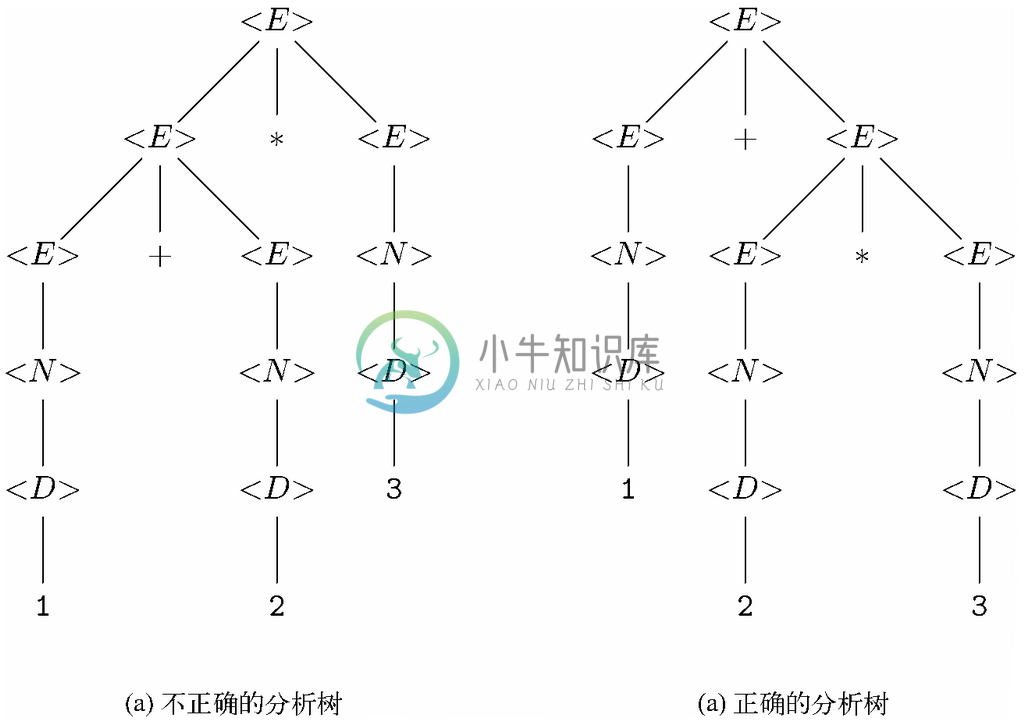
图 11-21 表示表达式1+2*3的两棵分析树
11.5.2 表示表达式的无二义文法
就像表示平衡括号串的文法(11.2)可以被视作文法(11.1)的无二义版本那样,也可以为示例11.5中的表达式文法构建一个无二义版本。“窍门”就是定义有着如下直觉含义的3个语法分类。
1. <因式>生成了不能被“提取出”的表达式,也就是说,因式要么是单个操作数,要么是加了括号的表达式。
2. <项>生成了因式的积或商。单个因式是项,因此一列由*或/运算符分隔的因式也是项。12和12/3<因式>*45都是项。
3. <表达式>生成了一项或多项的和或差。单个项就是个表达式,因此一列由+或-运算符分隔的项也是表达式。12、12/3*45和12+3*45-6都是表达式。
图11-22就是表示表达式、项和因式间关系的文法。我们用简写<E>、<T>和<F>分别代表<因式>、<项>和<表达式>。
(1) <E> → <E> + <T> | <E> - <T> | <T>
(2) <T> → <T> * <F> | <T>/<F> | <F>
(3) <F> → (<E>) | <N>
(4) <N> → <N><D> | <D>
(5) <D> → 0 | 1 | … | 9
图 11-22 表示算术表达式的无二义文法
例如,第(1)行的3个产生式定义了表达式要么是较小的表达式后面跟上+或-以及另一项,要么是单独的项。如果将这些概念融为一体,那么该产生式是说,每个表达式都是项后面跟上0个或更多由一个+或-以及一项构成的配对。同样,第(2)行表示项是由较小的项后面跟上*或/以及因式构成的。也就是说,项是由因式后面跟上0个或更多由一个*或/加上一个因式组成的配对。第(3)行说的是因式或者是数字,或者是由括号包围的表达式。而第(4)行和第(5)行则像之前所做的那样定义了数字和数码。
之所以在第(1)行和第(2)行中使用了诸如
<E>→<E>+<T>
这样的产生式,而没有使用看似与之等价的<E>→<T>+<E>,就是为了强制这些项从左起分组。因此,我们看到像1-2+3这样的表达式会被正确地分组为(1-2)+3。同样,像1/2*3这样的项也能被正确地分组为(1/2)*3。图11-23展示了用图11-22中的文法表示表达式1-2+3的唯一分析树。请注意,1-2必须首先被组合为表达式。如果像图11-20b中那样先组成2+3,是没办法用图11-22所示的文法将1-附加到该表达式上的。
表达式、项和因式之间的区别使得处于不同优先级的运算符能被正确分组。例如,表达式1+2*3对应的分析树只有图11-24所示的那棵,它像图11-21b所示的树那样先组合了子表达式2*3,而不是像图11-21a所示的错误的树那样首先组合1+2。
就像之前提到的平衡括号串问题那样,我们没有证明图11-22所示的文法是无二义的。习题中包含了更多例子,应该有助于说服读者相信该文法不仅是无二义的,而且为各个表达式给出了正确的组合方式。我们还表述了该文法的思路如何扩展到更全面的表达式家族。
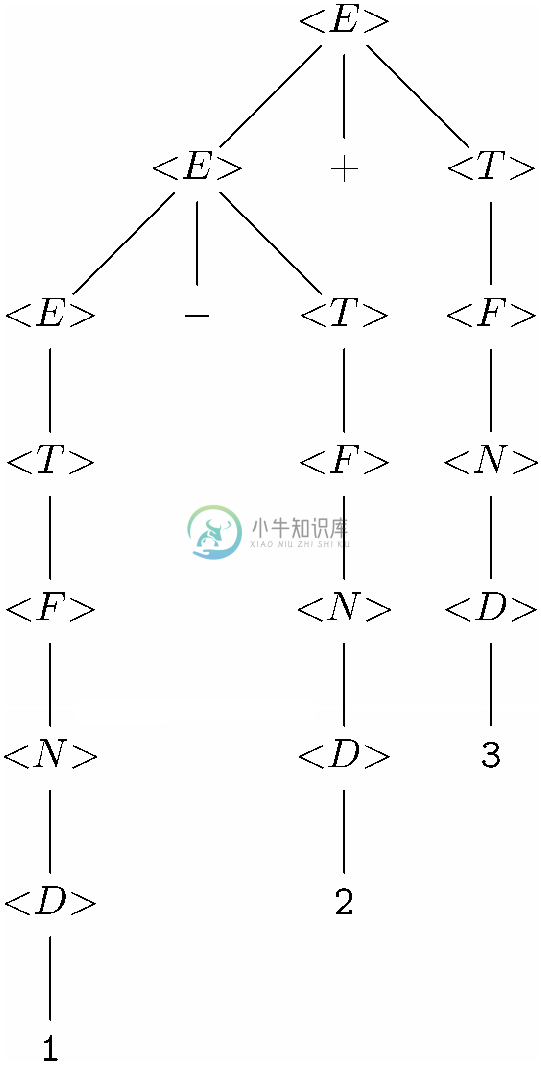
图 11-23 用图11-22中的无二义文法表示表达式1-2+3的分析树
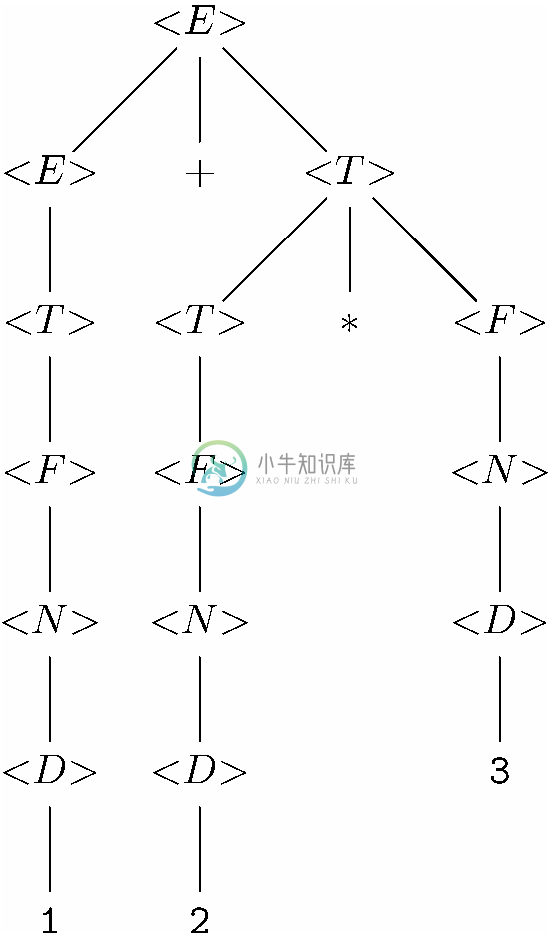
图 11-24 用图11-22中的无二义文法表示表达式1+2*3的分析树
11.5.3 习题
1. 用图11-22所示的文法,为下列各表达式给出唯一的分析树。
(a) (1+2)/3
(b) 1*2-3
(c) (1+2)*(3+4)
2. * 图11-22所示文法的表达式有两级优先级,+和-在第一级,而*和/在更高的第二级。一般而言,我们可以利用k+1个语法分类处理具有k 个优先级的表达式。修改图11-22中的文法,使其包含乘方运算符^,它的优先级比*和/更高。作为提示,大家要定义是操作数或带括号表达式的要素,并重新把因式定义为一个或多个要素由乘方运算符连接而成。请注意,乘方的组合是从右起而不是从左起的,也就是说,2^3^4表示的是2^(3^4),而不是(2^3)^4。我们该如何确保在要素中是从右起进行组合的?
3. * 扩展该无二义表达式文法,允许=、<=等比较运算符,这些比较运算符都具有同样的优先级而且是左关联的,它们的优先级在+和-之下。
4. 扩展图11-22中的表达式文法,使其包含一元减号。请注意,这一运算符的优先级要比其他运算符的优先级更高,例如,-2*-3就被组合为(-2)*(-3)。
5. 扩展习题3中得出的文法,已包含逻辑运算符&&、||和!。其中&&和*有着相同优先级,而||的优先级与+相同,而!的优先级则比一元的-更高。&&和||这两个二元运算符都是从左起组合的。
6. * 不是每个表达式按照11.2节图11-2所示的二义性文法都有一棵以上的分析树。给出一些根据该文法只有唯一分析树的表达式。大家能否给出一条规则,说明什么时候表达式会具有唯一的分析树?
7. 以下文法定义了只有0和1组成的字符串的集合(不含ε)。
<字符串>→<字符串><字符串> | 0 | 1
在该文法中,字符串010有几棵分析树?
8. 给出与习题7中文法具有相同语言的无二义文法。
9. * 文法(11.1)对空串来说有多少分析树?给出对应空串的3种不同的分析树。
11.6 分析树的构造
文法和正则表达式一样,都可以描述语言,但都不能直接给出算法来确定某字符串是否在所定义的语言中。对正则表达式来说,我们在第10章中已经了解到如何先把正则表达式转换成非确定自动机,接着转换成确定自动机,而这一确定自动机就可以直接实现为程序。
对文法来说,也存在多少有些相似的处理过程。一般来说,根本不可能把文法转换成确定自动机,在11.7节中我们会讨论一些可以进行这种转换的例子。不过,通常可以把文法转换成类似自动机的程序,从头至尾读取输入,并呈现该输入字符串是否在该文法的语言中的决策。这类技术中最重要的就是“LR分析”(LR代表从左至右扫描输入),但它不在本书要讨论的范围之内。
11.6.1 递归下降分析
这里要介绍的是一种更加简单但不那么强大的分析技术——“递归下降分析”,在这种分析中,文法会被一系列相互递归的函数替代,每个递归函数都对应文法中的一个语法分类。对应语法分类<S>的函数S 的目标是读入构成语言L(<S>)中字符串的字符序列,并返回指向该字符串分析树根节点的指针。
产生式的右部可以看作找到左部的语法分类中的字符串所必须满足的一系列目标——终结符和语法分类。例如,考虑表示平衡括号串的无二义文法,我们在图11-25中将其重现。
(1) <B> → ε
(2) <B> → ( <B> ) <B>
图 11-25 表示平衡括号串的文法
产生式(2)表述了弄清平衡括号串是否依次满足以下4个条件的一种方法。
1. 找到字符(;
2. 然后找到平衡括号串;
3. 然后找到字符);
4. 最后找到另一个平衡括号串。
一般而言,如果发现某终结符是下一个输入符号,终结符的目标就得到满足了,但如果下一个输入符号是其他内容,这一目标就不会被满足了。要弄清右部中的语法分类是否得到满足,可以调用对应该语法分类的函数。
根据文法构建分析树的安排如图11-26所示。假设要确定某终结符序列X1X2…Xn 是否为语法分类<S>中的字符串,而且如果是还要给出它的分析树。然后我们在输入文件中放入X1X2…Xn ENDM,其中ENDM是一个不属于终结符的特殊符号。2ENDM叫作端记号(endmarker),它的作用是表示待检查的整个字符串已经被读入了。例如,在C语言程序中,通常会使用EOF或EOS字符作为端记号。
2在实际用于编程语言的编译器中,整个输入可能不是一次性放入一个文件中的,而是由每次检查源程序中一个字符的“词法分析器”这种预处理器一次找到一个终结符。
X1 X2 … Xn ENDM
↑
调用S
图 11-26 初始化在输入中发现<S>的程序
输入游标(input cursor)标记了要被处理的终结符,也就是当前的终结符。如果输入是字符串,那么游标可以是指向字符的指针。分析程序首先要调用对用语法分类<S>的函数S,而且输入游标是在输入的开头位置。
每当处理产生式右部,并在产生式中遇到终结符a的时候,就要在输入游标指示的位置查找相匹配的终结符a。如果找到a,就把输入游标移至输入中的下一个终结符。如果当前的终结符是a之外的内容,就是匹配失败,就不能为该输入字符串给出分析树。
另一方面,如果处理产生式右部并遇到了语法分类<T>,就要调用与<T>对应的函数T。如果T“失败”,那么整个分析也失败,而该输入就被视为不在待分析的语言中。如果T 成功,它就会“消灭”某一输入,把输入游标向前移动对应该输入的0个或更多位置。从T 被调用时的位置直到T 离开游标之前的位置都要被销毁。T 还会返回一棵树,就是与该被销毁输入对应的分析树。
当我们处理完产生式右部中的各个符号后,就要为该产生式表示的那部分输入生成分析树。要完成这一工作,就需要创建一个新的根节点,并以该产生式的左部作为其标号。该根节点的子节点是成功调用与右部中语法分类对应的函数所返回的树的根节点,而且要为右部中的每个终结符创建相应的叶子节点。
11.6.2 用于平衡括号串的递归下降分析器
现在来考虑一个扩展过的例子,看看如何为图11-25所示文法中的语法分类<B>设计递归函数B。在某个输入位置被调用的函数B,会销毁从那个位置开始的某个平衡括号串,并把输入光标留在紧临该平衡括号串之后的那个位置。
难点在于,要满足确定<B>这一目标,到底是使用可以立即成功的产生式(1),<B>→ε,还是使用产生式(2),也就是<B>→(<B>)<B>。而我们要遵循的策略是,只要下一个终结符为(,就使用产生式(2),只要下一个终结符是)或是端记号,就使用产生式(1)。
函数B如图11-27b所示,在它之前的图11-27a中是一些重要的辅助要素,这些元素包括以下几点。
1. 常量FAILED被定义为函数B 没能在输入中找到平衡括号串时的返回值。FAILED的值与NULL相同。后者的值也表示一棵空树。不过,如果B成功的话,它返回的分析树不会为空,所以FAILED的这一定义是不可能有二义性的。
2. 类型NODE和TREE的定义。节点是由标号字段(字符),以及指向最左子节点和右兄弟节点的指针组成的。标号‘B’表示标号为B 的节点,‘(‘和’)’分别表示标号为左括号和右括号的节点,而‘e’则表示标号为ε 的节点。与5.3节中最左子节点右兄弟节点结构不同的是,这里为指向节点的指针选择的类型是TREE而非pNODE,因为这里的这些指针多用来作为树的表示。
3. 下面要描述的3个辅助函数和函数B 的原型声明。
4. 两个全局变量。第一个是parseTree,存放着由对B 的第一次调用返回的分析树。第二个是nextTerminal,它是输入游标,指向输入终结符串中的当前位置。请注意,nextTerminal具有全局性是很重要的,这样当B的一次调用返回时,输入游标所在的位置对执行这次调用的B的副本而言就是已知的。
5. main函数。在这一简单的演示中,main将nextTerminal置为指向特定测试串()()开头的位置,而且调用B 的解雇被放置在parseTree中。
6. 3个辅助函数可以创建树节点,而且,如果需要的话,可以组合子树以形成更大的树。它们分别是
(a) makeNode 0(x)函数创建的节点没有子节点,也就是说,它创建的是叶子节点,而且用符号x 作为该叶子节点的标号。返回的是由这一个节点组成的树。
(b) makeNode 1(x,t )函数创建的节点具有一个子节点。新节点的标号为x,而且其子节点是树t 的根节点。返回的是根节点为所创建节点的树。请注意,makeNode1要利用makeNode0创建根节点,然后让树t 的根节点成为所创建根节点的最左子节点。我们假设所有的最左子节点和右兄弟节点指针一开始都是NULL,而且它们就是,因为它们都是由makeNode0创建的,该函数显然将它们置为了NULL。因此,makeNode1并不一定要把NULL存储到树t 根节点的rightSibling字段中,不过这样做是明智的安全之举。
(c) 函数makeNode 4(x,t1,t2,t3,t4)创建的节点具有4个子节点。该节点的标号是x,而其子节点按照从左到右的次序分别是树t1、t2、t3和t4的根节点,返回的是用所创建节点作为根节点的树。请注意,makeNode4要利用makeNode1创建一个新的根节点,并将t1附加到该节点上,然后用右兄弟节点指针把其余的树串联起来。
#define FAILED NULL
typedef struct NODE *TREE;
struct NODE {
char label;
TREE leftmostChild, rightSibling;
};
TREE makeNode0(char x);
TREE makeNode1(char x, TREE t);
TREE makeNode4(char x, TREE t1, TREE t2, TREE t3, TREE t4);
TREE B();
TREE parseTree; /* 存放分析的结果 */
char *nextTerminal; /* 输入字符串中的当前位置 */
void main()
{
nextTerminal = "()()"; /* 在实际应用中,终结符串是从输入读取的 */
parseTree = B();
}
TREE makeNode0(char x)
{
TREE root;
root = (TREE) malloc(sizeof(struct NODE));
root->label = x;
root->leftmostChild = NULL;
root->rightSibling = NULL;
return root;
}
TREE makeNode1(char x, TREE t)
{
TREE root;
root = makeNode0(x);
root->leftmostChild = t;
return root;
}
TREE makeNode4(char x, TREE t1, TREE t2, TREE t3, TREE t4)
{
TREE root;
root = makeNode1(x, t1);
t1->rightSibling = t2;
t2->rightSibling = t3;
t3->rightSibling = t4;
return root;
}
图11-27(a) 递归下降分析器的辅助函数
TREE B()
{
(1) TREE firstB, secondB;
(2) if(*nextTerminal == '(') /* 遵循产生式2 */ {
(3) nextTerminal++;
(4) firstB = B();
(5) if(firstB != FAILED && *nextTerminal == ')') {
(6) nextTerminal++;
(7) secondB = B();
(8) if(secondB == FAILED)
(9) return FAILED;
else
(10) return makeNode4('B',
makeNode0('('),
firstB,
makeNode0(')'),
secondB);
}
else /* 对B的第一次调用失败了 */
(11) return FAILED;
}
else /* 遵循产生式 1 */
(12) return makeNode1('B', makeNode0('e'));
}
图11-27(b) 为平衡括号串构建分析树的函数
现在可以一行行考虑图11-27b所示的程序了。第(1)行是两个局部变量firstB和secondB的声明,这两个局部变量的作用是存放在尝试产生式(2)的情况下对B 的两次调用所返回的分析树。第(2)行会测试输入的下一个终结符是否为(。如果是,我们就将在产生式(2)的右部中查找实例,如果不是,就要假设使用的是产生式(1),而且ε 就是该平衡串。
在第(3)行,我们要递增nextTerminal,因为当前输入(已经匹配上了产生式(2)右部中的(。我们现在已经让输入游标处在恰当的位置,它对应的对B 的调用将为产生式(2)右部中的第一个<B>找到平衡串。对B的这次调用是在第(4)行发生的,而该调用返回的树被存储在变量firstB中,它随后会被装配成与当前对B 的调用对应的分析树。
第(5)行要检查是否仍然有能力找到平衡串。也就是说,首先要确定第(4)行对B 的调用没有失败。然后测试nextTerminal当前的值是否为)。回想一下,当B返回时,nextTerminal指向要用来形成平衡串的下一个输入终结符。如果要匹配产生式(2)的右部,而且已经匹配了(与第一个<B>,那么就必须匹配),这就解释了该测试的第二部分。只要该测试的任何一部分失败,当前对B 的调用就会在第(11)行失败。
若通过了第(5)行的测试,则在第(6)和第(7)行要把输入游标移过刚发现的右括号,并再次调用B,以匹配产生式(2)中的最后一个<B>。返回的树被临时存储在secondB中。
如果第(7)行对B 的调用失败,secondB的值就会是FAILED。第(8)行会检测这种情况,而且当前对B 的调用也会失败。
第(10)行代表的是成功找到平衡括号串的情况。我们要返回由makeNode4构建的树。该树具有标号为‘B’的根节点以及4个孩子。第一个是标号为(的叶子节点,它是由makeNode0构造的。第二个是存储在firstB中的树,它是通过第(4)行对B 的调用产生的分析树。第三个是标号为)的叶子节点,第四个则是由第(7)行对B 的第二次调用返回的分析树,它存储在secondB中。
只有在第(5)行的测试失败时,才会使用第(11)行。第(12)行处理的是第(1)行的初始测试没能在第一个字符的位置找到(的情况。在这种情况下,假设产生式(1)是正确的。该产生式的右部为ε,因此我们没有销毁任何输入,但返回了一个由makeNode1创建的节点,其标号为B 而且有一个标号为ε 的子节点。
示例 11.9
假设在输入中有终结符串()()ENDM。这里的ENDM代表字符'\0',它是在C语言中用来标记字符串结尾的。图11-27a中main函数对B的调用确定了(是当前的输入,而且第(2)行的测试会成功。因此,nextTerminal在第(3)行会前移,而且第(4)行会进行对B的第二次调用,表示为图11-28中的“调用2”。

图 11-28 在处理输入()()ENDM时进行的调用
在调用2中,第(2)行的测试失败,因此在第(12)行会返回图11-29a所示的树。现在回到调用1,其中在第(5)行时,nextTerminal指向的是),而且图11-29a的树在firstB中。因此,第(5)行的测试会成功。我们在第(6)行前移nextTerminal,并在第(7)行调用B。这是图11-28中所示的“调用3”。
在调用3中,我们在第(2)行成功,在第(3)行前移nextTerminal,并在第(4)行调用B,该调用就是图11-28中的“调用4”。就和调用2一样,调用4也会在第(2)行的测试失败,并在第(12)行返回一棵类似图11-29a的树但有所不同。
我们现在回到了调用3,其中nextTerminal仍然指向),firstB(是此次对B的调用的局部变量)存放着一棵类似图11-29a这样的树,而且有着第(5)行的控制。这次测试会成功,而且我们会在第(6)行前移nextTerminal,所以它现在指向的是ENDM。我们在第(7)行进行对B的第五次调用。该调用在第(2)行的测试会失败,并在第(12)行返回图11-29a的另一个副本。这棵树称为对应调用3的secondB的值,并且第(8)行的测试也失败了。因此,在调用3的第(10)行,我们要构建如图11-29b所示的树。
至此,调用3在第(8)行成功地返回到调用1,这时调用1的secondB存放着图11-29b中的树。就像在调用3中那样,第(8)行的测试会失败,而且我们在第(10)行要构建一棵有着新根节点的树,其第二个孩子是图11-29a所示树的一个副本(这棵树被存放在调用1的firstB中),而且它的第四个孩子是图11-29b中的树。得到的树被main函数放置在parseTree中,它的样子如图11-29c所示。
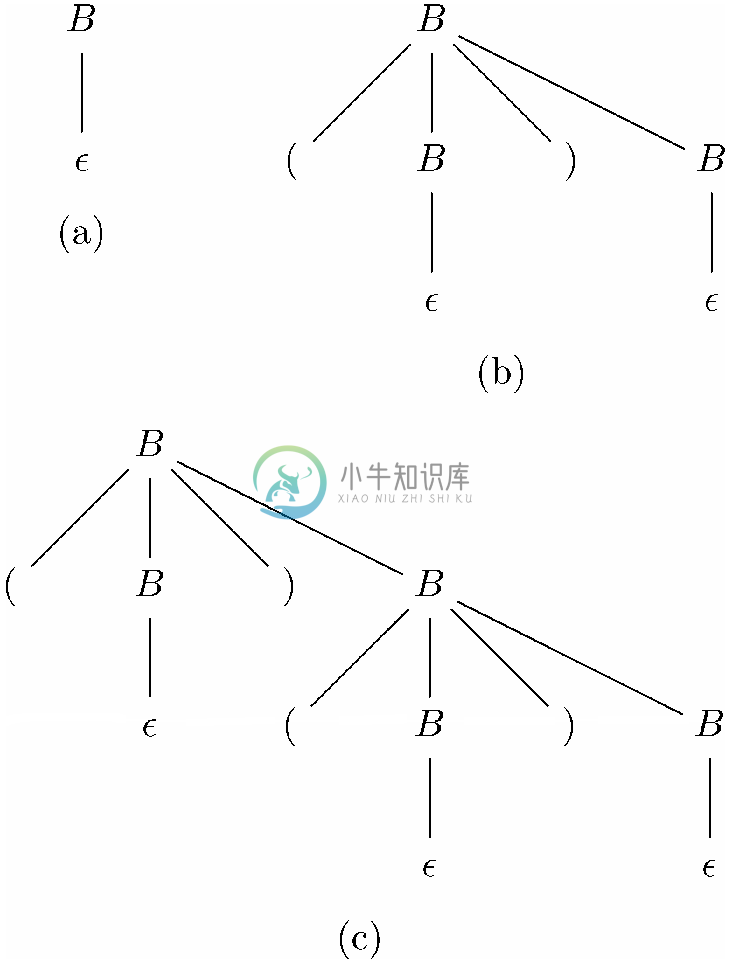
图 11-29 由对B 的递归调用构建的树
11.6.3 递归下降分析器的构建
虽然不能针对所有文法,但可以将图11-27中用到的技术扩展到适用于很多文法。关键要求是,对各语法分类<S>,如果存在不止一个以<S>为左部的产生式,那么通过查看当前唯一的终结符(通常被称为前瞻符号),就可以确定那个需要得到尝试的以<S>为左部的产生式。例如,在图11-27中,我们的决策就是,只要前瞻符号是(,就选取右部为(<B>)<B>第二个产生式,而要是前瞻符号为)或ENDM,就选定右部为ε 的第一个表达式。
一般来说,我们不可能弄清对某定义文法而言是否存在总能做出正确决定的算法。对图11-27来说,我们声明所陈述的策略是行得通的,但并未对此加以证明。不过,如果拥有自己相信行得通的决策,那么就可以按照如下方式为各语法分类<S>设计函数S。
1. 检查前瞻符号,并决定要尝试哪个产生式。假设被选中的产生式右部为X1X2…Xn。
2. 对i=1、2、…、n,为Xi 进行以下操作。
(a) 如果Xi 是终结符,检查前瞻符号是否为Xi 。如果是,则前移输入游标。如果不是,那么这次对S 的调用就失败了。
(b) 如果Xi 是语法分类,比方说是<T>,就调用对应该语法分类的函数T。如果T 以失败状态返回,就说明对S 的调用失败了。如果T 成功返回,就把返回的树存储起来以待随后使用。
如果在考虑完所有的Xi 之后都没有失败,就创建各孩子按次序分别对应X1、X2、…Xn 的新节点,以组成一棵要返回的分析树。如果Xi 是终结符,那么Xi 的孩子就是新创建的以Xi 为标号的叶子节点。如果Xi 是语法分类,那么Xi 的子节点就是在与Xi 对应的函数完成调用时返回的树的根节点。图11-29就是这种树构建过程的示例。
如果语法分类<S>表示所含字符串有待识别和分析的语言,就要在第一个输入的终结符处放置输入游标,开始分析过程。如果输入在语言L(<S>)中,对函数S 的调用就会使得对应该输入的分析树被构建起来,而如果不在的话,对S 的调用就会返回失败。
11.6.4 习题
1. 给出针对以下输入,图11-27所示的程序所执行的调用序列,其中每种情况下最后都跟着端记号ENDM符号。
(a) (())
(b) (()())
(c) ())(
2. 考虑以下表示数字的文法。
<数字>→<数码><数字> | ε
<数码>→0 | 1 | … | 9
设计对应该文法的递归下降分析器,也就是说,编写两个函数,其中一个对应<数字>,另一个对应<数码>。大家可以遵照图11-27中的格式,并假设存在makeNode1这种根节点具有指定数目子节点的树。
3. ** 假设把习题2中对应<数字>的生成式写为
<数字>→<数码><数字> | <数码>
或
<数字>→<数字><数码> | ε
是否还能够设计递归下降分析器?为什么?
(1) <L> → ( <E> <T>
(2) <T> → , <E> <T>
(3) <T> → )
(4) <E> → <L>
(5) <E> → 原子
图 11-30 对应表结构的文法
4. * 图11-30所示的文法定义了非空表,表的元素是由逗号分隔并由括号包围的。元素可以是原子或表结构体。在这里,<E>代表元素,<L>表示表,而<T>则对应“尾部”,也就是,要么是闭合的),要么是由逗号和以)结尾的元素构成的配对。为图11-30中的文法编写递归下降分析器。
11.7 表驱动分析算法
正如我们在6.7节中看到过的,递归函数调用通常是用活动记录栈实现的。因为递归下降分析器中的函数完成的工作非常具体,所以可以用一个检查表并操作栈的函数来代替这些函数。
要记得,对应语法分类<S>的函数S 首先要决定使用哪个产生式,然后经过一系列步骤,每个步骤都对应着所选产生式右部中的一个符号。因此,可以维持一个大致与活动记录栈对应的文法符号栈,而符号和语法分类都被放置在该栈中。当语法分类<S>位于栈顶时,首先要确定正确的产生式。然后用所选产生式的右部替换<S>,其中右部的左端位于栈顶。如果是终结符位于栈顶,就要确定它是否与当前输入符号匹配。如果是,我们就将其弹出栈并前移输入游标。
要从直觉上了解这种安排为何起作用,先假设递归下降分析器刚调用过对应语法分类<S>的函数S,而且选定的产生式右部为a<B><C>。那么对应S的这一活动记录会在以下4个时候处于活动状态。
1. 在检验a是否在输入中时;
2. 在进行对B 的调用时;
3. 在该调用返回而且C 被调用时;
4. 在对C 的调用返回而且S 完成调用时。
如果我们在表驱动分析器中直接用右部的符号(本例中是a<B><C>)替换<S>,那么该活动记录栈会在控制权返回对应递归下降分析器中S 的活动时的输入位置曝光这些符号。
1. 第一次曝光的是a,而且我们会检测a是否在输入中,就像函数S 所做的那样。
2. 第二次,紧接第一次之后发生,S 会调用B,而<B>会位于栈顶,这会造成相同的行为。
3. 第三次,S 调用C,不过这里是<C>在栈顶,而且完成的是相同的工作。
4. 第四次,S 返回,而且我们不会发现更多替代<S>的符号。因此,活动记录栈中此点以下的符号之前存放在<S>中,但现在被暴露在外了。类似地,在S 的活动记录以下的活动记录在递归下降分析器中会得到控制权。
11.7.1 分析表
如果不想写一系列的递归函数,也可以构建分析表(parsing table),它的每一行都对应着语法分类,每一列对应着可能的前瞻符号。在表示语法分类<S>的那一行中,对应前瞻符号X 的项是前瞻符号为X 时展开<S>必须用到的以<S>为左部的产生式的编号。
分析表中的某些项可能为空。假设需要展开的语法分类<S>,而且前瞻符号为X,但我们发现表示<S>的那行中对应X 的那一项为空,就说明分析已经失败了。这种情况下,可以确定该输入不在此语言中。
示例 11.10
图11-31表示了对应图11-25所示平衡括号串无二义文法的分析表。该分析表相当简单,因为其中只有一个语法分类。该表所表示的策略与11.6节中的示例所采用的策略是相同的。如果前瞻符号是(,那么展开时用到的是产生式(2),也就是<B>→(<B>)<B>,否则展开时就要借助产生式(1),或者说<B>→ε 。我们很快就会看到这样的分析表是如何使用的。
| ( ) |
|
|---|---|---|
<B> | 2 1 | 1 |
图 11-31 对应平衡括号串文法的分析表
示例 11.11
图11-32所示的是另一个分析表,它对应着图11-33所示的文法,该文法是图11-6所示语句文法的一个变种。
| w | c | { | } | s | ; |
|
|---|---|---|---|---|---|---|---|
<S> | 1 |
| 2 |
| 3 |
|
|
<T> | 4 |
| 4 | 5 | 4 |
|
|
图 11-32 对应图11-33所示文法的分析表
图11-33中的文法之所以具有这种形式,是为了可以用递归下降(或者等价地,用这里描述的表驱动分析算法)进行分析。要知道为什么这种形式是必要的,首先考虑一下图11-6所示文法中对应<L>的产生式。
<L>→<L><S>|ε
如果当前的输入是开始语句的s这样的终结符,那么可知<L>一定至少由右部为<L><S>第一个生成式展开一次。不过,如果不检查接下来的输入并弄清语句列中共有多少条语句,就没法确定要进行多少次展开。
(1) <S> → w c<S>
(2) <S> → { <T>
(3) <S> → s ;
(4) <T> → <S><T>
(5) <T> → }
图 11-33 可进行递归下降分析的、表示简单语句的文法
我们在图11-33中用到的方法是,记住程序块是由左花括号后面跟上0条或更多语句以及右花括号组成的。我们把这0条或更多语句以及右花括号称为“尾部”(tail),并用语法分类<T>表示它。图11-33中的产生式(2)说明,语句可以由左花括号后面加上尾部构成。产生式(4)和产生式(5)则表示尾部要么是语句后面跟上尾部,要么直接就是个右花括号。
决定用产生式(4)还是产生式(5)展开<T>是件非常简单的事。只有在右花括号是当前输入时,产生式(5)才行得通,而产生式(4)只在当前输入可以开始语句时才有效。在我们的简单文法中,开始语句的终结符只有w、{和s。因此,在图11-32中可以看到,在对应语法分类<T>的那行中,为这3个前瞻符号选择了产生式(4),而为前瞻符号}选择了产生式(5)。对其他的前瞻符号而言,我们不可能用它们作为尾部的开头,所以就要在对应<T>的那行中把对应其他前瞻符号的位置留空。
同样,语法分类<S>的决定也很简单。如果前瞻符号为w,那么只有产生式(1)能起作用。如果前瞻符号为{,产生式(2)就是唯一可行的选择。而对前瞻符号s来说,只有产生式(3)是可行的。对其他前瞻符号来说,相应的输入是没法形成语句的。这些结论解释了图11-32中对应<S>的那一行。
11.7.2 表驱动分析器的工作原理
所有的分析表都可以被实质上的同一程序用作数据。这一驱动器程序具有同时存放着终结符和文法分类的文法符号栈。该栈可以被视作剩下的输入必须满足的目标,这些目标一定是按照从栈顶到栈底的次序得到满足的。
1. 通过确定某终结符是输入的前瞻符号,可以满足终结符的目标。也就是说,只要终结符x在栈顶位置,就要检查前瞻符号是否为x,如果是,就从栈中弹出x,并读取要成为新前瞻符号的下一个输入终结符。
2. 通过查询分析表中行对应<S>且列对应前瞻符号的项,可以满足语法分类目标<S>。
(a) 如果相应的项为空,那么就不能为该输入得出分析树,这样驱动器程序就失败了。
(b) 如果相应的项含有产生式i,就要把<S>从栈顶位置弹出,并把产生式i 右部中的各个符号压入栈中。右部中的符号是按照从右至左的顺序被压入栈的,这样一来,右部的第一个符号最终就会处在栈顶的位置,而第二个符号就紧邻其下,以此类推。作为特例,如果右部为ε,就只要把<S>从栈中弹出即可。
假设想确定字符串s是否在L(<S>)中。在这种情况下,要用输入中的s ENDM字符串3启动驱动器,并读取第一个终结符作为前瞻符号。活动记录栈一开始只由语法分类<S>组成。
3有时候端记号ENDM符号也是必要的,它可以作为告知我们已经到达输入末端的前瞻符号,其他时候它只是用来捕捉错误。例如,在图11-31中ENDM是必要的,因为我们在平衡括号串之后总有更多的括号,但在图11-32中它不是必要的,对应ENDM的那列中没有任何项就证明了一切。
示例 11.12
我们对输入{w c s ; s ; }ENDM使用图11-32中的分析表。图11-34展示了表驱动分析器所执行的处理步骤。表中所示栈的内容是按照栈顶内容位于最左侧的方式排列的,这样一来,当我们把栈顶位置的语法分类替换为它某一产生式的右部时,该右部就会出现在栈顶的位置,其中的符号都是按照正常次序排列。
| 栈 | 前瞻符号 | 剩余输入 |
|---|---|---|---|
1) | <S> | { |
|
2) | {<T> | { |
|
3) | <T> | w |
|
4) | <S><T> | w |
|
5) | wc<S><T> | w |
|
6) | c<S><T> | c |
|
7) | <S><T> | s |
|
8) | s;<T> | s |
|
9) | ;<T> | ; |
|
10) | <T> | s |
|
11) | <S><T> | s |
|
12) | s;<T> | s |
|
13) | ;<T> | ; |
|
14) | <T> | } |
|
15) | } | } |
|
16) | ε | ENDM | ε |
图 11-34 使用图11-32所示表格的表驱动分析器的处理步骤
图11-34中的第(1)行展示了初始情况。因为要测试字符串{wcs;s;}是否属于语法分类<S>,所以一开始活动记录栈中只存放着<S>。给定字符串的第一个符号{是前瞻符号,而且字符串的其余部分跟上ENDM就构成了剩下的输入。
如果查看图11-32中对应语法分类<S>和前瞻符号{的项,就知道必须按照产生式(2)展开<S>。该产生式的右部是{<T>,而且在我们到达第(2)行时,可以看到这两个文法符号已经替换了栈顶的<S>。
现在栈顶位置是终结符{。因此要将其与前瞻符号加以比较。因为栈顶和前瞻符号相符,所以我们要弹出栈顶内容,并将输入游标前移到下一个输入符号w,这样它就成了新的前瞻符号。这些改变反映在第(3)行中。
接下来,<T>位于栈顶而且w是前瞻符号,查阅图11-32可知恰当的行动是用产生式(4)展开。因此将<T>从栈中弹出,并压入<S><T>,如第(4)行中所见。同样,现在处于栈顶的<S>会被产生式(1)的右部替代,因为这是由图11-32中对应<s>的行与对应前瞻符号w的列决定的,这一改变反映在第(5)行中。在第(5)行和第(6)行之后,栈顶的终结符会与当前的前瞻符号相比较,因为每一对都能匹配,所以它们被弹出,而且输入游标前移。
这里要遵照第(7)到第(16)行,核实每一步都是根据分析表可以采取的合适行为。因为在各终结符到达栈顶时会与当时的当前前瞻符号匹配,所以我们不会失败。因此,字符串{wcs;s;}在语法分类<S>中,也就是说,它是语句。
11.7.3 分析树的构建
上面描述的算法可以分辨给定字符串是否在给定语法分类中,不过它并不会生成分析树。不过,对该算法进行简单的修改,它就能在输入字符串在初始化活动记录栈所用的语法分类中时给出相应的分析树。11.6节中描述过的递归下降分析器是从下向上构建分析树的,也就是说,从叶子节点开始,并在函数调用返回时逐渐将其组合成更大的子树。
而对表驱动分析器来说,自上而下地构建分析树要更方便。也就是说,我们从根节点开始,并且随着我们不断选择用来展开栈顶位置语法分类的产生式,就同时为构建中的分析树的节点创建了子节点,这些子节点对应着所选产生式右部中的符号。构建分析树的规则如下所述。
1. 一开始,活动记录栈中只含有某个语法分类,比方说是<S>。我们将分析树初始化为只含一个标号为<S>的节点。栈中的<S>对应着正在构建的分析树中的一个节点。
2. 一般情况下,如果活动记录栈含有符号X1X2…Xn,而且X1在栈顶,那么当前分析树的叶子节点标号从左到右排列可以组合成以X1X2…Xn 为后缀的字符串s。分析树的后n个叶子节点对应着栈中的符号,所以每个栈符号Xi 都与标号为Xi 的叶子节点对应。
3. 假设语法分类<S>位于栈顶,而且选择用产生式<S>→Y1Y2…Yn 的右部替代<S>。我们会找到分析树中对应这一<S>的叶子节点(它是以语法分类为标号的最左子节点),并给它n 个从左至右标号分别为Y1、Y2、…、Yn 的子节点。而在右部为ε 的特例中,我们会创建一个标号为ε 的子节点。
示例 11.13
我们按照图11-34中的步骤进行处理,并在这一过程中构建分析树。首先,在第(1)行,活动记录栈只由<S>组成,而且对应的树是如图11-35a所示的单个节点。在第(2)行要用产生式<S>→{<T>展开<S>,因此就为图11-35a中的叶子节点赋予了两个子节点,从左至右分别以{和<T>为标号。对应第(2)行的树如图11-35b所示。
图 11-35 构建分析树的前几步
第(3)行不会对分析树带来改变,因为我们匹配的是终结符,不会展开语法分类。不过在第(4)行要将<T>展开为<S><T>,所以要为图11-35b中标号为<T>的叶子节点添加两个以这些符号为标号的子节点,如图11-35c所示。然后在第(5)行<S>被展开为wc<S>,这会让图11-35c中标号为<S>的叶子节点得到3个子节点。大家可以自行继续这一过程。最终的分析树如图11-36所示。
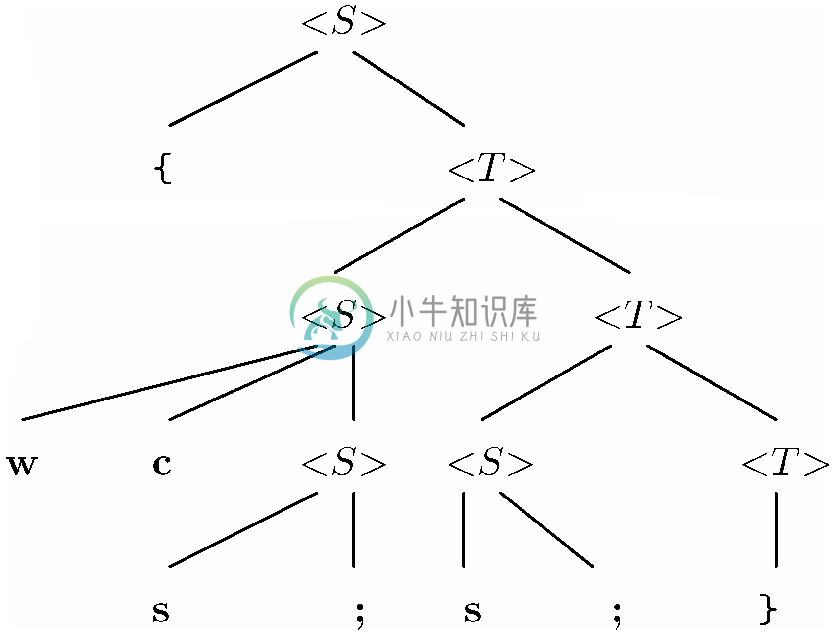
图 11-36 对应图11-34中分析过程的完整分析树
11.7.4 让文法变得可分析
正如我们已经看到的,很多文法需要进行一些修改才能用我们在11.6和11.7这两节中了解的递归下降或表驱动方法进行分析。尽管无法保证任何文法都能修改为可用这两种方法分析,但有一些值得了解的小窍门,它们可以让这种使文法变得可分析的修改工作变得更高效。
第一个窍门是消除左递归。我们已经在示例11.11中指出过,产生式<L>→<L><S>|ε 是不能用这些方法分析的,因为没办法弄清应用第一个产生式的次数。一般来说,只要对应某语法分类<X>的产生式的右部以<X>自身开头,我们就不清楚为了展开<X>要应用该产生式多少次。这种情况就叫作左递归。不过,通常可以重新排列有问题产生式的右部中的符号,使得<X>排在靠后的位置。这一步骤就叫作左递归的消除。
示例 11.14
在之前讨论过的示例11.11中,我们看到<L>表示0个或更多<S>。因此可以通过调换<S>和<L>的位置消除左递归,这样一来就有
<L>→<S><L>|ε
再举个例子,考虑一下表示数字的产生式:
<数字>→<数字><数码>|<数码>
给定数码作为前瞻符号,就不知道要展开<数字>需要使用第一个产生式多少次。不过,我们看到数字是一个或多个数码,这样就可以重新排列第一个产生式的右部,得到
<数字>→<数码><数字>|<数码>
这一对产生式就消除了左递归。
不过,示例11.14中的产生式还是不能用我们提过的方法分析。要让它们变得可分析,就需要用到第二个窍门——提取左因子(leftfactoring)。当对应语法分类<X>的两个产生式具有以相同符号C 开头的右部时,只要前瞻符号是来自共有符号C 的,我们就没法弄清该使用哪个产生式。
要为这些产生式提取左因子,就要创建表示这些产生式“尾部”,即表示右部中C 之后的部分的语法分类<T>。然后把这两个对应<X>的产生式替换为<X>→C<T>和两个以<T>为左部的两个产生式。这两个产生式的右部是之前所说的“尾部”,也就是对应<X>的两个产生式中C 之后的内容。
示例 11.15
考虑一下示例11.14中设计的对应<数字>的产生式:
<数字>→<数码><数字>|<数码>
这两个产生式是以相同符号<数码>开始的。因此,当前瞻符号为数码时,我们没法分辨要使用哪个产生式。不过,如果提取左因子,得到
<数字>→<数码><尾部>
<尾部>→<数字>|ε
就可以服从这些决定了。在这里,对应<尾部>的这两个产生式让我们选择对应<数字>的第一个产生式的尾部,也就是<数字>本身,或者第二个对应<数字>的产生式的尾部,即ε。
现在,当必须扩展<数字>,并以数码作为前瞻符号时,就会用<数码><尾部>替换<数字>,匹配该数码,然后可以根据数码后面跟着的内容选择如何展开尾部。也就是说,如果后面跟着另一个数码,那么就用<尾部>的第一个选择展开,而如果后面跟着的内容不是数码,则可知已经看到整个数字,并用ε 来替换<尾部>。
11.7.5 习题
1. 为下列输入字符串模拟使用图11-32所示分析表的表驱动分析器。
(a) {s;}
(b) wc{s;s;}
(c) {{s;s;}s;}
(d) {s;s}
2. 对习题1中取得成功的那些分析,给出分析过程中构建分析树的过程。
3. 利用图11-31中的分析表,对11.6节习题1中的输入串模拟表驱动分析器。
4. 给出习题3的分析过程中分析树的构建情况。
5. * 如下文法
(a) <语句> → if(条件)
(b) <语句> → if(条件)<语句>
(c) <语句> → 简单语句
表示C语言中的选择语句。它是没法用递归下降分析器和表驱动分析器进行分析的,因为如果有前瞻符号if,就没办法确定要使用前两个产生式中的哪一个。为该文法提取左因子,使它可以用11.6节和本节介绍的算法分析。提示:在提取左因子时,就得到了具有两个产生式的新语法分类。一个的右部为ε,而另一个的右部则以else开头。显然,当else作为前瞻符号时,要选择第二个产生式。其他前瞻符号都不能让我们选择这一产生式。不过,如果看看有哪些前瞻符号让我们用右部为ε的产生式展开,就会发现这些前瞻符号中也有else。不过,也可以强行规定,在前瞻符号为else时决不展开为ε。该选择对应着“else匹配之前未匹配的then”这一规则,因此这是“正确的”选择。你可能想找到一个在前瞻符号为else且展开为ε时还能让分析器完成分析的例子。不过你会发现,在任意一次这样的分析中,构建的分析树总会为else匹配“错误的”then。
6. ** 如下文法
<结构体>→struct{<字段列>
<字段列>→类型 字段名;<字段列>
<字段列>→ε
需要一些修改才可以用本节和11.6节介绍的方法进行分析。重写该文法,使其可由递归下降和表驱动的方法分析,并构建相应的分析表。
11.8 文法与正则表达式
文法和正则表达式都是用于描述语言的表示法。我们在第10章中已经看到,正则表达式表示法与确定自动机和非确定自动机表示法是等价的,因为可由这3种表示法描述的语言集合是相同的。文法是否有可能是另一种与我们已经见过的这些表示法都等价的表示法?
答案是“不可能”,因为文法要比我们在第10章中介绍的正则表达式之类的表示法更强大。这里要分两步展现文法的表现力。首先,我们将证实每种能用正则表达式描述的语言也都能用文法来描述。接着我们会给出一种可以由文法描述,但不能用正则表达式描述的语言。
11.8.1 用文法模拟正则表达式
这种模拟背后的直觉思路就是,正则表达式中的3种运算符(取并、串接和闭包)分别可以用一个或两个产生式“模拟”。正式地讲,可以通过对正则表达式R 中出现的运算符的数量n 进行完全归纳,证明如下命题。
命题。对每个正则表达式R 来说,都存在某一文法,满足对文法中的语法分类<S>而言,有L(<S>)=L<R>
也就是说,由正则表达式表示的语言也是语法分类<S>的语言。
依据。依据情况是n=0,也就是正则表达式R 中未出现运算符的情况。R 要么是单个符号,比方说x,要么是ε 或∅。我们创建一个新的语法分类<S>。在R=x的第一种情况下,还要创建产生式<S>→x。因此,L(<S>)={x},而且L<R>也是相同的单字符串语言。如果R是ε,同样可以为<S>创建产生式<S>→ε,而如果R=∅,则根本不用为<S>创建产生式。这样当R 为ε 时,L(<S>)是{ε };而当R 是∅时,L(<S>)是∅。
归纳。假定归纳假设对具有不超过n 个运算符的正则表达式成立。设R 是其中出现n+1个运算符的正则表达式。总共有3种情况,具体取决于构建R 所应用的最后一个运算符是取并、串接还是闭包。
1. R=R1|R2。因为这里有一个运算符(即取并运算符|)既不属于R1也不属于R2,所以可知R1和R2中运算符的个数都不可能超过n。因此,归纳假设适用于R1和R2,而且我们可以找到具有语法分类<S1>的文法G1,以及具有语法分类<S2>的文法G2,分别满足L(<S1>)=L(R1)和L(<S2>)=L(R2)。为了避免出现两个文法相互融合的巧合出现,我们可以假设,在构造新文法的过程中,所创建的语法分类的名称一直都不会在另一个文法中出现。这样一来,G1和G2中就不会有相同的语法分类。创建一个新的语法分类<S>,它既未出现在G1和G2中,也没有出现在为其他正则表达式构建的其他文法中。除了对应G1和G2的两个产生式外,我们还要添加两个产生式
<S>→<S1>|<S2>
那么<S>的语言只由<S1>和<S2>的语言中所有的字符串组成。这两个语言分别是L(R1)和L(R2),所以有
L(<S>)=L(R1)∪L(R2)=L(R)
这正是我们想要的结果。
2. R=R1R2。就像情况(1)那样,假设存在文法G1和G2,它们分别具有语法分类<S1>和<S2>,满足L(<S1>)=L(R1)和L(<S2>)=L(R2)。然后创建新的语法分类<S>,并在G1和G2产生式的基础之上添加产生式
<S>→<S1><S2>
然后就有L(<S>)=L(<S1>)L(<S2>)。
3. R=R1*。设G1是具有语法分类<S1>的文法,满足L(<S1>)=L(R1)。创建新语法分类<S>,并添加两个产生式
<S>→<S1><S>|ε
因为<S>可生成由0个或更多<S1>构成的串,所以有L(<S>)=(L(<S1>))*。
示例 11.16
考虑正则表达式a|bc*。首先要为该表达式中的3个符号创建语法分类。4因此,就得到产生式
4如果这些符号出现两次或多次,并不需要为符号的每次出现创建新的语法分类,只需要为每种符号创建一个语法分类就足够了。
<A>→a
<B>→b
<C>→c
根据正则表达式的组合规则,我们的表达式会被分组为a|(b(c)*)。因此,首先要创建对应c*的文法。根据之前所述的规则(3),我们要在产生式<C>→c(就是对应正则表达式c的文法)的基础之上添加产生式
<D>→<C><D>|ε
这里的语法分类<D>是随意选择的,可以是除了已经被使用过的<A>、<B>和<C>之外的任何语法分类。要注意到
L(<D>)=(L(<C>))*=c *
现在我们需要对应bc*的文法。可以取只由产生式<B>→b组成的对应b的文法,以及对应c*的文法,即
<C>→c
<D>→<C><D>|ε
我们要创建新的语法分类<E>,并添加产生式
<E>→<B><D>
之所以使用该产生式,是因为之前提到的对应串接情况的规则(2)。它的右部包含<B>和<D>,因为它们分别是对应正则表达式b和c*的语法分类。因此对应bc*的文法是
<E>→<B><D>
<D>→|ε
<B>→b
<C>→c
而且语法分类<E>的语言就是所需的。
最后,要得到对应整个正则表达式的文法,就要用到对应取并运算的规则(1)。这要引入新的语法分类<F>,以及产生式
<F>→<A>|<E>
请注意,语法分类<A>对应子表达式a,而<E>则对应子表达式bc*。得到的文法就是
<F>→<A>|<E>
<E>→<B><D>
<D>→<C><D>|ε
<A>→a
<B>→b
<C>→C
而语法分类<F>的语言就是给定正则表达式所表示的语言。
11.8.2 有文法但没有正则表达式的语言
现在要证实文法并非只有正则表达式那么强大。我们要通过展示一种只有文法但没有正则表达式的语言来做到这一点。我们将这一语言称为E,它是由一个或更多0后面跟上相等数量的1组成的字符串的集合。也就是说
E={01,0011,000111,...}
要描述E 中的字符串,有一种基于指数的实用表示方法。设sn(其中s 是字符串而n 是整数)代表ss…s(n 个s),也就是说,s 与它自身串接n 次。那么
E={0111,0212,0313,...}
或者使用集合形成法表示就是
E={0n 1n|n≥1}
首先,我们要相信可以用文法描述E。以下文法就可以完成这一工作。
(1) <S>→0<S>1
(2) <S>→01
大家可以使用依据产生式(2)说明01在L(<S>)中。在第二轮中,我们可以使用产生式(1),用01替换右部中的<S>,这样就为L(<S>)得到了0212。再一次应用产生式(1),用0212替换右部中的<S>,就说明0313也在L(<S>)中,等等。一般来说,0n1n要求使用产生式(2)一次,并随后使用产生式(1)n-1次。因为我们用这两个产生式不能产生别的字符串,所以可知E=L(<S>)。
11.8.3 证明E不能用任何正则表达式定义
现在要证明E 不能用正则表达式描述。这里证明E 不能用任何确定有限自动机描述要更容易些。这一证明过程也能证明E 没有正则表达式,因为如果E 是正则表达式R 的语言,我们就可以利用10.8节中的技巧将R 转换成等价的确定有限自动机。该确定有限自动机就定义了语言E。
因此,假设E 是某确定有限自动机A 的语言。那么A 就会有若干数量的状态,比方说是m 个状态。考虑一下当A 接收输入000…时会发生什么。我们这里把该未知自动机A 的初始状态叫作S0。A 一定有针对输入0的、从状态S0到某个我们称之为S1的状态的转换。从该状态出发,另一个0可以把A 带到称为S2的状态,等等。一般地说,在读入i 个0后就处在状态S0中,如图11-37所示。5
5大家应该记住,我们其实并不知道A 的状态的名称,而是只知道A 具有m 个状态(其中m 为某整数)。因此,s0、…、sm并不是A中状态的真正名称,而只是我们为了方便称呼而为这些状态赋予的名称。这并不像看起来这么奇怪。打个比方,我们一般会创建数组s,用0到m 作为索引,并在s[i ]中存储某值,该值可以是自动机A 的状态名称。然后可以在程序中用s[i ]代指该状态,而不是用它本身的名称。
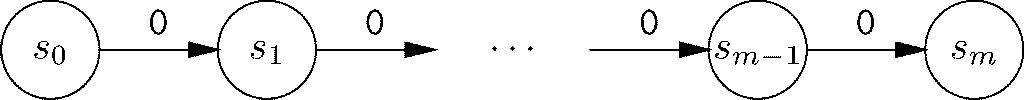
图 11-37 为自动机A 输送0
鸽巢原理
证明语言E 没有确定有限自动机的过程要用到称作鸽巢原理(pigeonhole principle)的技巧,我们通常将该原理陈述为:
“如果m+1只鸽子飞进m 个鸽巢,那么至少有一个巢中有两只鸽子。”
在这种情况下,鸽巢就相当于自动机A 的状态,而鸽子就是A 在看到0个、1个、2个直至m 个0后所处的m 个状态。
请注意,为了应用鸽巢原理,这里的m 必须是有限的。7.11节中讲过的无限酒店的故事告诉我们,对立的命题对无限集来说是可以成立的。在那个例子中,我们看到一家有着无数个房间(对应鸽巢)的酒店,以及数量比房间数多1的客人(对应鸽子),不过还是有可能为每个客人分配一个房间,而不用把两个客人安排到同一房间中。
现在假设A 刚好有m 个状态,而且s0、s1、…、sm总共有m+1个状态。因此不可能让这些状态全都不同。在0到m 的范围中,肯定存在两个不同的整数i 和 j,使得si 和sj 其实为相同状态。如果假设i是i和j之间的较小者,那么图11-37的路径之中一定至少存在一条环路,如图11-38所示。在实际应用中,可能存在比图11-38中更多的环路和状态重复。还要注意,i 可以是0,在这种情况下,图11-38所示的从s0到si 的路径起始就是一个节点。同样,sj 可以是sm,这种情况下从sj 到sm 的路径就只是个节点。
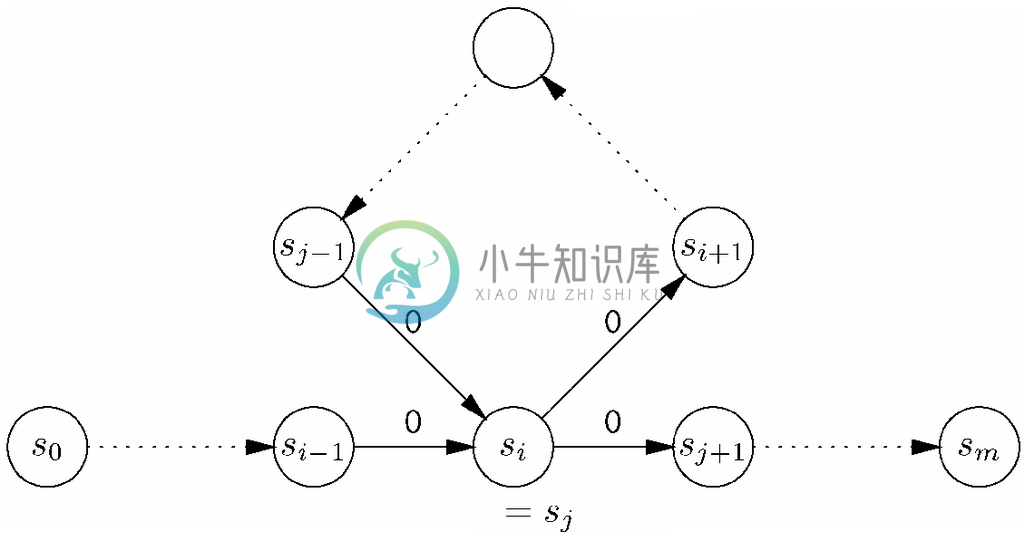
图 11-38 图11-37中的路径一定含有环路
图11-38暗示了自动机A 不能“记住”自己已经看到过多少个0。如果处在状态sm中,它可能已经刚好看到了m 个0,这样的话,如果我们从状态m 开始,并为A 提供刚好m 个1,那么A 一定会到达接受状态,如图11-39所示。
不过,假设我们为A 提供了一个有m+j-i 个0的串。看看图11-38,就会发现i 个0可以将A 从s0带到与sj 相同的si 。我们还会看到m-j 个0会把A 从状态sj 带到sm。因此,m-j+i 个0就可以把A 从状态s0带到sm,如图11-39中靠上方的路径那样。
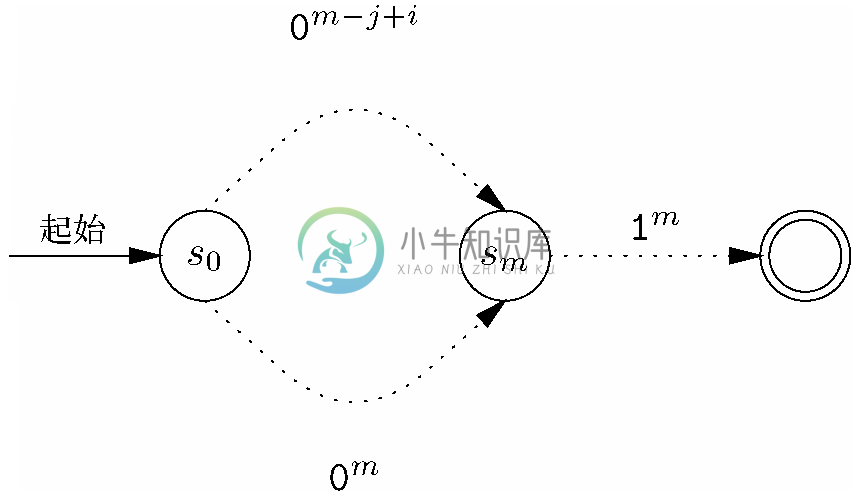
图 11-39 自动机A 不能区分它到底是看到了m 个0还是m-j+1个0
因此,m-j+i 个0后面跟上m 个1也可以把A 从s0带到接受状态。换句话说,字符串0m-j+i1m 也在A 的语言中。但因为 j 比i 大,所以该串中的1要比0多,这样就不在语言E 中。因此可得出A 的语言并不是E 的结论,正如我们所假设的那样。
因为一开始只假设了E 具有确定有限自动机,而且最终推出了矛盾,所以可推断出假设不成立,也就是说,E 没有确定有限自动机。因此,E 也没有正则表达式。
语言{0n 1n|n≥1}只是无数种可由文法指定但不能用正则表达式表示的语言中的一个例子。本节习题中还会给出另外一些例子。
11.8.4 习题
1. 给出定义以下正则表达式语言的文法。
(a) (a|b)*a
(b) a*|b*|(ab)*
(c) a*b*c*
文法不能定义的语言
有人可能会问文法是否为描述语言的最强大表示法,答案是:“绝不可能!”我们可以证明一些简单语言并不具有文法,尽管证明技巧并不在本书要介绍的范围之内。这种的语言的一个例子就是由相同数量的0、1和2按次序构成的串形成的集合,也就是
{012, 001122, 000111222, …}要举一个更强大的语言描述方法的例子,可以考虑一下C语言本身。对任意文法,以及它的任一语法分类<S>来说,都可以写出C语言程序以确定字符串是否在L(<S>)中。此外,确定字符串是否在上述语言中的C语言程序也不难编写。
但还是有C语言程序不能定义的语言。“不可判定问题”这一高雅理论就可用来证明某些问题是不能用任何计算机程序解决的。我们将在14.10节中简要讨论不可判定性以及一些不可判定问题的例子。
2. * 证明平衡括号串集合不能由任何正则表达式定义。提示:这一证明过程与上述针对语言E 的证明过程类似。假设平衡括号串集合具有含m 个状态的确定有限自动机。为该自动机提供m 个(,然后检查它进入的状态。证明该自动机可能被“愚弄”去接受某个不平衡的括号串。
3. * 证明由形如0n 10n 的字符串(也就是两列等长的0由一个1分开)组成的语言是不可以用正则表达式定义的。
4. * 大家有时候可能会看到一些谬误的断言,声称像本节中E 这样的语言可以用正则表达式描述。推理过程是,对各个n 而言,0n 1n 就是定义只含0n 1n 这一个字符串的语言的正则表达式。因此下列正则表达式就是描述E 的。
01 | 0212 | 0313 | …
这一论证过程错在何处?
5. * 另一个和语言有关的谬误论证声称E 具有以下有限自动机。该自动机具有一个状态a,它既是起始状态又是接受状态。存在从a 到它自身的针对符号0和1的转换。那么显然字符串0i 1i 能把自动机从状态a 带到状态a,这样该字符串就被接受了。为什么这一论证过程没有证明E 是某有限自动机的语言?
6. ** 证明下列语言不能用正则表达式定义。
(a) {ww R|w 是由a 和b 组成的字符串,w R 是与w 排列次序相反的字符串}
(b) {0i |i 是完全平方数}
(c) {0i |i 是质数}
其中哪些语言可以用文法定义?
11.9 小结
在阅读过本章之后,大家应该注意以下要点。
(上下文无关)文法如何定义语言。
如何构建可以表示字符串文法结构的分析树。
二义文法有何歧义,为什么编程语言的规范中不需要二义文法。
可用来为某些类型的文法构建分析树的递归下降分析技术。
用于实现递归下降分析器的表驱动方式。
为什么文法与正则表达式或有限自动机相比是更强大的描述语言的表示法。
11.10 参考文献
上下文无关文法首先是由Chomsky [1956] 作为描述自然语言的范式研究的。同样的范式也被用来定义两种最早的重要编程语言的语法,这两种语言分别是Fortran (Backus et al. [1957]) 和Algol 60 (Naur [1963])。因此,上下文无关文法通常也称为巴科斯范式 (Backus-Naur Form, BNF)。Bar-Hillel, Perles and Shamir [1961]首先通过上下文无关文法的数学属性对其进行了研究。对上下文无关文法及其应用更为深入的研究见Hopcroft and Ullman [1979]或Aho, Sethi and Ullman [1986]。
递归下降分析器已经用于很多编译器和编译器编写系统中(见Lewis, Rosenkrantz and Stearns [1974])。Knuth [1965]首先确定了LR文法,这是可以按照从左到右扫描输入的方式被确 定分析的文法的最大自然分类。
Aho, A. V., R. Sethi, and J. D. Ullman [1986]. Compiler Design: Principles, Techniques, and Tools, Addison-Wesley, Reading, Mass.
Backus, J. W. [1957]. “The FORTRAN automatic coding system,” Proc. AFIPS Western Joint Computer Conference, pp. 188–198, Spartan Books, Baltimore.
Bar-Hillel, Y., M. Perles and E. Shamir [1961]. “On formal properties of simple phrase structure grammars,” Z. Phonetik, Sprachwissenschaft und Kommunikationsforschung 14, pp. 143–172.
Chomsky, N. [1956]. “Three models for the description of language,” IRE Trans. Information Theory IT-2:3, pp. 113–124.
Hopcroft, J. E. and J. D. Ullman [1979]. Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, Reading, Mass.
Knuth, D. E. [1965]. “On the translation of languages from left to right,” Information and Control 8:6, pp. 607–639.
Lewis, P. M., D. J. Rosenkrantz, and R. E. Stearns [1974]. “Attributed translations,” J. Computer and System Sciences 9:3, pp. 279–307.
Naur, P. (ed.) [1963]. “Revised report on the algorithmic language Algol 60,” Comm. ACM 6:1, pp. 1–17.