第 5 章　树

优质

小牛编辑

114浏览

2023-12-01

在很多情况下，信息会具有家谱或组织图中那样的分层结构或嵌套结构。为分层结构建模的抽象被称为树，而且这种数据结构是计算机科学领域中最为基础的内容之一。它是包括Lisp在内的数种程序设计语言的底层模型。

本书很多章节中介绍了不同类型的树。例如，在1.3节中，我们看到一些计算机系统中的目录和文件是如何被组织成树形结构的。2.8节中，我们利用树展示了如何递归地分割表，并在归并排序算法中将其重组。3.7节中，我们用树说明了程序中的简单语句是如何一步步组合成更为复杂的语句的。

5.1　本章主要内容

本章讨论的主要内容如下。

与树相关的术语和概念（5.2节）。
用于在程序中表示树的基础数据结构（5.3节）。
对树中节点进行操作的递归算法（5.4节）。
结构归纳法——对树进行归纳证明的方法，在这种归纳中要用小树逐渐构建成更大的树（5.5节）。
二叉树，树的一种变种，每个节点都只有两个子树（5.6节）。
二叉查找树，维护一组要进行插入和删除操作的元素的数据结构（5.7节和5.8节）。
优先级队列是一个可以向其中添加元素的集合，不过每次只能从中删除最大的元素。偏序树（partially ordered tree）是为了实现优先级队列而引入的一种高效数据结构，而利用被称为“堆”的平衡偏序树数据结构得到的堆排序算法，在为n个元素排序时所花的时间为O(n logn)。

5.2　基本术语

树是被称为节点的点与被称为边的线的集合。一条边连接着两个不同的节点，要形成树，这一系列的节点和边必须满足某些属性，图5-1就是树的示例。

{%}

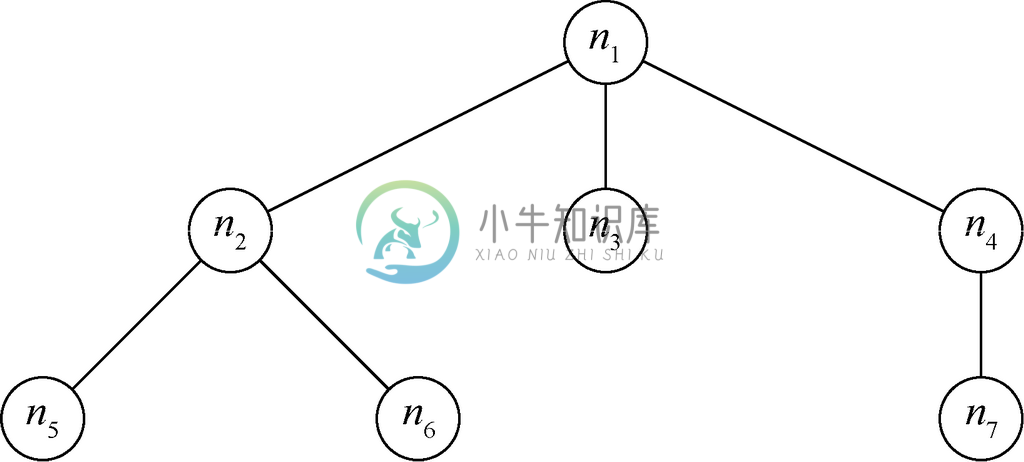
图 5-1　有7个节点的树

1. 在树中，有一个节点是与众不同的，它被称为根。树的根通常画在其顶端。在图5-1中，根为n₁。

2. 除根之外的每个节点c 都由一条边连接到某个称为c 的父节点的节点p。我们也将节点c 称为p 的子节点。节点的父节点要画在该节点的上方。例如，在图5-1中，n₁就是n₂、n₃和n₄的父节点，而n₂是n₅和n₆的父节点。换个角度讲，n₂、n₃和n₄都是n₁的子节点，而n₅和n₆是n₂的子节点。

3. 如果从除根之外的任一节点n 开始，移动到n 的父节点，再到n的父节点的父节点，以此类推，最终到达树的根节点，就说树是连通的。例如，从n₇ 开始，移动到它的父节点n₄，然后移动到n₄的父节点，也就是根节点n₁。

5.2.1　树的等价递归定义

利用由较小树构成较大树的归纳定义，还可以递归地定义树。

依据。单个节点n 就是一棵树，我们说n 就是这棵单节点树的根。

归纳。设r 是一个新节点，并设T₁、T₂、…、T_k 分别是根为c₁、c₂、…、c_k 的树。这里要求任何节点在T_i 中的出现次数都不会超过一次，而且r 是个“新”节点，一定不会在这些树中出现。可以按照以下规则用r 和T₁、T₂、…、T_k 组成新的树T。

(a) 用r 作为树T 的根。

(b) 从r 添加连接到c₁、c₂、…、c_k 的边，使得这些节点都成为根节点r 的子节点。还可以将本步骤视为让r 成为T₁、T₂、…、T_k 些树的根节点的父节点。

示例 5.1

我们可以使用这一递归定义构建图5-1中的树，而这一构建过程也验证了图5-1中的结构为树。根据依据规则，单个节点可被视为树，所以节点n₅和n₆本身都是树。接着，可以利用归纳规则创建新树，其中n₂作为根节点r，而节点n₅就是树T₁，节点n₆则是树T₂，它们是r 这一新根节点的子节点。节点c₁和c₂分别是n₅和n₆，因为它们就是树T₁和T₂的根。这样一来，我们就得出如下结构

是树的结论，而且它的根是n₂。

同样，根据依据n₇就是一棵树，而且根据归纳规则，如下结构

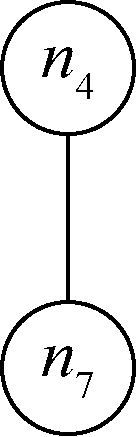
是一棵树，其中n₄是它的根。

节点n₃本身也是一棵树。最后，如果将节点n₁作为r，并将n₂、n₃和n₄视作刚提到的3棵树的根，就能创建出图5-1中的结构，并验证它确实是棵树。

5.2.2　路径、祖先和子孙

这种父子关系可以自然而然地扩展为祖先和子孙的关系。粗略地讲，节点的祖先就是从节点到其父节点，再到其父节点的父节点，以此类推，顺着这样一条唯一路径找到的那些节点。严格地讲，节点本身也是其自身的祖先节点。而子孙关系则是祖先关系的反向关系，像父子关系这样就是互为反向关系。也就是说，当且仅当节点a 为节点d 的祖先节点时，节点d 才是节点a 的子孙节点。

更严谨地讲，假设m₁、m₂、…、m_k 是树中的一系列节点，其中m₁是m₂的父节点，m₂是m₃的父节点，以此类推，直到m_k-1是m_k 的父节点。那么m₁、m₂、…、m_k 就是该树中从m₁到m_k 的一条路径。路径的长度为k-1，比路径上的节点数小1。请注意，路径可能是由单个节点构成的，这种情况下路径的长度就为0。

示例 5.2

在图5-1中，n₁、n₂、n₆是从根节点n₁到节点n₆的一条长度为2的路径，n₁是从n₁到它自己的一条长度为0的路径。

如果m₁、m₂、…、m_k是树中的一条路径，节点m₁就是m_k 的祖先，而节点m_k 则是m₁的子孙。如果该路径的长度不小于1，那么m₁就是m_k 的真祖先，而m_k 则是m₁的真子孙。还要记住，路径长度可能为0，在这种情况下，我们就可以得出m₁是其自身的祖先也是其自身的子孙这一结论，虽然它不是自己的真祖先或真子孙。树的根节点是树中每个节点的祖先，而树中每个节点都是根节点的子孙。

示例 5.3

在图5-1中，7个节点全都是n₁的子孙，而n₁是所有节点的祖先。此外，除n₁之外的所有节点都是n₁的真子孙，而n₁也是除了它自己之外的所有节点的真祖先。n₅、n₂和n₁都是n₅的祖先。而n₄的子孙有n₄和n₇。

具有相同父节点的节点有时也称为兄弟节点。例如，在图5-1中，n₂、n₃和n₄就互为兄弟节点，而n₅和n₆互为兄弟节点。

5.2.3　子树

在树T 中，某个节点n，与其所有真子孙（若存在的话），就构成了T 的子树。而节点n 就是该子树的根节点。请注意，子树要满足3个条件才能构成树：它有根节点；子树中其他节点在该子树中都有唯一的父节点；此外，沿着该子树中任意节点的父节点回溯，最终都能达到该子树的根节点。

示例 5.4

再来看图5-1，节点n₃自己就是棵子树，因为n₃除了它自己之外没有别的子孙。而节点n₂、n₅和n₆也构成了一棵子树，因为这些节点都是n₂的子孙。不过，在没有节点n₅的情况下，n₂和n₆两个节点本身是不能构成子树的。最后，图5-1中的整棵树都是它自己的子树，其中根节点为n₁。

5.2.4　叶子节点和内部节点

树中没有子节点的节点就是叶子节点。内部节点是指至少有一个子节点的节点。因此，树中的每个节点要么是叶子节点，要么是内部节点，但不可能同时是这两者。树的根节点通常是内部节点，不过，如果该树只由一个节点组成，那么该节点就既是根节点也是叶子节点。

示例 5.5

在图5-1中，n₅、n₆、n₃和n₇都是叶子节点，而n₁、n₂和n₄则是内部节点。

5.2.5　高度和深度

在树中，节点n 的高度是指从n 到叶子节点最长路径的长度，树的高度就是根节点的高度。而节点n 的深度，或者说等级（level），就是从根节点到n 的路径的长度。

示例 5.6

在图5-1中，节点n₁的高度为2，n₂的高度为1，而叶子节点n₃的高度为0。其实，任意叶子节点的高度都为0。图5-1中，树的高度为2。节点n₁的深度为0，n₂的深度为1，n₅的深度为2。

5.2.6　有序树

另外，可以为任意节点的子节点指定从左到右的顺序。例如，图5-1中n₁的子节点最左边是n₂，然后是n₃，再然后是n₄。这一从左到右的排列方式可以扩展到为树中的所有节点排列顺序。如果m和n是兄弟节点，而m在n的左边，那么m的子孙全都在n的子孙的左边。

示例 5.7

在图5-1中，根为n₂的子树中所有节点（也就是n₂、n₅和n₆）都在根为n₃和n₄的子树所有节点的左边。因此，n₂、n₃和n₆都在n₃、n₄和n₇的左边。

在树中选择任意两个互不存在祖先关系的节点x 和y。由于有着“在左边”的定义，x 和y 中其中有一个是在另一个的左边。要分辨哪个在哪个左边，就要从x 和y 开始沿着路径向根节点回溯。而在某一点，可能是根节点，也可能是较低的点，这两条路径会在某个如图5-2所示的节点z 相遇。从x 和y 到z 的路径分别要经过两个不同的节点m 和n，可能有m=x且（或）n=y，但一定有m≠n，否则这两条路径在z 以下的某个位置就融合了。

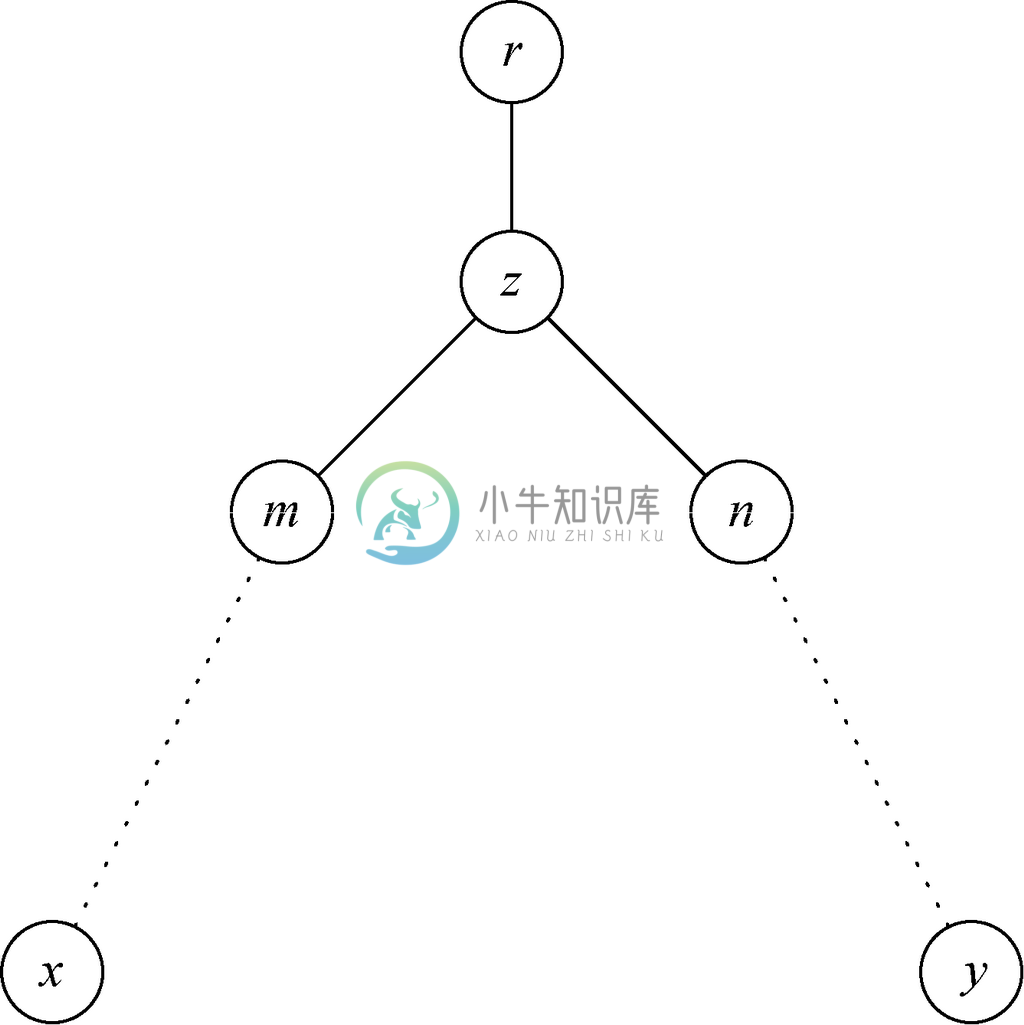
图 5-2　节点x 在节点y 的左边

假设m 在n 的左边。那么因为x 在根为m 的子树中，而y 在根为n 的子树中，所以有x 在y 的左边。同样，如果m 在n 的右边，那么x 也就在y 的右边。

示例 5.8

因为叶子节点不可能是其他叶子节点的子孙节点，所以所有叶子节点的顺序都遵循“从左起”的原则。例如，图5-1中所有叶子节点的顺序是n₅、n₆、n₃、n₇。

5.2.7　标号树

标号树（labelled tree）是指树中每个节点都有与之关联的标号或值的树。我们可将标号视为与给定节点相关联的信息。标号可以是很简单的内容，比如一个整数；也可以是复杂的内容，比如整个文档中的文本。我们可以改变节点的标号，但不能改变节点的名称。

如果节点的名称不重要，就可以用节点的标号来表示它。不过，标号并不总是能为节点提供唯一名称，因为若干个节点可能有着同一标号。因此，很多时候在绘制节点时既会标上其标号，也会标上其名称。下面的一些图展示了标号树的概念，并提供了一些示例。

5.2.8　表达式树——一类重要的树

算术表达式可以用标号树表示，而且将表达式直观表示为树往往是非常有意义的。其实，表达式树（expression tree）顾名思义就是以统一的方式指定了表达式的操作数与操作符之间的关联，不论这种关联是表达式中括号的放置需要的，还是所涉及运算符的优先级和结合规则需要的。

回想一下2.6节中对表达式的讨论，特别是示例2.17，我们在该例中给出了涉及常见算术运算符的表达式的递归定义。通过对表达式递归定义的模拟，就可以递归地定义对应的标号树。大致的概念就是通过将运算符应用到较小表达式上以构成更大的表达式，我们会创建标号为该运算符的新节点。该新节点就成为了表示较大表达式的树的根节点，而它的子节点就是表示较小表达式的树的根节点。

例如，可以按照如下方式，定义表示使用二元运算符+、-、×、/及一元运算符-的算术表达式的标号树。

依据。单个原子操作数（比如一个变量、一个整数或一个实数，如2.6节介绍的）是表达式，它的树就是标号为该操作数的一个节点。

{%}

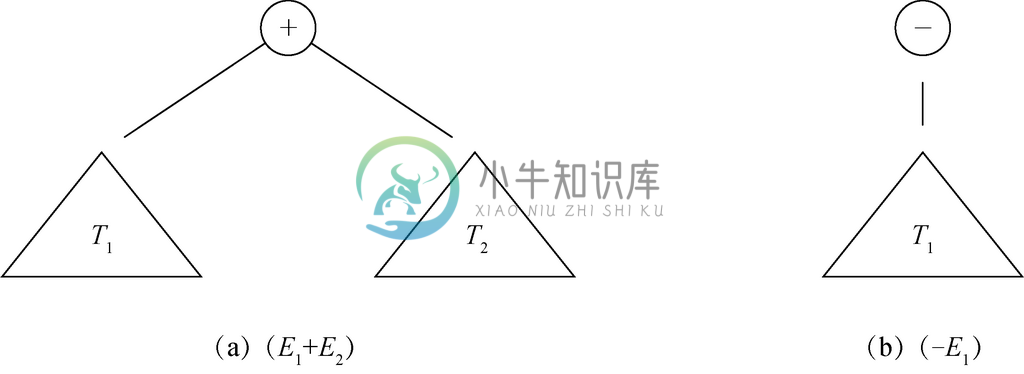
图 5-3　(E₁(E₂)和-E₁的表达式树

归纳。如果E₁和E₂这两个表达式分别是由树T₁和T₂表示的，那么表达式(E₁+E₂)就是由图5-3a所示的树表示的，其根节点标号为+。该根节点有两个子节点，依次分别是树T₁和T₂的根节点。同样，表达式(E₁-E₂)、(E₁×E₂)和(E₁/E₂)分别有着根节点标号-、×和/，且子树均为T₁和T₂的表达式树。最后，可以将一元减号运算符应用到表达式E₁上。这里引入了标号为-的根节点，而其唯一的子节点是T₁的根节点，表示(-E₁)的树如图5-3b所示。

示例 5.9

在示例2.17中，我们按照依据和递归规则对一系列6个表达式的递归构建进行过讨论。图2-16列出过的这些表达式分别是：

　 (i)　x　　　　　　(iv)　(-(x+10))
　(ii)　10　　　　　　(v)　y
　(iii)　(x+10) 　　　(vi)　(y×(-(x+10)))

表达式(i)、(ii)和(v)都是单个操作数，因此依据规则就说明了图5-4a、图5-4b、图5-4e中的树分别是表示这些表达式的。请注意，这些树都是由一个节点组成的，节点的名称分别为n₁、n₂和n₅，而节点的标号则是圆圈中的操作数。

{%}

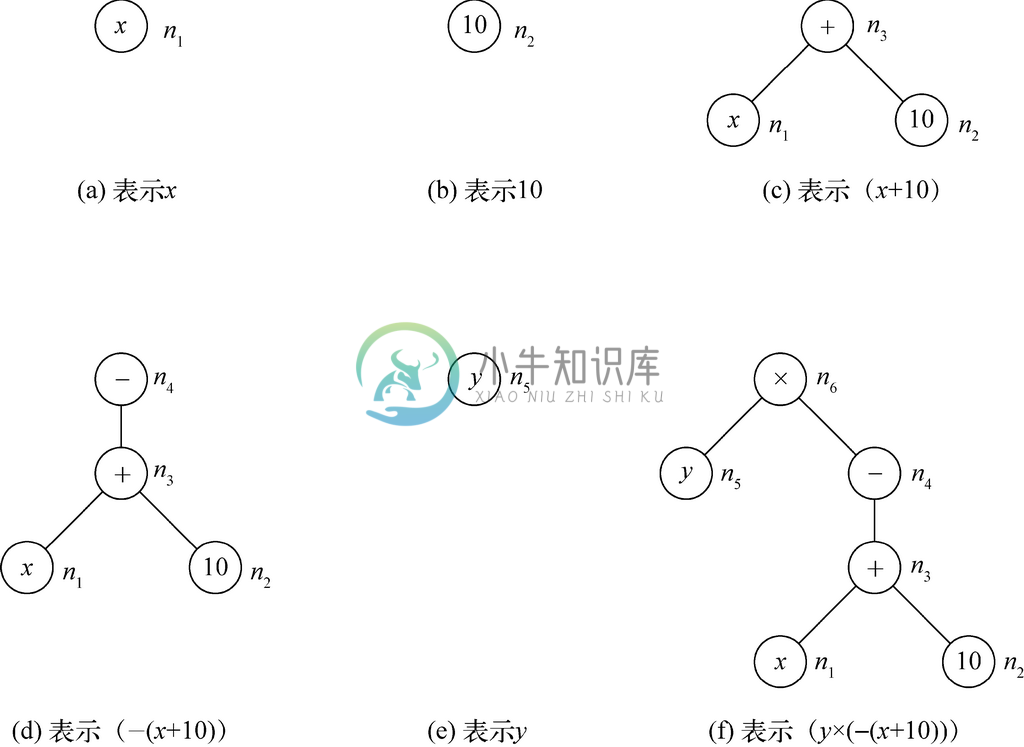
图 5-4　表达式树的构建

表达式(iii)是对操作数x 和10应用操作符+得到的，所以可以看到图5-4c所示的表示该表达式的树根节点标号为+，而图5-4a和5-4b中树的根节点则作为其子节点。表达式(iv)是对表达式(iii)应用一元的-，所以图5-4d中表示(-(x+10))的树在表示(x+10)的树的基础之上，多了标号为-的根节点。最后，图5-4f所示的是表示表达式(y×(-(x+10)))的树，其根节点标号为×，且其子节点依次为图5-4e和5-4d所示树的根节点。

5.2.9　习题

1. 在图5-5中有一棵树，分别指出如下内容描述的各是什么。

(a) 该树的根节点。

(b) 该树的叶子节点。

(d) 节点6的兄弟节点。

(e) 以节点5为根节点的子树。

(f) 节点10的祖先。

(g) 节点10的子孙。

(h) 节点10左边的节点。

(i) 节点10右边的节点。

(j) 该树中的最长路径。

(k) 节点3的高度。

(l) 节点13的深度。

(m) 该树的高度。

{%}

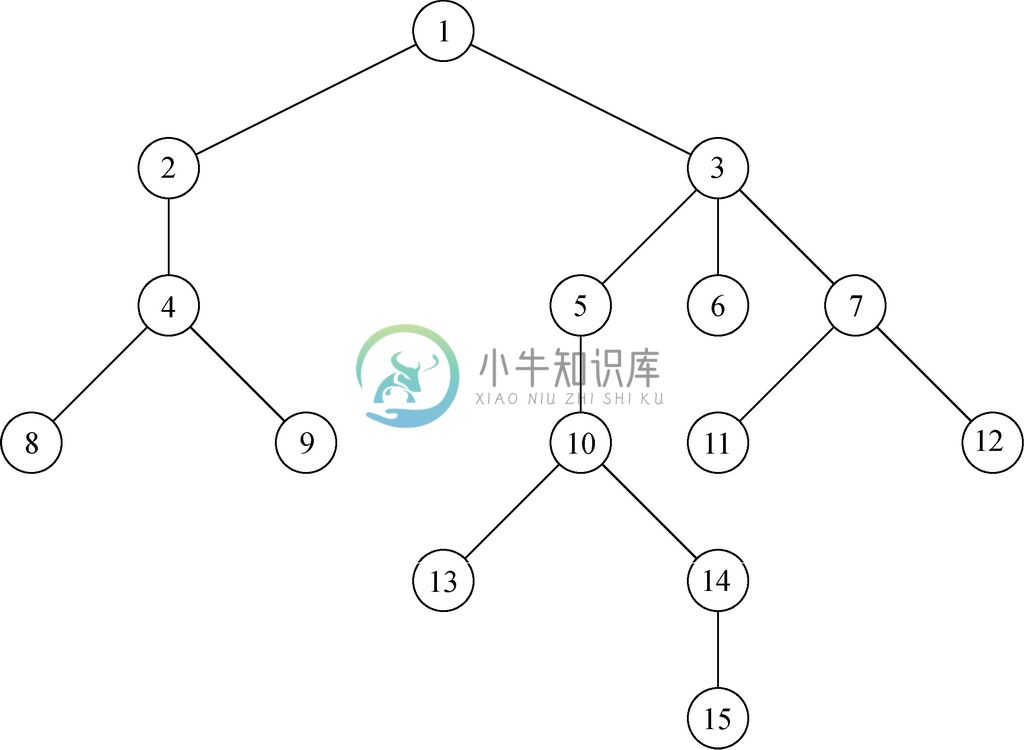
图 5-5　习题(1)的树

2. 树中的叶子节点能否有(a)子孙；(b)真子孙？

3. 证明：在树中，任何叶子节点都不可能是其他叶子节点的祖先。

4. *证明：本节中树的两种定义是等价的。提示：要证明由非递归定义生成的树就是根据递归定义生成的树，就要利用到对树中节点数的归纳。在相反的方向上，要利用对递归定义中递归轮数的归纳。

5. 假设有由4个节点r、a、b 和c 组成的图。节点r 是个孤立的点，没有边连通它。其余3个节点构成了一个循环，也就是说，有一条边连通a 和b，有一条边连通b 和c，还有一条边连通c 和a。为何该图不是树？

6. 在很多种树中，在内部节点和叶子节点（确切地说是这两种节点的标号）之间有着明显的区别。例如，在表达式树中，内部节点表示运算符，而叶子节点表示原子操作数。给出以下各种树的内部节点和叶子节点间的区别。

(a) 如1.3节中所述，表示目录结构的树。

(b) 如2.8节中所述，表示归并排序中表的分割和合并的树。

7. 给出表示以下表达式的表达式树。请注意，出于习惯性的表达，题目中的表达式省略了多余的括号，大家首先必须利用运算符的优先级和结合性恢复适当的括号。

(a) (x+1)×(x-y+4)

(b) 1+2+3+4+5+6

8. 证明：如果x 和y 是有序树中两个不同的节点，那么以下条件中一定刚好有一个是成立的。

(a) x 是y 的真祖先。

(b) x 是y 的真子孙。

(d) x 在y 的右边。

5.3　树的数据结构

很多数据结构可用来表示树。应该选用哪种数据结构，取决于想要执行的特定操作。举个简单的例子，如果想要做的只是定位节点的父节点，那么可以用由标号组成的结构体，加上指向表示节点之父节点的结构体的指针来表示每个节点。

作为一般规则，树的节点可以用结构体表示，这些结构体中的字段以某种方式将节点链接在一起，这种链接方式与节点在抽象的树中的连接方式类似，而树本身则可由指向表示根节点的结构体的指针来表示。因此，在谈到对树的表示时，我们主要是对节点的表示方式感兴趣。

表示方式的一种差异体现在表示节点的结构体在计算机内存中的位置上。在C语言中，可以使用标准库stdlib.h中的malloc函数为表示节点的结构体创建空间，这种情况下，节点都“漂泊”在内存中，并只能通过指针来访问。此外，可以创建由结构体组成的数组，并用数组中的元素来表示节点。这里节点还是根据它们在树中的位置链接起来的，不过也可以沿着数组的顺序来访问这些节点。因此，可以不沿着树中的路径来访问节点。基于数组的表示方式的弊端，在于没办法创建一棵节点数超过数组所含元素数量的树。接着，我们会假设这些节点都是由malloc创建的，虽然在树的大小有限制的情况下，由相同类型的结构体组成数组是可行的，而且有可能是首选方案。

5.3.1　树的指针数组表示

表示树的最简单方式之一就是为每个节点使用一个由表示节点标号的字段组成的结构体，后面再跟上指向该节点子节点的指针组成的数组。图5-6就表示了这样的结构。常量bf 是该指针数组的大小，它表示节点可以具有的最大子节点数，这个量就是分支系数（branching factor）。某节点对应数组的第i 个位置含有指向该节点第i 个子节点的指针，不存在的子节点可用NULL指针表示。

{%}

图 5-6　用指针数组表示的节点

在C语言中，该数据结构可以用如下类型声明来表示。

typedef struct NODE *pNODE;
struct NODE {
    int info;
    pNODE children[BF];
};

在这里，字段info表示构成节点标号的信息，而BF则表示分支系数的常量。在本章中我们还将看到该声明的多个变种。

在这种表示树的数据结构和多数表示树的数据结构中，都将树表示为指向根节点的指针。因此，pNODE还是树的类型。其实，可以在pNODE的位置使用类型TREE，而且在5.6节开始介绍二叉树时，我们将采纳这一约定。不过，现在还是要使用pNODE这个名称代表“指向节点的指针”类型，因为在某些数据结构中，指向节点的指针除了表示树之外还用于其他用途。

指针数组表示使我们能在O(1)的时间内访问任意节点的第i 个子节点。然而，当树中只有少量节点有很多子节点时，这种表示会非常浪费空间。在这种情况下，数组中的多数指针都是NULL。

试着记住trie
术语trie（单词查找树）来源于单词retrieval（检索）的中间部分。它本来被人们读作tree，好在现在常见读法已经将其读为发音有区别的try了。

示例 5.10

树可以用来表示一系列单词，其表示方式可以使检查给定字符序列是否为存在的单词变得非常有效率。在这类称为单词查找树的树中，除了根节点之外，每个节点都有与之相关联的字母。由某个节点n 表示的字符串，就是从根节点到n 的路径上的字母序列。给定一组单词，单词查找树的节点就是那些表示该集合中某个单词的前缀的字符串。节点的标号是由表示该节点的字母，以及表明从根节点到该节点的字母串能否构成完整单词的布尔值组成的。如果能，就用布尔值1表示，如果不能，就用0表示。1

1在5.2节中，介绍过的标号都只有一个值。不过，值可以是任意类型的，而且标号可以是由两个或多个字段组成的结构体。在本例中，标号有一个字段是个字母，而第二个字段则是一个值要么为0要么为1的整数。

例如，假设我们的“字典”是由4个单词he、hers、his和she组成的。这些单词的单词查找树如图5-7所示。要确定单词he是否在集合中，可以从根节点n₁开始，移动到标号为h的子节点n₂，再从节点n₂移动到标号为e的子节点n₄。因为这些节点都出现在树中，而且n₄的标号中还有1，所以可以得出he在该集合中的结论。

{%}

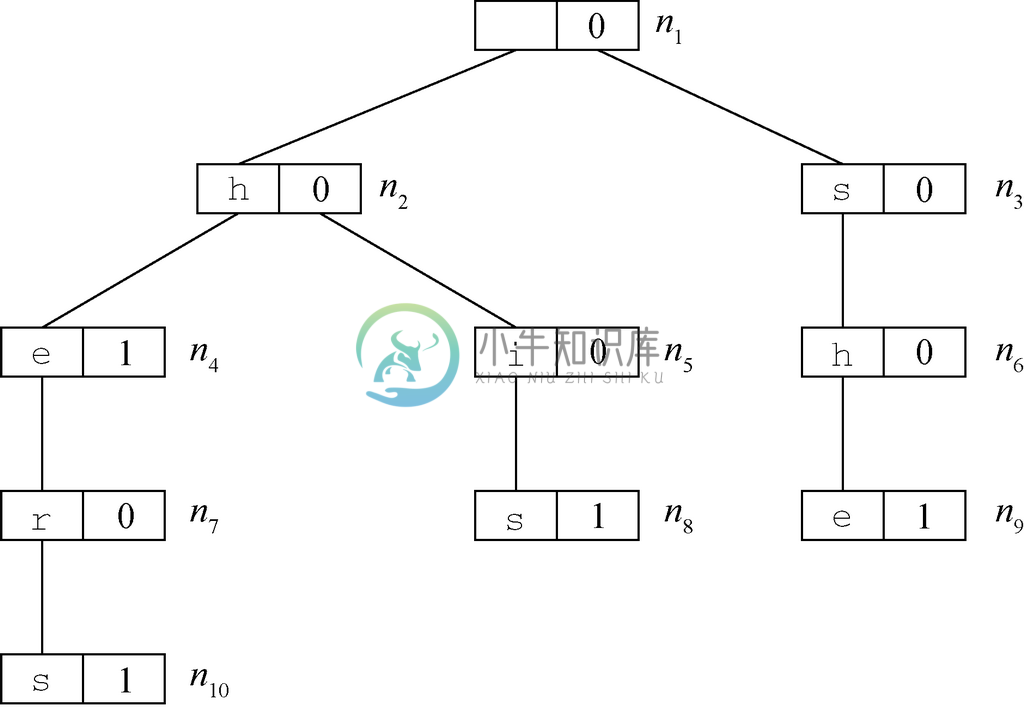
图 5-7　单词he、hers、his和she的单词查找树

再举一个例子，假设想要确定him是否在该集合中。可以从根节点开始沿着路径移动到n₂，再移动到n₅，这是表示前缀hi的。不过在节点n₅处找不到对应字母m的子节点。所以可以得出him不在该集合中的结论。最后，如果查找单词her，那么可以找出从根节点到节点n₇的路径。该节点存在，但标号不含1。因此可以得出her不在该集合中的结论，虽然以它为真前缀的单词hers在该集合中。

单词查找树中众节点的分支系数就等于构成这些单词的字母表中不同字符的数目。例如，如果不区分大小写字母，而且单词中不含撇号这样的特殊字符，那么分支系数就等于26。包含两个标号字段的节点的类型可以按照图5-8中所示的方式定义。在数组children中，可以假设字母a是用下标0表示的，而下标1表示字母b，以此类推。

typedef struct NODE *pNODE;
struct NODE {
    char letter;
    int isWord;
    pNODE children[BF];
};

图 5-8　字母单词查找树的定义

图5-7中抽象形式的单词查找树可以用图5-9所示的数据结构表示。通过展示前两个字段letter和isWord，以及数组children中那些具有非NULL指针的元素，从而表示节点。在children数组中，对每个非NULL的元素，标记该数组的字母是由指向子节点的指针上方的项表示的，不过该字母实际上没有出现在该结构中。请注意，根节点的letter字段是无关紧要的。

{%}

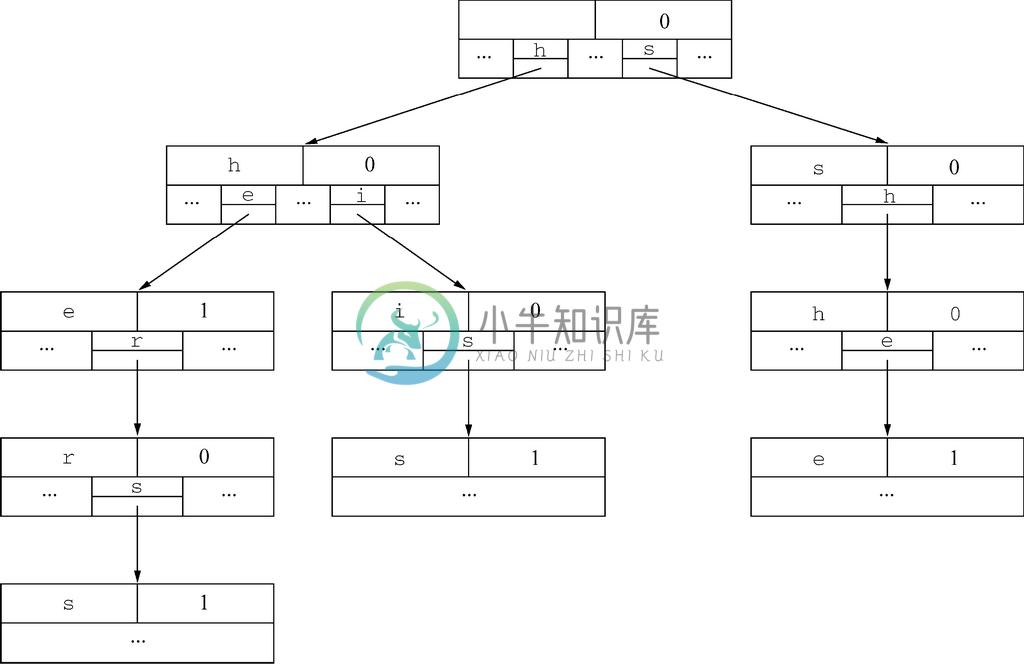
图 5-9　图5-7中所示单词查找树的数据结构

5.3.2　树的最左子节点右兄弟节点表示

使用指针数组表示节点的空间利用率可能很低，因为通常情况下，绝大多数指针都会是NULL。图5-9显然就是这种情况，其中没有哪个节点有两个以上非NULL指针。事实上，如果想想这种情况，就会发现，在任何基于26个字母的字母表的单词查找树中，指针的数量都会是表示节点的指针的数量的26倍。因为没有哪个节点会有两个父节点，而且根节点是没有父节点的，所以N个节点中只有N-1个非NULL的指针，也就是说，每26个指针中只有不到1个是有用的。

要克服树的指针数组表示空间利用率低的问题，方法之一就是使用链表来表示节点的子节点。节点对应链表所占据的空间是与该节点子节点的数量成正比的。不过，这种表示方式在时间上要付出代价，访问第i 个子节点所需时间为O(i )，因为在到达第i 个节点之前必须遍历长度为i-1的链表。与之相比，使用指针数组表示子节点的话，就可以在O(1)时间内到达第i 个子节点，跟i 完全没有关系。

在树的这种最左子节点右兄弟节点（leftmost-child-right-sibling）表示中，要为每个节点放入一个指向其最左子节点的指针，而节点没有指向它其他子节点的指针。要找到节点n 的第二个及后续的子节点，可以为这些节点创建一个链表，其中每个子节点c 都指向n 的子节点中紧挨在c 右侧的那个，该节点称为c 的右兄弟节点。

示例 5.11

在图5-1中，n₃是n₂的右兄弟节点，n₄是n₃的右兄弟节点，n₄没有右兄弟节点。沿着n₁指向其最左子节点n₂的指针，然后移到指向n₂右兄弟节点n₃的指针，接着再到指向n₃右兄弟节点n₄的指针，就能找出n₁的子节点。接着就会发现一个为NULL的右兄弟节点指针，并知道n₁没有更多子节点了。

图5-10简要绘出了图5-1所示树的最左子节点右兄弟节点表示。向下的箭头是指最左子节点链接，而向右的箭头则是右兄弟节点链接。

图 5-10　图5-1中所示树的最左子节点右兄弟节点表示

在树的最左子节点右兄弟节点表示中，节点是按照如下方式定义的。

typedef struct NODE *pNODE;
struct NODE {
    int info;
    pNODE leftmostChild, rightSibling;
};

info字段存放着与节点相关联的标号，而且可以是任一类型的。字段leftmostChild和rightSibling指向最左子节点以及相应的右兄弟节点。请注意，尽管leftmostChild给出了有关该节点自身的信息，但节点的rightSibling字段才是真正表示该节点父节点全部子节点的链表的那一部分。

示例 5.12

现在将图5-7中的单词查找树表示成最左子节点右兄弟节点的形式。首先，节点的类型如下。

typedef struct NODE *pNODE;
struct NODE {
    char letter;
    int isWord;
    pNODE leftmostChild, rightSibling;
};

根据示例5.10中描述过的模式，前两个字段是表示信息的。图5-7中的单词查找树可表示为图5-11所示的数据结构。请注意，每个叶子节点都有为NULL的最左子节点指针，而每个最右子节点都有为NULL的右兄弟节点指针。

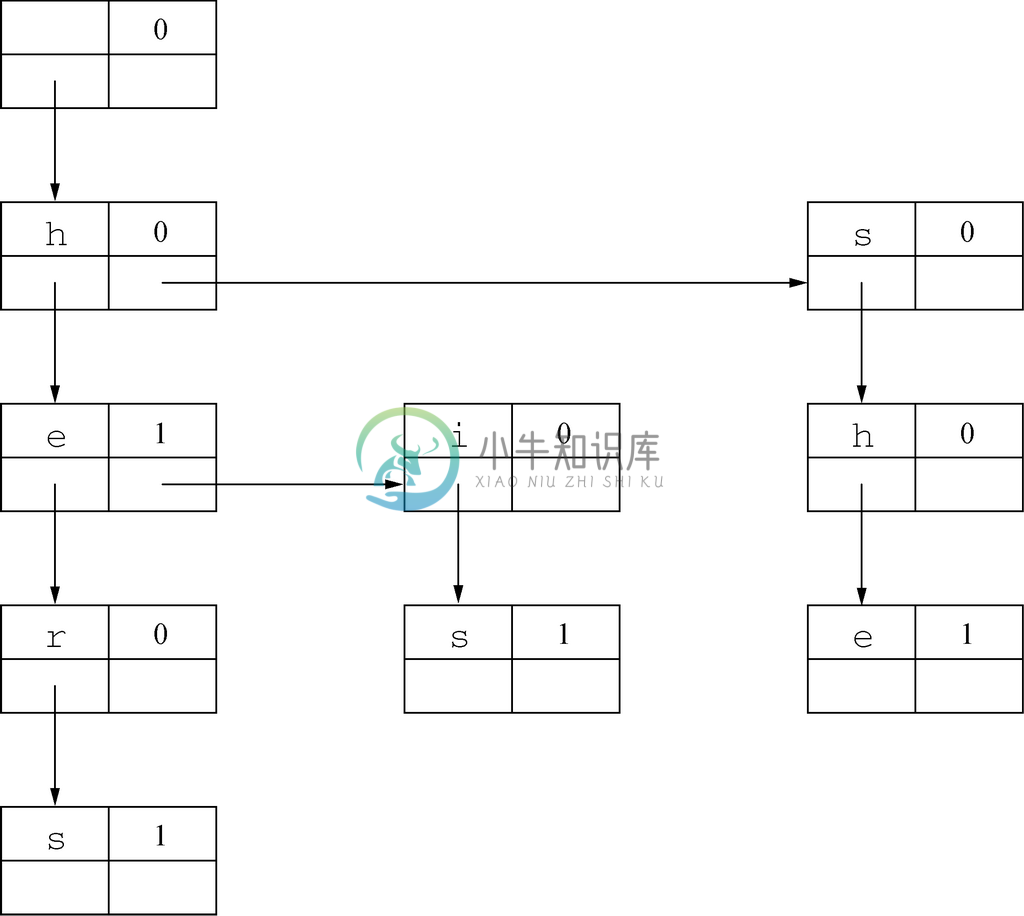
图 5-11　所示单词查找树的最左子节点右兄弟节点表示

举个与最左子节点右兄弟节点表示的用途有关的例子。在图5-12中，函数seek(let,n)会接受字母let 以及指向节点n 的指针作为参数。它会返回一个指针，指向n 的子节点中letter字段里有let 的那个子节点，如果不存在这样的节点，返回的就是NULL指针。如果发现let，或是检查过所有的子节点，就会达到第(6)行，并跳出该循环。不管是哪种情况，c都存放着正确的值，如果存在存放了let 的子节点，就是指向该节点的指针，如果不存在，就是NULL指针。

请注意，seek函数的运行时间与找到所要找的子节点所必须检查的子节点数成正比，如果根本找不着这样的节点，那么运行时间就与节点n的子节点数成正比。与之相比的是，如果使用树的指针数组表示，seek会直接返回字母let对应的数组元素的值，花的时间为O(1)。

     pNODE seek(char let, pNODE n)
     {
(1)      c = n->leftmostChild;
(2)      while (c != NULL)
(3)          if (c->letter == let)
(4)              break;
             else
(5)              c = c->rightSibling;
(6)      return c;
     }

图 5-12　找到所需字母对应的子节点

5.3.3　父指针

有些时候，在表示节点结构体中包含指向其父节点的指针是很有用的，而根节点的父指针为NULL。例如，示例5.12中的结构体就成了

typdef struct NODE *pNODE;
struct NODE {
    char letter;
    int isWord;
    pNODE leftmostChild, rightSibling, parent;
};

有了这种结构体，就可以确定某给定节点表示的单词了。不断回溯父指针，直到到达根节点，我们就可以确认根节点，因为只有它的parent指针的值是NULL。这一路下来的letter字段就倒着拼出了该单词。

5.3.4　习题

1. 对图5-5所示树中的每个节点，它们的最左子节点和右兄弟节点。

2. 请进行下列操作。

(a) 将图5-5中的树表示为分支系数为3的单词查找树。

(b) 用最左子节点指针和右兄弟节点指针来表示图5-5中的树。

每种表示方式各需要多少字节的内存？

3. 考虑英语中单数人称代词的如下集合：I、my、mine、me、you、your、yours、he、his、him、she、her、hers。对图5-7所示的单词查找树加以补充，从而将这13个单词都包含在内。

4. 假设某部完整的英语词典包含了2 000 000个单词，以及1 000 000个单词前缀——也就是在其尾部加上0个或多个字母便能构成单词的字母串。

(a) 这部词典的单词查找树共有多少个节点？

(b) 假设使用示例5.10中的结构体表示节点。设指针需要4字节，且信息字段letter和isWord各需要1字节，那么这棵单词查找树需要多少字节？

5. 假设用示例5.12中的结构体（最左子节点右兄弟节点表示）来表示习题(4)中描述的词典。假设指针和信息字段占据的空间与习题(4)的(b)小题中的假设相同，那么这种表示中这棵树需要占据多少空间？在该空间中NULL指针占的比例又是多少？

6. 在树中，如果节点c 同为x 和y 的祖先，而且c 的真子孙中没有一个同时是x 和y 的祖先，那么就说c 是x 和y 的最低共同祖先。编写程序，使其能找出给定的树中任一对节点的最低共同祖先。在这种程序中使用什么数据结构表示树比较好？

树的表示的对比
这里总结了树的指针数组表示（单词查找树）与最左子节点右兄弟节点表示的相对优势。
指针数组表示带来了更快的子节点访问速度，不管有多少子节点，到达任意子节点都只需要O(1)的时间。
最左子节点右兄弟节点表示占用的空间更少。以图5-7所示的单词查找树为例，如果使用指针数组表示，那么每个节点含有26个指针，而如果使用最左子节点右兄弟节点表示，每个节点只含两个指针。
最左子节点右兄弟节点表示不要求对节点的分支系数加以限制，因此可以在不改变数据结构的前提下表示具有任一分支系数的树。然而，如果使用指针数组表示，一旦选择了数组的大小，就不能表示具有更大分支系数的树了。

5.4　对树的递归

对树进行的递归操作可以自然清晰地写下来，这样的操作数量之多突显了树的实用性。图5-13展示了接受树的节点n 作为参数的递归函数F (n)的一般形式。F 首先会执行一些步骤（也可能不执行任何步骤），我们将其表示为操作A₀。接着，F 会对n 的第一个子节点c₁调用它自身。在这次递归调用中，F 将会“探索”以c₁为根节点的子树，进行F 对树进行的任何操作。当该调用返回对节点n 的调用时，就会执行另一个操作A₁。接着F 会在n 的第二个子节点上被调用，引起对第二棵子树的探索，以此类推，就是对n 的操作与在n 的子节点对F 的调用交替着进行。

{%}

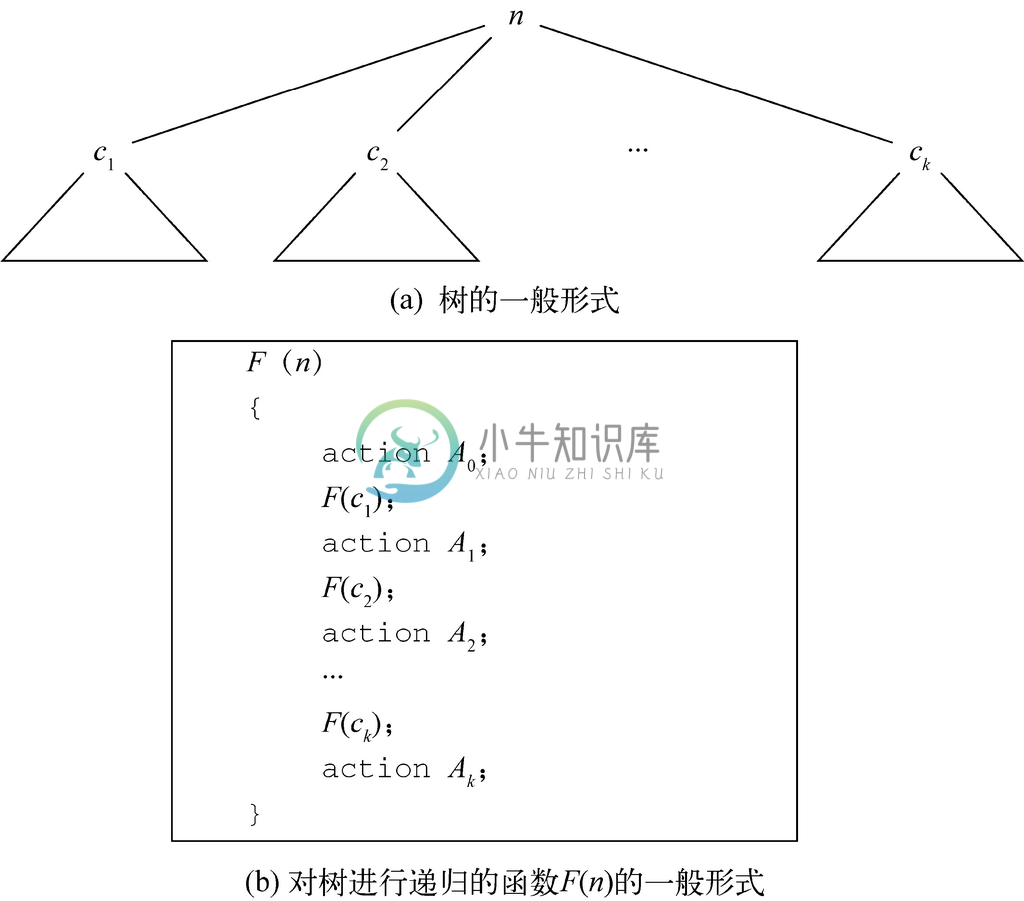
图 5-13　对树进行递归的函数

示例 5.13

对树进行简单的递归会产生树的节点标号的前序排列（preorder listing）。这里的操作A₀是打印节点的标号，而其他的操作也无非是些“分门别类进行记录”的操作，这些操作可以让我们访问给定节点的每个子节点。效果就是，如果从根节点开始逆时针环游访问树中的每个节点，在第一次遇到这些节点时会将它们的标号打印出来。请注意，只有在第一次访问某个节点时才将其标号打印出来。这种环游如图5-14中的箭头所示，访问这些节点的顺序是+a+*-b-c-*d*+。这一节点标号序列的前序排列是+a*-bcd。

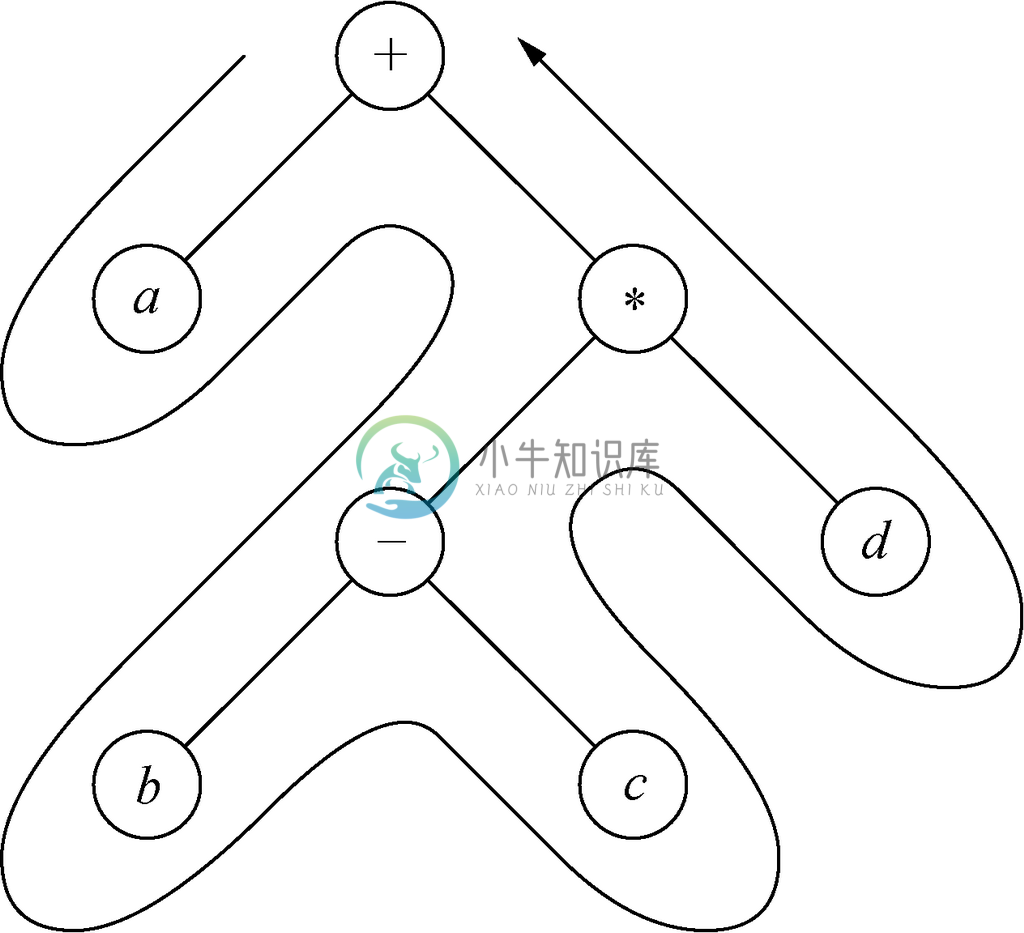
图 5-14　表达式树及其环游

假设为表达式中标号为一个字母的节点使用最左子节点右兄弟节点的表示方式。内部节点的标号是该节点处的算术运算符，而叶子节点的标号是表示操作数的字母。节点和指向节点的指针可以按照如下方式定义。

typedef struct NODE *pNODE;
struct NODE {
    char nodeLabel;
    pNODE leftmostChild, rightSibling;
};

函数preorder如图5-15所示。在随后的解说中，可以很自然地将指向节点的指针看作节点本身。

           void preorder(pNODE n)
           {
               pNODE c; /* 节点 n 的子节点 */

(1)            printf("%c\n", n->nodeLabel);
(2)            c = n->leftmostChild;
(3)            while (c != NULL) {
(4)                preorder(c);
(5)                c = c->rightSibling;
               }
           }

图 5-15　前序遍历函数

操作“A₀”由图5-15所示程序的以下几个部分组成。

1. 在第(1)行，打印节点n 的标号；

2. 在第(2)行，将c 初始化为n 的最左子节点；

3. 在第(3)行，执行第一次c != NULL的测试。

第(2)行会初始化一个循环，在该循环中，c 会依次成为n 的每个子节点。请注意，如果n 是叶子节点，那么c 就会在第(2)行被赋上NULL值。

第(3)行到第(5)行的while循环会一直进行，直到遍历完n 的所有子节点。对每个子节点而言，会在第(4)行对该节点递归地调用函数preorder，接着在第(5)行行进到下一个子节点。i≥1的每个操作A_i，都是由让c 在n 的子节点中移动的第(5)行，以及测试是否遍历完子节点的第(3)行组成的。这些操作都只是分门别类地记录而已，与此相比，第一行中的操作A₀完成的是关键步骤：打印标号。

对图5-14中所示树的根节点调用preorder的一系列事件可总结为图5-16所示的情形。每一行左侧的字符就是在对preorder(n)的调用正在被执行时节点n 的标号。因为没有哪两个节点的标号会相同，所以使用节点的标号作为其名称是没有问题的。请注意，打印出的字符是+a*-bcd，这一打印顺序就和环游的顺序一样。

     调用 preorder(+)
(+)      打印 +
(+)      调用 preorder(a)
(a)           打印 a
(+)      调用 preorder(*)
(*)           打印 *
(*)           调用 preorder-)
(-)               打印 -
(-)               调用 preorder(b)
(b)                    打印 b
(-)               调用 preorder(c)
(c)                    打印 c
(*)           调用 preorder(d)
(d)               打印 d

图 5-16　递归函数preorder对图5-14所示树进行的操作

示例 5.14

另一种为树中节点排序的常见方式是后序，对应图5-14所示树的环游，不过会列出最后访问的节点，而不是第一次访问的节点。例如，在图5-14中，后序排列就是abc-d*+。

要生成节点的后序排列，需要由最后的操作来完成打印，这样才会在对节点的所有子节点从左起依次调用后序排列函数之后，再打印该节点的标号。其他的操作则会初始化穿越子节点或移动到下一子节点的循环。请注意，如果某个节点是叶子节点，那么要做的只有列出标号，而不存在任何递归调用。

如果使用示例5.13介绍的节点表示方式，就可以通过图5-17中的递归函数postorder构建后序排列。在对图5-14所示树的根节点调用该函数时的操作如图5-18所示，这里使用了与图5-16中一致的节点名称转换方式。

     void postorder(pNODE n)
     {
         pNODE c; /* 节点 n 的子节点 */

(1)      c = n->leftmostChild;
(2)      while (c != NULL) {
(3)          postorder(c);
(4)          c = c->rightSibling;
         }
(5)      printf("%c\n", n->nodeLabel);
     }

图 5-17　递归的后序函数

     调用 postorder(+)
(+)       调用 postorder(a)
(a)            打印 a
(+)       调用 postorder(*)
(*)            调用 postorder(-)
(-)                 调用 postorder(b)
(b)                      打印 b
(-)                 调用 postorder(c)
(c)                      打印 c
(-)                 打印 -
(*)                调用 postorder(d)
(d)                 打印 d
(*)            打印 *
(+)       打印 +

图 5-18　递归函数postorder对图5-14所示树进行的操作

示例 5.15

接下来的例子要求我们在对子树进行的所有递归调用中执行一些重大操作。假设给定一棵表达式树，其中以整数为操作数，并使用二元运算符，而且希望得出该树表示的表达式的数值。我们可以通过对该表达式树执行以下递归算法达成这一目的。

依据。对于一个叶子节点，得出该节点的值作为树的值。

归纳。假设要计算以某个节点n 为根节点的子树形成的表达式的值。我们要为以n 的子节点为根节点的子树所对应的子表达式求值，这两个值是节点n 处的运算符对应的操作数的值。接着就可以对这两个子树的值应用标号为n 的运算符，这样就得到了以n 为根节点的整棵子树的值。

前缀表达式和后缀表达式
如果以前序列出表达式树的标号，就得到了给定表达式的前缀表达式。同样，以后序列出表达式树的标号就得出等价的后缀表达式。而普通概念的表达式，就是二元运算符出现在操作数之间的表达式，称为中缀表达式。例如，图5-14中表达式树的中缀表达式为a+(b-c)*d。正如我们在示例5.13和示例5.14中所见，等价的前缀表达式是+a*-bcd，等价的后缀表达式是abc-d*+。
有个有关前缀和后缀概念的有趣事实，只要每个运算符都有唯一的参数数量（比如，不能同时使用一元和二元的减号），那么就算没有括号，也还是能清楚地将运算符与它们对应的操作数进行分组。
可以按照如下方式由前缀表达式构建中缀表达式。在前缀表达式中，可以看到运算符后跟着所需数量的操作数，而没有内嵌的运算符。例如，在前缀表达式+a*-bcd 中，子表达式-bc 就是这样一个字符串，因为这个减号像此例中的所有运算符一样是二元的。我们可以用新符号来代替该子表达式，比如说设x=-bc，接着再重复这一确定运算符后跟其对应操作数的过程。在本例中，就是要对+a*xb进行处理。在这里可以确定子表达式y=*xd，并将剩余的字符串缩减为+ay。现在剩下的字符串就只有一个运算符和它的操作数了，这样就可以转换为中缀表达式a+y。
现在就可以通过重现这些步骤来重建中缀表达式中剩下的部分了。可以看到子表达式y=*xd 的中缀形式为x*d，所以可以将a+y 中的y 替换为x*d，这样就得到了a+(x*d)。请注意，一般来说，中缀表达式里是需要括号的，虽然在本例中在为操作数分组时因为*的优先级比+高所以省略了这对括号。接着将x=-bc 替换为中缀表达式b-c，便可得到最终的表达式为a+((b-c)*d)，这与图5-14中的树表示的表达式是相同的。
对后缀表达式来说，可以利用相似的算法。唯一的区别就是在分解后缀表达式时是要看运算符以及放在它们前面的必要数量的操作数。

我们将指向节点的指针与节点定义如下。

typedef struct NODE *pNODE;
struct NODE {
    char op;
    int value;
    pNODE leftmostChild, rightSibling;
};

字段op存放的要么是表示算术运算符的字符，要么是字符i，这里的i代表integer（整数），并确认节点为叶子节点。如果该节点是叶子节点，那么value字段就存放着该节点表示的整数，在处理内部节点时是用不上value的。

这一概念允许运算符具有任意数量的参数，虽然我们在编写代码时会出于简便性的考虑而假设所有运算符都是二元的。代码如图5-19所示。

     int eval(pNODE n)
     {
         int val1, val2; /* 第一棵子树和第二棵子树的值 */

(1)      if (n->op) == ’i’) /* n points to a leaf */
(2)          return n->value;
         else {/* n 指向内部节点 */
(3)          val1 = eval(n->leftmostChild);
(4)          val2 = eval(n->leftmostChild->rightSibling);
(5)          switch (n->op) {
(6)              case '+': return val1 + val2;
(7)              case '-': return val1 - val2;
(8)              case '*': return val1 * val2;
(9)              case '/': return val1 / val2;
             }
         }
     }

图 5-19　为算术表达式求值

如果节点n是叶子节点，第(1)行的测试会成功，并在第(2)行返回该叶子节点的整数标号。如果该节点不是叶子节点，那么会在第(3)行给它的左操作数求值，并在第(4)行给它的右操作数求值，分别将结果存入val1和val2。联系第(4)行的表示，可以注意到节点n的第二个子节点就是节点n最左子节点的右兄弟节点。第(5)行到第(9)行形成了一个switch语句，在该语句中要决定n处为何种运算符，并为左操作数和右操作数的值应用合适的运算。

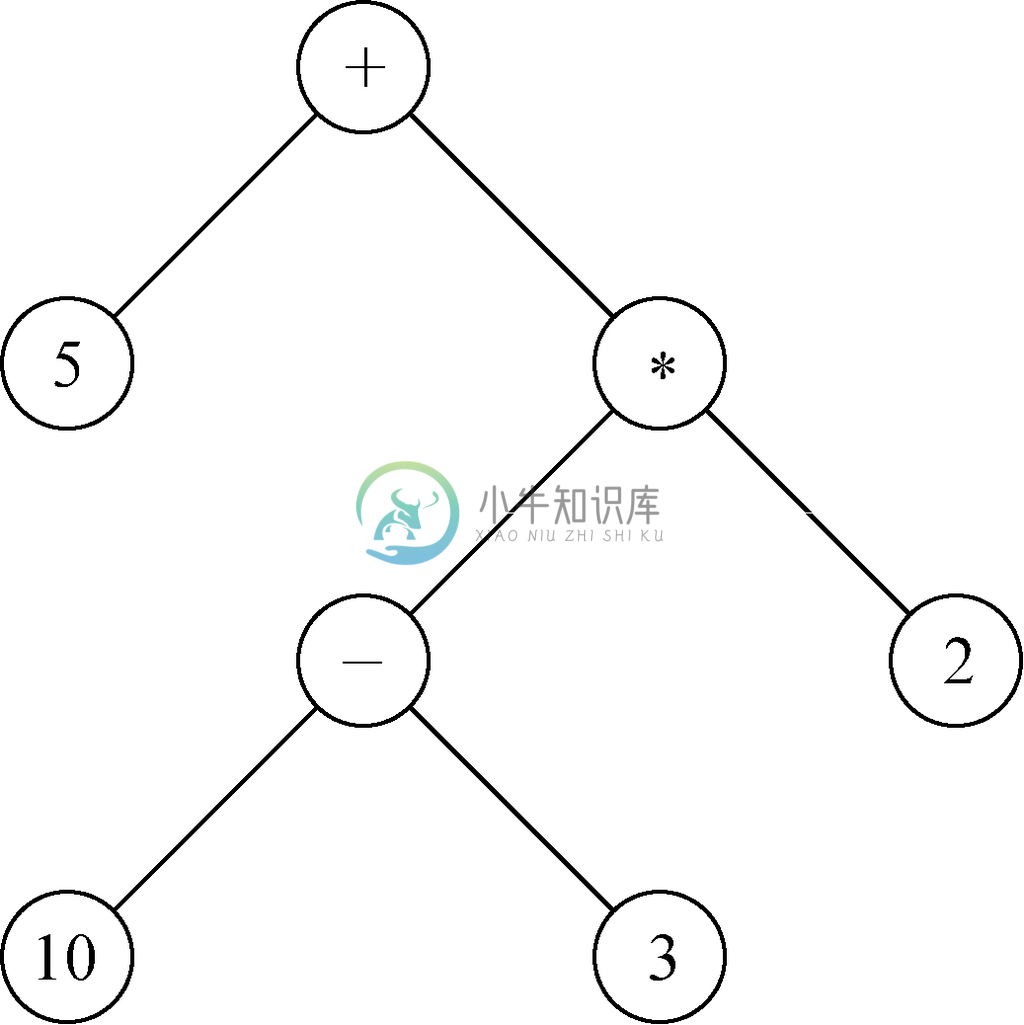
图 5-20　操作数为整数的表达式树

例如，考虑图5-20中所示的表达式树。在图5-21中我们还会看到在为该表达式求值时，每个节点处进行的调用和返回的序列。和以往一样，要利用到节点标号是唯一的这一事实，并用它们的标号来为其命名。

      调用 eval(+)
 (+)      调用 eval(5)
 (5)          返回 5
 (+)      调用 eval(*)
 (*)          调用 eval(-)
 (-)               调用 eval(10)
(10)                  返回 10
 (-)               调用 eval(3)
 (3)                  返回 3
 (-)               返回 7
 (*)             调用 eval(2)
 (2)               返回 2
 (*)             返回 14
 (+)         返回 19

图 5-21　函数eval在图5-20所示树的每个节点处进行的操作

示例 5.16

有时需要确定树中各节点的高度，节点的高度可由以下函数递归地定义。

依据。叶子节点的高度为0。

归纳。内部节点的高度要比其子节点最大的高度大1。

可以将这一定义转换成递归程序，该程序会将每个节点的高度计算出来存放到height字段中。

依据。在叶子节点处，将高度置为0。

归纳。在内部节点，递归地计算子节点的高度，找出最大值，加上1，并将结果存储到height字段中。

该程序如图5-22所示，假设节点是具有如下形式的结构体。

typedef struct NODE *pNODE;
struct NODE {
    int height;
    pNODE leftmostChild, rightSibling;
};

computeHt函数接受指向节点的指针作为参数，并计算出该节点的高度存放到height字段中。如果在树的根节点处调用该函数，就会计算该树中所有节点的高度。

           void computeHt(pNODE n)
           {
               pNODE c;

(1)            n->height = 0;
(2)            c = n->leftmostChild;
(3)            while (c != NULL) {
(4)                computeHt(c);
(5)                if (c->height >= n->height)
(6)                    n->height = 1+c->height;
(7)                c = c->rightSibling;
               }
           }

图 5-22　计算树中所有节点高度的例程

在第(1)行，我们会将n 的高度初始化为0。如果n 是叶子节点，计算就算完成了，因为第(3)行的测试将会立即失败，所以算出的任何叶子节点的高度都为0。第(2)行会将c 置为（指向）n 的最左子节点（的指针）。随着不断进行第(3)行至第(7)行的循环，c 依次成为n 的每个子节点。第(4)行会递归地计算c 的高度。随着计算的进行，n->height中的值会比目前最高的子节点高度大1，不过如果没有子节点，这个值就是0。因此，第(5)行和第(6)行在发现比之前的子节点更高的子节点后会增加n 的高度。此外，对第一个子节点，第(5)行的测试是肯定会被满足的，而且我们会将n->height置为比第一个子节点的高度大1。在因为处理完所有子节点而跳出循环后，n->height就会被置为比n 子节点中的最大高度大1。

程序设计还要更具防御性
图5-19中的程序有若干方面表现出了一种粗心的编程风格，这是应该避免的。具体来说，我们在没有首先检查指针是否为NULL的情况下就一路前进了。因此，在第(1)行，n是可能为NULL的。我们真应该将程序以如下形式开头。
if (n != NULL) /* then do lines (1) to (9) */
else /* print an error message */
即便n不是NULL，在第(3)行还是可能看到它的leftmostChild字段是NULL，因此应该检测一下n->leftmostChild是否为NULL，如果是，就打印出错误消息，而且不去调用eval。同样，即便n的最左子节点存在，该子节点也可能没有右兄弟节点，所以在第(4)行之前还需要检查
n->leftmostChild->rightSibling != NULL
而且该程序还依赖于树中节点所含信息是正确的这一假设。例如，如果某个节点是内部节点，它的标号为二元运算符，而且我们已经假设它具有两个子节点，并且第(3)行和第(4)行的指针不可能为NULL。不过，运算符标号有可能是不正确的。要正确处理这种情形，就应该在switch语句中加入default情况，以检测意料之外的运算符标号。
作为一般规则，对程序的输入永远正确这一假设的依赖过分简单了；在现实中，“只要有可能出错，就肯定会出错。”如果某个程序要使用多次，势必会遇到那些形式不符合程序员预想的数据。在实践中多么小心都不为过。盲目地接受NULL指针，或假设输入数据总是正确的，都是常见的编程错误。

习题

1. 编写递归程序，计算用最左节点指针和右兄弟节点指针表示的树的节点数量。

2. 编写递归程序，找到树中具有最大标号的节点。假设该树节点的标号都为整数，而且是用最左子节点右兄弟节点指针表示的。

3. 修改图5-19中的程序，使其能处理含有一元减号节点的树。

4. * 编写递归程序，为最左子节点右兄弟节点指针表示的树计算左右对的数量。所谓左右对，就是指节点n 在m 左侧这样的一对节点n 和m。例如，在图5-20中，节点5就在标号为*、-、10、3和2的节点左侧，而节点10在节点3和节点2左侧，节点-在节点2左侧。因此，该树的左右对共有8对。提示：在对节点n 调用编写的递归函数时，要让该函数返回两个部分，以n 为根节点的子树中左右对的数量，还有以n 为根节点的子树中节点的数量。

5. 以(a)前序和(b)后序列出图5-5中（见5.2节的习题）树的节点。

6. 对如下各表达式

(i) (x+y)*(x+z)

(ii) ((x-y)*z+(y-w))*x

(iii) ((((a*x+b)*x+c)*x+d)*x+e)*x+f

完成以下操作：

(a) 构建表达式树；

(b) 写出等价的前缀表达式；

7. 将后缀表达式ab+c *de-/f 转换为(a)中缀表达式和(b)前缀表达式。

8. 编写函数，使其可以“环游”树，并在经过节点时打印节点的名称。

9. 图5-17中的后序函数进行的操作A₀、A₁等各是什么？（“操作”就是如图5-13所指的那些。）

5.5　结构归纳法

第2章和第3章已经介绍了不少有关整数属性的归纳证明。可以假设某一命题对n 来说为真，或者假设命题对所有小于等于n 的整数都成立，并使用该归纳假设证明同一命题对n+1也成立。“结构归纳法”与之类似但不尽相同，适用于证明与树有关的属性。结构归纳法模拟了对树的递归算法，而且这种形式的归纳法在想要证明一些与树有关的命题时是最易于使用的。

假设要证明命题S(T )对所有的树T 都为真。作为依据，要证明S(T )对由单一节点组成的树T 为真。而对归纳部分来说，要假设T 是一棵以r 为根节点，并有子节点c₁、c₂、…、c_k（k≥1）的树。如图5-23所示，设T₁、T₂、…、T_k分别是以c₁、c₂、…、c_k为根节点的T 的子树。那么归纳步骤就是假设S(T₁)、S(T₂)、…、S(T_k)都为真，并证明S(T )。如果完成了这一证明，就可以得出S(T )对所有的树T 都成立的结论。这种形式的论证就叫作结构归纳法。请注意，除了要区分依据部分（1个节点）和归纳步骤（多于1个节点），结构归纳法不会提及树中具体的节点数。

{%}

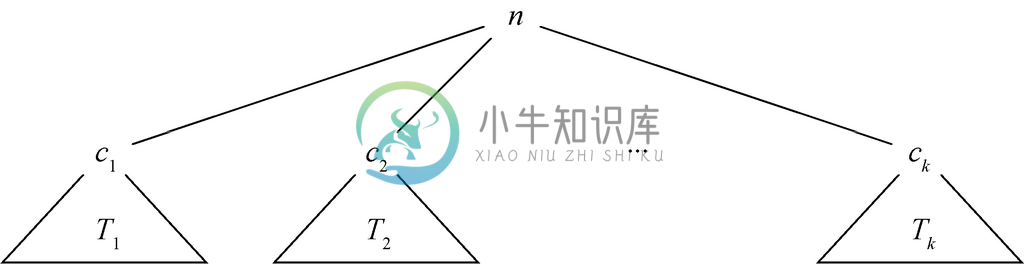
图 5-23　树及其子树

示例 5.17

一般情况下，在证明对树进行操作的递归程序时会需要用到结构归纳法。举例来说，可以再次看看图5-19所示的eval函数，图5-24重现了该函数的函数体。只要将指向T 根节点的指针赋值给该函数的参数n，就可将该函数应用于树T。然后它就会计算由T 表示的表达式的值。接下来要用结构归纳法证明如下命题。

(1)      if (n->op) == 'i') /* n 指向叶子节点 */
(2)          return n->value;
         else {/* n 指向内部节点 */
(3)          val1 = eval(n->leftmostChild);
(4)          val2 = eval(n->leftmostChild->rightSibling);
(5)          switch (n->op) {
(6)              case '+': return val1 + val2;
(7)              case '-': return val1 - val2;
(8)              case '*': return val1 * val2;
(9)              case '/': return val1 / val2;
             }
         }

图 5-24　图5-19中eval(n)函数的函数体

命题S(T )。在对T 的根节点调用eval时，返回的值是T 所表示的算术表达式的值。

依据。作为依据，T 由单个节点组成。也就是说，参数n 是一个（指向）叶子节点（的指针）。因为在该节点表示操作数时，op字段具有值“i”，图5-24中第(1)行的测试会成功，第(2)行会返回操作数的值。

归纳。假设节点n 不是（指向）叶子节点（的指针）。归纳假设就是，S(T' )以n的某个子节点为根节点的每棵树T' 都为真。必须使用这一推理证明S(T )对以n 为根节点的树T 成立。

因为假设运算符都是二元的，所以n有两棵子树。根据归纳假设，第(3)行和第(4)行计算出val1和val2的值，分别是左子树和右子树的值。图5-25展示了这两棵子树，val1存放着T₁的值，val2存放着T₂的值。

图 5-25　调用eval(n)返回T₁和T₂的值的和

如果看看第(5)行到第(9)行的switch语句，就会发现不管根节点n 处出现什么运算符，它都会被应用到val1和val2这两个值上。例如，如果根节点处存放着+，如图5-25所示，那么第(5)行返回的值就是val1+val2，正如这应该是树T₁和T₂对应表达式的和。现在就完成了归纳步骤。

因此可以得出S(T )对所有的表达式树T 都成立的结论，eval函数能正确地求出表示表达式的树的值。

示例 5.18

现在来考虑一下图5-22中的computeHt函数，图5-26重现了该函数的函数体。该函数接受（指向）节点n（的指针）作为参数，并计算n 的高度。我们将通过结构归纳法证明以下命题。

(1)        n->height = 0;
(2)        c = n->leftmostChild;
(3)        while (c != NULL) {
(4)            computeHt(c);
(5)            if (c->height >= n->height)
(6)                n->height = 1+c->height;
(7)            c = c->rightSibling;
           }

图 5-26　图5-22中computeHt(n)函数的函数体

命题S(T )。在对指向树T 根节点的指针调用computeHt时，T 中每个节点的正确高度都会被存储在该节点的height字段中。

依据。如果树T 只有一个节点n，那么在图5-26中的第(2)行，c 会被赋上NULL值，因为n 没有子节点。因此，第(3)行的测试会立即失败，而且while循环的循环体永远都不会执行。因为第(1)行会将n->height置为0（这对叶子节点而言是正确的值），所以可以得出结论，当T 只有一个节点时S(T )成立。

归纳。现在假设n 是有多个节点的树T 的根节点，那么n 至少有一个子节点。我们可以在归纳假设中假定，在第(4)行调用computeHt(c)时，以c 为根节点的子树中每个节点（包括c 本身）的height字段中都被装入了正确的高度。现在需要证明，第(3)行到第(7)行的while循环可以正确地将n->height置为比n 的子节点的最大高度大1。要做到这一点，就需要执行另一次归纳，这是嵌套在该结构归纳法证明过程中的，就像是程序中循环嵌套在另一个循环中那样。该归纳使用的是“普通的”归纳法而不是结构归纳法，它的命题如下。

命题S' (i )。在第(3)到第(7)行的循环执行i 次之后，n->height的值要比n 前i 个子节点的最大高度大1。

依据。依据是i=1的情况。因为n->height在循环外——第(1)行——会被置为0，并且肯定不会有比0还小的高度，所以第(5)行的测试会得到满足。第(6)行就会将n->height置为比n 的第一个子节点的高度大1。

归纳。假设S' (i )为真。也就是说，在循环的迭代i 次之后，n->height会比前i 个子节点的最大高度大1。如果有第i+1个子节点，那么第(3)行的测试会成功，而且会第i+1次执行循环体。第(5)行的测试会将新的高度与之前的最大高度相比较。如果新高度c->height比前i 个高度中最大值加1要小，就不用对n->height进行任何改变。这是对的，因为前i+1个子节点的最大高度是可以与前i 个子节点的最大高度相同的。不过，如果新的高度比之前的最大值大，第(5)行的测试就会成功，这样n->height就会被置为比第i+1个子节点的高度大1，这是正确的。

现在可以回到结构归纳了。当第(3)行的测试失败时，就已经考虑过n 的所有子节点了。内层的归纳S' (i )说明，当子节点的总数为i 时，n->height要比n 各子节点的最大高度大1。这就是n 的正确高度。将归纳假设S 应用于n 的各子节点，就得到结论：正确的高度已经存储到每个子节点的height字段中。因为已经得知n 的高度也已经正确地计算出来，所以可以得出结论：T 中所有节点都被赋上了它们正确的高度值。

现在已经完成了结构归纳法的归纳步骤，并得出结论：对每棵树调用computeHt都可以正确地计算树中每个节点的高度。

结构归纳法的模板
下面简述了进行正确的结构归纳法证明的过程。
1. 指定要证明的命题S(T )，其中T 是一棵树。
2. 证明依据，也就是只要T 是一棵单节点的树，S(T )就为真。
3. 建立归纳步骤，设T 是以r 为根节点的树，而且有k≥1棵子树，分别为T₁、T₂、…、T_k。表示假定有归纳假设，即S(T_i )对每棵子树T_i（i=1、2、…、k）都为真。
4. 证明在(3)中提到的假设下S(T )为真。

5.5.1　结构归纳法为何有效

要说明结构归纳法为何是一种有效的证明方法，其原因与普通归纳法有效的原因类似：如果结论为假，那么就会有个最小的反例，而且该反例既有可能违背依据，也可能违背归纳过程。也就是说，假设有命题S(T )，已经证明了它的依据和结构归纳步骤，而存在一棵树或多棵树可以让S 为假。设T₀是可以让S(T₀)为假的这样一棵树，并设T₀与让S 为假的任一棵树的节点一样少。

有两种情况。第一种，假设T₀由单个节点组成。那么根据依据，有S(T₀)为真，所以这种情况不可能发生。

现在就只剩下T₀有多个节点的情况了，这里假设T₀有m个节点，那么T₀就是由根节点r 与一个或多个子节点构成。设以这些子节点为根的树分别是T₁、T₂、…、T_k 。这里可以声明T₁、T₂、…、T_k 的节点数均不超过m-1。因为如果某棵树（假如是T_i）的节点数达到或超过m，那么由T_i（可能还有其他子树）和根节点r 组成的T₀就至少会有m+1个节点。这与T₀刚好有m 个节点的假设是矛盾的。

因为T₁、T₂、…、T_k 这些子树的节点数都不超过m-1，所以就可以知道这些树都不能违背S，因为选择了T₀是让S为假的最小子树。因此可知S(T₁)、S(T₂)、…、S(T_k)都为真。而假设已经得到证明的归纳步骤说明了S(T₀)也为真，这样又与T₀违背S 的假设产生了矛盾。

在考虑完这两种可能的情况后，我们就知道：不管一棵树只有一个节点还是有多个节点，T₀都不可能是S 的例外。因为S 是没有例外的，所以S(T )一定对所有的树T 都为真。

5.5.2　习题

1. 通过结构归纳法证明：

(a) 图5-15的前序遍历函数会以前序打印出树的标号；

(b) 图5-17中的后序函数会以后序列出标号。

2. * 假设分支系数为b 的单词查找树是用具有图5-6中所示格式的节点表示的。用结构归纳法证明：如果树T 有n 个节点，那么它的节点中有1+(b-1)n 个NULL指针。那么，共有多少非NULL指针？

3. * 节点的度是指节点所具有的子节点的数目。2用结构归纳法证明：在任意树T 中，节点的数目都要比节点的度之和大1。

2分支系数和度是相关的概念，但它们是不同的，分支系数是树中各节点度的最大值。

4. * 用结构归纳法证明：在任意树T 中，叶子节点的数目都要比具有右兄弟节点的节点的数目大1。

5. * 用结构归纳法证明：在任意用最左子节点右兄弟节点的数据结构表示的树T 中，NULL指针的数目都要比节点的数目大1。

6. * 在5.2节开始的部分，我们给出了树的递归定义和非递归定义。使用结构归纳法证明：每棵以递归方式定义的树在非递归定义下也是同样的树。

7. ** 证明习题(6)的逆命题：每棵以非递归方式定义的树在以递归方式定义时也是相同的树。

树的归纳的谬误形式
我们常常会想着对树的节点数进行归纳，就是假设命题对具有n 个节点的树成立，并证明它对具有n+1个节点的树也成立。如果不够谨慎，就很可能作出这种荒谬的证明。
在第2章中对整数进行归纳证明时，我们提出了一种合理的方法，就是试着用S(n)证明命题S(n+1)，并称这种方法为“后靠”。有时候有人可能把这一过程看作从S(n)开始并证明S(n+1)，称这种方法为“前推”。在整数的情况下，这基本上是相同的意思。不过，对树而言，我们不能先假设命题对具有n 个节点的树成立，并在某个位置加上一个节点，然后就说证明了结果对所有具有n+1个节点的树都成立。
例如，声明S(n)：“所有具有n 个节点的树都有一条长度为n-1的路径。”n=1的依据情况显然为真。在错误的“归纳”中，可能会作出如下论证：“假设有一棵具有n 个节点的树T，它有一条长n-1的路径，假如说是到节点v 的。给v 加上子节点u。现在就有了一棵具有n+1个节点的树，而且它有一条长度为n 的路径，这样就证明了归纳步骤。”
当然，上述论证是谬误的，因为它没有证明结果对所有具有n+1个节点的树都为真，而只是证明了对选出的一些树为真。正确的证明不能是从n个节点“前推”到n+1个节点，因为我们不会从这一过程得出所有可能的树。我们必须从任意具有n+1个节点的树开始“后靠”，小心地选出一个节点，并将其删除，从而得到一棵具有n个节点的树。

5.6　二叉树

本节展现了另一种树——二叉树，它和5.2节介绍的“普通”树是不同的。在二叉树中，节点最多有两个子节点，而且并不是自然地从左起为子节点计数，而是有两个“槽”，其中一个用来存放左子节点，另一个用来存放右子节点。这两个槽中可能有一个为空，也可能两个都为空。

图 5-27　两棵各只有两个节点的二叉树

示例 5.19

图5-27展示了两棵二叉树。它们均以n₁为根节点。第一棵树以n₂为左子节点，且没有右子节点。而第二棵树则没有左子节点，n₂是其根节点的右子节点。在这两棵树中，n₂都是既没有左子节点也没有右子节点。它们均为只有两个节点的二叉树。

接下来将按照如下方式递归地定义二叉树。

依据。空树是二叉树。

归纳。如果r 是节点，而且T₁和T₂都是二叉树，那么以r 为根节点，T₁为左子树，T₂为右子树可以组成一棵二叉树，如图5-28所示。也就是说，T₁的根节点就是r的左子节点，除非T₁是空树，因为这种情况下r 没有左子节点。同样地，T₂的根节点是r 的右子节点，除非T₂是空树，因为这种情况下r没有右子节点。

图 5-28　二叉树的递归定义

5.6.1　二叉树的术语

5.2节引入的路径、祖先和子孙的概念也适用于二叉树。也就是说，左子节点和右子节点都归为“子节点”。路径仍然是节点m₁、m₂、…、m_k 按照m_i+1是m_i（i=1,2,…,k-1）的（左或右）子节点的方式串联起来的序列。这条路径称为从m₁到m_k 的路径。k=1的情况也是可以的，这样的话路径上就只有一个节点。

如果某个节点存在两个子节点，那么这两个子节点就互为兄弟节点。叶子节点是指既没有左子节点也没有右子节点的节点，还可以认为叶子节点是左子树和右子树都为空树的节点。内部节点则指不是叶子节点的节点。

路径长度、高度和深度的定义与普通的树是完全相同的。二叉树路径的长度要比节点数小1，也就是说，长度就是路径上父子关系对的数量。节点n 的高度是指n 到其子孙叶子节点最长路径的长度。二叉树的高度就是其根节点的高度。节点n 的深度是指从根节点到n 的路径的长度。

示例 5.20

图5-29展示了具有3个节点的二叉树可能形成的5种形状。在图5-29所示的每棵二叉树中，n₃都是n₁的子孙，并存在从n₁到n₃的路径。n₃在每棵树中都是叶子节点，而n₂在中间那棵树中是叶子节点，在其他4棵树中都是内部节点。

n₃在每棵树中的高度都为0，n₁除了在中间那棵树的高度为1之外，在其他树中的高度都为2。每棵树的高度都与n₁在那棵树中的高度一致。节点n₃除了在中间那棵树的深度为1之外，在其他树中深度都为2。

{%}

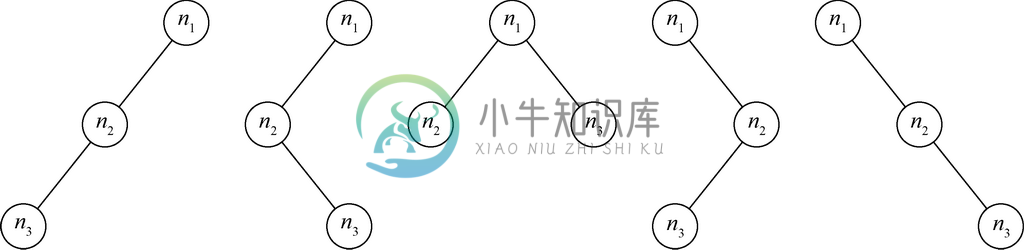
图 5-29　具有3个节点的5种二叉树

（普通）树和二叉树的区别
尽管二叉树要求区分子节点是左子节点还是右子节点，但普通的树却没有这样的限制，理解这一点是很重要的。也就是说，二叉树不仅是节点的子节点数全都不多于两个的树。图5-27中的两棵树不仅是互不相同，而且与由根节点及根节点的子节点组成的如下普通树也没有关系。
这里还存在一个技术上的区别。尽管树的定义中表示树至少有一个节点，但二叉树中可以存在空树，也就是没有节点的树。

5.6.2　二叉树的数据结构

有一种很自然的方式可以用于表示二叉树。节点可以表示为具有leftChild和rightChild这两个分别指向左子节点和右子节点的字段的记录。出现在这两个字段中的NULL指针就表示对应的左子树或右子树为空——也就是说节点没有左子节点或右子节点。

二叉树可以表示为指向其根节点的指针。空二叉树很自然地就被表示为NULL。因此，如下类型定义就表示二叉树。

typedef struct NODE *TREE;
struct NODE {
    TREE leftChild, rightChild;
};

在这里，“指向节点的指针”类型名为TREE，因为这一类型最常见的用途就是表示树和子树。我们既可以将leftChild和rightChild字段解释为指向子节点的指针，也可以将其解释为指向左右子树本身的指针。

此外，还可以为表示NODE的结构体添加标号字段，并（或）可以添加指向父节点的指针。请注意，父指针的类型是*NODE，或是TREE的等价类型。

5.6.3　对二叉树的递归

有很多针对二叉树的自然算法可以通过递归的方式来定义。这里递归的模式要比图5-13中普通树的递归模式更具局限性，因为操作只能发生在左子树被探索之前、两棵子树的探索之间，或是两棵子树都探索完之后。对二叉树进行递归的模式如图5-30所示。

{
    action A₀;
    对左子树的递归调用;
    action A₁;
    对右子树的递归调用;
    action A₂;
}

图 5-30　二叉树递归算法的模板

示例 5.21

具有二元运算符的表达式树可以用二叉树表示。这些二叉树是很特殊的，因为节点要么有两个子节点，要么就没有子节点（一般而言，二叉树可以有只有一个子节点的节点）。例如，图5-31重现了图5-14中的表达式树，这棵表达式树可以视作二叉树。

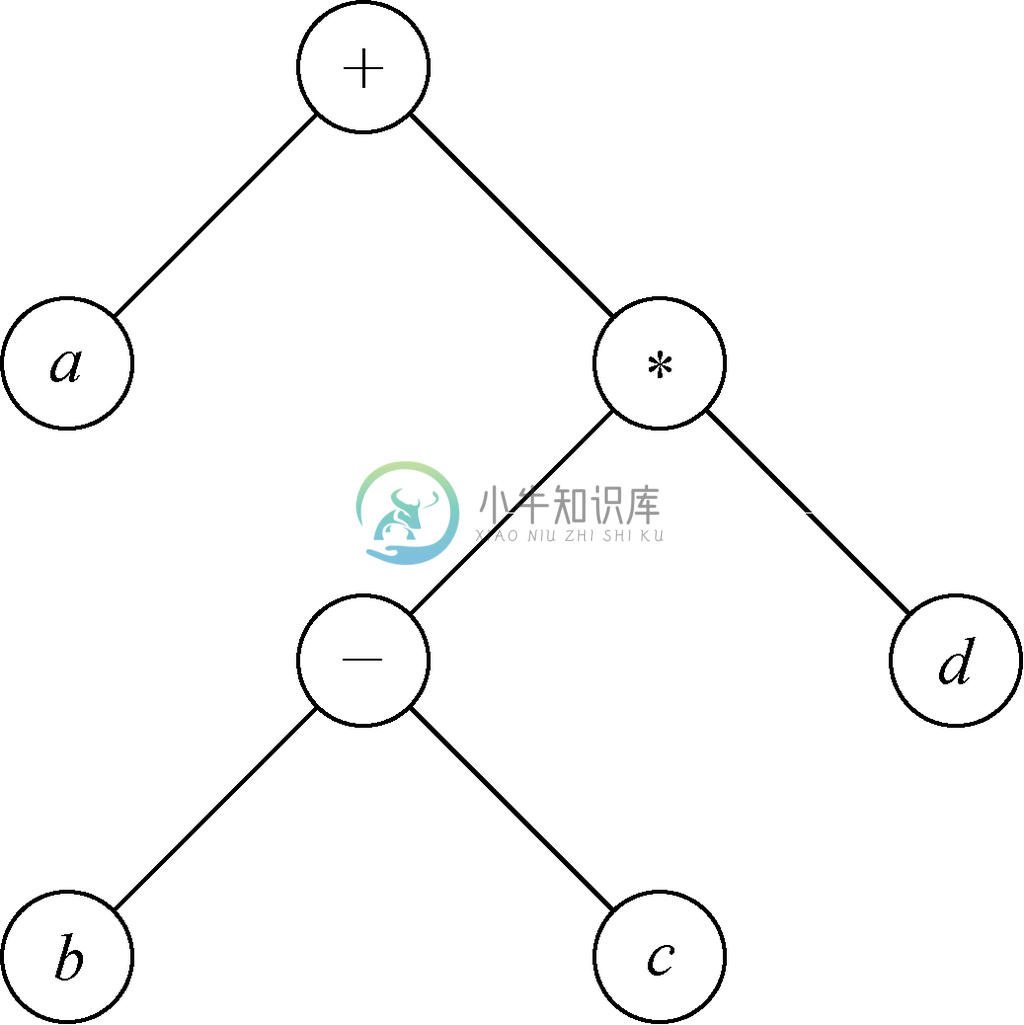
图 5-31　由二叉树表示的表达式a+(b-c )*d

假设为节点和树定义如下类型：

typedef struct NODE *TREE;
struct NODE {
    char nodeLabel;
    TREE leftChild, rightChild;
};

那么图5-32就展示了用来以前序列出二叉树T 中各节点标号的递归函数。

     void preorder(TREE t)
     {
(1)      if (t != NULL) {
(2)          printf("%c\n", t->nodeLabel);
(3)          preorder(t->leftChild);
(4)          preorder(t->rightChild);
         }
     }

图 5-32　二叉树的前序排列

该函数的行为与图5-15中用于处理普通树的同名函数相似。主要区别在于，当图5-32中的函数遇到叶子节点时，它会对（缺失的）左右子节点调用自身。这些调用会立即返回，因为当t为NULL时，整个函数体只有第(1)行的测试会执行。如果将图5-32中的第(3)行和第(4)行替换为：

(3)  if (t->leftChild != NULL) preorder(t->leftChild);
(4)  if (t->rightChild != NULL) preorder(t->rightChild);

就可以多节省一些调用。不过，这样就不能防止其他函数以NULL为参数调用preorder了。因此，为了安全起见，要保留第(1)行的测试。

5.6.4　习题

1. 编写函数，使其能打印出二叉树节点（标号）的中序排列。假设这些节点是用如本节所描述那样具有左子节点和右子节点指针的记录表示的。

2. 编写函数，使其接受二叉表达式树，并打印出它所表示的表达式带有全部括号的版本。假设这里使用了与习题1相同的数据结构。

3. * 重复习题2，但只打印所需的括号，假设这里使用的是常用的算术运算符优先级和结合性。

4. 编写函数，使其能得出二叉树的高度。

5. 如果二叉树的节点同时具有左子节点和右子节点，那么就说该节点是完全的。用结构归纳法证明：二叉树中完全节点的数量，要比叶子节点的数量少1。

6. 假设用左子节点右子节点记录类型表示二叉树。用结构归纳法证明：NULL指针的数量要比节点的数量大1。

7. ** 树可以用来表示递归调用。每个节点都表示某个函数F的一次递归调用，而其子节点则表示F执行的调用。在本题中，要考虑对4.5节给出的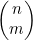 $\begin{pmatrix}n\\m\end{pmatrix}$ 进行递归，根据的递归关系是 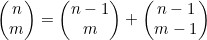$\begin{pmatrix}n\\m\end{pmatrix}=\begin{pmatrix}n-1\\m\end{pmatrix}+\begin{pmatrix}n-1\\m-1\end{pmatrix}$ 。每次调用都可以用一棵二叉树表示。如果某个节点对应着 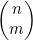$\begin{pmatrix}n\\m\end{pmatrix}$ 的计算，而且不属于依据情况（m=0和m=n），那么其左子节点就表示 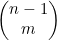$\begin{pmatrix}n-1\\m\end{pmatrix}$ ，而右子节点表示 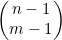$\begin{pmatrix}n-1\\m-1\end{pmatrix}$ 。如果该节点表示的是依据情况，那么它就既没有左子节点，也没有右子节点。

(a) 通过结构归纳法证明：根节点对应着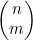 $\begin{pmatrix}n\\m\end{pmatrix}$ 的二叉树刚好有 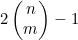$2\begin{pmatrix}n\\m\end{pmatrix}-1$ 个节点。

(b) 利用(a)证明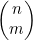： $\begin{pmatrix}n\\m\end{pmatrix}$ 对应递归算法的运行事件是 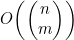$O\biggl(\begin{pmatrix}n\\m\end{pmatrix}\biggr)$ 。请注意，该运行时间因此也就是O(2ⁿ)，不过后者是平滑但非紧边界。

中序遍历
除了二叉树的前序排列和后序排列外，二叉树就只有一种有意义的节点排列方式了。在二叉树中，探索完左子树之后，而在探索右子树之前（即图5-30中操作T₁的位置）列出每个节点，这样就形成了二叉树节点的中序排列。例如，在图5-31所示的树中，中序排列就是a+b-c *d。
对表示表达式的二叉树进行前序遍历，得到的就是该表达式的前缀形式，对同样的树进行后序遍历，则会得到表达式的后缀形式。而中序遍历则几乎会产生原始的，或者说是中缀形式的表达式，不过该表达式是没有括号的。也就是说，图5-31中的树表示的表达式a+(b-c ) *d 与其中序排列a+b-c *d 是不同的，差别只是后者中少了必要的括号而已。
要确保所需的括号出现，可以为所有的运算符加上括号。在这种修改后的中序遍历中，在探索左子树之前执行的操作A₀，会检查节点的标号是否为运算符，而且，如果是运算符的话，就会打印“(”，也就是左括号。同样地，如果标号是运算符，探索完两棵子树后执行的操作A₂就会打印右括号“)”。将该规则应用于图5-31所示的二叉树，得到的结果会是(a+((b-c)*d))，这就有了b-c 两侧一对必要的括号，以及两对多余的括号。

对二叉树进行结构归纳
与普通树一样，结构归纳法也适用于二叉树。其实还可以使用更简单的模式，这种模式下的依据是空树。下面就是对这一技巧的总结。
1. 指定要证明的命题S(T )，其中T 是一棵二叉树。
2. 证明依据，即证明若T 是空树，则S(T )为真。
3. 设T 是以r 为根节点，并以T_L 和T_R 为子树的二叉树，以此构建归纳步骤。声明假定有归纳假设，即S(T_L)和S(T_R)为真。
4. 在(3)中提到的假设下证明S(T )为真。

5.7　二叉查找树

各种计算机程序中有一种同样的活动，就是维护这样一组值，用户希望：

1. 向这组值中插入元素；

2. 从这组值中删除元素；

3. 查找某元素，看看它是否在这组值中。例子之一是英语词典，我们时不时地会往里面插入一些新单词，比如fax；删除一些不再使用的单词，比如aegilops；或者是要查找一串字母，看看其是否为单词，例如，这是拼写检查器程序的一部分。

因为这个例子是我们非常熟悉的，所以不管其具体用途是什么，只要是可以按照上述定义对其执行插入、删除和查找操作的一组值，都叫作词典。再举个词典的例子，某教授可能要记录选修某课程学生的花名册。偶尔会有学生被加入这门课程（插入），或是退出该课程（删除），或是需要弄清某个学生是否选修了该课程（查找）。

二叉查找树这种带标号的二叉树是实现词典的一个好方法。假设节点的标号是按照“小于”顺序（我们会将其写作<）从一组值中选出的。例子包括具有一般小于顺序的实数或整数，或是有着用<表示的词典顺序或字母表顺序的字符串。

二叉查找树（Binary Search Tree，BST）是一种带标号的的二叉树，以下属性对这种二叉树的每个节点x 都成立：x 的左子树中所有节点的标号都小于x 的标号，而其右子树中所有节点的标号都大于x 的标号。这种属性被称为二叉查找树属性。

示例 5.22

图5-33展示了对应着集合｛Hairy，Bashful，Grumpy，Sleepy，Sleazy，Happy｝的二叉查找树，其中<顺序是词典顺序。请注意，根节点左子树在词典顺序上都小于Hairy，而右子树在字典顺序上都大于它。这一属性对该树中的每个节点都成立。

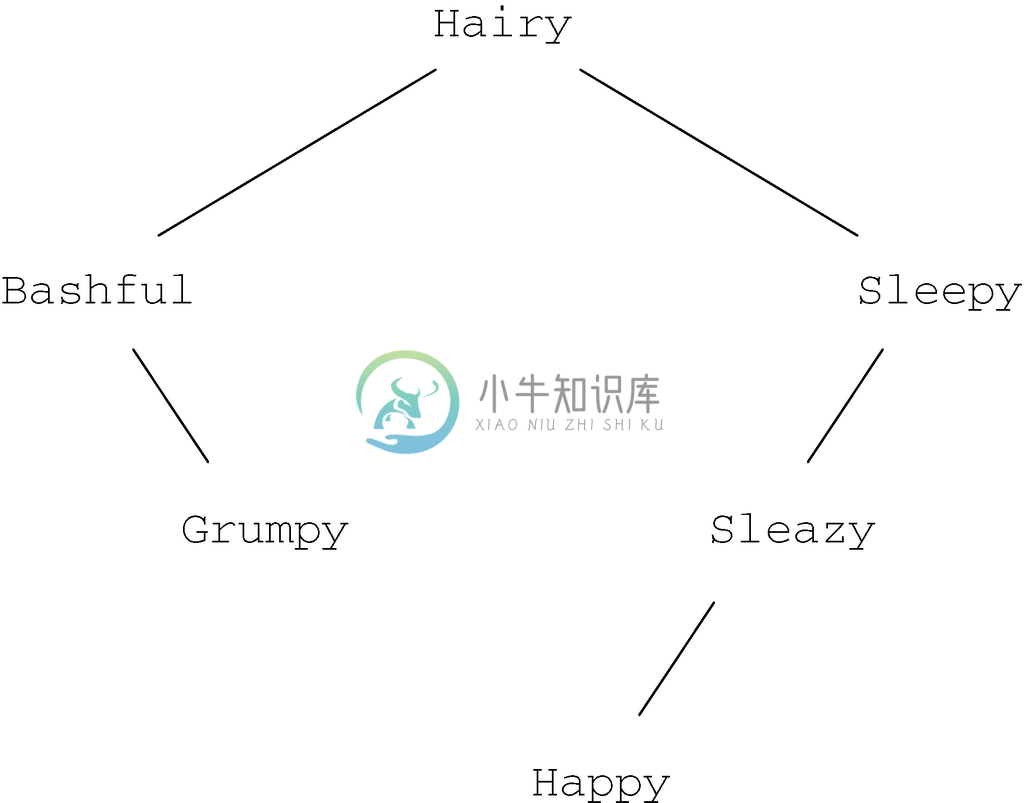
图 5-33　具有6个带字符串标号的节点的二叉查找树

5.7.1　用二叉查找树实现词典

我们可以将二叉查找树表示为任何带标号的二叉树。例如，可以按如下形式定义NODE类型。

typedef struct NODE *TREE;
struct NODE {
    ETYPE element;
    TREE leftChild, rightChild;
};

二叉查找树被表示为指向二叉查找树根节点的指针。元素的类型ETYPE应该得到合理的设置。在本章所有的程序中，都将假设ETYPE为int类型，从而使元素间的比较可以直接用算术比较运算符<、==和>完成。在涉及词典顺序比较的例子中，可以假设程序中的比较由诸如2.2节中讨论过的lt、eq 和gt 这样的比较函数完成。

5.7.2　二叉查找树中元素的查找

假设想在由二叉查找树T 表示的某词典中查找某个元素x。如果将x 与T 的根节点处的元素加以比较，就可以利用二叉查找树属性快速找到x，或确定x 没有出现。如果x 在根节点处，就完成了查找。否则，如果x 比根节点处的元素小，x 就只可能在左子树中被找到（根据二叉查找树属性），而如果x 比根节点处的元素大，x 就只可能出现在右子树中（还是因为二叉查找树属性）。也就是说，可以通过以下递归算法表示查找操作。

依据。如果树T 是空树，那么x 未出现。如果树T 非空，而且x 在根节点，那么x 就出现了。

归纳。如果T 非空而x 未在根节点位置，设y 是T 根节点处的元素。如果x< y，则只在根节点的左子树中查找x；如果x>y，则只在y 的右子树中查找x。二叉查找树属性保证x 不可能出现在没有查找的那棵子树中。

抽象数据类型
诸如插入、删除和查找这种可能对一组对象或特定类别执行的一系列操作，有时称为抽象数据类型或ADT。这一概念也会被称为类或模块。我们将在第7章中研究若干抽象数据类型，而在本章中，我们会看到其中一个：优先级队列。
ADT可以有多种抽象实现。例如，在本节中可看到二叉查找树是一种实现词典ADT的好方法。表是另一种看似可靠实则经常效率低下的实现词典ADT的方式。7.6节将介绍散列，另一种不错的词典实现方式。
每种抽象实现依次可通过若干种不同的数据类型来具体实现。举例来说，可以使用二叉树的左子节点右子节点实现作为实现二叉查找树的数据结构。这一数据结构，加上用于插入、删除和查找的恰当函数，就成了词典ADT的一种实现。
在程序中使用ADT的一个重要原因是，ADT底层的数据只能通过ADT的操作（比如插入）来访问。这一限制是防御性编程的一种形式，可以防止操作数据的函数以意料之外的方式对数据进行偶发变更。使用ADT的第二个重要原因在于，ADT让我们可以重新设计数据结构和实现其操作的函数，在不担心会为程序其余部分引入错误的前提下，这样可能提高操作的效率。如果只有用于ADT操作的接口函数被正确地重写，就不会出现新的错误。

示例 5.23

假设想要在图5-33的二叉查找树中查找Grumpy。将Grumpy与根节点处的Hairy相比较，发现Grumpy在词典顺序上要先于Hairy，因此要对左子树调用lookup。

左子树的根节点是Bashful，而将该标号与Grumpy相比，发现前者要先于后者。因此要对Bashful的右子树递归地调用lookup。现在发现Grumpy在这一子树的根节点处，并返回TRUE。这些步骤是由具有图5-34模式的词典顺序比较函数执行的。

     BOOLEAN lookup(ETYPE x, TREE T)
     {
(1)      if (T == NULL)
(2)          return FALSE;
(3)      else if (x == T->element)
(4)          return TRUE;
(5)      else if (x < T->element)
(6)          return lookup(x, T->leftChild);
         else /* x 一定是大于T->element */
(7)          return lookup(x, T->rightChild);
     }

图 5-34　如果x 在T 中，函数lookup(x,T)会返回TRUE，否则返回FALSE

更具体地讲，图5-34中的递归函数lookup(x,T)使用左子节点右子节点数据结构实现了这一算法。请注意，lookup返回的是BOOLEAN类型的值，这一类型实际上与int相同，不过它定义的值只有TRUE和FALSE，分别定义为1和0。BOOLEAN类型是在1.6节中引入的。此外，请注意，这里的lookup函数只接受能由=、<等运算符比较的类型。如果要让它处理示例5.23中用到的字符串那样的数据，就需要重写。

在第(1)行，lookup会确定T 是否为空。如果不为空，那么lookup在第(3)行会确定x 是否存储在当前节点。如果x 不在该节点，那么lookup就会根据x 是小于还是大于当前节点存储的元素，递归地查找左子树或右子树。

5.7.3　二叉查找树元素的插入

向二叉查找树T 中增加一个新元素x 是很简单的，以下递归算法简要描述了处理思路。

依据。如果T 是空树，用一棵由单个节点构成的树替代T，并在该节点处放上x。如果T 非空而且其根节点处有元素x，那么x 已经在字典中，不需要再做任何事情。

归纳。如果T 非空，而且x 不在其根节点处，那么如果x 小于根节点处的元素，就将x插入左子树，如果x 大于根节点处的元素，就将x 插入右子树。

如图5-35所示的insert(x,T)函数为左子节点右子节点数据结构实现了这一算法。在第(1)行发现T的值为NULL时，就会新建一个节点，该节点就成了树T。第(2)到第(5)行会创建该树，并在第(10)行返回。

      TREE insert(ETYPE x, TREE T)
      {
 (1)      if (T == NULL) {
 (2)          T = (TREE) malloc(sizeof(struct NODE));
 (3)          T->element = x;
 (4)          T->leftChild = NULL;
 (5)          T->rightChild = NULL;
          }
 (6)      else if (x < T->element)
 (7)          T->leftChild = insert(x, T->leftChild);
 (8)      else if (x > T->element)
 (9)          T->rightChild = insert(x, T->rightChild);
(10)      return T;
      }

图 5-35　insert(x,T)函数将x 添加到T 中

如果在T 的根节点处没找到x，那么在第(6)到第(9)行，会根据相应的情况对左子树或右子树调用insert函数。被该插入操作修改过的子树，会分别在第(7)或第(9)行成为T 的根节点的左子树或右子树的新值。第(10)行会返回增加过元素的树。

请注意，如果x 在T 的根节点，那么第(1)、第(6)和第(8)行的测试都不会成功。这种情况下，insert会在什么都不做的情况下返回T，这是正确的，因为x 已经在树中了。

示例 5.24

继续示例5.23的问题，从技术上理解，对字符串进行比较需要的代码与图5-35相比稍有不同，图5-35中<这样的算术比较要替代为对lt 这样恰当定义的函数的调用。图5-36展示了向图5-33插入Filthy后的二叉查找树。首先对根节点调用insert，发现Filthy<Hairy。因此，在图5-35的第(7)行，对左子节点调用insert。结果发现Filthy>Bashful，所以接着在第(9)行对右子节点调用insert。这样就到了Grumpy，它从词典顺序上在Filthy之后，因此就要对Grumpy的左子节点调用insert。

指向Grumpy左子节点的指针为NULL，所以在第(1)行必须创建一个新节点。这棵单节点树会返回给Grumpy节点处对insert的调用，而且在第(7)行该树会被安置为Grumpy左子节点的值。带有Grumpy和Filthy的修改过的树会返回给标号为Bashful的节点处对insert的调用。然后，以Bashful为根节点的新树就成了整棵树根节点的左子树。最终的树如图5-36所示。

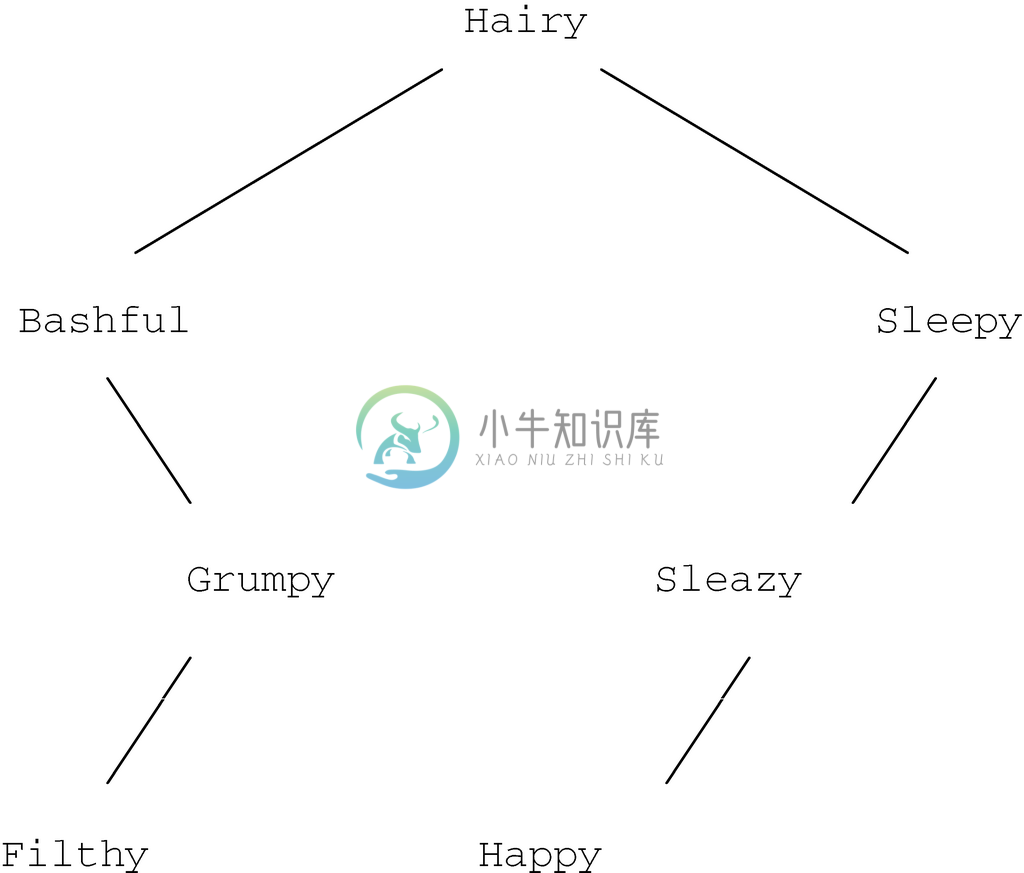
图 5-36　插入Filthy之后的二叉查找树

5.7.4　二叉查找树元素的删除

从二叉查找树中删除某个元素x 要比查找或插入复杂一些。首先，要找出含有x 的节点；如果没有这样的节点，就算是完事了，因为x 不在这棵要处理的树里头。如果x 在叶子节点处，那么直接删除该叶子节点就行了。不过，如果x 是某个内部节点n，就不能直接删除该节点，因为这样做会破坏树的连通性。

我们必须以某种方式对树进行重新排列，从而在维持二叉查找树属性的同时让x 从树中消失。这会有两种情况。第一种，如果n 只有一个子节点，就用该子节点代替n，这样二叉查找树的属性就得到了保持。

第二种情况，假设n 的两个子节点都存在。一种策略就是找到标号为y 的节点m，它是n 右子树中最小的元素，并在节点n 处用y 代替x，如图5-37所示。然后就可以从右子树中删除节点m。

{%}

图 5-37　要删除x，先删除包含右子树中最小元素y 的节点，然后将节点n处的标号由x 替换为y

此时二叉查找树属性继续成立。原因在于，x 比n 的左子树中的所有元素都大，而y 大于x（因为y 在n 的右子树中），所以y 也比n 左子树的所有元素都大。因此，就n 的左子树而言，y 是适合于位置n 的元素。而对n 的右子树来说，y 也是适合作为根节点的，因为选出的y 是右子树中的最小元素。

     ETYPE deletemin(TREE *pT)
     {
         ETYPE min;

(1)      if ((*pT)->leftChild == NULL) {
(2)          min = (*pT)->element;
(3)          (*pT) = (*pT)->rightChild;
(4)          return min;
         }
         else
(5)          return deletemin(&((*pT)->leftChild));
     }

图 5-38　deletemin(pT)函数会删除并返回T 的最小元素

如图5-38所示，可以很方便地定义deletemin(pT)函数从非空二叉查找树中删除含最小元素的节点，并返回最小元素的值。我们给该函数传入的参数是指向树T 的指针的地址。该函数中所有对T 的引用都是通过该指针间接完成的。

我们给函数传入的参数，是指向某个位置的指针，而在这个位置可以找到指向节点（即树）的指针，这种风格的树操作叫作按引用调用。这在图5-38中是很关键的，因为第(3)行的指针指向左子节点为NULL的节点m，我们希望将这一指针替代为另一个指针，节点m 的rightChild字段中的指针。如果deletemin的参数是指向节点的指针，那么这种改变就会在对deletemin的调用中发生，而且树中的指针其实不会改变。顺便说一下，也可以使用按引用调用来实现插入操作。在那种情况下，可以直接对树进行修改，而不必像图5-35中所做的那样返回修改过的树。这里将这一修订过的insert函数留作本节习题。

现在来看看图5-38的工作原理。沿着左子节点向下寻找，直到在图5-38的第(1)行找到左子节点为NULL的节点，就找到了最小的元素。在该节点m 处的元素y 一定是该子树中最小的元素。原因在于，这里完全是循着左子节点向下寻找的，这样一来y 要比m 在该子树中的任一祖先都小。而子树中其他节点要么是在m 的右子树中，根据二叉查找树属性这些元素肯定大于y，要么是在m 的某个祖先的右子树中。右子树中的元素肯定比m 的某个祖先处的元素大，因此也就大于y，如图5-39所示。

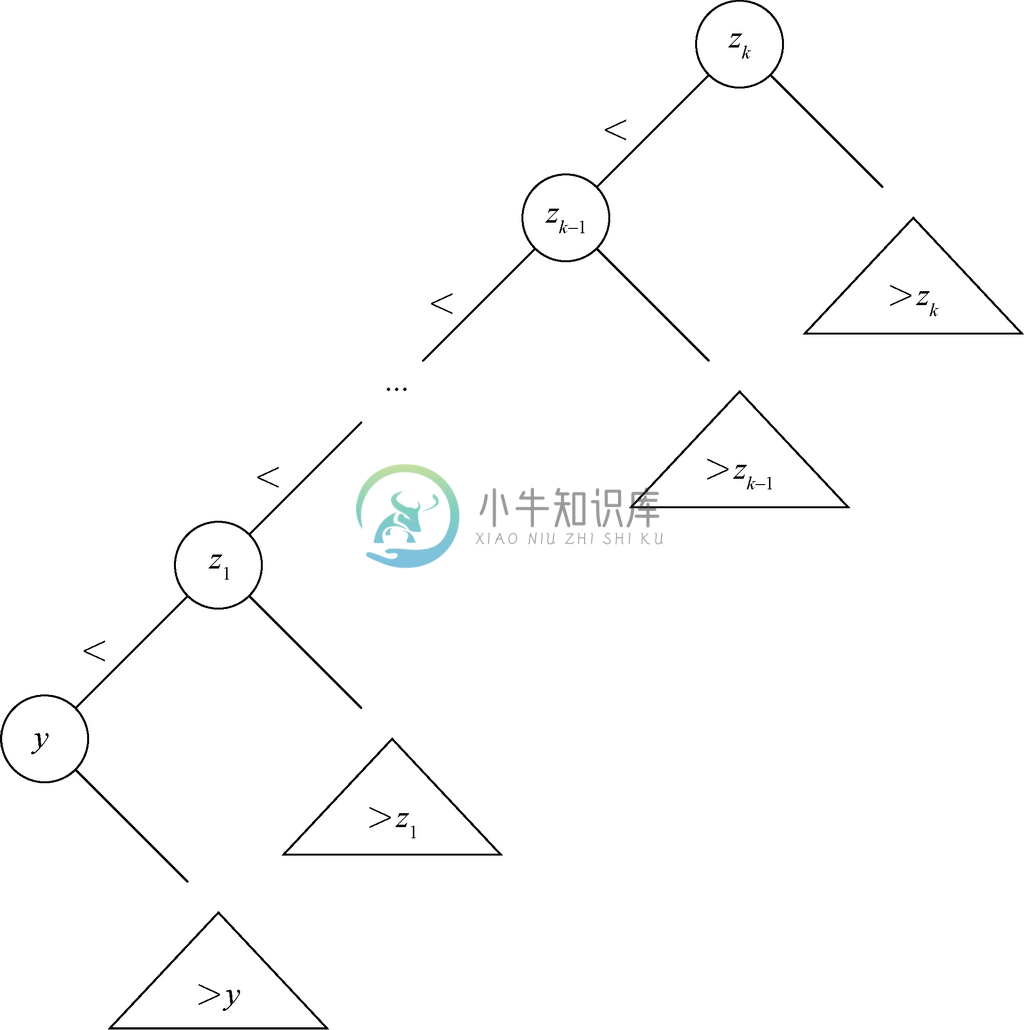
图 5-39　右子树中所有其他元素都大于y

在子树中找到最小的元素后，在第(2)行会记录下它的值，并在第(3)行用它的右子树代替最小元素所在节点。请注意，在从子树中删除最小元素时，总是有着最简单的删除情况，因为不存在左子树。

还有一点与deletemin相关的内容就是，当第(1)行的测试失败时，就意味着还没到达最小元素，就要继续处理左子节点。这一步骤是通过第(5)行的递归调用完成的。

deletemin(x,pT)函数如图5-40所示。如果pT指向空树T，就没什么要做的，而且第(1)行的测试会确保什么事都没做。此外，第(2)行和第(4)行的测试会处理x 不在根节点的情况，会根据具体情况重定向到左子树或右子树。如果到达第(6)行，那么x 就一定在T 的根节点位置，而且我们必须替换该根节点。第(6)行会测试左子节点是否可能为NULL，若为NULL，那么就可以在第(7)行直接将T 替换为其右子树。同样地，如果在第(8)行发现右子节点为NULL，那么就用T 的左子树来替代T。请注意，如果根节点的两个子节点都为NULL，那么就在第(7)行将T 替换为NULL。

      void delete(ETYPE x, TREE *pT)
      {
 (1)      if ((*pT) != NULL)
 (2)          if (x < (*pT)->element)
 (3)              delete(x, &((*pT)->leftChild));
 (4)          else if (x > (*pT)->element)
 (5)              delete(x, &((*pT)->rightChild));
              else /* 这里，x 在(*pT)的根节点处 */
 (6)              if ((*pT)->leftChild == NULL)
 (7)                  (*pT) = (*pT)->rightChild;
 (8)              else if ((*pT)->rightChild == NULL)
 (9)                  (*pT) = (*pT)->leftChild;
                  else /* 这里的两个子节点都不为NULL */
(10)                  (*pT)->element =
                              deletemin(&((*pT)->rightChild));
      }

图 5-40　delete(x,pT)函数从T 中删除元素x

两个子节点均不为NULL的情况是在第(10)行处理的。在这里会调用deletemin，返回右子树的最小元素y，并从该子树中删除y 。第(10)行的赋值操作会在T 的根节点处用y 代替x 。

示例 5.25

如果使用类似delete（但能够比较字符串）的函数从图5-36中的二叉查找树删除Hairy，结果如图5-41所示。因为Hairy在具有两个子节点的节点中，所以delete会调用deletemin函数，从根节点的右子树中删除并返回最小的元素Happy，然后Happy就成了曾存放Hairy的该树根节点的标号。

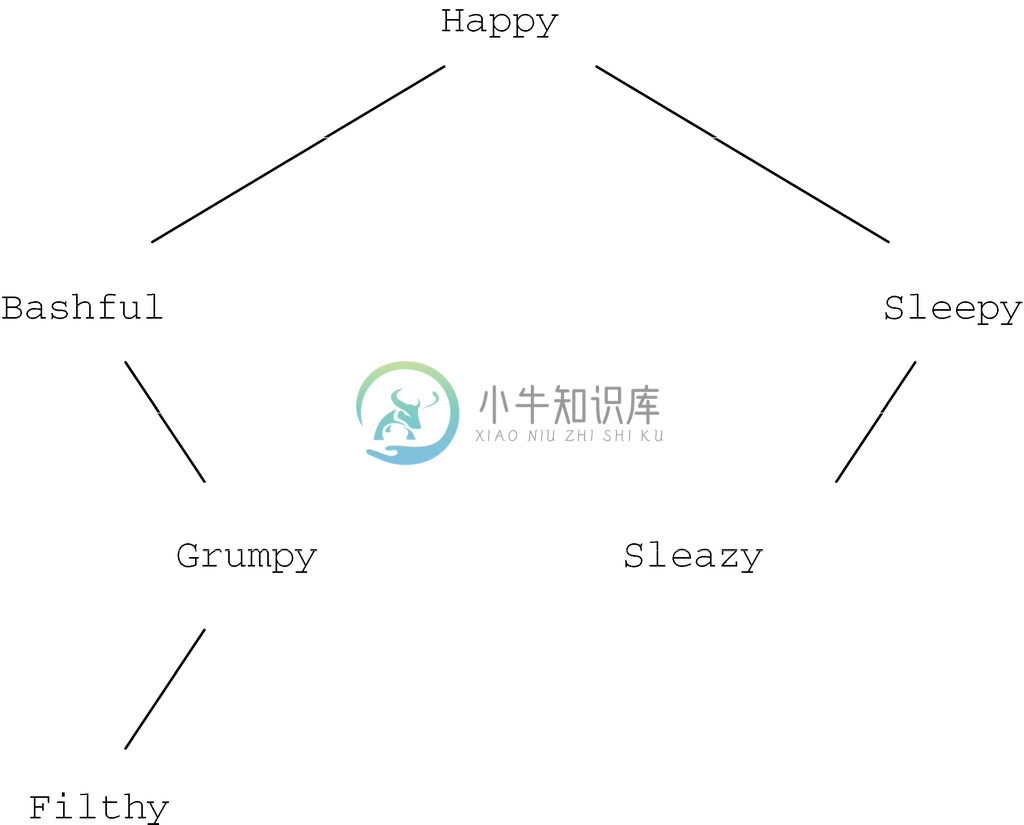
图 5-41　删除Hairy后的二叉查找树

5.7.5　习题

1. 假设使用最左子节点右兄弟节点表示法实现二叉查找树。重新编写适用于这一数据结构的实现了插入、删除和查找这些词典操作的函数。

2. 如果按顺序插入单词：Doc、Dopey、Inky、Blinky、Pinky和Sue，会使图5-33中的二叉查找树变成什么样？然后，依次删除Doc、Sleazy和Hairy后又会怎样？

3. 用对字符串的词典比较代替对整数的算术比较，重新编写lookup、insert和delete函数。

4. * 重新编写insert函数，使得树参数可以按引用传递。

5. * 在本节中，我们曾以“按引用调用”的方式编写过delete函数。不过，也可以用编写insert函数的风格编写该函数，即接受树作为参数，而不是接受指向树的指针作为参数。编写这一版本的delete操作。注意：让deletemin返回修改过的树并非真正可能，因为它还必须返回最小的元素。我们可以重新编写deletemin，使其返回同时具有新树和最小元素的结构体。

6. 要删除带有两个子节点的节点，除了通过在右子树中找到最小元素，还可以在左子树中找到最大的元素，并用它替代删除的元素。重新编写来自图5-38和图5-40的delete和deletemin函数，从而融入这种修改。

7. * 在需要删除某个具有父节点p、（非空的）左子节点l 和（非空的）右子节点r 的节点n 处的元素时，另一种处理删除操作的方式是，找出n 的右子树中存放最小元素的节点m。接着，让r 代替n 成为p 的左子节点或右子节点，并让l 成为m 的左子节点。请注意，m 之前不能有左子节点。证明这一系列改变为何会保留二叉查找树属性。大家是否愿意选择这一策略替代5.7节中描述过的那种？提示：对这两种方式而言，考虑它们对路径长度的影响。正如我们将在5.8节中看到的，短路径会让操作运行得更迅速。

8. * 在本习题中，考虑图5-39所示的二叉查找树。通过对i 的归纳证明，如果1≤i≤k，那么y< z_i 。然后，证明y 是以z_k 为根节点的树中最小的元素。

9. 编写完整的C语言程序，实现存储整数的词典。接受形为xi 的命令，其中x是字母i（插入）、d（删除）和l（查找）中的一个。整数i 是该命令的参数，就是有待插入、删除或查找的整数。

5.8　二叉查找树操作的效率

二叉查找树提供了一种相当快速的词典实现。首先请注意，插入、删除和查找操作各会进行若干次递归调用，调用次数等于所经过的路径的长度。但该路径必须包含达到右子树最小元素的路线，以防deletemin被调用。对lookup、insert、delete和deletemin函数进行简单的分析，可知各操作都花费O(1)的时间，而且要加上一次递归调用的时间。此外，因为该递归调用总是在当前节点的子节点处进行的，所以每次成功调用中节点的高度至少要减少1。

因此，如果以指向某个高度为h 的节点的指针调用这些函数所花的时间为T(h)，就有以下递推关系来为T(h)确定上界。

依据。T(0)=O(1)。也就是说，在对叶子节点调用函数时，该调用要么终止，不再有进一步的调用，要么以NULL参数进行一次递归调用，接着会返回而不再继续调用。这些工作所花时间为O(1)。

归纳。对h≥1，T(h)≤T(h-1)+O(1)。也就是说，对任何内部节点调用函数所花的时间，都等于O(1)加上对高度至多为h-1的节点进行一次递归调用所花的时间。如果作出T(h)会随着h 的增加而增加这一合理假设，那么该递归调用的时间不会大于T(h-1)。

该递推关系的解是O(h)，正如3.9节中讨论过的那样。因此，对具有n 个节点的二叉查找树执行词典操作的运行时间至多与该树的高度成比例。不过具有n 个节点的二叉查找树通常高度为多少呢？

5.8.1　最坏情况

在最坏的情况下，二叉树的所有节点都排列在一条路径上，就像图5-42所示的树那样。例如，取一列有序的k个元素，将这些元素一个个地依次插入一棵空树，就可以形成这样的树。也有不全由右子节点组成，而是由左右子节点混合组成的单路径树，其路径上的内部节点既可能是左子节点也可能是右子节点。

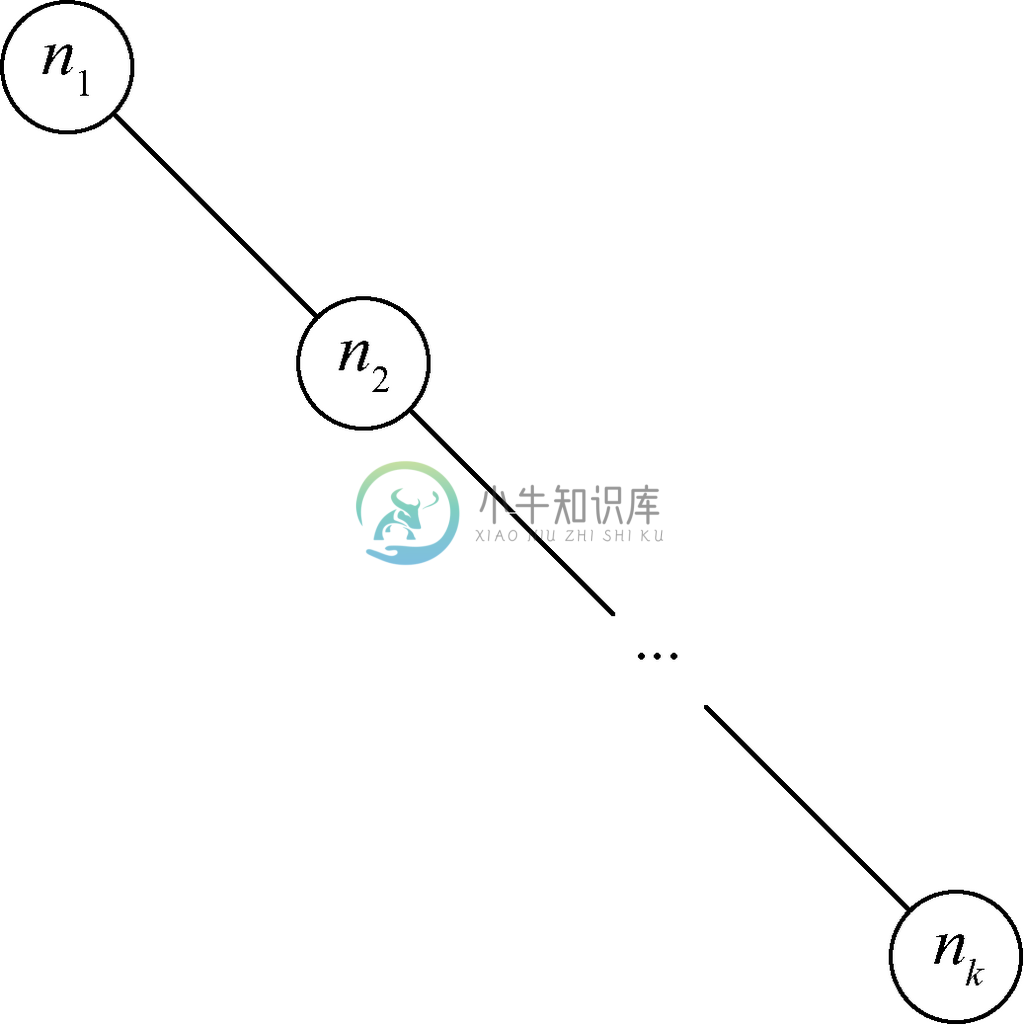
图 5-42　退化的二叉树

像图5-42这样具有k 个节点的树的高度显然为k-1。因此可以预见，如果具有k 个元素的词典的表示不幸是这些树中的一种，那么查找、插入和删除操作所花时间都会是O(k)。从直觉上讲，如果需要查找某个元素x，平均需要走过一半路径才会找到它，需要查看k/2个节点。如果这还没有找到x，就需要继续向下搜索该树，直到到达x所在的位置为止，平均也要走过该路线的一半。因为查找、插入和删除操作都涉及元素的查找，所以可知，在给定图5-42所示树的最坏情况下，这些操作平均要花的时间都是O(k)。

5.8.2　最佳情况

不过，二叉树不一定非得像图5-42这样又高又瘦，它也可以是图5-43这种分枝丛生的低矮样式。而后者这样的树，每个内部节点向下到某层的两个子节点都存在，而且下一层的所有叶子节点也都存在，这样的结构叫作完全树或完整树。

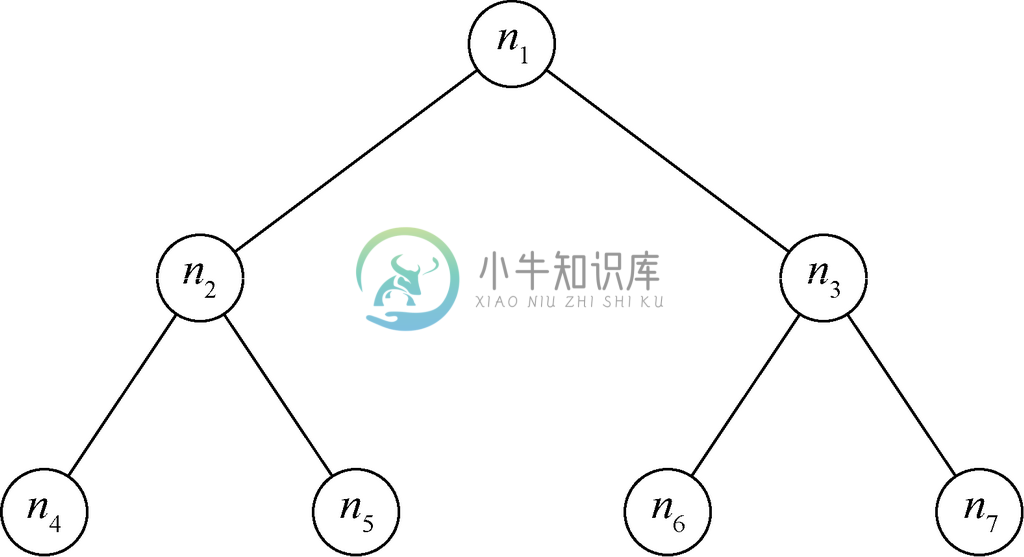
图 5-43　有7个节点的完全二叉树

高度为h 的完全二叉树共有2^h+1-1个节点。我们可以通过对高度h 的归纳证明这一声明。

依据。如果h=0，那么该树由一个节点组成。因为2⁰⁺¹-1=1，所以依据情况成立。

归纳。假设高度为h 的完全二叉树有n^h+1-1个节点，并考虑高度为h+1的完全二叉树。该树有一个根节点，并由两棵高度为h 的完全二叉树分别作为其左右子树。例如，图5-43中高度为2的完全二叉树包含根节点n₁，由n₂、n₄和n₅3个节点构成的左子树（高度为1的完全二叉树），以及由其余3个节点构成的右子树（另一棵高度为1的完全二叉树）。根据归纳假设，两棵高度为h 的完全二叉树共有2(2^h+1-1)个节点。在加上根节点后，可知高度为h+1的完全二叉树共有2(2^h+1-1)+1=2^h+2-1个节点，这就证明了归纳步骤。

现在可以将这一关系反转，说一棵具有k=2^h+1-1个节点的完全二叉树高度为h。这样一来，k+1=2^h+1。两边取对数，就有log₂(k+1)=h+1，或者大致可以说h 是O(logk )。因为查找、插入和删除的运行时间都与树的高度成比例，所以这些操作所花的时间是节点数的对数。这样的性能要比图5-42所示最糟情况所花的线性时间强多了。随着词典的大小越来越大，词典操作运行时间的增长要比集合中元素的增长慢得多。

5.8.3　一般情况

图5-42所示情况和图5-43所示情况哪个更普遍？其实，两者在实践中都不常见，不过图5-43中的完全树提供的词典操作效率与一般情况的效率是近似的。也就是说，平均情况下，查找、插入和删除花费的都是对数时间。

要证明一般二叉树可以提供对数时间的词典操作是很难的。证明的要点在于，从这样的树的根节点到某个随机节点的路径长度的期望值是O(logn)。本节习题中将给出这一期望值的递推等式。

不过，我们可以直观地看出这为什么应该是正确的运行时间，理由如下。二叉树的根节点会将除它自己之外的节点分为两棵子树。在最平均的分布中，一棵有k 个节点的树将会有两棵各有约k/2个节点的子树。如果根节点元素刚好是在一列有序元素的正中位置，就会形成这种情况。而在最坏的分布中，根节点元素是词典中的第一个或最后一个元素，这样就会使一棵子树为空，而另一棵子树中有k-1个元素。

平均而言，可以预期根节点是在已排序表正中和极端之间，而且可以预期约有k/4个节点在较小的子树中，另外的3k/4个节点在较大子树中。假设在向下探索树的过程中，每次递归调用时始终移动到较大子树的根节点，而且类似的假设适用于每层元素的分布。在第一层，较大子树会按照1:3的比例划分，在第二层留下共有(3/4)(3k/4)，即9k/16个节点的最大子树。因此，可以预见在第d 层的最大子树约有(3/4)^dk 个节点。

如果d 变得足够大，那么(3/4)^dk 的量会接近1。而且可以预见，在这一层，最大子树将是由一个叶子节点组成的。因此要问，d 为什么值可以使(3/4)^dk≤1？如果取以2为底的对数，就得到

d log₂(3/4)+log₂k≤log₂1　　　　　　(5.1)

现有log₂1=0，且log₂(3/4)是一个负常数，约为-0.4。因此可将(5.1)式重新写为log₂k≤0.4d，或a≥(log₂k )/0.4=2.5log₂k。

换句话说，在深度约为节点数以2为底的对数的2.5倍的位置（或是在更高的层数），就有望全是叶子节点了。这一论述证实了（但并未证明）一般二叉查找树的高度与该树节点数的对数成正比这一陈述。

5.8.4　习题

1. 如果树T 高度为h，而且分支系数为b，那么树T 最多可以有多少个节点，最少有多少个节点？

2. ** 进行如下实验，从n 个不同值的n !种顺序中任选一种，并按照这一顺序将这些值插入一棵空的二叉查找树中。设P(n)是实验后这n 个值中某个特定值v 所在节点的深度的期望值。

(a) 证明，对n≥2，

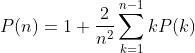
$P(n)=1+\frac{2}{n^2}\sum^{n-1}_{k=1}kP(k)$

(b) 证明P(n)是O(logn)。

5.9　优先级队列和偏序树

到目前为止，我们只看到一种抽象数据类型——词典，以及它的一种实现——二叉查找树。本节将研究另一种抽象数据类型以及它最有效率的一种实现。这种叫作优先级队列的抽象数据类型是各自有优先级与之关联的一组元素。例如，这些元素可以是一些记录，而优先级则可能是记录中某个字段的值。与优先级队列ADT有关的两种操作如下：

1. 向集合中插入一个元素（insert）；

2. 从集合中找出优先级最高的元素并将其删除（这种组合操作称为deletemax），被删除的元素由该函数返回。

示例 5.26

分时操作系统从多个来源接受服务请求，而这些作业的优先级可能不尽相同。例如，优先级最高的可能是系统进程，这些进程中可能包含监控传入数据（比如在终端的按键动作生成的信号，或是局域网上数据包的到达所生成的信号）的“守护进程”。接着可能是用户进程，那些由普通用户发出的指令。再下来就可能是某些特定的后台作业，比如向磁带备份数据，或是用户已指定以低优先级运行的长计算。

作业可以表示为记录，这种记录由对应作业的整数ID和对应作业优先级的整数组成。也就是说，可以使用如下结构体

struct ETYPE {
    int jobID;
    int priority;
};

表示优先级队列中的元素。在初始化新的作业时，它会得到一个ID和一个优先级。然后对等待服务的作业构成的优先级队列执行这一元素的插入操作。当处理器资源可用时，系统就会来到优先级队列，并执行deletemax操作。由该操作返回的元素就是等待服务的作业中优先级最高的作业，而该作业正是接下来要执行的。

示例 5.27

我们可以使用优先级队列ADT实现排序算法。假设有一列整数a₁、a₂、…、a_n 要排序，可以将这些整数放入一个优先级队列，分别使用这些元素的值作为各自的优先级。如果随后执行deletemax操作n 次，这些整数就会按照从大到小的顺序依次被选出来。5.10节还会更详细地讨论这种称为堆排序的算法。

5.9.1　偏序树

实现优先级队列的一种有效方式是使用偏序树（Partially Ordered Tree，POT），这是一种具有如下属性的带标号二叉树。

1. 节点的标号是具有“优先级”的元素，该优先级可以是元素的值，也可以是元素某个组成部分的值。

2. 存储在节点中的元素的优先级，不小于存储在其子节点中的元素的优先级。

属性(2)说明，任何子树根节点处的元素总是该子树中最大的元素。我们将属性(2)称为偏序树属性，或POT属性。

示例 5.28

图5-44展示了一棵具有10个元素的偏序树。在这里以及本节的其他部分中，我们都将用元素的优先级来表示它们，就像元素和它们的优先级是一回事那样。请注意，相等的元素可能出现在树中的不同层级。要说明偏序树属性在根节点得到满足，请注意，根节点处的元素18不小于其子节点处的元素18和16。同样，可以验证在该树的每个内部节点处偏序树属性都成立。因此，图5-44是一棵偏序树。

偏序树为优先级队列提供了一种实用的抽象实现。简单地说，要执行deletemax操作，就要找到根节点，它肯定是最大的，并用底层的最右节点代替它。不过，这样做时，偏序树属性可能被破坏，因此必须还原偏序树属性，要让新放置在根节点处的元素“向下沉”，直到它到达合适的层次，使得它小于它的父节点，并且不小于它的子节点。要执行插入操作，就要在底层尽可能左的位置增加一个新的叶子节点，如果底层没有空位置，就要新添加一个层级，并将该节点放在新一层的左端。这样也可能对偏序树属性造成破坏，如果造成破坏，就要让新元素“向上冒”，直到它找到合适的位置。

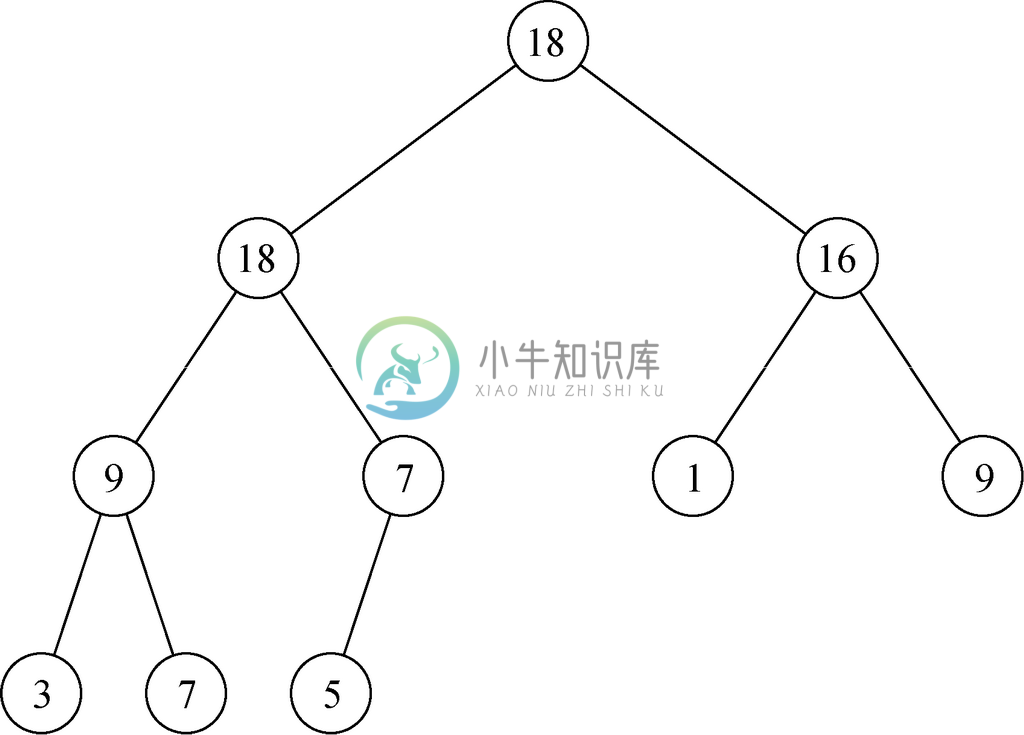
图 5-44　有10个节点的偏序树

5.9.2　平衡偏序树和堆

如果偏序树除最下层之外的所有层级的节点全存在，而且最下层的叶子节点尽可能集中在左侧，那么这样的偏序树就是平衡的。这一条件说明，如果该树有n 个节点，那么从根节点到任何节点的路径都不可能比log₂n 长。图5-44中的树就是平衡偏序树。

平衡偏序树可以用称为堆的数组数据结构实现，这种数据结构提供了一种迅速、紧凑的优先级队列ADT实现。堆就是对元素下标有着特殊解释的数组A。首先从A[1]中的根节点开始，并未使用A[0]。在根节点之后，各层级依次出现。在同一层级中，节点按照从左到右的顺序排列。

因此，根节点的左子节点是在A[2]中，而根节点的右子节点在A[3]中。一般而言，A[i ]处节点的左子节点在A[2i ]中，而其右子节点在A[2i+1]中，如果这些子节点在偏序树中都存在的话。这种树的平衡性质使这种表示成为可能。这些元素的偏序树属性说明，如果A[i ]有两个子节点，那么A[i ]不小于A[2i ]和A[2i+1]，如果A[i ]只有一个子节点，那么A[i ]不小于A[2i ]。

图 5-45　图5-44对应的堆

实现的层次
对词典和优先级队列这两种ADT进行比较，并注意到每种情况下只给出了一种抽象实现以及对应该抽象实现的一种数据结构，这样做是很有意义的。每种ADT都有其他的抽象实现，而每种抽象实现也都有其他的数据结构。之前已经说过，在本书随后的内容中还将讨论词典的其他抽象实现，比如散列表，而且在5.9节的习题中表示过，二叉查找树对优先级队列而言也是种合适的抽象实现。下表总结了目前为止我们对词典和优先级队列的抽象实现及数据结构的了解。
ADT
抽象实现
数据结构
词典
二叉查找树
左子节点右子节点结构
优先级队列
平衡偏序树
堆

ADT	抽象实现	数据结构
词典	二叉查找树	左子节点右子节点结构
优先级队列	平衡偏序树	堆

示例 5.29

表示图5-44所示平衡偏序树的堆如图5-45所示。例如，A[4]存放着值9，这一数组元素表示图5-44中根节点的左子节点的左子节点。而该节点的子节点则在A[8]和A[9]中。它们的元素分别是3和7，都不大于9，正如偏序树属性所要求的。数组元素A[5]对应着根节点左子节点的右子节点，它的左子节点在A[10]的位置。它可以有存放在A[11]中的右子节点，但图5-44中的偏序树只有10个元素，所以A[11]并不是该堆的一部分。

尽管这里展示的树节点和数组元素似乎就只是优先级本身，但原则上讲树节点或数组中出现的是完整的记录。正如我们将要看到的，在偏序树或其堆表示的父子节点间要进行很多元素交换。因此，如果数组元素是指向表示优先级队列中各对象的记录的指针，并将这些记录存储在堆“之外”的另一个数组中，就会更有效率。这样就可以在不调整记录本身的情况下直接对指针进行交换。

5.9.3　优先级队列操作在堆上的执行

在5.9节和5.10节中，会用全局整数数组A[1..MAX]表示堆。这里假设元素都是整数，而且都等于它们的优先级。当元素是记录时，可将指向记录的指针存储在数组中，并根据记录中的某个字段来确定元素的优先级。

假设有一个满足偏序树属性的具有n-1个元素的堆，我们要向A[n]中添加第n 个元素。偏序树属性在各处都继续成立，除了在A[n]和它的父节点间可能有例外。因此，如果A[n]大于其父节点位置的元素A[n/2]，就必须交换这些元素。而A[n/2]与其父节点间也可能违背偏序树属性。如果这样的话，就要让新元素递归地“冒泡”，直到它到达父节点有一个更大元素的位置，或是到达根节点位置。

执行这一操作的C语言函数bubbleUp如图5-46所示。它使用swap(A,i,j)函数交换A[i ]和A[ j ]处的元素，该函数也是在图5-46中定义的。bubbleUp的操作很简单。给定表示节点的参数i，它表示的节点与其父节点有可能违背偏序树属性，测试是否有i =1，也就是测试是否为根节点，在根节点的话就不会破坏偏序树属性。如果不是，则测试A[i ]是否大于其父节点处的元素；如果是，就在其父节点处递归地调用bubbleUp，交换A[i ]与其父节点。

void swap(int A[], int i, int j)
{
    int temp;

    temp = A[i];
    A[i] = A[j];
    A[j] = temp;
}

void bubbleUp(int A[], int i)
{
    if (i > 1 && A[i] > A[i/2]) {
        swap(A, i, i/2);
        bubbleUp(A, i/2);
    }
}

图 5-46　swap函数交换数组元素，而bubbleUp函数则将堆中的新元素推到它的右侧位置

示例 5.30

假设有图5-45所示的堆，并向其添加了优先级为13的第11个元素。该元素会出现在A[11]中，就有了如下数组

调用bubbleUp(A,11)，对A[11]和A[5]进行比较，因为A[11]更大，所以必须交换这两个元素。也就是说A[5]和A[11]违背了偏序树属性。因此，数组就成了

调用bubbleUp(A,5)，对A[2]和A[5]进行比较，因为A[2]更大，所以不会违背偏序树属性，bubbleUp(A,5)不会进行任何操作。这样就已经恢复了该数组的偏序树属性。

现在介绍如何实现优先级队列的插入操作。设n 是优先级队列中当前的元素数，并假设数组A[1..n]已经满足偏序树属性。增加n，并将待插入的元素存储到新的A[n]中。最后，调用bubbleUp(A,n)。表示插入操作的代码如图5-47所示。参数x是待插入的元素，而参数pn是指向优先级队列当前大小的指针。请注意，n 必须按引用传递，也就是说，通过指向n 的指针传递，这样当n 增加时，改变才不只是在插入操作局部造成影响。这里省略了对n<MAX 的检查。

void insert(int A[], int x, int *pn)
{
    (*pn)++;
    A[*pn] = x;
    bubbleUp(A, *pn);
}

图 5-47　在堆上实现的优先级队列插入操作

要实现优先级队列的deletemax操作，需要对堆或偏序树进行另一项操作，这次是让根节点处可能违背偏序树属性的元素向下沉。假设A[i ]可能违背偏序树属性，在它中的元素可能小于其子节点A[2i ]和A[2i+1]中的一个或两个。我们可以将其与其中一个子节点交换，不过一定要注意是与哪一个交换。如果与两个子节点中较大的那个交换，那么肯定不会在A[i]曾经的两个子节点间引入偏序树属性的破坏，因为较大的那个现在已经是较小那个的父节点了。

图5-48中的bubbleDown函数实现了这一操作。在选择了与A[i ]进行交换的子节点后，它会递归地调用自身，以消除新位置上的元素A[i ]（也就是现在的A[2i ]或A[2i+1]）与其新子节点之间可能存在的偏序树属性的破坏。参数n 是堆中的元素数，或者说是最后一个元素的下标。

这个函数有点棘手。如果A[i ]有两个子节点，就必须决定将其与哪个子节点交换，所以首先要在图5-48的第(1)行假设较大的子节点是A[2i ]。而如果右子节点存在（即child<n），并且右子节点更大，第(2)行的测试就会得到满足，并在第(3)行让child 成为A[i ]的右子节点。

在第(4)行有两项需要测试的内容。首先，A[i ]在该堆中有可能真的没有子节点。因此要通过检测是否有child≤n 来确定A[i ]是否为内部节点。第第二项测试是检测A[i ]是否小于A[child ]。如果两项条件都满足，那么在第(5)行就要将A[i ]与它较大的那个子节点交换，并在第(6)行递归地调用bubbleDown，如果有必要的话，就将违背偏序树属性的元素进一步向下压。

     void bubbleDown(int A[], int i, int n)
     {
         int child;

(1)      child = 2*i;
(2)      if (child < n && A[child+1] > A[child])
(3)          ++child;
(4)      if (child <= n && A[i] < A[child]) {
(5)          swap(A, i, child);
(6)          bubbleDown(A, child, n);
         }
     }

图 5-48　bubbleDown会将违背偏序树属性的元素压到合适的位置

可以按照图5-49所示的方式用bubbleDown实现优先级队列的deletemax操作。deletemax函数接受数组A 和指向堆中当前元素数n 的指针pn 作为参数。这里省略了对n>0的测试。

在第(1)行，将根节点处要删除的元素与最后的元素（在A[n]中）交换。技术上讲，应该返回删除的元素，不过，正如所看到的，将其放入不再属于该堆的A[n]也是可以的。

在第(2)行，将n 减少1，实际上就是删除现在处于旧的A[n]中的最大元素。因为现在的根节点可能会违背偏序树属性，所以在第(3)行调用bubbleDown(A,1,n)，它会递归地将违背偏序树属性的元素向下压，直到该元素到达一个不再小于它子节点的位置或是成为叶子节点，不管哪种情况，都不再会违反偏序树属性了。

     void deletemax(int A[], int *pn)
     {
(1)      swap(A, 1, *pn);
(2)      --(*pn);
(3)      bubbleDown(A, 1, *pn);
     }

图 5-49　用堆实现的优先级队列deletmax操作

示例 5.31

假设对图5-45中的堆执行deletemax操作。在交换了A[1]和A[10]之后，将n 置为9。这样堆就变成了

在执行bubbleDown(A,1,9)时，会将child 置为2。因为A[2]≥A[3]，所以在图5-48的第(3)行不用增加child 。然后，因为child≤n 而且A[1]<A[2]，所以交换这两个元素，得到数组

接着调用bubbleDown(A,2,9)。这要求我们在第(2)行对A[4]和A[5]加以比较，比较的结果是前者更大。因此，在图5-48的第(4)行，child=4。又因为可知A[2]<A[4]，所以交换这两个元素，并对如下数组调用bubbleDown(A,4,9)。

再下来要比较A[8]和A[9]，结果后者更大，所以bubbleDown(A,4,9)的第(4)行有child=9。因为A[4]<A[9]，所以再次进行交换，得到数组

随后调用bubbleDown(A,9,9)。在第(1)行将child 置为18，而且因为child<n 为假，第(2)行的第一个测试会失败。同样，第(4)行的测试也会失败，所以不用再进行交换或递归调用。这一数组现在已经是还原偏序树属性的堆了。

5.9.4　优先级队列操作的运行时间

优先级队列堆实现的每次插入或deletemax操作的运行时间是O(logn)。要知道原因，首先考虑一下图5-47所示的insert程序。该程序前两步花的时间显然是O(1)，此外还要加上对bubbleUp的调用所花的时间。因此，需要确定bubbleUp的运行时间。

粗略地讲，我们注意到每次bubbleUp递归调用自身时，就是离根节点更近了一个节点的位置。因为平衡偏序树的高度大约是log₂n，所以递归调用的次数是O(log₂n)。因为对bubbleUp的每次调用花的时间是O(1)外加递归调用的时间（如果有的话），所以总时间应该为O(logn)。

更严格地讲，设T (i )是bubbleUp(A,i)的运行时间，那么可以构建如下T (i )的递推关系。

依据。如果i=1，那么T(i )是O(1)，因为很容易看出，在这种情况下，图5-46中的bubbleUp程序不会执行任何递归调用，只是执行了if语句的测试。

归纳。如果i>1，那么if语句的测试可能会失败，因为A[i ]不再需要继续上升了。若该测试成功，则花O(1)的时间执行swap，并以参数i /2（若i 为奇数则略小于i /2）递归调用bubbleUp一次。因此T(i )≤T(i /2)+O(1)。

所以可以说，对于某些常数a 和b，递推关系

T(1)=a
T(i )=T(i /2)+b, i>1,

能作为bubbleUp运行时间的上界。如果将T(i /2)展开，就得到，对每个j，有

T(i )=T(i /2 ^j )+bj　　　　　　(5.2)

如3.10节中那样，可以对j 的值加以选择，使得T(i /2^j )最为简单。在这种情况下，可以令j 等于logi，这样一来i/2^j=1。因此，(5.2)式就成了T(i )=a+b log₂i，也就是说T(i )是O(logi )。因为bubbleUp的运行时间是O(logi )，所以插入操作的运行时间也是O(logi )。

现在考虑deletemax。从图5-49中可以看出，deletemax 的运行时间是O(1)加上bubbleDown的运行事件。对图5-48所示bubbleDown函数的分析基本上与对bubbleUp的分析相同。这里就不再赘述分析过程，直接得出bubbleDown和deletemax 的运行时间也是O(logn)这一结论。

5.9.5　习题

1. 考虑图5-45中的堆，说明在下列情况下分别会发生什么。

(a) 插入3

(b) 插入20

(d) 再次删除最大元素

2. 通过对i 的归纳证明(5.2)式。

3. 通过对违背偏序树属性的节点的深度进行归纳，证明图5-46中的bubbleUp函数可以正确地将有一处违背偏序树属性的树还原为具有偏序树属性的树。

4. 证明：如果A之前是大小为n-1的堆，那么insert(A,x,n)函数可以使A变为大小为n 的堆。

5. 通过对违背偏序树属性的节点的高度进行归纳，证明图5-48中的bubbleDown函数可以正确地将有一处违背偏序树属性的树还原为具有偏序树属性的树。

6. 证明：deletemax(A,n)可以让大小为n 的堆变为大小为n-1的堆。如果A之前不是堆，会发生什么？

7. 证明：bubbleDown(A,1,n)处理长度为n 的堆所花时间是O(logn)。

8. ** 随机选出不同优先级的n 个元素构成堆，该堆是偏序树的概率是多少？如果没法总结出一般规则，就编写递归函数计算这一表示为n 的函数的概率。

9. 实现偏序树不一定要使用堆。假设使用之前用于二叉树的常规的左子节点右子节点数据结构。展示如何使用这一结构实现bubbleDown、insert和deletemax函数。

10. * 二叉查找树也可以用作优先级队列的抽象实现。展示如何使用具有左子节点右子节点数据结构的二叉查找树实现插入和deletemax操作。这些操作在最坏情况下以及在一般情况下的运行时间分别是多少？

5.10　堆排序：利用平衡偏序树排序

现在要介绍被称为堆排序的算法。它会分两个阶段为数组A[1..n]排序。在第一个阶段，堆排序会给A 偏序树属性。堆排序的第二个阶段会反复从堆中选出剩余元素中的最大元素，直到堆只由最小的元素构成，这样就完成了对数组A 的排序。

图 5-50　堆排序过程中数组A 的情况

图5-50展示了处于第二阶段的数组A。数组的开头部分具有偏序树属性，而剩下的部分则是以非递减次序排好序的元素。此外，已排序部分是数组中前n-i大的元素。在第二阶段，i的值可以从n减到1，从而让一开始为整个数组A的堆，最终减少到只剩下位于A[1]的最小元素。更详细地讲，第二阶段由如下步骤组成。

1. 将A[1..i]中最大元素A[1]与A[i ]交换。因为A[i+1..n]中所有元素都不小于A[1..i]中的元素，而且我们刚刚将A[1..i]中最大的元素移动到了位置i，所以可知A[i..n]是数组中前n-i-1大的元素，而且已经是排好次序的。

2. i 的值是递减的，每次将堆的大小减少1。

3. 通过下压根节点处的元素（就是刚移动到A[1]的元素），还原开头部分的偏序树属性。

示例 5.32

考虑图5-45中的数组，它是具有偏序树属性的。这里从第二阶段的第一次迭代开始分析。在第一步中，要将A[1]与A[10]交换，得到：

第二步是将堆的大小减小为9，而第三步则是通过调用bubbleDown(1)还原前9个元素的偏序树属性。在这次调用中，A[1]和A[2]进行了交换。

接着，A[2]与A[4]进行了交换。

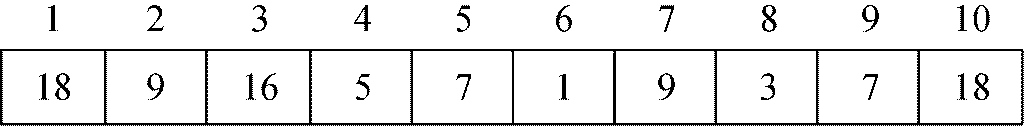
最后，A[4]和A[9]交换：

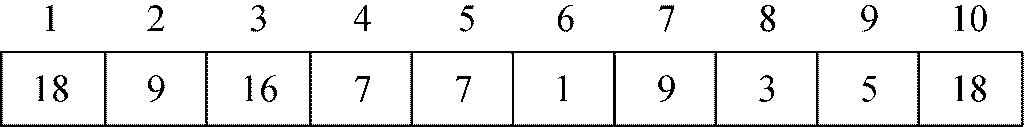
至此，A[1..9]具有了偏序树属性。

第二阶段的第二次迭代首先要交换A[1]中的元素18与A[9]中的元素5。在将5往下压到合适位置后，数组就成了

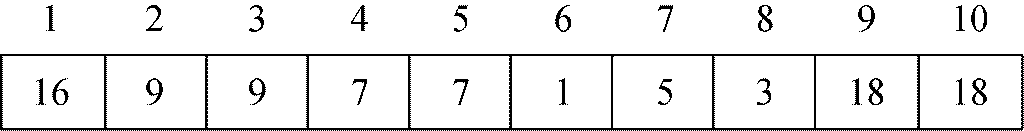
到这里，数组中最后两个元素已经是最大的两个元素，而且是已经排好次序的。

第二阶段会不断继续，直到完成对数组的排序。

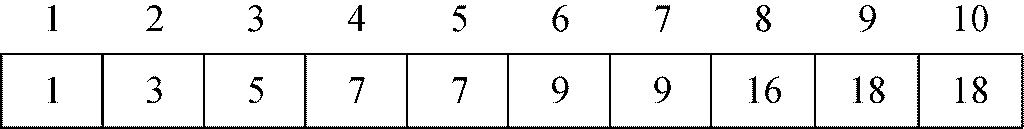
5.10.1　数组的堆化

可以非正式地将堆排序描述为：

for (i = 1; i <= n; i++)
　　insert (a_i );
for (i = 1; i <= n; i++)
　　deletemax

要实现这一算法，先将待排序的n 个元素a₁、a₂、…、a_n插入一个最初为空的堆中。然后执行n 次deletemax操作，按从大到小的次序取出元素。图5-50所示的安排让我们可以随着数组中堆部分的萎缩，在数组的尾部存储已删除的元素。

我们已经在5.9节中论证过插入和deletemax操作的运行时间都是O(logn)，而且每种操作显然都要执行n 次，所以这是一种可与归并排序媲美的O(n logn)排序算法。其实，在只需要最大的几个元素，而不需要整个已排序表的情况下，堆排序还能优于归并排序。原因在于，要让数组变成堆，如果使用图5-51所示的heapify函数，只需要O(n)的时间就能完成，而不是O(n logn)。

void heapify(int A[], int n)
{
    int i;

    for (i = n/2; i >= 1; i--)
        bubbleDown(A, i, n);
}

图 5-51　数组的堆化

5.10.2　`Heapify`的运行时间

首先，图5-51中对bubbleDown的n/2次调用总时间看起来应该是O(n logn)，因为我们了解的bubbleDown运行时间上界只有logn 这一个。不过，如果利用向下压元素的序列大多非常短这一事实，就可以得到更紧的边界——O(n)。

一开始，甚至都不必堆数组的后半部分调用bubbleDown，因为那里的节点全部是叶子节点。如果数组的第二个四分之一部分——也就是A[(n/4)+1..n/2]——中的元素存在比它们的子节点小的，就可以调用bubbleDown一次。不过，它们的子节点是在数组后半部分，都是叶子节点，因此，在A 的第二个四分之一中，最多调用一次bubbleDown。同样，在数组的第二个八分之一中，最多调用两次bubbleDown。在数组个区域中调用bubbleDown的次数如图5-52所示。

{%}

图 5-52　随着数组下标不断变大，对bubbleDown的调用次数迅速减少

现在来计算一下heapify调用了多少次bubbleDown，其中包括递归调用。从图5-52可看出，可以将A分为若干个区段，其中第i 个区段是由大于n/2ⁱ⁺¹且不大于n/2ⁱ 的 j 对应的A[j]组成。因此，区段i 中的元素数就是n/2ⁱ⁺¹，而且区段i 中每个元素至多调用i 次bubbleDown。此外，i>log₂n 的区段都为空，因为它们至多包含n/2^1+log₂n=1/2个元素。A[1]是区段log₂n 中唯一的元素，因此需要计算和值

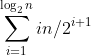$\sum^{\log_2n}_{i=1}in/2^{i+1}$ 　　　　　　(5.3)

将(5.3)的有限和扩展为无限和，并提取出因式n/2，就可以给出该和值的上界

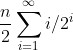
$\frac{n}{2}\sum^{\infty}_{i=1}i/2^i$

现在必须得出(5.4)式中和值的上界。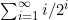 $\sum^{\infty}_{i=1}i/2^i$ 可以写为

(1/2)+(1/4+1/4)+(1/8+1/8+1/8)+(1/16+1/16+1/16+1/16)+…

可以将这些2的乘方的倒数写为如图5-53所示的三角形。每一行都是公比为1/2的无穷几何级数，而其和则是级数中第一项的两倍，正如图5-33右侧所示。各行之和又形成了另一个几何级数，而它的和是2。

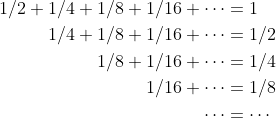
$\begin{align*}1/2+1/4+1/8+1/16+\cdots&=1\\1/4+1/8+1/16+\cdots&=1/2\\1/8+1/16+\cdots&=1/4\\1/16+\cdots&=1/8\\\cdots&=\cdots\end{align*}$

图 5-53　将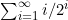 $\sum^{\infty}_{i=1}i/2^i$ 排列为三角和

这样一来，(5.4)的上界为(n/2)×2=n。也就是说，在函数heapify中调用bubbleDown的次数不超过n。因为已经得出每次调用花费的时间为O(1)，不含任何递归调用，所以可以得出结论：heapify花的总时间为O(n)。

5.10.3　完整的堆排序算法

堆排序C语言程序如图5-54所示。它使用整数数组A[1..MAX]表示堆。待排序的元素被插入A[1..n]中。图5-54中函数声明的定义包含在5.9节和5.10节中。

     #include <stdio.h>

     #define MAX 100

     int A[MAX+1];

     void bubbleDown(int A[], int i, int n);
     void deletemax(int A[], int *pn);
     void heapify(int A[], int n);
     void heapsort(int A[], int n);
     void swap(int A[], int i, int j);

     main()
     {
         int i, n, x;

         n = 0;
         while (n < MAX && scanf("%d", &x) != EOF)
             A[++n] = x;
         heapsort(A, n);
         for (i = 1; i <= n; i++)
             printf("%d\n", A[i]);
     }

     void heapsort(int A[], int n)
     {
         int i;

(1)      heapify(A, n);
(2)      i = n;
(3)      while (i > 1)
(4)          deletemax(A, &i);
     }

图 5-54　对数组进行堆排序

第(1)行调用heapify，它将待排序的n个元素变成一个堆。第(2)行将标记堆尾的i初始化为n。第(3)和第(4)行的循环将deletemax应用n-1次。我们应该重新审视图5-49中的代码，会看到deletemax(A,i)会将当前堆中最大的元素（永远是A[1]）与A[i ]交换。这样一来，i 每次会减少1，所以堆的大小也会缩小1。在第(4)行被deletemax“删除”的元素现在成为数列已排序尾部的一部分。它不大于之前的尾部A[i+1..n]中的任何元素，而不小于仍在堆中的任意元素。因此，声明的属性得到保持，堆中的所有元素都先于尾部的所有元素。

5.10.4　堆排序的运行时间

刚刚已经确定了第(1)行中的heapify函数花的时间与n 成比例。第(2)行显然花了O(1)的时间。因为第(3)行和第(4)行的循环每进行一次，i 就减少1，所以循环要进行n-1次。第(4)行中对deletemax的调用花的时间是O(logn)。因此，整个循环的总运行时间为O(n logn)。这一时间主导了第(1)行和第(2)行的运行时间，所以heapsort函数处理n 个元素的运行时间是O(n logn)。

5.10.5　习题

1. 对3、1、4、1、5、9、2、6、5这列元素应用堆排序。

2. * 给出一个运行时间是O(n)的算法，使其从具有n个元素的表中找出前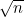 $\sqrt{n}$ 大的元素。

5.11　小结

读者应该从本章中获取如下要点。

树是一种用于表示层次化信息的重要数据模型。
多种涉及数组和指针结合的数据结构可用于实现树，选择何种数据结构取决于要对树进行哪种操作。
树节点最重要的两种表示分别是最左子节点右兄弟节点表示和单词查找树（指向子节点的指针数组）。
递归算法和证明也适用于树。结构归纳法是普通归纳模式的一种变形，可以有效地对树中的节点数进行完全归纳。
二叉树是树模型的一种变形，它的每个节点最多可以有左子节点和右子节点。
二叉查找树是带标号的二叉树，它具有“二叉查找树属性”，即节点左子树的所有标号都先于该节点的标号，而且节点右子树的所有标号都后于该节点的标号。
词典抽象数据类型是可以对其执行插入、删除和查找操作的集合。二叉查找树可以有效地实现词典。
优先级队列是另一种抽象数据类型，是可以对其执行插入和deletemax操作的集合。
偏序树是种带标号的二叉树，它具有任意节点的标号都不小于其子节点标号的属性。
平衡偏序树除最下层之外的各层都被节点占满，而最下层只有靠左侧的位置被占据，它可以通过被称为堆的数组结构实现。这一结构提供了一种复杂度为O(logn)的优先级队列实现，并带来了一种复杂度为O(n logn)的排序算法——堆排序。

5.12　参考文献

树的单词查找树表示来自Fredkin [1960]。二叉查找树是由若干人各自独立发明的，而读者可以参考Knuth [1973]来了解二叉查找树的历史以及大量与各类查找树有关的信息。要了解树的更多高级应用，参见Tarjan [1983]。

Williams [1964]率先设计了平衡偏序树的堆实现。Floyd [1964] 描述了堆排序的一个高效版本。

Floyd, R. W. [1964]. “Algorithm 245: Treesort 3,” Comm. ACM 7:12, pp. 701.

Fredkin, E. [1960]. “Trie memory,” Comm. ACM 3:4, pp. 490–500.

Knuth, D. E. [1973]. The Art of Computer Programming, Vol. III, Sorting and Searching, 2nd ed., Addison-Wesley, Reading, Mass.

Tarjan, R. E. [1983]. Data Structures and Network Algorithms, SIAM Press, Philadelphia.

Williams, J. W. J. [1964]. “Algorithm 232: Heapsort,” Comm. ACM 7:6, pp. 347–348.

第 5 章 树

5.1 本章主要内容

5.2 基本术语

5.2.1 树的等价递归定义

示例 5.1

5.2.2 路径、祖先和子孙

示例 5.2

示例 5.3

5.2.3 子树

示例 5.4

5.2.4 叶子节点和内部节点

示例 5.5

5.2.5 高度和深度

示例 5.6

5.2.6 有序树

示例 5.7

示例 5.8

5.2.7 标号树

5.2.8 表达式树——一类重要的树

示例 5.9

5.2.9 习题

5.3 树的数据结构

5.3.1 树的指针数组表示

示例 5.10

5.3.2 树的最左子节点右兄弟节点表示

示例 5.11

示例 5.12

5.3.3 父指针

5.3.4 习题

5.4 对树的递归