第 9 章 图数据模型
从某种意义上讲,图就是二元关系。不过,它利用一系列由线(称为边)或箭头(称为弧)连接的点(称为节点)提供了强大的视觉效果。在这方面,图就是我们在第5章中研究过的树数据模型的泛化。和树一样,图也有多种形式:有向图/无向图,以及标号图/无标号图。
图还和树一样可以解决大范围的问题,比如距离的计算、关系中环的查找,以及连通性的确定。我们在第2章中已经见识过用图来表示程序的结构。而第7章也用到图来表示二元关系,并用图展示了关系的某些属性,比如交换律。在第10章中将看到用图表示自动机,而在第13章中会看到用图表示电路。而图除上述这些之外的若干重要应用将在本章中讨论。
9.1 本章主要内容
本章的主要内容包括以下这些。
与有向图和无向图有关的定义(9.2节和9.10节)。
表示图的两种重要数据结构:邻接表和邻接矩阵(9.3节)。
用来在无向图中找出连通分支的算法和数据结构(9.4节)。
找出最小生成树的技巧(9.5节)。
名为“深度优先搜索”的用于探索图的实用技巧(9.6节)。
应用深度优先搜索测试有向图是否有环路,找出无环图的拓扑次序,以及确定是否存在从一个节点到另一节点的路径(9.7节)。
用来找出最短路径的迪杰斯特拉算法(9.8节)。该算法可找出从某个“源”节点到每个节点的最小距离。
找出任意两个节点间最小距离的弗洛伊德算法(9.9节)。
本章中的很多算法都是比解决问题的直观方法更加高效的实用技巧。
9.2 基本概念
有向图,是由节点集合N 以及N 上的二元关系A 组成的。我们将A 称为有向图弧的集合,因此弧是节点的有序对。
绘出的图如图9-1所示。各节点是用圆圈表示的,节点的名称就在圆圈中央。我们通常会用从0开始的整数为节点命名,或者使用等效的枚举。在图9-1中,节点集合N={0,1,2,3,4}。
A中的弧(u,v)都是由从u 到v 的箭头表示的。在图9-1中,弧的集合是
A={(0,0),(0,1),(0,2),(1,3),(2,0),(2,1),(2,4),(3,2),(3,4),(4,1)}

图 9-1 有向图的示例
在文本中,一般习惯将弧(u,v)表示为u→v。我们将v 称为弧的头部,而将u 称为弧的尾部,以适应v 在箭头的头部而u 在其尾部的概念。例如,0→1就是图9-1中的一条弧,它的头部是节点1,而尾部是节点0。另一条弧是0→1,这样一条从某节点通向其自身的弧就叫作自环(loop)。对该弧而言,头部和尾部都是节点0。
9.2.1 前导和后继
当u→v 是弧时,还可以说u 是v 的前导(predecessor),而且v 是u 的后继(successor)。因此,弧0→1就表示0是1的前导而1是0的后继,而弧0→0则表示0同时是其本身的前导和后继。
9.2.2 标号
就像对树那样,也可以为图的各节点附加标号(label)。标号是绘制在所对应的节点附近的。同样,可以在靠近弧中点的位置为弧放置标号。节点的标号或弧的标号可以是任意类型的。例如,图9-2就展示了节点名为1,标号为“狗”,节点名为2,标号为“猫”,而且有一条标号为“咬”的弧1→2。

图 9-2 含两个节点的标号图
和树一样,不应该把节点的名称与其标号弄混。同一幅图中各节点的名称必须是唯一的,但可能有不止一个节点的标号相同。
9.2.3 路径
有向图中的路径是一列节点(v1,v2,…,vk),其中每个节点都有到下一节点的弧,也就是vi →vi+1,i=1,2,…,k-1。该路径的长度是k-1,也就是这条路径上弧的数量。例如,图9-1中的(0,1,3)就是一条长度为2的路径。
k=1的情况也是可以存在的。也就是说,任何节点v 本身都是一条从v 到v 的长度为0的路径。该路径上没有弧。
9.2.4 有环图和无环图
有向图中的环路(cycle)是指起点和终点为同一节点的长度不为0的路径。环路的长度就是这条路径的长度。请注意,路径长度为0的情况不是环路,虽然“其起点和终点是同一节点”。然而,由一条弧v→v 构成的路径是一条长度为1的环路。
示例 9.1
考虑图9-1中的图。因为有自环0→0,存在一条长度为1的环路(0,0)。还有一条长度为2的环路(0,2,0),因为有弧0→2和2→0。同样,(1,3,2,1)是一条长度为3的环路,而(1,3,2,4,1)则是长度为4的环路。
请注意,环路的起点和终点可以是其中的任一节点。也就是说,环路(v1,v2,…,vk ,v1)也可以写为(v2,…,vk ,v1,v2),或者写为(v3,…,vk ,v1,v2,v3),等等。例如,环路(1,3,2,4,1)也可以写为(2,4,1,3,2)。
在每条环路中,第一个节点和最后一个节点都是相同的。如果环路(v1,v2,…,vk ,v1)的节点v1、…、vk 中没有一个出现一次以上,就说该环路是简单环路,也就是说,简单环路的唯一重复出现在最终节点处。
示例 9.2
示例9.1中的环路都是简单环路。在图9-1中,环路(0,2,0)是简单环路。不过,也有些环路不是简单环路,比如环路(0, 2, 1, 3, 2, 0)中节点2就出现了两次。
给定含有节点v的非简单环路,就能找到含有v的简单环路。要知道原因,可以假设有一条起点和终点都是v的环路(v,v1,v2,…,vk ,v1)。如果该环路不是简单环路,就只会是以下两种情况之一。
(1) v出现了3次或3次以上;
(2) 存在某个v 之外的节点u,它出现了两次,也就是,环路肯定是(v,…,u,…,u,…,v)这样的。
在第(1)种情况下,可以直接删除倒数第二次出现v 的位置之前的所有节点,结果是一条从v 到v 的更短环路。在第(2)种情况中,可以删除从u 到u 的部分,将其用一个u 替代,得到环路(v,…,u,…,v)。不管哪种情况,得到的结果肯定仍然是环路,因为结果中的每条弧都是原环路中的,因此肯定是出现在该图中的。
在让环路成为简单环路之前,可能有必要多次重复该变形。因为环路在每次迭代后总会变得更短,所以最终一定能得到简单环路。我们刚刚已经证明了,如果图中有一条环路,那么一定至少含有一条简单环路。
示例 9.3
给定环路(0,2,1,3,2,0),可以删除第一个2以及它后面的1和3,这样就得到了简单环路(0,2,0)。从实际情况上讲,该环路是从0开始,到达2,然后是1,再是3,回到2,最后回到0。第一次到达2时,可以假装这是第二次到达2,跳过了1和3,然后直接回到0。
再举个例子,考虑非简单环路(0,0,0)。因为0出现了3次,所以可以删除第一个0,也就是删除倒数第二个0之前的所有内容。实际上我们是将绕着自环0→0行进两次的路径替换为绕行一次的路径。
如果图中含一条或多条环路,就说该图是有环的。如果不含环路,就说该图是无环的。而根据刚才有关简单环路的论证,当且仅当图中含有简单环路时,该图为有环图,因为如果该图有环路,那么它肯定有简单环路。
示例 9.4
我们在3.8节中提到过,可以用名为“调用图”的有向图表示由一系列函数执行的调用。图中的节点就是函数,而如果函数p 调用了函数Q,就有一条弧P→Q。例如,图9-3展示了与2.9节中的归并算法对应的调用图。

图 9-3 归并排序算法的调用图
调用图中出现的环路意味着算法中的递归。在图9-3中有4条简单环路,分别是围绕节点MakeList、MergeSort、split和merge的长度为1的环路。而且每条环路都是自环。回想一下,这些函数都调用了自己,因此都是递归的。到目前为止,函数调用自己的递归是最常见的类型,而且这些递归在调用图中都是以自环的形式出现的。我们将这种递归称为直接递归。不过,大家偶然会看到间接递归,也就是调用图中环路长度大于1的递归。例如,下图就表示函数P 调用了函数Q,而函数Q 调用了函数R,函数R 回过头来又调用了函数P。

9.2.5 无环路径
如果路径中没有节点出现一次以上,就说该路径是无环的。我们刚才在证明对每条环路而言都存在一条简单环路时给出的论证也说明了以下原则。如果存在从u 到v 的路径,就存在从u 到v 的无环路径。要知道原因,首先看看从u 到v 的任意路径。如果存在某个节点w(它可能是u 或v)出现了两次,就可以将两个w 以及这两个w 之间的所有内容用一个w 替代。就像环路的情况那样,我们可能不得不多次重复该过程,但最终会将该路径简化为无环路径。
示例 9.5
再次考虑图9-1中的图。路径(0,1,3,2,1,3,4)是从0到4的包含了环路的路径。我们可以将注意力放在两个节点1上,并将它们及其之间的3和2替换为1,留下(0,1,3,4),这是条无环路径,因为没有节点出现了两次。将注意力放在两个节点3上也可以得到同样结果。
9.2.6 无向图
有时候也可以用没有方向的线条(称为边)连接节点。正式地讲,边是两个节点组成的集合。边{u,v }表示节点u 和v 是双向连通的。1如果{u,v }是边,那么节点u 和v 就是邻接的或者说是邻居。带有边的图,也就是有着对称弧关系的图,就称为无向图。
1请注意,边必须刚好有两个节点。由一个节点构成的单一集不是边。因此,虽然从一个节点到其自身的边是可以存在的,但从一个节点到其自身的自环边是不能存在的。不过某些“无向图”的定义也允许这种自环存在。
示例 9.6
图9-4表示了夏威夷群岛的部分公路图。城市之间的公路就是用边表示的,而且边的标号表示的是行车距离。将公路表示为边而不是弧是很自然的,因为公路通常是双向的。

图 9-4 表示夏威夷群岛中瓦胡岛、毛伊岛和夏威夷岛(左起顺时针排列)上的公路的无向图
9.2.7 无向图中的路径和环路
无向图的路径是各节点与下一节点间都由边连通的节点列(v1,v2,…,vk)。也就是说,对i=1,2,…,k-1而言,{vi,vi+1}是边。请注意,边作为集合,其中的元素是没有特定次序的。因此,边{vi,vi+1}也可以表示为{vi+1,vi }。
路径(vi,v2,…,vk)的长度是k-1。就像有向图那样,节点本身是一条长度为0的路径。
在无向图中定义环路是有点棘手的。问题在于,我们不希望将诸如(u,v,u)这样只要存在边{u,v}就存在的路径视作环路。同样,如果(vi,v2,…,vk)是条路径,我们可以来回穿越该路径,但肯定不想把如下路径视为环路。
(v1,v2,…,vk-1,vk,vk-1,…,v2,v1)
在无向图中定义简单环路的最简单方式可能是指长度不小于3而且起点和终点为同一节点,而且预期最后的节点不会与任何节点重复的路径。而无向图中非简单环路的概念通常不怎么使用,所以后面就不继续讲这个概念了。
和有向环路一样,如果两条无向环路是由次序相同的相同节点构成,就可以将它们视作相同环路。如果两条无向环路是由次序相反的相同节点构成,那么它们也是相同的环路。正式地讲,对从1到k 的每个i,简单环路(v1,v2,…,vk)与环路(vi,vi+1,…,vk,v1,v2,…,vi-1)及环路(vi,vi-1,…,v1,vk,vk-1,…,vi+1)都是等价的。
示例 9.7
在图9-4中,(瓦西阿瓦,珍珠城,迈里,瓦西阿瓦)是长度为3的简单环路。而如果从迈里开始并沿着同样的次序行经环路,它也可以写为等价的(迈里,瓦西阿瓦,珍珠城,迈里)。同样,也可以从珍珠城开始,并沿着相反方向行经环路,得到等价的环路(珍珠城,迈里,瓦西阿瓦,珍珠城)。
再举个例子,(拉耶,瓦西阿瓦,珍珠城,檀香山,卡内奥赫,拉耶)是一条长度为5的简单环路。

图 9-5 习题(1)和习题(2)对应的有向图
9.2.8 习题
1. 考虑图9-5中的图。
(a) 总共有多少条弧?
(b) 从节点a 到节点d 共有多少条无环路径?它们分别是什么?
(c) 节点b 的前导是什么?
(d) 节点b 的后继是什么?
(e) 总共有多少条简单环路?列出它们。不要重复只有起点不同的路径(见习题8)。
(f) 列出长度最多到7的所有非简单环路。
2. 通过将弧u→v 替换为边{u,v },把图9-5所示的图转换为无向图。
(a) 找出从a 到d 的所有无重复节点的路径。
(b) 包含全部6个节点的简单环路有几条?列出这些环路。
(c) 节点a 的邻居有哪些?
3. * 如果某图有10个节点,那么它最多可以有多少条弧?它最少可能有多少条弧?一般来说,如果图有n 个节点,那么它最多和最少分别可能含有多少条弧?
4. * 针对无向图的边重复习题3。
5. ** 如果某有向图是无环的而且有n 个节点,那么它最多可能有多少条弧?
6. 在目前为止本书介绍过的内容中找出一个函数间间接递归的例子。
7. 以所有可能的方式写出环路(0,1,2,0)。
8. * 设G 是有向图,并设R 是G 的环路上的关系,当且仅当(u1,…,uk ,u1)和(v1,…,vk ,v1)表示相同环路时有(u1,…,uk ,u1)R(v1,…,vk ,v1)。证明R 是G 的环路上的等价关系。
9. * 如果S 是定义在某图节点上的关系,当且仅当u=v 或者存在同时包含节点u 和v 的环路时有uSv,证明关系S 是该图节点上的等价关系。
10. * 当讨论无向图中的简单环路时,我们提到过如果两条环路有着相同的节点,不管是次序相同还是次序相反,这两条环路其实都是相同的。证明:由表示相同简单环路的有序对组成的关系R 是等价关系。
9.3 图的实现
实现图的标准方式有两种。一种叫作邻接表,大致上与二元关系的实现方法类似。第二种叫作邻接矩阵,是一种表示二元关系的新方法,而且更适合表示那些有序对数量占据了可能在某给定定义域中浮动的有序对总数很大一部分的关系。我们将首先为有向图考虑这些表示,然后再为无向图考虑。
9.3.1 邻接表
设节点是由整数0、1、…、MAX-1或者等价的枚举类型命名的。一般而言,我们会使用NODE作为节点的类型,不过可以假设NODE跟int是一回事。那么就可以使用7.9节介绍的一般化的特征向量法表示弧的集合,这种表示就叫邻接表。我们将链表的节点定义如下:
typedef struct CELL *LIST;
struct CELL {
NODE nodeName;
LIST next;
};
然后创建数组:
LIST successors[MAX];
也就是说,successor[u]这一项包含了一个指针,指向由节点u 的所有后继组成的链表。
示例 9.8
图9-1中的图可以用图9-6中的邻接表表示。我们已经通过节点编号为这些邻接表排过序了,不过节点的后继可能以任意次序出现在其邻接表中。

图 9-6 图9-1中的图的邻接表表示
9.3.2 邻接矩阵
另一种常见的有向图表示方式是邻接矩阵。我们可以创建如下二维数组:
BOOLEAN arcs[MAX][MAX];
其中如果存在弧u→v,则arcs[u][v]的值为TRUE,否则该值为FALSE。
示例 9.9
图9-1中的图对应的邻接矩阵如图9-7所示。用1表示TRUE,用0表示FALSE。

图 9-7 表示图9-1中的图的邻接矩阵
9.3.3 对图的操作
如果考虑一些简单的图操作,就可以看到图的这两种表示方法间的不同。最基本的操作也许就是确定从节点u 到节点v 是否存在弧u→v。在邻接矩阵中,要查找arcs[u][v]看该项是否为TRUE只需要0 (1)的时间。
邻接矩阵与邻接表的对比
当图很稠密时,也就是,当弧的数量接近最大可能数字时(对有n 个节点的图来说是n2),就倾向于选择邻接矩阵表示。不过,如果图是稀疏的,也就是说,如果可能存在的弧大多数并未出现,那么用邻接表表示法就可能节省空间。要知道原因,请注意表示含n 个节点的图的邻接矩阵有n2位,假设用1位来表示
TRUE和FALSE,而不是像本节中已经做过的那样用整数表示。在一般的计算机中,像邻接表单元这样的结构体是由整数和指针构成的,每个结构体会使用32位表示整数,并用32位表示指针,总共需要64位。因此,如果弧的数量为a,就需要64a 位存储该链表,而且存放n 个表头的数组还需要32n 位。如果有32n+64a< n2,也就是如果有a< n2/64-n/2,邻接表就要比邻接矩阵节省空间。如果n 很大的话,就可以舍掉n/2这项,并近似地将之前的不等式视作a< n2/64,也就是说,如果可能存在的弧只有不到1/64实际出现,邻接表就要比邻接矩阵节省空间。我们在讨论对图的操作时将更为详细地论证这两种表示法的优劣。下表总结了为多种操作优先选择的表示法。
操作
稠密图
稀疏图
查找弧
邻接矩阵
皆可
找后继
皆可
邻接表
找前导
邻接矩阵
皆可
使用邻接表的话,就要找到对应u 的邻接表的表头,需要0(1)的时间。然后,如果v 不在表中,就要遍历该表直到末端,或者如果v 存在的话平均要浏览该表的一半。如果该图中有a 条弧和n 个节点,那么平均要花O(1+a/n)的时间来完成这样的查找。如果a 不大于n 乘以某个常数因子,这个量就是O(1)。不过,在与n 相比时,a 越大,使用邻接表表示法验证弧是否出现所花的时间就越长。在a 大约是n2(其最大可能值)的极端情况下,每个邻接表中都将近有n 个节点。这种情况下,找到某给定的弧平均要花O(n)的时间。换句话说,当我们需要查找某给定的弧时,图越稠密,就越愿意选择邻接矩阵而不是邻接表。
另一方面,我们经常需要找到某给定节点u 的所有后继。要用邻接表找到所有的后继,就要行向successor[u]并遍历该表,平均耗时O(a/n)。如果a 和n 是近似的,就可以在O(1)的时间内找到u 的所有后继。不过如果使用邻接矩阵,就必须检查节点u 所在的那一整行,不管a 是多少都要花O(n)的时间。因此,对每个节点只有少量边与之连接的图来说,在需要检查某给定节点的后继时,使用邻接表要比使用邻接矩阵快得多。
不过,假设想要找到某给定节点v 的全部前导。如果用邻接矩阵表示,就需要检查v 所在的那一整列,如果u 所在那行的位置是1,就意味着u 是v 的前导。这一检查要花费0(n)的时间。而邻接表表示在查找前导时也帮不上忙。必须检查对应每个节点u 的邻接表,看看该表中是否含有v。因此,我们可能要检查所有邻接表的所有单元,而且很可能将检查大多数的单元。因为整个邻接表结构中单元的数量等于a,也就是图中弧的数量,所以使用邻接表在含a 条弧的图中找前导的时间就是O(a)。在这里,邻接矩阵表示法是占优势的,而且图越稠密,这种优势就越大。
度的问题
从节点v 出发的弧的数量就叫作v 的出度。因此,节点的出度等于其邻接表的长度,还等于相应的邻接矩阵中对应v 的那行中1的数量。进入节点v 的弧的数量叫作v 的入度。入度衡量的是节点v 在某节点的邻接表中出现的次数,而且是相应的邻接矩阵中对应v的那列中1的数量。
在无向图中,我们不会区分边是从节点出发还是进入节点。对无向图而言,节点v 的度就是v 的邻居的数量,也就是含有v 的边{u,v }的数量。请记住,在集合中,成员的次序是不重要的,所以{u,v }和{v,u }是相同的边,因此只能计算一次。而无向图的度则是该图中节点的度的最大值。例如,如果将二元关系看作无向图,那么它的度就是3,因为节点最多只能与它的父节点、左子节点和右子节点之间有边。对有向图而言,可以说有向图的入度是其节点入度的最大值,同样,有向图的出度是其节点出度的最大值。
9.3.4 无向图的实现
如果图是无向图,可以假装每条边都被替代为两个方向上的弧,并将得到的有向图用邻接表或邻接矩阵表示出来。如果使用邻接矩阵,那么该矩阵是对称的。也就是说,如果称该矩阵为edges,那么edges[u ][v ]=edges[v ][u ]。如果使用邻接表表示法,那么边{u,v }就会被表示两次。我们可以在邻接表中找到对应u 的v,也可以在该表中找到对应v 的u。这种排列通常是实用的,因为不可能事先分辨出{u,v }这条边是更可能从u 到v,还是更可能从v 到u。
示例 9.10
考虑一下如何表示图9-4的无向图中最大那部分,也就是表示瓦胡岛6个城市的那部分。在这里我们要忽略边的标号。对应的邻接矩阵表示就如图9-8所示。请注意,该矩阵是对称的。
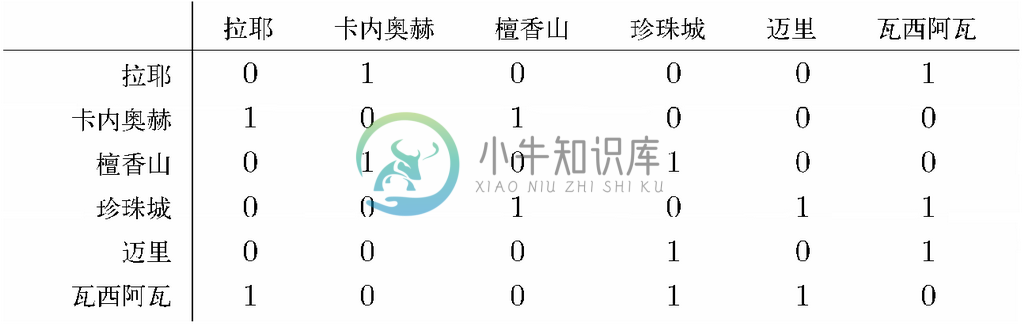
图 9-8 图9-4中的无向图的邻接矩阵表示
图9-9展示了该无向图的邻接表表示。在两种情况下,我们都要用到枚举类型
enum CITYTYPE {Laie, Kaneohe, Honolulu, PearlCity, Maili, Wahiawa};
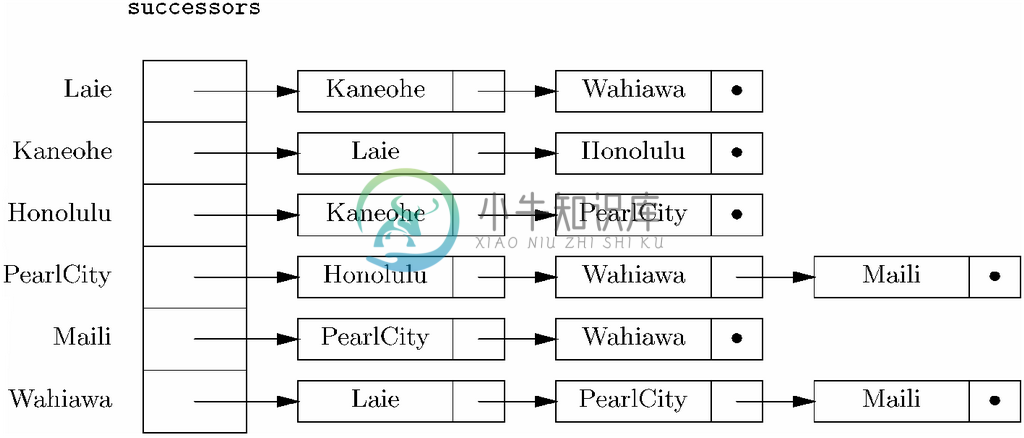
图 9-9 图9-4中无向图的邻接表表示
来作为数组的索引。这种安排多少有些刻板,因为这样定义就没法对该图的节点集合进行任何改动。不过我们很快就会给出用整数显式命名节点并用城市名作为节点标号的相似示例,这样在改变节点集合方面会更具灵活性。
9.3.5 标号图的表示
假设图的弧(如果是无向图就是边)带有标号。在使用邻接矩阵时,就可以将表示弧u→v 在图中出现的1替换为该弧的标号。而且必须要有一些可作为矩阵的项但又不会与标号混淆的值,我们要用该值表示弧未出现的情况。
如果用邻接表表示图,就要为构成各链表的单元添加一个nodeLabel字段。如果存在标号为L 的弧u→v,那么在对应节点u 的邻接表中就会找到nodeName字段为v 而且nodeLabel字段为L 的单元。nodeLabel字段的值就表示该弧的标号。
我们要用另一种方式表示节点的标号。对邻接矩阵来说,只要创建另一个名为NodeLabels的数组,并设NodeLabels[u]是节点u 的标号。在使用邻接表时,已经有了以节点为索引的表头数组。我们要把该数组的元素改为结构体,一个字段为节点标号,而另一个字段为指向邻接表开头的指针。
示例 9.11
我们要再次表示图9-4所示图的较大部分,不过这次要加上边的标号,也就是距离。此外,要给出节点的整数名称,从对应拉耶的0开始,按照顺时针方向排列。城市的名称是用节点的标号表示的。要将节点标号的类型定义为长度为32的字符数组。这种表示方式要比示例9.10的方式更灵活,因为如果要在数组中分配额外的位置,就可以在想要添加城市时如愿以偿。得到的图重绘为图9-10的样子,而对应的邻接矩阵表示如图9-11所示。

图 9-10 节点名称为整数而标号为城市名的瓦胡岛地图
请注意,这一表示其实有两个部分,cities数组,指示从0到5的整数代表的城市,以及distances矩阵,指示边是否出现以及出现的边的标号。我们用不会被误解为标号的值-1表示未出现的边,因为在本例中,标号是表示城市间距离的,它肯定是正数。

图 9-11 有向图的邻接矩阵表示
可以将该结构体声明如下:
typedef char CITYTYPE[32];
typedef CITYTYPE cities[MAX];
int distances[MAX][MAX];
这里的MAX 是至少为6的某个数字,它限制了可以出现在图中的节点数。CITYTYPE被定义为长度为32的字符数组,而且数组cities给出了各节点的标号。例如,可以预期cities[0]是"Laie"(拉耶)。
还可以用邻接表表示图9-10所示的图。假设常量MAX 和CITYTYPE类型都与上面的定义相同。我们可以将CELL和LIST类型定义为
typedef struct CELL *LIST;
struct CELL {
NODE nodeName;
int distance;
LIST next;
};
接下来,要将cities数组声明为
struct {
CITYTYPE city;
LIST adjacent;
} cities[MAX];
图9-12展示了用这种方式表示的图9-10所示的图。

图 9-12 具有节点标号和边标号的图的邻接表表示
9.3.6 习题
1. 分别用
(a) 邻接表
(b) 邻接矩阵
表示图9-5(见9.2节的习题)所示的图,在每种情况下都给出合适的类型定义。
2. 假设图9-5中的弧都是边,即将图变成无向图。针对该无向图重复习题1。
3. 为图9-5中有向图的弧加上标号,标号是由弧的尾部跟上弧的头部组成的长度为2的字符串。例如,弧a→b 的标号就是字符串ab。还有,假设节点的标号是对应其名称的大写字母。比如名为a 的节点的标号就是A。针对该带标号的有向图重复习题1。
4. * 无标号图的邻接矩阵表示与弧集合的特征向量表示有何关系?
5. * 通过对n 的归纳证明,在含n 个节点的无向图中,节点度的和是边数的两倍。注意。不使用归纳法也是可以证明该命题的,不过这里要求大家使用归纳法证明。
6. 设计算法,在有向图的(a)邻接矩阵;(b)邻接表表示中插入和删除弧。
7. 针对无向图重复习题6。
8. 我们可以为有向图或无向图的邻接表表示增加“前导表”。在执行以下哪些操作时,会选择这种表示?
(a) 查找弧。
(b) 找出所有后继。
(c) 找出所有前导。
在分析中要同时考虑稠密图和稀疏图的情况。
9.4 无向图的连通分支
我们可以将任意无向图分解为一个或多个连通分支(connected component)。连通分支是节点的集合,分支的任意成员之间都是存在路径的。此外,连通分支是极大的,也就是说,连通分支中的节点没有与分支外的任意节点连接的路径。如果图是由单个连通分支组成的,那么就说该图是连通图。
连通分支的物理解释
如果给定了绘制出的无向图,就很容易看出连通分支。将边想象成弦。如果拿起任一节点,包含该节点作为成员的连通分支就会随之而来,而其他连通分支中的成员则会待在原地。当然,这些“眼球”很容易完成的任务让计算机完成起来却不一定很容易。找出图中连通分支的算法是本节的重要主题。
示例 9.12
再次考虑图9-4中有关夏威夷群岛的图。其中含有3个连通分支,分别对应3个岛。最大的分支是由拉耶(Laie)、卡内奥赫(Kaneohe)、檀香山(Honolulu)、珍珠城(Pearl City)、迈里(Maili)和瓦西阿瓦(Wahiawa)组成的。这些城市都是在瓦胡岛上,而且它们显然是由公路(也就是边的路径)相互连接。还有,瓦胡岛上的公路是没法连接到其他岛的。按照图论的说法就是,在图9-4中,不存在从上面提到的这6个城市到其他城市的路径。
第二个分支是由毛伊岛上的城市拉海纳(Lahaina)、卡胡卢伊(Kahului)、哈纳(Hana)和凯奥凯阿(Keokea)组成的。第三个分支是夏威夷“大岛”上的城市希洛(Hilo)、科纳(Kona)和卡姆埃拉(Kamuela)。
9.4.1 作为等价类的连通分支
另一种看待连通分支的实用方式就是将其视为等价关系P 上的等价类,其中P 是定义在无向图节点上的关系,当且仅当存在从u 到v 的路径时有uPv。很容易验证P 是等价关系。
1. P 是自反的,也就是说,对任意节点u 有uPu,因为从任意节点到其自身都有长度为0的路径。
2. P 是对称的。如果uPv,那么存在从u 到v 的路径。因为该图是无向图,所以相反的节点序列也是路径。因此有vPu。
3. P 是传递的。假设uPw 和wPv 都成立,那么存在从u 到w 的路径,比方说是
(x1,x2,…,xj )
这里有u=x1且w=xj 。还有,存在从w 到v 的路径(y1,y2,…,yj ),其中w=y1而且v=yj 。如果将这些路径连接在一起,就得到了从u 到v 的路径,即
(u =x1,x2,…,xj =w =y1,y2,…,yk =v )
示例 9.13
考虑图9-10中从檀香山到迈里的路径(檀香山,珍珠城,瓦西阿瓦,迈里)。再考虑该图中从迈里到拉耶的路径(迈里,珍珠城,瓦西阿瓦,拉耶)。如果将这两条路径连在一起,就得到了从檀香山到拉耶的路径:
(檀香山,珍珠城,瓦西阿瓦,迈里,珍珠城,瓦西阿瓦,拉耶)
这条路径刚好是条环路。正如在9.2节中提过的,我们总是能删除环路得到无环路径。在这种情况下,要消除环路,一种方法就是将两个瓦西阿瓦以及它们之间的节点用一个瓦西阿瓦替代,得到从檀香山到拉耶的无环路径
(檀香山,珍珠城,瓦西阿瓦,拉耶)
因为P 是等价关系,所以它把问题中无向图节点的集合分成了等价类。包含节点v 的类就是满足vPu 的所有节点u 的集合。此外,等价类的其他属性还有,如果节点u 和v 在不同的等价类中,那么不可能有uPv,也就是说不存在从一个等价类中的某节点到另一等价类中节点的路径。因此,由“路径”关系P 定义的各等价类就是该图的各连通分支。
9.4.2 计算连通分支的算法
假设我们想构建图G 的连通分支。一种方式是从G 中没有边的节点组成的图G0开始。然后考虑G 的边,一次一条,构建一系列的图G0、G1、…,其中Gi 是由G 的节点和G 的前i 条边构成的。
依据。G0是由G 中没有边的节点组成。每个节点本身是一个分支。
归纳。假设在考虑了前i 条边后得到了图Gi 的连通分支,现在考虑第i+1条边:{u,v }。
1. 如果u 和v 在Gi 的同一分支中,那么Gi+1有着与Gi 相同的连通分支集合,因为这条新的边不会连接到任何尚未连通的节点。
2. 如果u 和v 在不同分支中,我们可以合并包含u 和v 的分支,得到Gi+1的连通分支。图9-13解释了为什么存在从u 所在分支中任一节点x 到v 所在分支中任一节点y 的路径。我们沿着第一个分支中从x 到u 的路径走,然后到边{u,v },最后经过已知存在于第二个分支中的从v 到y 的路径。
当以这种方式考虑过所有的边时,就得到了全图的连通分支。
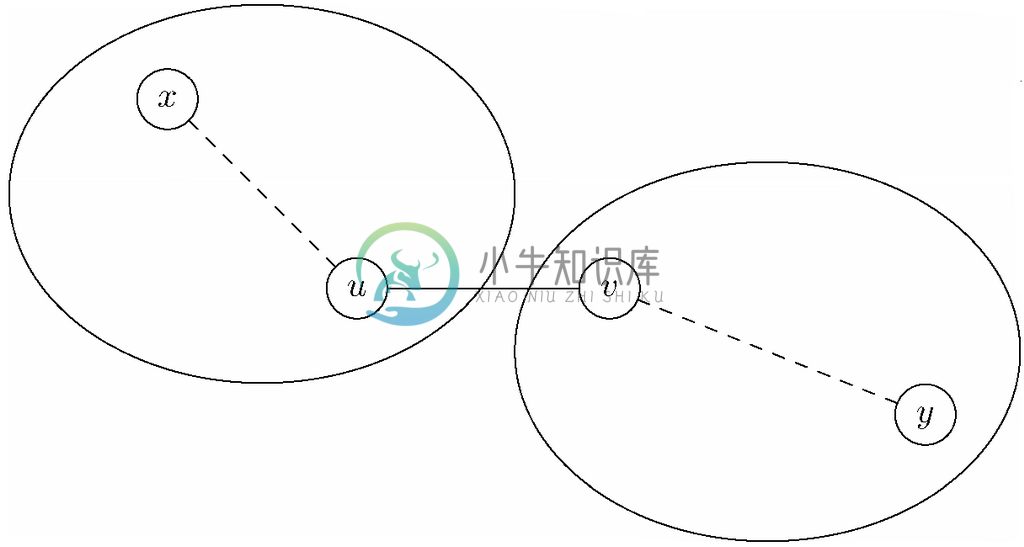
图 9-13 添加连接了含u 的分支与含v 的分支的边{u,v }
示例 9.14
来考虑一下图9-4中的图。虽然我们能够以任意次序考虑这些边,不过为了9.5节中某一算法的需要,在这里按照边标号从小到大的次序列出了这些边。边的列表如图9-14所示。
首先,所有13个节点都在它们各自的分支中。当考虑1号边{卡内奥赫,檀香山}时,我们就将这两个节点合并到了一个分支中。而第二条边{瓦西阿瓦,珍珠城}则合并了这两个城市。第三条边是{珍珠城,檀香山},这条边把包含这两个城市的分支合并了。至此,这些分支各含两个城市,所以就有了具有4个城市的分支,即{瓦西阿瓦,珍珠城,檀香山,卡内奥赫}。而所有其他城市都还在它们自己的分支中。
边 | 城市1 | 城市2 | 距离 |
|---|---|---|---|
1 | 卡内奥赫 | 檀香山 | 11 |
2 | 瓦西阿瓦 | 珍珠城 | 12 |
3 | 珍珠城 | 檀香山 | 13 |
4 | 瓦西阿瓦 | 迈里 | 15 |
5 | 卡胡卢伊 | 凯奥凯阿 | 16 |
6 | 迈里 | 珍珠城 | 20 |
7 | 拉海纳 | 卡胡卢伊 | 22 |
8 | 拉耶 | 卡内奥赫 | 24 |
9 | 拉耶 | 瓦西阿瓦 | 28 |
10 | 科纳 | 卡姆埃拉 | 31 |
11 | 卡姆埃拉 | 希洛 | 45 |
12 | 卡胡卢伊 | 哈纳 | 60 |
13 | 科纳 | 希洛 | 114 |
图 9-14 以标号为次序的图9-4中的边
4号边是{迈里,瓦西阿瓦},并且将迈里添加到大分支中。第5条边是{卡胡卢伊,凯奥凯阿},它将这两个城市合并到一条分支中。当考虑6号边{迈里,珍珠城}时,我们看到了新现象:这条边的两端已经存在于相同的分支中。因此我们不再合并6号边。
7号边是{拉海纳,卡胡卢伊},它将节点拉海纳添加到了分支{卡胡卢伊,凯奥凯阿}上,形成了分支{拉海纳,卡胡卢伊,凯奥凯阿}。而8号边则将拉耶添加到了最大的分支上,最大分支现在就成了:
{拉耶,卡内奥赫,檀香山,珍珠城,瓦西阿瓦,迈里}
第九条边{拉耶,瓦西阿瓦}连接了该分支中的两个城市,因此被忽略掉。
10号边将卡姆埃拉和科纳组成一条分支,而且11号边为这一分支添加了希洛。12号边则将哈纳添加到了{拉海纳,卡胡卢伊,凯奥凯阿}这一分支中。最后,13号边{希洛,科纳}连接的是已经存在于同一分支中的两个城市。因此,最后总共有如下几个连通分支。
{拉耶,卡内奥赫,檀香山,珍珠城,瓦西阿瓦,迈里}
{拉海纳,卡胡卢伊,凯奥凯阿,哈纳}
{卡姆埃拉,希洛,科纳}
9.4.3 用于形成分支的数据结构
如果非正式地考虑9.4.2节中描述的算法,我们需要能迅速完成以下两项工作:
1. 给定某节点,找出其当前所在分支;
2. 将两个分支合并为一个分支。
有很多种数据结构可以支持这些操作。我们将研究一种简单却又能带来极佳性能的想法。关键在于将每个分支中的节点都放进一棵树中。2分支是由树的根表示的。上述两项操作现在可以按照如下方式实现。
2请务必理解,在接下来的内容中,“树”和“图”指的是不同的结构。图的节点与树的节点间存在一一对应,也就是说,每个树节点都表示一个图节点。不过,树中父子节点之间的边并不一定是图中存在的边。
1. 要找到图中节点的分支,就要找到该节点在树中的代表,然后沿着树中的路径到达表示该分支的根节点。
2. 要合并两个不同的分支,我们就要让一个分支的根节点成为另一分支根节点的子节点。
示例 9.15
我们遵循示例9.14介绍的步骤,展示按照特定步骤创建的树。首先,每个节点本身都是一棵单节点树。而第一条边{卡内奥赫,檀香山}会让我们把两棵单节点树{卡内奥赫}和{檀香山}合并为一棵双节点树{卡内奥赫,檀香山}。任何一个节点都可以作为另一个的子节点。不过在这里假设檀香山是根节点卡内奥赫的子节点。
同样,第二条边{瓦西阿瓦,珍珠城}合并了两棵单节点树,而且可以假设珍珠城是根节点瓦西阿瓦的子节点。至此,当前的分支集合可以用图9-15所示的两棵树以及9棵单节点树来表示。

图 9-15 合并分支得到的前两棵重要的树
第三条边{珍珠城,檀香山}合并了这两个分支。假设瓦西阿瓦是另一个根节点卡内奥赫的子节点。那么得到的分支就可以用图9-16中的树表示。

图 9-16 表示含4个节点的分支的树
当考虑第四条边{瓦西阿瓦,迈里}时,就要把迈里合并到用图9-16中的树表示的分支中。既可以把迈里作为卡内奥赫的子节点,也可以将卡内奥赫当作迈里的子节点。不过这里选择前者,因为这样可以让树的高度保持比较小的值,而让大分支的根节点作为小分支根节点的子节点会让树中的路径变得更长。在确定节点的分支时,长路径会让我们要花更多时间才能沿着路径到达根节点。通过遵循这样的策略,并在分支高度相同时作出任意觉得,我们可能得到图9-17中表示3条最终连通分支的3棵树。

图 9-17 使用树合并算法表示最终连通分支的树
遵循示例9.15中的经验,我们制订了这样的策略,在合并两棵树时,高度较小的根节点要成为高度较大的根节点的子节点。如果出现高度相等的情况就任选一种方式。从这一策略中得到的重要收获就是树的高度只能以树中节点数对数的速度增长,而且在实践中,树的高度往往还更小。因此,当沿着一条路径从树的节点到达其根节点时,所花的时间最多与树中节点数的对数成比例。我们可以通过对高度h 的归纳证明如下命题,从而得出这一对数边界。
命题S(h)。按照将较低高度合并到较高高度的策略形成的高度h 的树,至少有2h个节点。
依据。依据是h=0。这样的树肯定只有一个节点,而且因为20=1,所以命题S(0)成立。
归纳。假设S(h)对某个h≥0成立,并考虑高度为h+1的树T。在通过合并形成T 的过程中的某个时刻,树的高度第一次达到h+1。让树的高度达到h+1的唯一方式就是让某高度为h 的树T1的根节点成为某树T2根节点的子节点。T 是T1加上T2,可能还要加上一些后来要加上的其他节点,如图9-18所示。
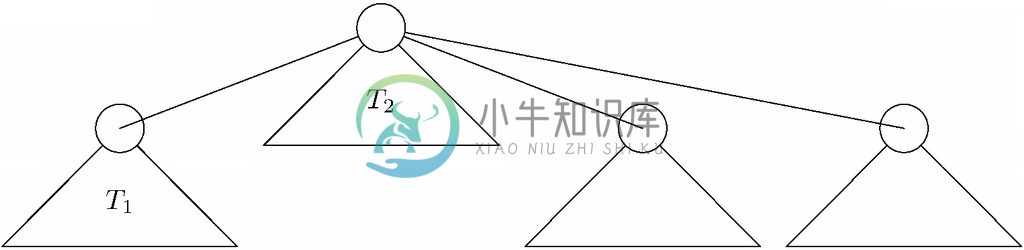
图 9-18 形成高度为h+1的树
现在,根据归纳假设,T1至少有2h个节点。因为它的根节点成为了T2根节点的子节点,所以T2的高度也至少是h。因此,T2也至少有2h个节点。T是T1加上T2,可能还有更多节点组成的,所以T 至少有2h+2h=2h+1个节点。这就是S(h+1),所以我们证明了归纳步骤。
现在就知道了,如果一棵树有n 个节点且高度为h,那么肯定有n≥2h。如果在两边取对数,就得到log2n≥h,也就是说,树的高度不可能大于节点数的对数。这样一来,当我们沿着任意路径从节点到达树的根节点时,都要花O(logn)的时间。
现在要更详细地描述实现这些想法的数据结构。首先,假设用NODE类型来表示节点。就像以前那样,我们假设NODE的类型为int,而且MAX至少是图中所含节点的数量。对图9-4中的例子而言,要设MAX为13。
还要假设由EDGE类型的单元组成的链表edges,这些单元是由如下声明定义的
typedef struct EDGE *EDGELIST;
struct EDGE {
NODE node1, node2;
EDGELIST next;
};
最后,对图中的每个节点而言,还需要一个与之对应的树节点。树节点是TREENODE类型的结构体,由以下内容组成。
1. 父指针,让我们能在该图的节点上构建树,并沿着树到达其根节点。父指针为NULL就标识该节点为根节点。
2. 以给定节点为根节点的树的高度。只有该节点是根节点时才使用该高度。
因此可以将TREENODE类型定义为:
typedef struct TREENODE *TREE;
struct TREENODE {
int height;
TREE parent;
}:
我们还要定义数组
TREE nodes[MAX];
以便将每个图节点与树中某个节点关联起来。应当明白,数组nodes中的每一项都是指向树中节点的指针,而该数据项也是图中节点的唯一代表。
图9-19展示了两个重要的辅助函数。第一个是find,它接受节点a,取指向其对应树节点x 的指针,沿着x 的父指针及其祖先向上,直到到达根节点。这种对根节点的搜索是由第(2)行和第(3)行执行的。如果找到了根节点,就会在第(4)行返回指向该根节点的指针。请注意,在第(1)行,NODE类型一定是int,这样才能用它来作为nodes数组的索引。
/* 返回树的根节点位置,该位置含有对应
图节点a的树节点x */
TREE find(NODE a, TREE nodes[]);
{
TREE x;
(1) x = nodes[a];
(2) while (x->parent != NULL)
(3) x = x->parent;
(4) return x;
}
/* 让根节点较低的树成为根节点较高的树的子树,
从而将根节点分别
为x和y的树合并为一棵树 */
void merge(TREE x, TREE y)
{
TREE higher, lower;
(5) if (x->height > y->height) {
(6) higher = x;
(7) lower = y;
}
else {
(8) higher = y;
(9) lower = x;
}
(10) lower->parent = higher;
(11) if (lower->height == higher->height)
(12) ++(higher->height);
}
图 9-19 辅助函数find和merge
第二个函数是merge,3它接受指向两个树节点的指针x 和y,要让函数正常工作,它们一定是需要合并的两棵树的根节点。第(5)行的测试确定了哪个根节点的高度更大,如果相等就直接选择y。在第(6)行至第(7)行或第(8)行至第(9)行,会根据具体的情况将较高的根节点赋值给局部变量higher,而较低的根节点则被赋值给局部变量lower。接着在第(10)行较低的根节点会成为较高根节点的子节点,而在第(11)行和第(12)行,如果T1和T2的高度相等,较高根节点(也就是现在合成的树的根节点)的高度要增加1。较低根节点的高度保持不变,不过现在这个值已经没有意义了,因为较低根节点现在已经不再是根节点了。
3不要把该函数与第2章和第3章中用于归并排序的同名函数弄混了。
找出连通分支的算法的核心内容如图9-20所示。假设函数makeEdges()会把手头的图转换成由图中的边组成的链表,这里并未展示该函数的代码。
#include <stdio.h>
#include <stdlib.h>
#define MAX 13
typedef int NODE;
typedef struct EDGE *EDGELIST;
struct EDGE {
NODE node1, node2;
EDGELIST next;
};
typedef struct TREENODE *TREE;
struct TREENODE {
int height;
TREE parent;
};
TREE find(NODE a, TREE nodes[]);
void merge(TREE x, TREE y);
EDGELIST makeEdges();
main()
{
NODE u;
TREE a, b;
EDGELIST e;
TREE nodes[MAX];
/* 初始化节点,使得每个节点都在由其自身构成的树中 */
(1) for (u = 0; u < MAX; u++) {
(2) nodes[u] = (TREE) malloc(sizeof(struct TREENODE));
(3) nodes[u]->parent = NULL;
(4) nodes[u]->height = 0;
}
/* 将e初始化为存放图中各边的表 */
(5) e = makeEdges();
/* 检查每条边,如果边的的端点在不同组分中,就将它们
合并 */
(6) while (e != NULL) {
(7) a = find(e->node1, nodes);
(8) b = find(e->node2, nodes);
(9) if (a != b)
(10) merge(a, b);
(11) e = e->next;
}
}
图 9-20 用来找出连通分支的C语言程序
用来找出连通分支的更优算法
我们会在9.6节中研究深度优先搜索时看到,其实还有更好的方法来计算连通分支,它只需要花费O(m)的时间,而不是O(m logn)的时间。不过,9.4节中给出的数据结构本身也很实用,我们在9.5节中就要看到另一个使用该数据结构的程序。
图9-20的第(1)行到第(4)行会浏览数组nodes,而在第(2)行会为每个节点创建一个树节点。在第(3)行其parent字段会被置为NULL,表示它是其自身构成的树的根节点,而在第(4)行会将其height字段置为0,以反映出在由该节点自己构成的树中就只有它这一个节点。
然后第(5)行会把e初始化为指向边链表中的第一条边,而且第(6)行到第(11)行的循环会一次检查每一条边。在第(7)行和第(8)行,我们找到了当前边两个端点的根节点。接着在第(9)行要测试这些根节点是否为不同的树节点。如果是,那么当前边的两个端点在不同分支中,而且我们要在第(10)行合并这些分支。如果该边的两个端点在同一分支中,就跳过第(10)行,因此就不会对树集合造成任何改变。最后,第(11)行会带着我们沿着边链表行进。
9.4.4 连通分支算法的运行时间
我们来确定一下图9-20所示的算法处理一幅图要花多长时间。假设该图有n 个节点,并设节点数和边数的较大者为m。4首先看看这些辅助函数。我们论证过,将高度较低的树合并到高度较高的树中的策略可以保证从任意树节点到达其根节点的路径都不会比logn长。因此,find会花费O(logn)的时间。
4把m 当作边的数量是很正常的,不过在某些图中,节点比边更多。
接下来要查看图9-19中的函数merge。它的每条语句都花费O(1)的时间。因为其中不含循环或函数调用,所以整个函数也只花O(1)的时间。
最后来看看图9-20所示的主程序。第(1)行到第(4)行的for循环循环体要花费O(1)的时间,而且该循环要迭代n 次。因此,第(1)行到第(4)行所花的时间是O(n)。假设第(5)行要花费O(m)的时间。最后,考虑一下第(6)行到第(11)行的while循环。在循环体中,第(7)和第(8)行每行都要花费O(logn)的时间,因为它们都调用了函数find,而我们刚刚已经确定过find要花费O(logn)的时间。第(9)行和第(11)行显然只要O(1)的时间。第(10)行同样只要O(1)的时间,因为我们刚刚确定了merge花费O(1)的时间。因此,整个循环体要花费O(logn)的时间。而while循环会迭代m 次,其中m 是边的数量。因此,该循环的运行时间就是O(m logn),也就是迭代的次数乘以循环体运行时间的边界。
然后,一般来说,整个程序的运行时间可以表示为O(n+m+m logn)。不过,m 至少是n,所以m logn 这一项就主导了其他两项。因此,图9-20所示程序的运行时间就是O(m logn)。
9.4.5 习题
1. 图9-21列出了密歇根州的一些城市以及它们之间的公路里程数。就本习题的目的而言可以忽略里程数。以本节描述的方式检查每条边,构建该图的连通分支。
2. * 通过对k 的归纳证明,有k 个节点的连通分支至少有k-1条边。
城市1 | 城市2 | 距离 |
|---|---|---|
马凯特(Marquette) | 苏圣玛丽(Sault Ste. Marie) | 153 |
萨吉诺(Saginaw) | 弗林特(Flint) | 31 |
大急流城(Grand Rapids) | 兰辛(Lansing) | 60 |
底特律(Detroit) | 兰辛(Lansing) | 78 |
埃斯卡诺巴(Escanaba) | 苏圣玛丽(Sault Ste. Marie) | 175 |
安娜堡(Ann Arbor) | 底特律(Detroit) | 28 |
安娜堡(Ann Arbor) | 巴特尔克里克(Battle Creek) | 89 |
巴特尔克里克(Battle Creek) | 卡拉马祖(Kalamazoo) | 21 |
梅诺米尼(Menominee) | 埃斯卡诺巴(Escanaba) | 56 |
卡拉马祖(Kalamazoo) | 大急流城(Grand Rapids) | 45 |
埃斯卡诺巴(Escanaba) | 马凯特(Marquette) | 78 |
巴特尔克里克(Battle Creek) | 兰辛(Lansing) | 40 |
弗林特(Flint) | 底特律(Detroit) | 58 |
图 9-21 密歇根州某些城市间的距离
3. * 有一种更简单的方法实现“合并”和“寻找”,在使用这种方法时,要使用以节点为索引的数组,给出每个节点的分支。一开始,每个节点都在由它自己构成的分支中,而且我们要用相应的节点来为这种分支命名。要找到节点的分支,只要查找对应的数组项即可。要合并分支,就要沿数组向下行进,将所有出现第一个分支的地方都改为第二个分支。
(a) 编写C语言程序实现这一算法。
(b) 该程序的运行时间是多少?将其表示为节点数n与节点数和边数较大值m的函数。
(c) 对某些边数和节点数而言,这种实现其实比本章中描述的实现还要好。什么时候这种实现更好?
4. * 假设本节的连通分支算法中不是将较低的树合并到较高的树中,而是将节点较少的树合并到节点较多的树中。这种连通分支算法的运行时间是否仍为O(m logn)?
9.5 最小生成树
连通分支问题有个很重要的推广,其中给定了以数字(整数或实数)作为边标号的无向图。我们不仅要找到连通分支,而且要为各分支找到连接分支中各节点的树。此外,该树一定是最小的,意味着边标号的和是尽可能小的。
这里讨论的树与第5章讨论过的树不太一样。这里的树中没有节点会被指定为根节点,而且没有子节点或子节点次序的概念。本节中提到“树”时,指的是没有根没有次序的树,就是那些不含简单环路的无向图。
无向图G 的生成树是由G 的节点与G 的边的子集按照如下要求一起构成的。
1. 连通节点,也就是说,任意两个节点之间都存在只用生成树中的边构成的路径。
2. 形成无根且无次序的树,也就是说,树中没有(简单)环路。
如果G 是单个连通分支,就总是存在生成树。最小生成树是给定图对应的任意生成树中边标号的和最小的那个。
示例 9.16
设图G 是如图9-4或图9-10所示对应瓦胡岛的连通分支。图9-22展示了一种可能的生成树。它是通过删除{迈里,瓦西阿瓦}和{卡内奥赫,拉耶}这两条边并剩下其余5条边形成的。这棵树的权(也就是边标号之和)为84。正如我们将要看到的,这不是最小值。

图 9-22 对应瓦胡岛的生成树
有根树与无根树
无根树的概念似乎不应该很奇怪。其实我们可以从无根树中任选一个节点作为根节点。这样就为所有的边给出了远离根节点,或者是从父节点到子节点的方向。从物理意义上讲,这就像是从无根树的某个节点提起该树,让该树其他部分从选定的节点处吊起来。例如,可以将珍珠城作为图9-22所示生成树的根节点,它就成了下面这样
如果愿意的话,可以为每个节点的子节点排定次序,不过这种次序是任意的,与原来的无根树之间没有关系。
9.5.1 找到最小生成树
有多种用于找到最小生成树的算法。我们将研究其中一种,名为克鲁斯卡尔算法(Kruskal's algorithm),它是对9.4节中讨论过的寻找连通分支算法的一种简单扩展。需要进行的修改如下所述。
1. 需要按照边标号的递增次序考虑这些边。我们在示例9.14中刚好选择了这种次序,不过对连通分支而言这不是必要的。
2. 在考虑边时,如果边的两个端点在不同分支中,就要选择该边构成生成树并且合并两个分支,正如9.4节的算法中所做的。否则,就不选择这条边构成生成树,当然也就不用合并分支。
示例 9.17
Acme Surfboard Wax 公司在如图9-4所示的13个城市中都有办公地点。它希望从电话公司租用专用的数据传输线路,我们假设电话线路是沿着图9-4中的边表示的公路架设的。在不同的岛屿之间,该公司必须使用卫星传输,而成本与分支数量是成正比的。不过,对地面传输线路来说,电话公司是按里程收费的。5 6因此,我们希望为图9-4所示的图中各连通分支找出最小生成树。
5这是一种为租用的电话线路收费的可行方式。人们可以找出连接这些所需场所的最小生成树,且收费是根据该树的权得出的,而不用考虑提供电话连接的实际方式。
6请注意,如果将树中的弧看作存在从父节点到子节点的方向,树就可以被当作有向图的一个特例。其实,树还总是无环图。
如果按照分支分开这些边,就可以分别为各分支运行克鲁斯卡尔算法。不过,如果我们尚不知道有哪些分支,就必须将所有的边放在一起考虑,从最小的标号开始,按照图9-14的次序进行。正如9.4节中那样,我们先从由节点本身构成的分支中的各节点开始。
首先考虑标号最小边{卡内奥赫,檀香山}。这条边将这两个城市合并到一个分支中,而且因为我们执行了合并操作,所以就选择了该边用来构成最小生成树。2号边是{瓦西阿瓦,珍珠城},而且因为这条边也是合并了两个分支,所以它也被选来构成该生成树。同样,第三条边{珍珠城,檀香山}和第四条边{瓦西阿瓦,迈里}也合并了分支,因此也被放入生成树。
第五条边{卡胡卢伊,凯奥凯阿}合并了这两个城市,而且也被接纳到生成树中,虽然这条边是要成为表示毛伊岛分支的生成树的一部分,而不是和前四条边那样是瓦胡岛分支的一部分。
第六条边{迈里,珍珠城}连接着已经出现在同一分支中的两个城市。因此,该边会被生成树拒之门外。即便我们必须选择某条标号更大的边,也不能选择{迈里,珍珠城},因为这样一来就会在迈里、瓦西阿瓦和珍珠城间形成一条环路。在生成树中是不可以有环路的,所以这3条边中必须有一条被排除在外。随着我们按照标号的次序考虑这些边,最后的边肯定有着最大的标号,也是最佳方案要排除掉的。
第七条边{拉海纳,卡胡卢伊}和第八条边{拉耶,卡内奥赫}都被生成树接纳,因为它们合并了分支。而9号边{拉耶,瓦西阿瓦}会因为它的端点在同一分支中而不被接受。我们会接受10号边和11号边,它们形成了表示“大岛”分支的生成树,而且我们会接纳12号边以完成毛伊岛分支。13号边不会被接纳,因为它连接的科纳和希洛已经被10号边和11号边连接到同一分支中了。得到各分支的生成树如图9-23所示。
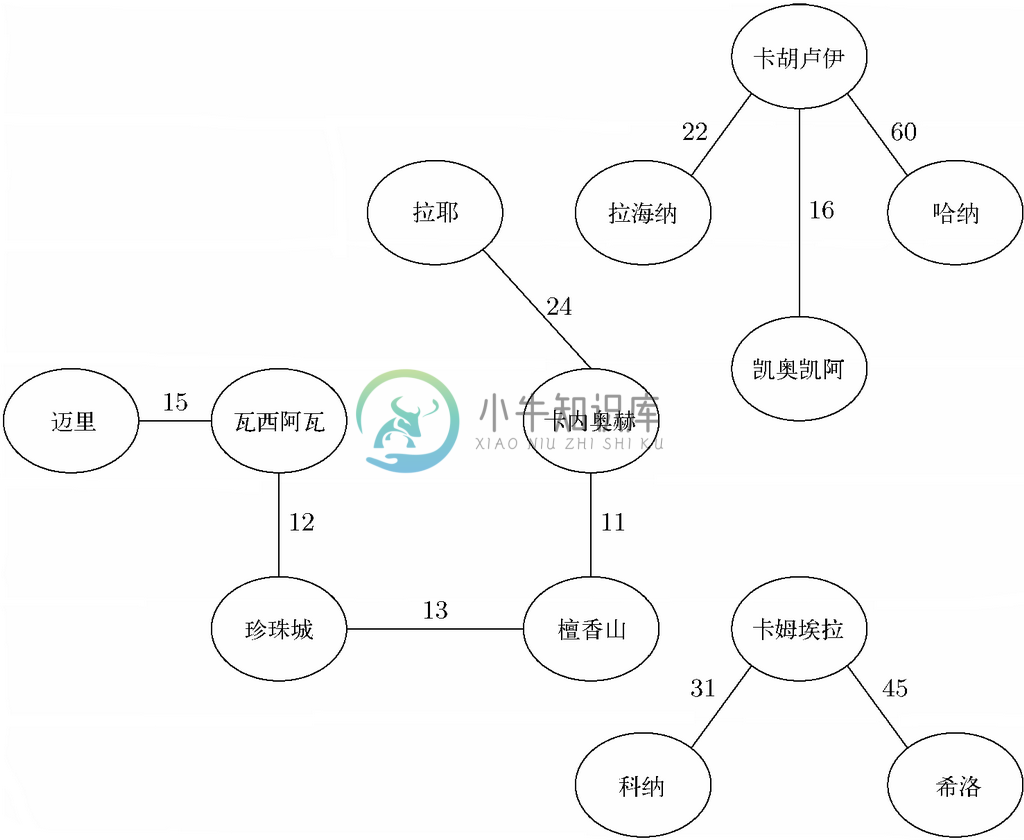
图 9-23 图9-4所示的图对应的生成树
9.5.2 克鲁斯卡尔算法起效的原因
可以证明,克鲁斯卡尔算法可为某给定图生成权最小的生成树。设G 是无向连通图。简便起见,如果需要,我们会为某些标号加上一些极小的量,使得所有标号都是不同的,而且添加的各极小量的和要小于G 中任意不同标号之间的差。这样一来,带有新标号的G 就会有唯一的最小生成树,它将会是带原有权的G 所有最小生成树中的一棵。
接着,设e1、e2、…、em 是G 的所有边,而且是按照标号从小到大的顺序排列的。请注意,这个次序也是克鲁斯卡尔算法处理这些边依照的次序。设K 是带有用克鲁斯卡尔算法生成的调整后标号的图G 对应的生成树,并设T 是G 唯一的最小生成树。
我们要证明K 和T 其实是相同的。如果它们是不同的,一定至少存在一条边在其中一棵树而不在另一棵中。设ei 是这一系列边中第一条这样的边,也就是说,e1、…、ei-1要么同在K 和T 中,要么都不在K 和T 中。这里有两种情况,取决于ei 是在K 中还是在T 中。我们在每种情况下都能得出矛盾,因此就能得出ei 是不存在的,因此K=T,而且K 是G 的最小生成树。
贪婪有时是有用的
克鲁斯卡尔算法是贪婪算法的一个好例子,在贪婪算法中我们会做出一系列的决定,每次都做出当时最佳的选择。这些局部的决定是决定哪条边要被添加到正在成形的生成树中。在各情况下,我们都要选择那条标号最小但又不会因为产生环路而破坏“生成树”定义的边。通常,局部最优选择的整体效果不是全局上最适合的。然而,在克鲁斯卡尔算法的情况中,可以证明结果从全局上讲也是最佳的,也就是一棵权最小的生成树。
情况1。边ei 在T 中而不在K 中。如果克鲁斯卡尔算法不接受ei,那么ei 肯定与之前为K 选择的边中某路径P 形成了环路,如图9-24所示。因此,组成P 的边都能在e1、…、ei-1中找到。不过,T 和K 对这些边是一致的,也就是说,如果P 的边在K 中,那么这些边也在T 中。不过因为T 中含有ei,P 加上ei 就在T 中形成了环路,这与我们说T 是生成树的假设是矛盾的。因此,ei 在T 中而不在K 中是不可能的。

图 9-24 路径P(实线)在T和K中,边ei只在T中
情况2。边ei 在K 中而不在T 中。设ei 连接了节点u 和v。因为T 是连通的,所以在T 中节点u 和v 之间一定存在某条无环路径,假设称其为Q。因为Q 没有用到边ei,所以Q 加上ei 在图G 中形成了简单环路。这里存在两种子情况,具体取决于ei 的标号是否比路径Q 上所有边的标号都大。
(a)边ei 有着最高的标号。那么Q 上的所有边都在{e1,…,ei-1}中。请记住,T 和K 在ei 之前的所有边都是一样的,所以Q 中所有的边也是K 中的边。不过ei 也在K 中,这表示K 是一条环路。因此我们排除了ei 的标号比Q 中任何边的标号都高的可能。
(b)路径Q 上的某边f 的标号比ei 的标号高。假设f 连接节点w 和x。图9-25展示了树T 中的这种情况。如果将边f 从T 中删除,并加上边ei,就不会形成环路,因为路径Q 因f 被删除而中断了。得到的边的集合权要比T 低,因为f 有着比ei 更高的标号。我们声明得到的这些边仍然连通所有节点。要知道原因,请注意w 和x 仍然是连通的,有一条路径沿着Q 从w 到u,然后沿着边ei,然后再沿着路径Q 从v 到x。因为{w,x }是唯一一条被删除的边,如果它的终点仍然是连通的,那么显然所有节点都是连通的。因此,边的新集合是生成树,而它的存在与T 是最小生成树的假设相矛盾。
现在就已经证明了ei 不可能在K 中而不在T 中。这样就排除了第二种情况。因为ei 不可能在T 和K 中,所以可以得出结论,K 其实就是最小生成树T。也就是说,克鲁斯卡尔算法总是能找到最小生成树。

图 9-25 路径Q(实线)在T 中,我们可以将边ei 添加到T 中并删除边f
9.5.3 克鲁斯卡尔算法的运行时间
假设对某一含n 个节点的图运行克鲁斯卡尔算法。就像9.4节那样,设m 是节点数与边数的较大者,但请记住,通常边数是较大者。假设该图是用邻接表表示的,这样就可以在O(m)的时间内找到所有的边。
首先,必须用标号为边排序,如果使用了诸如归并排序这样的高效排序算法,就要花上O(m logm)的时间。接着要考虑这些边,花上O(m logn)的时间进行所有的合并与寻找,就像在9.4节中讨论过的那样。因此看起来克鲁斯卡尔算法的总运行时间是O(m(logn+logm))。
不过,要注意到m≤n2,因为只存在n(n-1)/2个节点对。因此,logm≤2logn,这样一来m(logn+logm)≤3m logn。因为在大O 表达式中常数因子是可以省略掉的,所以可以得出结论:克鲁斯卡尔算法的运行时间是O(m logn)。
9.5.4 习题
1. 如果瓦西阿瓦被选为根节点,画出表示图9-22的树。
2. 使用克鲁斯卡尔算法为边和标号都如图9-21(见9.4节习题)所示的各分支找到最小生成树。
3. ** 证明,如果图G 是有n 个节点的无向连通图,而且T 是G 的生成树,则T 有n-1条边。提示:我们需要对n 进行归纳。难点在于证明T 一定有某个度为1的节点v,也就是说,T 刚好只有一条边含节点v。考虑如果对每个节点u 都至少有两条T 的边含有u 会发生什么。沿着边进出一系列的节点,最终会找到一条环路。因为假设T 是生成树,所以它不可能含有环路,这样一来就形成矛盾了。
4. * 一旦我们选定了n-1条边,就不需要考虑将更多的边纳入该生成树了。描述克鲁斯卡尔算法的一个变种,它不会为所有边排序,但会将它们放入优先级队列中,将边标号的相反数作为其优先级(也就是最短的边会首先被deleteMax 选中)。证明,如果生成树可以在前m/logm 条边中找到,那么这一版本的克鲁斯卡尔算法就只需要花O(m)的时间。
5. * 假设为图G 找到了最小生成树T,然后向G 添加权为w 的边{u,v }。在什么情况下T 仍是新图的最小生成树?
6. ** 无向图G 的欧拉回路是起止点为同一节点而且刚好含有图G 中每条边一次的路径。
(a) 证明,当且仅当每个节点都为偶数度时,无向连通图含有欧拉回路。
(b) 设G 是有m 条边而且每个节点都为偶数度的无向图。给出运行时间是O(m)的为图G 构建欧拉回路的算法。
9.6 深度优先搜索
我们现在要描述一种对有向图而言很实用的图探索方法。在5.4节中我们讨论过树的前序遍历和后序遍历,其中从根节点开始,递归地探索了访问过的每个节点的子节点。我们几乎可以将同样的思路应用到任意有向图上。①从任意节点出发,可以递归地探索其后继。
不过,必须小心图中存在环路的情况。如果存在环路,我们可能会绕着环路永远地递归调用探索函数。例如,考虑图9-26中的图。从节点a 开始,我们可能决定接下来探索节点b。从b 出发可能会先探索c,然后从c 出发可能要先探索b。这样就会导致无限递归,反复地探索b 和c。其实,我们选择按照什么次序探索b 和c 的后继是不重要的。要么会困在其他的环路中,要么最终会无限地从b 探索c 并从c 探索b。

图 9-26 有向图的示例
这一问题有个简单的解决方案:在访问节点的过程中为其做上标记,并永不再次访问标记过的节点。这样一来,我们从起始节点起可以到达的任何节点都会被探索到,而之前已经访问的节点不会被再次访问。我们将看到这种探索所花的时间是与被探索的弧的数量成比例的。
这种搜索算法叫作深度优先搜索,因为我们会尽可能快地行进到离初始节点尽可能远(尽可能“深”)的节点。这可以通过一种简单的数据结构实现。这里要再次假设使用NODE类型为节点命名,而且该类型就是int类型。我们用邻接表表示弧。因为需要为每个节点添加一个“标记”,其值是从VISITED和UNVISITED中二选一,所以要创建一个结构体数组来表示该图。这些结构体要同时包括这里所说的标记以及邻接表的表头。
enum MARKTYPE {VISITED, UNVISITED};
typedef struct {
enum MARKTYPE mark;
LIST successors;
} GRAPH[MAX];
其中LIST为邻接表,是按照以下习惯方式定义的
typedef struct CELL *LIST;
struct CELL {
NODE nodeName;
LIST next;
};
一开始要将所有的节点标记为UNVISITED。图9-27所示的递归函数dfs(u,G)会处理某幅在外部定义的GRAPH类型的图G 中的节点u。
在第(1)行我们将u 标记为VISITED,这样就不用再次对它调用dfs了。第(2)行会初始化指针p,它指向节点u 的邻接表的第一个单元。第(3)行至第(7)行的循环会带p 沿着邻接表向下行进,依次考虑u 的各后继v。
void dfs(NODE u, GRAPH G)
{
LIST p; /* 沿着u对应的邻接表下行 */
NODE v; /* 由p指向的单元中存放的节点 */
(1) G[u].mark = VISITED;
(2) p = G[u].successors;
(3) while (p != NULL) {
(4) v = p->nodeName;
(5) if (G[v].mark == UNVISITED)
(6) dfs(v, G);
(7) p = p->next;
}
}
图 9-27 递归的深度优先搜索函数
第(4)行会将v 置为节点u“当前”的后继。在第(5)行,我们会测试v 之前是否已经被访问过。如果是,就跳过第(6)行的递归调用并在第(7)行中将p 移动到邻接表的下一个单元。不过,如果v 从未被访问过,就要在第(6)行从节点v 开始进行深度优先搜索。最后,完成对dfs(v,G)的调用。然后执行第(7)行,让p 沿着u 的邻接表向下移动并进行循环。
示例 9.18
假设G是图9-26所示的图,而且为了简化问题,假设各邻接表中的节点都是按照字母表顺序排列的。一开始,所有节点都会被标记上UNVISITED。调用dfs(a),7节点a 在第(1)行会被标记为VISITED,而且我们在第(2)行要初始化指针p,它指向a 的邻接表的第一个单元。在第(4)行v 被置为b,因为b 是第一个单元中的节点。由于b 当前处于未被访问的状态,所以第(5)行的测试会成功,并且要在第(6)行调用dfs(b)。
7在接下来的内容中,我们将省略dfs的第二个参数,因为它永远都是图G。
现在,要以b 为参数开始一次对dfs的新调用,而u=a 的旧调用处于休眠状态而并未终止。因为c 是b 的邻接表中的第一个节点,所以在第(4)行c 成了v 的值。节点c 是未访问过的,所以我们在第(5)行会成功并在第(6)行调用dfs(c)。
现在激活了对dfs的第三次调用,而且要开始dfs(c),我们将c 标记为VISITED,并在第(4)行将v 置为b,因为b 是c 的邻接表中第一个也是唯一的一个节点。不过,b 已经在对dfs(b)的调用的第(1)行中被标记为VISITED了,所以我们要跳过第(6)行,并在第(7)行将p 沿着c 的邻接表向下移动。因为c 没有更多后继了,这样p 就成了NULL,所以第(3)行的测试就会失败,对dfs(c)的调用就完成了。
现在又回到对dfs(b)的调用。指针p 在第(7)行被前移,现在它指向b 的邻接表的第二个单元,这个单元存放着节点d。我们在第(4)行将v 置为d,因为d 是未被访问过的,所以在第(6)行要调用dfs(d)。
在执行dfs(d)时,我们会将d 标记为VISITED。那么v 首先会被置为c。但因为c 是被访问过的,因此下一次进行循环时会有v=e。这会引发对dfs(e)的调用。节点e 只有c 这么一个后继,所以在将e 标记为VISITED后,dfs(e)就会返回到dfs(d)。接下来在dfs(d)的第(4)行进行v=f 的赋值,并调用dfs(f)。在把f标记为VISITED后,我们会发现f 也只有c 这么一个后继,而c 又是被访问过的。
现在就完成了对dfs(f)的调用。因为f 是d 的最后一个后继,所以我们完成了对dfs(d)的调用,而且由于d 是b 的最后一个后继,这样也就完成了对dfs(b)的调用。这样就把我们带回了dfs(a)。节点a 还有另一个后继d,不过该节点是被访问过的,所以我们也就完成了对dfs(a)的调用。
图9-28总结了dfs对图9-26所示图的操作。我们展示了对dfs进行调用的情况,并在右侧给出了当前处于活跃状态的调用。我们还表示了每一步执行的活动,并展示了与当前活跃的调用相关联的局部变量v 的值,或者是给出p = NULL,表示没有相应的v 值。

图 9-28 在深度优先搜索期间所执行调用的记录
9.6.1 构建深度优先搜索树
因为我们标记了节点以防访问它们两次,这样一来在探索图的过程中图就像树那样了。其实,也可以绘出一棵树,其父子节点之间的边就是被搜索的图G 中的某些弧。如果我们在对dfs(u)的调用中,而且它会带来对dfs(v)的调用,那么我们就让v 成为u 在该树中的子节点。u 的子节点是按照对这些子节点调用dfs 的次序从左向右出现的。而第一次dfs调用所针对的节点就是该树的根节点。不会对任何节点调用dfs 两次,因为在第一次调用后这些节点就会被标记为VISITED。因此,这样定义的结构真是棵树。我们可以称这样的树是某给定图的深度优先搜索树(depth-firstsearchtree)。
示例 9.19
图9-29所示的树展示了图9-28总结的对图9-26所示的图的探索过程。我们把代表父子关系的树向弧(tree arc)表示为实线,图中的其他弧被表示为虚线箭头。这里我们应该忽略节点标号的数字。

图 9-29 图9-26所示的图的一种可能的深度优先搜索树
9.6.2 深度优先搜索树弧的分类
当我们为图G 构建深度优先搜索树时,可以把G 中的弧分为4组。应该不难理解,这种分类是就某棵特定的深度搜索树而言的,或者说,是针对各邻接表中节点的某种特定次序(形成对G 的一次特定探索)而言的。这4类弧分别如下。
1. 树向弧,满足dfs(v)被dfs(u)调用的弧u→v。
2. 前向弧(forward arc),满足v 是u 的真子孙但又不是u 的子节点的弧u→v。例如,在图9-29中,弧a→b 就是唯一的前向弧。树向弧都不是前向弧。
3. 后向弧(backward arc),满足v 是u 在该树中的祖先(u=v 也是可以的)的弧u→v。图9-29中,弧c→b 是唯一的后向弧。任何自环,也就是节点到其自身的弧都被分类为后向弧。
4. 横向弧(cross arc),满足v 既不是u 的祖先也不是其子孙的弧u→v。图9-29中有3条这样的弧:d→c、e→c 和f→c。
在图9-29中,每条横向弧都是从右至左的。这种情况并非巧合。假设在某深度优先搜索树中有一条横向弧u→v 满足u 在v 的左侧。考虑一下在调用dfs(u)期间会发生什么。到完成对dfs(u)的调用之时,我们应该已经考虑过从u 到v 的弧了。如果v 尚未被放置到树中,那么它就会成为u 在该树中的子节点。因为这种情况显然不会发生(这样v就不会在u 的右侧了),所以在考虑弧u→v 时,v 肯定已经在该树中了。

图 9-30 在考虑弧 u→v 时构建的树的一部分
不过,图9-30展示了当dfs(u)处于活动状态时存在的树的一部分。因为子节点会按照从左至右的次序添加进来,所以迄今为止节点u 的真祖先没有子节点在u 的右侧。因此,v 只可能是u 的祖先,u 的子孙,或者是在u 左侧的某个位置。因此,如果u→v 是横向弧,v 就一定是在u 的左侧,而不可能像我们最初假设的那样在u 的右侧。
9.6.3 深度优先搜索森林
在示例9.19中,我们特别幸运,从节点a 开始,就能够到达图9-26所示图的全部节点。但假设我们从其他节点开始,就可能没法到达a,a 就不会出现在深度优先树中。因此,探索图的一般方式是构建一系列的树。我们从某个节点u 开始并调用dfs(u)。如果还有节点未被访问过,就再选择一个节点,比方说是v,并调用dfs(v)。只要还有节点未被分配到任一树中,就继续重复该过程。
在所有节点都被分配到一棵树中后,我们就按照构建这些树的先后次序,把构建出的树从左到右列出来。这一列树就叫作深度优先搜索森林(depth-firstsearchforest)。利用之前定义的NODE和GRAPH数据类型,可以通过图9-31所示的函数,从所需的那么多根节点开始搜索,对完全从外部定义的图G 进行探索。这里我们假设NODE类型为int类型,而且MAX 是G 中的节点数。
void dfsForest(GRAPH G);
{
NODE u;
(1) for (u = 0; u < MAX; u++)
(2) G[u].mark = UNVISITED;
(3) for (u = 0; u < MAX; u++)
(4) if (G[u].mark == UNVISITED)
(5) dfs(u, G);
}
图 9-31 通过探索所需的那么多树对图进行探索
在第(1)行和第(2)行中,我们会把所有节点初始化为UNVISITED。然后,在第(3)行到第(5)行的循环中,要依次考虑各节点u。在考虑u 时,如果该节点尚未被添加到任何树中,那么在进行第(4)行的测试时它仍然会被标记为未被访问过。在这样的情况下,我们就会在第(5)行调用dfs(u,G),并探索以u 为根节点的深度优先搜索树。特别要说的是,第一个节点总是会成为树的根节点。不过,如果在执行第(4)行的测试时u 已经被添加到树中,那么u 就会被标记为VISITED,因此不会创建以u 为根节点的树。
示例 9.20
假设将上述算法应用到图9-26所示的图上,但是设d 是名称为0的节点,也就是说,d 是该深度搜索生成森林中树的第一个根节点。调用dfs(d),这会构建图9-32中的第一棵树。现在除了a 之外的所有节点都已经被访问过。当u 在图9-31第(3)行到第(5)行的循环中成为各节点时,除了u=a 时之外第(4)行的测试都会失败。然后,我们会创建如图9-32所示的单节点第二棵树。请注意,在调用dfs(a)时,a 的两个后继都带有VISITED标记,因此我们不再从dfs(a)进行任何递归调用。

图 9-32 深度优先搜索森林
当把图中的节点表示为深度优先搜索森林时,前向弧、后向弧与树向弧的概念还像之前那样。不过,横向弧的概念必须扩展到包含那些从一棵树到其左侧的树的弧。这种横向弧的例子包括图9-32中的a→b 和a→d。
横向弧总是从右至左的这一规则继续成立。原因还是一样的。如果存在从一棵树到其右侧树的横向弧u→v,那么考虑一下当调用dfs(u)时会发生什么。因为v没有被添加到当时正在形成的树中,所以它肯定已经在某棵树中。但是u 右侧的树尚未创建,因此v 不可能是这些树的一部分。
尽善尽美的深度优先搜索
无论节点数和弧数之间存在什么的关系,对图的深度优先探索需要的时间是与图的“大小”(也就是节点数与弧数之和)成正比的。因此,深度优先搜索与其他任意“查看”图的算法在速度上只有常数因子的差异。
9.6.4 深度优先搜索算法的运行时间
设G 是有n 个节点的图,并设m 是节点数与弧数之间的较大者。图9-31所示的dfsForest就要花O(m)的时间。这一事实的证明需要一点小花招。在计算对dfs(u)的调用所花的时间时,我们不会将图9-27第(6)行中对dfs的递归调用所花的时间计算在内,就像3.9节中所建议的那样。不过,不难看出要为每个u 值调用dfu(u)一次。因此,如果将每次调用的开销加起来,除掉其递归调用,就能得到将所有调用视作一个整体所花的总时间。
请注意,除掉在对dfs的递归调用中所花的时间,图9-27中第(3)行到第(7)行的while循环所花的时间是可以变化的,因为节点u 的后继数量可能是从0到n 的任一数字。假如设mu 是节点u 的出度,也就是u 的后继的数量。那么在执行dfs(u)期间进行该循环的次数就肯定是mu。在评估dfs(u)的运行时间时,并不会把第(6)行执行dfs(v,G)的时间计算在内,而除该调用之外,整个循环体只要花O(1)的时间。因此,除去在递归调用上花的时间,第(3)行到第(7)行的循环花的总时间就是O(1+mu),这个附加的1是必要的,因为mu 可能为0,在这种情况下我们仍然需要为第(3)行的测试花上O(1)的时间。因为第(1)行和第(2)行的dfs要花O(1)的时间,所以可以得出结论,忽略递归调用,dfs(u)要花O(1+mu )的时间完成调用。
现在可以看到,在运行dfsForest期间,刚好要为每个u 值调用dfs(u)一次。因此,花在所有这些调用上的总时间是花在每次调用上的时间之和的大O,也就是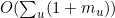 。但是
。但是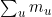 就是图中弧的数量,也就是最多为m,8因为每条弧都是都某一个节点发出的。节点数为n,所以
就是图中弧的数量,也就是最多为m,8因为每条弧都是都某一个节点发出的。节点数为n,所以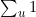 就是n。由于n≤m,因此所有对
就是n。由于n≤m,因此所有对dfs的调用花的总时间就是O(m)。
8其实,mu 的和刚好是m,除非节点数大于弧数。回想一下,m 是节点数与弧数间的较大者。
最后,必须考虑dfsForest花的时间。图9-31所示的该程序由各要迭代n次的两个循环组成。不难看出,除去对dfs的调用,循环体所花的时间是O(1),因此这些循环的开销都是O(n)。这一时间会被对dfs的调用所花的O(m)时间主导。因为我们已经弄清了dfs调用所花的时间,所以可以得到dfsForest,再加上其所有对dfs的调用,要花O(m)的时间。
9.6.5 有向图的后序遍历
一旦有了深度优先搜索树,就可以按后序为其节点编号。不过,还有一种在搜索期间进行编号的简单方法。只要把为节点u 加上编号当作dfs(u)完成前我们要做的最后一件事即可。然后,在节点的所有子节点被编号后,它自己就会被编上号,正好是按照后序编号的。
示例 9.21
图9-29所示的树,也就是我们对图9-26中的图进行深度优先搜索所建立的树,有着后序编号的节点标号。如果查看图9-28的过程,就会发现最先要返回的调用是dfs(c),而且节点c 会被编为1号。然后我们会访问d,接着是e,并从对e 的调用返回。因此,e 的编号是2。同样,我们会访问f 并从其返回,它会被编为3号。至此,已经完成了对d 的调用,它会得到4这个编号。这样就完成了对dfs(b)的调用,因此b 的编号就是5。最后,最开始对a 的调用返回,给了a 编号6。请注意,这一次序刚好就是我们以后序遍历该树会得到的。
我们可以对目前所编写的深度优先算法进行一些简单改动,从而为节点指定后序编号,这些改动如图9-33所总结。
int k; /* 为已访问过的节点计数 */
void dfs(NODE u, GRAPH G)
{
LIST p; /* 指向u的邻接表的单元 */
NODE v; /* 由p指向的单元中存放的节点 */
(1) G[u].mark = VISITED;
(2) p = G[u].successors;
(3) while (p != NULL) {
(4) v = p->nodeName;
(5) if (G[v].mark == UNVISITED)
(6) dfs(v, G);
(7) p = p->next;
}
(8) ++k;
(9) G[u].postorder = k;
}
void dfsForest(GRAPH G)
{
NODE u;
(10) k = 0;
(11) for (u = 0; u < MAX; u++)
(12) G[u].mark = UNVISITED;
(13) for (u = 0; u < MAX; u++)
(14) if (G[u].mark == UNVISITED)
(15) dfs(u, G);
}
图 9-33 以后序为有向图的节点编号的例程
1. 在GRAPH类型中,需要为每个节点增加一个名为postorder的字段。对图G 而言,我们要将节点u 的后序编号放在G[u].postorder中。这一赋值是在图9-33的第(9)行完成的。
2. 我们使用全局变量k按后序为节点计数。这一变量是在dfs和dfsForest的外部定义的。正如在图9-33中所见,我们在dfsForest的第(10)行将k 初始化为0,并刚好在赋值后序编号之前,在dfs中的第(8)行将k 递增1。
请注意,这样一来,当深度优先搜索森林中不止有一棵树时,第一棵树就会得到最低的编号,而紧接着的那棵树就会按顺序得到接下来的编号,以此类推。例如,在图9-32中,a 会得到后序编号6。
9.6.6 后序编号的特殊属性
横向弧不能从左向右说明了与后序编号和图的深度优先表示中4种弧相关的一些有趣而实用的信息。在图9-34a中,我们看到图的深度优先表示中有u、v 和w 3个节点。节点v 和w 是u 的子孙,而且w 在v 的右侧。图9-34b展示了分别为这3个节点调用dfs各自的活动持续时间。

图 9-34 树中位置间的关系和调用的持续时间
我们可以得出一些观点。首先,对子孙节点(比如v)进行的对dfs的调用,只在对祖先节点(比如u)的调用期间的某个子时间区间内是活动的。特别要指出的是,对dfs(v)的调用会在对dfs(u)的调用之前终止。因此,只要v 是u 的真子孙,v 的后序编号肯定要比u 的后序编号小。
其次,如果w 在v 的右侧,那么对dfs(w)的调用必须等到对dfs(v)的调用终止后才会开始。因此,只要v 在w 的左侧,v 的后序编号就要比w 的后序编号小。虽然图9-34中没有表示出来,但即便v 和w 在深度优先搜索森林的不同树中,只要v 所在的树在w 所在的树的左侧,同样的结论也是成立的。
我们现在可以为每条弧u→v 考虑u 和v 后序编号之间的关系了。
1. 如果u→v 是树向弧或前向弧,那么v 是u 的子孙,所以v 按后序要先于u。
2. 如果u→v 是横向弧,那么我们知道v 在u 的左侧,因此按后序v 还是先于u。
3. 如果u→v 是后向弧而且u≠v,那么v 是u 的真祖先,因此按后序v 在u 之后。不过,对后向弧而言v=u 是有可能的,因为自环也是后向弧。因此,一般来说,对后向弧u→v 而言,我们知道v 的后序编号是不会小于u 的后序编号的。
总之,我们看到,弧头部按后序是要先于尾部的,除非该弧是后向弧,在弧是后向弧的情况中,尾部按后序是不会在头部之后的。因此,只要找到那些尾部按后序不大于头部的弧,就可以认定它们是后向弧。我们在9.7节中将看到这一概念的若干应用。
9.6.7 习题
1. 为图9-5中的树(见9.2节的习题)给出两棵从节点a 出发的深度优先搜索树。给出从节点d 出现的深度优先搜索树。
2. * 不管从图9-5中的哪个节点开始,我们最后都只得到深度优先搜索森林中的一棵树。简要解释对这幅特定的图为什么一定是这种情况。
3. 对9.6节习题1中的各棵树,指出哪些弧是树向弧、前向弧、后向弧和横向弧。
4. 对9.6节习题1中的各棵树,给出节点的后序编号。
5. * 考虑含a、b、c 这3个节点以及a→b 和b→c 这两条弧的图。为这幅图给出所有可能的深度优先搜索森林,为每棵树考虑所有可能的起始节点。每个森林的节点后序编号各是怎样的?
6. * 考虑把习题5的图一般化为具有a1、a2、…、an 这n 个节点和a1→a2、a2→a3、…、an-1→an 这些弧。通过对n 的完全归纳证明,该图具有2n-1种不同的深度优先搜索森林。提示:记住对i ≥0有1+1+2+4+8+…+2i=2i+1是能帮上忙的。
7. * 假设从图G 开始,并为G 添加一个新节点x,它是原来的图G 中所有节点的前导。如果从节点x 开始对新图运行图9-31中的dfsForest,就只得到一棵树。如果接着将x 从该树中删除,就可以得到若干棵树。这些树与原图G 的深度优先搜索森林之间有什么联系?
8. ** 假设有一幅有向图G,我们已经通过图9-31所示的算法从这幅有向图的表示构建了深度优先生成森林F。现在将弧u→v 添加到图G 中形成新图H,除了节点v 出现在节点u 相应邻接表中的某个位置,图H 的表示与图G 的表示如出一辙。如果现在对H 的这种表示运行图9-31所示的算法,在什么条件下会构建出相同的深度优先森林F?也就是说,H 的树向弧什么时候会刚好与G 的树向弧相同?
9.7 深度优先搜索的一些用途
在本节中,我们会看到如何利用深度优先搜索快速解决一些问题。就像之前那样,这里也是用n 表示图的节点数,并用m 表示节点数与弧数间的较大者,特别要指出的是,假设n≤m 总是成立的。这里介绍的算法对用邻接表表示的图来说都要花O(m)的时间。第一个算法可以确定有向图是否为无环的。然后对那些无环图,我们会看到如何找出其节点的拓扑排序(拓扑排序在7.10节讨论过,我们会找个恰当的时机回顾一下其定义)。我们还要展示如何计算图的传递闭包(概念还是见7.10节),以及如何比用9.4中给出的算法更快地找到无向图的连通分支。
9.7.1 有向图中环路的寻找
在对有向图G 进行深度优先搜索期间,可以在O(m)的时间内为所有节点指定后序编号。回想一下9.6节的内容,我们发现尾部按后序小于等于其头部的弧只有后向弧。只要某图存在后向弧u→v,其中v 的后序编号不小于u 的后序编号,该图中就一定存在环路,如图9-35所示。这条环路是由从u 到v 的弧以及树中从v 到其子孙u 的路径组成的。

图 9-35 每条后向弧都可以与树向弧一起构成环路
这个命题反过来也是成立的,也就是说,如果图中存在环路,那么就肯定存在后向弧。要知道原因,先假设存在某环路,比方说v1→v2→…→vk→v1,并设对i=1、2、…、k,节点vi 的后序编号为pi 。如果k=1,也就是说,环路为一条弧,那么在图G 的任意深度优先表示中v1→v1都肯定是后向弧。
如果k>1,假设v1→v2,v2→v3,等等,直到vk-1→vk 这些弧都不是后向弧。那么每条弧的头部按后序都先于其尾部,而且后序编号p1、p2、…、pk 形成了递减序列。特别要说的是,pk< p1。然后考虑完成该环路的弧vk→v1。其尾部的后序编号为pk,要小于其头部的后序编号p1,所以这条弧是后向弧。这就证明了在环路中肯定存在后向弧。
这样一来,在计算了所有节点的后序编号后,只要检查所有弧,看看有没有弧的尾部按后序小于等于其头部。如果有,我们就找到了后向弧,而且该图是有环图。如果没有这样的弧,该图就是无环图。图9-36展示了测试外部定义的图G 是否为无环图的函数,它所使用的表示图的数据结构与9.6节中描述的相同。它还利用了图9-33中定义的dfsForest函数计算G 中节点的后序编号。
BOOLEAN testAcyclic(GRAPH G)
{
NODE u, v; /* u会行经所有的节点 */
LIST p; /* p指向与u对应的邻接表中的各个单元,
v是该邻接表中的节点 */
(1) dfsForest(G);
(2) for (u = 0; u < MAX; u++) {
(3) p = G[u].successors;
(4) while (p != NULL) {
(5) v = p->nodeName;
(6) if (G[u].postorder <= G[v].postorder)
(7) return FALSE;
(8) p = p->next;
}
}
(9) return TRUE;
}
图 9-36 确定图G 是否无环的函数
在第(1)行调用dfsForest计算后序编号之后,我们会在第(2)行到第(8)行的循环中检查各节点u。指针p 会沿着u 对应的邻接表向下行进,而且在第(5)行,v 会依次成为u 的各个后继。如果在第(6)行发现u 按后序等于或先于v,就找到了后向弧u→v,并在第(7)行返回FALSE。如果没有找到这样的弧,就在第(9)行返回TRUE。
9.7.2 无环测试的运行时间
和之前一样,设n 是图G 中节点的数量,并设m 是节点数与弧数之间的较大者。我们已经知道在图9-36的第(1)行中对dfsForest的调用要花O(m)的时间。而第(5)到第(8)行是while循环的循环体,显然要花O(1)的时间。要得到while循环本身运行时间的良好边界,就必须用到我们在9.6节中为深度优先搜索的时间确定边界时用到的小诀窍。设mu 是节点u 的出度,那么第(4)行到第(8)行的循环就要进行mu 次。因此,第(4)行到第(8)行所花的时间是O(1+mu)。
第(3)行只要花O(1)的时间,因此第(2)行到第(8)行的for循环所花的时间是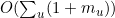 。正如在9.6节中验证过的,这些1的和是O(n),mu 的和则是m。由于n≤m,所以第(2)到第(8)行的
。正如在9.6节中验证过的,这些1的和是O(n),mu 的和则是m。由于n≤m,所以第(2)到第(8)行的for循环的运行时间就是O(m)。正如深度优先搜索本身那样,检测环路的时间与查看整幅图所花的时间也只有常数因子的差别。
9.7.3 拓扑排序
假设我们知道有向图G 是无环的。就像对任意图那样,可以为G 找到一个深度优先搜索森林,并为G 的节点确定后序编号。假设(v1,v2,…,vn)是图G 的节点按后序反向排列的表,也就是说v1是后序编号为n 的节点,v2的编号为n-1,而且一般而言,vi 是后序编号为n-i+1的节点。
该表中节点的次序具有这样的属性,G 中所有弧都是按照该次序向前行进的。要知道原因,假设vi →vj 是G 中的弧。因为G 是无环图,所以其中肯定不存在后向弧。因此,对每条弧而言,其头部按后序都是先于尾部的。也就是说,vj 按后序要先于vi 。不过表是与后序反向的,所以在表中vi 要先于vj 。也就是说,按照表的次序每条弧的尾部都要先于其头部。
具有图中每条弧的尾部都先于头部这种属性的图G 中,节点的次序叫作拓扑次序,而为这些节点找到这一次序的过程就叫作拓扑排序。只有无环图才有拓扑次序,而且正如我们已经看到的,通过深度优先搜索,可以在O(m)的时间内为无环图生成拓扑次序,其中m 是节点数和弧数之间的较大者。如果要为某节点给定后序编号,也就是要完成对该节点的dfs调用,我们会将该节点压入栈中。在完成所有调用后,该栈就成了节点按后序出现的表,其中编号最大的节点位于栈顶(前端)。这就是我们所需要的反向后序。因为深度优先搜索要花O(m)的时间,而且将节点压入栈只需要O(n)的时间,所以整个过程要花费O(m)的时间。
拓扑次序和环路查找的应用
本节中讨论的算法在不少情况下是很实用的。当执行用节点表示的特定任务所依照的次序有约束时,拓扑排序就会变得很方便。如果在执行任务v 之前必须执行u,就画一条从u到v的弧,然后拓扑次序就是我们执行所有任务所依照的次序。
非递归函数集合的调用图也是相似的例子,在这种情况下我们要在分析了某函数调用的函数之后再分析该函数。因为弧是从调用者到被调用函数的,所以拓扑次序的相反次序,也就是后序本身是我们分析函数所依照的次序,以确保我们只会在处理完某函数调用的函数后再来处理该函数。
在其他情况下,运行该环路测试也是有效的。例如,表示任务优先级的图中所含的环路就表示执行所有任务是没有次序可依照的,而调用图中的环路表示存在递归调用。
示例 9.22
在图9-37a中有一幅无环图,而在图9-37b中是按照字母表次序考虑节点后得到的深度优先搜索森林。我们在图9-37b中还展示了从这次深度优先搜索中得到的后序编号。如果最先把后序编号最高的节点列出来,我们就得到拓扑次序(d,e,c,f,b,a)。读者应该自行验证一下图9-37a的8条弧中每条弧的尾部按照该表的次序都先于其头部。而这幅图恰好还有另外3种拓扑次序,比如(d,c,e,b,f,a)。
9.7.4 可达性问题
对于有向图可以提出一个很自然的问题:给定一个节点u,沿着有向图中的弧从u 可以到达哪些节点?我们将该节点集合称为节点u 的可达集。其实,如果对图中每个节点u 都询问这一可达性问题,就能知道对哪些节点对(u,v )而言存在从u 到v 的路径。
解决可达性问题的算法很简单。如果我们对节点u 感兴趣,就将所有节点标记为UNVISITED并调用dfs(u)。然后可以再次检测所有节点。那些标记上VISITED的节点就是从u 可达的节点,而其他节点则不是。如果想找到从另一个节点u 可达的节点,就将所有节点再次置为UNVISITED,并调用dfs(u)。我们可以为所有想要处理的节点重复该过程。
示例 9.23
考虑图9-37a。如果从节点a 开始进行深度优先搜索,我们哪里都去不了,因为没有从a 发出的弧。因此,dfs(a)会立即终止。因为只有a 被访问过,所以可以得出结论,a 是从a 可达的唯一节点。
如果从b 开始,可以到达a,但这也就是全部了,所以b 的可达集就是{a,b }。同样,从c 开始可以到达{a,b,c,f },从d 则可以到达所有节点,从e 可以到达{a,b,e,f },而从f 只可以到达{a,f }。
再举个例子,考虑一下图9-26。从a 可以到达所有的节点。不过从除了a 之外的任意节点出发,可以到达除了a 之外的所有节点。

图 9-37 无环图的拓扑排序
9.7.5 可达性测试的运行时间
假设有向图G 含n 个节点与m 条弧。还假设G 是用9.6节中的GRAPH数据类型表示的。首先,假设我们想为某节点u 找到其可达集。将所有节点初始化为UNVISITED需要O(n)的时间。对dfs(u,G)的调用要花O(m)的时间,而且再次检查所有节点看哪些节点被访问过需要O(n)的时间。在检查节点之时,我们还可以创建由从节点u 可达的节点组成的表,这仍然只用花O(n)的时间。因此,为一个节点找到可达集要花O(m)的时间。
现在假设需要为所有n 个节点找出可达集。我们可以重复该算法n 次,为每个节点执行一次该算法。因此,总时间为O(mn)。
9.7.6 通过深度优先搜索寻找连通分支
在9.4节中,我们给出了为节点数为n 且节点数与边数较大值为m 的无向图寻找连通分支的算法,该算法的运行时间为O(m logn)。我们用于合并分支的树结构本身是很有意义的,例如,可以利用它帮助实现克鲁斯卡尔的最小生成树算法。不过,如果使用深度优先搜索,我们可以更高效地找到连通分支。正如接下来将要看到的,O(m)的时间就足够了。
思路就是把无向图当作边被两个方向上的弧替代后的有向图。如果用邻接表表示图,那么甚至不用对这种表示进行任何修改。现在为该有向图构建深度优先搜索森林,森林中的每棵树都是该无向图的一个连通分支。
传递闭包和自反传递闭包
设R 是集合S 上的二元关系。可达性问题就可以视作计算R 的自反传递闭包,通常将其表示为R *。关系R *是满足以下条件的有序对(u,v )的集合,在由R 表示的图中,从节点u 到节点v 存在长度为0或0以上的路径。
另一种非常类似的关系是R+,也就是R 的传递闭包,它是满足如下条件的有序对(u,v )的集合。在由R 表示的图中,从节点u 到节点v 存在长度为1或1以上的路径。R *和R+之间的区别在于,(u,u)对S 中的每个u 而言都在R *中,而当且仅当从u 到u 之间存在一条长度为1或1以上的环路时,(u,u)才在R+中。要从R *计算R+,只需要检查每个节点u 是否有来自其可达节点(包括它本身)的进入弧(enteringarc),如果没有,就将u 从它自己的可达集中删除。
要知道原因,首先要注意到有向图中的弧u→v 的出现表示存在边{u,v }。因此,树中的所有节点都是连通的。
现在我们必须证明反向的命题,也就是如果两个节点是连通的,那么它们在同一棵树中。假设在无向图中存在连通不同树中两个节点u 和v 的路径。假如u 的树是首先构建起来的。那么在有向图中存在从u 到v 的路径,这表明v 和该路径上的所有节点都应该已经被添加到含u 的树中。因此,当且仅当无向图中的节点在同一棵树中时,它们才是连通的,也就是说,这些树都是连通分支。
示例 9.24
再次考虑图9-4中的无向图。图9-38展示了我们可以为该图构建的一种可能的深度优先搜索森林。要注意这3棵深度优先搜索树是如何与3个连通分支对应的。
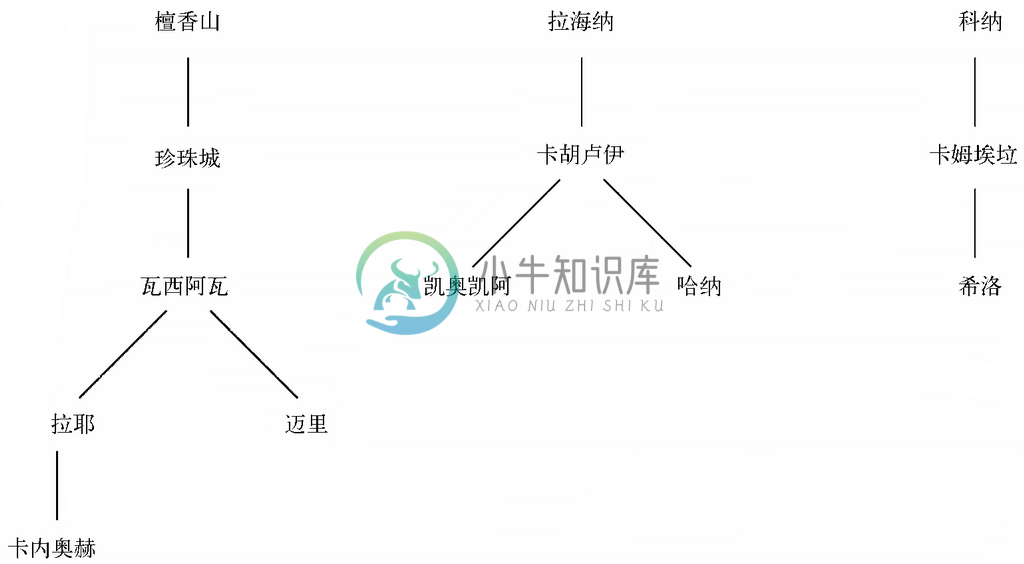
图 9-38 深度优先搜索森林将无向图分为连通分支
9.7.7 习题
1. 为图9-37所示的图找出所有拓扑次序。
2. * 假设R 是定义域D 上偏序关系。我们可以用R 的图来表示R,其中节点是D 中的元素,而且只要uRv 且u≠v 就存在弧u→v。设(v1,v2,…,vn)是R 的图的拓扑次序。设关系T 是这样定义的,只要i≤j,就有viTvj 。证明下列命题。
(a) T 是全序关系。
(b) R 中的有序对是T 中有序对的子集,也就是,T 是包含了偏序关系R 的全序关系。
3. 对图9-21所示的图(在将其转换为对称的有向图之后)应用深度优先搜索,找出其连通分支。
4. 考虑含有弧a→c,b→a,b→c,d→a 和e→c 的图。
(a) 对该图进行环路测试。
(b) 为该图找出所有的拓扑次序。
(c) 为每个节点找出可达集。
5. * 在9.8节中,我们会考虑找到从源节点s出发的最短路径的一般问题。也就是说,如果从s 到各个节点u 的最短路径存在,我们希望弄清这些最短路径的长度。如果是有向无环图,这个问题就要简单一些。给出算法,计算有向无环图G 中从节点s 到各节点u 的最短路径的长度,如果这样的路径不存在则是无限长。大家设计的算法应花费O(m)的时间,其中m 是图G 中节点数和弧数的较大者。证明自己的算法具有该运行时间。提示:首先对G 进行拓扑排序,依次访问每个节点。在访问节点u 时,根据已经计算出的s 到u 的前导的最短距离来计算从s 到u 的最短距离。
6. * 为有向无环图G 给出计算以下几项内容的算法。大家给出的算法应该有O(m)的运行时间,其中m 是G 中节点数和弧数的较大者,而且大家应该证明这一运行时间就是自己设计的算法所需要的。提示:对习题(5)中的思路加以改造。
(a) 对每个节点u,找到从u 到任意节点的最长路径的长度。
(b) 对每个节点u,找到从任意节点到u 的最长路径的长度。
(c) 对给定的源节点s 和G 的所有节点u,找到从s 到u 的最长路径的长度。
(d) 对给定的源节点s 和G 的所有节点u,找到从u 到s 的最长路径的长度。
(e) 对每个节点u,找到经过u 的最长路径的长度。
9.8 用于寻找最短路径的迪杰斯特拉算法
假设有一幅图,它既可能是有向图也可能是无向图,它的弧(或边)都带有表示弧(或边)的“长度”的标号。图9-4就是个例子,它展示了夏威夷群岛的特定公路的距离。想知道两个节点间的最小距离是特别平常的事,例如,地图上通常会带有行车距离的表格,从而指示出人们一天中可以开多远,或是有助于确定经过不同的中间城市的两条路线中哪条更短。类似的问题会给每条弧关联上沿着该弧行进所花的时间,或者可能关联上经过该弧的开销。那么两个节点间的最小“距离”就分别对应着出行的时间或费用。
一般而言,路径的距离是该路径上所有弧(或边的)标号之和。而从节点u 到节点v 的最小距离是从u 到v 的任意路径的距离中最小的那个。
示例 9.25
考虑一下图9-10中瓦胡岛的地图。假设想要找出从迈里到卡内奥赫的最小距离,有若干路径可供我们选择。有一个实用的观点,只要弧的标号是非负的,那么最小距离路径中就绝对不会有环路。我们可以跳过环路,并在同样的两个节点间找到一条距离不超过含环路路径距离的路径。因此,我们只需要考虑如下路径。
1. 经过珍珠城和檀香山的路径。
2. 经过瓦西阿瓦、珍珠城和檀香山的路径。
3. 经过瓦西阿瓦和拉耶的路径。
4. 经过珍珠城、瓦西阿瓦和拉耶的路径。
这些路径的距离分别是44、51、67和84。因此,从迈里到卡内奥赫的最小距离是44。
如果想找到从某给定节点(称为源节点)到图中所有节点的最小距离,可以使用的最有效的技巧之一就是迪杰斯特拉算法,这也就是本节的主题。事实证明,如果我们想要的就是从一个节点u 到另一个节点v 的距离,最佳方式就是以u 为源节点运行迪杰斯特拉算法,并在得出到v 的距离时停止算法。如果我们想找到每个节点对之间的最小距离,就要用到9.9节中将要介绍的算法,弗洛伊德算法,该算法有时要比以每个节点为源节点运行迪杰斯特拉算法更值得选择。
迪杰斯特拉算法的本质就是,我们按照这些最小距离从小到大的次序,也就是最近的节点最先的次序,找到从源节点到其他节点的最小距离。随着迪杰斯特拉算法的进行,就有了类似图9-39所示的情形。在图G 中,存在某些特定的节点是已解决的,也就是说,它们的最小距离是已知的,这一集合总包括源节点s。对未解决的节点v,我们要记录最短特殊路径的长度,所谓特殊路径,就是从源节点出发,只经过已解决节点,然后在最后一步跳出已解决区域直接到达v 的路径。
我们要为每个节点u 记录dist(u)值。如果u 是已解决节点,那么dist(u)就是从源节点到u 的最短路径的长度。如果u 不是已解决的,那么dist(u)就是从源节点到u 的最短特殊路径的长度。一开始,只有源节点是已解决的,而且dist(s)=0,因为只由s 自己构成的路径的长度肯定是0。如果存在从s 到u 的弧,那么dist(u)就是该弧的标号。请注意,在只有s 是已解决节点时,特殊路径只包含那些从s 出发的弧,所以如果存在从s 到u 的弧,dist(u)就应该是弧s→u 的标号。我们还将使用定义的常量INFTY,该常量要比图G 中任意路径的距离都要大。INFTY是作为“无限的”值使用的,表示尚未发现特殊路径。也就是说,如果一开始不存在弧s→u,就有dist(u)=INFTY。

图 9-39 迪杰斯特拉算法执行过程中的中间阶段
现在假设我们有些已解决节点和一些未解决节点,如图9-39所示。我们发现节点v是未解决的,但在所有未解决节点中具有最小的dist值。可以通过以下方式“解决”v。
(1) 接受dist (v )作为从s 到v 的最小距离。
(2) 对所有尚未解决的节点u,调整dist (u )的值,以表明v 现在已解决这一事实。
第(2)步所要求的调整如下所述。我们要对dist (u )的旧值与dist (v )加上弧v→u 的标号的和进行比较,如果后者所述的和较小,就将dist (u )替换为该和。如果不存在弧v→u,就不用调整dist (u )。
示例 9.26
考虑一下图9-10中的瓦胡岛地图。该图是无向图,不过可以假设图中的边是两个方向上的弧。设源节点为檀香山。那么一开始,只有檀香山是已解决的,而且其距离为0。我们可以将dist(珍珠城)置为13并将dist(卡内奥赫)置为11,不过对其他城市来说,没有从檀香山出发到这些城市的弧,所以它们与檀香山的距离就是INFTY。这种情形如图9-40的第一列所示。距离值上的星号表示该节点是已解决的。
| 城市 | 轮次 | ||||
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| 檀香山 | 0\* | 0\* | 0\* | 0\* | 0\* |
| 珍珠城 | 13 | 13 | 13\* | 13\* | 13\* |
| 迈里 | INFTY | INFTY | 33 | 33 | 33\* |
| 瓦西阿瓦 | INFTY | INFTY | 25 | 25\* | 25\* |
| 拉耶 | INFTY | 35 | 35 | 35 | 35 |
| 卡内奥赫 | 11 | 11\* | 11\* | 11\* | 11\* |
dist 的值
图 9-40 迪杰斯特拉算法执行过程中的各个阶段
在这些未解决节点中,具有最小距离的节点现在为卡内奥赫,所以这节点就是已解决的。存在从卡内奥赫到檀香山和拉耶的弧。到檀香山的弧是派不上用场的,不过dist(卡内奥赫)的值11,加上从卡内奥赫到拉耶的弧的标号24,总共为35,要小于当前dist(拉耶)的值——“无限大”。因此,在第二列中,我们已经把到拉耶的距离减小到35。而卡内奥赫现在是已解决节点了。
在下一轮处理中,具最小距离的未解决节点是珍珠城,其距离为13。在我们解决珍珠城时,还必须考虑珍珠城的邻居,也就是迈里和瓦西阿瓦。我们可以将到迈里的距离减至33(13和20的和),并将到瓦西阿瓦的距离减至25(13和12的和)。现在的情况就如第(3)列所示。
接下来要解决的是瓦西阿瓦,其距离为25,在当前的未解决节点中是最小的。不过,该节点不允许我们减少到其他节点的距离,所以第(4)列与第(3)列有着相同的距离项。同样,接着要解决迈里,其距离为33,不过它也不能减少任何距离,所以第(5)列的各距离项也与第(4)列的相同。严格地说,必须解决最后一个节点,拉耶,不过最后一个节点不可能影响到其他距离,所以第(5)列就给出了从檀香山到所有6个城市的最短距离。
9.8.1 迪杰斯特拉算法起效的原因
为了证明迪杰斯特拉算法是起作用的,必须假设弧的标号都是非负的。9我们将通过对k的归纳证明,在存在k 个已解决节点时,下列命题成立。
9如果允许标号是负值,我们就可以找到一些迪杰斯特拉算法会给出错误答案的图。
(a) 对每个已解决节点u 来说,dist(u)是从s 到u 的最小距离,而且到u 的最短路径只由已解决节点组成。
(b) 对每个未解决节点u 来说,dist(u)是从s 到u 的任意特殊路径的最小距离,如果不存在这样的路径则为INFTY。
依据。对k=1,s 是唯一的已解决节点。我们将dist(s)初始化为0,这满足了(a)。而对其他每个节点u,如果弧s→u 存在,我们就将dist(u)初始化为该弧的标号,如果不存在就初始化为INFTY。因此,(b)也得到满足。
归纳。现在假设(a)和(b)在k 个节点被解决后还成立,并设v 是第k+1个被解决的节点。我们声明(a)仍然成立,因为dist(v)是从s 到v 的任意路径的最短距离。假设不是,根据归纳假设的(b)部分,当有k 个节点已解决时,dist(v)是到v 的任意路径的最小距离,而且一定存在到距离更短的到v 的非特殊路径。如图9-41所示,这一路径一定会在某个节点w(可能是节点s)离开已解决节点,并行向某个未解决节点u。从那里开始,该路径可能反复进出已解决节点,直到它最终到达节点v。

图 9-41 假设的经过w和u到达v的更短路径
不过,v 被选定为第k+1个已解决节点。这就意味着这时的dist(u)不会小于dist(v),否则就要选择u 作为第k+1个节点。根据归纳假设的(b)部分,dist(u)是到u 的任意特殊路径的最小距离。不过图9-41中从s 到w 再到u 的路径是条特殊路径,所以该路径的距离至少为dist(u)。因此,假设的经过w 和u 的从s 到v 的更短路径的距离至少为dist(v),因为该路径从s 到u 那部分的距离已经是dist(u)了,而且有dist(u)≥dist(v)。10因此,(a)对k+1个节点也是成立的,也就是说,当我们将v 纳入已解决节点的行列时,(a)继续成立。
10请注意,所有标号都非负的事实是至关重要的,如果不这样的话,该路径从u 到v 的部分的距离有可能为负值,这样就会得到一条到v 的更短路径。
现在必须证明当把v 添加到已解决节点中时,(b)仍然成立。考虑当把v 添加到已解决节点中时仍然未解决的某个节点u。在到u 的最短特殊路径上,肯定存在某倒数第二个节点,这个节点既可能是v 也可能是其他某个节点w。这两种可能如图9-42所示。

图 9-42 到u 的最短特殊路径上倒数第二个节点是什么
首先假设倒数第二个节点是v。那么图9-42中所示从s 到v 再到u 的路径的长度就是dist(v)加上弧v→u 的标号。
另外,假设倒数第二个节点是其他某节点w。根据归纳假设(a),从s 到w 的最短路径只由v 之前的已解决节点组成,因此,v 没有出现在这条路径上。所以,当把v 添加到已解决节点中时,到u 的最短特殊路径不会改变。
现在回想一下,当解决v 时,会把每个dist(u)值调整为dist(u)的旧值与dist(v)加上弧v→u 的标号这两者中的较小者。前者表示的是除v 之外的某个节点w 作为倒数第二个节点的情况,而后者则是v 为倒数第二个节点的情况。因此,(b)部分也成立,这样就完成了归纳步骤。
9.8.2 迪杰斯特拉算法的数据结构
现在要展示迪杰斯特拉算法的一种高效实现,它利用了5.9节的平衡偏序树结构。11这里要使用两个数组,一个是表示该图的graph数组,另一个是表示偏序树的potNodes。这样做的目的是,对图中的各节点u,都有一个与之对应的偏序树节点a,其优先级就等于dist (u)。不过,和5.9节不同的是,我们将按照最低优先级而不是最高优先级来组织该偏序树。或者,我们可以取-dist (u)为a 的优先级。图9-43展示了这种数据结构。
11其实,当弧的数量要比节点数的平方(也就是能达到的弧的最大数量)小一些时,这种实现是唯一的好方法。我们将在习题中讨论用于稠密图情况的一种简单实现。
我们用NODE作为图节点的类型。和往常一样,将用从0开始的整数为节点命名,还将使用POTNODE作为偏序树中节点的类型。就像在5.9节中那样,为了方便,我们会假设偏序树中的节点是用从1开始的整数编号的。因此,NODE和POTNODE类型就等同于int。

图 9-43 用来表示对应迪杰斯特拉算法的图的数据结构
GRAPH数据类型定义如下
typedef struct {
float dist;
LIST successors;
POTNODE toPOT;
} GRAPH[MAX];
这里,MAX是图中的节点数,而LIST则是由CELL类型的单元组成的邻接表的类型。因为需要加上为浮点数标号的标签,所以就应该像下面这样定义CELL类型
typedef struct CELL *LIST;
struct CELL {
NODE nodeName;
float nodeLabel;
LIST next;
};
我们将数据类型POT声明为图中节点组成的数组
typedef NODE POT[MAX+1];
我们现在可以定义以下关键数据结构
GRAPH graph;
POT potNodes;
POTNODE last;
结构体数组graph含有图中的节点,而数组potNodes则包含了偏序树中的节点,而变量last则表示偏序树(存放在数组potNodes[1..last]中)当前的末端。
直觉上讲,偏序树的结构是用数组potNodes中的位置表示的,就像平常表示偏序树那样。该数组中的元素让我们通过引用回图本身来区分节点的优先级。特别要说的是,在potNodes[a]中放置的是所表示图节点的索引u。而dist字段graph[u].dist给出了节点a在偏序树中的优先级。
9.8.3 迪杰斯特拉算法的辅助函数
我们需要若干辅助函数来让实现运转起来。最基础的函数是swap,它会交换偏序树中的两个节点。这个问题并不像5.9节中的那么简单。在这里,graph的toPOT字段必须继续记录数组potNodes中的值,如图9-43所示。也就是说,如果graph[u].toPOT的值为a,那么还肯定有potNodes[a]的值为u。
swap函数的代码如图9-44所示。它接受的参数包括图G、偏序树P,以及偏序树中的两个节 点a和b。这里将检验该函数交换偏序树a 和b 两项中的值并交换对应图节点的toPOT字段的工作留给读者作为练习。
void swap(POTNODE a, POTNODE b, GRAPH G, POT P)
{
NODE temp; /* 用来交换偏序树节点 */
temp = P[b];
P[b] = P[a];
P[a] = temp;
G[P[a]].toPOT = a;
G[P[b]].toPOT = b;
}
图 9-44 交换偏序树中两个节点的函数
我们将需要让节点在偏序树中上冒与下沉,就像在5.9节中所做的那样。其主要区别在于,这里的数组potNodes中元素的值不是优先级。这个值会把我们带到graph数组中的节点,而在表示该节点的结构体中可以找到字段dist,它会告诉我们优先级。因此我们还需要辅助函数priority返回合适节点对应的dist。我们还将在本节内容中作出如下假设,较小的优先级会上升到偏序树的顶端,而非5.9节中那样是较大优先级。
图9-45展示了priority、bubbleUp和bubbleDown函数,它们都是对5.9节中同名函数进行简单修改后得到的。这些函数都接受图G和偏序树P作为参数。而函数bubbleDown还需要整数参数last,用来表示数组P中当前偏序树的末端。
float priority(POTNODE a, GRAPH G, POT P)
{
return G[P[a]].dist;
}
void bubbleUp(POTNODE a, GRAPH G, POT P)
{
if ((a > 1) &&
(priority(a, G, P) < priority(a/2, G, P))) {
swap(a, a/2, G, P);
bubbleUp(a/2, G, P);
}
}
void bubbleDown(POTNODE a, GRAPH G, POT P, int last)
{
POTNODE child;
child = 2*a;
if (child < last &&
priority(child+1, G, P) < priority(child, G, P))
++child;
if (child <= last &&
priority(a, G, P) > priority(child, G, P)) {
swap(a, child, G, P);
bubbleDown(child, G, P, last);
}
}
图 9-45 偏序树中节点的上冒与下沉
9.8.4 初始化
我们将假设对应图中各节点的邻接表已经创建,而且指向图节点u 的邻接表的指针已经出现在graph[u].successors中。还要假设节点0是源节点。如果接受图节点i 与偏序树节点i+1对应,数组potNodes就恰如其分地被初始化为偏序树。也就是说,偏序树的根节点表示图的源节点,也就是我们给定优先级0的节点,而且我们要为所有其他节点给定优先级INFTY,这是定义为“无限”的常量。
带异常的初始化
请注意,在图9-46的第(2)行中,我们将
dist[1]以及所有其他距离都置为INFTY。接着在第(5)行,再将该距离修正为0。与测试每个i 值以确定其是否为异常情况相比,这种方式要更具效率。诚然,如果我们将第(2)行替代为if (i == 0) G[i].dist = 0; else G[i].dist = INFTY;就可以消除第(5)行,不过这样一来不仅增加了代码,还会增加运行时间,因为这样修改就必须进行n 次测试和n 次赋值,而不是像图9-46中的第(2)行和第(5)行那样只用进行n+1次赋值而不用进行测试。
正如我们将要看到的,在迪杰斯特拉算法的第一轮处理中,我们选择“解决”源节点,这样就创造了可以作为非正式介绍中起始点的条件,其中源节点是已解决的,而且dist[u]只有在存在从源节点到u 的弧时才不是无限长。初始化函数如图9-46所示。正如本节中之前的函数那样,initialize接受图和偏序树作为参数,还要接受指向整数last的指针pLast,所以该函数可以将pLast初始化为MAX,也就是该图中节点的数量。回想一下,last表示的是与当前正使用的偏序树对应的数组中最后一个位置。
void initialize(GRAPH G, POT P, int *pLast);
{
int i; /* i既作为图节点,也作为树节点, */
(1) for (i = 0; i < MAX; i++) {
(2) G[i].dist = INFTY;
(3) G[i].toPOT = i+1;
(4) P[i+1] = i;
}
(5) G[0].dist = 0;
(6) (*pLast) = MAX;
}
图 9-46 迪杰斯特拉算法的初始化
请注意,偏序树的索引是1到MAX,而对图来说,这些索引就是从0到MAX-1。因此,在图9-46的第(3)行和第(4)行中,必须一开始就把图中的节点i 对应到偏序树的节点i+1。
9.8.5 迪杰斯特拉算法的实现
图9-47展示了迪杰斯特拉算法的代码,利用到了我们之前已经编写的所有函数。要为对应偏序树potNodes以及带有指示偏序树末端的整数last的图graph执行迪杰斯特拉算法,就要初始化这些变量,然后调用
Dijkstra(graph, potNodes, &last)
函数Dijkstra的工作原理如下。在第(1)行我们要调用initialize。其余代码,也就是第(2)行到第(13)行是个循环,该循环每次迭代都对应迪杰斯特拉算法的一轮处理,在迭代中我们要选择一个节点v 并将其解决。在第(3)行选择的节点v 总是对应树节点为偏序树根节点的那个。在第(4)行,通过交换v 与偏序树当前的最后一个节点,我们把v 从偏序树中取出。第(5)行其实是通过递减last将v 删除。然后第(6)行通过对我们刚放置到根节点位置的节点调用bubbleDown,还原了偏序树属性。事实上,未解决节点会出现在last 之下,而已解决节点则出现在last 及last 以上的位置。
void Dijkstra(GRAPH G, POT P, int *pLast)
{
NODE u, v; /* v 是我们要解决的节点 */
LIST ps; /* ps 沿着v的后继表下行,u是ps
指向的那个后继 */
(1) initialize(G, P, pLast);
(2) while ((*pLast) > 1) {
(3) v = P[1];
(4) swap(1, *pLast, G, P);
(5) --(*pLast);
(6) bubbleDown(1, G, P, *pLast);
(7) ps = G[v].successors;
(8) while (ps != NULL) {
(9) u = ps->nodeName;
(10) if (G[u].dist > G[v].dist + ps->nodeLabel) {
(11) G[u].dist = G[v].dist + ps->nodeLabel;
(12) bubbleUp(G[u].toPOT, G, P);
}
(13) ps = ps->next;
}
}
}
图 9-47 迪杰斯特拉算法的主函数
在第(7)行我们开始调整距离,以反映v 现在已被解决的事实。指针p 被初始化为指向节点v 邻接表的开头。在第(9)行把变量u 置为v 的某一后继之后,我们在第(10)行测试了到u 的最短特殊路径是否经过v。只要该数据结构中由G[u].dist表示的dist (u )的旧值大于dist (v )加上弧v→u 标号的和,就有这一最短特殊路径经过节点v。如果这样,那么在第(11)行,将dist (u )置为新的更小的值,并在第(12)行调用bubbleUp。所以,如果需要的话,u 可以在偏序树中上升到反映其新优先级的位置。在第(13)行中随着p 沿着v 的邻接表向下移动,该循环就随之完成了。
9.8.6 迪杰斯特拉算法的运行时间
正如之前所述那样,假设图具有n 个节点,而且m 是弧数与节点数的较大者。这里将会按照描述这些函数的次序分析每个函数的运行时间。首先,swap函数显然花费O(1)的时间,因为它只由赋值语句组成。同样priority函数也花费O(1)的时间。
bubbleUp函数是递归函数,但它的运行时间是O(1)加上对到根节点一半距离的节点递归调用该函数的时间。正如我们在5.9节中验证过的,至多存在logn 次调用,而且每次调用需要O(1)的时间,所以bubbleUp的总运行时间就是O(logn)。同样,bubbleDown也花费O(logn)的时间。
initialize函数要花O(n)的时间。具体来说就是,第(1)行到第(4)行的循环要迭代n 次,而其循环体每次迭代要花O(1)的时间。这就给了该循环O(n)的时间。第(5)行和第(6)行各自贡献了O(1)的时间,不过我们在大O表达式中可以将其省略掉。
现在把注意力转移到图9-47中的Dijkstra函数上。设mv是节点v的出度,或者说是v的邻接表的长度。我们首先分析第(8)行到第(13)行的内层循环。第(9)行到第(13)行的各行都要花O(1)的时间,除了第(12)行对bubbleUp的调用之外,我们论证过该调用要花O(logn)的时间。因此,该循环的循环体要花O(logn)的时间。该循环进行的次数等于v对应的邻接表的长度,之前已经将其表示为mv了。因此,第(8)行到第(13)行的循环的运行时间可以表示为O(1+mv logn),1这一项表示的是v没有后继,也就是mv=0的情况,不过我们还是要进行第(8)行的测试。
现在考虑第(2)行到第(13)行的外层循环。我们已经验证过第(8)行到第(13)行了。第(6)行调用bubbleDown需要的时间。而循环体的其他各行都只要O(1)的时间,因此整个循环体需要花上O((1+mv)logn)的时间。
外层循环刚好要迭代n-1次,因为last的范围是从n 减少到2。1+mv 中的1这一项因此要贡献n-1,或者说是O(n)的时间。不过,mv 这项一定要为各个节点v 相加,因为所有节点(除了最后一个节点)都要被选作一次v。因此,mv 对外层循环所有迭代的总贡献是O(m),因为有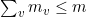 。由此可以得出外层循环要花O(m logn)的时间。第(1)行对
。由此可以得出外层循环要花O(m logn)的时间。第(1)行对initialize的调用要花O(n)的时间,不过可以将其省略。这样一来就得到迪杰斯特拉算法的运行时间为O(m logn),也就是说,至多是查看图中的节点和弧所花时间的logn 倍。
9.8.7 习题
1. 按照图9-21中所示的图(见9.4节的习题),找到从底特律到其他城市的最短距离。如果某城市是从底特律不可达的,则这个最小距离为“无限”。
2. 有时候我们希望计算从一个节点到另一个节点遍历的弧的数量。例如,我们可能希望把在乘飞机或坐公交车出行过程中的换乘次数减少到最小。如果给每条弧标记上1,那么最小距离计算就会变成数弧的过程。为图9-5中的图(见9.2节的习题)找出从节点a到达各节点所需要的最小弧数。
3. 图9-48a中有7个灵长类物种以及它们名称的缩写。这些物种中的某些物种已知要先于其他物种出现,因为在同一地点代表时间流逝的不同地层中发现了它们的化石。图9-48b中的表给出的三元组(x,y,t )表示物种x 与物种y 是在同一地点被发现,不过x 要比y 早t 百万年出现。
(a) 画出表示图9-48中数据的有向图,其中弧是从较早的物种到达较晚的物种,弧的标号就表示物种间的时间差异。
(b) 以AF为源节点,对(a)小题画出的图运行迪杰斯特拉算法,找到AF之后的各其他物种与它相差的最短时间。
4. * 我们给出的迪杰斯特拉算法的实现需要O(m logn)的时间,这一时间要小于O(n2)的时间,除了弧的数量接近n2的情况之外。如果m 很大,就可以谋划另一种不需要用到优先级队列的实现,这样在每一轮处理中就不再需要O(n)的时间选择要解决的节点,而只需要O(mu)的时间,也就是与从已解决节点u 出发的弧的数量成正比的时间,来更新dist。得到的是一种O(n2)时间的算法。完善这里提出的思路,并为迪杰斯特拉算法的这种实现编写C语言程序。
Australopithecus Afarensis(最早南方古猿) | AF |
|---|---|
Australopithecus Africanus(非洲南方古猿) | AA |
Homo Habilis(能人) | HH |
Australopithecus Robustus(粗壮南方古猿) | AR |
Homo Erectus(直立人) | HE |
Australopithecus Boisei(鲍氏南方古猿) | AB |
Homo Sapiens(智人) | HS |
(a) 物种及其缩写
物种1 | 物种2 | 时间 |
|---|---|---|
AF | HH | 1.0 |
AF | AA | 0.8 |
HH | HE | 1.2 |
HH | AB | 0.5 |
HH | AR | 0.3 |
AA | AB | 0.4 |
AA | AR | 0.6 |
AB | HS | 1.7 |
HE | HS | 0.8 |
(b) 物种1先于物种2的时间
图 9-48 灵长类物种之间的关系
5. ** 如果某些弧的标号为负值,迪杰斯特拉算法就不是永远都能奏效了。给出一幅能让迪杰斯特拉算法给出错误最小距离的带负值标号的图。
6. ** 设G 是我们已经为其运行过迪杰斯特拉算法并以某种次序解决了其中节点的图。假设要为G 添加一条权为0的弧u→v,以形成新图G' 。在什么情况下迪杰斯特拉算法为G' 解决节点的次序与为G 解决节点的次序相同?
7. ** 在本节中我们采用的方法是把表示图G 的数组与存储整数(作为指向其他数组索引)的偏序树关联起来。另一种方式是使用指向数组元素的指针。使用指针替代整数索引,重新实现迪杰斯特拉算法。
9.9 最短路径的弗洛伊德算法
如果想知道含n 个节点的非负标号图中所有节点对之间的最小距离,可以把每个节点n 作为源节点来运行迪杰斯特拉算法。因为运行一次迪杰斯特拉算法所需的时间为O(m logn),其中m 是节点数和弧数的较大者,那么用这种方式找出所有节点对之间的最小距离就要花掉O(mn logn)的时间。此外,如果m 接近其最大值n2,就可以使用9.8节的习题(4)中讨论过的迪杰斯特拉算法O(n2)时间的实现,这样要为每个节点对都找到最小距离,就需要运行n 次成为O(n3)时间的算法。
还有一种找出所有节点对之间最小距离的算法——弗洛伊德算法。这种算法要花O(n3)的时间,因此从本质上讲不比迪杰斯特拉算法更好,而且当弧的数量远小于n2时要比前者更糟。不过,弗洛伊德算法是基于邻接矩阵,而不是基于邻接表的,它从概念上讲要比迪杰斯特拉算法简单得多。
弗洛伊德算法的本质是,依次将图的每个节点u 作为枢纽。当u 是枢纽时,我们会试着利用u 作为所有节点对之间的中间节点,如图9-49所示。对每个节点对(比方说是v 和w)而言,如果弧v→u 和u→w 的标号的和,即图9-49中的d+e,要小于当前从v 到w 的弧的标号f,那么就将f 替换为d+e。

图 9-49 使用节点u 作为枢纽,以改善某些节点对之间的距离
实现弗洛伊德算法的代码片段如图9-50所示。和之前一样,假设节点使用从0开始的整数命名,并且还是使用NODE作为节点的类型,不过这里要假设该类型为整数或等价的枚举类型。我们还要假设有n×n 的数组arc,满足arc[v][w]是给定图中弧v→w 的标号。不过,对其对角线上所有的节点v 来说,即便存在弧v→v,也有arc[v][v]=0。原因在于,从一个节点到其自身的最短距离总是0,而且我们根本不希望沿着这些弧行进。如果没有从v 到w 的弧,我们就让arc[v][w]为INFTY,就是要比其他任意标号都大很多的一个特殊值。还有一个相似的数组dist,在其末端存放着最小距离,dist[v][w]将成为从节点v 到节点w 的最小距离。
NODE u, v, w;
(1) for (v = 0; v < MAX; v++)
(2) for (w = 0; w < MAX; w++)
(3) dist[v][w] = arc[v][w];
(4) for (u = 0; u < MAX; u++)
(5) for (v = 0; v < MAX; v++)
(6) for (w = 0; w < MAX; w++)
(7) if (dist[v][u] + dist[u][w] < dist[v][w])
(8) dist[v][w] = dist[v][u] + dist[u][w];
图 9-50 弗洛伊德算法
第(1)行到第(3)行会将dist初始化为arc。第(4)行到第(8)行构成了一个循环,其中每个节点u 会依次被取作枢纽。对各枢纽u,在v 和w 上的双重循环中,我们考虑了每个节点对。第(7)行会测试从v 经过u 到达w 是否比从v 直接到w 更近,如果是这样,那么第(8)行就会将dist[v][w]降低为从v 到u 的距离及从u 到w 的距离之和。
示例 9.27
考虑一下9.3节图9-10中的图。使用0到5的数字表示节点,其中0表示拉耶,1表示卡内奥赫,等等。图9-51展示了arc矩阵,标号INFTY表示相应的节点对之间没有边连通。而arc矩阵也是dist矩阵的初始值。
沃夏尔算法
有时候,我们只对分辨两个节点间是否存在路径感兴趣,而不去管最小距离是多少。如果这样,就可以使用元素类型为
BOOLEAN(即int)的邻接矩阵,其中TRUE(1)表示弧的存在,而FALSE(0)表示弧不存在。同样,dist矩阵的元素也是BOOLEAN类型的,其中TRUE表示问题中已知的节点间存在路径,而FALSE表示它们之间不存在路径。我们需要对弗洛伊德算法进行的唯一修改就是把图9-50中的第(7)行和第(8)行替换为(7) if (dist[v][w] == FALSE) (8) dist[v][w] = dist[v][u] && dist[u][w];如果
dist[v][w]还不是TRUE,只要dist[v][u]和dist[u][w]都是TRUE,这两行代码就会把它置为TRUE。得到的算法名为沃夏尔算法(Warshall's Algorithm),可以在O(n3)的时间内为含n 个节点的图计算自反闭包和传递闭包。这一算法从来都不会优于9.7节中利用了深度优先搜索的O(mn)时间的算法。不过,沃夏尔算法使用的是邻接矩阵而非邻接表,而且如果m 接近n2,它实际上会因为其简单性而比乘法的深度优先搜索更有效率。
请注意,图9-10中的图是无向图,所以矩阵是对称的,也就是说arc[v][w]=arc[w][v]。如果图是有向图,就可能不存在这种对称性,不过弗洛伊德算法并未利用到对称性,因此处理有向图或无向图都是可以的。
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
0 | 0 | 24 |
|
|
| 28 |
1 | 24 | 0 | 11 |
|
|
|
2 |
| 11 | 0 | 13 |
|
|
3 |
|
| 13 | 0 | 20 | 12 |
4 |
|
|
| 20 | 0 | 15 |
5 | 28 |
|
| 12 | 15 | 0 |
图 9-51 arc矩阵,它是dist矩阵的初始值
第一个枢纽是u=0。因为INFTY与任意值的和都是INFTY,所以唯一的节点对v 和w,两者都不为u。而且有dist[v][u]+dist[u][w]小于INFTY的节点对,就是v=1和w=5,反之亦然。12因为此时dist[1][5]是INFTY,我们就将dist[1][5]用dist[1][0]+dist[0][5]的和52替换掉。同样,要将dist[5][1]替换为52。其他距离都不能借助枢纽0得到改善,这样一来就得到如图9-52所示的dist矩阵。
12如果v 和w 中有一个为u,就很容易看出dist[v][w]永远不可能借助经过u 而得到改进。因此,在查找经过中枢w 能够改进距离的节点对时,可以忽略那些形如(v,u )或(u,w )的有序对。
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
0 | 0 | 24 |
|
|
| 28 |
1 | 24 | 0 | 11 |
|
| 52 |
2 |
| 11 | 0 | 13 |
|
|
3 |
|
| 13 | 0 | 20 | 12 |
4 |
|
|
| 20 | 0 | 15 |
5 | 28 | 52 |
| 12 | 15 | 0 |
图 9-52 在使用0作为枢纽后的dist矩阵
现在以节点1作为枢纽。在如图9-52所示的当前dist矩阵中,节点1分别存在到节点0(距离24)、节点2(距离11)和节点5(距离52)的非无限连接。我们可以将这些边组合起来,从而将节点0到节点2的距离从INFTY减少到24+11=35。还可以把节点2和节点5之间的距离减少到11+52=63。请注意,63是从檀香山到卡内奥赫,然后到拉耶,最后到瓦西阿瓦的路径的距离,不过这一最短路线只经过了目前已经成为过枢纽的节点。最终,我们会发现经过珍珠城的更短路线。当前的dist矩阵如图9-53所示。
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
0 | 0 | 24 | 35 |
|
| 28 |
1 | 24 | 0 | 11 |
|
| 52 |
2 | 35 | 11 | 0 | 13 |
| 63 |
3 |
|
| 13 | 0 | 20 | 12 |
4 |
|
|
| 20 | 0 | 15 |
5 | 28 | 52 | 63 | 12 | 15 | 0 |
图 9-53 在使用1作为枢纽后的dist矩阵
现在用2作为枢纽。节点2当前与节点0(距离35)、节点1(距离11)、节点3(距离13)和节点5(距离63)之间存在非无限连接。在这些节点中,节点0和节点3之间的距离可以改善为35+13=48,而且节点1和节点3之间的距离可以改善为11+13=24。因此,当前的dist矩阵如图9-54所示。
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
0 | 0 | 24 | 35 | 48 |
| 28 |
1 | 24 | 0 | 11 | 24 |
| 52 |
2 | 35 | 11 | 0 | 13 |
| 63 |
3 | 48 | 24 | 13 | 0 | 20 | 12 |
4 |
|
|
| 20 | 0 | 15 |
5 | 28 | 52 | 63 | 12 | 15 | 0 |
图 9-54 使用节点2作为枢纽后的dist矩阵
接下来,节点3成为枢纽。图9-55展示了节点3与其他各节点之间当前的最佳距离。13通过行经节点3,可以作出如下距离上的改善。
13读者应该将图9-55与图9-49加以比较。后者展示了如何在有向图的一般情况下使用枢纽节点,其中进出枢纽节点的弧可能有着不同标号。而图9-55则利用了示例图的对称性,让我们使用节点3与其他各节点之间的边来表示进入节点3的弧,就像图9-49左侧那样,以及从节点3出发的弧,就像图9-49右侧那样。
1. 节点1和节点5之间地距离被减小到36。
2. 节点2和节点5之间的距离被减小到25。
3. 节点0和节点4之间的距离被减小到68。
4. 节点1和节点4之间的距离被减小到44。
5. 节点2和节点4之间的距离被减小到33。

图 9-55 到节点3的当前最佳距离
当前的dist矩阵如图9-56所示。
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
0 | 0 | 24 | 35 | 48 | 68 | 28 |
1 | 24 | 0 | 11 | 24 | 44 | 36 |
2 | 35 | 11 | 0 | 13 | 33 | 25 |
3 | 48 | 24 | 13 | 0 | 20 | 12 |
4 | 68 | 44 | 33 | 20 | 0 | 15 |
5 | 28 | 36 | 25 | 12 | 15 | 0 |
图 9-56 使用节点3作为枢纽后的dist矩阵
使用节点4作为枢纽不能改善任何距离。当节点5作为枢纽时,我们可以改善节点0和节点3之间的距离,因为在图9-56中有
dist[0][5] + dist[5][3] = 40
这要小于dist[0][3]的值48。就具体的城市而言,这就相当于发现,从拉耶出发经过瓦西阿瓦到珍珠城,要比经过卡内奥赫和檀香山到珍珠城更近。同样,可以把节点0和节点4之间的距离从68改善到43。最终的dist矩阵如图9-57所示。
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
0 | 0 | 24 | 35 | 40 | 43 | 28 |
1 | 24 | 0 | 11 | 24 | 44 | 36 |
2 | 35 | 11 | 0 | 13 | 33 | 25 |
3 | 40 | 24 | 13 | 0 | 20 | 12 |
4 | 43 | 44 | 33 | 20 | 0 | 15 |
5 | 28 | 36 | 25 | 12 | 15 | 0 |
图 9-57 最终的dist矩阵
9.9.1 弗洛伊德算法为何奏效
正如我们所见,在弗洛伊德算法的任何阶段,从节点v 到节点w 的距离都将是只由做过枢纽的节点组成的路径中最短路径的距离。最终,所有的节点都成为过枢纽,而且dist[v][w]存放着所有可能路径的最小距离。
我们可以将从节点v 到节点w 的k 路径定义为满足从v 到w 的中间节点编号不大于k 的路径。请注意,并不需要限制v 或w 一定是k 或更小。
k=-1的情况是个重要特例。因为假设节点的编号是从0开始的,所以(-1)路径是没有中间节点的。它只可能是一条弧,或是作为0长度路径起止点的一个节点。
图9-58展示了k 路径的样子,不过端点v 和w 既可以在k 之上,也可以在k 以下。在该图中,线的高度表示了从v 到w 的路径上各节点的编号。
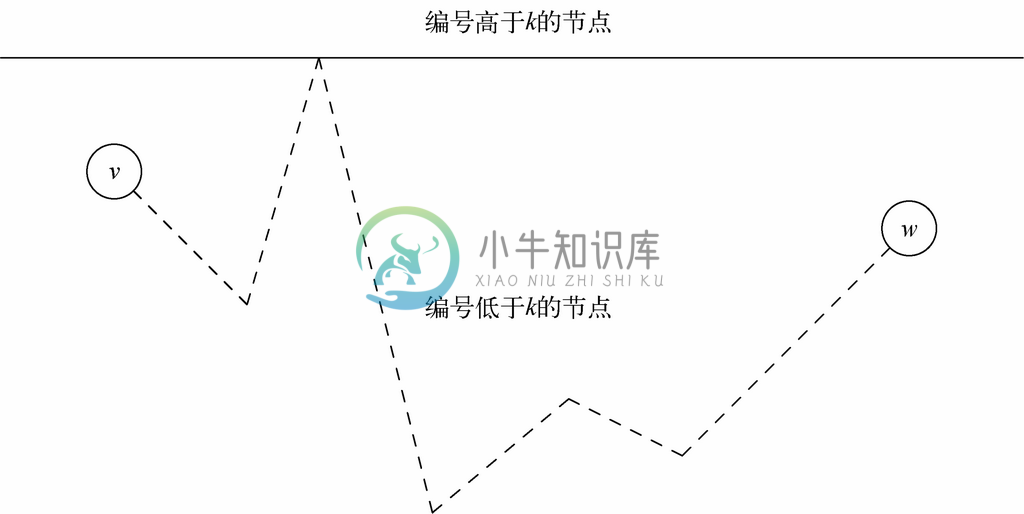
图 9-58 除了端点(可能高于k)外,k 路径上的节点不会高于k
示例 9.28
在图9-10中,路径0、1、2、3是一条2路径。中间节点1和2都不大于2。这一路径也是3路径,4路径和5路径。但它不是1路径,因为中间节点2大于1。同样,它也不是0路径或(-1)路径。
因为假设节点的编号是从0到n-1,所以(-1)路径不可能有中间节点,因此它一定是一条弧或一个节点。而n-1路径则可以是任意路径,因为在节点编号为0到n-1的图中,任何路径中间节点的编号都不会大于n-1。这里将通过对k 的归纳证明该命题。
命题S(k )。如果弧的标号都是非负的,那么在图9-50第(4)行到第(8)行的循环将u 置为k+1之前,dist[v][w]是从v 到w 的最短k 路径的长度,如果没有这样的路径,其长度就是INFTY。
依据。依据是k=-1。我们在第一次执行该循环的循环体之前将u 置为0。在第(1)行到第(3)行中我们已经把dist初始化为arc。因为由一个节点构成的弧和路径只有(-1)路径,所以依据成立。
归纳。假设S(k )成立,考虑u=k+1时循环迭代期间dist[v][w]发生的情况。假设P 是从v 到w 的最短k+1路径。有两种情况,具体取决于P 是否经过k+1号节点。
1. 如果P 是k 路径,也就是说P 其实没有经过k+1号节点,那么根据归纳假设,在经过k 次迭代之后dist[v][w]已经等于P 的长度。因为没有更短的(k+1)路径,所以我们在以k+1号节点为枢纽的这轮处理中不能改变dist[v][w]。
2. 如果P 是k+1路径,我们可以假设P 只经过节点k+1一次,因为环路永远都不可能减少距离。回想一下,我们要求所有标号都是非负的。因此,P 是由从v 到节点k+1的k 路径Q,后面跟上从节点k+1到w 的k 路径R 组成的,如图9-59所示。根据归纳假设,dist[v][k+1]和dist[k+1][w]分别是在第k 次迭代之后路径Q 和R 的长度。

图 9-59 (k+1)路径可以分为两条k 路径,Q 后面跟上R
首先要看到dist[v][k+1]和dist[k+1][w]在第k+1次迭代中不可能改变。原因在于所有的标号都是非负的,这样所有路径的长度都是非负的,因此图9-50中第(7)行的测试在u(即节点k+1)是v 或w 其中之一时一定会失败。
所以,当我们以u=k+1对任意的v 和w 应用第(7)行的测试时,自从第k 次迭代结束之后dist[v][k+1]和dist[k+1][w]的值就不再改变。也就是说,第(7)行的测试会对最短k 路径的长度及从v 到k+1和k+1到w 的最短k 路径长度之和进行比较。在第(1)种情况下,路径P 不经过k+1,前者更短,而在情况(2)中,P 经过k+1,后者是图9-59中路径Q 和路径R 长度之和,因此要更短。
可以得出结论:第k+1次迭代会把dist[v][w]置为对所有的节点v 和w 而言最短k+1路径的长度。这就是命题S(k+1),所以我们得出了归纳的结论。
要完成证明,设k=n-1。也就是说,我们知道在完成全部n 次迭代后,dist[v][w]是任意从v 到w 的n-1路径的最短距离,这样就证明了dist[v][w]是从v 到w 的任意路径中最小的距离。
9.9.2 习题
1. 假设图9-5(见9.2节习题)中所有的弧标号都为1,使用弗洛伊德算法得出各节点对间最短路径的长度。给出以每个节点作为枢纽后的距离矩阵。
2. 对图9-5中的图应用沃夏尔算法,计算其自反闭包和传递闭包。给出以每个节点作为枢纽后的可达性矩阵。
3. 使用弗洛伊德算法为图9-21(见9.4节习题)中的图找到各城市对之间的最短距离。
4. 使用弗洛伊德算法为图9-48(见9.8节习题)中的各灵长类物种找出它们之间可能间隔的最短时间。
5. 有时我们想只考虑有一条或多条弧的路径,而将单个节点排除在弧的范畴之外。如何修改arc矩阵的初始化部分,使得在查找从节点到其自身的最短路径时只考虑长度为1或1以上的路径?
6. * 找出图9-10中所有的无环2路径。
7. * 为什么当弧上的正负开销都存在时弗洛伊德算法就不起作用了?
8. ** 给出能找到两个给定节点间最长无环路径的算法。
9. ** 假设对图G 运行弗洛伊德算法。然后,我们将弧u→v 的标号降为0,以构建新图G'。当对图G 和图G' 应用弗洛伊德算法时,怎样的节点s 和t 组成的节点对会使每一轮处理中对应的两个dist[s][t]都相同?
9.10 图论简介
图论是专门研究图属性的数学分支。在之前的几节中,我们已经展示了图论的基本定义,以及计算机科学家开发的一些可以高效计算图关键属性的基础算法。我们已经看到计算最短路径、生成树和深度优先搜索树的算法。本节要介绍图论中一些更重要的概念。
9.10.1 完全图
每一对不同的节点之间都存在边的无向图就叫作完全图。含n个节点的完全图就叫作Kn。图9-60展示了从K1到K4的完全图。
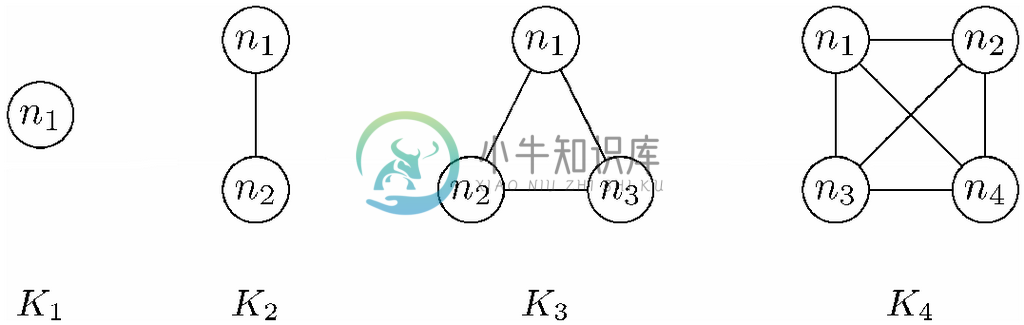
图 9-60 前4个完全图
Kn中的边数是n(n-1)/2,或者说是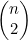 。想知道原因,可以考虑Kn 的边{u,v }。可以选择n 个节点中的任意一个作为u,并从其余n-1个节点中任选一个作为v,因此总的选择数为n(n-1)。不过,这样一来每条边都数了两次,一次是{u,v },第二次是{v,u },所以必须在总选择数上除以2,以得出正确的边数。
。想知道原因,可以考虑Kn 的边{u,v }。可以选择n 个节点中的任意一个作为u,并从其余n-1个节点中任选一个作为v,因此总的选择数为n(n-1)。不过,这样一来每条边都数了两次,一次是{u,v },第二次是{v,u },所以必须在总选择数上除以2,以得出正确的边数。
也存在完全有向图的定义。这种图具有从每个节点到每个其他节点(包括其自身)的弧。n个节点的完全有向图有n2条弧。图9-61展示了含3个节点和9条弧的完全有向图。

图 9-61 含3个节点的完全有向图
9.10.2 平面图
如果可以将无向图的所有节点都放在一个屏幕上,而且可以将它的边画为连续的线而没有边交叉,就说该无向图是平面图。
示例 9.29
图9-60中的K4在画出来时有两条相交的对角边。不过,K4是平面图,正如我们看到的图9-62中这种画法一样。在图9-62中,通过重新把一条对角边画在外面,就避免了两条边相交的情况出现。可以说图9-62是图K4的平面表示,而图9-60则是图K4的非平面表示。请注意,在平面表示中边可以不是直线。

图 9-62 K4的平面表示
在图9-63中看到两种最简单的非平面图,也就是没有任何平面表示的图。一个是K5,有5个节点的完全图。而另一个是K3,3,它的形成方式是,取两组3个节点,并用一组的各个节点与另一组的各个节点连接,但不连接同组中的节点。读者应该试着重画这两种图,看看有没有办法使得任意两条边都不会交叉,以感受一下它们为什么不是平面图。

图 9-63 两种最简单的非平面图
库拉托斯基定理说过,任何非平面图都至少含有这两种图中一种的“副本”。不过,我们在解释副本的概念时一定要小心一点,因为要在任意的非平面图G 中找到K5或K3,3的副本,可能必须要将图9-63所示的某些边与图G 中的路径关联起来。
9.10.3 平面性的应用
平面性在计算机科学中是举足轻重的。例如,很多图或相似的图表需要在计算机屏幕或纸上表现出来。为了清楚起见,是需要制出图的平面表示的,或者如果图不是平面图,就需要尽可能减少交叉边的数量。
读者可能会在第13章中看到我们画的一些相当复杂的电路图,它们其实就是以门和线路连接点为节点而且以线路为边的图。因为这些电路一般而言都不是平面的,所以必须制定一些约定,让线路可以在不连接的情况下交叉,而且用点来表示线路的连接。
相关的应用涉及集成电路的设计。集成电路,或者说“芯片”,把第13章中讨论过的那些逻辑电路都实物化了。它们不需要逻辑电路被刻画为平面表示,但存在相似的限制让我们可以为边指定若干“层”,通常是3或4层。在第一层上,表示电路的图必须有平面表示,边是不允许有交叉的。不过,不同层级上的边是可以交叉的。
9.10.4 图着色
为图G 着色的图着色问题就是给每个节点指定一种“颜色”,使得由边连通的两个节点不会被指定相同的颜色。然后我们可能要问以这种方式为图着色需要多少种不同的颜色。为图G 着色所需的最小颜色数量就叫作图G 的色数(chromaticnumber),通常表示为χ(G)。可以用不超过k 种颜色着色的图被称为可着k 色的。
示例 9.30
如果图是完全图,那么它的色数就等于节点的数量,也就是说χ(Kn)=n。要证明这一点很简单,因为任意两个节点u 和v 之间都是有边连通的,所以不可能为它们着上相同的颜色。因此,每个节点都要有其自己的颜色。对每个k≥n 而言,Kn 都是可着k 色的,不过如果k< n,则Kn 不是可着k 色的。请注意,可以说K4是可着5色的,即便没法为图K4的4个节点用上所有5种颜色。然而,严格地讲,只要图可以用k 种或更少的颜色着色,而不是说刚好可用k 种颜色着色,就可以说图是可着k 色的。
再举个例子,图9-63所示的图K3,3的色数为2。比方说可以把左边组中的节点全着上红色,而将右边那组中的节点全着上蓝色。那么所有的边都是在红色和蓝色节点间的。K3,3就是二分图(bipartitegraph)的例子,也就是可以用两种颜色着色的图。所有这样的图都可以把它们的节点分成两组,其中同一组的成员间是没有边连接的。
最后再举个例子,图9-64中6节点图的色数为4。要知道原因,可以注意到中心的节点不能与其他任何节点颜色相同,因为它与所有节点都是连通的。因此要为它单独使用一种颜色,比方说红色。我们还至少需要两种别的颜色来为环上的节点着色。不过,如果我们试着像图9-64中所做的那样交替着色,比方着上蓝色和绿色,就会遇到问题,第五个节点的邻居既有蓝色也有绿色,因此这个例子中就需要第四种颜色——黄色。

图 9-64 色数为4的图
9.10.5 图着色的应用
找出一种好的图着色方案是计算机科学中另一个热门问题。例如,在第1章的全书内容简介中,我们考虑过将课程分配到时间段中,从而使学生不可能选到同一时段上课的两门课程。这样做的动机是在安排期末考试时保证学生不可能在同一时间需要参加两科考试。我们可以画一幅节点是各门课程的图,其中如果有学生同时选修了某两门课程,在表示这两门课程的节点间就存在边。
这样一来,需要多少个时段来安排考试的问题就成了计算该图的色数是多少的问题。所有颜色相同的节点都可以被安排在同一时段,因为它们之间不存在边。反过来讲,如果有一套对任何学生来说都不会引起时间冲突的安排,那么就可以把所有可安排在同一时段的课程涂成相同的颜色,因此就生成了一种颜色数量与考期时段数相同的图着色方案。
在第1章中,我们试探过基于寻找最大独立集安排考试的方法。这对寻找为图着色的好方案来说也是一种合理的试探。大家可能会期待可以为小到像图1-1中5节点图那样的图尝试所有可能的颜色,其实这是可以的。不过,随着节点数的增加,图可能着色的种数是呈指数式增加的,而且,在找寻最少可能颜色的过程中,为那些非常大的图考虑所有可能的着色并不可行。
9.10.6 团
无向图G 的团(clique)是G 中满足每对节点之间都存在边的所有节点组成的集合。含k 个节点的团就叫作k 点团(k-clique)。图中最大团的大小就叫作该图的团数(clique number)。
示例 9.31
举个简单的例子,任意完全图Kn 都是由全部n 个节点组成的团。事实上,对所有的k≤n 来说,Kn 都有k 点团,但如果k>n,则没有k 点团。
图9-64中的图有大小为3的团,但没有更大的团了。这些3点团都是三角形的。因为没法再将其他节点纳入环中,所以该图中不可能有4点团。每个环节点都只连接到其他3个节点,所以4点团必定会包含环上的某个节点v、它在环上的邻居,以及中心节点。不过,v 在环上的邻居之间没有边,所以没有4点团。
举个团的应用的例子,假设不像图1-1那样表示课程的冲突,而是用两个节点之间的边表示这两门课程没有学生同时选择。如此,两门有边连接的课程可以在同一时间考试。然后我们可以查找极大团(maximal clique),即不是更大的团的子集的团,而且要为同时段课程的极大团
安排考试。
9.10.7 习题
1. 对图9-4中的图而言:
(a) 色数是多少?
(b) 团数是多少?
(c) 给出一个最大团的例子。
2. 如果将(a)图9-5;(b)图9-26中的图变成无向图,那么它们的色数各是多少?可将弧当作边。
3. 图9-5不是用平面方式表示的。该图是否为平面图?也就是说,能否重画该图,从而使该图中没有交叉的边?
4. * 与无向图相关的3个量分别是它的度(任意节点的最大邻居数)、它的色数和它的团数。推导这3个量之间一定成立的不等关系。并解释这些关系为何一定成立。
5. ** 设计算法,接受含n 个的节点而且节点数和边数较大者为m 的图,并在O(m)的时间内能分辨该图是否为二分图(可着2色的图)。
6. * 我们可以把图9-64中的图一般化为具有一个中心节点以及k 个在同一环上的节点,其中环上的每个节点都只与其在环上的邻居以及中心节点相连。给出该图的色数,用k 的函数表示。
7. * 对像在9.5节中讨论过的那样的无序无根树的色数有什么说法?
8. ** 设Ki,j 是取一组i 个节点以及另一组 j 个节点,并把一组中各个节点和另一组中的每个节点用边连接后形成的图。我们看到如果i=j=3,那么得到的图就不是平面图。那么对什么样的i 和 j 来说Ki,j 是平面图?
9.11 小结
图9-65中的表对我们在本章中解决的各种问题、解决这些问题的算法,以及这些算法的运行时间进行了总结。在该表中,n 是图中的节点数,而m 是图中节点数与弧(边)数之间的较大者。除非另外标明,否则假设图是由邻接表表示的。
问题 | 算法 | 运行时间 |
|---|---|---|
最小生成树 | 克鲁斯卡尔算法 | O(m logn) |
检测环路 | 深度优先搜索 | O(m) |
拓扑排序 | 深度优先搜索 | O(m) |
单一源可达性 | 深度优先搜索 | O(m) |
连通分支 | 深度优先搜索 | O(m) |
传递闭包 | n 次深度优先搜索 | O(mn) |
单一源最短路径 | 使用偏序树实现的迪杰斯特拉算法 | O(m logn) |
| 使用9.8节习题(4)实现的迪杰斯特拉算法 | O(n2) |
所有节点对的最短路径 | n 次利用使用偏序树实现的迪杰斯特拉算法 | O(mn logn) |
| n 次利用使用9.8节习题(4)实现的迪杰斯特拉算法 | O(n3) |
| 利用使用邻接矩阵表示的弗洛伊德算法 | O(n3) |
图 9-65 图算法的总结
除此之外,我们还为读者介绍了图论中最关键的一些概念,包括:
路径和最短路径;
生成树;
深度优先搜索树和森林;
图着色和色数;
团和团数;
平面图。
9.12 参考文献
更多与图算法有关的材料见Aho, Hopcroft,and Ullman [1974,1983]。Hopcroft and Tarjan [1973]中首先引入了深度优先搜索来创建高效的图算法。迪杰斯特拉算法来源于Dijkstra [1959],弗洛伊德算法来源于Floyd [1962],克鲁斯卡尔算法来源于Kruskal [1956],而沃夏尔算法来源于 Warshall [1962]。
Berge [1962]涵盖了数学领域的图论。Lawler [1976],Papadimitriou and Steiglitz [1982],以及 Tarjan [1983]展示了高端的图优化技术。
Aho, A. V., J. E. Hopcroft, and J. D. Ullman [1974]. The Design and Analysis of Computer Algorithms, Addison-Wesley, Reading, Mass.
Aho, A. V., J. E. Hopcroft, and J. D. Ullman [1983]. Data Structures and Algorithms, Addison-Wesley, Reading, Mass.
Berge, C. [1962]. The Theory of Graphs and its Applications, Wiley, New York.
Dijkstra, E. W. [1959]. “A note on two problems in connexion with graphs,” Numberische Mathematik 1, pp. 269–271.
Floyd, R. W. [1962]. “Algorithm 97: shortest path,” Comm. ACM 5:6, pp. 345.
Hopcroft, J. E., and R. E. Tarjan [1973]. “Efficient algorithms for graph manipulation,” Comm. ACM 16:6, pp. 372-378.
Kruskal, J. B., Jr. [1956]. “On the shortest spanning subtree of a graph and the traveling salesman problem,” Proc. AMS 7:1, pp. 48–50.
Lawler, E. [1976]. Combinatorial Optimization: Networks and Matroids, Holt, Rinehart and Winston, New York.
Papadimitriou, C. H., and K. Steiglitz [1982]. Combinatorial Optimization: Algorithms and Complexity, Prentice-Hall, Englewood Cliffs, New Jersey.
Tarjan, R. E. [1983]. Data Structures and Network Algorithms, SIAM, Philadelphia.
Warshall, S. [1962]. “A theorem on Boolean matrices,” J. ACM 9:1, pp. 11-12.


