第五章：条件和递归

优质

小牛编辑

127浏览

2023-12-01

这章的中心话题是能够根据程序的状态执行不同命令的if语句。但是首先我想介绍两个新的运算符 : 地板除（floor division）和求余（modulus）。

地板除和求余

地板除 运算符(floor division operator) // 先做除法，然后将结果保留到整数。例如，如果一部电影时长105 分钟，你可能想知道这代表着多少小时。传统的除法操作会返回一个浮点数：

>>> minutes = 105
>>> minutes / 60
1.75

但是，用小时做单位的时候，我们通常并不写出小数部分。地板除丢弃除法运算结果的小数部分，返回整数个小时:

>>> minutes = 105
>>> hours = minutes // 60
>>> hours
1

如果你希望得到余数，你可以从除数中减去一个小时也就是60分钟:

>>> remainder = minutes - hours * 60
>>> remainder
45

另一个方法就是使用 求余运算符(modulus operator) % ，它会将两个数相除，返回余数。

>>> remainder = minutes % 60
>>> remainder
45

求余运算符比看起来更加有用。例如，你可以查看一个数是否可以被另一个数整除——如果　x % y　的结果是 0，那么 x 能被 y　整除。

此外，你也能获得一个数的最右边一位或多位的数字。例如， x % 10 返回 x 最右边一位的数字（十进制）。类似地，x % 100 返回最后两位数字。

如果你正在使用　Python 2, 那么除法就会和前面的介绍有点不同。除法运算符 /　在被除数和除数都是整数的时候，会进行地板除，但是当被除数和除数中任意一个是浮点数的时候，则进行浮点数除法。(译者注：在 Python3 中，无论任何类型都会保持小数部分)

布尔表达式

布尔表达式（boolean expression）的结果要么为真要么为假。下面的例子使用 == 运算符。它比较两个运算数，如果它们相等，则结果为 True ，否则结果为 False 。

>>> 5 == 5
True
>>> 5 == 6
False

True 和 False 是属于bool类型的特殊值；它们不是字符串。

>>> type(True)
<class 'bool'>
>>> type(False)
<class 'bool'>

== 运算符是关系运算符（relational operators）之一；其他关系运算符还有：

x != y               # x 不等于 y
x > y                # x 大于 y
x < y                # x 小于 y
x >= y               # x 大于或等于 y
x <= y               # x 小于或等于 y

虽然这些运算符对你来说可能很熟悉，但是Python的符号与数学符号不相同。一个常见的错误是使用单独一个等号（=）而不是双等号（==）。请记住，= 是赋值运算符，== 是关系运算符。没有类似 =< 或 => 的东西。

逻辑运算符

有三个逻辑运算符（logical operators）：and 、or 和 not。这些运算符的含义和它们在英语的意思相似。例如，x > 0 and x < 10 只在x大于0并且小于10时为真。

n%2 == 0 or n%3 == 0中如果 一个或两个 条件为真，那么整个表达式即为真。也就是说，如果数字n能被2或者3整除，则为真。

最后，not 运算符对一个布尔表达式取反，因此，如果 x > y 为假，也就是说x小于或等于y，则 not (x > y) 为真。

严格来讲，逻辑运算符的运算数应该是布尔表达式，但是Python并不严格要求。任何非0的数字都被解释成为真（ True ）。

>>> 42 and True
True

这种灵活性很有用，但有一些细节可能容易令人困惑。你可能需要避免这种用法（除非你知道你正在做什么）。

有条件的执行

为了写出有用的程序，我们几乎总是需要能够检测条件，并相应地改变程序行为。 条件语句（Conditional statements）给予了我们这一能力。最简单的形式是 if 语句：

if x > 0:
    print('x is positive')

if 之后的布尔表达式被称作条件（condition）。如果它为真，则缩进的语句会被执行。如果不是，则什么也不会发生。

if 语句和函数定义有相同的结构：一个语句头跟着一个缩进的语句体。类似的语句被称作复合语句（compound statements）。

语句体中可出现的语句数目没有限制，但是至少得有一个。有时候，一条语句都没有的语句体也是有用的（通常是为你还没写的代码占一个位子）。这种情况下，你可以使用 pass 语句，它什么也不做。

if x < 0:
    pass          # 待完成：需要处理负数值！

二选一执行

if 语句的第二种形式是二选一执行（alternative execution），此时有两个可能的选择，由条件决定执行哪一个。语法看起来是这样：

if x % 2 == 0:
    print('x is even')
else:
    print('x is odd')

如果x除以2的余数是0，那么我们知道x是偶数，然后程序会打印相应的信息。如果条件为假，则执行第二部分语句。由于条件要么为真要么为假，两个选择中只有一个会被执行。这些选择被称作分支（branches），因为它们是执行流程的分支。

链式条件

有时有超过两个可能的情况，于是我们需要多于两个的分支。表示像这样的计算的方法之一是链式条件（chained conditional）：

if x < y:
    print('x is less than y')
elif x > y:
    print('x is greater than y')
else:
    print('x and y are equal')

elif 是“else if”的缩写。同样地，这里只有一个分支会被执行。 elif 语句的数目没有限制。如果有一个 else 从句，它必须是在最后，但这个语句并不是必须。

if choice == 'a':
    draw_a()
elif choice == 'b':
    draw_b()
elif choice == 'c':
    draw_c()

程序将按顺序逐个检测条件，如果第一个为假，检测下一个，以此类推。如果它们中有一个为真，相应的分支被执行，并且语句结束。即便有不止一个条件为真，也只执行第一个为真的分支。

嵌套条件

一个条件可以嵌到另一个里面。我们可以这样写前一节的例子：

if x == y:
    print('x and y are equal')
else:
    if x < y:
        print('x is less than y')
    else:
        print('x is greater than y')

外层的条件（outer conditional）包括两个分支。第一个分支包括一条简单的语句。第二个分支又包括一个 if 语句，它有自己的两个分支。那两个分支都是简单的语句，当然它们也可以是条件语句。

虽然语句的缩进使得结构很明显，但是仍然很难快速地阅读嵌套条件（nested conditionals） 。当你可以的时候，避免使用嵌套条件是个好办法。

逻辑运算符通常是一个简化嵌套条件语句的方法。例如，我们可以用一个单一条件重写下面的代码：

if 0 < x:
    if x < 10:
        print('x is a positive single-digit number.')

只有我们通过了两个条件检测的时候，print语句才被执行，因此我们可以用 and 运算符得到相同的效果：

if 0 < x and x < 10:
    print('x is a positive single-digit number.')

对于这样的条件，Python 提供了一种更加简洁的写法。

if 0 < x < 10:
    print('x is a positive single-digit number.')

递归

一个函数调用另一个是合法的；一个函数调用它自己也是合法的。这样的好处可能并不是那么明显，但它实际上成为了程序能做到的最神奇的事情之一。例如，看一下这个程序：

def countdown(n):
    if n <= 0:
        print('Blastoff!')
    else:
        print(n)
        countdown(n-1)

如果n是0或负数，程序输出单词“Blastoff!”。否则，它输出n然后调用一个名为 countdown 的函数—即它自己— 传递n-1作为实参。

如果我们像这样调用该函数会发生什么呢？

>>> countdown(3)

countdown开始以n=3执行，由于n大于0，它输出值3，然后调用它自己…

countdown开始以n=2执行，由于n大于0，它输出值2，然后调用它自己…
countdown开始以n=1执行，既然n大于0，它输出值1，然后调用它自己…
countdown开始以n=0执行，由于n不大于0，它输出单词“Blastoff!”，然后返回。
获得n=1的 countdown 返回。
获得n=2的 countdown 返回。

获得n=3的 countdown 返回。

然后你回到__main__中。因此整个输出类似于：

3
2
1
Blastoff!

一个调用它自己的函数是递归的（recursive）；这个过程被称作递归（recursion）。

再举一例，我们可以写一个函数，其打印一个字符串n次。

def print_n(s, n):
    if n <= 0:
        return
    print(s)
    print_n(s, n-1)

如果 n <= 0 ，return语句 退出函数。执行流程马上返回到调用者，函数剩余的语句行不会被执行。

函数的其余部分和 countdown 相似：它打印s的值，然后调用自身打印s n-1次。因此，输出的行数是 1 + (n - 1) ，加起来是n。

对于像这样简单的例子，使用for循环可能更容易。但是我们后面将看到一些用for循环很难写，用递归却很容易的例子，所以早点儿开始学习递归有好处。

递归函数的堆栈图

在堆栈图一节中，我们用堆栈图表示了一个函数调用期间程序的状态。这种图也能帮我们理解递归函数。

每当一个函数被调用时，Python生成一个新的栈帧，用于保存函数的局部变量和形参。对于一个递归函数，在堆栈上可能同时有多个栈帧。

图5-1：堆栈图展示了一个以n = 3调用 countdown 的堆栈图。

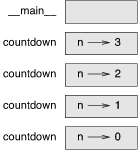
图5-1：堆栈图

通常，堆栈的顶部是__main__栈帧。因为我们在__main__中没有创建任何变量，也没有传递任何实参给它，所以它是空的。

对于形参n，四个 countdown 栈帧有不同的值。 n=0的栈底，被称作基础情形（base case）。它不再进行递归调用了，所以没有更多的栈帧了。

接下来练习一下，请画一个以s = 'Hello'和 n=2 调用print_n的堆栈图。写一个名为do_n的函数，接受一个函数对象和一个数n作为实参，能够调用指定的函数n次。

无限递归

如果一个递归永不会到达基础情形，它将永远进行递归调用，并且程序永远不会终止。这被称作无限递归（infinite recursion），通常这不是一个好主意。下面是一个最简单的无限递归程序：

def recurse():
    recurse()

在大多数编程环境里，一个具有无限递归的程序并非永远不会终止。当达到最大递归深度时，Python会报告一个错误信息：

  File "<stdin>", line 2, in recurse
  File "<stdin>", line 2, in recurse
  File "<stdin>", line 2, in recurse
                  .
                  .
                  .
  File "<stdin>", line 2, in recurse
RuntimeError: Maximum recursion depth exceeded

此回溯比我们在前面章节看到的长一些。当错误出现的时候，在堆栈上有1000个递归栈帧！

如果你不小心遇到了无限递归，检查你的函数，确保基础情形没有继续调用递归。同时如果确实有基础情形，请检查基础情形是不是能够出现这种情形。

键盘输入

到目前为止，我们所写的程序都不接受来自用户的输入。每次它们都只是做相同的事情。

Python 提供了一个内建函数 input ，可以暂停程序运行，并等待用户输入。当用户按下回车键(Return or Enter)，程序恢复执行，input以字符串形式返回用户键入的内容。在Python 2中，这个函数的名字叫raw_input。

>>> text = input()
What are you waiting for?
>>> text
What are you waiting for?

在从用户那儿获得输入之前，打印一个提示告诉用户输入什么是个好办法。 input接受提示语作为实参。

>>> name = input('What...is your name?\n')
What...is your name?
Arthur, King of the Britons!
>>> name
Arthur, King of the Britons!

提示语最后的\n表示一个新行（newline），它是一个特别的字符，会造成换行。这也是用户的输入出现在提示语下面的原因。

如果你期望用户键入一个整型数，那么你可以试着将返回值转化为 int ：

>>> prompt = 'What...is the airspeed velocity of an unladen swallow?\n'
>>> speed = input(prompt)
What...is the airspeed velocity of an unladen swallow?
42
>>> int(speed)
42

但是，如果用户输入不是数字构成的字符串，你会获得一个错误：

>>> speed = input(prompt)
What...is the airspeed velocity of an unladen swallow?
What do you mean, an African or a European swallow?
>>> int(speed)
ValueError: invalid literal for int() with base 10

我们后面将介绍处理这类错误的方法。

调试

当出现语法错误和运行时错误的时候，错误信息中会包含了很多的信息，但是信息量有可能太大。通常，最有用的部分是：

是哪类错误，以及
在哪儿出现。

语法错误通常很容易被找到，但也有一些需要注意的地方。空白分隔符错误很棘手，因为空格和制表符是不可见的，而且我们习惯于忽略它们。

>>> x = 5
>>>  y = 6
  File "<stdin>", line 1
    y = 6
    ^
IndentationError: unexpected indent

在这个例子中，问题在于第二行缩进了一个空格。但是错误信息指向y，这是个误导。通常，错误信息指向发现错误的地方，但是实际的错误可能发生在代码中更早的地方，有时在前一行。

运行时错误也同样存在这个问题。假设你正试图计算分贝信噪比。公式是SNR_{db} = 10 \log_{10} (P_{signal} / P_{noise})。在Python中，你可能会写出这样的代码：

import math
signal_power = 9
noise_power = 10
ratio = signal_power // noise_power
decibels = 10 * math.log10(ratio)
print(decibels)

但是，当你运行它的时候，你却获得一个异常。

Traceback (most recent call last):
  File "snr.py", line 5, in ?
    decibels = 10 * math.log10(ratio)
ValueError: math domain error

该错误信息指向第5行，但是那一行没什么错误。为了找到真正的错误，打印 ratio 的值也许会有用，结果发现它实际上是0。那么问题是在第4行，使用了地板除而不是浮点数除法。

你应该花些时间仔细阅读错误信息，但是不要轻易地认为错误信息的提示都是准确的。

术语表

地板除:

一个操作符,用 // 表示，表示对两个数做除法同时向0取整。

求余运算符:

一个运算符，用百分号 % 表示，返回两个数相除的余数

布尔表达式:

一个值要么为真要么为假的表达式。

关系运算符:

对其运算符进行比较的运算符： ==，!=，>，<，>=，<=。

逻辑运算符:

将布尔表达式组合在一起的运算符: and，or，和 not。

条件语句:

一段根据某个条件决定程序执行流程的语句。

条件:

决定哪个分支会被执行的布尔表达式

复合语句:

由语句头和语句体组成的语句。语句头以 : 结尾，语句体相对语句头缩进。

分支:

条件语句中的选择性语句序列。

链式条件:

由一系列替代分支组成的条件语句。

嵌套条件:

出现另一个条件语句某个分支中的条件语句。

返回语句：: 结束函数执行并且将结果返回给调用者的语句。

递归:

调用正在执行的函数本身的过程。

基本情形:

在递归函数中，不进行递归调用的条件分支。

无限递归:

没有基本情形或者无法出现基本情形的递归函数。最终无限递归会导致运行时错误。

练习题

习题 5-1

time 模块提供了一个可以返回当前格林威治标准时间的函数，名字也是time。这里的格林威治标准时间用纪元(the epoch)以来的秒数表示，纪元是一个任意的参考点。在 Unix 系统中，纪元是1970年1月1号。

>>> import time
>>> time.time()
1437746094.5735958

请写一个脚本读取当前时间，并且将其转换为纪元以来经过了多少天、小时、分钟和秒。

习题 5-2

费马大定理（Fermat’s Last Theorem ）称，没有任何整型数a、b和c能够使

a^n + b^n = c^n

对于任何大于2的n成立。

写一个名为check_fermat的函数，接受四个形参——a，b，c以及n ——检查费马大定理是否成立。如果n大于2且等式
a^n + b^n = c^n
成立，程序应输出“Holy smokes, Fermat was wrong!”。否则程序应输出“No, that doesn’t work.”。
写一个函数提示用户输入a，b，c以及n的值，将它们转换成整型数，然后使用check_fermat检查他们是否会违反了费马大定理。

习题 5-3

如果你有三根棍子，你有可能将它们组成三角形，也可能不行。比如，如果一根棍子是12英寸长，其它两根都是1英寸长，显然你不可能让两根短的在中间接合。对于任意三个长度，有一个简单的测试能验证它们能否组成三角形：

如果三个长度中的任意一个超过了其它二者之和，就不能组成三角形。否则，可以组成。（如果两个长度之和等于第三个，它们就组成所谓“退化的”三角形。）

写一个名为is_triangle的函数，其接受三个整数作为形参，能够根据给定的三个长度的棍子能否构成三角形来打印“Yes”或“No”。
写一个函数，提示用户输入三根棍子的长度，将它们转换成整型数，然后使用 is_triangle检查给定长度的棍子能否构成三角形。

习题 5-4

下面程序的输出是什么？画出展示程序每次打印输出时的堆栈图。

def recurse(n, s):
    if n == 0:
        print(s)
    else:
        recurse(n-1, n+s)

recurse(3, 0)

如果你这样调用函数： recurse(-1,0) ，会有什么结果？
请写一个文档字符串，解释调用该函数时需要了解的全部信息（仅此而已）。

习题 5-５

后面的习题要用到第四章中的Turtle：

阅读如下的函数，看看你能否看懂它是做什么的。然后运行它（见第四章的例子）。

def draw(t, length, n):
    if n == 0:
        return
    angle = 50
    fd(t, length*n)
    lt(t, angle)
    draw(t, length, n-1)
    rt(t, 2*angle)
    draw(t, length, n-1)
    lt(t, angle)
    bk(t, length*n)

习题 5-６

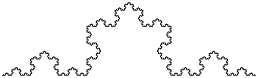
图5-2：科赫曲线（Koch Curve）。

科赫曲线（Koch Curve）是一个看起来类似图5-2的不规则碎片几何体（fractal）。要画一个长度为x的科赫曲线，你只需要：

画一个长度为x/3的科赫曲线。
左转60度。
画一个长度为x/3的科赫曲线。
右转120度。
画一个长度为x/3的科赫曲线。
左转60度。
画一个长度为x/3的科赫曲线。

例外情况是x小于3的情形：此时，你只需要画一道长度为x的直线。

写一个名为 koch 的函数，接受一个海龟和一个长度作为形参，然后使用海龟画一条给定长度的科赫曲线。
写一个名为 snowflake 的函数，画出三条科赫曲线，构成雪花的轮廓。
答案：http://thinkpython.com/code/koch.py 。
科赫曲线能够以多种方式泛化。点击http://en.wikipedia.org/wiki/Koch_snowflake 查看例子，并实现你最喜欢的那种方式。

贡献者

翻译：@iphyer
校对：@bingjin
参考：@carfly