第七章:迭代
本章介绍迭代,即重复运行某个代码块的能力。我们已经在递归一节接触了一种利用递归进行迭代的方式;在简单的重复一节中,接触了另一种利用 for 循环进行迭代的方式。在本章中,我们将讨论另外一种利用 while 语句实现迭代的方式。 不过,首先我想再多谈谈有关变量赋值的问题。
重新赋值
可能你已发现对同一变量进行多次赋值是合法的。新的赋值会使得已有的变量指向 新的值(同时不再指向旧的值)。
>>> x = 5 >>> x 5 >>> x = 7 >>> x 7
第一次打印 x 时, 它的值为 5;第二次打印时,它的值是 7。
图7-1状态图展示了 重新赋值 在状态图中看起来是什么样子。
这里我想探讨一个常见的疑惑点。由于 Python 用等号(=)来赋值,所以很容易将 a = b 这样的语句理解为数学上的相等命题;即a 和 b 相等。但是这种理解是错误的。
首先,相等是一种对称关系,赋值不是。例如,在数学上,如果 a=7, 则 7=a。但是在 Python 中,语句 a = 7 是合法的,7 = a 则不合法。
此外,数学中,相等命题不是对的就是错的。如果 a=b,那么 a 则是永远与 b 相等。在 Python 中,赋值语句可以使得两个变量相等, 但是这两个变量不一定必须保持这个状态:
>>> a = 5 >>> b = a # a 和 b 现在相等 >>> a = 3 # a 和 b 不再相等 >>> b 5
第三行改变了 a 的值,但是没有改变 b 的值,所以它们不再相等了。
给变量重新赋值非常有用,但是需要小心使用。对变量频繁重新赋值会使代码难于阅读, 不易调试。
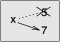
图7-1状态图
更新变量
重新赋值的一个常见方式是 更新(update),更新操作中变量的新值会取决于旧值。
>>> x = x + 1
这个语句的意思是,“获得 x 的当前值,加1,然后将 x 的值更新为新的值。”
如果试图去更新一个不存在的变量,则会返回一个错误。这是因为 Python 是先求 式子右边的值,然后再把所求的值赋给 x:
>>> x = x + 1 NameError: name 'x' is not defined
在更新变量之前,你得先 初始化(initialize) 它,通常是通过一个简单的赋值实现:
>>> x = 0 >>> x = x + 1
通过加1来更新变量叫做 递增(increment);减1叫做 递减(decrement)。
while 语句
计算机经常被用来自动处理重复性的任务。计算机很擅长无纰漏地重复相同或者相似的任务, 而人类在这方面做的不好。在计算机程序中,重复也被称为**迭代(iteration)**。
所以 Python 提供了使其更容易实现的语言特性。其中之一就是我们在简单的重复一节看到的 我们已经见过两个利用递归来迭代的函数: `countdown 和 print_n。由于迭代如此普遍, 所以 Python 提供了使其更容易实现的语言特性。其中之一就是我们在简单的重复一节看到的 for 语句。后面我们还会继续介绍。
另外一个用于迭代的语句是 while 。下面是使用 while 语句实现的 countdown:
def countdown(n):
while n > 0:
print(n)
n = n - 1
print('Blastoff!')
你可以像读英语句子一样来读 `while 语句。它的意思是:“只要 n 的值大于 0, 则打印出 n 的值,然后让 n 减1。当 n 递减至 0 时,打印单词 Blastoff!”。
更正式地来说,while 语句的执行流程如下:
- 首先判断条件为真还是为假。
- 如果为假,退出
while语句,然后执行接下来的语句; - 如果条件为真,则运行
while语句体,运行完再返回第一步;
这种形式的流程叫做循环(loop),因为第三步后又循环回到了第一步。
循环主体应该改变一个或多个变量的值,这样的话才能让条件判断最终变为假, 从而终止循环。不然的话,循环将会永远重复下去,这被称为**无限循环(infinite loop)**。 在计算机科学家看来,洗发水的使用说明——“抹洗发水, 清洗掉,重复”便是个无限循环,这总是会让他们觉得好笑。
对于 countdown 来说,我们可以证明循环是一定会终止的:当 n 是 0 或者负数,该循环就不会执行;不然 n 通过每次循环之后慢慢减小,最终也是会变成 0 的。
有些其他循环,可能就没那么好理解了。例如:
def sequence(n):
while n != 1:
print(n)
if n % 2 == 0: # n 是偶数
n = n / 2
else: # n 是奇数
n = n*3 + 1
循环的条件是 n != 1,所以循环会一直执行到 n 等于 1,条件判断为假时循环才终止。
每次循环,该程序打印出 n 的值,然后检查它是偶数还是奇数。如果它是偶数, 那么 n 可以被2整除;如果是奇数,则它的值被替换为 n*3 + 1。例如,如果传递给 sequence 的实参为3,那么打印出的结果将会是:3、10、5、16、8、4、2、1。
由于 n 的值时增时减,所以不能轻易保证 n 会最终变成 1,或者说这个程序能够终止。 对于某些特殊的 n 的值,可以很好地证明它是可以终止的。例如,当 n 的初始值是 2 的倍数时,则每次循环后 n 一直为偶数,直到最终变为 1。上一个示例中,程序就打印了类似的序列,从16开始全部为偶数。
难点是能否证明程序对于 所有 的正整数 n 都会终止的。目前为止, 还没有人证明 或者 证伪该命题。(见: http://en.wikipedia.org/wiki/Collatz_conjecture 。)
我们做个练习,利用迭代而非递归,重写之前递归一节中的 print_n 函数。
break
有些时候循环执行到一半你才知道循环该结束了。这种情况下,你可以使用 break 语句 来跳出循环。
例如,假设你想从用户那里获取输入,直到用户键入“done”。你可以这么写:
while True:
line = input('> ')
if line == 'done':
break
print(line)
print('Done!')
循环条件是True,其总是为真,所以该循环会一直执行直到碰到 break。
每次循环时,程序都会给出一个尖括号(>)提示。如果用户输入“done”,执行 break 语句 跳出循环。否则,程序就会一直打印出用户所输入的内容并且跳到循环开始,以下是一个运行示例:
> not done not done > done Done!
while循环的这种写法很常见,因为你可以在循环的任何地方判断条件 (而不只是在循环开始),而且你可以积极地表达终止条件(“当出现这个情况是终止”), 而不是消极地表示(“继续运行直到出现这个情况”)。
平方根
循环常用于计算数值的程序中,这类程序一般从一个大概的值开始,然后迭代式地进行改进。
例如,牛顿法 (Newton’s method) 是计算平方根的一种方法。 假设你想求a的平方根。如果你从任意一个估算值x开始,则可以利用下面的公式计算出更为较为精确的估算值:
y = \frac{x + a/x}{2}
例如,假定 a 是 4,x 是 3:
>>> a = 4 >>> x = 3 >>> y = (x + a/x) / 2 >>> y 2.16666666667
可以看到,结果与真实值(\sqrt{4} = 2)已经很接近了,如果我们用这个值 再重新运算一遍,它将得到更为接近的值。
>>> x = y >>> y = (x + a/x) / 2 >>> y 2.00641025641
再通过多几次的运算,这个估算可以说已经是很精确了。
>>> x = y >>> y = (x + a/x) / 2 >>> y 2.00001024003 >>> x = y >>> y = (x + a/x) / 2 >>> y 2.00000000003
一般来说,我们事先不知道要多少步才能得到正确答案,但是我们知道当估算值不再变动时,我们就获得了正确的答案。
>>> x = y >>> y = (x + a/x) / 2 >>> y 2.0 >>> x = y >>> y = (x + a/x) / 2 >>> y 2.0
当 y == x 时,我们可以停止计算了。下面这个循环就是利用一个初始估值 x, 循序渐进地计算,直到估值不再变化。
while True:
print(x)
y = (x + a/x) / 2
if y == x:
break
x = y
对于大部分a的值,这个程序运行正常,不过一般来说,检查两个浮点数是否相等比较危险。浮点数只能大约表示:大多数有理数,如1/3,以及无理数, 如\sqrt{2},是不能用浮点数来精确表示的。
与其检查 x 和 y 的值是否完全相等,使用内置函数 abs 来计算二者之差的绝对值或数量级更为安全:
if abs(y-x) < epsilon:
break
这里,变量 epsilon 是一个决定其精确度的值,如 0.0000001。
算法
牛顿法就是一个 算法(Algorithm) 示例:它是解决一类问题的计算机制 (这个例子中是计算平方根)。
为了理解算法是什么,先了解什么不是算法或许有点帮助。你在学习一位数乘法时, 可能背出了乘法表。实际上,你只是记住了100个确切的答案。这种知识并不是算法性的。
不过,如果你比较 “懒”,你可能就会找到一些诀窍。比如说为了计算n和 9 的乘积,你可以把 n-1 作为乘积的第一位数,再把10-n作为第二位数,从而得到它们的乘积。这个诀窍是将任意个位数 与 9 相乘的普遍解法。这就是一种算法。
类似地,你所学过的进位加法、借位减法、以及长除法都是算法。算法的特点之一 就是不需要过多的脑力计算。算法是一个机械的过程,每一步都是依 据一组简单的规则跟着上一步来执行的。
执行算法的过程是很乏味的,但是设计算法就比较有趣了,不但是智 力上的挑战,更是计算机科学的核心。
人们轻轻松松或者下意识自然而然做的一些事情,往往是最难用算法来表达的。理解自然语言就是个很好的例子。我们每个人都听得懂自然语言,但是目前还没有人能够解释我们是 怎么 做到的,至少不是以算法的形式解释。
调试
当你开始写更为复杂的程序时,你会发现大部分时间都花费在调试上。更多的 代码意味着更高的出错概率,并且会有更多隐藏bug的地方。
减少调试时间的一个方法就是“对分调试”。例如,如果程序有100行,你一次检查一行,就需要100步。
相反,试着将问题拆为两半。在代码中间部分或者附近的地方,寻找一个可以检查的中间值。加上一行 print 语句(或是其他具有可验证效果的代码),然后运行程序。
如果中间点检查出错了,那么就说明程序的前半部分存在问题。如果没问题,则说明是后半部分出错了。
每次你都这样检查,就可以将需要搜索的代码行数减少一半。经过6步之后(这比100小多了),你将会找到那或者两行出错的代码,至少理论上是这样。
在实践中,可能并不能很好的确定程序的 “中间部分” 是什么,也有可能并不是那么好检查。 计算行数并且取其中间行是没有意义的。相反,多考虑下程序中哪些地方比较容易出问题,或者 哪些地方比较容易进行检查。然后选定一个检查点,在这个断点前后出现bug的概念差不多。
术语表
重新赋值(reassignment):
给已经存在的变量赋一个新的值。
更新(update):
变量的新值取决于旧值的一种赋值方法。
初始化(initialize):
给后面将要更新的变量一个初始值的一种赋值方法。
递增(increment):
通过增加变量的值的方式更新变量(通常是加 1)。
递减(decrement):
通过减少变量的值的方式来更新变量。
迭代(iteration):
利用递归或者循环的方式来重复执行代一组语句的过程。
无限循环(infinite loop):
无法满足终止条件的循环。
算法(algorithm):
解决一类问题的通用过程。
练习题
习题7-1
复制平方根一节中的循环,将其封装进一个叫 mysqrt 的函数中。这个函数接受 a 作为形参,选择一个合适的 x 值,并返回 a 的平方根估算值。
为测试上面的函数,编写一个名为 test_squre_root 的函数,打印出如下表格:
a mysqrt(a) math.sqrt(a) diff - --------- ------------ ---- 1.0 1.0 1.0 0.0 2.0 1.41421356237 1.41421356237 2.22044604925e-16 3.0 1.73205080757 1.73205080757 0.0 4.0 2.0 2.0 0.0 5.0 2.2360679775 2.2360679775 0.0 6.0 2.44948974278 2.44948974278 0.0 7.0 2.64575131106 2.64575131106 0.0 8.0 2.82842712475 2.82842712475 4.4408920985e-16 9.0 3.0 3.0 0.0
其中第一列是 a 的值;第二列是通过 mysqrt 计算得到的 a 的平方根;第三列是用 math.sqrt 计算得到的平方根;第四列则是这两个平方根之差的绝对值。
习题7-2
内置函数 eval 接受一个字符串,并使用 Python 解释器来计算该字符串。例如:
>>> eval('1 + 2 * 3')
7
>>> import math
>>> eval('math.sqrt(5)')
2.2360679774997898
>>> eval('type(math.pi)')
<class 'float'>
编写一个名为 eval_loop 的函数,迭代式地提示用户输入,获取输入的内容,并利用 eval 来计算其值,最后打印该值。
该程序应持续运行,知道用户输入 'done',然后返回它最后一次计算的表达式的值。
习题7-3
数学家斯里尼瓦瑟·拉马努金(Srinivasa Ramanujan) 发现了一个可以用来生成 1 / \pi 近似值的无穷级数(infinite series):
\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}
编写一个名为 estimate_pi 的函数,利用上面公式来估算并返回 \pi 的值。这个函数应该使用 while 循环来计算所有项的和,直到最后一项小于 1e-15 (Python 中用于表达 10^{-15} 的写法)时终止循环。你可以将该值与 math.pi 进行比较,检测是否准确。
答案: http://thinkpython2.com/code/pi.py 。

