K-Means 聚类算法

优质

小牛编辑

116浏览

2023-12-01

全部代码

1、聚类过程

聚类属于无监督学习，不知道 y 的标记分为 K 类

K-Means算法分为两个步骤

第一步：簇分配，随机选 K 个点作为中心，计算到这 K 个点的距离，分为 K 个簇

第二步：移动聚类中心：重新计算每个簇的中心，移动中心，重复以上步骤。

如下图所示：

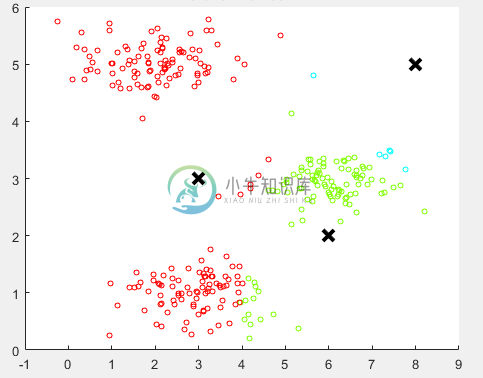
随机分配的聚类中心

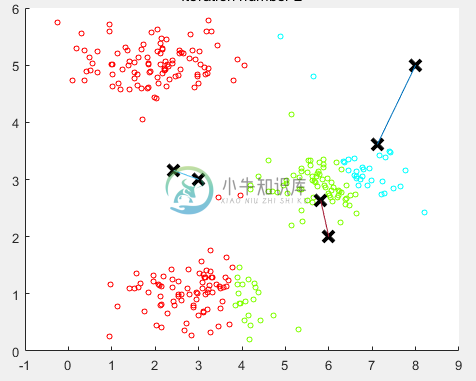
重新计算聚类中心，移动一次

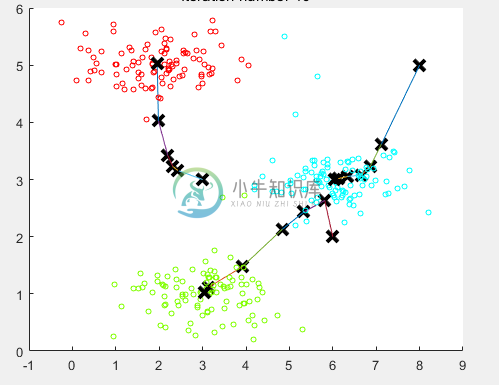
最后 10 步之后的聚类中心

计算每条数据到哪个中心最近实现代码：

# 找到每条数据距离哪个类中心最近  
def findClosestCentroids(X,initial_centroids):
  m = X.shape[0]          # 数据条数
  K = initial_centroids.shape[0]  # 类的总数
  dis = np.zeros((m,K))       # 存储计算每个点分别到K个类的距离
  idx = np.zeros((m,1))       # 要返回的每条数据属于哪个类
  
  '''计算每个点到每个类中心的距离'''
  for i in range(m):
    for j in range(K):
      dis[i,j] = np.dot((X[i,:]-initial_centroids[j,:]).reshape(1,-1),(X[i,:]-initial_centroids[j,:]).reshape(-1,1))
  
  '''返回dis每一行的最小值对应的列号，即为对应的类别
  - np.min(dis, axis=1)返回每一行的最小值
  - np.where(dis == np.min(dis, axis=1).reshape(-1,1)) 返回对应最小值的坐标
   - 注意：可能最小值对应的坐标有多个，where都会找出来，所以返回时返回前m个需要的即可（因为对于多个最小值，属于哪个类别都可以）
  '''  
  dummy,idx = np.where(dis == np.min(dis, axis=1).reshape(-1,1))
  return idx[0:dis.shape[0]]  # 注意截取一下

计算类中心实现代码：

# 计算类中心
def computerCentroids(X,idx,K):
  n = X.shape[1]
  centroids = np.zeros((K,n))
  for i in range(K):
    centroids[i,:] = np.mean(X[np.ravel(idx==i),:], axis=0).reshape(1,-1)   # 索引要是一维的,axis=0为每一列，idx==i一次找出属于哪一类的，然后计算均值
  return centroids

2、目标函数

也叫做失真代价函数
$$J({c^{(1)}}, \cdots ,{c^{(m)}},{u_1}, \cdots ,{u_k}) = \frac{1}{m}\sum\limits_{i = 1}^m {||{x^{(i)}} - {u_{{c^{(i)}}}}|{|^2}} $$
最后我们想得到：
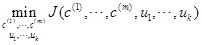
其中 $${c^{(i)}}$$ 表示第 i 条数据距离哪个类中心最近，
其中 $${u_i}$$ 即为聚类的中心

3、聚类中心的选择

随机初始化，从给定的数据中随机抽取K个作为聚类中心
随机一次的结果可能不好，可以随机多次，最后取使代价函数最小的作为中心

实现代码：(这里随机一次)

# 初始化类中心--随机取K个点作为聚类中心
def kMeansInitCentroids(X,K):
  m = X.shape[0]
  m_arr = np.arange(0,m)    # 生成0-m-1
  centroids = np.zeros((K,X.shape[1]))
  np.random.shuffle(m_arr)  # 打乱m_arr顺序  
  rand_indices = m_arr[:K]  # 取前K个
  centroids = X[rand_indices,:]
  return centroids

4、聚类个数K的选择

聚类是不知道y的label的，所以不知道真正的聚类个数

肘部法则（Elbow method）

作代价函数J和K的图，若是出现一个拐点，如下图所示，K 就取拐点处的值，下图此时 K=3

若是很平滑就不明确，人为选择。

第二种就是人为观察选择

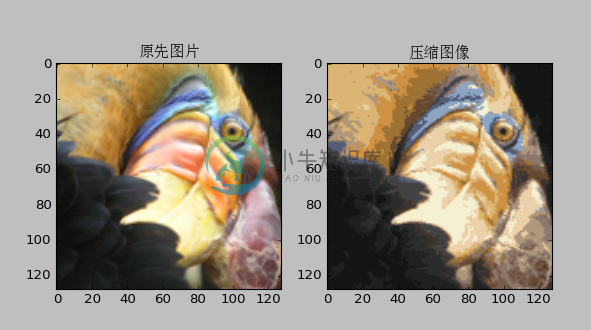
5、应用——图片压缩

将图片的像素分为若干类，然后用这个类代替原来的像素值

执行聚类的算法代码：

# 聚类算法
def runKMeans(X,initial_centroids,max_iters,plot_process):
  m,n = X.shape           # 数据条数和维度
  K = initial_centroids.shape[0]  # 类数
  centroids = initial_centroids   # 记录当前类中心
  previous_centroids = centroids  # 记录上一次类中心
  idx = np.zeros((m,1))       # 每条数据属于哪个类
  
  for i in range(max_iters):    # 迭代次数
    print u'迭代计算次数：%d'%(i+1)
    idx = findClosestCentroids(X, centroids)
    if plot_process:  # 如果绘制图像
      plt = plotProcessKMeans(X,centroids,previous_centroids) # 画聚类中心的移动过程
      previous_centroids = centroids  # 重置
    centroids = computerCentroids(X, idx, K)  # 重新计算类中心
  if plot_process:  # 显示最终的绘制结果
    plt.show()
  return centroids,idx  # 返回聚类中心和数据属于哪个类

6、使用 scikit-learn 库中的线性模型实现聚类

导入包

  from sklearn.cluster import KMeans

使用模型拟合数据

  model = KMeans(n_clusters=3).fit(X) # n_clusters指定3类，拟合数据

聚类中心

  centroids = model.cluster_centers_  # 聚类中心

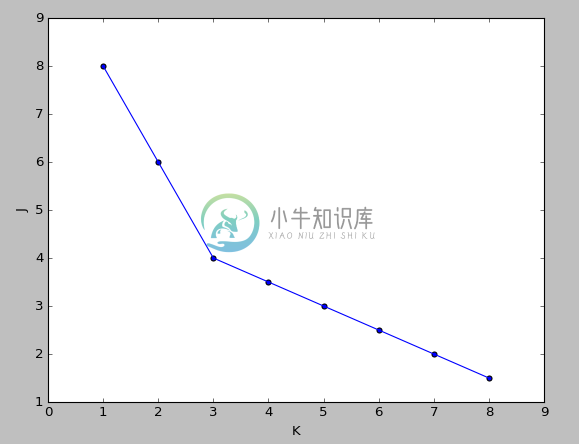
7、运行结果

二维数据类中心的移动

图片压缩